Reference

                                                           STRUTTURA RETICOLARE SPAZIALE

                                                                           MODELLAZIONE

Le travi reticolari, grazie alla loro geometria triangolare, consentono di creare strutture in grado di superare grandi luci per mezzo di un numero limitato di appoggi. Per questa esercitazione ho preso in esame un ponte largo 10m la cui campata misura 100 m.

Per la modellazione utilizzo il software AutoCad, creo un nuovo layer chiamato "Telaio" e sul piano XY traccio una linea di 100m, il cui punto medio è situato nell'origine, questo permetterà un maggiore controllo del modello una volta esportato su SAP2000; dal punto medio traccio una linea di 10m lungo Y e successivamente disegno un arco a tre punti passante per quest'ultimo e per gli estremi della linea tracciata precedentemente.

Una volta tracciato l'arco utilizzo il comando dividi sezionando l'arco in 40 parti, partendo da uno degli estremi disegno una per una le linee che collegano i punti precedentemente ottenuti dividendo l'arco, generando così una spezzata; a questo punto posso eliminare l'arco sottostante e passare alla visualizzazione 3d. Copio la spezzata disegnata finora in direzione Y ad una distanza di 2,5m e in seguito collego i vertici delle linee prima ottenuti a formare quadrati (le basi della nostra piramide) e poi triangoli (i controventamenti). Andiamo ora a disegnare un altro arco a tre punti avente come punti i punti medi della prima, della centrale e dell'ultima diagonale, tracciato l'arco lo spostiamo in basso lungo Z di 2,5m; utilizziamo ancora il comando dividi sezionandolo questa volta in 39 parti ottenendo in questo modo i vertici delle nostre piramidi.

Ora basterà unire ognuno di questi vertici ai 4 punti che compongono le rispettive basi ottenendo la prima campata di piramidi.

A questo punto copio per quattro volte ciò che ho disegnato finora, lungo Y con l'accortezza di non creare linee sovrapposte e di dare ad ognuna delle file di piramidi disegnate successivamente controventamenti incidenti e non paralleli rispetto al filare precedente.

Unisco infine i vertici delle piramidi anche lungo Y (formando anche qui dei quadrati) e vado a disegnare anche su questi quadrati dei controventamenti che seguano quelli superiori. Nota: Anche quì, come in tutto il modello, ad ogni linea corrisponde un'asta, quando colleghiamo perciò i vertici delle piramidi disegneremo tutte linee singole (in questo caso tre) e non un'unica linea onde evitare che poi SAP riconosca quelle come un'unica asta con conseguente generazione di taglio e momento. Mi ci soffermo in quanto questo problema ed in particolare la sua individuazione mi ha dato non pochi grattacapi nello svolgimento dell'esercitazione.

A questo punto salvo il file in formato .dxf con la versione più vecchia per non avere problemi nell'importazione.

                                               IMPORTAZIONE E DEFINIZIONE DEL MODELLO IN SAP 2000

Avviato il programma, creo un nuovo modello e seleziono come unità di misura l'opzione Kn,m,C e imposto il foglio bianco (blank).

 

Importo il file .dxf da File>Importa>Autocad .dxf file e dal menù a tendina scelgo prima l'unità di misura precedentemente impostata e poi alla schermata successiva, sotto la voce Frame, seleziono il nome del layer su cui ho disegnato in Cad ("Telaio" nel mio caso).

                        

Il nostro modello sarà importato in SAP. Selezioniamo tutta la struttura e tramite Edita>Edita Punti>Unisci Nodi elimineremo le imperfezioni che ad occhio nudo potrebbero sfuggirci; imposto come valore 0,5.

                                                 

Ora rilascio i momenti ai vertici delle aste in modo da impostare le cerniere interne. Seleziono tutto poi vado su Assegna>Frame>Rilasci/Rigidezze Parziali. Quindi spunto le caselle  di inizio e fine per Momento 2.2 (minore) e Momento 3.3 (maggiore).

                           

Tutti gli estremi delle singole aste a questo punto saranno contrassegnati da un punto verde.

Assegniamo i vincoli esterni, cerniere: per farlo bisogna selezionare i punti in cui le si vuole posizionare e andare su Assegna>Nodo>Vincoli Esterni e scegliere la cerniera appunto.

                                                       

Le strutture reticolari  si caricano con delle forza puntuali concentrate sui nodi. Per creare queste forze clicco su Assegna>Carichi nodo>Forze e creo un nuovo caso di carico chiamato F con un moltiplicatore di peso proprio uguale a zero.

Dopo aver creato un nuovo caso di carico torno automaticamente alla schermata precedente dove devo assegnare un valore e la componente lungo cui si sviluppa (Z). Nel mio caso decido di caricare i nodi centrali con una forza di 60 Kn e i nodi lungo l'estremità della struttura con una forza di 30 Kn. Questo perchè l'area d'influenza dei nodi esterni è la meta di quella dei nodi interni.

 

Infine seleziono tutte le aste e assegno un profilo andando su Assegna>Frame>Sezione frame>Aggiungi nuova proprietà, seleziono il materiale che voglio usare e scelgo un tipo di profilato, (in questo caso acciaio a sezione tubolare circolare cava), gli do un nome assegnandogli in seguito delle dimensioni di predimensionamento.

Una volta premuto su ok ci apparirà la finestra Proprietà Frame. Selezioniamo la sezione ASTA e quindi premendo ok la sezione sarà assegnata a tutti i frame.

                                                                  ESECUZIONE DELL'ANALISI

A questo punto si è pronti per eseguire l'analisi del modello con il tasto Run; nella finestre che si apre selezioniamo DEAD e MODAL e clicchiamo su Esegui/Non Eseguire Caso e scegliamo di non farli partire,saranno perciò contrasssegnati dalla dicitura "Do Not Run". Poi selezioniamo F e clicchiamo su Esegui Ora.

Finita l'analisi il software mi mostrerà la Deformata.

Verifico di aver realizzato in modo corretto la struttura, seleziono Mostra sollecitazioni>Frame>Momento 3-3 e controllo che il grafico del momento sia pari a zero. Se il momento è nullo anche il taglio sarà nullo. L’unica cosa che apparirà sarà perciò lo sforzo assiale.

Per visualizzare le tabelle andiamo su Visualizza>Mostra Tabelle e ci si aprirà una finestra, seleziono il solo schema di carico che ci interessa  deselezionando DEAD e selezionando F, diamo Ok; successivamente nella finestra Scegli Tabelle da Mostrare sotto la voce Risultati dell' analisi spuntiamo la casella Output Elemento, quindi diamo Ok.

Il software creerà quindi la tabella dei risultati della struttura (Elements forces-frame) con le relative sollecitazioni associate ad ognuna delle aste che compongono la struttura; ora non mi resta che esportare i risultati su excel andando su File>Esporta Tabella Corrente>Su Excel

                         DIMENSIONAMENTO DEGLI ELEMENTI DELLA STRUTTURA SU EXCEL

A questo punto quello che dovrò fare è dimensionare le aste assegnando ad ognuna di esse un profilato riferendomi alle tabelle delle aziende produttive che riportano dimensioni e caratteristiche. La tabella scelta per questa esercitazione è stata presa dal sito Oppo.it

Una volta importato il file su excel, quello che faccio è ordinare le aste sulla base dello Sforzo Normale in modo tale da poter distinguere le aste tese ( quelle con il segno +) da quelle compresse (quelle con il segno -); mi creo quindi un nuovo documento excel e con il copia e incolla faccio un foglio excel per le aste tese ed un altro per quelle compresse. Il passo successivo sarà quello di eliminare dalle tabelle tutti i dati inutili mantenenendo solamento il numero del frame, il valore dello sforzo normale e la lunghezza totale dell'asta ( SAP infatti creerà delle tabelle che ci aggiornano sullo stato tensionale della singola asta ogni tot. metri; ma trovandoci nel caso di uno sforzo normale costante avremo dei dati ridondanti che possiamo cancellare, manterremo solamente il dato che ci indica la lunghezza totale dell'asta perchè ci tornerà utile nel dimensionamento delle aste compresse).

ASTE TESE:

Una volta creati i due fogli, inizio con il dimensionamento delle aste tese. Scelgo la classe di Acciaio che voglio usare (S235) e scrivo in una nuova casella il valore limite caratteristico fyk, nella casella successiva metto il valore gamma s (1,05) e nella terza casella scrivo il valore fyd che sarà uguale a fyk/gamma s. E' possibile a questo punto trovare l'Area minima che l'asta dovra avere facendo N/fyd ed infine scelgo dai profilari una sezione con un area immediatamente maggiore rispetto a quella minima. Naturalmente si è deciso di non scegliere una sezione particolare per ogni asta ma di creare delle macrocategorie.

in arancione le aste più sollecitate

ASTE COMPRESSE:

Passo ora al foglio delle aste compresse, trovo anche qui l'Area minima con il metodo precedentemente spiegato ma essendo questo tipo di aste esposte al problema del Carico critico di punta ( Instabilità Euleriana), dovrò fare una serie di considerazione aggiuntive prima di poter dimensionare l'asta. I dati che andrò ad aggiungere alla tabella saranno il modulo di elasticità E (210000 N/mm2), il coefficente β (1 nel nostro caso), il valore L0 (uguale ad L x β), una volta scritti questi valori posso determinare λ*, ρmin, Imin. Ora posso scegliere la sezione da assegnare all'asta che dovrà però rispettare non solo il valore di area minima ma sottostare anche alle condizioni per cui [ρdesign > ρmin]  [Idesign > Imin]   [λdesign < 200(limite di legge)]. Anche qui non vado a dimensionare ogni asta ma creo delle macrocategorie facendo attenzione che però tutte le condizioni poste siano rispettate.

in arancione le aste più sollecitate

Per la struttura presa in esame le aste sono state dimensionate nel seguente modo:

124 aste --- 457,2 x 8,0

239 aste ---355,6 x 6,3

111 aste --- 273,0 x 5,6

139 aste --- 219,1 x 5,0

458 aste --- 88,4 x 4,0

363 aste --- 33,7 x 2,6

 

1. Parto dalla base di un triangolo equilatero e con il comando RUOTA, e impostando la copia alla rotazione, mi creo l’esagono dalla quale sono partito per creare il modulo del mio arco.
   

   ---

   

   ---

   ---

    

2. Con il comando OFFSET creo un secondo esagono ( di poco più grande della metà ) e lo RUOTO di 90°.
   

   ---

   

   ---

   ---

    

3. Creo un ARCO di ampiezza a piacere e con il comando DIVIDI lo suddivido in 20 parti ( 10 per l’esagono più piccolo e 10 per quello più grande ).
   

   ---

   

   ---

   ---

    

4. Sempre con il comando RUOTA ( e copia ), partendo dal centro dell’arco, ripeto gli esagoni nelle posizioni individuate dai punti. 
   

   ---

   

   ---

   ---

    

5. Eseguo la stessa operazione per l’esagono più piccolo  ( per una sola volta in modo da creare il modulo che verrà ripetuto per tutto l’arco) e collego i vertici degli esagoni.
   

   ---

   

   ---

   ---

    

6. Una volta uniti tutti i vertici utilizzando di nuovo COPIA con ROTAZIONE completo l’arco. 
   

   ---

   

   ---

   ---

    

7. Analizzo il modulo utilizzato selezionando un asta alla volta per individuare le lunghezze tipo di tutte le aste e ne cambio il colore trovando così 8 lunghezze diverse che mi serviranno per il dimensionamento successivo.
   

   ---

   

   ---

   ---

    

8. Esporto il file in .DWG assicurandomi di aver creato tutte aste singole, lo apro con Autocad e lo salvo in .DXF; Apro Sap2000, importo il file e dichiaro il Layer al quale deve fare riferimento per le aste e imposto come unità di misura KN, m, C. Seleziono i punti delle due basi e assegno i vincoli nei Joint del tipo Cerniera.
   

   ---

   

   ---

   ---

    

9. Seleziono tutte le aste e assegno i rilasci sia all’inizio che alla fine delle aste. 
   

   ---

   

   ---

   ---

    

10. Seleziono tutte le aste e assegno alle aste una sezione tubolare cava in acciaio. 
    

    ---

    

    ---

    ---

     

11. Imposto dei carichi puntuali “ f ” simmetrici tra loro (in questo caso senza considerare il peso del materiale)  in modo da permettere al programma di calcolare gli sforzi alla quale sarà sottoposta la struttura.
    

    ---

    

    ---

    ---

     

12. Avvio l’analisi e mi assicuro che la struttura abbia solo degli sforzi assiali.
    

    ---

    

    ---

    ---

     

13. Con lo short-cut Ctrl+T si aprirà una finestra nella quale metterò la spunta sulla voce ANALYSIS RESULTS e su SELECT LOAD PATTERN imposto la visualizzazione solo della forza “ f “ per mettere in tabella l’analisi fatta dal programma che ci permetterà di effettuare il dimensionamento. 
    

    ---

    

    ---

    ---

     

14. Nel menù a tendina in alto a destra scelgo la voce Element Forces – Frames, la quale mi restituirà tutti i valori di sforzo per ogni singola asta e lo esporto in excel. 
    

    ---

    

    ---

    ---

     

15. Elimino tutte le colonne successive alla quinta avente indice P, la quale rappresenta gli sforzi assiali ( quelli che interessano a noi per questa analisi ); seleziono tutta la colonna STATION e la dispongo in ordine crescente ed elimino tutti i valori diversi da zero per isolare i le aste e i relativi valori di sforzo.
    

    ---

    

    ---

    ---

     

16. Separo le aste che si comportano a trazione da quelle a compressione, scarico il file excel dal portale di meccanica riguardante il dimensionamento di pilastri, prelevo la tabella dalla sezione Acciaio, elimino le colonne precedenti alla voce N, la incollo di fianco alla tabella ottenuta da Sap2000.
    

    ---

    ---

     

17. ASTE SOGGETE A TRAZIONE: Inserisco i valori della mia tabella superiori allo Zero, scelgo un tipo di acciaio (S275) con coefficiente di snervamento fyk = 275 MPa e coefficiente di sicurezza γ_m = 1.05; da questi troverò la tensione di progetto f_yd = fgk/ym e A_min = N/fyd e scegliendo quindi un A_design adatta.
    

    ---

    

    ---

    ---

     

18. ASTE SOGGETTE A COMPRESSIONE: Effettuo le stesse operazioni delle aste soggette a trazione solo che per queste dovrò ricavarmi anche i valori I_min (momento di inerzia), ρ_min (il raggio di inerzia minimo della sezione) e λ* (snellezza dell’asta) avendo come dati anche E = 210000 Mpa (modulo di elasticità) e un coefficiente β che dipende dalle condizioni di vincolo (β = 1). Da qui dovrò andare a scegliere sulla tabella dei profili dei ρdesin, A_design e I_design in modo che siano tutti superiori dei loro rispettivi minimi e trovare quindi λ.
    

    ---

    

1.Modellazione su SAP2000

A partire da un modulo di misure 2mx2mx2m, ho creato una trave reticolare 12mx12m copiando il primo elemento  6 volte lungo l'asse y e  6 volte lungo l'asse x.

 

 

Dopo aver selezionato tutta la trave, cliccando su Assign-Frame-Releases/Partial fixity, ho assegnato una cerniera interna a tutti i nodi della struttura rimuovendo  i vincoli riguardanti il Momento (Moment 22 e Moment 33) ad inizio e fine di agni asta.

 

In seguito, ho assegnato 3 cerniere che vincolassero esternamente la struttura scegliendo 3 punti distinti e non allineati e cliccando su Assign-Joint-Restraint.

 

 Successivamente ho creato un nuovo load pattern ( f ) e ho selezionato tutti i nodi interni assegnandogli una forza concentrata pari a 100 kN da Assign-Joint Loads-Forces . I nodi di bordo invece, avendo metà area di influnza rispetto a quelli interni,li ho caricati con una forza pari a 50 kN.

 

Dopo aver selezionato l'intera struttura, andando su Define-Section Properties-Frame Section, ho definito la sezione (tubolari in acciaio).

 

 

Cliccando su Assign-Frame-OutputStations ho posto 1 come valore su Min Number Stations per evitare troppi valori duplicati nella tabella dei risultati.

 

Infine ho lanciato l'analisi (play-RunNow) e ho ottenuto i valori dello sforzo normale ai quali è sottoposta la struttura e la sua configurazione deformata.

 

Cliccando su Display-ShowTables ho visualizzato la tabella riportante i valori delle sollecitazioni di sforzo normali agenti sulle aste della struttura e l'ho importata su Excel.

Ho riordinato la colonna riportante gli sforzi normali, ordinandoli dal più piccolo al più grande, e l'ho poi importa insieme a quella relativa alle lunghezze delle aste (Station m) sulla tabella excel  " sul dimensionamento dei pilastri" scaricata da questo portale.

A partire dagli sforzi normali (considerati per il loro valore assoluto (inserendo la funzione modulo dei valori della colonna P  nella colonna N) ho dimensionato le aste utilizzando un acciaio S275 ponendo il coeff.di vincolo β = 1, essendo gli elementi incernierati su entrambi gli estremi. Ottenuta l' Area minima (Amin= N / fyd) ho scelto profilati in acciaio tubolari con Area di sezione maggiore o uguale dell'Area minima e, tenendo anche conto dell'instabilità alla quale possono essere soggette le aste sollecitate a compressione, ho selezionato dei profilati che avessero anche il Momento di Inerzia (I_design  ) ed il raggio di inerzia (ρ_design) maggiori di quelli minimi.

Apro il programma e apro un nuovo file. Seleziono Grid only e controllo che le unità di misura siano KN,m,C. 

scrivo le dimensioni del volume che voglio disegnare

ho il volume e lo ricalco disegnando le aste e controventandole

copio il volume senza una faccia e lo incollo a 2 metri, attaccato a quello esistente

 lo copio e incollo finché non ho 32 volumi da 2x4x6.

Define, Section Properties, Frame section e add new property e scelgo Pipe in acciaio

seleziono tutto, assign, frame, frame section 

assign, frame, release. Rilascio i momenti 22 e 33. 

 Assegniamo i vincoli esterni, mi metto a quota z=0 

metto in pianta i vincoli sui nodi. Assign, joint, restraints e seleziono la cerniera. 

mi metto in 2d view ad altezza z=6 e seleziono la parte centrale.

Assign, joint loads, forces. Creo un nuovo load pattern: lo chiamo f e gli assegno un peso proprio pari a 0.  Lungo z metto -100 KN, il valore è negativo perché è diretto verso il basso. 

 A questo punto seleziono solo i nodi perimetrali e faccio la stessa cosa ma assegno un carico pari alla metà di quello che influisce sui nodi precedenti. L’area di influenza dei nodi perimetrali è la metà rispetto a quella dei nodi centrali. 

Sempre su f assegno -50 KN. Controllo che i carichi siano stati assegnati bene andando su Display, show load assigns e joint. Seleziono f e se posso premere ok allora è corretto.

Seleziono tutto, vado su assign, frame, output station e metto station 1.  

Analyze e seleziono il caso f, vado su run now e salvo il file. Controllo i grafici e verifico che il momento sia nullo. Seleziono lo sforzo assiale.

display, show table, seleziono load pattern solo quello che mi serve, quindi f, così anche select load cases e prendo i risultati delle analisi. Si apre una tabella e seleziono elements, forces, frames. Esporto la tabella su Excel da file, export current table to excel. Elimino dalla casella F in poi perché mi serve solo lo sforzo assiale. Con ctrl, shift e freccia in basso seleziono tutta la casella station e ordino dal minore, in questo modo elimino tutti i valori che  sono 0. Ordino anche i valori degli sforzi normali nella colonna P dal più piccolo al più grande e li copio nel file del dimensionamento. 

Calcolo l' area minima da sforzo normale di compressione. Ricopio i valori dalla tabella del profilato controllando che l'area di progetto sia maggiore dell'area minima, così come il momento di inerzia e ρ min. Essendo una trave doppiamente appoggiata, il coifficiente β è 1. Ho cambiato i segni ai valori di N per avere un'area positiva. 

Ho scelto un profilato in acciaio.

Calcolo dell'area minima da sforzo normale di trazione. In questo caso devo controllare solo che l'area di progetto sia maggiore dell'area minima. 

q

1. Imposto la mia griglia con una dimensione di 2 metri in tutte le direzioni, disegno le aste e i controventi. Lo ripeto nello spazio copiandolo in direzione X per sei volte e in direzione Y una volta sola. Assegno le cerniere interne rilasciando il momento in tutti i punti, sia all’inizio che alla fine delle travi. 
2. Assegno i vincoli esterni. I sostegni non sono allineati e sono in corrispondenza dei nodi. 
3. Assegno i carichi concentrati nei nodi. Al centro della struttura assegno una forza di 140KN e a quelli esterni la metà, perché hanno metà dell’area di influenza.
4. Vado a definire la sezione degli elementi strutturali. Aggiungendone una nuova, tubolare in acciaio, assegnadola a tutte le aste. 
5. Uso il comando Run Now per verificare la deformazione della struttura. 
6. Verifico anche i grafici di taglio e momento che devono essere entrambi zero.
7. Esporto la Tabella "Element Forces Frame" su Excel. (Ctrl+T) 
8. Creo una nuova tabella Excel dove inserisco i dati della struttura esportata da SAP ed i dati presenti nel foglio Excel scaricato dal Portale di Meccanica sul dimensionamento dei pilastri.
9. Tramite SAP trovo le lunghezze delle mie aste diagonali: 2,83m. Successivamente importo anche questi dati su Excel.
10. Per la compilazione della tabella utilizzo i dati del sito  http://www.oppo.it dei profilati metallici a sezione circolare.

11. Compilo la tabella partendo dalle aste a compressione (sforzo normale negativo), successivamente quelle soggette a trazione (sforzo normale positivo).

12. Aste a compressione: inserisco i valori delle tabelle “oppo” nelle colonne Adesign, Idesign e ῤminimo che corrispondono alla sezione metallica, al momento d'Inerzia ed al raggio d’inerzia così da trovarmi il valore λ che indica la snellezza del profilato che non deve essere inferiore a 200. Il momento d'inerzia e l'area del profilato devono essere maggiori del momento d'inerzia minimo e dell'Area minima dell'asta. Di conseguenza scelgo il profilato più adatto.
13. Aste a trazione: il procedimento è simile al precedente, ma questa volta prendo in considerazione solo l’Area minima per il dimensionamento, che deve essere sempre minore della sezione metallica del mio profilato.                                                         

Per lo svolgimento di questa esercitazione prenderemo in considerazione gli stessi modelli di solai (nelle tre differenti tecnologie costruttive: latero-cemento, acciaio, legno) presi in esame per gli esercizi precedenti.

 

Bisogna innanzi tutto chiarire che un’asta (più precisamente un pilastro nel nostro caso) può subire due tipi di sforzo normale centrato, agente assialmente rispetto alla sua lunghezza: trazione (se la forza agente tende a provocare un allungamento dell’asta) o compressione (se la forza agente tende a provocare un accorciamento dell’asta).

Nel primo caso il progetto si limita al calcolo dell’area minima di sezione che garantisce la resistenza a trazione.

Nel secondo caso invece il progetto prevede il calcolo dell’area minima di sezione resistente a compressione, e del momento d’inerzia minimo capace di contrastare il fenomeno d’instabilità euleriana. Inoltre, soltanto nel caso del pilastro in calcestruzzo armato, bisognerà eseguire una verifica a pressoflessione: questo perché i nodi in una struttura in cemento armato sono di tipo a incastro, quindi la trave sottoposta a flessione trasferisce momento anche al pilastro.

I pilastri del progetto che dovremo affrontare sono compressi, quindi svolgeremo i calcoli come indicato nel secondo caso.

Di seguito è rappresentato il modello strutturale dell’edificio tipo che andremo ad analizzare.

 

 

Per ogni tecnologia partiremo dimensionando la trave maggiormente sollecitata (nel nostro caso sul corrente 2 la A-B o la B-C di luce 4m) utilizzando il foglio excel fornitoci per la prima esercitazione.

 

1.  CALCESTRUZZO ARMATO

Per questo tipo di tecnologia costruttiva è stato scelto un solaio in latero cemento. Di seguito è rappresentato graficamente completo di tutte le sue parti costitutive.

 

 

Verrà calcolato tutto per una porzione di solaio pari a 1m².

 

analisi dei carichi

 

q_s (carichi strutturali)

_caldana in calcestruzzo: [(0,04*1,00*1,00)m³ + (0,16*0,20*1,00)m³]/m² * 2300kg/m³ = 165,60 kg/m² = 1,66 kN/m²

_rete elettrosaldata (maglia 15cm*15cm  ø8): 5,3 kg/m² = 0,053 kN/m²

_travetti: 2,00ml/m² * 10,50kg/ml = 21,00 kg/m² = 0,21 kN/m²

_pignatte (8 pz/m²): 66,4 kg/m² = 0,66 kN/m²

----------------------------------------------------------------------------------------------------------------------------------

_totale:    q_s = 2,58 kN/m²

 

q_p (carichi permanenti)

_pavimento in cotto (10 pz/m²): 42,0 kg/m² = 0,42 kN/m²

_massetto in sabbia e cemento: (0,04*1,00*1,00)m³/m² * 1800kg/m³ = 72,0 kg/m² = 0,72 kN/m²

_isolamento acustico: 5 kg/m² = 0,05 kN/m²

_intonaco: 13,3kg/m² = 0,13 kN/m²

_incidenza tramezzi: 0,5 kN/m²

_incidenza impianti: 1,0 kN/m²

----------------------------------------------------------------------------------------------------------------------------------

_totale:    q_p = 2,82 kN/m²

 

q_a (carichi accidentali)

_carichi accidentali in ambiente residenziale: 2,0 kN/m²

----------------------------------------------------------------------------------------------------------------------------------

_totale:    q_a = 2,00 kN/m²

 

Inserendo nella tabella i dati trovati, otterremo le dimensioni di sezione della trave resistente a flessione secondo i dati di carico da noi imposti. Come possiamo vedere di seguito la sezione della nostra trave avrà una sezione rettangolare con base “b = 25 cm” e altezza “H = 45 cm”.

 

 

Decidiamo inoltre di attribuire questi valori dimensionali sia alle travi principali che a quelle secondarie per rendere uniforme l’impalcato.

A questo punto possiamo iniziare i passaggi che ci permetteranno di calcolare le dimensioni del nostro pilastro maggiormente sollecitato a sforzo normale.

Il riquadro rosso evidenzia l’analisi dimensionale: inseriamo le luci delle travi principali e di quelle secondarie gravanti sul pilastro studiato e dal prodotto delle luci ricaviamo l’area della porzione di solaio oggetto del nostro studio.

Il riquadro verde evidenzia l’analisi dei carichi: inseriamo il peso specifico kN/m delle travi (ricavato con il foglio excel del dimensionamento della trave) e ricavo il peso delle travi q_trave grazie alla seguente formula.

q_trave = ∑  (1,3 * P trave_i * L_i)              con        P trave=peso unitario della trave (kN/m)          L=luce trave

Inseriamo poi i dati che si riferiscono al carico strutturale “q_s”, al carico permanente “q_p” ed al carico accidentale “q_a” ricavati precedentemente. In questo modo il foglio excel calcola il peso totale del solaio come somma dei singoli carichi per il rispettivo coefficiente di sicurezza, il cui risultato viene a sua volta moltiplicato per l’area del solaio gravante sul pilastro.

Definendo il numero dei piani possiamo ricavare quindi il carico N agente sul pilastro più sollecitato con la seguente formula:

N = (q_trave + q_solaio)*n_piani

 

 

Ora scegliamo una classe di resistenza caratteristica del cemento “f_ck” e ricaviamo la resistenza di progetto f_cd. Sappiamo che una resistenza è più genericamente una tensione, quindi la sua formula è:

f_cd = N/A 

dove N nel nostro caso è proprio il carico normale “N” che grava sul nostro pilastro, ed “A” è l’area su cui agisce il carico. Ma dato che stiamo ragionando in termini di resistenza massima del materiale l’area in questione è la più piccola che mi è permesso utilizzare per resistere a tale entità di carico: ciò vuol dire che un’area uguale o superiore a quella nella formula mi garantisce che la struttura resista. Per questo diciamo che ciò che cerchiamo è l’area minima resistente. Dall’area trovata possiamo ricavare i lati della sezione del nostro pilastro semplicemente facendo la radice quadrata del risultato ottenuto.

A_min = N/f_cd            -------->               b_min = √A_min 

 

 

Avendo trovato l’area minima di sezione resistente, passiamo ora a studiare il fenomeno dell’instabilità euleriana. Studiamo quindi quel livello di tensione dovuto a N_cr di compressione che provoca l’inflessione del pilastro. Stiamo quindi ipotizzando che:

f_cd =

DIMENSIONAMENTO DI UN PILASTRO

 Si dimensioni un pilastro nelle tre diverse tecnologie: legno, acciaio e cemento armato.

Osservando una generica pianta di carpenteria, il pilastro centrale sarà quello maggiormente sollecitato  in quanto ha un area di maggiore influenza.

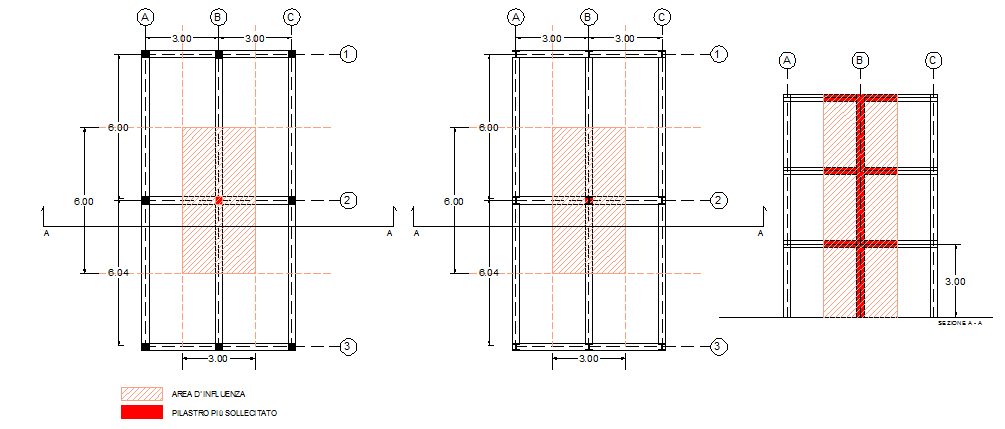
Pilastro: 2B

A_i= L₁ x L₂ = 6 m x 3 m = 18 m²

LEGNO

FASE 1°_ CALCOLO DELLO SFORZO NORMALE N AGENTE SUL PILASTRO

Fornisco alcuni dati necessari al foglio Excel, affinchè calcoli N:

_peso unitario delle due travi  (dipende dalla loro sezione) =

P x A

Si ottiene moltiplicando il peso specifico del materiale della trave per l’ area della sezione, essendo le due travi della stessa dimensione ed entrambe in legno i due valori saranno identici.

trave _p _  peso unitario della trave 1

trave _s _  peso unitario della trave 2

calcolo l’ area della sezione ( h = 50 cm; b= 30 cm)

50 cm x 30 cm= 1500 cm² = 0,15 m²  

Essendo il peso specifico del legno,

P legno = 8 KN/m³

Si ottiene il peso unitario delle travi:

8 KN/m³ x 0,15 m²   = 1,2 KN/m

_ valori dei carichi che gravano sul solaio

Questi dati posso ricavarli dalla prima esercitazione)

q_s = 0,39 KN/m2

q_p = 3,80 KN/m2

q_a = 2 KN/m2

Adesso il foglio Excel calcola il q_tot allo stato limite ultimo.

Inserendo il numero dei piani, ovvero il numero di solai che gravano sul pilastro

_ n piani = 3

il foglio calcolerà N sul pilastro maggiormente sollecitato con la seguente formula:

                         N= [ q_tot x A_i + t₁ x l₁ + t₂ x l₂ ] n piani

Dove :

t₁ = peso della trave 1

l₁ = lunghezza della trave 1

t₂ = peso della trave 2

l₂ = lunghezza della trave 2

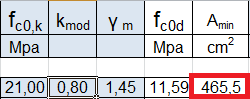
FASE 2°_ CALCOLO DELL’ AREA MINIMA CHE DEVE AVERE LA SEZIONE DEL PILASTRO PER EVITARE CHE IL MATERIALE ENTRI IN CRISI

Fornisco alcuni dati necessari al foglio Excel, affinchè calcoli A_min:

_ fc0,k = 21 Mpa resistenza caratteristica parallela alle fibre del legno

_k_mod= 0,8 (ricavato dalle tabelle in base alla durata del carico, classe di durata/ classe di servizio)

_{_}γ_m= 1, 45 (coefficiente parziale di sicurezza)

Il foglio calcolerà A_min che poi andrò ad ingegnerizzare.

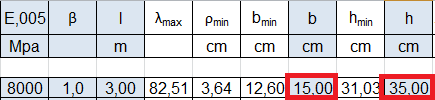
FASE 3°_ DETERMINAZIONE DELLA b E DELL’ ALTEZZA h

Fornisco alcuni dati necessari al foglio Excel, affinchè calcoli b e h:

E005 = 8000 Mpa modulo di elasticità del materiale

β= 1 coefficiente adimensionale che riflette l’ influenza dei vincoli, avendo due cenrniere, il suo valore sarà pari a 1

l= 3 m altezza del pilastro

I foglio calcolerà:

_λ_max, la snellezza dalla seguente formula

λ_max = 3,14 √(E /fcd)  

_ρ_min , il raggio minimo d ‘inerzia dato dal rapporto tra la luce libera d’ inflessione e la snellezza

ρ_min = l₀/ λ_max

_ b_min  la base minima della sezione del pilastro che andrò ad ingegnerizzare e che ricava attraverso:

ρ_min= √[(1/2)b]   =>   b= ρ_min  2 √3

_ h_min , l’ altezza minima della sezione del pilastro che andrò ad ingegnerizzare con h > h_min

FASE 4°_ VERIFICA

Avendo ora definito la b e l’ h del pilastro con b < h,

il foglio Excel ricava:

_ A_design, l’ area di progetto, fattore che mi garantisce che l’ elemento non entri in crisi se

                                                        A_design > A_min

_ Idesign, il momento d’inerzia di design che mi garantisce che l’ elemento non si infletta

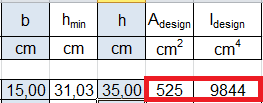
Verifica:

A_design = 525 cm²

A_min = 465,5 cm²

quindi     525 cm² > 465,5 cm²  => VERIFICATA!

ACCIAIO

FASE 1°_ CALCOLO DELLO SFORZO NORMALE N AGENTE SUL PILASTRO

Fornisco alcuni dati necessari al foglio Excel, affinchè calcoli N:

_carico dovuto al peso proprio delle travi (lo si ricava dalle tabelle)

trave _p (IPE400)=  66,3 kg/m = 0,66 KN/m

trave _s (IPE 120) = 10,4 kg/m =0,10 KN/m

_ valori dei carichi che gravano sul solaio

Questi dati posso ricavarli dalla prima esercitazione)

q_s = 1,03 KN/m2

q_p = 2,49 KN/m2

q_a = 2 KN/m2

Adesso il foglio Excel calcola il q_tot allo stato limite ultimo.

Inserendo il numero dei piani, ovvero il numero di solai che gravano sul pilastro

_ n piani = 3

il foglio calcolerà N sul pilastro maggiormente sollecitato con la seguente formula:

                       N= [ q_tot x A_i + t₁ x l₁ + t₂ x l₂ ] n piani

 

FASE 2°_ CALCOLO DELL’ AREA MINIMA CHE DEVE AVERE LA SEZIONE DEL PILASTRO PER EVITARE CHE IL MATERIALE ENTRI IN CRISI

Fornisco alcuni dati necessari al foglio Excel, affinchè calcoli A_min:

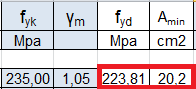
_ f_yk = 235 MPa tensione di snervamento

_γ_m = 1,05 coefficiente parziale di sicurezza

FASE 3°_ DETERMINAZIONE DEL MOMENTO Dì INERZIA MINIMO I_min

Consultando le tabelle, fornisco alcuni dati necessari al foglio Excel:

E =  210.000 N/mm2   modulo di elasticità del materiale

β= 1 coefficiente adimensionale che riflette l’ influenza dei vincoli, avendo due cenrniere, il suo valore sarà pari a 1

l= 3 m altezza del pilastro

I foglio calcolerà:

_λ_max, la snellezza massima

_ρ_min , il raggio minimo d ‘inerzia

_ I_min = Ax (ρ_min)²

Confrontando le tabelle vado a scegliere il profilato che ingegnerizza i valori ρ_min e I_min ricavati dal foglio, ovvero quello i cui valori superino quelli ricavati dal foglio di calcolo.

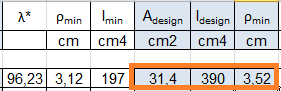
_Scelgo il profilo HEA 140 e vado ad inserire i valori :  A_design ; I_design ; ρ_design

FASE 4°_ VERIFICA

Il profilo è verificato se e solo se  A_design > A_min

A_design = 31,4 cm²

A_min= 20,2 cm²

quindi                A_design > A_min   => VERIFICATA!

 

CEMENTO ARMATO

FASE 1°_ CALCOLO DELLO SFORZO NORMALE N AGENTE SUL PILASTRO

Fornisco alcuni dati necessari al foglio Excel, affinchè calcoli N:

_carico dovuto al peso proprio delle travi

A x P (prodotto tra area della sezione della trave per il peso specifico del suo materiale)

A = 20 cm x 35 cm = 700 cm²  => A = 0,07 m²

P= 2 4 KN /m³

trave _p = 0,07 m² x 24 KN/m³ = 1,68 KN/m

trave _s= 0,07 m² x 24 KN/m³ =1,68 KN/m

_ valori dei carichi che gravano sul solaio

Questi dati posso ricavarli dalla prima esercitazione)

q_s = 2,45 KN/m2

q_p = 3,53 KN/m2

q_a = 2 KN/m2

Adesso il foglio Excel calcola il q_tot allo stato limite ultimo.

Inserendo il numero dei piani, ovvero il numero di solai che gravano sul pilastro

_ n piani = 3

FASE 2°_ CALCOLO DELL’ AREA MINIMA  CHE DEVE AVERE LA SEZIONE DEL PILASTRO PER EVITARE CHE IL MATERIALE ENTRI IN CRISI E LA BASE MINIMA

Affinchè  il foglio calcoli A_min:

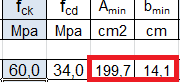
_ devo inserire f_ck = 60 MPa tensione di snervamento

FASE 3°_ DETERMINAZIONE DEL MOMENTO Dì INERZIA MINIMO I_min

fornisco alcuni dati necessari al foglio Excel:

_ E =21.000 N / mm²

_β = 1

_ l = 3 m

I foglio calcolerà:

_λ_max, la snellezza massima

_ρ_min , il raggio minimo d ‘inerzia

_ b_{min, la base minima} che andrò ad ingegnerizzare

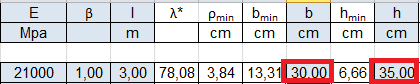
Essendo ora nota la base della sezione del pilastro posso determinare anche l ‘ altezza h_min che devo sempre ingegnerizzare.

 

FASE 4°_ VERIFICA

Essendo noti la base e l’ altezza della sezione del pilastro (b < h) il foglio  Excel ricava:

A_design ;I_design ;I_max ;W_max ;Q_t ;M_t ;δ_max

Affinchè la sezione sia verificata, dovranno essere soddisfatte due condizioni di verica:

1° condizione di verifica : A_design > A_min

2° condizione di verifica :  δ_max ≤ f_cd  

(Viene effettuata questa seconda verifica in quanto nel c. a. il nodo trave – pilastro,essendo  un incastro, determina un momento e quindi sottopone il pilastro al fenomeno di presso-flessione)

entrambe le due condizioni risultano soddisfatte ,la sezione è VERIFICATA!

 

Nella prima esercitazione abbiamo progettato la stratigrafia di tre solai di differenti tecnologie costruttive (cls armato, acciaio, legno). Disegnando poi un semplice telaio strutturale abbiamo individuato al suo interno la trave doppiamente appoggiata maggiormente sollecitata in un piano tipo, per poi dimensionarla secondo i parametri di carico stabiliti. Abbiamo quindi progettato la suddetta trave prendendo in considerazione la resistenza massima del materiale, cioè nello Stato Limite Ultimo ovvero in quello stato appena precedente al cedimento della struttura a seguito della rottura delle sue parti..

In questo caso considereremo dei solai con identica stratigrafia di quelli dell’esercitazione 1 ma individuando questa volta la trave a sbalzo maggiormente sollecitata. La dimensioneremo in base ai parametri di carico stabiliti ed eseguiremo una verifica a deformabilità: verificheremo cioè che lo spostamento verticale massimo della mensola in questione sia inferiore ai valori massimi permessi dalla normativa. In questo caso lavoreremo perciò in regime di Stato Limite d’Esercizio, cioè in quello stato subito dopo il quale la struttura non si rompe, ma a causa di spostamenti e deformazioni cambia nella sua conformazione limitando la possibilità d’utilizzo dell’edificio.

 

1.  CALCESTRUZZO ARMATO

Per questo tipo di tecnologia costruttiva è stato scelto un solaio in latero cemento. Di seguito è rappresentato graficamente completo di tutte le sue parti costitutive.

 

analisi dei carichi

 

q_s (carichi strutturali)

_caldana in calcestruzzo: [(0,04*1,00*1,00)m³ + (0,16*0,20*1,00)m³]/m² * 2300kg/m³ = 165,60 kg/m² = 1,66 kN/m²

_rete elettrosaldata (maglia 15cm*15cm  ø8): 5,3 kg/m² = 0,053 kN/m²

_travetti: 2,00ml/m² * 10,50kg/ml = 21,00 kg/m² = 0,21 kN/m²

_pignatte (8 pz/m²): 66,4 kg/m² = 0,66 kN/m²

-----------------------------------------------------------------------------------------------------------

_totale:    q_s = 2,58 kN/m²

 

q_p (carichi permanenti)

_pavimento in cotto (10 pz/m²): 42,0 kg/m² = 0,42 kN/m²

_massetto in sabbia e cemento: (0,04*1,00*1,00)m³/m² * 1800kg/m³ = 72,0 kg/m² = 0,72 kN/m²

_isolamento acustico: 5 kg/m² = 0,05 kN/m²

_intonaco: 13,3kg/m² = 0,13 kN/m²

_incidenza tramezzi: 0,5 kN/m²

_incidenza impianti: 1,0 kN/m²

-----------------------------------------------------------------------------------------------------------

_totale:    q_p = 2,82 kN/m²

 

q_a (carichi accidentali)

_carichi accidentali in ambiente residenziale: 2,0 kN/m²

-----------------------------------------------------------------------------------------------------------

_totale:    q_a = 2,00 kN/m²

 

Il valore di carico da utilizzare per il progetto della trave non è dato dalla sola somma q_s+q_p+q_a: i valori trovati devono ora essere moltiplicati per i rispettivi coefficienti stabiliti dalla normativa; i loro risultati poi andranno sommati e daranno come risultato q_tot /m² ovvero il carico di progetto ma relativo ad 1m² di solaio. Per ottenere q_u /ml (cioè il carico agente su un metro lineare di trave) sarà sufficiente moltiplicare q_tot /m² per la misura dell’interasse: conosceremo così quindi il carico della superficie disegnata in blu più scuro (1m² * interasse) in figura 1c.

 

q_tot /m² = Ɣ_G1q_s + Ɣ_G2q_p + Ɣ_Q1q_a                                              Ɣ_G1=1,3    Ɣ_G2=1,5    Ɣ_Q1=1,5

q_tot /m² = (1,3 * 2,58) + (1,5 * 2,82) + (1,5 * 2,00) = 10,58 kN/m²

q_u /ml = q_tot /m² * interasse = 10,58 kN/m² * 3m        --------------->        q_u /ml = 31,75 kN/m

 

 

Passiamo adesso al calcolo del momento flettente massimo della nostra trave: essendo una trave a sbalzo la formula del momento flettente massimo è la stessa di quello della mensola ed è nota:  M_max = ql²/2.

 

M_max = [(31,75 kN/m) * (3m)²]/2         ---------------------------------->        M_max = 142,88 kNm

 

Ora scegliamo il tipo di calcestruzzo e di acciaio che vogliamo utilizzare per sviluppare il nostro progetto. Entrambi saranno caratterizzati da una resistenza caratteristica: moltiplicando tali resistenze caratteristiche per i relativi coefficienti maggiorativi otterremo i valori delle loro resistenze di progetto (f_cd per il calcestruzzo, f_yd per l’acciaio: la “_y” sta per yield = snervamento, la “_d” per design = progetto).

 

f_cd = α_cc*f_ck/Ɣ_m = 0,85*(40 N/mm²)/1,5      ---------------------------->        f_cd = 22,67 N/mm²

f_yd = f_yk/ Ɣ_y = (450 N/mm²)/1,15                ---------------------------->        f_yd = 391,3 N/mm²

 

Adesso abbiamo tutti i dati necessari a ricavare la l’altezza della trave. Lo faremo sfruttando la relazione che intercorre tra il concetto di momento flettente (Bernoulli) e il concetto di tensione (Navier). Fisso arbitrariamente un valore per la base (in questo caso scelgo b= 25 cm).

 

x_c : h_u = f_cd : (f_cd + f_yd/n)       --->       x_c= h_u* [f_cd*(f_cd + f_yd/n)]          con       α = f_cd*(f_cd + f_yd/n)       --->        x_c = α  * h_u

h_u = √ 2/[f_cd*(1-α/3)*α] * √ M/b          con          r = √ 2/[f_cd*(1-α/3)*α]                h_u = r * √ M/b

 

Sommando al valore di h_u trovato quello dell’altezza del copriferro “δ” otteniamo la nostra h_min. I calcoli effettuati hanno preso in considerazione la massima resistenza del materiale, quindi per i dati di carico e misura della base da noi scelti, l’altezza trovata è l’altezza minima resistente “h_min”. Le misure di progettazione del calcestruzzo sono espresse in multipli di 5 cm, per questo l’altezza che sceglieremo sarà un valore multiplo di 5 subito più grande dell’h_min trovata. Nel nostro caso:

 

h_u = 35,83 cm     δ = 5 cm     ------>    h_min = h_u + δ = (35,83 + 5)cm = 40,83 cm     ---->       H = 45,00 cm

 

Terminata la fase di progetto passiamo alla fase di verifica. Adesso andremo ad aggiungere il peso proprio della trave alla somma dei carichi portati dalla trave stessa, calcoleremo il momento massimo, e verificheremo poi se la sezione scelta sarà adatta anche a queste nuove carattristiche di carico.

 

p_t/ml = 2,59 kN/m           lo moltiplico per Ɣ_G1 = 1,3

q_u’ = q_u + (2,59 kN/m*1,3) = (31,75 + 3,37) kN/m           -------------------->       q_u’ = 35,12 kN/m

M’_max = q_u’ * l² / 2     ------>    M’_max = (35,12 kN/m) * (3m)² / 2    ----------->       M’_max = 158,02 kNm

M’ = C*B* = T*B*     ------>    h’_u = √ 2/[f_cd*(1-α/3)*α] * √ M’/b      ----------->       h’_u = 37,68 cm

h’_min = h’_u + δ = (37,68 + 5)cm = 42,68cm      ----------------------------------->       H’ = 45,00 cm

La sezione scelta risulta quindi verificata in quanto       ---------------------->       H = H’ = 45,00 cm

 

Passiamo adesso alla parte concernente questa esercitazione, cioè la verifica a deformabilità. Dobbiamo trovare il valore dello spostamento verticale massimo “v_max” della trave a sbalzo. In questo caso, trattandosi di una trave a sbalzo: v_max=(q_e*l⁴)/(8*E*I_x), con q_e che comprende i carichi del solaio + il peso proprio della trave in stato d’esercizio ed E = 21000 N/mm². Lo spostamento verticale è inversamente proporzionale al momento d’inerzia, perciò più grande è il momento d’inerzia minore sarà lo spostamento causato dal carico sulla trave. Calcoliamo perciò il momento d’inerzia rispetto all’asse x perchè la trave è disposta con la lunghezza maggiore in verticale. In questo modo il momento d’inerzia è maggiore in quanto l’altezza nella formula è espressa alla quarta, e quindi oltre alle caratteristiche di resistenza del materiale anche la conformazione geometrica della trave l’aiuta a resistere meglio ai carichi su di essa applicati.

 

q_e = [(q_s + q_p +