Esercitazione

Progettazione Strutturale 1M - a.a. 2017/2018
prof.ssa Ginevra Salerno - studente: Antonio Tripodo [462841] con Francesco Varano [475968]

Seconda Esercitazione: Dimensionamento di un telaio in tre tecnologie – Parte 2

Vento

L’azione del vento sulla struttura è descrivibile attraverso un andamento (co)sinusoidale in quanto agente naturale variabile. La NTC 2008 consente di studiare l’intensità di questo fenomeno attraverso la formula della Pressione Cinetica di riferimento

P = 0,5 ρ(v)^2

nella quale P rappresenta la pressione esercitata dal vento sull’edificio [N/m^2], ottenuta dal prodotto di ρ (valore di densità dell’aria = 1,25 Kg/m^3) e il quadrato di v (velocità di riferimento del vento, calcolata in m/s).
Per una analisi di massima consideriamo un apporto di 0,4 KN/m^2 sulla facciata controvento e 0,2 KN/m^2 sulla facciata sottovento, valori moltiplicati per l’area di influenza dei rispettivi pilastri perimetrali.

Sisma

L’azione sismica viene descritta come un carico linearmente distribuito, crescente con l’altezza dell’edificio, e calcolata per ogni livello attraverso le formule

Fi = Fs (zi Wi / Szi Wi)

Fs = cW

dove Fs rappresenta l’intensità del sisma ed è ottenuta dal prodotto di c (rapporto fra l’accelerazione sismica e quella gravitazionale = 0,3 per questa zona) e W (la somma del peso strutturale, il 20% di un eventuale Carico Neve e il 30% dei Carichi di Destinazione). Questa viene a sua volta moltiplicata per il rapporto fra il prodotto del livello considerato con la sua W e la sommatoria di prodotti fra i vari livelli dei piani e i loro rispettivi W.
Se l’interpiano rimane costante per tutto l’edificio il calcolo di Fi si limita al prodotto di Fs e il rapporto fra il livello del piano considerato e la somma dei livelli di ogni piano.

z =interpiano (costante), 4 piani

F1 = Fs (z/10z) = Fs/10
F2 = Fs (2z/10z) = Fs (2/10)
F3 = Fs (3z/10z) = Fs (3/10)
F4 = Fs (4z/10z) = Fs (4/10)

Il sisma nella realtà si concentra in un unico punto dell’edificio, detto Centro di Massa, vicino ma non corrispondente al baricentro geometrico della struttura. Per l’analisi su SAP2000 vengono individuati più punti, ciascuno situato nel Centro di Area di Impalcato di ogni piano.
Nel caso in cui la geometria del piano non fosse regolare, le sue coordinate vengono calcolate attraverso la formula

C(Xc, YC)

Xc = x1(A1) + x2(A2) / (A1 + A2)

Yc = y1(A1) + y2(A2) / (A1 + A2)

altrimenti il Centro di Area coincide con il baricentro geometrico del piano. Questo punto costituisce una prosecuzione del vincolo interno Diaphram.

Si procede con la verifica della risposta dei tre modelli di telaio sottoposti ad azioni combinate:

a) CARICO VERTICALE SLU e AZIONE VENTO dir. X
b) CARICO VERTICALE SLU e AZIONE VENTO dir. Y
c) CARICO VERTICALE SLU e AZIONE SISMA dir. X
d) CARICO VERTICALE SLU e AZIONE SISMA dir. Y

 

TELAIO IN ACCIAIO

Carico verticale SLU

Qs = 1,7 KN/m^2 (1,3) (5 m) = 11,05 KN/m

Qp = 2,635 KN/m^2 (1,5) (5 m) = 19,8 KN/m

Qa = 2 KN/m^2 (1,5) (5 m) = 15 KN/m

Azione Vento dir. X

Pilastro controvento
P = 0,4 KN/m^2 (5 m) = 2 KN/m

Pilastro sottovento
P = 0,2 KN/m^2 (5 m) = 1 KN/m

Azione Vento dir. Y

Pilastro controvento
P = 0,4 KN/m^2 (8 m) = 3,2 KN/m

Pilastro sottovento
P = 0,2 KN/m^2 (8 m) = 1,6 KN/m

Azione Sisma dir. X e Y

Fs = (0,3) (15584,2 KN + 120 KN + 1440 KN) = 5143,26 KN

F1 = 514,33 KN
F2 = 1028,652 KN
F3 = 1542,99 KN
F4 = 2057,304 KN

C (15, 10)
 

TELAIO IN CLS ARMATO

Carico verticale SLU

Qs = 3,21 KN/m^2 (1,3) (3 m) = 12,52 KN/m

Qp = 2,34 KN/m^2 (1,5) (3 m) = 10,53 KN/m

Qa = 2 KN/m^2 (1,5) (3 m) = 9 KN/m

Azione Vento dir. X

Pilastro controvento
P = 0,4 KN/m^2 (3 m) = 1,2 KN/m

Pilastro sottovento
P = 0,2 KN/m^2 (3 m) = 0,6 KN/m

Azione Vento dir. Y

Pilastro controvento
P = 0,4 KN/m^2 (5 m) = 2 KN/m

Pilastro sottovento
P = 0,2 KN/m^2 (5 m) = 1 KN/m

Azione Sisma dir. X e Y

Fs = (0,3) (12043,4 KN + 187,2 KN + 62,4 KN) = 3688 KN

F1 = 368,8 KN
F2 = 737,6 KN
F3 = 1106,4 KN
F4 = 1475,2 KN

C (13, 6)

 

TELAIO IN LEGNO

Carico verticale SLU

Qs = 0,3562 KN/m^2 (1,3) (3 m) = 1,38918 KN/m

Qp = 2,635 KN/m^2 (1,5) (3 m) = 11,85 KN/m

Qa = 2 KN/m^2 (1,5) (3 m) = 9 KN/m

Azione Vento dir. X

Pilastro controvento
P = 0,4 KN/m^2 (3 m) = 1,2 KN/m

Pilastro sottovento
P = 0,2 KN/m^2 (3 m) = 0,6 KN/m

Azione Vento dir. Y

Pilastro controvento
P = 0,4 KN/m^2 (5 m) = 2 KN/m

Pilastro sottovento
P = 0,2 KN/m^2 (5 m) = 1 KN/m

Azione Sisma dir. X e Y

Fs = (0,3) (5859,55 KN + 187,2 KN + 62,4 KN) = 1832,75 KN

F1 = 183,28 KN
F2 = 366,56 KN
F3 = 549,84 KN
F4 = 733,12 KN

C (13, 6)

 

 

Impostate le 3 tecnologie di telaio su SAP, con le sezioni predimensionate nella scorsa esercitazione, per prima cosa si applicano tutti i carichi verticali sulla struttura (Qs,Qp e Qa) distribuiti linearmente sulle travi principali di ogni piano, poi anche del carico neve solo sul solaio di copertura.

Definita la combinazione di carico SLU+NEVE = Qs*1,3+Qp*1,5+Qa*1,5 + neve , si avvia l'analisi ed importate le tabelle su excel si verificano le sezioni del pilastro, trave e aggetto con Nmax e Mmax dato dall'analisi.

Successivamente su SAP si aggiungono anche i carichi orizzontali, sisma e vento.
Il vento viene distribuito lungo i pilastri, con valori 0,4 in compressione e 0,2 in decompressione.
La forza sismica viene calcolata con la seguente formula: Fs = c * W
Dove c è il coefficiente di intensità sismica, mentre W è il peso
W = P (peso della struttura ps+pp) + 20% N (neve) + 30% Q (sovraccarichi accidentali)
Fs si distribuisce con valori diversi in base alla quota del piano (F1=Fs/10; F2=Fs*2/10; F3=Fs*3/10; etc..) e viene applicata nel centro di massa. Sia il vento che il sisma vengono calcolati per entrambe le direzioni ortogonali, non essendo possibile prevedere la direzione dell'azione.

Vengono definite le combinazioni anche per i carichi orizzontali ed avviata l'analisi.

Per la verifica a pressoflessione dei pilastri bisogna distinguere in base alla tecnologia:
Per il cls, viene prima determinata l'eccentricità e=M/N e si distinguono 3 casi: e<H/6, H/6<e<H/2, e>H/2. In questo caso e>H/2, l'eccentricità era molto forte, quindi si è verificato il pilastro a flessione senza compressione.
Per il legno è bastato verificare che la somma dei rapporti tra le tensioni  e resistenze del materiale fosse minore o uguale a 1 :
σc / fcd + σf / ffd < 1
il legno essendo un materiale anisotropo (su SAP considerato come ortotropo) ha 3 diversi valori di resistenza caratteristica (fc, ft, ff).
Per l'acciaio invece :
σ = N/A +/- M/W < fd

In allegato il file pdf con l'esercitazione in dettaglio, immagini e calcoli.

Esercitazione_3

Svolta con Alessandro Valentini

 

_Imposto il telaio su SAP:

Per prima cosa disegno su SAP il telaio preso in analisi nell’ ES_2

 

Affinchè tale struttura agisca come telaio vado ad applicare dei “Costrain” sui punti di intersezione dei “Frame”, avrò “Costrain” diversi per i punti appartenenti a solai diversi. Questa operazione elimina le rotazioni attorno l’asse Z.

Ora assegno le sezioni corrispondenti ai “Frame”, quindi creo 3 file diversi dello stesso telaio per le 3 differenti tecnologie utilizzate: acciaio, legno e calcestruzzo. Le sezioni assegnate a travi e pilastri corrispondono a quelle di prima dimensione prodotte nella ES_2.

Applico i carichi Qa, Qp, Qs. I primi due saranno gli stessi per tutte e tre le tecnologie, il Qs varia in base al materiale utilizzato. Tali carichi sono applicati solo alle travi principali secondo la relativa area d’ influenza.

La combinazione di questi tre carichi sarà la seguente:

 Qs x 1,3 + Qp x 1,5 + Qa x 1,5

Procedo ora ad applicare le azioni del vento e del sisma sui telai, il procedimento è lo stesso per tutte le tecnologie.

 

_Azione del vento:

Applico l’azione del vento sulle facciate esposte: sopravento e sottovento. Tale azione va applicata ai pilastri come una Forza lineare omogenea su tutta la loro altezza, considerando l’area d’ influenza che copre ogni pilastro.

Sopravento: 0,4 x area d’influenza

Sottovento: 0,2 x area d’influenza

Il procedimento si ripete due volte per le due possibili direzioni del vento: lungo gli assi X e Y

 

_Azione del sisma:

 Per applicare l’azione del sisma sul telaio di SAP è necessario per prima cosa creare dei punti in corrispondenza dei centri di massa di ogni solaio. A Questi verrà applicato quindi il “Costrain” corrispondente al solaio di appartenenza per farlo funzionare come parte integrante dello stesso.

A questo punto vanno individuate le forze da applicare sui diversi centri di massa. Queste variano in base alla distanza del solaio da terra e all’ interpiano tra i solai:

F,i = F,s (z,i / Σz,i)      

dove “z” è la misura dell’interpiano. In questo caso l’interpiano è sempre di 4m e i solai sono 4

Per ricavare F,s, è necessario attuare una combinazione di carichi specifica per l’azione del sisma:

F,s = cW = c ( Qp + Qs + 20%Neve + 30%Qa)

dove “c “ è una costante il cui valore corrisponde a

0,2 x 9,8 m/s2

(9,8 m/s2  =  accelerazione di gravità).

Il procedimento si ripete due volte per le due possibili direzioni del sisma: lungo gli assi X e Y.

 

 

Acciaio:

Per verificare che la dimensione dei pilastri del telaio in acciaio sia adeguata a resistere alle sollecitazioni di vento e sisma procedo con la verifica a presso flessione di tali sezioni.

Le verifiche di sisma e vento si fanno separatamente e tali azioni si uniscono alla combinazione dei carichi Qa, Qp e Qs con aggiunta di un ulteriore carico accidentale: il carico neve

 

_Verifica sisma:

Per verificare i pilastri del telaio sotto azione del sisma viene analizzato il pilastro con le maggiori sollecitazioni a pressione e a flessione, a questo quindi viene applicata la verifica a presso-flessione.

La direzione del sisma utilizzata è quella nella direzione Y. Tale condizione è la più svantaggiosa per i pilastri che sono dei profilati HEA orientati con l’anima lungo l’asse X. DI conseguenza presenteranno una resistenza a flessione inferiore lungo Y.

La tensione data dalla combinazione di flessione e pressione è inferiore alla Fyd quindi la sezione è verificata.

 

_Verifica vento:

Per verificare le sezioni dei pilastri sotto l’azione del vento applico lo stesso procedimento: Elemento più sollecitato con applicazione del vento nella direzione di Y.

La tensione data dalla combinazione di flessione e pressione è inferiore alla Fyd quindi la sezione è verificata.

 

Legno:

Per verificare che la dimensione dei pilastri del telaio in legno sia adeguata a resistere alle sollecitazioni di vento e sisma procedo con la verifica a presso flessione di tali sezioni.

La verifica di sisma e vento si fa separatamente e tali azioni si uniscono alla combinazione dei carichi Qa, Qp e Qs con aggiunta di un ulteriore carico accidentale: il carico neve

 

_Verifica sisma:

Per verificare i pilastri sotto azione del sisma viene analizzato il pilastro con le maggiori sollecitazioni a pressione e a flessione, a questo quindi viene applicata la verifica a presso-flessione.

La direzione del sisma presa in considerazione in questo caso sarà esclusivamente quella in cui i pilastri soffrono di maggiore sforzo a momento flettente. Dal momento che sono di sezione quadrata e non hanno una direzione di maggior resistenza a flessione rispetto all’altra.

 

 _Verifica vento:

Per verificare le sezioni dei pilastri sotto l’azione del vento applico lo stesso procedimento: Elemento più sollecitato con applicazione del vento nella direzione con maggiore flessione.

 

Calcestruzzo:

Per verificare che la dimensione dei pilastri del telaio in c.l.s. sia adeguata a resistere alle sollecitazioni di vento e sisma procedo con la verifica a presso flessione di tali sezioni.

La verifica di sisma e vento si fa separatamente e tali azioni si uniscono alla combinazione dei carichi Qa, Qp e Qs con aggiunta di un ulteriore carico accidentale: il carico neve.

Per verificare il pilastro in calcestruzzo è necessario individuare l’eccentricità

e = M/N

attraverso questa è possibile stabilire il tipo di reazione della sezione

Caso_1: e < H/6                 → compresso

Caso_2: H/6 < e < H/2      → compresso e flesso

Caso_3: e > H/2                 → flesso

Quindi si applica la verifica opportuna al caso.

 

_Verifica sisma:

La direzione del sisma presa in considerazione in questo caso sarà esclusivamente quella in cui i pilastri soffrono di maggiore sforzo a momento flettente. Dal momento che sono di sezione quadrata e non hanno una direzione di maggior resistenza a flessione rispetto all’altra.

 

_Verifica vento:

Per verificare le sezioni dei pilastri sotto l’azione del vento applico lo stesso procedimento: Elemento più sollecitato con applicazione del vento nella direzione con maggiore flessione.

La seconda parte dell' esercitazione 2 consiste nella creazione in SAP dei telai  precedentemente dimensionati e nella successiva verifica delle sezioni mediante i valori esportati dal software. Anche in questo caso sono stati presi in considerazione due tipi di telai, uno per l'acciaio e l'altro per calcestruzzo armato e legno.  L'analisi delle strutture e la conseguente verifica è stata fatta inserendo i carichi neve, vento e sisma.

In allegato il commento in pdf.

L'esercitazione è stata svolta in collaborazione con Claudia Belliscioni.

Si tratta della seconda parte dell'esercitazione precedente relativa al dimensionamento di un edificio nelle tre tecnologie, in questo caso siamo andati a verificare tramite il programma SAP2000 la deformata e lo sforzo normale e flettente, introducendo i carichi sisma, neve e vento.

L'esercitazione è stata svolta con Elena Monaco e Filippo Merlani.

 

 

 

 

 

 

Svolta con Pietro Sircana

In allegato il commento e gli excel usati per le verifiche
 

In questa esercitazione si cerca di verificare i telai calcolati nella precedente esercitazione con l’utilizzo dei  dati delle analisi di SAP2000.

 

ACCIAIO

Come prima analisi ci occupiamo degli effetti di un sisma su una struttura a telai piani in acciaio. Come prima operazione è stato calcolato il centro di massa di tutti i solai della struttura, punto nel quale scarica la forza orizzontale del sisma.

X_C= (576X18)+(320x10)/896= 15,14m

Y_C= (576x8)+(320x24)/896= 13,71m

Successivamente è stato calcolato il peso (W) di ogni solaio, massa dell’edificio, per calcolarne il peso totale.

W= (q_sx896)+(q_px896)+30%(q_ax896)=  (3,1x896)+(2,67x896)+30%(2x896)= 2777,6+2392,32+537,6= 5707,2KN

W_tetto= (q_sx896)+(q_px896)+30%(q_ax896)+20%(q_{a neve}x869)= (3,1x896)+(2,67x896)+30%(2x896)+20%(0,5x869)= 2777,6+2392,32+537,6+89,6= 5796,8KN

W_tot= (5707,2x3)+ 5796,8= 22828,8KN

F_s= 22828,8x0,3= 6848,64KN

F₁= 6848,64x1/10= 684,86KN

F₂= 6848,64x2/10= 1369,73KN

F₃= 6848,64x3/10= 2054,59KN

F₄= 6848,64x4/10= 2739,54KN

Assegnate le forze nei centri precedentemente trovati e inserito un diaphram ad ogni solaio compreso il centro di massa si creano due combinazioni di carico una per il sisma in direzione x e una in direzione y.

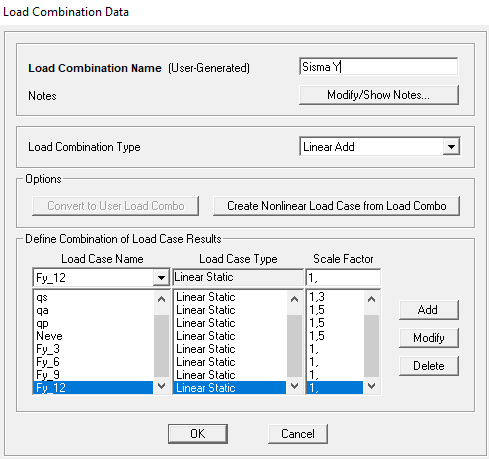
Ora possiamo avviare l'analisi ed esportare le tabelle di calcolo su Excel. Si prosegue con la verifica.

SISMA X

M= 520KNm =520000000Nmm

N= 1642KN= 1642000N

A= 112,5cm²= 11250mm²

W= 3069cm³= 3069000mm³

F_yd=261,9

Sigma= N/A= 1642000/11250= 146N/mm²

Sigma_max= M/W= 520000000/3069000= 169N/mm²

Sigma_tot= 146+169= 315N/mm²  f_yd<Sigma_tot

Non verificato, si ha bisogno di un profilo maggiore del HEA 300

 

SISMA Y

M= 565KNm =565000000Nmm

N= 2330KN= 2330000N

A= 112,5cm²= 11250mm²

W= 3069cm³= 3069000mm³

F_yd=261,9

Sigma= N/A= 2330000/11250= 207N/mm²

Sigma_max= M/W= 565000000/3069000= 184N/mm²

Sigma_tot= 207+184= 391N/mm²  f_yd<Sigma_tot

Non verificato, si ha bisogno di un profilo maggiore del HEA 300

 

CLS armato

Come prima analisi ci occupiamo degli effetti di un sisma su una struttura a telai piani in CLS armato. Come prima operazione è stato calcolato il centro di massa di tutti i solai della struttura, punto nel quale scarica la forza orizzontale del sisma.

X_C= (225x11,25)+(125x6,25)/350= 9,46m

Y_C= (225x5)+(125x15)/350= 8,57m

Successivamente è stato calcolato il peso (W) di ogni solaio, massa dell’edificio, per calcolarne il peso totale.

W= (q_sx350)+(q_px350)+30%(q_ax350)=  (3,2x350)+(2,97x350)+30%(2x350)= 1120+1039,5+210= 2369,5KN

W_tetto= (q_sx350)+(q_px350)+30%(q_ax350)+20%(q_{a neve}x350)= (3,2x350)+(2,97x350)+30%(2x350)+20%(0,5x350)= 1120+1039,5+210+35= 2404,5KN

W_tot= (2369,5x3)+ 2404,5= 9513KN

F_s= 9513x0,3= 2853,9KN

F₁= 2853,9x1/10= 285,39KN

F₂= 2853,9x2/10= 570,78KN

F₃= 2853,9x3/10= 856,17KN

F₄= 2853,9x4/10= 1141,56KN

Assegnate le forze nei centri precedentemente trovati e inserito un diaphram ad ogni solaio compreso il centro di massa si creano due combinazioni di carico una per il sisma in direzione x e una in direzione y.

Ora possiamo avviare l'analisi ed esportare le tabelle di calcolo su Excel. Si prosegue con la verifica.

SISMA X

N= 968KN = 968000N

M= 215KNm =215000000Nmm

H=40cm = 400mm

e= 215000000/968000= 222mm  Fuori dalla sezione

SISMA Y

N= 1053KN= 1053000N

M= 198KNm= 198000000Nmm

H= 40cm= 400mm

e= 198000000/1053000= 188mm   H/6<e<H/2

Sigma_max= 2N/3uxB= 2x1053000/36x400= 146,25N/mm²

3u= 3(H/2xB)= 36mm

Sigma_max>Sigma_cd  

Non verificato, bisogna incrementare la sezione in direzione y, direzione anche delle travi principali, portandola a 60cm il pilastro è verificato.

 

LEGNO

Come prima analisi ci occupiamo degli effetti di un sisma su una struttura a telai piani in Legno. Come prima operazione è stato calcolato il centro di massa di tutti i solai della struttura, punto nel quale scarica la forza orizzontale del sisma.

X_C= (225x11,25)+(125x6,25)/350= 9,46m

Y_C= (225x5)+(125x15)/350= 8,57m

Successivamente è stato calcolato il peso (W) di ogni solaio, massa dell’edificio, per calcolarne il peso totale.

W= (q_sx350)+(q_px350)+30%(q_ax350)=  (0,66x350)+(2,99x350)+30%(2x350)= 231+1046,5+210= 1487,5KN

W_tetto= (q_sx350)+(q_px350)+30%(q_ax350)+20%(q_{a neve}x350)= (0,66x350)+(2,99x350)+30%(2x350)+20%(0,5x350)= 231+1046,5+210+35= 1522,5KN

W_tot= (1487,5x3)+ 1522,5= 5985KN

F_s= 5985x0,3= 1785KN

F₁= 1785x1/10= 178,5KN

F₂= 1785x2/10= 357KN

F₃= 1785x3/10= 535,5KN

F₄= 1785x4/10= 714KN

Assegnate le forze nei centri precedentemente trovati e inserito un diaphram ad ogni solaio compreso il centro di massa si creano due combinazioni di carico una per il sisma in direzione x e una in direzione y.

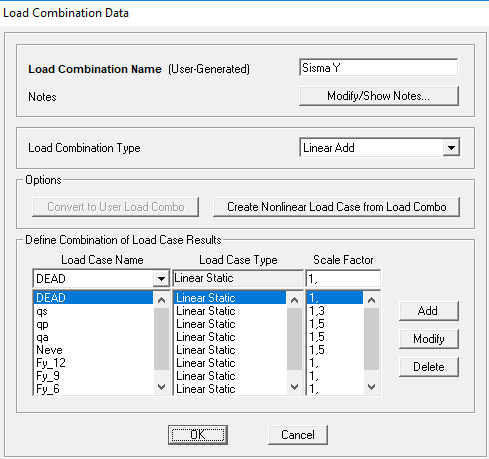
Ora possiamo avviare l'analisi ed esportare le tabelle di calcolo su Excel. Si prosegue con la verifica.

 

SISMA X

M= 149KNm =149000000N/mm

N= 606KN= 606000N

A= 900cm²= 90000mm²

W=4500cm³= 4500000mm³

W= bxh²/6= 30x30²/6= 4500cm³

Sigma_c= N/A= 606000/90000= 6,7N/mm²

Sigma_f= M/W= 149000000/4500000=33N/mm²

f_cd= 0,8x21/1,5= 11,2N/mm²

f_fd= 0,8x24/1,5= 12,8N/mm²

Sigma_c/f_cd+Sigma_f/f_fd < 1 => 6,7/11,2+33/12,8 < 1 => 3,2 < 1 

Non verificata la sezione deve essere aumentata, con una sezione 30x60 il valore viene verificato. 

 

SISMA Y

M= 230KNm =230000000N/mm

N= 798KN= 798000N

A= 900cm²= 90000mm²

W=4500cm³= 4500000mm³

Sigma_c= N/A= 798000/90000= 8,9N/mm²

Sigma_f= M/W= 230000000/4500000= 51N/mm²

f_cd= 0,8x21/1,5= 11,2N/mm²

f_fd= 0,8x24/1,5= 12,8N/mm²

Sigma_c/f_cd+Sigma_f/f_fd < 1 => 6,7/11,2+51/12,8 < 1 => 4,6 < 1

Non verificata la sezione deve essere aumentata, con una sezione 30x60 il valore viene verificato. 

 

 

Per quanto riguarda la verifica alla spinta del vento si vanno a calcolare i carichi distribuiti sui pilastri.

CLS e LEGNO

0,5KN/m² x 5m= 2,5KN/m x 0,8= 2KN/m parete in pressione

0,5KN/m² x 5m= 2,5KN/m x 0,4= 1KN/m parete in depressione

ACCIAIO

0,5KN/m² x 8m= 4KN/m x 0,8= 3,2KN/m parete in pressione

0,5KN/m² x 8m= 4KN/m x 0,4= 1,6KN/m parete in depressione

Inseriti i carichi distribuiti si va a creare una combinazione di carico del vento x e uno per il vento y.

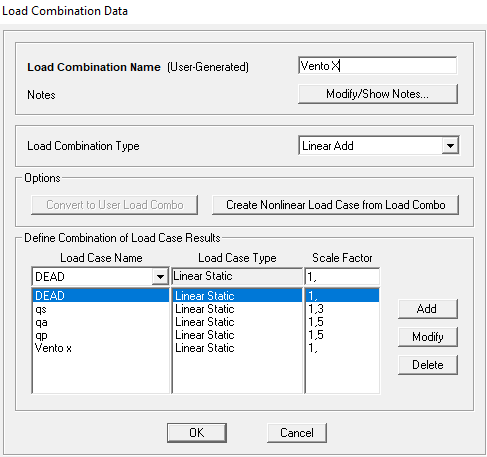
Una volta create le combinazioni di carico, ho cercato di calcolare le tabelle, ma non so per quale motivo queste non vengono fuori, come se la mia combinazione di carico sia nulla. Per questo problema non sono riuscito a verificare il telaio sotto l'azione del vento.

Palombo Giustino. 

Realizzata con Lucrezia Rodriguez.

In allegato il commento in pdf e gli excel usati per la verifica

L'esercitazione è stata svolta in collaborazione con Fabiana Rasile e Filippo Merlani.