Analisi di tre tipologie di struttura ad arco.
Abbiamo analizzato diverse tipologie di strutture ad arco, dove sono stati creati e messi a confronto tre sistemi strutturali vincolati in egual modo, dove l’unico elemento che cambiava era la forma.
Uno è l’arco parabolico, uno l’arco a tutto sesto e arco ribassato.
Gli archi sono tutti definibili come archi a tre cerniere. L’unico elemento quindi, che li contraddistingue , e dunque li fa lavorare diversamente, è la loro forma.
Essendo tutti archi, tutti e tre rispondono ai carichi verticali per compressione più che per flessione.
Lavorano quindi come strutture spingenti, esercitando cioè la cosiddetta forza di spinta nella sezione in chiave.
La forza di spinta è data da una formula parametrizzata, pari a:
H= ql^2/2f
Da cui si capisce bene che i parametri da cui dipende la forza di spinta sono la luce l e la freccia f.
La formula spiega come, da una relazione di luce e freccia dell’arco è possibile ricavare la forza centrale che fa perno sulla sommità dell’arco , la quale, in assenza di vincoli rischia di provocare dunque una possibile perdita di forma e dunque una deformata.
Ma ciò non accade, perché la controspinta delle cerniere all’imposta dell’arco esercita una forza uguale e contraria a quella in sommità, impedendole di sbilanciare la struttura.
Per svolgere l’esercitazione su SAP, sono stati seguiti degli step.
Innanzitutto il disegno dell’arco realizzato su autocad , uno per ogni tipo di arco, tutti spezzati in chiave.
Essi sono stati successivamente riportati in SAP , dove sono seguite le seguenti fasi in tutti e tre i casi:
-Rilascio dei momenti nel punto centrale interno all’arco
( assign --> frame --> release partial fixity --> spunta sulla casella m3-3 peima start , poi end , in due riprese differenti, questo dopo aver selezionato i due segmenti ai lati del punto di chiave in sommità uno per volta)
-Impostazione dei vincoli cerniere all’imposta dell’arco ( seleziono punti di imposta -->assign -->joint -->restraints-->selezione del vincolo cerniera.)
-Assegnazione del materiale e delle caratteristiche di sezione
( Seleziono la struttura per intero --> assign --> frame --> frame section --> add new -->scelta del materiale concrete --> assegnazione base e altezza)
-Assegnazione del carico uniformemente distribuito di valore q=10KN/m (selezione completa dello schema strutturale-->assign --> frame loads--> distributed --> add new (carico self multiplier =0) , selezionare la spunta dal menù a tendina gravity pojected - assegnazione del valore nella stringa “load”)
-Avvio dell’analisi ( Run Analysis)
-Visualizzazione dei valori di sforzo assiale , taglio, momento flettente (show forces, frame)
-Verifica dei valori delle reazioni vincolari in cerniera
Di seguito gli screenshot delle varie fasi descritte in precedenza, affrontate per ogni tipo di arco :
Arco a tutto sesto :
l= f = r = 1 m
q=10 KN/m
H=ql^2/2f = (10 KN/m*1m)^2/2f =50 KN
ql ( reazione vincolare verticale cerniera all’imposta ) = 10 kN/m *1,00 m =10kN
 Rilascio momenti
Rilascio momenti
 Impostazione cerniere
Impostazione cerniere
 Impostazione sezione
Impostazione sezione

Forza uniformemente distribuita
 Configurazione deformata
Configurazione deformata
 Grafici sforzi assiali
Grafici sforzi assiali
Arco ribassato :
l = 3 m
f = 2 m
q=10 KN/m
H=ql^2/2f = (10 KN/m*1m)^2/2f =50 KN
ql ( reazione vincolare verticale cerniera all’imposta ) = 10 kN/m *1,00 m =10kN
Immagine 3d arco ribassato
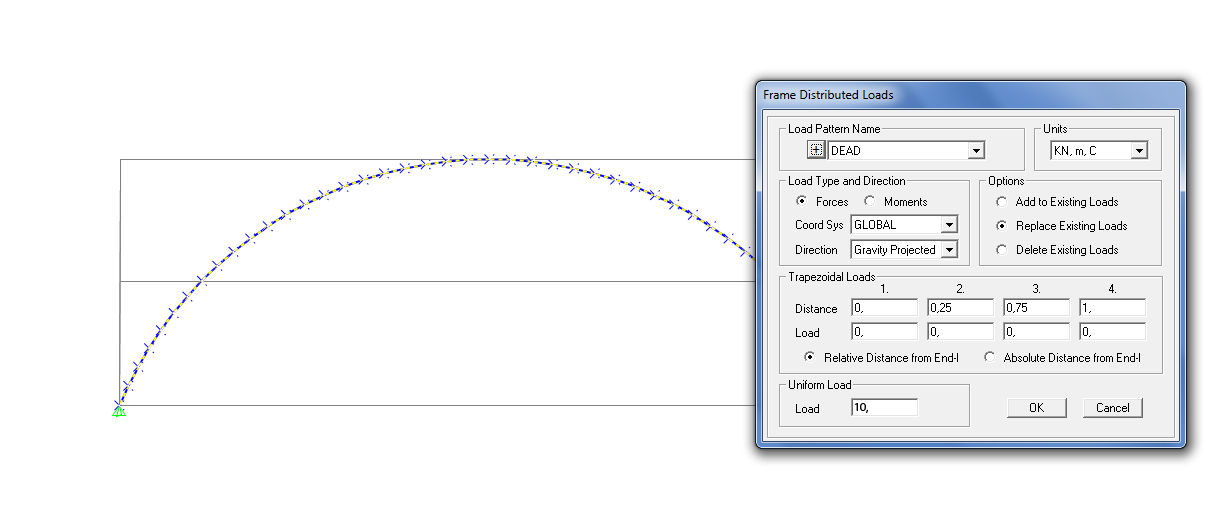
Arco ribassato applicazione carico uniformemente distribuito
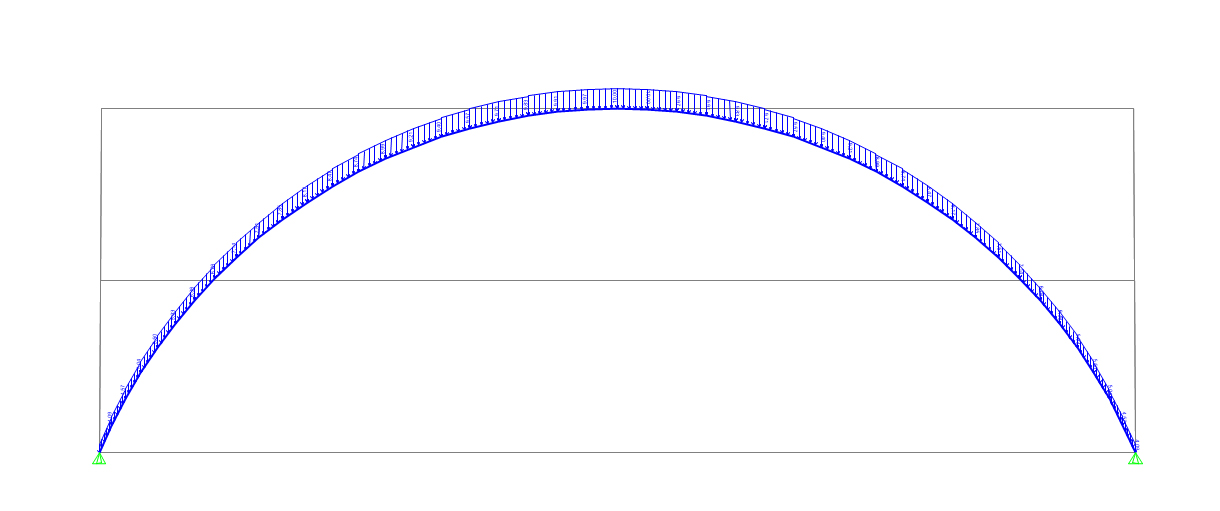
Arco ribassato con carico distribuito agente
 Arco ribassato deformata
Arco ribassato deformata

Arco ribassato grafici sforzo assiale
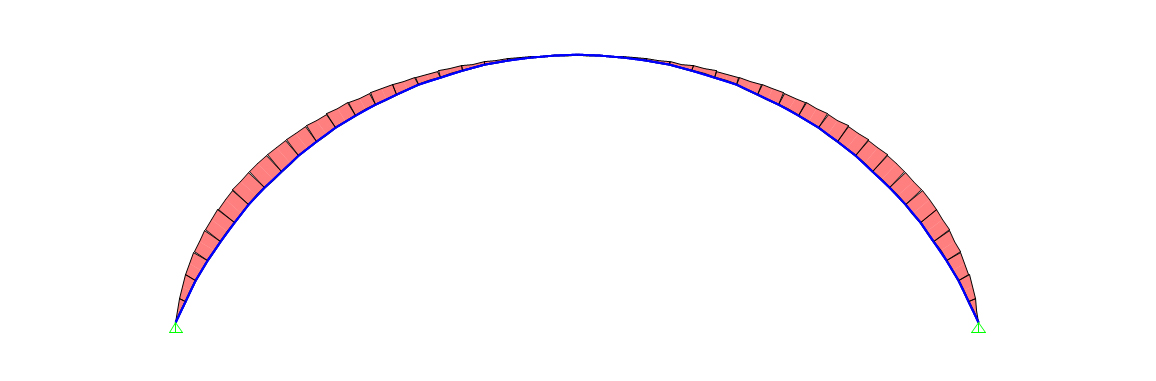
Arco ribassato grafici momento
Arco parabolico :
l = 2 m
f = 3 m
q=10 KN/m
H=ql^2/2f = (10 KN/m*3m)^2/2*3 = 150 KN
ql ( reazione vincolare verticale cerniera all’imposta ) = 10 kN/m *1,00 m =10kN
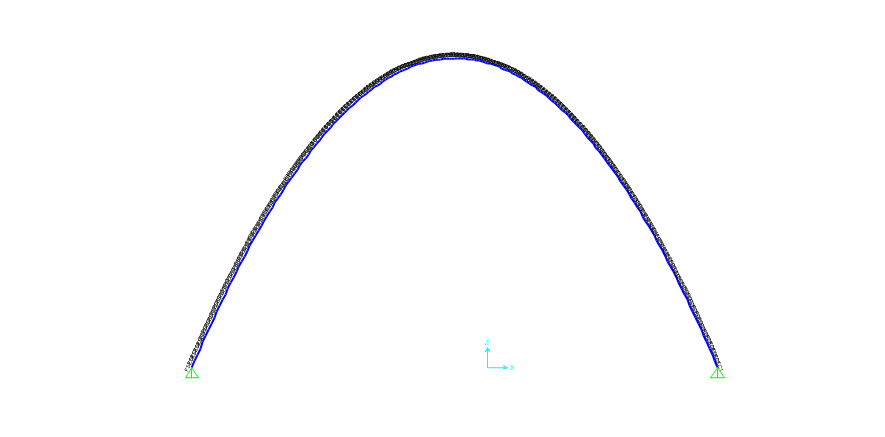
Arco parabolico sezione applicata
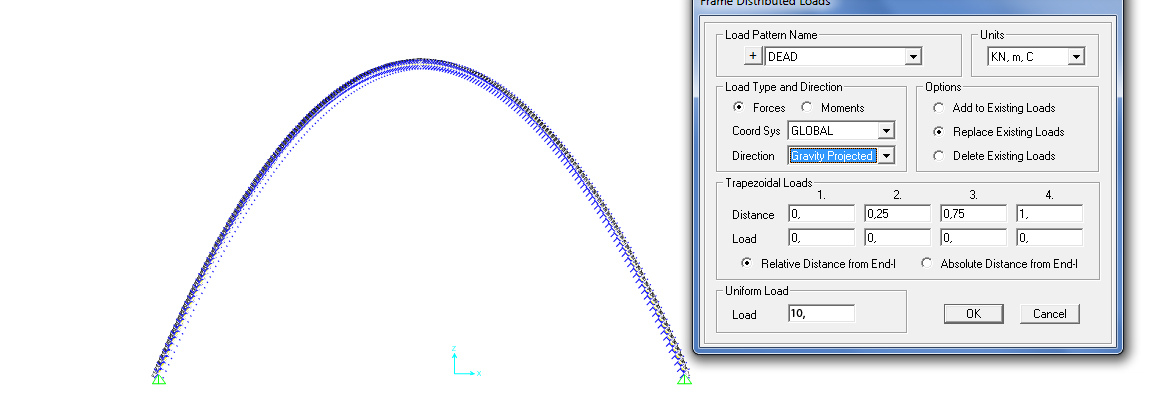
Arco parabolico carico uniformemente distribuito applicato

Arco parabolico deformata

Arco parabolico grafici sforzo assiale
Commenti recenti