Blog

Per poter resistere a forze sismiche, cioè orizzontali, è necessario che le strutture siano in qualche modo controventate, e in generale ogni telaio dell'edificio rappresenta un controvento. In questo caso i telai sono di tipo Shear-type, modello teorico ideale di telaio, dove i nodi sono tutti incastri e la trave è infinitamente rigida (molto resistente a flessione) con momento di inerzia maggiore di quello dei pilastri: essa prende la maggior parte del momento e del taglio. La deformata vedrà quindi la trave soggetta solo a traslazione orizzontale rigida (con solo spostamento) e non a deformazione assiale, e avendo rotazione nulla all'incastro essa "trascinerà" i pilastri che quindi si deformeranno in quanto soggetti a flessione.

Alla forza orizzontale che agisce sull'impalcato (che diventa corpo rigido piano), il telaio reagirà con altrettante forze orizzontali, cioè i tagli che nascono in corrispondenza di ogni pilastro. Il legame che sussiste tra il taglio in quel punto e lo spostamento della trave è la rigidezza k del controvento. In corrispondenza di ogni controvento della struttura è perciò rappresentata una molla, che indica la rigidezza di ogni controvento della struttura.

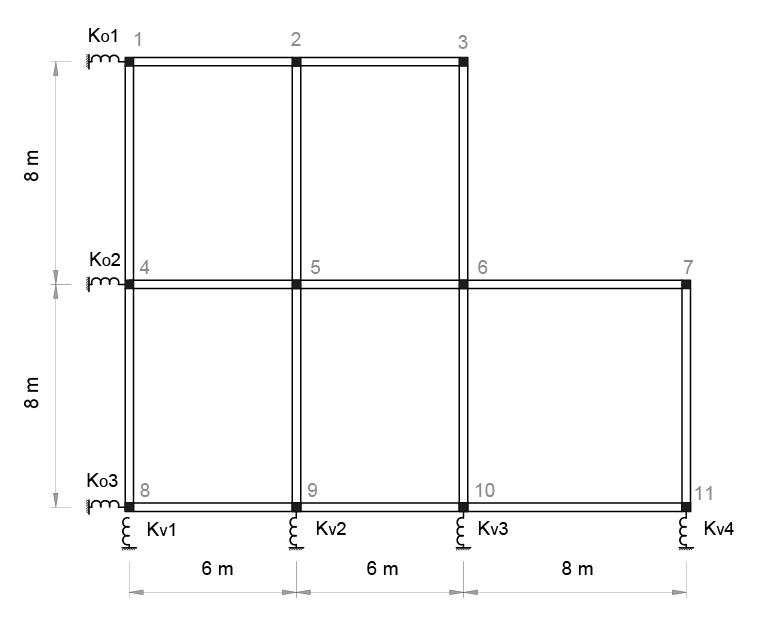Decisa l'altezza dei pilastri pari a 4 m e la loro sezione pari a 40 cm x 40cm, e il materiale, ( c.a.), con il supporto di un foglio excel si determina il centro delle rigidezze del telaio e la ripartizione delle forze sismiche.

STEP 1: si calcolano le rigidezze traslanti dei controventi dell'edificio analizzando telaio per telaio. Si inseriscono quindi i valori di E, H, I, e ottengo la rigidezza di ogni telaio.

E, modulo di elasticità del c.a. con classe di resistenza C 25-30 è pari a 31500 MPa (N/mm²)

H = 4 m

I = bh³/12= 213333 cm⁴

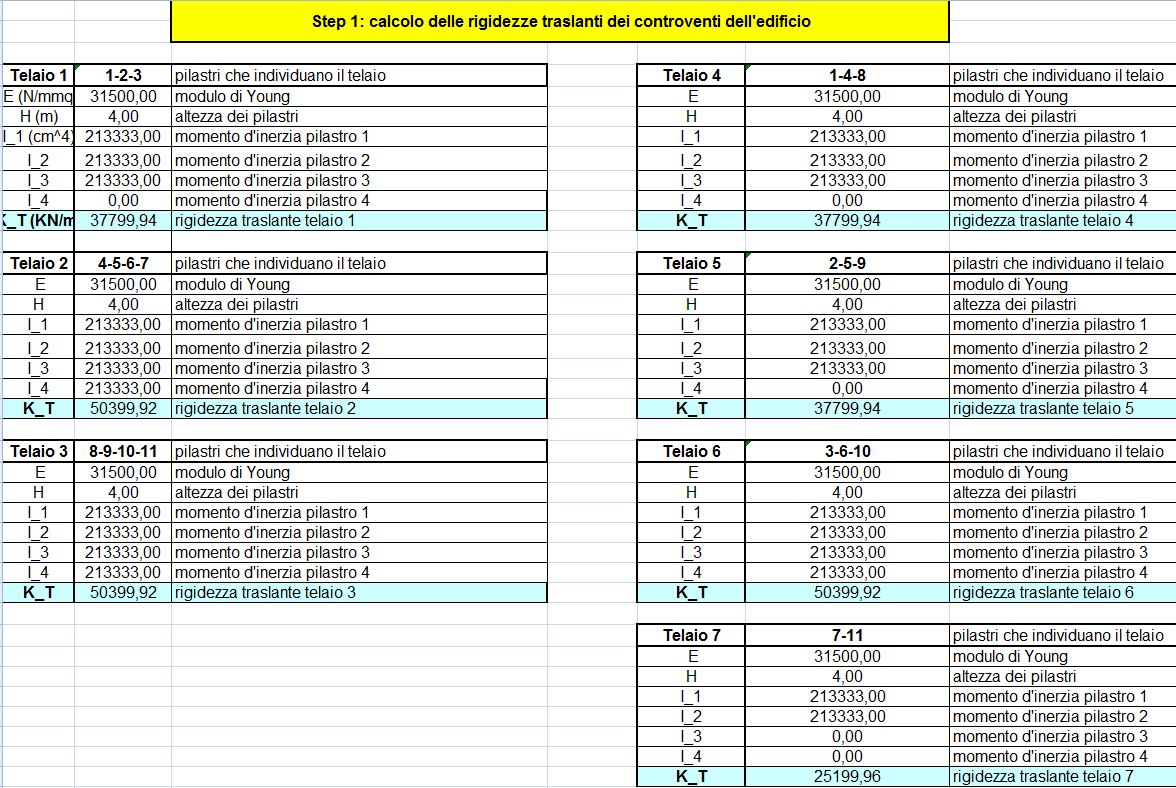
STEP 2: la tabella mostra tutte le rigidezze dei vari controventi, e le loro distanze dal punto di origine , cioè in corrispondenza del pilastro 8.

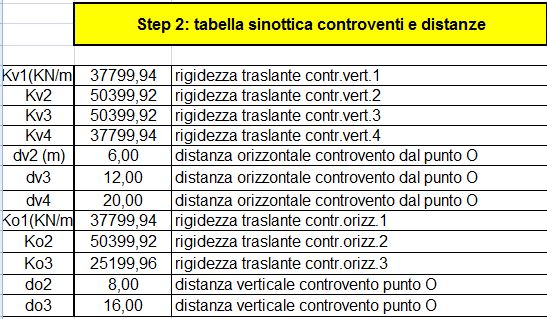
STEP 3:  calcolo delle coordinate del centro delle masse (baricentro, dove "confluiscono" le forze esterne applicate alla struttura). Si suddivide l'area totale dell'impalcato in aree più piccole, di cui si calcolano i singoli centri di massa, ottenendo poi le coordinate del centro di massa dell'intera struttura.

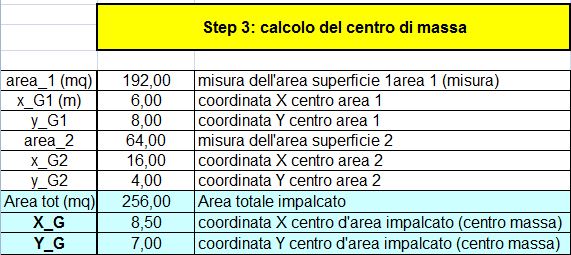
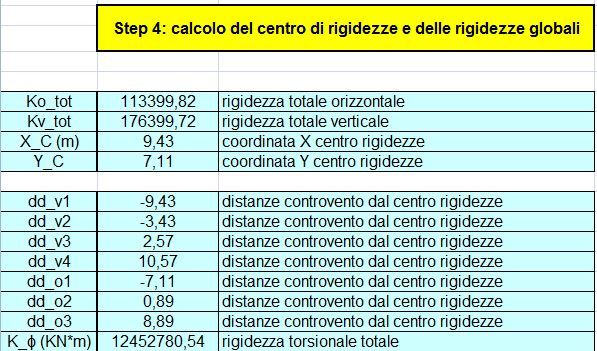
STEP 4:  calcolo delle coordinate del centro delle rigidezze

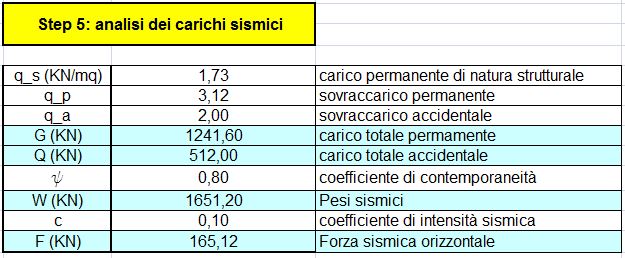
STEP 5:  dati i carichi di un solaio in c.a. (presi dalla scorsa esercitazione) e moltiplicati per l'area dell'impalcato si ottengono G e Q totali sulla struttura. Essi si moltiplicano per il coeff. di contemporaneità ottenendo i pesi sismici W, da moltiplicare a loro volta per il coeff. di intensità sismica, ottenendo la forza sismica totale agente.

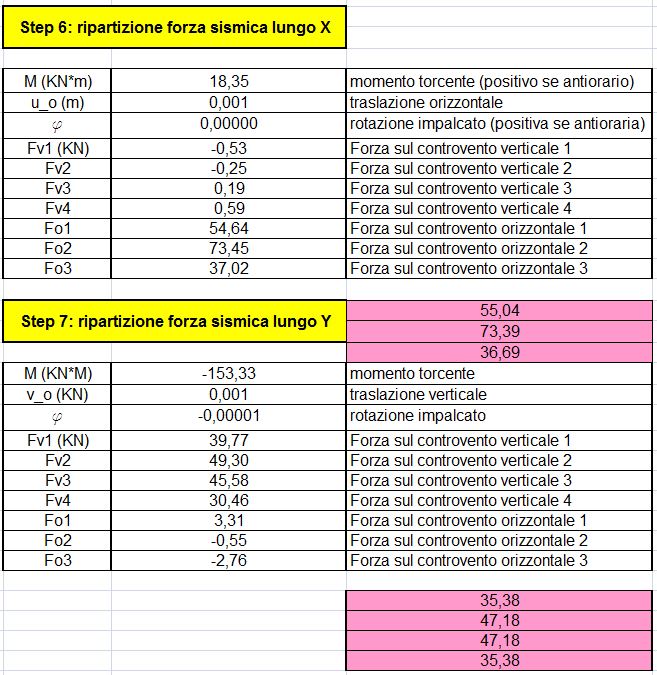
STEP 6-7:  si ottiene quindi la ripartizione delle forze sismiche Fx e Fy, il momento torcente Mx e My ricavati moltiplicando la forza sismica per la differenza tra le coordinate (le x per My e le y per Mx) del centro delle rigidezze e delle masse (quindi M_x= F(Y_C-Y_G) e M_y= F(X_C-X_G) ).

Lo spostamento traslante lungo la direzione x sul piano dove giace l'impalcato è pari a δ   ( da F= K x δ)

La rotazione dell’impalcato = Mx/ K_tot

Le forze su ciascun controvento si ricavano moltiplicando: rigidezza controvento * distanza dall’origine del controvento * rotazione impalcato.

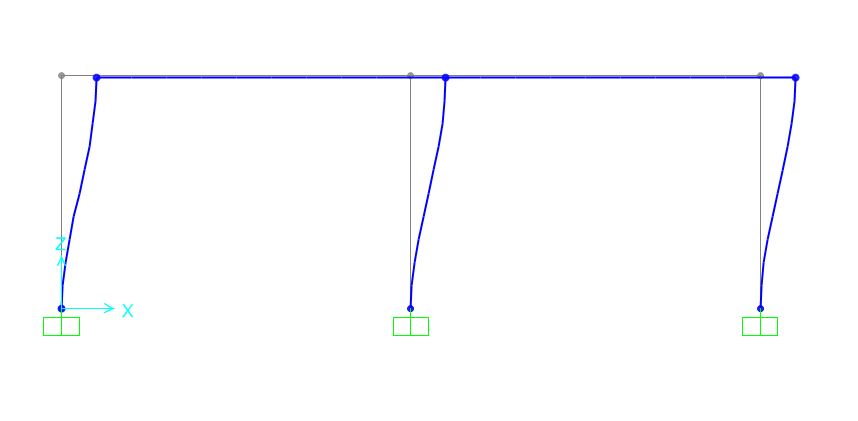
Si realizza la struttura su SAP per verificare la deformata e avere i valori delle sollecitazioni

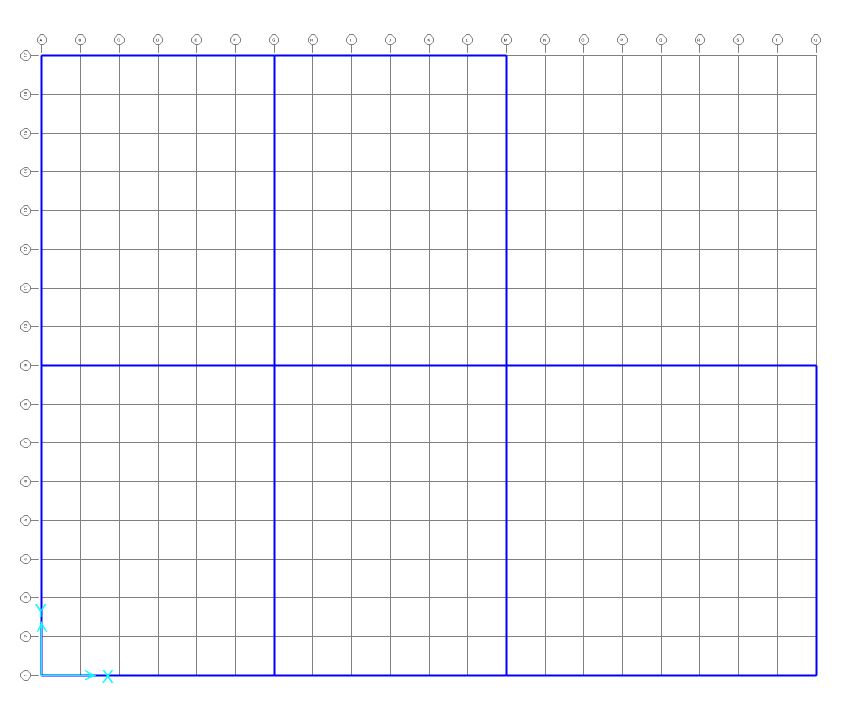
Attraverso lo strumento Grid Only realizzo una griglia di base su cui costruire i telai della struttura, e assegno poi vincolo di incastro alla base dei pilastri disegnati.

Si assegna poi la sezione dei pilastri e delle travi (per renderle idealmente infinitamente rigide vado ed aumentare il modulo E e l'altezza della sezione è anch'essa molto alta).

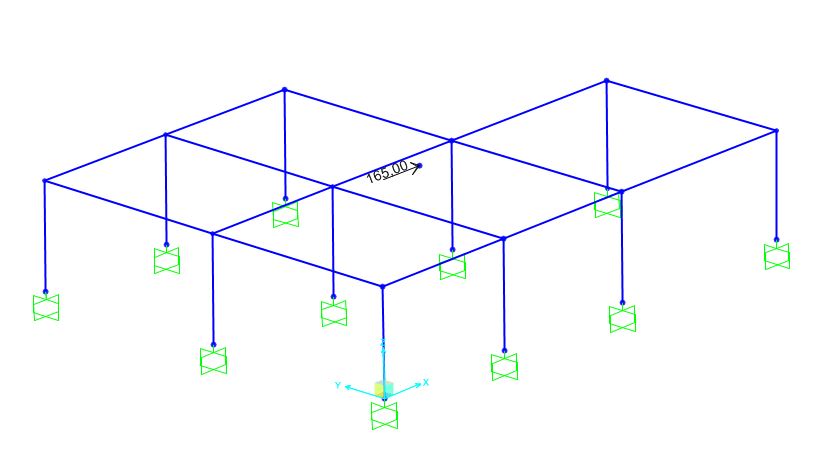
Si disegna poi il centro delle masse sul piano dell'impalcato dato dalle coordinate calcolate prima in excel.

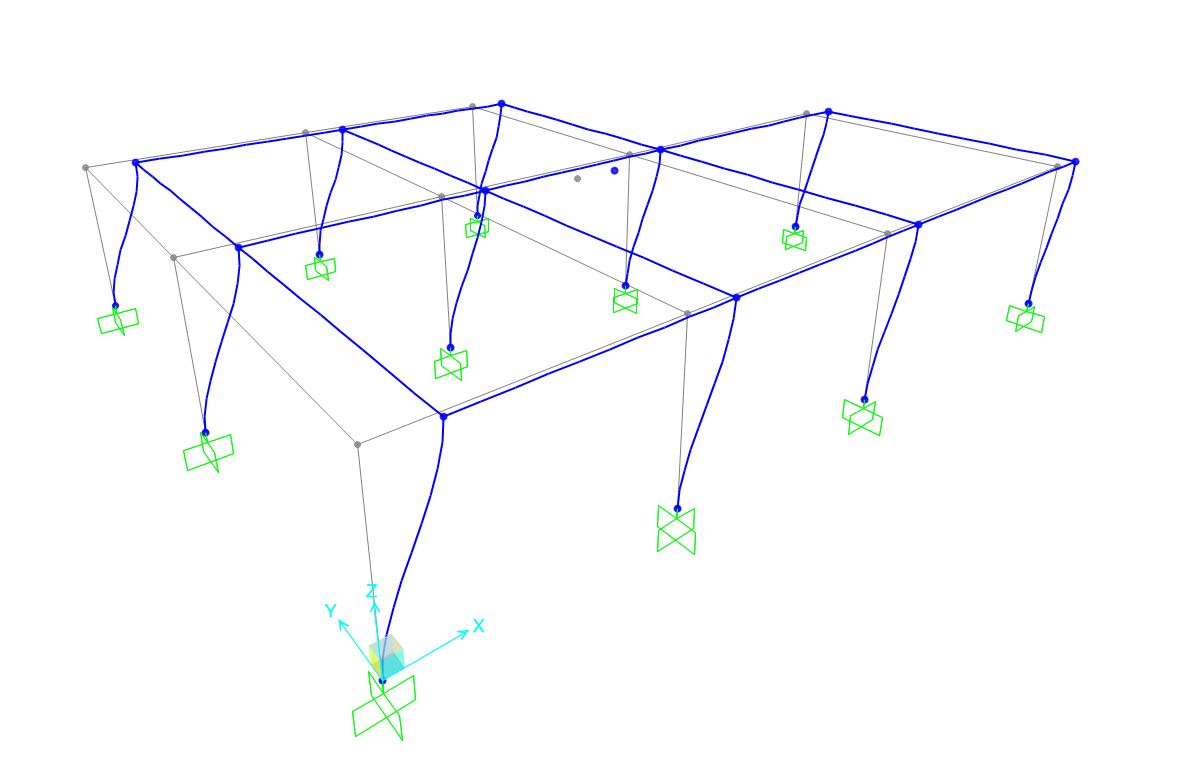
Dopo aver impostato la forza sismica agente sul centro delle rigidezze si ottiene la deformata classica del modello di telaio shear-type, dove ogni punto del piano orizzontale del solaio trasla orizzontalmente. Si nota anche una leggera rotazione dell'impalcato, dovuta al fatto che il centro delle masse non coincide precisamente con il baricentro della strutttura

EXE3_VERIFICA ABBASSAMENTO TRAVE A SBALZO:

Con riferimento alla pianta strutturale (sopra disegnata) di un solaio nel quale sono presenti delle travi a sbalzo e ipotizzandone tre tecnologie, siano esse: legno – acciaio – c.l.s. armato, verifichiamo, con quest’esercitazione, l’abbassamento della trave predisposta al sostenimento di tale sbalzo, in riferimento al rapporto di verifica che ci dice: abbassamento < luce_sbalzo/250.  

Consideriamo un interasse di 500 cm e una luce di 300 cm.

Con riferimento alle tecnologie scelte per l’EXE2, in precedenza postata, consideriamo che nel caso di trave incastrata, da un lato, e con un estremo libero, dall’altro (la così detta mensola), il momento flettente M è pari a ql²/2.

Tipologia di LEGNO: 

Utilizzo un tipo di legno lamellare con un modulo di resistenza a flessione (f_m,k) pari a 24 N/mm², e un modulo di elasticità (E) pari a 8000 N/mm², avremo: 

Il dimensionamento risulta corretto e il rapporto: abbassamento < luce_sbalzo/250 è verificato.

Tipologia di ACCIAIO: 

Utilizzo un valore pari a 275 N/mm² per la tensione/resistenza caratteristica di snervamento dell’acciaio (f_y,k), e  un modulo di elasticità (E) pari a 210000 N/mm², avremo:

Alla fine scegliamo una IPE400, della quale consideriamo:

Peso = 66,3 Kg/m

Momento d’inerzia (Jx) = 23130,0 cm⁴

Il dimensionamento risulta corretto e il rapporto: abbassamento < luce_sbalzo/250 è verificato.

Tipologia di C.L.S armato: 

Utilizzo modulo di resistenza a flessione (f_c,k) pari a 40 N/mm² ,della classe di resistenza del calcestruzzo ordinario C32/40, e un modulo di elasticità (E) pari a 21000 N/mm², avremo: 

Il dimensionamento risulta corretto e il rapporto abbassamento < luce_sbalzo/250 è verificato.

                                                                           - fine -

                                                                               A.

L'ARCO

Prendiamo in considerazione 3 archi: arco a tutto sesto, arco ribassato e arco parabolico.

Mantenendo la stessa luce di 6 metri e lo stesso carico, facciamo variare la freccia.

1. Arco a tutto sesto: L=6m; f=3m
2. Arco ribassato: L=6m; f=1,5m
3. Arco parabolico: L=6m; f=6m

In questo modo dovremmo capire meglio i comportamenti dei 3 archi. Dai risultati si dovrebbe evincere come un arco più è ribassato, più è “arco”. Infatti, gli archi lavorano prevalentemente a sforzo normale ed è l’arco ribassato che prende i carichi e li trasforma maggiormente in sforzi normali.

Per studiare il comportamento dei 3 archi, utilizziamo SAP. Disegniamo su Autocad 3D o Rhinoceros l’arco ed importiamolo in formato dxf su SAP.

Dopo averlo importato, speziamo l’arco nella sezione di chiave e facciamo il rilascio dei momenti in chiave a applichiamo un carico distribuito pari a 10KN.

1. ARCO A TUTTO SESTO:

L'arco a tutto sesto o semicircolare è un tipo di arco contraddistinto da una volta a semicerchio. È la tipologia più semplice di arco e prevede che il centro verso il quale convergono i giunti si trovi sulla linea d'imposta, cioè su quella linea che unisce i punti dove finiscono i sostegni e inizia l'arco.

Si avrà questa deformata:

Le reazioni vincolari saranno:

Il grafico degli sforzi assiali:

Il grafico dei momenti:

2. ARCO RIBASSATO:

Un arco si dice ribassato quando il centro verso il quale tendono i giunti dei cunei si trova più in basso della linea d'imposta.

Si avrà questa deformata:

Le reazioni vincolari saranno:

Il grafico degli sforzi assiali:

Il grafico dei momenti:

3. L'ARCO PARABOLICO:

Si avrà questa deformata:

Le reazioni vincolari e il grafico degli sforzi assiali saranno:

CONCLUSIONE

Se osserviamo i grafici degli sforzi normali possiamo dedurre:

Arco a tutto sesto:

• All’imposta: N=30,38 KN
• In chiave: N=15 KN

Arco ribassato:

• All’imposta: N=42,15 KN
• In chiave: N=30 KN

Arco parabolico:

• All’imposta: N=7 KN
• In chiave: N=30,92 KN

Per quanto riguarda le reazioni vincolari si può facilmente vedere come la struttura più spingente sia l’arco ribassato, infatti la reazione vincolare orizzontale è 30KN, mentre quella dell’arco a tutto sesto è 15KN (la metà), e quella dell’arco parabolico è 7,50KN (un quarto). Praticamente l’arco ribassato ha una spinta doppia rispetto all’arco circolare ed ha sforzo normale maggiore.

30KN>15KN>7,50KN

Dai grafici dei momenti si può vedere come l’arco ribassato ha più sforzo normale e quindi meno momento flettente rispetto all’arco circolare.

Studiamo su SAP il comportamento di tre tipi di archi prima modellati su rhinoceros poi importati come .dxf

L'arco fa parte di quel gruppo di strutture che reagisce alle forze esterne per FORMA. Sono strutture ottimizzate in quanto tendono a lavorare solamente a sforzo normale e questa caratteristica permette un'ottimizzazione del materiale al contrario delle strutture inflesse.

Per comportamento ad arco si intende una situazione in cui una struttura sottoposta a un carico esterno distribuito reagisce prevalentemente tramite sforzo normale, limitando taglio e momento che in alcuni casi sono nulli.

Per assurdo maggiore è l'altezza di un arco, minore è il suo comportamento ad arco in quanto diminuisce la spinta orizzontale e la struttura tende ad aumentare i valori di taglio e momento, avvicinandosi al comportamento di una trave inflessa. Al contrario si potrebbe pensare che un arco più è ribassato più si accivina al comportamento di una trave che resiste alla flessione tramite il momento d'inerzia della sua sezione, invece proprio in questi casi tendono ad abbassarsi o annullarsi i valori di taglio e momento lasciando la struttura con una compressione pura.

Questo ragionamento è espresso dalla formula della spinta orizzontale:

ql^2/2f, dove f è l'altezza dell'arco (imposta>chiave). Più cresce f minore sono la spinta orizzontale e il comportamento ad arco (le forze esterne saranno distribuite all'interno della struttura anche tramite taglio e momento). Più diminuisce f maggiore sono la spinta orizzontale e il comportamento arco (le forze esterne saranno distribuite all'interno della struttura prevalentemente tramite sforzo normale, rendendo nulli o quasi taglio e momento).

ARCO A TUTTO SESTO

ARCO PARABOLICO

ARCO CIRCOLARE RIBASSATO

Inserisco all'interno del foglio excel i dati della mia struttura,cercando di individuare il centro delle rigidezze.Una volta ottenuti i dati necessari verifico attraverso SAP il comportamento della mia struttura a seguito di una forza sismica 

Modifico il momento D'inerzia delle travi iper aumentarne la rigidezza

l'obiettivo di questa esercitazione è il calcolo del centro delle rigidezze di un telaio shear-type tramite l'uso di un foglio excell e la successiva verifica con SAP

il telaio è composto da pilastri di sezione 30x30 e da travi di sezione 30x60

all'interno della tabella sono stati inseriti il modulo di Young, l'altezza e il momento di inerzia dei pilastri, la rigidezza totale dei telai

le tabelle 3, 4 e 5 mostrano il calcolo del centro di massa e del centro delle rigidezze di tutta la struttura e la forza sismica orizzontale F da applicare al al centro delle rigidezze nella verifica su SAP

inserisco la struttura su SAP

dopo aver attribuito la sezione alle travi e ai pilastri, aggiungo tanti zeri al momento di inerzia per aumentare la rigidezza delle travi

trovo la posizione del centro delle rigidezze e per dare continuità alla struttura assegno il comando diaphragm, applico poi la forza sismica orizzontale F trovata con il foglio excell

ottengo la seguente deformata

la struttura sottoposta alla forza sismica trasla lungo l'asse dell'applicazione della forza ma non ruota    

Arco a tutto sesto:

Disegno un cerchio su Autocad lo taglio ed ottengo il mio arco, spezzo l'arco in chiave e dopo aver ruotato il mio arco in 3d di 90° lo salvo con il formato dxf2004.

Lo importo su Sap

1.assegno alle imposte le cerniere.

2.Seleziono i due segmenti in chiave e gli assegno la cerniera interna con il comando Frame_Release.

3.Seleziono l'arco e gli assegno una sezione, in questo caso in CLS 30X30cm

4. Assegno un carico distribuito di 100KN/m selezionando il comando Gravity Projected 

5. ora posso avviare l'analisi attraverso il comando Run e vedere la deformata, i grafici di M,T,N e le reazioni vincolari

T:

M:

N:

Arco ribassato:

Disegno un cerchio su Autocad lo taglio ed ottengo il mio arco, spezzo l'arco in chiave e dopo aver ruotato il mio arco in 3d di 90° lo salvo con il formato dxf2004.

Lo importo su Sap 

1.assegno alle imposte le cerniere. 

2.Seleziono i due segmenti in chiave e gli assegno la cerniera interna con il comando Frame_Release.

3.Seleziono l'arco e gli assegno una sezione, in questo caso in CLS 30X30cm

4. Assegno un carico distribuito di 100KN/m selezionando il comando Gravity Projected 

5. ora posso avviare l'analisi attraverso il comando Run e vedere la deformata, i grafici di M,T,N e le reazioni vincolari

T:

M:

N:

Ripartizione delle forze sismiche

Scopo dell'esercitazione è quello di verificare il comportamente di un impalcato a seguito di una sollecitazione orizontale, identificabile come la forza del vento o di un sisma.

Si prende ad esempio una struttura regolare con pilastri di sezione 30 cm x 30 cm, con un'inerzia di I: 67500 cm⁴ (bh³/12) ed un modulo di elasticità di 24855 N/mm²

Il primo passo è quello di calcolare le rigidezze traslanti dei controventi orizontali e verticali dell'impalcato.

Si prosegue scrivendo il valore di ogni controvento e la sua distanza dall'origine.

Trattandosi di un telaio Shear-Type, i pilastri contribuiscono alla ripartizione del momento grazie alle travi "infinitamente" rigide.

Prossimo passo è quello di definire il centro di massa G. Andando a suddividere l'impalcato in sottoaree più facilmente gestibili, è possibile trovare le coordinate x e y del centro di massa.

Ora calcoliamo il centro delle rigidezze C dove si andrà ad applicare la forza orizontale. Le coordinate del centro sono date dalla somma delle rispettive rigidezze traslanti per la distanza dall'origine fratto la somma totale dei controventi dell'altra coordinata.

La rigidezza rotazionale Kϕ è data dalla somma di ogni rigidezza per la distanza dall'origine al quadrato.

Andando ad analizzare i carichi sismici si trova la forza F da applicare orizzontalmente all'impalcato. Ogni controvento prenderà momento in mase alla sua rigidezza: un controvento più rigido prenderà più momento.

Il foglio excell ci dice come sono ripartiti i carichi sismici lungo x e y rispetto alle rigidezze dei controventi orizontali e verticali.

Andando su SAP

Disegnamo il nostro telaio e poniamo degli incastri come vincoli alla base dei pilastri. Una volta definito la sezione dei pilastri (30 cm x 30 cm) e delle travi (50 cm x 30 cm), andiamo a modificare la rigidezza delle travi cercando di renderle infinitamente rigide andando ad aumentare il momento di inerzia in entrambe le direzioni.

Dopo aver posizionato il centro delle rigidezze con le coordinate precedentemente trovate, applichiamo il Diaphragm su tutti i punti di un livello dell'impalcato. Il Diaphragm è un vincolo interno alla struttura che lega tra di loro i punti selezionati.

Dopo aver posizionato la forza sismica di 86.40 KN sul centro delle rigidezze mandiamo in verifica la struttura. Avendo applicato la forza sul centro delle rigidezze l'impalcato presenta solo traslazione orizontale e nessuna rotazione. Gli altri valori non sono nulli per l'impossibilità di rendere infinitamente rigide le travi.

Andando ad applicare la forza sismica sul centro delle masse, possiamo vedere come l'impalcato tende a ruotare in proporzione alla sua distanza dal centro delle rigidezze.