Blog

Esercitazione_3 - Deformabilità di uno sbalzo

Inviato da Simona.Mazzei il Dom, 18/05/2014 - 09:03

DIMENSIONAMENTO DI UNA TRAVE A SBALZO PER SOLAIO IN LEGNO, ACCIAIO E CLS

Dopo aver dimensionato una trave appoggiata, passiamo al dimensionamento di una trave a sbalzo.

Per il dimensionamento della trave a sbalzo utilizzeremo le tre tecnologie descritte nell’esercitazione precedente sia per quanto riguarda il legno, che per quanto riguarda l’acciaio e il calcestruzzo armato.

Il solaio preso in considerazione ha come interesse 4 metri e luce dello sbalzo 3 metri. Questi 2 valori andranno inseriti nella tabella excel rispettivamente nella casella interasse e nella casella luce.

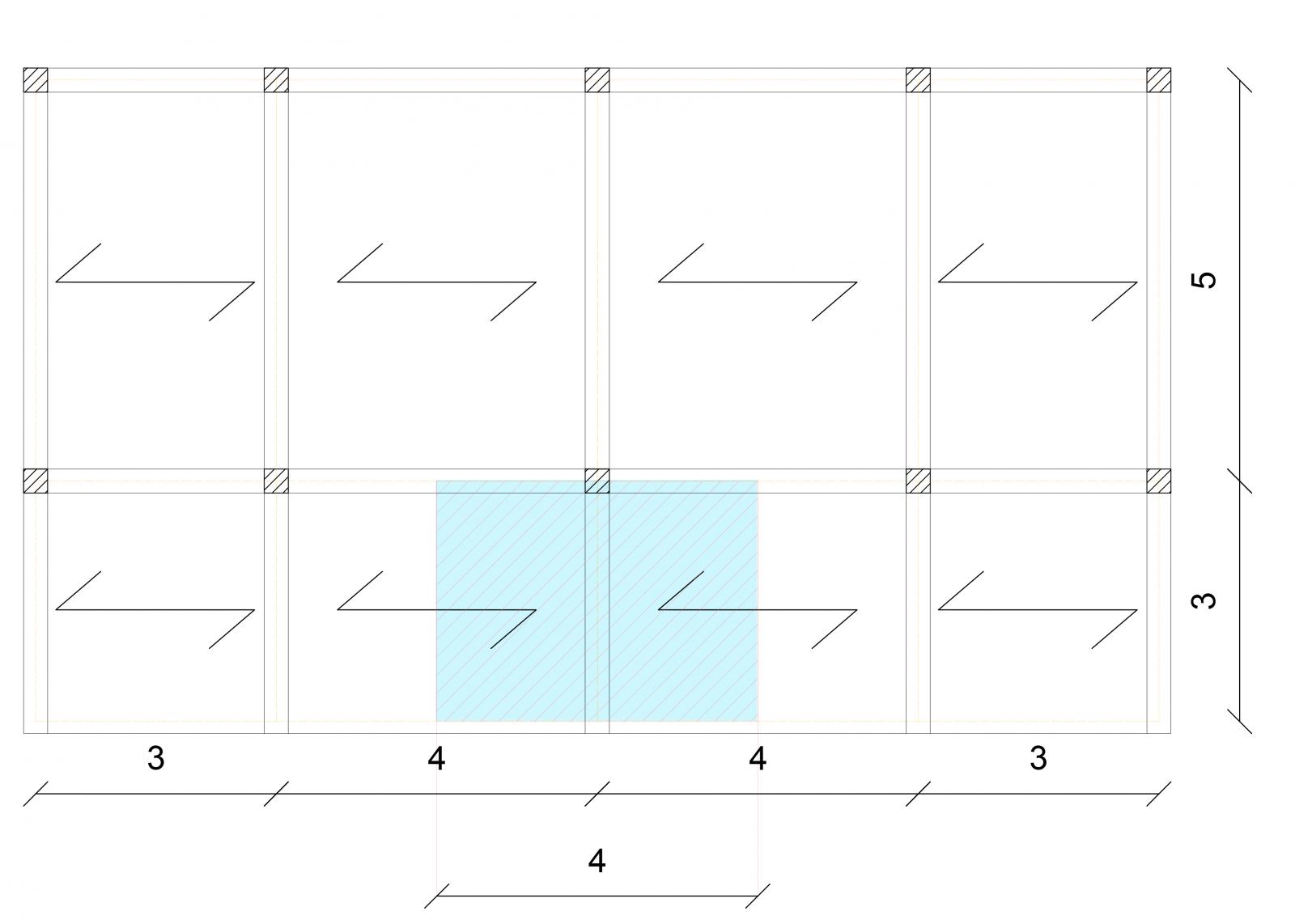
SOLAIO IN LEGNO

Prendo in considerazione il solaio in legno composto da:

Parquet

Travetto

Pilastrino in mattoni

Tavella in cotto

Massetto

Tavolato

Travetto

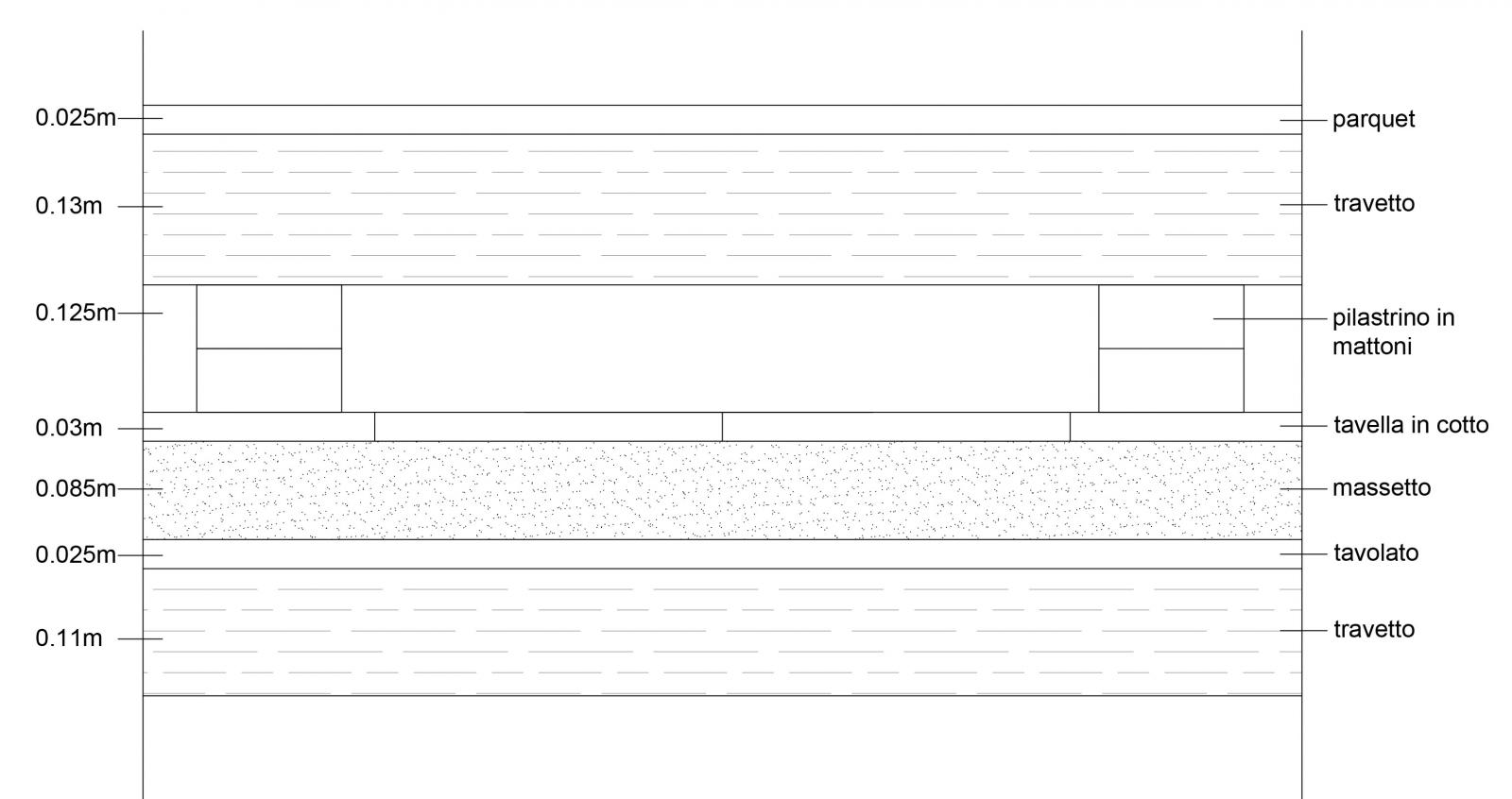
Ricordo che l’analisi dei carichi dava come risultati:

Carichi strutturali qs= 0,317 Kn/ m²

Carichi permanenti qp= 4,85 KN/m²

Carichi accidentali qa= 2KN/m² (ambiente ad uso residenziale)

Il carico q che ne uscirà fuori sarà la somma dei carichi precedentemente detti moltiplicati per dei coefficienti di sicurezza: 1,3 per i carichi strutturali qs e i carichi permanenti qp e 1,5 per i carichi accidentali qa.

Trattandosi di una trave a sbalzo, la tabella tiene conto del momento di una mensola M=ql²/2 (nell’esercizio precedente M=ql²/8 perché si trattava di una trave appoggiata) nel nostro caso pari a M= 174,91kNm

Come fatto nell’esercitazione precedente scegliamo il tipo di legno, in questo caso un legno lamellare GL 24h con resistenza a flessione fm,k = 24MPa, si troverà quindi la tensione ammissibile (sigma ammissibile). Impostando la base b=30cm si troverà l'altezza H= 51,40cm. Ingegnerizziamo la sezione portando l’altezza della nostra trave a 55cm.

Inserendo una trave di altezza 55cm avremo uno spostamento Vmax= 1,18cm, e la verifica per cui l/Vmax>250 risulta soddisfatta in quanto 253,66>250.

Adesso bisogna considerare il peso proprio della trave in modo tale da verificare se la trave appena dimensionata sia in grado di sopportare il peso proprio.

p= (0,30m x 0,55m x 1m)/m x 7KN/m³= 1,155 KN/m

Aggiungendo il peso proprio della trave la verifica l/Vmax>250 non risulta verificata. Possiamo quindi aumentare la sezione della trave, ricalcolare il peso proprio e reinserirlo nella tabella.

Prendiamo quindi una sezione di b=30cm e H=60cm

p= (0,30m x 0,60m x 1m)/m x 7KN/m³= 1,26 KN/m

Con una trave di altezza 60cm e base 30cm si riuscirà a superare lo sbalzo di 3m.

SOLAIO IN ACCIAIO

Prendo in considerazione il solaio in acciaio composto da:

pavimento

strato in cls alleggerito

getto in cls

lamiera grecata

trave secondaria IPE 180

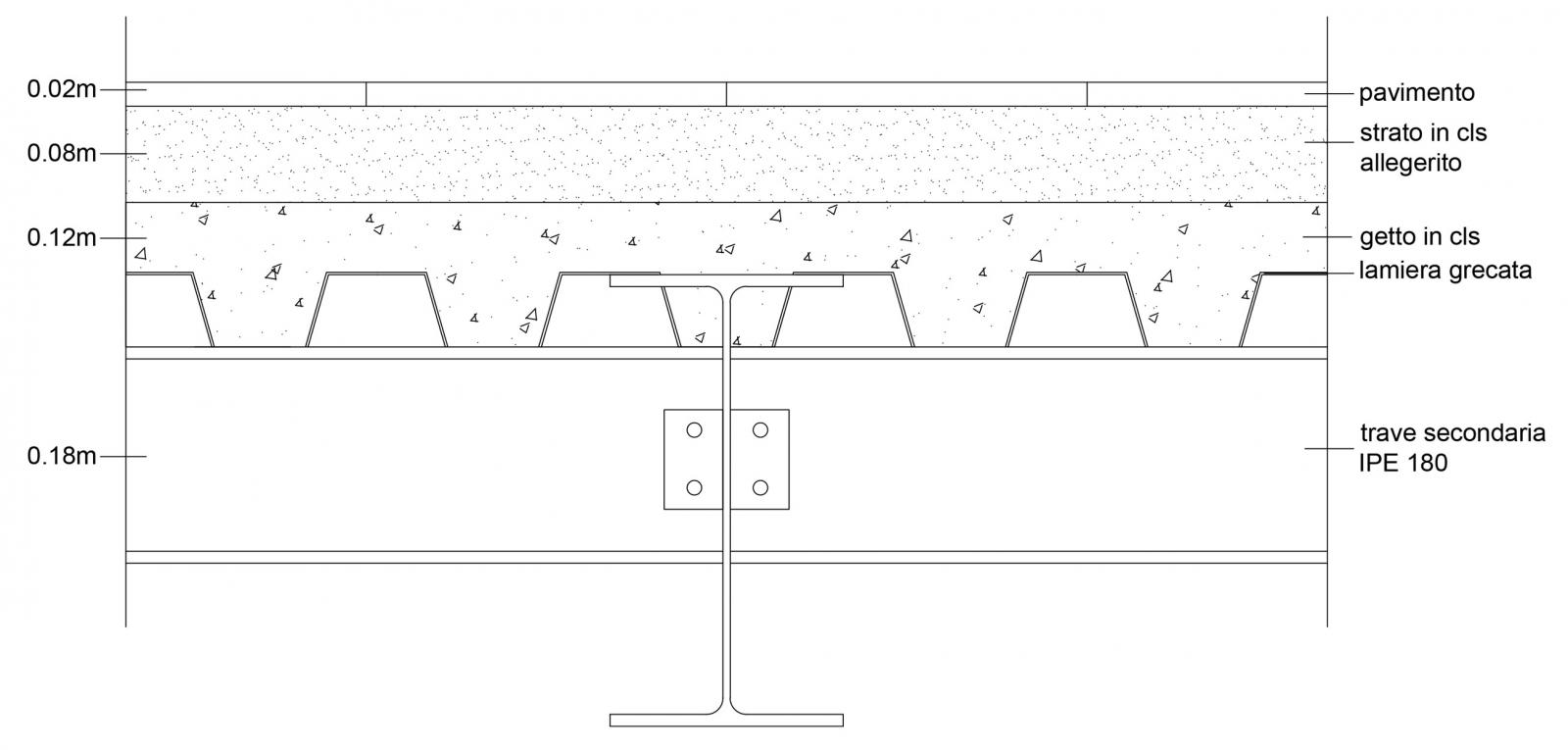
Ricordo che l’analisi dei carichi dava come risultati:

Carichi strutturali qs= 2,64KN/m²

Carichi permanenti qp= 3,48 KN/m²

Carichi accidentali qa= 2KN/m² (ambiente ad uso residenziale)

Il carico q che ne uscirà fuori sarà la somma dei carichi precedentemente detti moltiplicati per dei coefficienti di sicurezza: 1,3 per i carichi strutturali qs e i carichi permanenti qp e 1,5 per i carichi accidentali qa.

Trattandosi di una trave a sbalzo, la tabella tiene conto del momento di una mensola M=ql²/2 nel nostro caso pari a M= 197,21kNm

Per dimensionare la trave è necessario confrontare il modulo di resistenza Wx dato dalla tabella Excel con i moduli di resistenza dati dal profilario.

Possiamo quindi prendere come trave una IPE 360 con Wx=904cm³ e Ix=16270cm^4.

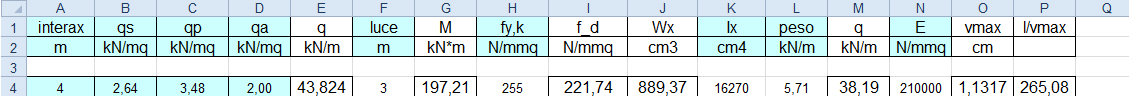
Inseriamo il peso proprio p della trave nella tabella Excel.

p= (0.00727m² x 1m)/m x 78,50 KN/m³=0,57 KN/m

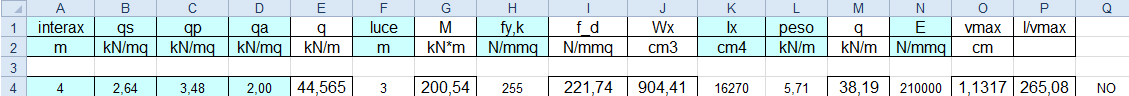
Il modulo di resistenza che ne risulta è di Wx= 904,41cm³ > 904cm³ dell’IPE 360. Devo quindi cambiare l’IPE scelta precedentemente.

Considero quindi un’ IPE 400 con peso proprio:

p= (0.00845m² x 1m)/m x 78,50 KN/m³=0,67 KN/m

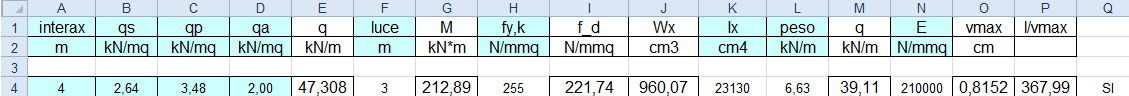
Il modulo di resistenza che ne risulta è di Wx= 960,07 cm³ < 1160cm³ dell’IPE 400. Inoltre l/Vmax>250 in quanto 367,99 > 250.

Con una trave IPE 400 si riuscirà a superare lo sbalzo di 3m.

SOLAIO IN CLS

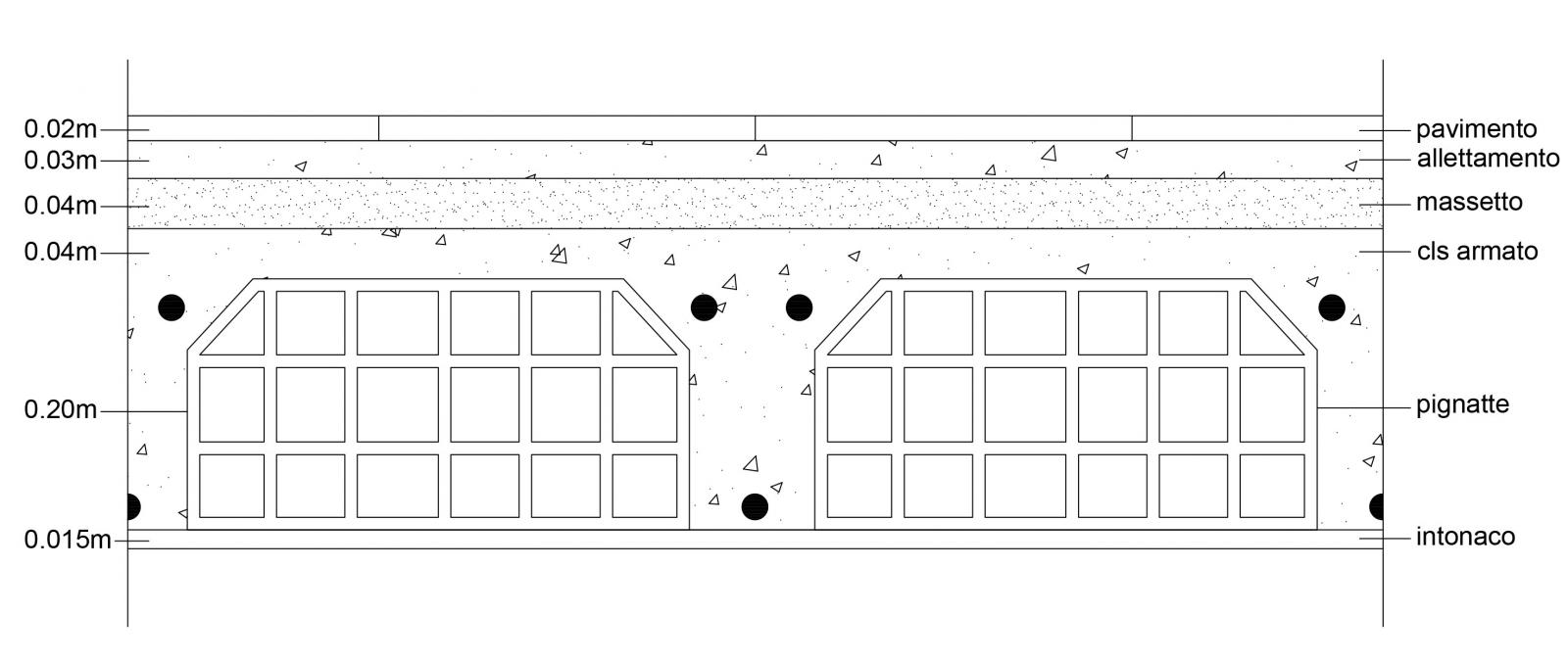
Prendo in considerazione il solaio in cls composto da:

pavimento

allettamento

massetto

cls armato

pignatte

intonaco

Ricordo che l’analisi dei carichi dava come risultati:

Carichi strutturali qs= 3,91 KN/m²

Carichi permanenti qp= 3,63 KN/m²

Carichi accidentali qa= 2KN/m² (ambiente ad uso residenziale)

Il carico q che ne uscirà fuori sarà la somma dei carichi precedentemente detti moltiplicati per dei coefficienti di sicurezza: 1,3 per i carichi strutturali qs e i carichi permanenti qp e 1,5 per i carichi accidentali qa.

Trattandosi di una trave a sbalzo, la tabella tiene conto del momento di una mensola M=ql²/2 nel nostro caso pari a M= 230,43KNm

Per le armature scelgo una resistenza caratteristica fyk=450 MPa mentre per il cls prendo C 40/50 con resistenza caratteristica a compressione Rck=50Mpa. Quindi con una base b=30cm, avrò un'altezza H=40,29cm. Ingegnerizziamo quindi la sezione portandola ad un'altezza H=45cm.

Sia p il carico proprio della trave.

p = (0,30m x 0,45m x 1m)/m x 25KN/m³ = 3,375 Kn/m

Avremo quindi una sezione di altezza H=41,77cm < 45cm. Inoltre l/Vmax>250.

Con una trave di altezza 45cm e base 30cm si riuscirà a superare lo sbalzo di 3m.

SdC(b) (LM PA)

Esercitazione

Es3_Verifica a deformabilità di una mensola

Inviato da laura.carlomagno il Dom, 18/05/2014 - 08:18

Esercitazione_Equazione della linea elastica

Inviato da laura.carlomagno il Dom, 18/05/2014 - 07:55

Esercitazione

ESERCITAZIONE 3: DEFORMABILITA' DI UNA MENSOLA.

Inviato da Giovanni.Saja il Sab, 17/05/2014 - 19:31

Considerato un telaio con uno sbalzo di luce pari a 3.00 m e interasse uguale calcolo il carico che agisce sulla trave più sollecitata verificando che la deformabilità della trave sia inferiore a 1/250 della sua luce. Si consideri come carichi strutturali , permanenti e accidentali i valori dell'esercitazione precedente nelle tre diverse tecnologie.

SOLAIO IN LEGNO

Qs=0,2 KN/mq; Qp=2,07 KN/mq; Qa=3,00 KN/mq

Lo sbalzo è verificato per una trave di 35x 45 cm in sezione.

SOLAIO IN ACCIAIO

Qs= 2,24 KN/mq; Qp= 3,54KN/mq; Qa=3,00KN/mq

Dal calcolo emerge che, rispetto al modulo di resistenza a flessione, il momento d'inerzia e il peso della trave ipotizzata non è sufficente a reggere lo sbalzo. Si procede allora considerando in tabella il valore immediatamente superiore sostituendo il momento d'inerzia e il peso della trave.

Lo sbalzo è verificato con una trave IPE 360.

SOLAIO IN CLS ARMATO.

Qs=1,50KN/mq; Qp=2,63KN/mq; Qa=6,00KN/mq

Dal calcolo inserendo la resistenza delle armature e la classe di resistenza del calcestruzzo emerge che lo sbalzo è verificato per una trave di 30x40 cm in sezione.

SdC(b) (LM PA)

Esercitazione

Esercitazione n°4 | Calcolo del centro di rigidezza

Inviato da Maria Luisa Regalo il Sab, 17/05/2014 - 17:02

La prima parte della quarta esercitazione analizza e mette al confronto il comportamento di una struttura simmetrica, sia dal punto di vista geometrico, che da quello meccanico, con una struttura simmetrica solo dal punto di vista geometrico.

STRUTTURA SIMMETRICA SIA GEOMETRICAMENTE CHE MECCANICAMENTE

La struttura costituita da travi e pilastri è vincolata a terra mediante degli incastri (FIG.01), le travi invece sono collegate ai pilastri con cerniere interne (FIG.02) e l'impalcato è rigido, in grado di ruotare solo intorno all'asse z (FIG.03).

Una volta che abbiamo assegnato la sezione (quindi anche il materiale) alle travi e ai pilastri, applichiamo una forza orizzontale pari a 100kN nel centro geometrico della struttura, che corrisponde anche al centro meccanico, poichè tutti i pilastri hanno la stessa rigidezza k=12EI_x/h³.

Dato che la forza è applicata sull'asse centrale delle rigidezze vi sarà una traslazione u che per la legge di Hooke è pari a u= F/k. (FIG.04)

F=100/3 kN= 33,33

k= 12 24855578 0,000675/ 27=7456,67 KN/m

u= 33,33kN/7456,67 kN/m = 0,0045 m

STRUTTURA SIMMETRICA SOLO GEOMETRICAMENTE

La struttura in FIG.06 resta simmetrica da un punto di vista geometrico, ma non lo è più dal punto di vista meccanico poichè la rigidezza, che dipende dal momento di inerzia della sezione, è maggiore nei pilastri rossi rispetto alla rigidezza dei pilastri blu. Ciò comporta uno spostamento dell'asse delle rigidezza verso i pilastri rossi; in questo modo la forza non è più applicata nel centro delle rigidezze e ciò determina un momento esterno generato dalla forza orizzontale F.

La deformata di questa struttura non sarà il risultato di una sola traslazione, ma dell'azione congiunta di una traslazione ed una rotazione (FIG.07).

Intuitivamente immaginiamo che i pilastri più rigidi sviluppano una reazione vincolare più grande e di conseguenza assorbono una quantità maggiore della F ( =100kN) iniziale. Per sapere effettivamente come si riparte la forza nei diversi controventi, consideriamo la loro rigidezza k=12EI_x/h³. A parità di materiale (E) e di altezza del pilastro (h), il rapporto k₁/k₂ = I₁/I₂

I₁=0,000675

I₂=0,0052

I₁=0,13 I₂

_k1=0,13 k₂

F = 2 k₁u + 1 k₂u

F= u(0,26 k₂ + 1k₂)

F= 1,26k₂ u

u= F/1,26k₂

F₁= 0,13 k₂(F/1,26k₂)= 10,32 kN

F₂= k₂(F/1,26k₂)= 79,36 kN

2F₁+1F₂=100kN

Perciò il telaio, con pilastri aventi sezione 50x50, si farà carico di quasi 4/5 della forza iniziale F, mentre agli altri telai, con pilastri aventi sezione 30x30, arriverà solo 1/10 della F iniziale.

La struttura in FIG.06 subisce la duplice azione di una traslazione e di una rotazione. Ciò è dovuto al fatto che il centro delle rigidezze non coincide più con i centro gerometrico della struttura.

FIG.08

Lo schema delle rigidezze della FIG.08 ed un foglio di calcolo Excel ci aiuteranno a calcolare la posizione precisa del centro delle rigidezze.

STEP 1 | Sono stati individuati i telai che svolgono la funzione di controventi, i pilastri e le loro caratteristiche: E definito dal materiale, I definito dalla sezione, h l'altezza del pilastro.

FIG.09

STEP 2 | La tabella sinottica dei controventi e delle distanze indica quali sono i valori delle rigidezze di ogni talaio e la distanza di questo da un punto di origine arbitrariamente stabilito. In questo caso in corrispondenza del pilastro 1.

STEP 3 | Si è voluto analizzare la struttura precedentemente studiata per le esercitazioni precedenti, che presenta una geometria molto semplice. Per questo motivo la ricerca del centro di massa non è particolarmente complicata. Nel caso in cui la struttura avesse presentato geometri più complesse, sarebbe stato necessario scomporre l'area iniziale in aree di base assimilabili a figure semplici, come ad esempio rettangoli, considerando il centro di ognuna di queste aree.

CdM ( 8 ; 4 )

STEP 4 | Per calcolare le coordinate del centro delle rigidezze è necessario moltiplicare la rigidezza di ogni telaio (orizzontale prima e verticale poi) per la distanza di questo dall'origine degli assi e una volta sommati tutti i valori ottenuti, si divide per la rigidezza totale (orizzontale prima e verticale poi). Una volta note le coordinate del centro delle rigidezze è facile ricavare la distanza di ogni controvento da questo.

Il centro delle rigidezze ha ascissa pari a quella del centro di massa perchè i controventi verticali presentano tutti e 4 la stessa rigidezza.

CdR ( 8 ; 1,24 )

STEP 5-6-7 | Dai carichi permanenti ed accidentali si ricava la forza sismica orizzontale (STEP 5), che potremmo avere sia nella direzione x (STEP 6) che nella direzione y(STEP 7). Possiamo notare come la forza sismica lungo y sia completamente assorbita dai controventi verticali e come i controventi orizzontali non svolgano nessun ruolo particolare nei confronti di questa forza. Ciò è dovuto al fatto che il centro delle rigidezze ha in comune con il centro di massa l'ascissa, e così nel caso in cui la forza sismica arrivi lungo y la struttura traslerebbe senza ruotare.