Esercitazione3_ Dimensionamento di una mensola
1_ Analisi edificio
L’edificio analizzato è una semplice abitazione (uso residenziale), dotato di schema strutturale composto da una trave appoggiata e da una mensola. In questo caso l’analisi è rivolta allo sbalzo. Il dato fondamentale, questa volta ancora più incisivo che nella trave appoggiata è la luce, in questo caso di 3m. È stata individuata in carpenteria una delle travi più sollecitate dotata di un interasse di 4m.
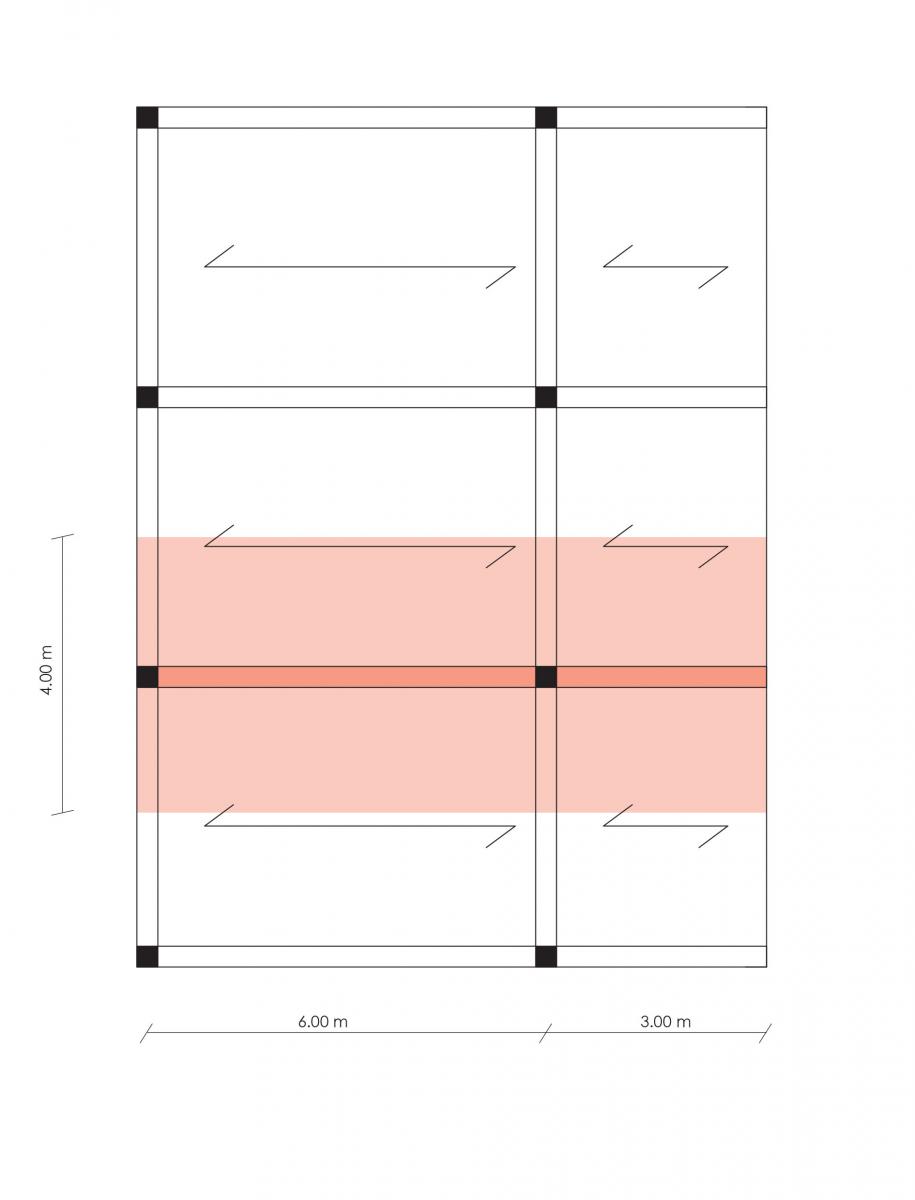
2_ Scelta del tipo di solaio
Si è scelto di fare un’analisi di questa trave, studiandola in relazione ai diversi materiali da costruzione: si sono perciò analizzate diverse stratigrafie di solaio in base alla trave che di volta in volta si vuole analizzare.
2.1_ Solaio in legno
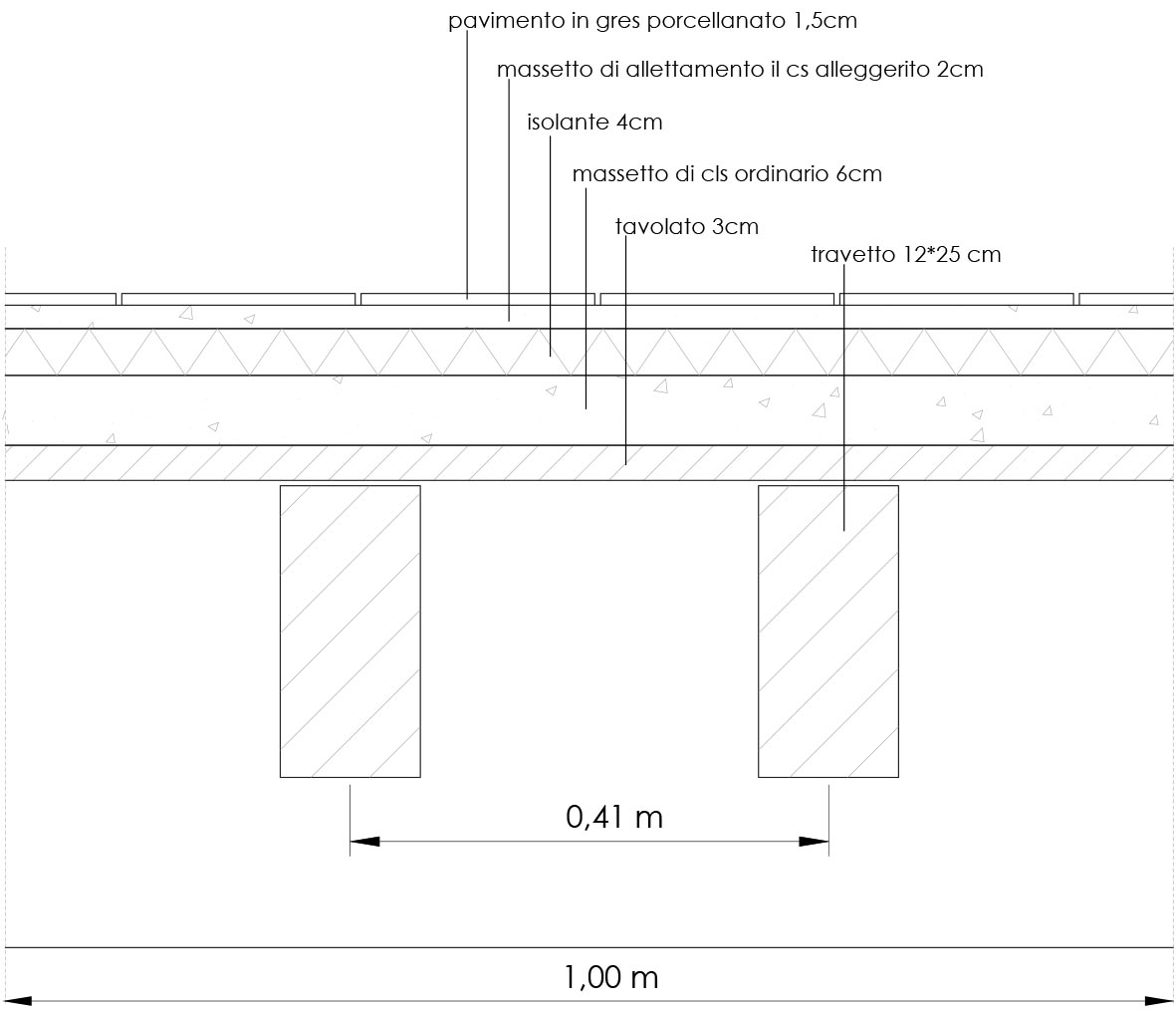
La tecnologia del solaio scelta è la medesima della scorsa esercitazione, per avere ancora più chiaro il paragone tra due diverse strutture. Vengono riportati di seguito, le rispettiva analisi dei carichi qs, qp, qA, (rispettivamente carichi strutturali, permanenti accidentali).
Analisi carichi solaio in legno
_carichi strutturali qs : tavolato, travetti
_tavolato 0,03 m * 4kN/m3 = 0,12 kN/m2
_travetti 2 * 0,25 m* 0,12 m * 6 kN/m3 = 0,36 kN/m2 (viene usato il valore al mq perché non c’è grande differenza con quello che si avrebbe al ml)
_totale qs = 0,48 kN/m2
_carichi permanenti qp : pavimento, allettamento, isolante, massetto, incidenza impianti e tramezzi
_pavimento in gres porcellanato 0,015 m * 20 kN/m3 = 0,3 kN/m2
_massetto in cls leggero 0,02 m * 14 kN/m3 = 0,28 kN/m2
_isolante 0,04 m * 0,4 kN/m3 = 0,016 kN/m2
_massetto cls 0,06 m * 24 kN/m3 = 1,44 kN/m2
_incidenza impianti 1 kN/m2
_incidenza tramezzi 0,5 kN/m2
_totale qp = 3,54 kN/m2
_carichi accidentali qA:
_ambiente residenziale 2,00 kN/m2
_totale qA: 2,00 kN/m2
_totale carichi 6,02 kN/m2
_coefficienti di sicurezza
Per aumentare la sicurezza del dimensionamento ogni carico va moltiplicato per un coefficiente di sicurezza (poco più grande di 1) e questi sono: γs = 1,3 γp = 1,3 γA= 1,5
_totale carichi (con coeff.sicurezza) = 8,23 kN/m2
_carico proprio della trave qs
In questa prima fase del dimensionamento non è stato considerato il peso proprio della trave, che incide nei carichi strutturali, in quanto non si conoscono le dimensioni della sezione. Tuttavia, una volta ricavata l’altezza della sezione con il predimensionamento ed ingegnerizzata, verrà moltiplicata per il peso specifico del materiale con cui è composta. Verrà poi effettuato un nuovo dimensionamento, aggiungendo il valore del peso della trave ai carichi strutturali, ottenendo così un nuovo momento flettente, e valutando così la resistenza della trave.
3.1_ Dimensionamento
Dal valore di carico calcolato su un mq di solaio, si è risaliti alla quantità di carico del pezzo di solaio che grava sulla trave scelta. (kN/m)
q = (qs * γs + qp *γp + qA *γA) * i = 8,23 kN/m2 * 4 m =
q =32,92 kN/m
Successivamente al calcolo del carico distribuito che insiste sulla trave, è possibile calcolare il momento massimo Mmax che insiste sulla sezione della stessa. In questo caso, la mensola a differenza della trave appoggiata possiede un momento Mmax = ql2/2:
Mmax = (32,92 kN/m * 32 m2 )/2 =
Mmax =148,07 kN * m
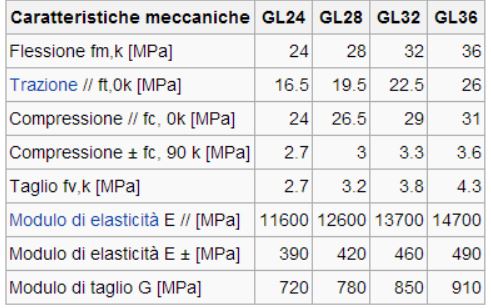
Definito il momento massimo di progetto, è necessario stabilire il materiale con cui si vuole realizzare la trave, dal quale dipenderà la resistenza fd. Nel caso del legno, la resistenza dipende dalla formula fd = ( kmod * fk ) / γm dove fk è la resistenza del materiale scelto(in questo caso legno lamellare classe GL 24 h), kmod è un coefficiente che tiene conto dell’effetto sia della durata del carico che dell’umidità sulla resistenza. Infine γm è il coefficiente di sicurezza del materiale (in questo caso 1,45).
fd = ( 0,8 * 24 N/mm2 ) /1,45 =
fd = 13,24 N/mm2
Una volta ricavata la resistenza di progetto del materiale è possibile effettuare il dimensionamento attraverso la formula di Navier : σamm= Mmax/ Wmax
Sapendo che Wmax = bh2/ 6, stabilendo un valore per la base della trave (=30 cm) è possibile ricavare, tramite la formula inversa l’altezza: h= √ (6 * Mmax) / (σamm * b)
h= √ (6 * 148,07 kNm) /[ (13,24 * 1000 kN/m2 ) * 0,3 m]
h= √ 888,42 kNm / 3972 kN /m
h= √0,2237 = 0,473 m
L’altezza minima per la trave è di 47,3 cm. Tuttavia visto che è un predimensionamento di minima, si sceglie di utilizzare una sezione di h= 50 cm.
4.1_ Analisi abbassamento
Il valore dell’abbassamento vmax non è altro che uno spostamento lineare, che perciò in una struttura isostatica può essere calcolato con il metodo degli spostamenti, che non è altro che una semplificazione del metodo della linea elastica.
L’equazione risolutiva di questo metodo è la seguente: Х(s)= d2v/ds2= M(s)/EJ
Questo significa che l’equazione dello spostamento v(s), data dalla doppia integrazione dell’equazione sovrascritta è fortemente dipendente sia dal modulo di Young, sia dal momento di inerzia della sezione stessa. È necessario perciò stabilire un valore di E, che dipende dalla tipologia di materiale scelto. Nel mio caso, la trave scelta di legno lamellare classe GL 24 h ha un valore di E= 11600 N/mm2. Invece, il valore Ix, modulo di inerzia della sezione è calcolato con la formula bh3/12, in quanto si tratta di una sezione rettangolare.
L’abbassamento totale è calcolabile attraverso la formula vmax= ql4/8EIx, in quanto il carico è uniformemente distribuito. A livello dimensionale:
[vmax] = [F] [L3]/ [F] [L-2] [L4] = [L]
In questo caso l’abbassamento misura:
vmax : 32,904 KN/m * 34 m4/ 8 * 11600 N/mm2 * 312500 cm4 = [(32,904*10) N/m * (34 *100) cm4] / 8* [(11600 * 100) N/cm2 * 312500 cm4] = 0,92 cm
Per verificare che l’abbassamento sia realmente accettabile da parte della struttura, è necessario che il rapporto tra vmax/ l ≤ 1/250. Nella tabella excel questo rapporto è invertito, perciò l’abbassamento è accettabile se l/ vmax ≥ 250. In questo caso il rapporto l/ vmax = 326,43 perciò questo abbassamento è accettato dalla struttura.
5.1_ Verifica del dimensionamento e dell’abbassamento
Per verificare il dimensionamento appena calcolato è necessario andare a ricalcolare i carichi, aggiungendo il peso proprio della trave, calcolato in base alla sezione per verificare se la struttura riesce a reggere lo sbalzo anche in questo caso. Il peso specifico del legno lamellare classe GL 24 h è di 380 kN/ m3.
Analisi carichi solaio in legno
_carichi strutturali qs : tavolato, travetti, trave
_tavolato 0,03 m * 4kN/m3 = 0,12 kN/m2
_travetti 2 * 0,25 m* 0,12 m * 6 kN/m3 = 0,36 kN/m2 (viene usato il valore al mq perché non c’è grande differenza con quello che si avrebbe al ml)
_trave 0,5 m * 0,3 m * 3,80 kN/m3 = 0,57 kN/ m2 (“ “ “ )
_totale qs = 1,05 kN/m2
_carichi permanenti qp : pavimento, allettamento, isolante, massetto, incidenza impianti e tramezzi
_pavimento in gres porcellanato 0,015 m * 20 kN/m3 = 0,3 kN/m2
_massetto in cls leggero 0,02 m * 14 kN/m3 = 0,28 kN/m2
_isolante 0,04 m * 0,4 kN/m3 = 0,016 kN/m2
_massetto cls 0,06 m * 24 kN/m3 = 1,44 kN/m2
_incidenza impianti 1 kN/m2
_incidenza tramezzi 0,5 kN/m2
_totale qp = 3,54 kN/m2
_carichi accidentali qA:
_ambiente residenziale 2,00 kN/m2
_totale qA: 2,00 kN/m2
_totale carichi (con coeff.sicurezza) = 8,97 kN/m2
_calcolo carico distribuito:
q = (qs * γs + qp *γp + qA *γA) * i = 8,97 kN/m2 * 4 m =
q =35,87 kN/m
_calcolo momento massimo:
Mmax = (35,87 kN/m * 62 m2 )/8 =
Mmax =161,4 kN * m
_calcolo h trave (in quanto il parametro della resistenza non ha subito variazioni):
h= √ (6 * 161,4 kNm) /[ (13,24 * 1000 kN/m2 ) * 0,3 m]
h= √ 968,4 / 3972 kN /m
h= √0,244= 0,493 m
La misura di altezza ingegnerizzata scelta in precedenza risulta essere valida, in quanto il peso della trave di legno è molto poco incidente a livello di carichi strutturali, che risultano appena raddoppiati. Per questo motivo, anche l’abbassamento della trave risulta minimamente aumentato, diventando vmax = 1,00 cm.
Il rapporto in questo caso l/ vmax = 299,45, quindi la struttura è definitivamente in grado di sopportare uno sbalzo di 3 metri con una trave a sezione uniforme di 30*50 cm di legno lamellare di classe GL 24 h.
5.1_ Dati di progetto nella tabella Excel

6.1_ Conclusioni
Dai due diversi dimensionamenti si è potuto constatare come aggiungendo il peso proprio della trave, si ha avuto un incremento dell’altezza della trave di oltre 2cm, che ha comportato un maggiore abbassamento, in quanto il carico ripartito uniformemente sulla trave è risultato maggiore nel secondo caso, e ha comportato un incremento di abbassamento di essa di 0,08 cm.
Tuttavia si è anche potuto notare che mantenendo invariata la sezione della trave, non è possibile fare cambiamenti significativi della luce (non può essere aumentata neanche di 50 cm), ma si può aumentare l’interasse della trave fino a 4,5m, arrivando così al limite di abbassamento della struttura di 1,13 cm.

2.2_ Solaio in laterocemento
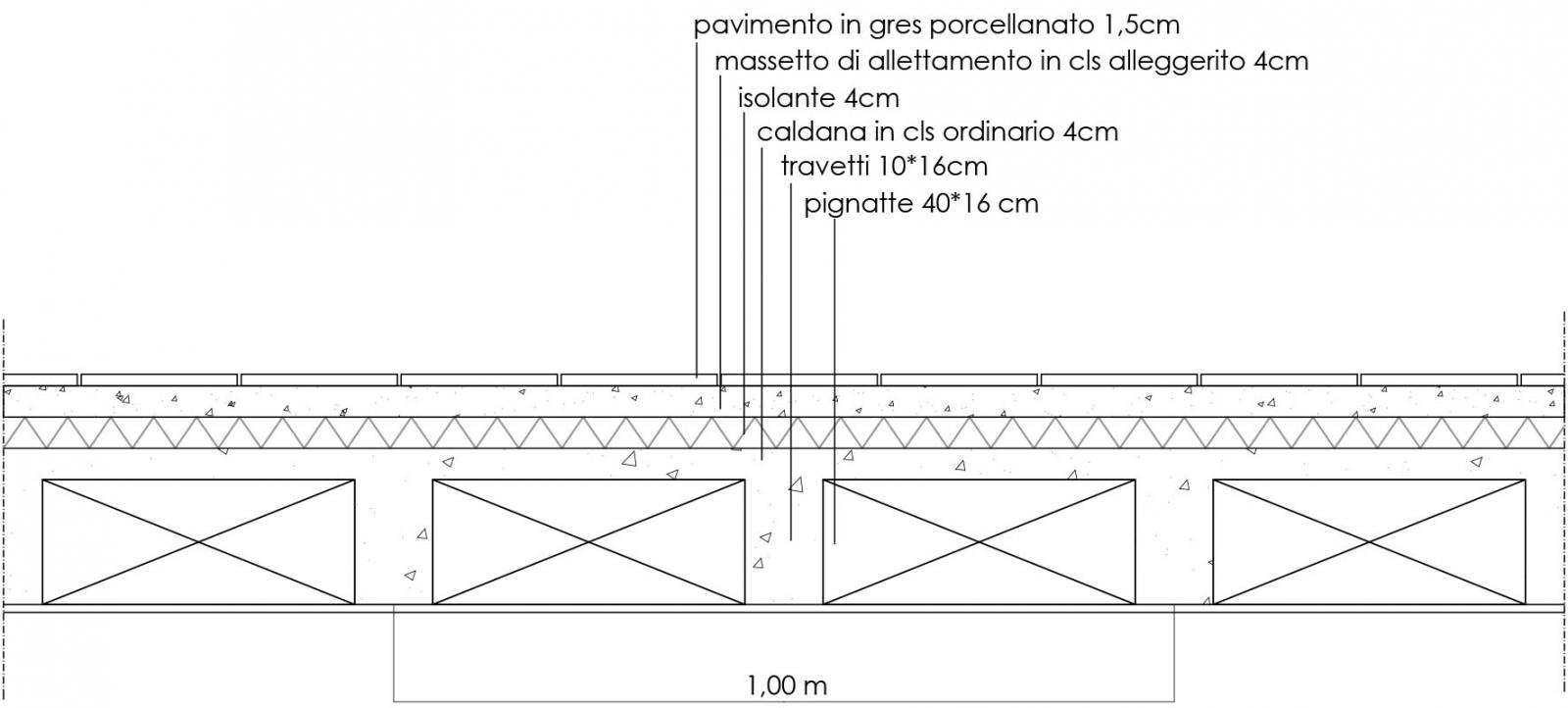
Analisi carichi solaio in laterocemento
_carichi strutturali qs : caldana, travetti
_caldana 0,04 m * 24kN/m3 = 0,96 kN/m2
_travetti 2 * 0,10 m* 0,16 m * 24 kN/m3 = 0,77 kN/m2 (viene usato il valore al mq perché non c’è grande differenza con quello che si avrebbe al ml)
_totale qs = 1,73 kN/m2
_carichi permanenti qp : pavimento, allettamento, isolante, pignatte, incidenza impianti e tramezzi
_pavimento in gres porcellanato 0,015 m * 20 kN/m3 = 0,3 kN/m2
_massetto in cls leggero 0,02 m * 14 kN/m3 = 0,28 kN/m2
_isolante 0,04 m * 0,4 kN/m3 = 0,016 kN/m2
_pignatte 2 * 0,4 m * 0,16 m * 8 kN/m3 = 1,02 kN/m2
_incidenza impianti 1 kN/m2
_incidenza tramezzi 0,5 kN/m2
_totale qp = 3,12 kN/m2
_carichi accidentali qA:
_ambiente residenziale 2,00 kN/m2
_totale qA: 2,00 kN/m2
_totale carichi 6,85 kN/m2
_coefficienti di sicurezza
Per aumentare la sicurezza del dimensionamento ogni carico va moltiplicato per un coefficiente di sicurezza (poco più grande di 1) e questi sono: γs = 1,3 γp = 1,3 γA= 1,5
_totale carichi (con coeff.sicurezza) = 9,30 kN/m2
_carico proprio della trave qs
In questa prima fase del dimensionamento non è stato considerato il peso proprio della trave, che incide nei carichi strutturali, in quanto non si conoscono le dimensioni della sezione. Tuttavia, una volta ricavata la sezione con il predimensionamento, verrà moltiplicata per il peso specifico del materiale con cui è composta. Verrà poi effettuato un nuovo dimensionamento, aggiungendo il valore del peso della trave ai carichi strutturali, ottenendo così un nuovo momento flettente, e valutando così la resistenza della trave.
3.2_ Dimensionamento
Dal valore di carico calcolato su un mq di solaio, si è risaliti alla quantità di carico del pezzo di solaio che grava sulla trave scelta. (kN/m)
q = (qs * γs + qp *γp + qA *γA) * i = 9,30 kN/m2 * 4 m =
q =37,2 kN/m
Successivamente al calcolo del carico distribuito che insiste sulla trave, è possibile calcolare il momento massimo Mmax che insiste sulla sezione della stessa. In questo caso, trattandosi di una mensola, il momento massimo è pari a Mmax = ql2/2:
Mmax = (37,2 kN/m * 32 m2 )/2 =
Mmax =167,4 kN * m
Definito il momento massimo di progetto, è necessario calcolare le resistenze dei due materiali che compongono la trave: l’acciaio fyd (che ha una resistenza specifica per le armature) ed è data dal rapporto fyd =fyk/ γs e il calcestruzzo fcd =αcc * fck/ γc
fyd = 450 N/mm2 / 1,15
fyd = 391,3 N/mm2
fcd =0,85 * 40 N/mm2 / 1,5
fcd = 22,86 N/mm2
Una volta ricavata la resistenza di progetto del materiale è possibile effettuare il dimensionamento attraverso l’equilibrio alla rotazione della sezione:
M= C * b* = T * b*
Dove b*=hu-Xc/3 Xc= α*hu α= σca/ (σca + σfa/n) n=15
M= C * (hu- α*hu /3)
M= σca * (b * α*hu)/2 * (hu- α*hu /3)
M= σca * b * α*hu/2 * (1 – α/3)hu
2M= σca * b * α * (1 – α/3)hu2
hu2= 2M / [σca * b * α * (1 – α/3)]
hu= √2M / [σca * b * α * (1 – α/3)]
Per calcolare l’altezza utile della sezione è necessario stabilire una base, in questo caso di 30 cm.
hu=√2 * 167,4 kNm / 103 * 22,86 kN/m2 * 0,3 m* 0,47 (1-0,47/3)
hu= 0,352 m = 35,2 cm
L’altezza minima per la trave è di 35,2 cm. Tuttavia nelle travi di cemento armato è necessario aggiungere un delta di 5 cm, che corrisponde all’altezza del copriferro e di metà della sezione dei tondini dell’armatura.
L’altezza che si ottiene dal predimensionamento quindi risulta essere H= hu+δ H= 35,2 + 5 cm = 40,2 cm. Si ingegnerizza la sezionale prevedendo un’altezza di H=45 cm.
Dall’altezza della trave è possibile ricavare attraverso il foglio Excel sia l’area, che il peso in KN/m, che poi viene sommato per ottenere il carico q definitivo 30,78 KN/mq.
4.2_ Analisi abbassamento
Il valore dell’abbassamento vmax non è altro che uno spostamento lineare, che perciò in una struttura isostatica può essere calcolato con il metodo degli spostamenti, che non è altro che una semplificazione del metodo della linea elastica.
L’equazione risolutiva di questo metodo è la seguente: Х(s)= d2v/ds2= M(s)/EJ
Questo significa che l’equazione dello spostamento v(s), data dalla doppia integrazione dell’equazione sovrascritta è fortemente dipendente sia dal modulo di Young, sia dal momento di inerzia della sezione stessa.
Il valore di E è 21000 N/mm2, mentre il modulo d’inerzia Ix anche questa volta viene calcolato con la formula bh3/12, e vale 227813 cm4.
L’abbassamento totale è calcolabile attraverso la formula vmax= ql4/8EIx, in quanto il carico è uniformemente distribuito.
In questo caso l’abbassamento misura:
vmax : 30,78 KN/m * 34 m4/ 8 * 21000 N/mm2 * 227813 cm4 = [(30,78*10) N/m * (34 *100) cm4] / 8* [(21000 * 100) N/cm2 * 227813 cm4] = 0,65 cm
Ora è necessario verificare che il rapporto l/ vmax sia ≥ 250.
In questo caso il rapporto l/ vmax = 460,60 perciò questo abbassamento è accettato dalla struttura, di conseguenza lo sbalzo è realizzabile.
5.2_ Dati di progetto nella tabella Excel

6.2_ Conclusioni
Il dimensionamento della mensola di cemento armato è stato già fatto, a differenza del legno, considerando il peso della trave all’interno del carico strutturale che agisce sullo sbalzo, in quanto il peso della trave di calcestruzzo è di molto maggiore rispetto a quello del legno.
[L’abbassamento tuttavia qui risulta minore, anche perché, nel termine q (carico totale che agisce sulla trave, peso della trave stessa compreso) non sono stati considerati i coefficienti di sicurezza γs ,γp ,γA , che al contrario avrebbero determinato un carico totale di è [1,3*(qs + qp )+ 1,5*qa]*4m+ 3,38 KN/m2 = 40,58 KN/m2.
Questo carico, comporterebbe al contrario un abbassamento:
vmax : 40,58 KN/m * 34 m4/ 8 * 21000 N/mm2 * 227813 cm4 = [(40,58*10) N/m * (34 *100) cm4] / 8* [(21000 * 100) N/cm2 * 227813 cm4] = 0,85 cm.
Anche in questo caso si è cercato di capire come reagiva la struttura al variare sia della luce che dell’interasse: la luce è aumentabile di 50 cm, ma solo nel caso dove nel carico q non sono considerati i coefficienti di sicurezza, mentre l’interasse può essere aumentato fino a 5 m, registrando un abbassamento rispettivo di 0,80 cm e 1,06 cm, che la struttura in entrambi i casi riesce a sostenere in quanto il rapporto l/ vmax è ≥ 250.

2.3_ Solaio in acciaio
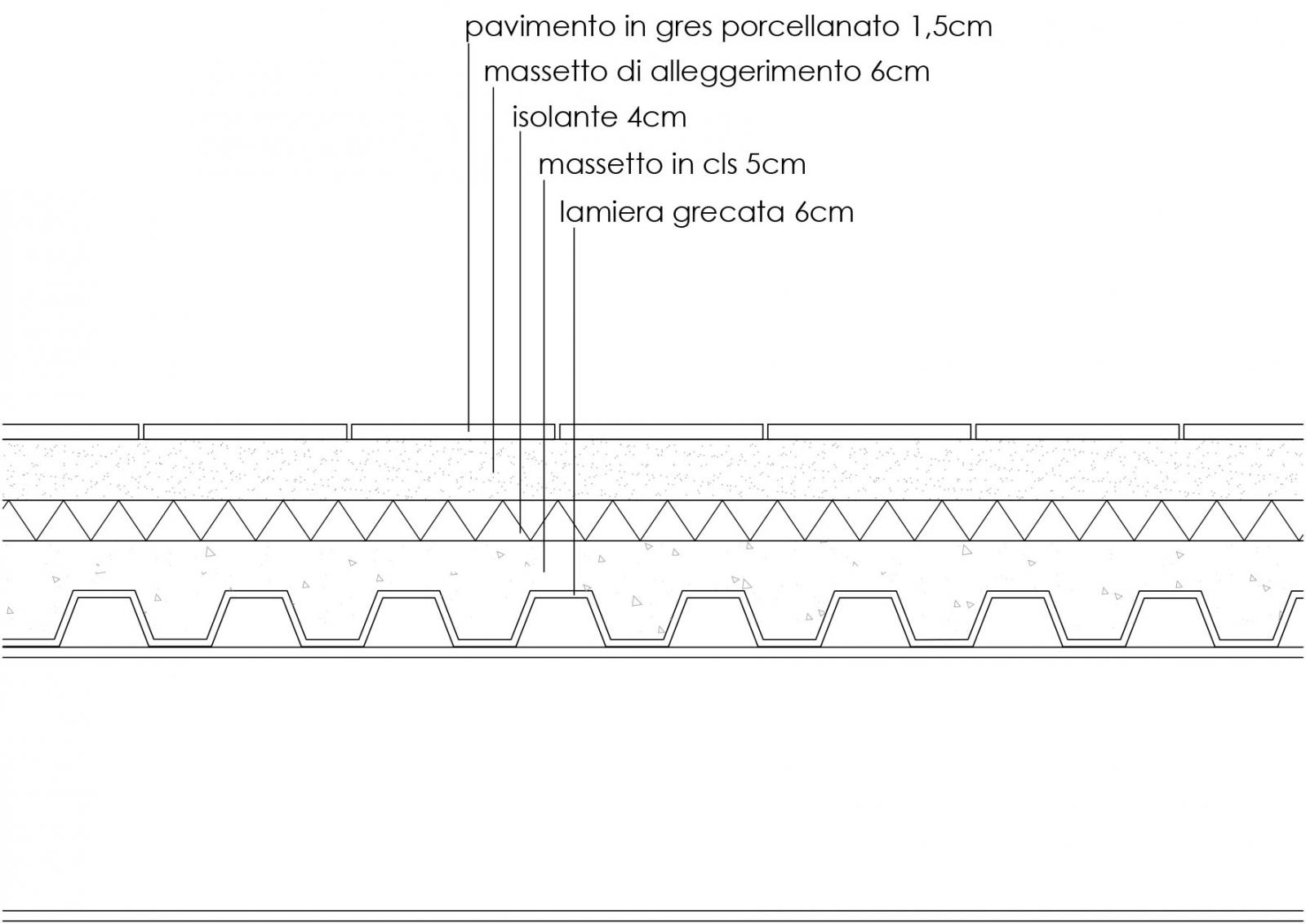
Analisi carichi solaio in acciaio
_carichi strutturali qs : massetto in cls, lamiera grecata
_massetto in cls spessore 0,11 m= 2,15 kN/m2
_lamiera grecata tipo HI-BOND spessore 0,7mm = 0,09 kN/m2
_totale qs = 2,24 kN/m2
_carichi permanenti qp : pavimento, allettamento, isolante, incidenza impianti e tramezzi
_pavimento in gres porcellanato 0,015 m * 20 kN/m3 = 0,3 kN/m2
_massetto in cls leggero 0,06 m * 14 kN/m3 = 0,84 kN/m2
_isolante 0,04 m * 0,4 kN/m3 = 0,016 kN/m2
_incidenza impianti 1 kN/m2
_incidenza tramezzi 0,5 kN/m2
_totale qp = 2,66 kN/m2
_carichi accidentali qA:
_ambiente residenziale 2,00 kN/m2
_totale qA: 2,00 kN/m2
_totale carichi 6,9 kN/m2
_coefficienti di sicurezza
Per aumentare la sicurezza del dimensionamento ogni carico va moltiplicato per un coefficiente di sicurezza (poco più grande di 1) e questi sono: γs = 1,3 γp = 1,3 γA= 1,5
_totale carichi (con coeff.sicurezza) = 9,37 kN/m2
_carico proprio della trave qs
In questa prima fase del dimensionamento non è stato considerato il peso proprio della trave, che incide nei carichi strutturali, in quanto non si conoscono le dimensioni della sezione. Tuttavia, una volta ricavata la sezione con il predimensionamento, verrà moltiplicata per il peso specifico del materiale con cui è composta. Verrà poi effettuato un nuovo dimensionamento, aggiungendo il valore del peso della trave ai carichi strutturali, ottenendo così un nuovo momento flettente, e valutando così la resistenza della trave.
3.3_ Dimensionamento
Dal valore di carico calcolato su un mq di solaio, si è risaliti alla quantità di carico del pezzo di solaio che grava sulla trave scelta. (kN/m)
q = (qs * γs + qp *γp + qA *γA) * i = 9,37 kN/m2 * 4 m =
q =37,48 kN/m
Successivamente al calcolo del carico distribuito che insiste sulla trave, è possibile calcolare il momento massimo Mmax = ql2/2:
Mmax = (37,48 kN/m * 32 m2 )/2 =
Mmax =168,66 kN * m
Definito il momento massimo di progetto, è necessario stabilire il materiale con cui si vuole realizzare la trave, dal quale dipenderà la resistenza fyd. Nel caso dell’acciaio, la resistenza dipende dalla formula fyd = fyk / γs dove fyk è la tensione di snervamento del materiale scelto (in questo caso Fe 430/S275), e γs è il coefficiente di sicurezza relativo dell’acciaio (1,15).
fyd = 275 N/mm2 /1,15 =
fyd = 239,13 N/mm2
Una volta ricavata la resistenza di progetto del materiale è possibile effettuare il dimensionamento attraverso la formula di Navier : σamm= Mmax/ Wmax
Avendo sia la tensione ammissibile che il momento massimo, posso utilizzare la formula inversa rcavandomi il modulo di resistenza minimo a flessione Wxmin
Wxmin= Mmax / σamm
Wxmin= 168,66 kNm / 103 * 239,13 kN/m2
Wxmin= 0,0007053 m3= 705,3 cm3
Attraverso il prontuario delle IPE è possibile trovare l’altezza della trave corrispondente al modulo di resistenza a flessione. Il valore appena superiore al Wxmin calcolato è di 713,0 cm3, che corrisponde ad un IPE330.
L’altezza della trave calcolata con il predimensionamento è di 33 cm.
Tramite il prontuario è possibile ricavare il peso della trave, pari a 0,491 KN/m2 , che viene sommato agli altri carichi strutturali ed utilizzato per il calcolo dell’abbassamento.
4.2_ Analisi abbassamento
Il valore dell’abbassamento vmax non è altro che uno spostamento lineare, che perciò in una struttura isostatica può essere calcolato con il metodo degli spostamenti, che non è altro che una semplificazione del metodo della linea elastica.
L’equazione risolutiva di questo metodo è la seguente: Х(s)= d2v/ds2= M(s)/EJ
Questo significa che l’equazione dello spostamento v(s), data dalla doppia integrazione dell’equazione sovrascritta è fortemente dipendente sia dal modulo di Young, sia dal momento di inerzia della sezione stessa.
Il valore di E è 210000 N/mm2, mentre il modulo d’inerzia Ix vale 11770 cm4.
L’abbassamento totale è calcolabile attraverso la formula vmax= ql4/8EIx, in quanto il carico è uniformemente distribuito.
In questo caso l’abbassamento misura:
vmax : 42,39 KN/m * 34 m4/ 8 * 210000 N/mm2 * 11770 cm4 = [(42,39*10) N/m * (34 *100) cm4] / 8* [(210000 * 100) N/cm2 * 11770 cm4] = 1,74 cm
Ora è necessario verificare che il rapporto l/ vmax sia ≥ 250.
In questo caso il rapporto l/ vmax = 172,77 perciò questo abbassamento non è accettabile a livello strutturale.
Si è scelto allora di cambiare la resistenza dell’acciaio, prendendo un materiale meno resistente Fe360/S235, per spingere la trave dotata di meno resistente ad aumentare la sua sezione, diventando di conseguenza più tozza.
Questa volta il dimensionamento ha portato alla scelta di una IPE360, dotata di peso pari a 0,571 KN/m2, e di modulo di inerzia Ix pari a 16270 cm4.
Dalla formula vmax= ql4/8EIx, risulta che vmax è pari a 1,127 cm.
In questo caso, il rapporto l/ vmax = 266,05 è maggiore di 250, di conseguenza la trave riesce a sostenere lo sbalzo.
5.3_ Dati di progetto nella tabella Excel

6.3_ Conclusioni
Si può quindi affermare, come scegliendo una resistenza caratteristica minore del materiale, che necessita perciò una sezione più tozza, si può ottenere una trave meno deformabile, dotata di maggiore momento di inerzia, che combatte perciò la flessione, e che è in grado di contenere l'abbassamento.
Commenti recenti