Blog

 La terza esercitazione consiste nel progetto di una trave a sbalzo nelle tre tecnologie di costruzione più comuni (legno, acciaio, cemento armato), con l’ausilio di un foglio elettronico Excel.

Piante di carpenteria di riferimento per solaio in legno,cls e acciaio

La prima carpenteria rappresenta un solaio in cls e legno; la seconda un solaio in acciao.

La trave a sbalzo maggiormente sollecitata è quella sull’asse B, con un’ area di influenza pari a 12 m² (luce: 3m, interasse: 4m).

Lo scopo dell’esercitazione è verificare che la deformabilità della trave non provochi un abbassamento (spostamento verticale) maggiore di 1/250 della luce della trave stessa; il foglio Excel ci permettere di conoscere il valore dello spostamento verticale della trave allo stato limite di esercizio.

Nel caso di una trave a sbalzo, si prende in considerazione il modello statico della mensola

il cui momento massimo è dato dalla formula  M_max = ql²/2

CEMENTO ARMATO

Considero i valori dei carichi strutturali, permanenti ed accidentali relativi al calcestruzzo della prima esercitazione:

q_s= 3,23 kN/m²

q_p= 2,64 KN/m²

q_a= 2kN/m²  

I tre carichi vengono sommati, moltiplicati per i loro coefficienti di sicurezza e moltiplicati per l’interasse ottenendo q_u pari a 44,64 kN/m. Conoscendo la luce (3 m) , si ottiene il valore del Momento massimo di una mensola  pari a  200,86 KNm.

Per le armature scelgo un acciaio con coefficiente di resistenza caratteristica pari a f_yk=450 MPa e un calcestruzzo con resistenza a compressione pari a f_ck=60 MPa. Imposto una base b pari a 25 cm; i calcoli del foglio Excel mi danno un’altezza minima della sezione che ingegnerizzo a 40 cm. Di conseguenza, ho una sezione di 25 cm X 40 cm.

Dopo aver dimensionato la sezione, effettuo la verifica a deformabilità controllando l’abbassamento massimo dell’elemento strutturale in rapporto alla sua luce.

Il procedimento, che è uguale in tutte e tre le tecnologie, si effettua allo SLE (Stato Limite di Esercizio) poiché la verifica è finalizzata a controllare che non vi siano spostamenti e deformazioni che possano limitare l’uso della costruzione, la sua efficienza e il suo aspetto.

A tal motivo i carichi incidenti sulla struttura vengono ricombinati seguendo la combinazione frequente, generalmente impiegata per gli stati limite di esercizio reversibili:

                                                               q_e= (G1 + G2 + ¥11 × Q1) × i

Nel cemento armato, il peso proprio dell’elemento strutturale veniva calcolato anche nella prima esercitazione, poiché era necessario verificare allo stato limite ultimo (SLU) che la sezione scelta fosse idonea a sopportare tutti i pesi gravanti su di sé anche dopo aver aggiunto il peso proprio. Dopo questa verifica, l’informazione relativa al peso verrà riutilizzata per calcolare il carico totale q_e.

Infine, per calcolare lo spostamento è necessario conoscere il modulo elastico del materiale E e il suo momento d’inerzia I_x

Calcolato il carico totale allo SLE q_e, specificato il modulo elastico E ed il momento di inerzia I_x, è ora possibile calcolare l’abbassamento massimo che è pari a:

                                                                        v_max = q_e* l⁴ / 8EI_x

e verificare che il rapporto tra la luce della trave e il suo spostamento massimo sia maggiore di 250, come imposto dalla normativa in base al tipo di elemento strutturale considerato:

                                                                             l / v_max ≥ 250

Lo spostamento verticale massimo è pari a 1,08 cm e il rapporto tra la luce e lo spostamento massimo è maggiore di 250.

LEGNO

q_s= 0,18 kN/m²

q_p= 3,74 KN/m²

q_a= 2kN/m²  

q_u pari a 35,376 kN/m

Conoscendo la luce (3 m) , si ottiene il valore del Momento massimo di una mensola  pari a  159,192 KNm

Dopo aver impostato il modulo elastico del materiale, scelgo una base di lunghezza pari a 25 cm; i calcoli del foglio Excel mi danno un’altezza minima della sezione che ingegnerizzo a 50 cm. Di conseguenza, ho una sezione di 25 cm X 50 cm. Dopo aver dimensionato la sezione, è necessario effettuare la verifica a deformabilità controllando l’abbassamento massimo dell’elemento strutturale in rapporto alla sua luce.

Nel caso del legno, per quanto riguarda il calcolo del carico totale allo stato limite di esercizio, il peso proprio della trave viene trascurato in quanto è un materiale leggero.

                                                          q_e= (G1 + G2 + ¥11 × Q1) × i = 20 kN/m

Calcolato il carico totale allo SLE q_e, specificato il modulo elastico E ed il momento di inerzia I_x, è ora possibile calcolare l’abbassamento massimo che è pari a:

                                                                    v_max = q_e l⁴/ 8EI_x= 0,96 cm.

Di conseguenza:

                                                                             l / v_max> 250

ACCIAO

q_s= 1,18 kN/m²

q_p= 1,74 kN/m²

q_a= 2kN/m²

q_u pari a 28,576 kN/m

Conoscendo la luce (3 m) , si ottiene il valore del Momento massimo di una mensola  pari a  128,592 KNm

Dopo aver definito la resistenza del materiale, dal foglio Excel si ottiene un modulo di resistenza a flessione W_x,min pari a 490,99 cm³. Quindi è opportuno utilizzare come profilato una IPE 300 che ha W_x pari a 557,0 cm³ e I_x pari a 8356 cm⁴. 

Dopo aver dimensionato la sezione, è necessario effettuare la verifica a deformabilità controllando l’abbassamento massimo dell’elemento strutturale in rapporto alla sua luce. Come per il cemento, anche per l’acciaio va considerato il peso proprio (0,422 KN/m); informazione che verrà riutilizzata per calcolare il carico totale q_e.

                                                    q_e= (G1 + G2 + ¥11 × Q1) × i = 16,102 kN/m

Calcolato il carico totale allo SLE q_e, specificato il modulo elastico E ed il momento di inerzia I_x, è ora possibile calcolare l’abbassamento massimo che è pari a:

                                                                   v_max = q_e l⁴/ 8EI_x= 0,929 cm.

Di conseguenza:

                                                                              l / v_max> 250

La travatura reticolare (o struttura reticolare) è una struttura composta da un insieme di aste vincolate ai nodi in modo da costituire un elemento resistente e indeformabile. La travatura reticolare ha tratto la propria origine dalla necessità di impiegare strutture sempre più leggere per superare luci sempre più grandi.

Nella seconda esercitazione ho dimensionato e analizzato una struttura reticolare tridimensionale con l’ausilio del software SAP2000 e di un foglio Excel.

In particolare, SAP2000 mi ha permesso di modellare una struttura reticolare e di ottenere, alla fine, i dati relativi agli sforzi assiali sulle singole aste; non troveremo, infatti, sollecitazioni di taglio e momento.

1. Avviato il programma, ho aperto un file New model, impostato l'unità di misura KN, m, C e scelto come spazio di lavoro Grid Only.

Ho creato una maglia rettangolare 6m x 8m composta da 12 campate 2m x 2m. Ho iniziato a modellare la mia struttura a base cubica collegando i vari vertici tra loro e controventando ogni singola faccia del cubo 

2.  il risultato è una struttura reticolare composta da 12 cubi di dimensioni 2m x 2m X 2m

3.  Ho completato la mia struttura assegnando, come vincolo esterno, una cerniera ai quattro spigoli inferiori e, tramite il comando Assign > Frame > Release partial fixity, ho trasformato tutti i nodi in cerniere interne.

4.  Successivamente ho assegnato il materiale (acciaio) alle aste della struttura, scegliendo un profilato a sezione circolare cava (Pipe)

5. cliccando su Define > Load pattern definisco un nuovo sistema di carichi inserendo un nuovo paramentro F con un Self Weight Multiplier uguale a 0.

6. Cliccando su Assigne > Joint loads > Forces assegno i carichi alla struttura, dopo aver selezionato esclusivamente i nodi superiori; la forza è pari a 100 kN (-100 kN in quanto è diretta verso il basso)

7.  Conclusa la prima fase di modellazione, si può procedere con l’analisi dei carichi selezionando esclusivamente la forza F

8. Ottengo così la struttura deformata e posso visualizzare i diagrammi (e i valori) dello sforzo assiale

9.  Cliccando su  Display > Show tables posso controllare i dati dell'analisi spuntando Analisys Results e selezionando il valore F

10. Infine esporto la tabella Element Forces - Frames in un file Excel per ottenere i dati utili al dimensionamento delle aste

Dopo un’operazione di “pulizia del file”, in cui ho eliminato i dati duplicati, ho ordinato i valori relativi allo sforzo normale dal più piccolo al più grande ed ho evidenziato i valori delle aste diagonali;  ora posso trasferirli nelle tabelle Excel preimpostate per trazione e compressione.

TRAZIONE

Prendo tutti i valori positivi dalla tabella esportata da Sap2000 e li incollo nel foglio Excel preimpostato nella sezione “acciao trazione”.

Per il dimensionamento delle aste, prendo in considerazione il valore massimo dello sforzo di trazione ed, in base a questo valore, il foglio Excel mi da un’area minima della sezione; quindi, dalla tabella dei profilati metallici circolari, scelgo una sezione con area maggiore rispetto all’area minima indicata.  

COMPRESSIONE

Prendo tutti i valori negativi dalla tabella esportata da Sap2000 e li incollo nel foglio Excel preimpostato nella sezione “acciao compressione”.

Per il dimensionamento delle aste compresse, prendo in considerazione:

1.    Valore massimo dello sforzo di compressione

2.    Area minima relativa all’asta soggetta allo sforzo di compressione maggiore

3.    Il valore massimo del momento d’inerzia minimo

Ingegnerizzando, verifico che il valore di lambda sia < 200.

In base a questi valori, per la mia struttura reticolare ho scelto un profilato metallico a sezione circolare cava di dimensioni 114,3 X 4,5 mm.

Questa esercitazione consiste nel dimensionamento e verifica di una trave a sbalzo, usando tre materiali differenti (legno, acciaio e cls).

Per comodità ho ripreso la stessa pianta di carpenteria della prima esercitazione dotandola di un aggetto di 3 m.

Il foglio excel da usare è composto di due parti di cui la prima uguale al foglio della prima esercitazione poichè riguarda i problemi legati allo Stato Limite Ultimo; mentre la seconda parte riguarda la deformabilità quindi lo Stato Limite d'Esercizio

SOLAIO IN LEGNO

Considero lo stesso solaio preso in considerazione nella prima esercitazione 

- Inizio a compilare la prima parte del foglio Excel con i valori dell'interasse, qs, qp, qa per ottenere quindi il qu = 37,797 Kn/m.

- Inserisco il valore dello sbalzo pari a 3 m per calcolare il momento massimo pari a Mmax = 170,08 KN*m

- inserisco ora i dati relativi al materiale ossia quello di un legno classe C24 (fmk = 24 N/mm² , Kmod = 0.8, γ m = 1.45) per ottenere un valore della tensione di progetto pari a f_dC = 13,24 N/mm² 

- scelgo una base di 35 cm ed ottengo una altezza di 46,33 cm che ingegnerizzo a 50 cm

- ora inizia la parte relativa allo SLE quindi inserisco un modulo elastico pari a E = 8000 N/mm² ed ottengo una Ix = 364583 cm⁴

- infine mi rendo conto che lo spostamento massimo v_max = 0,73 cm è verificato poichè il rapporto Ix/v_max >250

SOLAIO IN ACCIAIO

Come per il legno prendo in considerazione il pacchetto di solaio che avevo studiato per la prima esercitazione

- compilo la prima parte del foglio Excel come ho fatto per il legno per arrivare a trovare un valore di qu = 42,87 KN/m

- inserisco il valore della luce dello sbalzo e trovo un valore di Mmax = 192,95 KN*m

- per quanto riguarda il materiale ho scelto un acciaio di classe S235 che ha come caratteristiche una tensione fyk = 235 N/mm²

- trovato il valore di fd = 223,81 N/mm² calcoliamo il modulo di resistenza a flessione minimo uguale a Wx,min = 862,15 cm³

- consultando la tabella dei profilati IPE scelgo una IPE 360 sapendo che la resistenza a flessione deve essere più grande di quella trovata ( Wx = 904 cm³)

- Inserisco il valore di Ix ricavato dalla tabella Ix = 16270 cm⁴

- Dopo aver calcolato qe= 26,113 KN/m mi rendo conto che anche in questo caso il progetto è verificato poichè lo spostamento è uguale a v_max = 0,774 e quindi il rapporto  I_x/ v_max >250

SOLAIO IN CEMENTO ARMATO

- Compilo la prima parte del foglio Excel ed inserisco il valore dello sbalzo trovando così il valore del momento massimo Mmax= 225,54 KN*m

- Scelgo un acciaio di classe S450 ( fyk = 450 N/mm², fd = 391.30 N/mm² )

- Prendo un cls che abbia come tensione caratteristica fck = 60 N/mm² ed fcd = 34 N/mm²

- Prendo il valore di β=0.57 e di r=2.09 

- Considero una trave di base b = 30 cm e copriferro di 5 cm e trovo una altezza ingegnerizzata di H = 40 cm

- Il foglio excel verifica allora con i dati ottenuti se la trave presa in considerazione ha una tensione di progetto pari alla massima tensione esercitata in campata. La trave è verificata.

- Procediamo a calcolare la parte relativa allo SLE (qe = 33,6  KN/m)

- Anche questa volta la trave è verificata poichè  I_x/ v_max >250

Con la terza esercitazione vado a dimensionare una trave a sbalzo costituita da tre materiali, il legno, l'acciaio e il calcestruzzo armato. Ne verifico poi la deformabilità, calcolando l'abbassamento massimo della mensola attraverso il rapporto tra la luce della trave e il suo spostamento, sempre maggiore di 250.

La pianta della carpenteria segue alcune decisioni progettuali del Laboratorio di Progettazione 3 del Prof. Desideri e vuole indagare una delle possibilità di aggetto del nostro edificio.

SOLAIO IN LEGNO

Per il solaio prendo i carichi che ho ottenuto nella prima esercitazione per inserirli nel file excel.

In questo nuovo foglio di calcolo il momento massimo che risulta essere ql²/2 trattandosi di una mensola. Inoltre assumo la base della trave di 30 cm secondo un principio di continuità con i pilastri.

Dopo aver ingegnerizzato l'altezza, verifico la sezione allo Stato Limite di Esercizio. Nella verifica non si tiene conto del peso proprio della trave in legno.

La trave è verificata poichè il rapporto tra luce e spostamento (680) è maggiore di 250, secondo normativa.

SOLAIO IN ACCIAIO

Per l'acciaio, dopo aver trovato il modulo di resistenza a flessione minimo W_x per ingegnerizzare la sezione si inserisce nella colonna successiva il valore del momento di inerzia I_x del profilo, che ha come modulo di resistenza a flessione W_x un valore maggiore rispetto a quello trovato.

Come trave ho un IPE 360 di base 170 mm, con un momento di inerzia di 16270 cm⁴ e un peso di 57,1 kg/m, incluso quest'ultimo nei calcoli per il carico di esercizio q_e.

La trave è verificata poichè il rapporto tra luce e spostamento (340) è maggiore di 250, secondo normativa.

SOLAIO IN LATEROCEMENTO

Anche qui per la base della trave utilizzo i 30 cm del lato del pilastro, arrivando ad avere una trave alta 45 cm.

Per la deformabilità calcolo sempre il carico di esercizio q_e includendo il peso della trave.

La trave è verificata poichè il rapporto tra luce e spostamento (421) è maggiore di 250, secondo normativa.

Nella seconda esercitazione ho analizzato e dimensionato una struttura reticolare tridimensionale con l’ausilio del software SAP 2000 e di un foglio Excel.

Le aste reticolari sono sollecitate esclusivamente a sforzo normale (trazione e compressione).

Procedo con la descrizione dell’iter che, tramite SAP, mi ha permesso la modellazione della struttura reticolare e del calcolo degli sforzi sulle singole aste.

1) Apro un nuovo file cambiandone l’unità di misura in Kn,m,C scegliendo uno spazio di lavoro “Grid only”

2) Imposto la maglia strutturale con cubi di lato 3 m e dispongo 3 cubi lungo l'asse x ed y. Uso una griglia x=4 y=4 z=2

3) Inizio a modellare la mia struttura a base cubica collegando i vari vertici tra loro e controventando ogni singola faccia del cubo

4) Controllo se il mio modello non presenti aste duplicate cliccando su edit > edit points >merge duplicate

5) Correggo la tolleranza di 0,1 cliccando su edit > edit points > merge joints

6) Seleziono i quattro vertici inferiori e aggiungo delle cerniere tramite il comando assign > joint > restraints

7) Sblocco i nodi da sforzo flessionale selezionando la struttura e cliccando su Assign > Frame > Release partial fixity

8) Assegno il materiale alle aste che compongono la struttura tramite Frame > frame section > add ne property > pipe 

9) Imposto un nuovo schema di carichi cliccando su Define > Load pattern ed inserisco un nuovo parametro F coun un Self Weight Multiplier = 0

10) Seleziono esclusivamente i nodi superiori per caricarli aggiungendo una forza di -200 KN poichè diretta verso il basso. Clicco su Assigne > Joint loads > Forces

11) posso ora far partire l'analisi cliccando su Run analysis e selezionando esclusivamente la forza F come oggetto dell'indagine. Ottengo così la mia struttura deformata e posso controllare gli sforzi su di essa cliccando su Frame > Axiel force

12) Cliccando su  Display > Show tables posso controllare i dati dell'analisi spuntando Analisys Results e selezionando il valore F. Esportiamo adesso la tabella Element Forces - Frames in un file Excel per ottenere i dati utili al dimensionamento delle aste.

Per prima cosa elimino i dati ripetuti cliccando su Dati > rimuovi duplicati ed ordino gli sforzi dal più grande al più piccolo.

Adesso posso analizzare singolarmente gli sforzi di trazione (+) e gli sforzi di compressione (-)

TRAZIONE

- Nella prima colonna del foglio excel incollo gli sforzi normali delle aste per poi selezionare un acciaio di tipo S235 JR H con un valore di tensione di snervamento = 235 Mpa

- Aggingo il coefficiente y_s = 1,05 e ottengo un Fyd = 223,81 Mpa

- Ottenuta l'area minima di sezione procedo alla consultazione del profilario di aste a sezione circolare per il dimensionamento dei profili che avranno un'area maggiore rispetto a quella calcolata

COMPRESSIONE

- Per la compressione valgono gli stessi procedimenti descritti in precedenza ma con l'aggiunta del fenomeno di instabilità

- Aggiungo quindi il valore di E = 210000 Mpa e di beta = 1

- La lunghezza delle singole aste la ricavo facendo attenzione a quali di esse sono lati dei quadrati (3 m) e quali sono diagonali (4,24 m)

- Ottenuti i valori di Lambda, Rho min e I min procedo con il dimensionamento delle aste facendo attenzione che i valori del profilato siano superiori a quelli trovati

Per questa esercitazione bisogna dimensionare una mensola, usando tre tipi diversi di materiale (legno, acciaio, cemento armato), usando il programma Excel.

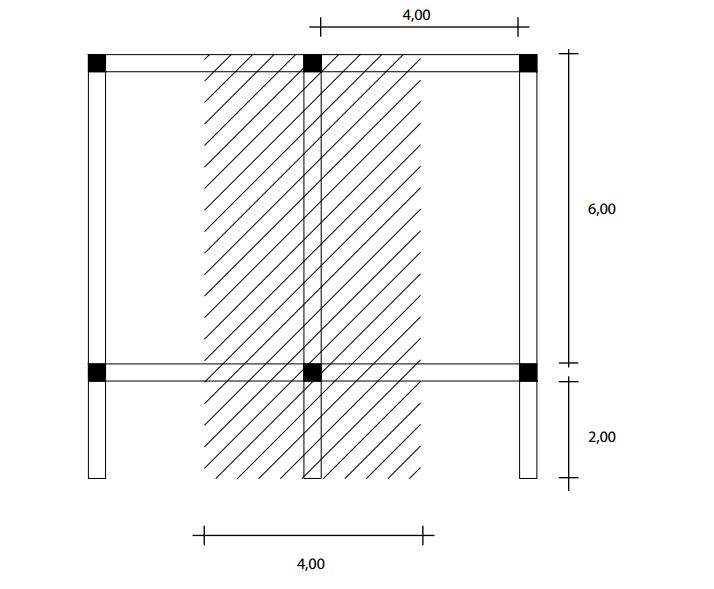
Riprendo la stessa pianta di carpenteria dell' Esercitazione I ( http://design.rootiers.it/strutture/node/1735 ) , una struttura composta da pilastri e travi, con l'aggiunta però dello sbalzo della mensola. La struttura è data da tre travi di luce 8m, delle quali 2m in aggetto. Prendo in esame la mensola maggiormente sollecitata, quella centrale.

Il foglio elettronico che prendiamo è diviso in due parti. Una parte uguale a quella della prima esercitazione, e quindi riguardanti problemi legati allo SLU, mentre nella seconda parte, quella che riguarderà la deformabilità, quindi ci troviamo in campo elastico, SLE.

Ovviamente le due analisi presuppongono coefficienti di sicurezza diversi, perchè nello stato limite ultimo si analizza il collasso, mentre nello stato limite di esercizio si considerano i fenomeni di deformabilità, ovvero fenomeni che non compromettono il funzionamento generale della struttura.

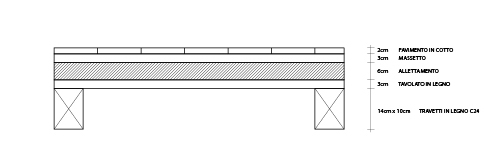
SOLAIO IN LEGNO

Prendo in esame lo stesso pacchetto di solaio della prima esercitazione, quindi la combinazione dei tre carichi, quello strutturale, non strutturale e variabile sono gli stessi.

Compilo quindi subito tutta la prima parte del file Excel.

Mi risulta quindi che: qu= 33,472 KN/m

e dopo aver posto la luce della mia mensola (2m) mi esce un valore del momento massimo pari

Mmax= 66,944 KN*m

Imposto ora i dati relativi al materiale di riferimento:

Scelgo un legno di classe C24, che ha come caratteristiche:

fmk = 24 N/mm2 (tensione caratteristica)

Kmod = 0.8

γ m = 1.45

ci troviamo a questo punto la tensione di progetto fd (N/mm2) = (Kmod x fmk) / γ m = 13.24

e ottengo per una base di 25cm un altezza minima di 34,83 cm che ingegnerizzo a 40cm.

Ora inizia la parte relativa allo SLE, ci troviamo il carico relativo al campo elastico qe.

Imposto il Modulo elastico pari a 8000 MPa ed ottengo una Ix = 133333 cm⁴

Infine arrivo a calcolarmi il mio spostamento massimo v_max= 0,35cm, che mi conferma il progetto poiché Ix/v_max >250.

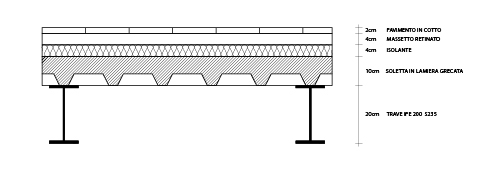
SOLAIO IN ACCIAIO

Prendo in esame lo stesso pacchetto di solaio della prima esercitazione, quindi la combinazione dei tre carichi, quello strutturale, non strutturale e variabile sono gli stessi.

Compilo quindi subito tutta la prima parte del file Excel.

Mi risulta quindi che: qu= 39.508 KN/m

e dopo aver posto la luce della mia mensola (2m) mi esce un valore del momento massimo pari

Mmax= 79.016 KN*m

Imposto ora i dati relativi al materiale di riferimento:

Scelgo un acciaio di classe S235, che ha come caratteristiche:

fyk = 235 N/mm2 (tensione caratteristica)

ci troviamo a questo punto la tensione di progetto fd (N/mm2) =  fyk / γ m ₀= 223.81 (con γ m ₀= 1.05)

Troviamo così il modulo di resistenza a flessione minimo uguale al rapporto Mmax/fd 

Wx,min = 353.05 cm³

Prendo la tabella delle sezioni IPE per trovare le dimensioni della trave portante, sapendo che la resistenza a flessione deve essere più grande di quella trovata.

Prendo una IPE 270, della quale il valore Ix= 5790 cm⁴

Adesso inizia la parte relativa allo SLE, poichè il foglio si calcola il q_e:
q_e =  23.921 KN/m
Come risultato avrò un v_max = 0,393 cm, dato che mi conferma il progetto poichè I_x/ v_max >250

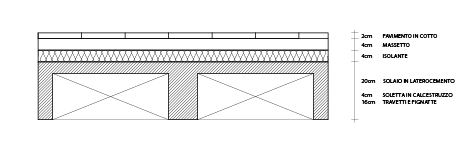
SOLAIO IN CEMENTO ARMATO

Prendo in esame lo stesso pacchetto di solaio della prima esercitazione, quindi la combinazione dei tre carichi, quello strutturale, non strutturale e variabile sono gli stessi.

Compilo quindi subito tutta la prima parte del file Excel.

dopo aver posto la luce della mia mensola (2m) mi esce un valore del momento massimo pari

Mmax= 83.66 KN*m

Scelgo un acciaio di classe S450, che ha come caratteristiche:

fyk = 450 N/mm2 (tensione caratteristica)

ci troviamo a questo punto la tensione di progetto fd (N/mm2) =  fyk / γ m = 391.30 (con γ m = 1.15)

Prendo un cls che abbia come tensione caratteristica fck = 60 N/mm^2, così da trovare la tensione di progetto

fcd= (0.85 x fck) / γm, con γm pari a 1.5.

Prendo il valore di β=0.57 e di r=2.09

Prendo un valore della base pari a 20cm per poi riuscire a trovare il valore di hu = 23.15 cm, con un copriferro δ di 4cm. L'Hmin viene di 27.15 cm che approssimo ad un altezza di 30cm.

Il foglio elettronico di excel verifica allora con i dati ottenuti se la trave presa in considerazione ha una tensione di progetto pari alla massima tensione esercitata in campata. In questo caso la trave è verificata.

Adesso inizia la parte relativa allo SLE, poichè il foglio si calcola il q_e:
q_e = (1qs + 1qp + 0,5qa) x interasse = 26.70 KN/m
Imposto il Modulo elastico del c.a. pari a 21000 MPa ed ottengo una I_x:
I_x = (b*h^3)/12 = 45000 cm⁴
Come risultato avrò un v_max = 0,57 cm, dato che mi conferma il progetto poichè I_x/ v_max >250