Portale di Meccanica

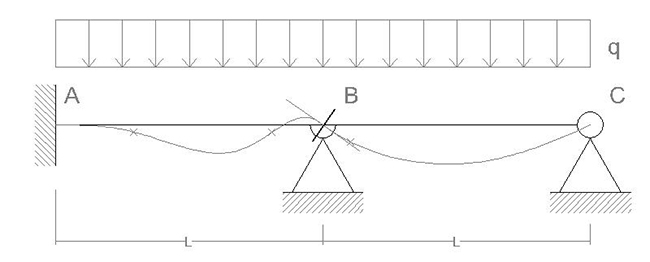
Questa struttura presenta alcune complicazioni che impongono di procedere con cautela, si tratta infatti di una struttura iperstatica priva di simmetrie e con una singolarità in mezzeria dovuta alla presenza di una cerniera che non interrompe la continuità della trave.

Possiamo comunque fare alcune ipotesi preliminari e poi valuteremo, applicando l’equazione della linea elastica, che queste ipotesi siano corrette.

LA DEFORMATA

Dal momento che la cerniera non interrompe la continuità della trave dobbiamo immaginare che localmente la deformata sia una curva continua, senza singolarità. Passando concettualmente dal modello di Bernoulli ad un modello tridimensionale, dobbiamo immaginare quello che fa la sezione in corrispondenza della cerniera B. Dal momento che la struttura non è simmetrica, dobbiamo immaginare che la sezione in B non stia ferma, ma ruoti dalla parte che è meno vincolata, quindi verso BC, verso destra, ovvero in senso orario.

Viceversa nell’ incastro A la rotazione è inibita dal vincolo ed invece è libera in C.

La deformata potrebbe essere quella di figura, poco proporzionata e molto accentuata.

IL MOMENTO

Alcune cose si possono dire anche del momento. Innanzitutto il carico è distribuito su entrambi i tratti della trave (tratti che definiamo non perché vi sia una discontinuità geometrica, ma vi è una discontinuità dovuta alla reazione vincolare in B) per questo motivo il momento sarà parabolico sia sul tratto AB che su quello BC. Le due parabole saranno diverse.

Entrambe si annulleranno nei punti di flesso (individuati in figura con delle X) poiché in essi cambia la curvatura della deformata. Dire che cambia la curvatura significa dire che la curvatura CAMBIA DI SEGNO. Il che vuol dire che in quel punto la curvatura si annulla. Visto che il momento è proporzionale alla curvatura (a meno del prodotto EJ che è costante e diverso da 0) nei punti dove si annulla la curvatura si annulla anche il momento.

Inoltre il momento si annulla anche nella cerniera C, mentre ha un valore nel punto B, in cui si trasmette momento per la continuità della trave. Nel punto B si ha un punto angoloso poiché in esso vi è una forza concentrata (la reazione vincolare) essa determinerà una irregolarità anche nel taglio.

IL TAGLIO

Il carico distribuito determina il fatto che il momento sia parabolico ed il taglio sia lineare, su entrambi i tratti, ma con inclinazioni ed andamenti diversi.

Quel che è certo è che in corrispondenza di B così come vi è un punto angoloso del momento, vi è un SALTO del taglio, salto che sarà uguale alla reazione vincolare della cerniera in B.

Infine il taglio si annullerà con certezza in due punti che sono i punti di vertice delle due parabole del momento, quella del tratto AB e quella del tratto BC. In questi punti infatti, la funzone momento, ha tangente orizzontale, il che equivale a dire che la derivata della funzione momento è nulla, ma la derivata della funzione momento è proprio la funzione taglio cambiata di segno, per cui in quei punti il taglio è nullo.

CONDIZIONI AL BORDO E DI CONTINUITA’

Innanzitutto dobbiamo chiederci di quante condizioni al bordo abbiamo bisogno. Per capirlo dobbiamo ricordarci che abbiamo diviso la trave idealmente in due tratti che si comportano in maniera diversa. A ciascuno dei due dobbiamo applicare l’Equazione della Linea Elastica, che integrata 4 volte presenterà 4 costanti di integrazione per tratto per un totale di 8.

E’ proprio di 8 condizioni che cerchiamo, e saranno sia di natura statica che cinematica.

BORDO A

In A c’è un incastro, è immediato dire che gli spostamenti sono inibiti, quindi anche quello verticale, come anche le rotazioni per cui:

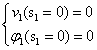
PUNTO B (condizioni di continuità)

In B, come abbiamo già visto, la continuità della trave è garantita, per cui, nonostante la presenza di una cerniera IL MOMENTO viene trasmesso e quindi NON E’ NULLO. Quel che è certo però è che esso è lo stesso sia a sinistra che a destra del vincolo.

Certamente sono inibiti gli spostamenti e quindi anche quelli verticali, e questa è una condizione doppia, poiché vale sia per il tratto AB che per quello BC.

Altra cosa che possiamo dire è che la continuità della trave ci dice che la ROTAZIONE RELATIVA è nulla, per cui la rotazione a destra e a sinistra è la stessa

Abbiamo quindi 4 condizioni, quelle sugli spostamenti e sulle rotazioni sono di natura cinematica, mentre quella sui momenti è di natura statica.

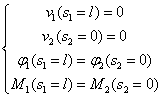
BORDO C

Nella cerniera sono libere le rotazioni quindi su di esse non possiamo dire nulla, sono inibiti gli spostamenti e quindi anche quelli verticali, ed è nullo il momento per cui:

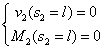
EQUAZIONE DELLA LINEA ELASTICA

L’ equazione della linea elastica è:

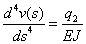
Essa va applicata ai due tratti, separatamente se le condizioni al bordo sono separate, e contemporaneamente quando le condizioni al bordo lo richiedono.

TRATTO AB	TRATTO BC

 

 

 

 

 

 

 

 

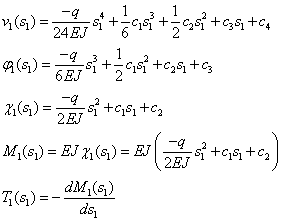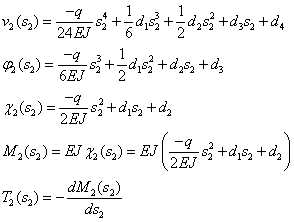Ora passiamo ad applicare alle giuste equazioni le condizioni al bordo:

PUNTO A

Dire che c’è un incastro in quel punto a sinistra, da dove iniziamo a contare le ascisse, equivale a dire che lo spostamento e la rotazione sono nulli, il che significa che le costanti c3 e c4 sono nulle.

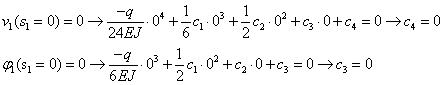
PUNTO B

Nel punto B avremo delle equazioni che comprendono sia le costanti c del primo tratto sia le costanti d del secondo tratto, mettendole in relazione tra loro, ma iniziamo con le equazioni che mantengono separate le costanti, che sono quelle riguardanti gli spostamenti:

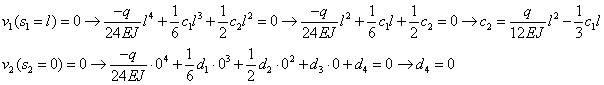
Vi sono poi le equazioni miste relative alle uguaglianze tra momenti e rotazioni. Per quanto riguarda il momento, stiamo considerando una trave continua, ma essa potrebbe essere continua anche se presentasse diversa sezione o se fosse di un diverso materiale nel primo e nel secondo tratto. Basterebbe infatti che fosse giuntata con continuità. Avremmo quindi dovuto considerare nei due tratti E1 e J1 ed E2 e J2 per diversi materiali e per diverse sezioni. Per semplificare però immaginiamo una trave continua per sezione e per materiale. Questo comporta che uguagliare i momenti significa in definitiva uguagliare le curvature, dal momento che nell’ uguaglianza dei momenti posso dividere a destra e a sinistra per EJ (che sono uguali nei due tratti).

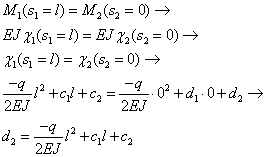
Infine passiamo all’ uguaglianza delle rotazioni (condizione inerente alla nullità della rotazione relativa).

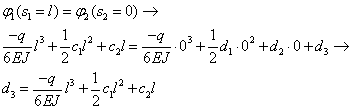
PUNTO C

Nel punto C abbiamo una condizione cinematica che riguarda la nullità dello spostamento e una condizione statica che riguarda la nullità del momento, a cui corrisponde la nullità della curvatura dal momento che EJ è sempre diverso da 0.

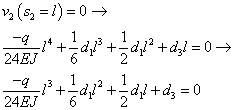
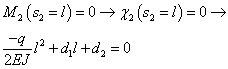
RIASSUMENDO

Ci ritroviamo con un sistema di 8 equazioni in 8 incognite, anzi, equazioni ed incognite sono di meno dal momento che alcune sono state definite come nulle. Indico con A il rapporto q/EJ.

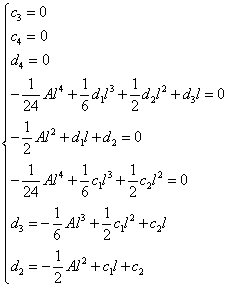
Se non avessi già apportato delle semplificazioni per l, quando necessario, mi accorgerei da dove proviene ciascuna delle equazioni, quelle di 4° grado in l derivano dagli spostamenti, quelle di 3° dalle rotazioni, quelle di 2° dai momenti.  Avendo abbassato di grado in alcuni casi non posso più determinarlo ad occhio.

E’ necessario risolvere il sistema:

Sostituiamo il d₂ della 8° equazione nella 5° equazione e troviamo d₁ in funzione di c₁ e c₂

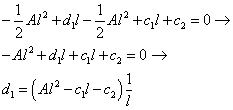
Sostituiamo il d₁ appena trovato ed i d₂ e d3 della 7° ed 8° equazione nella 4° equazione e troviamo c₂ in funzione di c₁

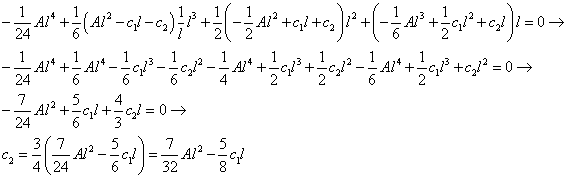
Sostituiamo il c₂ appena trovato nella 6° equazione e troviamo c₁:

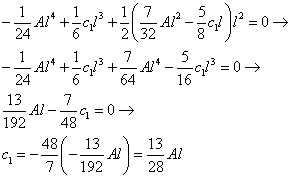
Sostituiamo il c₁ appena trovato nelle altre costanti che sono scritte in sua funzione e avremo tutte le costanti a cascata:

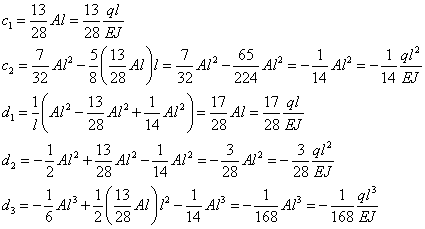
Ora che abbiamo tutte le costanti, riscriviamo le equazioni della linea elastica:

TRATTO AB	TRATTO BC

 

 

 

 

 

 

 

 

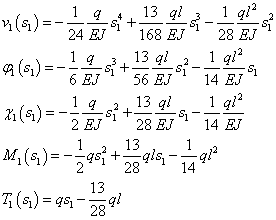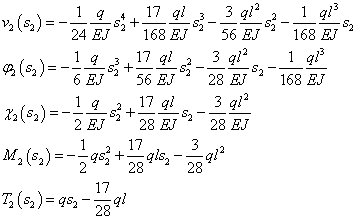Adesso che abbiamo tutte le funzioni possiamo descrivere il comportamento della struttura in ogni punto.

TAGLIO

Iniziamo dal taglio: valutare i punti dove si annulla significa trovare i punti di vertice delle parabole del momento. Calcoliamo il Taglio nei punti notevoli e poi vediamo dove si annulla:

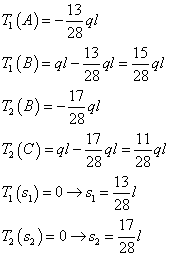
Se prima avevamo ipotizzato un andamento, ora possiamo disegnarlo quantitativamente:

MOMENTO

Per quanto riguarda il momento, nei punti dove si annulla il taglio avremo i vertici delle parabole, ma ci servono altri due punti notevoli, che sono quelli dove si annullano le curvature della deformata nei due tratti. Ci calcoliamo prima questi e poi il momento nei punti notevoli, iniziamo dal tratto AB

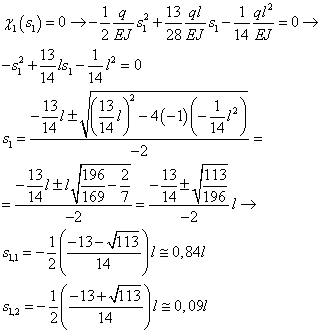
E poi il tratto BC:

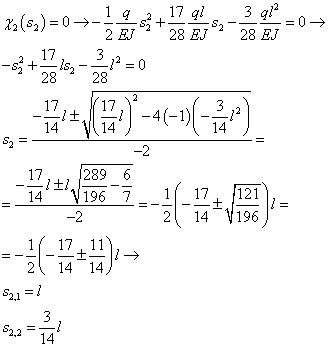
Calcoliamo il momento nei vincoli A e B (in C è 0) e nei punti di vertice delle parabole che sono quelli per cui si annulla il taglio:

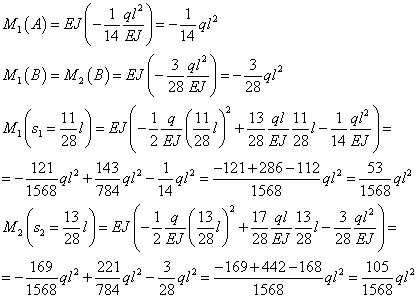
Ora è possibile disegnare il grafico del momento:

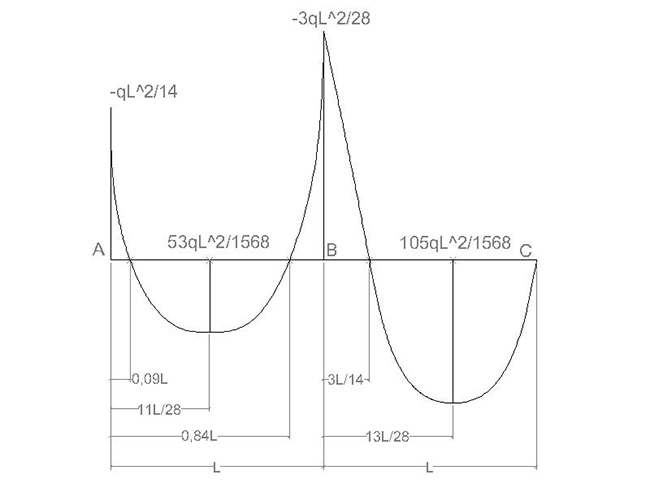
REAZIONI VINCOLARI

In ultimo, possiamo indicare i valori delle reazioni vincolari. Esse infatti sono le azioni di contatto che si trasformano in reazioni vincolari sui bordi, appena fuori dalle travi:

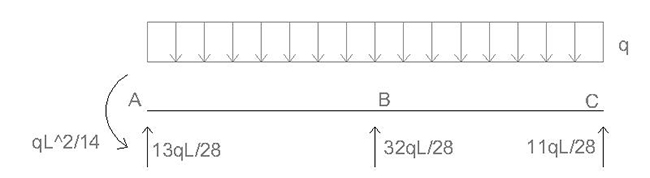
Come si vede, la reazione vincolare della cerniera in B è pari al salto che c’è nel taglio poiché essa si comporta, per il taglio e per il momento, come un carico concentrato, determinando un salto ed un punto angoloso. Essa è diretta verso l’alto, a dimostrazione del fatto che quel vincolo “lavora” per contrastare il desiderio della trave di inflettersi in quel punto.

Il sistema è equilibrato infatti le tre reazioni sono concordi e bilanciano alla traslazione verticale il carico così come accade per il momento.

Avremmo potuto praticare degli opportuni tagli di Cauchy per verificare che le reazioni vincolari sono esattamente queste, tenendo sempre conto della corretta convenzione di segno.

FIG. 01

La FIG. 01a mostra una trave 2 volte iperstatica soggetta ad un carico q, distribuito e costante, e la sua deformata. Aggiungendo 2gdv (cioè posizionando una cerniera al centro della trave) si ottiene una trave 4 volte iperstatica. Osservando le due deformate, si può intuire come la cerniera sviluppi una reazione vincolare F_By che tende a riportare la deformata (a) verso l'alto (b).  

La struttura, essendo iperstatica, non consente di calcolare immediatamente le reazioni vincolari, che si sviluppano in corrispondenza dei vincoli, con le sole equazioni di equilibrio, come si potrebbe fare in presenza di una struttura isostatica. Per arrivare a delle soluzioni quantitative sarà necessario ricorrere al metodo della linea elastica.

Per ora possiamo solo fare alcuni ragionamenti di tipo qualitativo, che saranno poi verifiati dai calcoli successivi.

La struttura è soggetta ad un carico distribuito di natura costante -> Taglio=lineare | Momento=parabolico

La deformata presenta 3 punti di flesso-> il momento si annullerà 3 volte in corrispondenza dei flessi

Vincolo di incastro -> rotazione nulla

Vincolo di cerniera -> momento nullo 

Queste informazioni insieme all'analisi dei tratti in cui le fibre superiori o inferiori sono tese ci permettono di suppore ed immaginare un diagramma dei momenti e del taglio come in FIG. 02

FIG. 02

Per studiare la struttura iperstatica della FIG. 01b è necessario applicare 2 volte il metodo degli spostamenti, poichè la struttura presenta una singolarità. In tal modo si avrà un'equazione della linea elastica per il primo tratto lungo L (che indicheremo con i pedici ₁) e un'altra equazione della linea elastica per il secondo tratto lungo sempre L (che indicheremo con i pedici ₂).

Nel caso specifico q₂= -q ed il modulo di elasticità E con il momento d'inerzia J, assumono lo stesso valore, trattandosi del medesimo materiale e della stessa sezione. Si ricavano le seguenti equazioni:

Abbiamo perciò 8 incognite, 4 per il primo tratto e altre 4 per il secondo tratto. Le prime vengono individuate con la lettera c e le seconde con la lettera d. Sarà necessario definire 8 condizioni al bordo, utili per ricavare le 8 incognite. 

Di conseguenza il punto A fornisce 2 informazioni che corrispondono alle 2 equazioni:

Il punto B fornisce 4 informazioni che corrispondono alle 4 equazioni:

Il punto C fornisce 2 informazioni che corrispondono alle 2 equazioni:

Le soluzioni che si ricavano da queste 8 equazioni sono:

Questi risultati li sostituiremo nelle equazione iniziali ottenendo v₁(s₁) e v₂(s₂):

 v₁(s₁) e v₂(s₂) forniscono tutte le informazioni necessarie a ricavare i diagrammi delle sollecitazioni, dai quali si possono ricavare le reazioni vincolari.

Iniziando dalle sollecitazioni di taglio, si va a calcolare il T₁(s₁) e T₂(s₂)in s=0 e in s=L, poichè in questo caso il Taglio è una funzione lineare bastano 2 valori per definirne il grafico:

Il momento invece è descritto da una funzione di secondo grado quindi è rappresentato da una parabola che per essere disegnata ha bisogno di tre valori. 

Una volta ricavati i valori possiamo disegnare i diagrammi:

Dai diagrammi ricaviamo le reazioni vincolari:

cari ragazzi

l'ulteriore revisione strutturale è fissata per mercoledì 23 Aprile, alle ore 12:30 presso il Laboratorio di Meccanica. 

la Prof.

Esercizio in classe:

La linea elastica:

Hp: trave a sezione costante e uniforme

1)analisi delle  condizioni al bordo ,incastro (A) cerniera (C) :

-condizioni cinematiche

-condizioni statiche

 

 

Condizione di CONTINUITA' della trave : cerniera (B)