ABSTRACT: Argomento del post saranno particolari di strutture 2D che agiscono per forma. Già sono state trattate in tal senso le strutture reticolari, le quali forzano e canalano le forze in termini di sforzo normale consentendo un'ottimizzazione del materiale e costi minori. In questo caso osserveremo il comportamento degli archi, particolari strutture caratterizzate nella loro modellazione più semplice da una iperstaticità esterna compensata da una labilità interna che si verifica nella cerniera esterna che collega le due travi di cui si compone, rendendo complessivamente l'arco complessivamente isostatico. Si vedranno tre tipologie di archi (a tutto sesto, ribassato e parabolico) e come nelle esercitazioni precedenti il risultato algebrico verrà verificato e confrontato con l'analisi computazionale.
Comincio con l'analizzare una gerica struttura ad arco riguardo le sue solo reazioni vincolari: per semplicità confronterò prima un arco a tutto sesto poi due mensole su pilastri vincolati alla base su cerniere e uniti da una cerniera interna. Si verificherà che indipendentemente dalla geometria le reazioni vincolari non cambiano data una freccia f (altezza dalla base), la proiezione dell'arco a terra l e un carico uniformemente distribuito q.
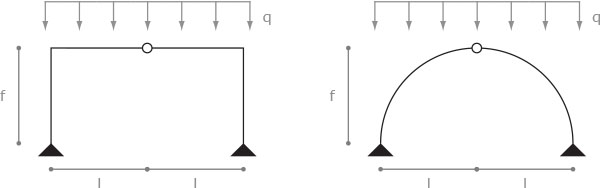
Studiamo il primo caso. Possiamo spezzare la struttura come segue ponendo attenzione alla compatibilità cinematica della struttura: dobbiamo porre infatti due forze c e d tali da garantire che la cerniera interna che essa sia compatibile anche con la parte non analizzata.
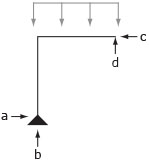d non può che essere nulla per simmetria della struttura perciò attraverso le 3 equazioni all'equilibrio possiamo risolvere il sistema nelle tre incognite a,b e c.
EQL alla traslazione verticale b-ql=0 ⇒ b=ql
EQL alla traslazione orizzontale a=c
EQL alla rotazione (rotazione in cerniera interna) a.f-b.l+ql2/2=0 ⇒ a=ql2/2f
Si osserva che i calcoli sono dipesi solo dai bracci d'applicazione perciò senza ripetere ridondanti conti possiamo dire di conoscere le reazioni vincolari attraverso f, l e q.
Analizziamo ora i tre casi studio presentati.
ARCO A TUTTO SESTO
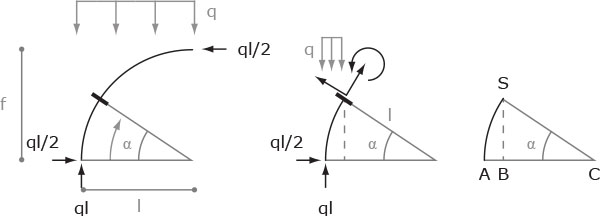
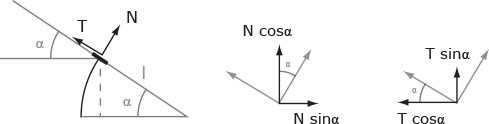
Dato un angolo α è possibile parametrizzare le sezioni dell'arco affinchè dipendano da esso. Per ogni sezione è così possibile scomporre nelle componenti verticali e orizzontali le azioni di contatto e conoscere l'entità agente del carico distribuito assegnato.
Se BC= l cos α e AB=AC-BC= l - cos α = l(1- cos α )f con α<π/2
EQL alla traslazione verticale N sinα- T cosα+ ql/2=0
EQL alla traslazione orizzontale N cosα+ T sinα+ ql - ql(1-cosα)=0
EQL alla rotazione M + ql2/2 sinα - ql l (1-cosα) - ql2(1-cosα)2/2=0
ARCO A SESTO RIBASSATO
I ragionamenti preliminari in questo particolare caso sono pressocchè analoghi ai precedenti se non per il fatto che α dovrà necessariamente essere maggiore di un α0 di partenza (e chiaramente minore di π/2) e che il centro di rotazione delle sezione è decentrato verticalmente.
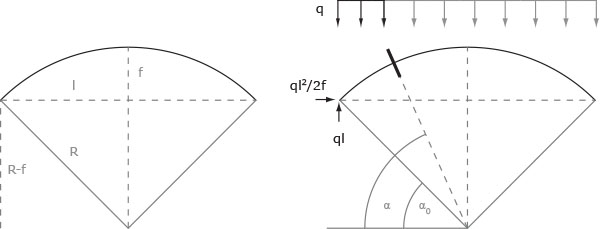
allora secondo il Teorema di Pitagora R2=(R-f)2+l2 ⇒ R2=R2 + f2-2Rf + l2 ⇒ R = l2 + f2 / 2f
e inoltre tg α0 = R-f / l
La sezione così schematizzata avrà che:
HC = R cosα
BH = BH - HC = l - R cosα
SH = R sinα
AS' = SH - AB = R sinα- R + f = R(sinα- 1) + f
EQL alla traslazione verticale N sinα- T cosα+ ql2/2f=0
EQL alla traslazione orizzontale N cosα+ T sinα+ ql - q(l-Rcosα)=0
EQL alla rotazione M + ((ql2/2f) (R(sinα- 1) + f) ) - q(l - R cosα)2/2 + ql (l - R cosα) =0
ARCO PARABOLICO
In questo ultimo particolare caso i ragionamenti riguardo la scelta dei parametri addetti al controllo delle sezioni lungo la trave sono dettati non da ragionamenti trigonometrici ma geometrico-analitici.
Dati infatti tre punti è possibile conoscere l'equazione della parabola corrispondente: attraverso la derivata di questa equazione conosciamo la tangente punto per punto e quindi l'angolo ß per il quale scomporre i vettori N e T.
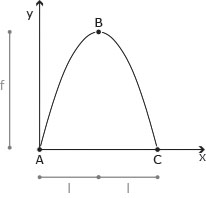A (0 , 0)
B (l , f)
C (2l , 0)
A, B, C ∈ P parabola di equazione generica ax2+bx+c=0
sostituendo i valori all'interno di P avremo 3 eqz in 3 incognite:
0=0+0+c
f=al2+bl+c
0=4al2+2bl+c
da cui ricaviamo mettendo a sistema l'equazione della parabola:
y= - fx2/l2+2fx/l
Calcoliamo ora la derivata y' per ottenere la tgßper ogni punto:
y'= tgß = - 2fx/l2+2f/l
Si nota che in x=0 tgß = 2f/l che è uguale al rapporto tra la componente verticale e orizzontale nel vincolo cerniera ql/ (ql2/2f) = tgα = 2f/l
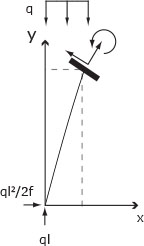
NB in questo caso specifo il disegno per la scomposizione delle forze in quanto differente rispetto i casi precedenti
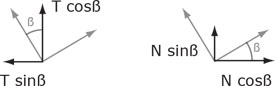
EQL alla traslazione verticale N cosß - T sinß+ ql2/2f=0
EQL alla traslazione orizzontale N sinß+ T cosß+ ql - qx=0
EQL alla rotazione -qlx + ql2/2f y + qx2/2 + M =0
È dovuto fare un'importante osservazione. Verifichiamo il comportamento del taglio: esplicitiamo nella prima equazione N per sostituirlo alla seconda.
N cosß / cosß = T sinß / cosß + ql2/2f . 1/ cosß = T tg ß + ql2/2f . 1/ cosß = 0
Sostituisco alla seconda equazione:
(T tg ß + ql2/2f . 1/ cosß) . sinß+ T cosß+ ql - qx = 0 ⇒
⇒ T (cosß + tg ß . sinß) - ql2/2f . (- 2fx/l2+2f/l) + ql - qx = 0
⇒ T (cosß + sinß . sinß / cosß) + qx - ql + ql - qx = 0
⇒ T (cosß2 + sinß2 )/ cosß = 0
⇒ T = 0 e quindi N = - ql2/(2f cosß)
Anche per il momento accade un fenomeno particolare:
-qlx + ql2/2f y + qx2/2 + M =0
⇒ ricordando che y=- fx2/l2+2fx/l ⇒ -qlx + ql2/2f . (- fx2/l2+2fx/l) + qx2/2 + M =0 = 0
⇒- qlx - qx2/2 + qlx + qx2/2 + M = 0
⇒M = 0
Per verificare attraverso SAP i risultati ottenuti e ottenere dei riscontri numerici relativi alle azioni interne N,T e M disegniamo in Autocad le tre tipologie.
Se per disegnare arco ribassato e a tutto sesto si dispone degli appositi strumenti non è la stessa cosa per il disegno della parabola (NB spezzare gli archi in prossimità della chiave). Inoltre SAP non accetta curve parametriche propriamente dette ma solo sue approssimazioni quindi dovremo disegnare la parabola come una serie di spezzate.
Per farlo ci serviremo di un foglio di calcolo in Excel il quale per come è stato realizzato fornirà una colonna di dati da copiare e incollare nel prompt dei comando durante il disegno di una polilinea (che dovrà poi essere esplosa).
Disegnate gli archi in Autocad li importiamo in SAP con le metologie già illustrate. Analogamente all'esercitazione sulla trave reticolare nel nodo in chiave applichiamo un rilascio del Momento attraverso la selezione del punto quindi Assign->Frames->Release/Partial Fixity, Moment 3-3
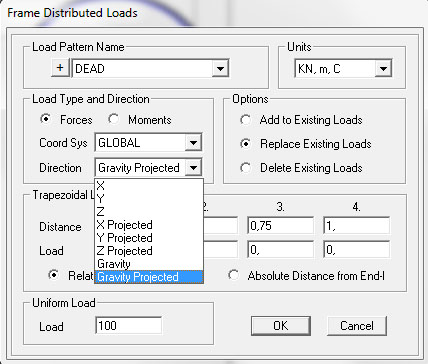
Applico inoltre una sezione 40x40 in Calcestruzzo con le caratteristiche di Default e applico un carico distribuito di 10KN in questo caso ponendo attenzione sulla spunta Gravity Projected analogamente a quanto viene realizzato durante lo svolgimento dei comuni esercizi.
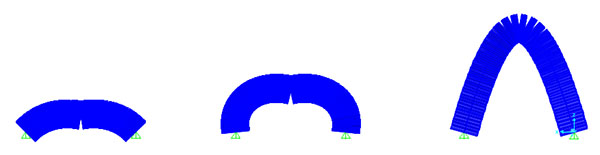
E qui i grafici dei risultati
DEFORMATA
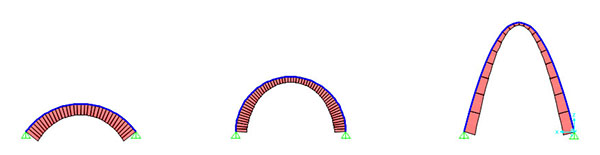
SFORZO NORMALE
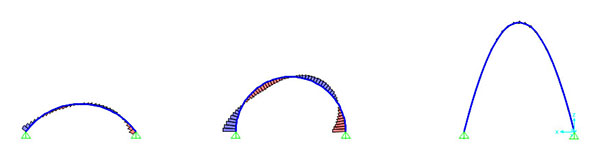
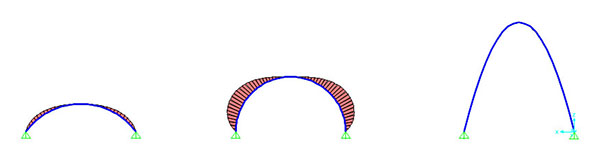
TAGLIO
MOMENTO
In allegato si può trovare la tabella relativa all'output delle azioni interne. Per capire a quale arco facesse riferimento i punti della tabella ho impostato diversi LoadPatterns e ho spuntato l'opzione Run uno alla volta.
SdC(b)
Commenti recenti