Portale di Meccanica

RISOLUZIONE DI UNA TRAVE VIERENDEEL MEDIANTE IL METODO DELLE RIGIDEZZE

Possiamo definire la RIGIDEZZA (K) il rapporto tra la FORZA (F) necessaria per imprimere uno spostamento e lo SPOSTAMENTO (δ).

F = k x δ

L’oggetto di questa esercitazione è la risoluzione di due travi di Vierendeel

 

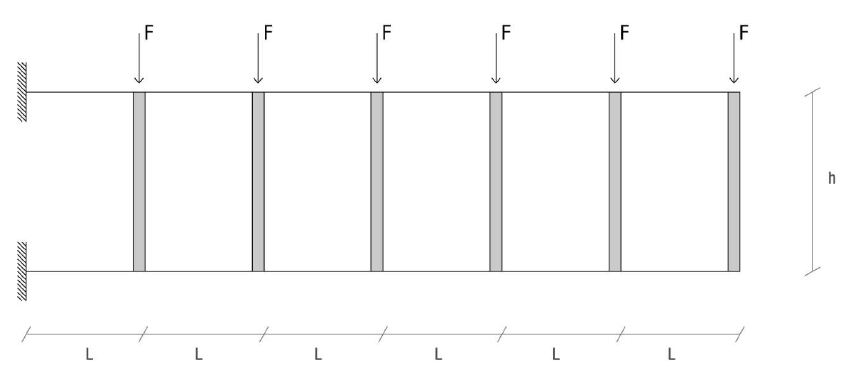
Dal punto di vista statico, il modello teorico della trave di Vierendeel si presenta come un telaio “SHEAR TYPE”

rovesciato. Nel telaio shear type la TRAVE presenta un’elevatissima RIGIDEZZA FLESSIONALE (infinita nel modello

ideale), mentre i PILASTRI sono ipotizzati INFINITAMENTE RIGIDI ASSIALMENTE (perché altrimenti la trave sarebbe

soggetta ad una rotazione rigida) pur consentendo le altre deformazioni. Pertanto, l’unico movimento che la trave può

compiere è la TRASLAZIONE ORIZZONTALE.

Una trave Vierendeel è una somma di telai Shear Type

La trave virendell  viene utilizzata perché il suo particolare comportamento permette di spezzare il diagramma del momento in ogni campata e ridurre i valori delle reazioni agli incastri.

Iniziamo con l’analizzare il modello shear type. Il portale ha una trave composta da un corpo rigido indeformabile, se applichiamo una forza F la trave non potendo ne deformarsi ne ruotare, è soggetta alla sola traslazione orizzontale  , che dipende dalla rigidezza dei pilastri.

La struttura si deforma come una trave doppiamente incastrata sottoposta a cedimento vincolare elastico sull'incastro.

Nonostante non ci siano carichi esterni, a causa del cedimento vincolare la trave si incurva. Dall’equazione della linea

elastica si ricavano i valori di rotazione, spostamento, momento flettente e taglio della trave.

TRAVE DI VIERENDEEL A MENSOLA

 

Dopo le considerazioni sopra riportate, posso dedurre che la deformazione della trave di Vierendeel a mensola sarà la seguente:

PILASTRI

 

In questo caso chiamo pilastri gli elementi orizzontali e travi gli elementi verticali.

Poiché i pilastri hanno la stessa rigidezza, le forze si ripartiranno in egual misura tra di essi.

Pertanto Il diagramma del taglio è il seguente:

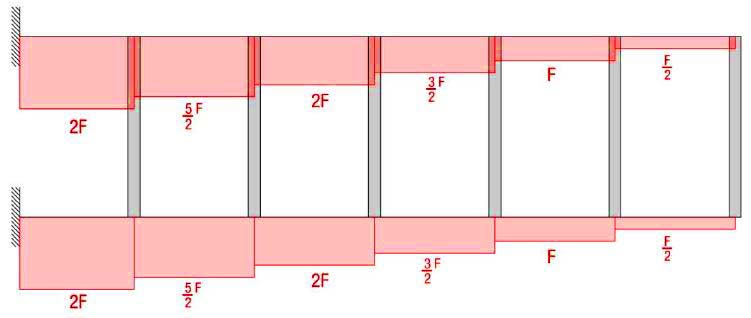
Per ottenere il momento flettente moltiplichiamo il taglio per la metà della luce

TRAVI

Attraverso l’equilibrio ai nodi posso calcolarmi taglio, momento e sforzo assiale degli elementi verticali.

 

Il diagramma dei MOMENTI nelle travi è il seguente:

Ottenuti i valori dei momenti, ci ricaviamo quelli del taglio facendo l'equilibrio alla rotazione dei pilastri, sommiamo i momenti e dividiamo per la luce del pilatro

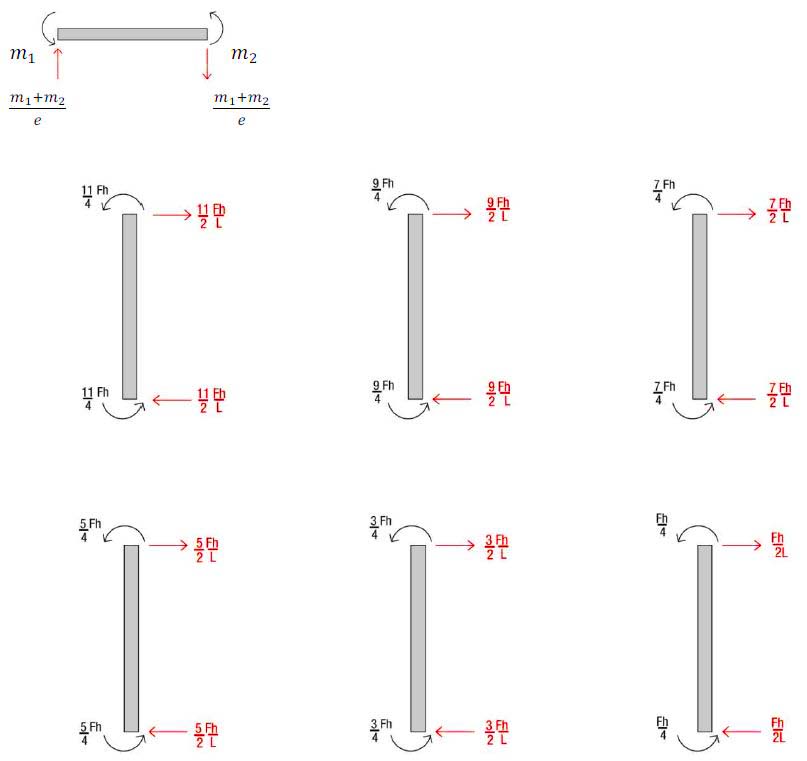
Il diagramma del TAGLIO nelle travi è il seguente:

SFORZO ASSIALE

Utilizzando l’equilibrio dei nodi, mi trovo lo sforzo assiale. Comincio dal CORRENTE SUPERIORE.

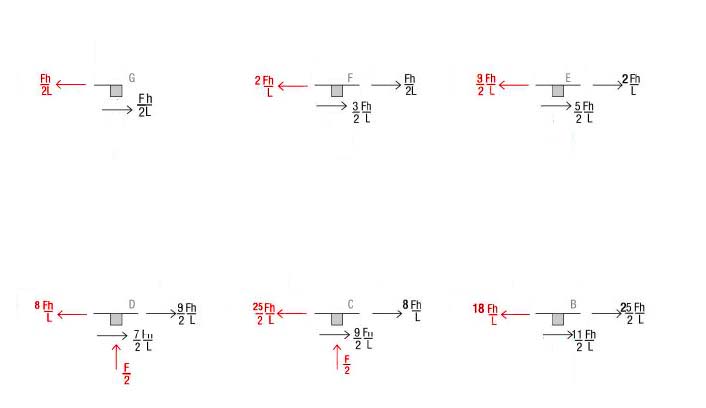
CORRENTE INFERIORE. Nel corrente inferiore i risultati saranno uguali ma opposti. Cioè i valori si ripeteranno nelle

aste del corrente inferiore, ma avranno verso opposto

diagramma degli SFORZI ASSIALI

Verifica dei risultati con SAP 2000

Verifico con SAP 2000 i risultati ottenuti dal calcolo manuale.

Dobbiamo però assegnare un materiale qualsiasi ed un profilo qualsiasi alle travi, mentre per i pilastri che devono essere INFINITAMENTE RIGIDI possiamo agire sulla sezione (cambiando così il momento d’inerzia) oppure sul materiale (cambiando il modulo elastico). In questo caso si è scelto di assegnare direttamente un modulo elastico “estremamente elevato” ed abbiamo ottenuto così i seguenti diagrammi e deformata.

Mando l’analisi e ottengo i seguenti risultati:

DEFORMATA

MOMENTO

TAGLIO

SFORZO ASSIALE

TRAVE DI VIERENDEEL DOPPIAMENTE INCASTRATA

A seguito delle considerazioni iniziali, posso facilmente ipotizzare che la struttura si deformerà nel seguente modo:

La struttura presenta SIMMETRIA geometrica e di carico. Nella trave D la forza esterna si ripartirà in ugual misura tra l’asta CD e l’asta DE (sia nel corrente superiore che in quello inferiore)

La forza si ripartisce in egual misura trai pilastri SOLO perché essi hanno tutti le stesse rigidezze.

Avrò 4 forze di F/4. Ora posso calcolarmi il taglio in tutti i pilastri.

TAGLIO: in una struttura con simmetria di CARICO e GEOMETRICA verrà specchiato e ribaltato (cioè i valori hanno segno opposto ma di ugual valore assoluto)

DIAGRAMMA DEL TAGLIO:

DIAGRAMMA DEL MOMENTO:

TRAVI: Tramite l’equilibrio ai nodi mi trovo TAGLIO e MOMENTO delle ASTE VERTICALI

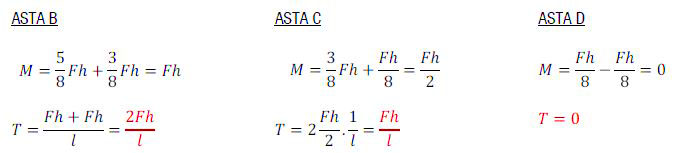
Ora posso disegnare il diagramma di TAGLIO e MOMENTO delle aste verticali (sempre seguendo le considerazioni fatte

precedentemente sui diagrammi di M e T in caso di simmetria geometrica e di carico):

DIAGRAMMA MOMENTO (travi):

DIAGRAMMA TAGLIO (travi):

Il titolo di questo seminario allude alla  consapevolezza che la progettazione strutturale è alla portata degli studenti e  delle studentesse di Architettura, a patto che si facciano i passi giusti all'interno di un processo di apprendimento graduale.

Il seminario si concentra solo sulla formula della flessione, ne analizza le implicazioni e crea un ponte concettuale tra le travi inflesse, le travature reticolari, le travi Vierendeel e le strutture ad arco. 

Anche uno studente che stia per terminare il corso di Fondamenti di Meccanica delle Strutture può seguire questo seminario e trarne frutto.

Buon lavoro
 

 

In allegato il PDF dello studio condotto per l'esame "Calcolo Automatico delle Strutture"

Graticcio di Travi

Un graticcio, al contrario di una gerarchia, è un modello composto da un sistema di travi ortogonali che collaborano tra loro reciprocamente.

Un parametro importante in un graticcio è la rigidezza torsionale (GJp/l) poichè la flessione in una direzione provoca inevitabilmente la torsione nella sua corrispettiva ortogonale.
Il termine Ip si riferisce al momento d'inerzia polare che varia a secondo della sezione presa in esame.

Mt = (GIp/l)ϕ

Il nodo ha 6 gradi di libertà: 3 traslazioni lungo i tre assi e 3 rotazioni intorno ai tre assi
In questo caso specifico avremo un abbassamento delle due travi che provocherà una rotazione nelle sezioni della trave AB che a sua volta provocherà una torsione della trave CD

Andiamo ad analizzare i due abbassamenti:

AB:

La forza F produce un abbassamento ᵟ della trave, conoscendo già i valori della rigidezza di una trave doppiamente appoggiata potremo ricavare gli sforzi di Taglio e Momento:

TAGLIO:  T= (12EJ/l³) ϭ              Ta= (324EJ/l³) ϭ               Tb= (81EJ/2l³) ϭ

MOMENTO: M= (6EJ/l²) ϭ              Ma= (54EJ/l²) ϭ               Mb= (27EJ/2l²) ϭ

BC:

Anche il nodo dell'asta CD, sotto il carico della forza F si abbassa senza ruotare:

TAGLIO:  T= (12EJ/l³) ϭ              Tc= (96EJ/l³) ϭ               Td= (96EJ/l³) ϭ

MOMENTO: M= (6EJ/l²) ϭ              Mc= (24EJ/l²) ϭ               Md= (24EJ/l²) ϭ

Ora andiamo ad analizzare la rotazione della sezione della trave AB:


Possiamo inserire i classici schemi notevoli già ricavati dalla questione della rigidezza flessionale per ricavare i momenti della trave:

 

MOMENTO: M= (4EJ/l) ϕ                 M= (2EJ/l) ϕ               

                  M1= (6EJ/l) ϕ               M2=Ma= (12EJ/l) ϕ

                  M3=Mb= (6EJ/l) ϕ         M4= (3EJ/l) ϕ

TAGLIO:     Ta= (54EJ/l²) ϭ             Tb= (27EJ/2l²) ϕLa rotazione della trave AB provoca una torsione della trave CD:

Il valore del momento torcente sarà:  (2GJp/l) ϕ

Conoscendo tutti i contributi degli sforzi di Taglio e Momento che agiscono sul nodo potremmo scrivere le due equazioni di equilibrio:

traslazione verticale:   ΣFz = 0     F= Taϭ- Taϕ+ Tcϭ+ Tbϭ+ Tbϕ+ Tdϭ          F= (1113EJ/2l³)ϭ- (81EJ/2l²)ϕ

equilibrio dei momenti:  ΣMy = 0     0=- Maϭ- Mbϭ + M2ϕ+ M3ϕ+ Mtϕ + Mtϕ          ϭ/2= ϕ[(38+8α)/81]

Sostituiamo ϭ/2 all'interno della prima equazione per trovare l'incognita rotazionale ϕ:

ϕ = Fl² / [EJ((1231/6)+(1484/27)α)]