Portale di Meccanica

RIPARTIZIONE DELLE FORZE ORIZZONTALI IN UNA STRUTTURA IN CEMENTO ARMATO

In questo esercizio si analizza una struttura a telaio in cemento armato, con lo scopo di ricavare la rigidezza nei confronti delle forze orizzontali di ciascun telaio di cui essa è composta, la posizione del centro di massa della struttura, quella del centro delle rigidezze e in base alla distanza tra questi ultimi gli spostamenti che la struttura compie sotto l’azione di un sisma, considerando come si ripartiscono le forze orizzontali sui diversi telai.

Il primo passo consiste nel calcolare la rigidezza di ogni telaio in cemento armato. Questo valore è strettamente legato alla rigidezza dei singoli pilastri che lo compongono, definita dalla geometria e il materiale di cui sono composti.

In questa tabella sono riassunti i valori delle rigidezze di nostro interesse e le distanze a cui i telai si trovano rispetto all’origine, fissata nel vertice inferiore sinistro della pianta.

Successivamente vengono calcolate le coordinate del centro di massa, mediante una semplice media ponderata che considera la posizione del baricentro e l’area di ognuna delle figure archetipe in cui la pianta è suddivisa.

Il calcolo della posizione del centro delle rigidezze dipende dalla rigidezza dei singoli telai e dalla loro posizione rispetto all’origine. Una seconda media ponderata, che tiene conto della rigidezza totale lungo i 2 assi cartesiani di riferimento.

La sommatoria del prodotto tra la rigidezza di ogni telaio e il quadrato della sua distanza dal centro delle rigidezze porta al valore della rigidezza rotazionale. A parità di rigidezza infatti maggiore è la distanza che il telaio ha rispetto al centro delle rigidezze e maggiore è il contributo che fornisce nella limitazione degli spostamenti.

L’analisi dei carichi è necessaria per determinare la forza sismica che agisce sulla struttura. Infatti come è noto sono le strutture pesanti a soffrire di più i sismi. I carichi al metro quadro dei pesi permanenti e accidentali, moltiplicati per l’area dell’impalcato, per il coefficiente di contemporaneità e successivamente divisi per il coefficiente di intensità sismica portano al valore della forza sismica orizzontale.

L’ultimo passo consiste nel ricavare la forza che si ripartisce sui singoli telai. La forza sismica orizzontale è applicata sul centro delle masse, generando una traslazione dell’impalcato nella sua direzione: essa si determina dividendo la forza per la rigidezza nella direzione corrispondente. Ma la non coincidenza del centro delle masse con il centro delle rigidezze provoca anche una rotazione dell’impalcato, per via del momento torcente che in questo modo si genera, che dipende proprio dal prodotto tra la forza orizzontale equivalente e la differenza tra le ascisse e le ordinate dei 2 centri (che quindi portano ad avere 2 valori di momenti torcenti).

L’entità della rotazione dell’impalcato si ottiene dividendo i momenti torcenti per la rigidezza rotazionale. Queste 2 grandezze sono dimensionalmente coerenti, infatti la rotazione è adimensionale.

Grazie ai dati ottenuti è possibile calcolare la forza orizzontale che ogni telaio sarà chiamato a controventare. Nell’esempio preso in considerazione essa è per la maggior parte dovuta allo spostamento e in minima parte alla rotazione, per via dell’enorme differenza che sussiste tra la rigidezza rotazionale e quelle di traslazione (tra le 20 e le 40 volte più piccola) e del valore del momento torcente, che è solo la metà della forza sismica orizzontale.

In questa esercitazione dovremo analizzare un impalcato strutturale soggetto a forze orizzontali. Lo studio verterà sul calcolo della rigidezza traslante K_δ, della traslazione δ lungo la direzione della forza agente, sulla rigidezza rotazionale K_φ e quindi sulla rotazione φ intorno al centro delle rigidezze.

Questo impalcato è formato da 7 telai ognuno dei quali comprende pilastri di grandezza 30x20cm, da cui i momenti d’inerzia:

STEP 1

In questo step si tabellano i telai dando ad ognuno dei dati precisi che sono: modulo di Young (E), altezza H e i valori dei momenti d’inerzia per ogni pilastro in base all’asse di rotazione. Si può quindi procedere al calcolo della rigidezza traslante K_δ di ogni telaio.

K_δ = ΣK_δ                Κ = 12EI/h³

STEP 2

In questo step raccoglieremo tutte le informazioni analitiche delle distanze dei vari telai da un punto di origine O e i valori delle rigidezze traslanti dei telai.

STEP 3

Ora bisognerà trovare il centro delle masse. Il passaggio è abbastanza semplice: si divide la forma della pianta in forme semplici con cui abbiamo facilità nel trovare il baricentro, a questo punto si tratta solo di attuare una media ponderata tra le aree delle suddette forme semplici e moltiplicarle con le distanze dal punto di origine.

G_X = [(X₁*A₁)+ (X₂*A₂)] / A_TOT

G_Y = [(Y₁*A₁)+ (Y₂*A₂)] / A_TOT

STEP 4

Quindi ora si passa alla determinazione del centro delle rigidezze (C).

X_C = (∑_i K_iv * d_iv) / K_{v_tot}                       Y_C = (∑_i K_io * d_io) / K_{o_tot}

Una volta trovato il centro delle rigidezze si dovranno calcolare le distanze di ogni telaio da C. A questo punto siamo in grado di calcolare la rigidezza torsionale K_φ.

Kφ = ∑i Ki * ddi2

STEP 5

Si esegue ora l’analisi dei carichi sismici allo SLE (perché non viene tenuto in conto γ) tramite il carico permanente totale G (somma dei carichi per l’area dell’impalcato) ed il carico totale accidentale Q (carico accidentale per l’area). Ne consegue che vi possiamo determinare i pesi sismici W: W = G + (Q * y).          y=coefficiente di contemporaneità.

Si procede dunque a trovare la forza sismica orizzontale F: F = W / c.    c=coefficiente di intensità sismica.

STEP 6-7

Siamo quindi in grado di quantificare la forza sismica orizzontale F lungo i due assi x/y per ogni controvento. Non essendo nello stesso punto il centro delle masse e il centro delle rigidezze il sistema ruoterà dando vita ad una traslazione δ ed una rotazione σ. Questa rotazione genera un momento torcente M che dovremo andare a calcolare.

Asse X:

M = F *(Y_c – Y_G)

F_oi = K_oi (u_x + dd_oi * φ)

F_vi = K_vi (dd_vi * φ)

Asse Y:

M = F *(X_c – Y_G)

F_oi = K_oi (dd_oi * φ)

F_vi = K_vi (u_y + dd_vi * φ)

Trave Vierendeel doppiamente appoggiata

Possiamo immaginare la nostra trave come una sequenza di cinque strutture shear-type unite insieme.
Un telaio shear-type prevede una trave infinitamente rigida che non si deforma con il deformarsi dei pilastri.

Per quanto riguarda i carichi immaginiamo di avere una sequenza di forze concentrate F sui nodi.

Prima di andare a calcolare tagli e momenti della struttura possiamo scinderla in due parti. Il comportamento sarà simmetrico
nelle due parti del telaio.

A questo punto vado a calcolare il taglio nelle tre aste (metà struttura):

T(0-1)=5F/4

T(1-2)=3F/4

T(2-3)=F/4

Faccio lo stesso per quanto riguarda il momento:

M(0-1)=5Fl/8

M(1-2)=3Fl/8

M(2-3)=Fl/8

Conoscendo tagli e momenti sarà ora possibile calcolare il momento in ogni singola trave dei vari telai shear-type che compongono la struttura.
Ogni asta è soggetta ai momenti dei due pilastri che la incontrano:

Asta(1) = [5Fl/8] + [3Fl/8] = Fl

Asta(2) = [3Fl/8] + [Fl/8]   = Fl/2

Asta(3) = Fl/8

Ora sapremo che nel calcolo dei tagli dei pilastri dovremo equilibrare i momenti agenti nei pilastri.

So che la rigidezza è uguale in tutti i pilasti [(12EJ/l^3)*δ]  mentre a variare è il taglio.

T(0-1)= 5F/4 = (12EJ/l^3)*δ           F(0-1)= 48EJδ/5l³                    δ= 5Fl³/48EJ                                     

T(1-2)=3F/4 = (12EJ/l^3)*δ            F(1-2)= 16EJδ/l³                      δ= Fl³/16EJ

T(2-3)=F/4 = (12EJ/l^3)*δ             F(2-3)= 48EJδ/l³                       δ= Fl³/48EJ

Trave Vierendeel doppiamente incastrata:

Come accennato all’inizio dell’esercitazione la seconda parte è dedita allo studio della stessa struttura analizzata in precedenza, con l’unica differenza che non sarà più a mensola ma sarà doppiamente incastrata agli estremi. In questo caso possiamo sfruttare la simmetria della struttura.

Lavoriamo come nell’esercizio precedente e quindi andiamo a calcolare il taglio sulle travi. In questo caso però bisognerà stare attenti perché nel punto 4, baricentro della simmetria, avremo una forza suddivisa in F/2 a destra e F/2 a sinistra.

Dal valore del taglio ne deriviamo quello di momento (moltiplico il taglio per metà della luce):

M₄= F/4 * L/2 = FL/8

M₅= 3F/4 * L/2 = 3FL/8

M₆= 5F/4 * L/2 = 5FL/8

A questo punto possiamo riportare i momenti agenti sui pilastri, ricordandoci di unire il momento nel punto 4 a destra e a sinistra:

Ovviamente i punti 3 e 2 saranno gli opposti dei punti 5 e 6.

Ora, avendo i valori dei momenti, determiniamo il valore del taglio dei pilastri:

T₆ = (FL + FL) / L = 2F

T₅ = (FL/2 + FL/2) / L = F

Andiamo quindi a calcolare il valore degli spostamenti:

F/4 = T = 12EI/L³ * δ₄ --> δ₄ = FL³/48EI

F = T = 12EI/L³ * δ₅ --> δ₅ = FL³/16EI

3F/2 = T = 12EI/L³ * δ₆ --> δ₆ = 5FL³/48EI

Possiamo quindi disegnare la nostra deformata:

            Verifica in SAP2000

Come abbiamo fatto per l’esercizio precedente risolviamo la struttura in SAP, ricordandoci sempre di dare una rigidezza infinita ai pilastri:

Deformata:

Taglio:

Momento:

In questa esercitazione andremo a studiare il comportamento di vari telai Shear Type sovrapposti l’uno all’altro e ribaltati in modo da costituire un sistema di trave che per la sua conformazione avrà delle sollecitazioni inferiori rispetto ad un sistema standard.

Studieremo due casi: il primo quando la nostra trave sarà disposta a mensola mentre il secondo quando la trave sarà incastrata da ambedue le parti.

Trave Vierendeel a mensola:

Come abbiamo detto prima la trave Vierendeel è costituita da vari telai Shear Type (nel nostro caso 6) sovrapposti l’uno sull’altro, questo ci consente di usufruire del metodo di risoluzione sfruttato nell’esercitazione del telaio Shear Type.

Il telaio Shear Type ci consente di avere un momento pari a 0 nella mezzeria del pilastro. Questo è un enorme aiuto nel caso si duplichi il telaio più volte dato che i vari segmenti sono disassociati l’uno rispetto all’altro e quindi i valori di momento e taglio diminuiscono ogni qual volta si studia il telaio successivo. Tutto questo ovviamente comporta che i vari segmenti siano della stessa sezione e materiale in modo che il coefficiente di rigidezza sia uguale per ogni segmento. Ciò comporta che ogni segmento abbia un taglio pari alla metà della forza agente. Ovviamente se nel telaio Shear Type si parlava di pilastri deformabili e travi non deformabili, nel sistema di trave Vierendeel sarà l’opposto.

Una volta saputo il taglio si può quindi procedere al calcolo del momento flettente massimo in corrispondenza degli incastri. Per far ciò è sufficiente moltiplicare il valore del taglio del segmento corrispondente per la metà del braccio, ossia L/2:

M₁= F/2 * L/2 = FL/4

M₂= F * L/2 = FL/2

M₁= 3F/2 * L/2 = 3FL/4

M₁= 2F * L/2 = FL

M₁= 5F/2 * L/2 = 5FL/4

M₁= 3F * L/2 = 3FL/2

Trovati i valori di momento sui segmenti di trave andiamo a vedere come gli stessi si trasmettono al pilastro indeformabile e quanto dovrà essere il momento contrastante di ogni pilastro:

Ne deriviamo cosi il diagramma degli sforzi di momento:

Una volta calcolati i momenti flettenti sul pilastro siamo pronti per calcolare il valore del taglio. Essendo ai due estremi del pilastro i valori del momento uguali possiamo sommare i valori tra di loro e dividerli per la luce in modo da avere il valore del taglio.

T₁ = (FL/4 + FL/4) / L = F/2

T₂ = (3FL/4 + 3FL/4) / L = 3F/2

T₃ = (5FL/4 + 5FL/4) / L = 5F/2

T₄ = (7FL/4 + 7FL/4) / L = 7F/2

T₅ = (9FL/4 + 9FL/4) / L = 9F/2

T₆ = (11FL/4 + 11FL/4) / L = 11F/2

Ora abbiamo il quadro completo. Tutte le forze e sollecitazioni sono state calcolate. Manca a questo punto solamente calcolare lo spostamento δ delle travi. Inizialmente avevamo imposto che tutte le travi avevano una sezione e un materiale uguale, questo implica che tutti i tratti di trave abbiano la medesima rigidezza che, come avevamo calcolato nell’esercizio del telaio Shear Type, ha un valore di 12EI/L³. Conoscendo, come già detto, il valore del taglio per ogni campata otteniamo:

F/2 = T = 12EI/L³ * δ₁ àδ₁ = FL³/24EI

F = T = 12EI/L³ * δ₂ àδ₂ = FL³/12EI

3F/2 = T = 12EI/L³ * δ₃ àδ₃ = FL³/8EI

2F = T = 12EI/L³ * δ₄ àδ₄ = FL³/6EI

5F/2 = T = 12EI/L³ * δ₅ àδ₅ = 5FL³/24EI

3F = T = 12EI/L³ * δ₆ àδ₆ = FL³/4EI

Da cui ne possiamo derivare la configurazione deformata:

            Verifica in SAP2000

Per la verifica in SAP2000 possiamo usare il modello “2D Frames”. Disegnamo la trave del nostro esercizio e impostiamo sezione e materiale. Per i pilastri però c’è bisogno di un coefficiente di rigidezza infinitamente elevato perché è indeformabile. Questo implica che il materiale assegnato ai pilastri sarà diverso rispetto a quello dato ai segmenti di trave. In questo modo sarà possibile determinare i valori giusti anche in SAP:

Deformata:

Taglio:

Momento:

Si chiama graticcio una struttura dove c’è una collaborazione tra due sistemi di travi più o meno ortogonali tra loro senza alcuna gerarchia, infatti l’intero sistema ha lo stesso momento d’inerzia (cioè i due sistemi di travi hanno la stessa sezione e stesso materiale) e i nodi sono tutti incastri che permettono il passaggio di momento e quindi il ripristino della continuità della trave.

Come già studiato nell’esercizio sulla rigidezza torsionale, anche nel graticcio questa entra in gioco grazie alla flessione di alcune  aste che provocano una torsione nella direzione a loro ortogonale.

La struttura analizzata è un graticcio semplice formato da due travi di lunghezza pari a 6m ortogonali tra loro e incastrate nell’asta BD nel punto di mezzeria, mentre nell’asta AC a 1/3 della lunghezza, con una forza F=10 KN applicata sul nodo centrale .

Se conosciamo gli spostamenti del nodo libero allora conosciamo anche quelli delle aste.

Trovandoci nello spazio tridimensionale, il nodo ha 6 gradi di libertà, esso può traslare e ruotare nelle direzioni x, y, z, ma per i vincoli che ci siamo dati sappiamo che in x e y il nodo non può traslare orizzontalmente altrimenti le aste si accorciano ed allungano, quindi è possibile il solo abbassamento  .

La rotazione attorno a z non ci sta perché non ci sono forze applicate, mentre abbiamo una rotazione attorno a y in quanto nell’asta AC la forza non è applicata al centro ma ad 1/3 quindi la tangente alla deformata non è orizzontale. Le incognite di spostamento che abbiamo sono due  ,

Con il metodo della sovrapposizione degli effetti possiamo studiare come la struttura reagisce ai nostri due parametri di spostamento facendoli agire uno per volta.

Facciamo agire solo l’abbassamento

Grazie agli schemi notevoli di una trave doppiamente incastrata possiamo ricavarci i valori di taglio e momento flettente.

Nell’asta BD i due momenti sono uguali e contrari e si annullano, infatti questi riguardano una eventuale rotazione attorno all’asse x che in questo caso non abbiamo.

Facciamo agire solo la rotazione

Sempre grazie agli schemi notevoli di una trave doppiamente incastrata con una rotazione applicata ad un estremo, possiamo ricavarci valori del taglio e momento

La flessione della trave AC intorno all’asse y corrisponde inevitabilmente alla torsione di quella BD:

Applicando la sovrapposizione degli effetti al nodo centrale, otteniamo le seguenti forze

Mettendo a sistema le due equazioni

VERIFICA IN SAP

Verifichiamo con SAP la sezione in calcestruzzo calcolata a mano, e come nell'esercizio della rigidezza torsionale fatto in precedenza, con le altre sezioni scelte, cioè:

.         Sezione RETTANGOLARE in CALCESTRUZZO ARMATO

·         Sezione CIRCOLARE PIENA in CALCESTRUZZO ARMATO

·         Sezione DOPPIA T in ACCIAIO

·         Sezione QUADRATA CAVA in ACCIAIO

·         Sezione TUBOLARE in ACCIAIO

DEFORMATA                                                                                     DIAGRAMMA MOMENTO

DIAGRAMMA TAGLIO                                                                              DIAGRAMMA TORSIONE

I risultati ottenuti sono stati riassunti in una tabella

Il telaio Shear Type indica la configurazione di una struttura di tipo “portale”. La caratteristica insita a questo telaio è l’indeformabilità della struttura orizzontale la quale fa si che il portale si possa deformare nei soli pilastri, che comunque hanno un movimento limitato dagli incastri alla base e al colmo degli stessi.

Prima di tutto però è bene definire il concetto di rigidezza (k) in quanto è il valore più influente per definire lo spostamento (δ).  La rigidezza è una costante derivata dal materiale che indica la quantità di forza necessaria ad imprimere una deformazione di spostamento unitario, difatti: F=k*δ . Quindi, maggiore è la rigidezza e maggiore dovrà essere la forza impressa per deformare il corpo.

Abbiamo detto dunque che la trave è indeformabile e che vi è mancanza di rotazione  agli estremi quindi và da se che la trave si muove con atto di moto rigido e le deformazioni sono insite nei soli pilastri. Essendo alla base ancorati al terreno, nel caso ci sia (come nel nostro caso) una forza orizzontale spingente (di cui tra l’altro si conosce il valore), l’unico spostamento sarà nel colmo del pilastro e sarà, per tutto quello che abbiamo detto prima, uguale a quello dell’altro pilastro. Lo spostamento derivato definirà il valore δ e darà vita a deformazione di curvatura χ e conseguente momento M, a prescindere dalla quantità del carico.

Tramite l’integrazione della linea elastica:

Essendo in questo caso in assenza dicarico:

Analizziamo le condizioni al bordo:

ESTREMO BASE

ESTREMO COLMO

Possiamo quindi riportare le equazioni di spostamento e rotazione:

Derivando la rotazione si avrà la curvatura e quindi il momento flettente M e il taglio T.

Da queste si possono diagrammare gli sforzi.

Qui sopra si possono vedere i valori delle reazioni vincolari nel pilastro, ma essendo strettamente collegate alla trave sappiamo che i valori vengono trasmessi all’interno della stessa:

Calcoliamo ora lo spostamento d tramite l’equilibrio alla traslazione orizzontale del corpo rigido (trave):

In questa esecitazione analizzeremo l’effetto della torsione su un telaio, 12 volte iperstatico e in seguito attraverso SAP2000 analizzeremo come la rigidezza torsionale del telaio varia in base alle scelte progettuali ( differenti materiali e geometria nella sezione delle travi e pilastri).

Analizzando il telaio preso in esempio e notiamo come il carico ripartito sull’asta AB produce una momento Ql²/2 corrispondente al nodo B.

Nel piano ZX la rotazione ϕ antioraria del momento provoca uno spostamento o una deformata che si traduce in FLESSIONE nella trave BC e pilastro BD. Dove c’è curvatura c’è momento flettente. Viene chiamata così in causa la rigidezza flessionale a rotazione della trave e del pilastro.

Nel piano XY il momento provoca una rotazione che si traduce in torsione della trave BE, quindi un momento torcente (Mt) momento uguale ed opposto al momento flettente al nodo B,  chiamando in causa la rigidezza torsionale della trave.

Rt = GJt/L

Analizzando il telaio preso in esempio e notiamo come il carico ripartito sull’asta AB produce una momento Ql²/2 corrispondente al nodo B.

Nel piano ZX la rotazione ϕ antioraria del momento provoca uno spostamento o una deformata che si traduce in FLESSIONE nella trave BC e pilastro BD. Dove c’è curvatura c’è momento flettente. Viene chiamata così in causa la rigidezza flessionale a rotazione della trave e del pilastro.

Analizzando il telaio preso in esempio e notiamo come il carico ripartito sull’asta AB produce una momento Ql²/2 corrispondente al nodo B.

 

Nel piano ZX la rotazione ϕ antioraria del momento provoca uno spostamento o una deformata che si traduce in FLESSIONE nella trave BC e pilastro BD. Dove c’è curvatura c’è momento flettente. Viene chiamata così in causa la rigidezza flessionale a rotazione  della trave e del pilastro.

 

Nel piano XY il momento provoca una rotazione che si traduce in torsione della trave BE, quindi un momento torcente (Mt) momento uguale ed opposto al momento flettente al nodo B,  chiamando in causa la rigidezza torsionale della trave. Rt= GJt/L

 

 

 

Equilibrio al Nodo (per trovarmi il valore di ϕ)

Ql²/2 - 4 EI/L ϕ - 4 EI/L ϕ - GJt/L ϕ = 0

Ql²/2 = (4 EI/L + 4 EI/L + GJt/L ) ϕ

dove  Kϕ= (8 EI/L + GJt/L ) (rigidezza al nodo)

a cui partecipano la rigidezza torsionale e la rigidezza flessionale

Allora come si ripartisce il momento esterno applicato provocato dalla trave a sbalzo?

Cerco ϕ 

ϕ= Ql²/2 *1/8 EI/L + GJt/L

dove:

Ql²/2= 15 kNm

E modulo di elasticità

I  momentod’inerzia

G modulo di elasticità tangenziale

L lunghezza della trave

Jt momento d’inerzia torsionale

Una volta trovato ϕ cerco tutti i valori delle rigidezze specifiche per ogni trave e pilastro.

Il momento applicato verrà ripartito a secondo delle diverse rigidezze.

trave BD= 3m; pilastro BC= 3m; trave BE= 1m;

Mf (trave BD)= 4 EI/L1ϕ

Mt (trave BE)= GJt/L ϕ

 

Mf (pilastro BC)= 4 EI/L ϕ

 

Esistono due tipologie di sezioni :

• •             Sezioni aperte
• •             Sezioni chiuse

Considerando diverse sezioni per la struttura, i valori dei due momenti ( flettente e torcente) varieranno al variare del materiale (acciao e cls ) e della geometria della sezione. Per esempio, il metodo dell’analogia idrodinamica studia il comportamento a torsione delle travi in funzione al loro tipo di  sezione  ( geometria del profilo).

 

Attraverso l’utilizzo di SAP2000 applicheremo profili in Cls ed Acciaio alla struttura per analizzare l’esito che il rispettivo momento d’inerzia ha sulla rigidezza torsionale momento di inerzia polare  Jt che dipende dalla sezione, e del modulo di elasticità tangenziale G che dipende dal materiale:

Iniziamo i nostri calcoli....prima a mano e poi li verificheremo su SAP2000.

CALCESTRUZZO

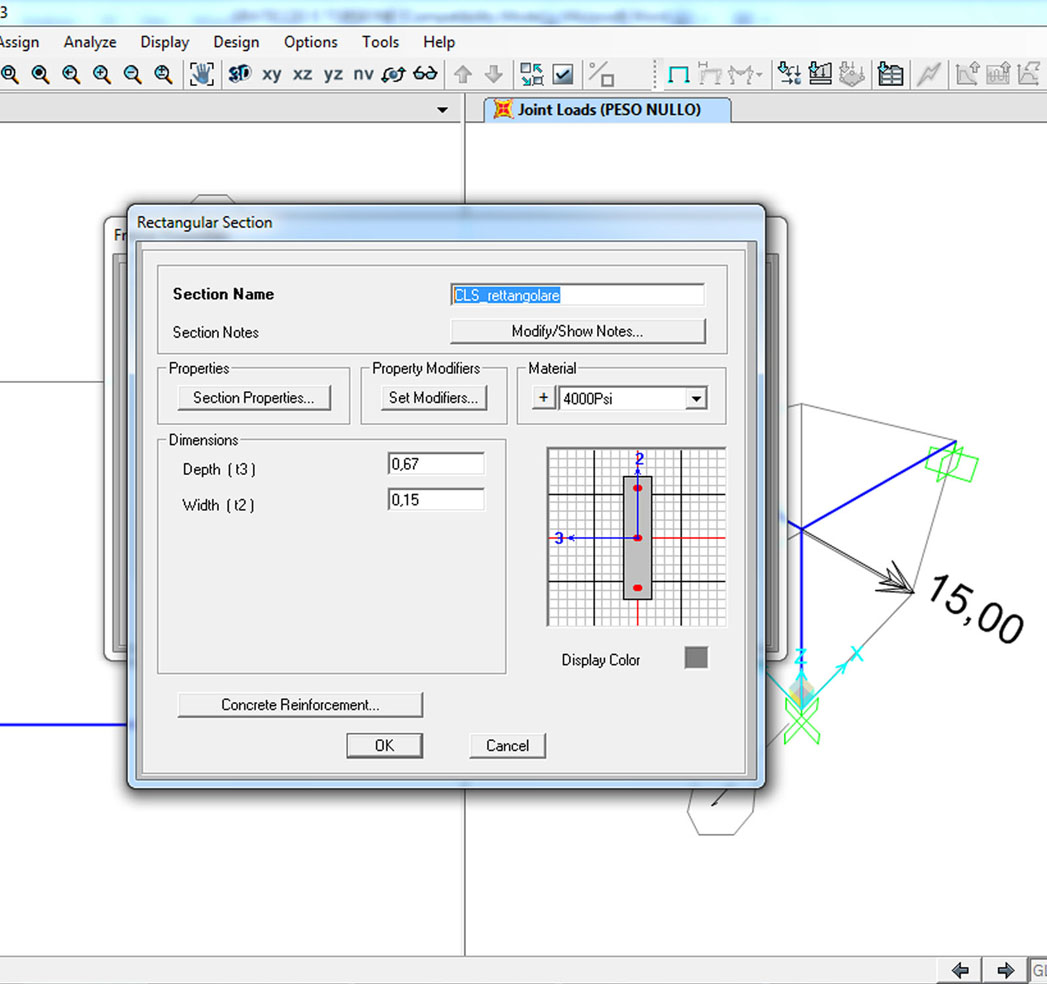
sezione RETTANGOLARE  67x15cm

Q= 30kN  Ql²/2 = 15kNm

E= 21 10⁶ kN/m²

I =bh³/12 = 0.15*(0.67)³/12 = 0.0037 m⁴

G =10.000 N/mm² = 10⁷ kN/m²

 

Inserisco  questi dati in SAP2000 “material property data”. G ha un nuovo valore cioè 8750000 kN/m²

L = trave BD = 3m; pilastro BC = 3m; trave BE = 1m;

Jt= C₂ab³                      C₂=a/b  (altezza/base) = 0.67/0.15= 4.46 quindi C₂=0,281

 

= 0,281( 0.67)(0.15)³ = 0,00064m⁴

 

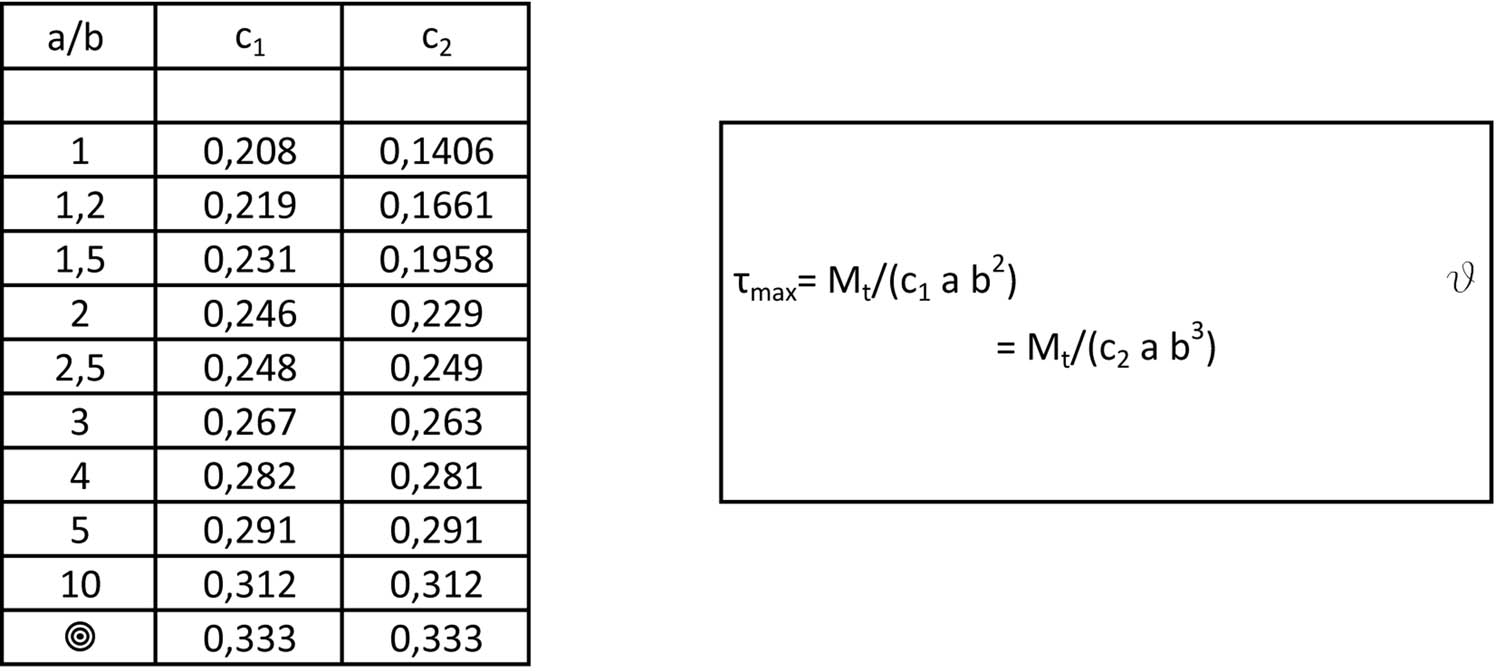
Cerco ϕ:

Equazione di Equilibrio al nodo:

RA = (8 EI/L + GJt/L )

RA = 8 (21 10⁶ * 0.0037)/3 + (8750000* 0,00064/3) ϕ

RA = (207200 + 1866.66) = 209066.66 kN/m

ϕA = 15/209066.66 = 0, 00007174

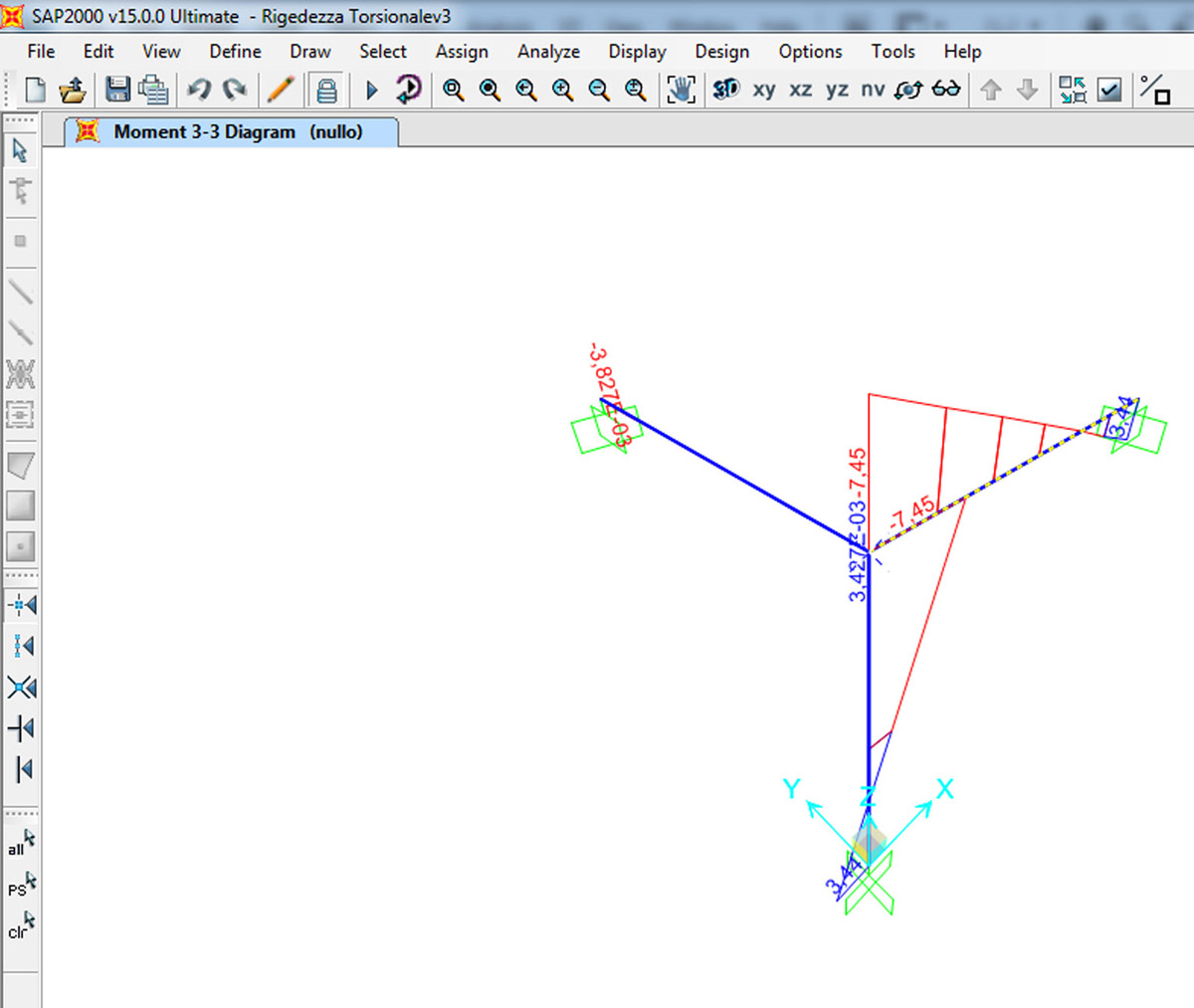
Mf (pilastro BC) =Mf (trave BD)= 4EI/L1 ϕ  con L=3m

(4*21 10⁶ * 0.0037/3)* 0, 00007174 = 7.432 kNm

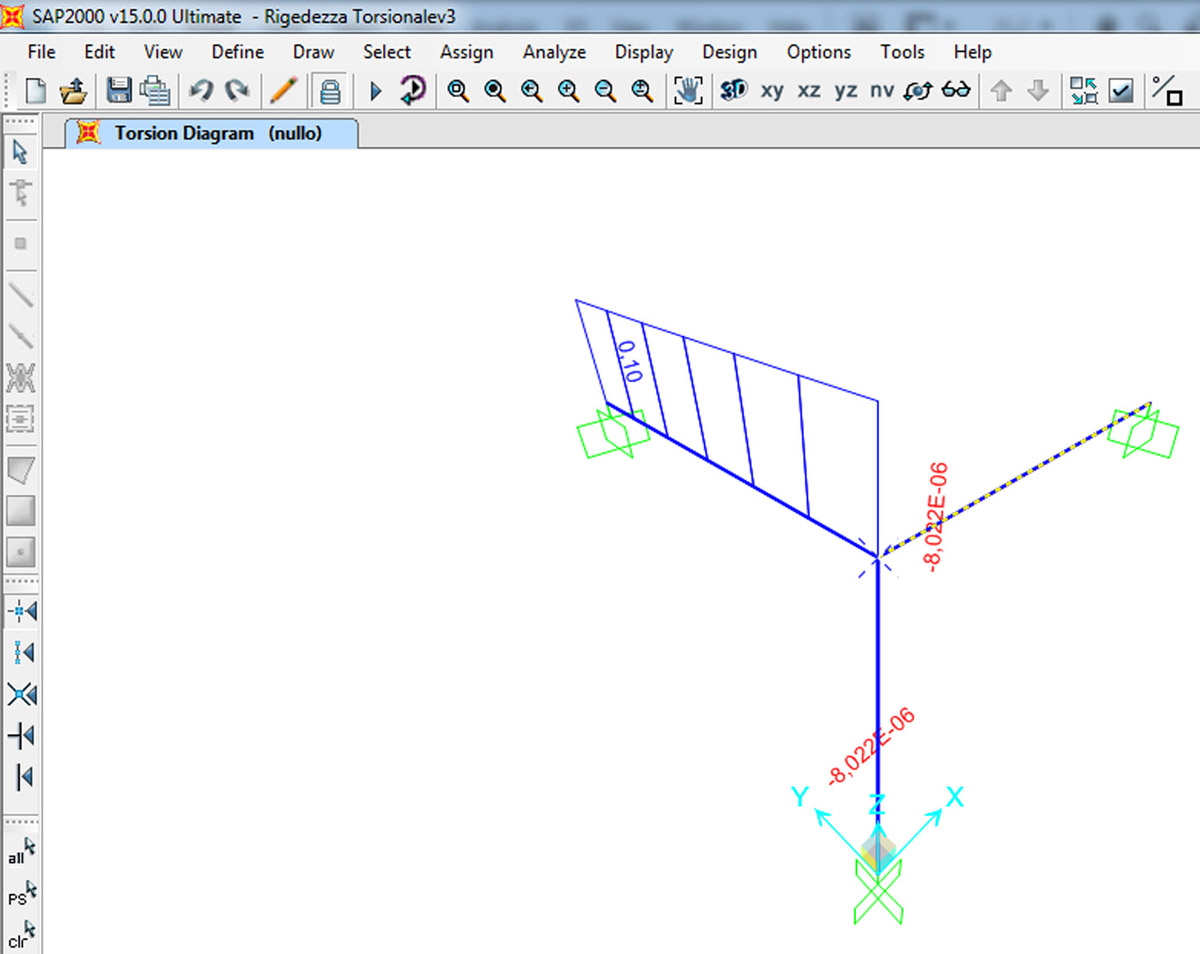
Mt (trave BE)= GJt/L ϕ con L=3m

(8750000* 0, 00064/3)* 0, 00007174 = 0,133 kNm

M1+M2+M3 = Ql²/2

7.432+7.432+ 0,133 = 15 kNm

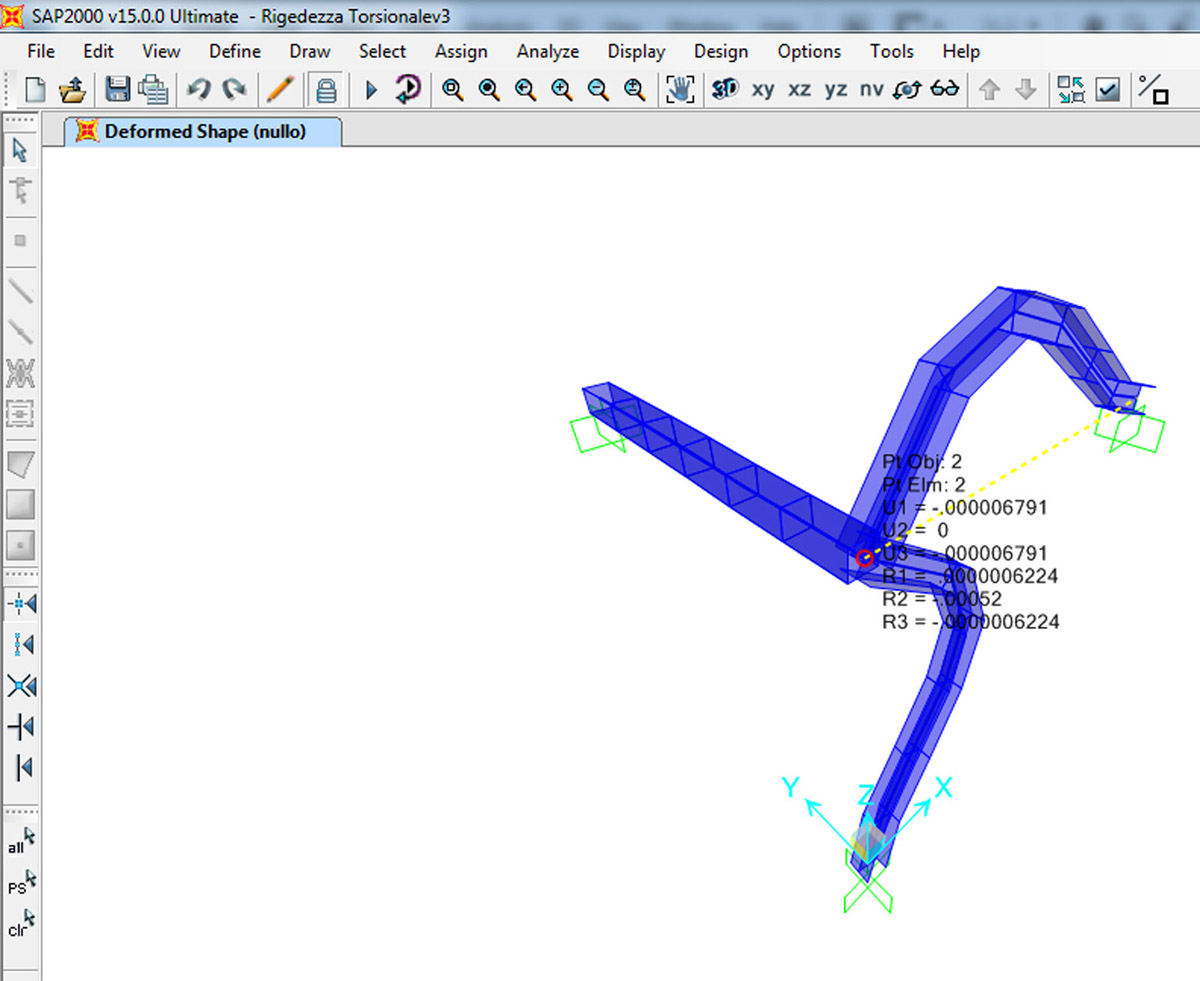
Su sap il nodo 3d con le 3 aste incastrate e un momento di 15 kNm applicato nel nodo B. Qui, tutte e tre le aste hanno una sezione in calcestruzzo rettangolare come per i calcoli manuali. nel definire la sezione è importante che anche su sap il cls abbia lo stesso modulo di elasticità e modulo di elasticità tangenziale.

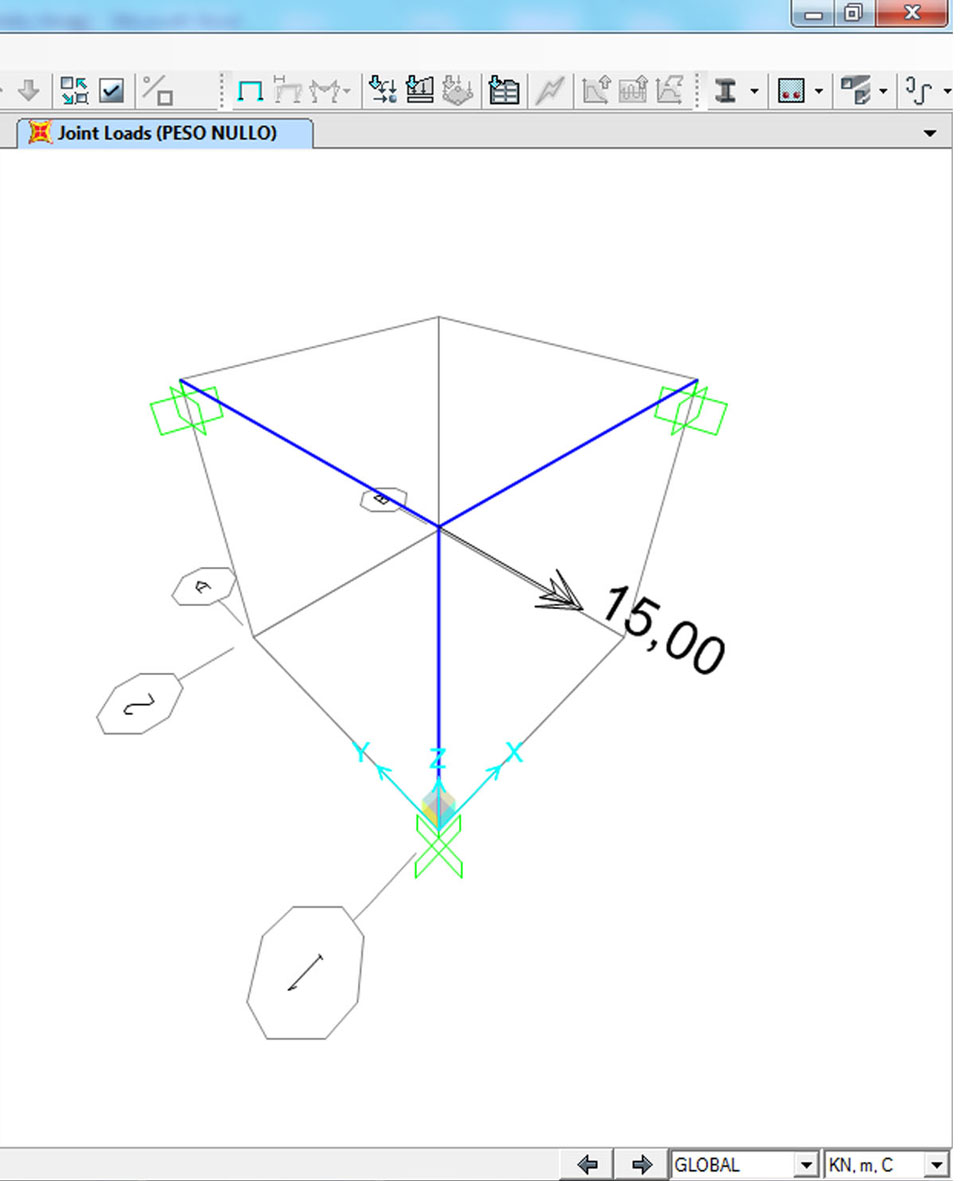
Le tre aste con la Forza di 15 kN applicata sul nodo B

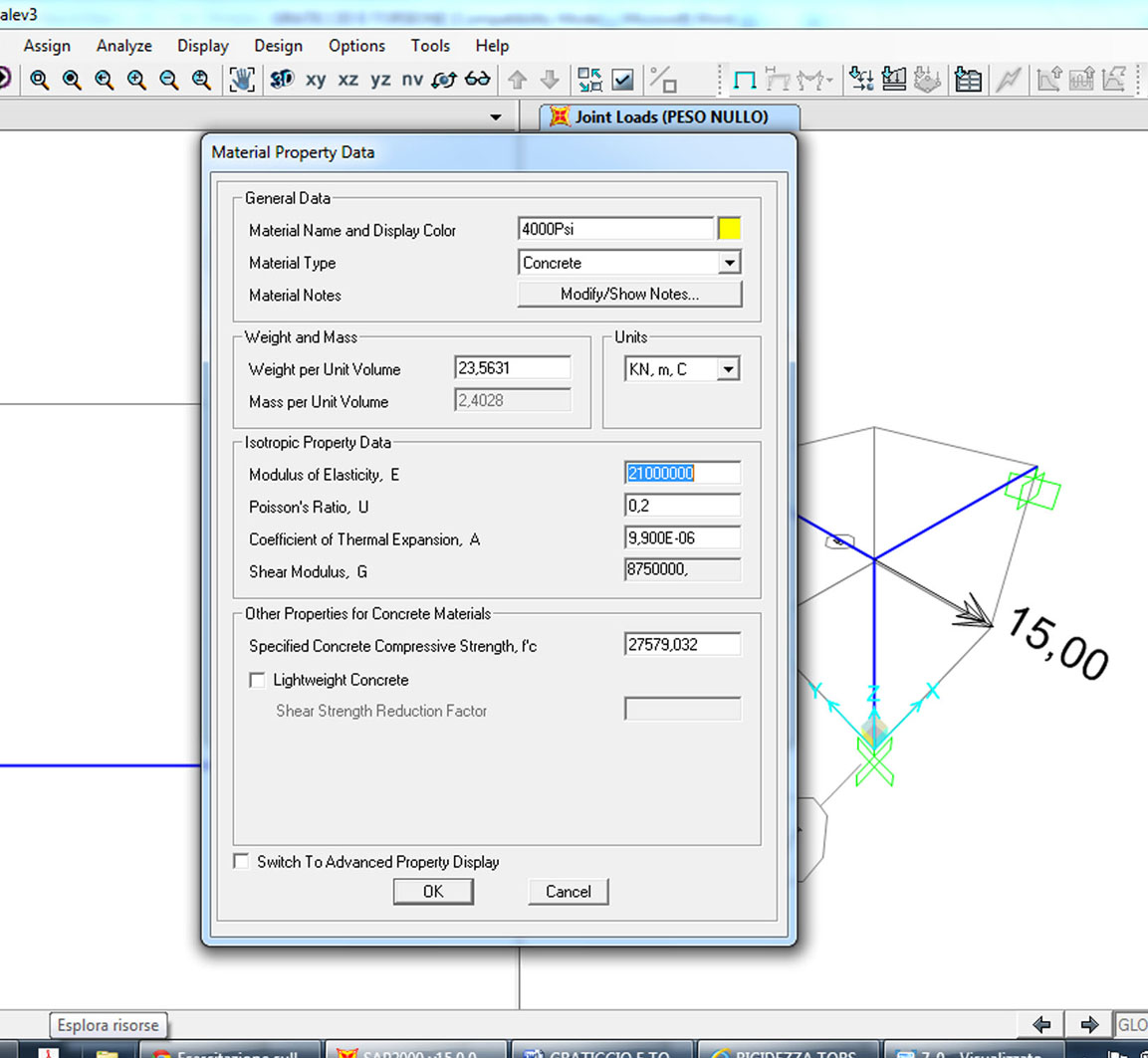
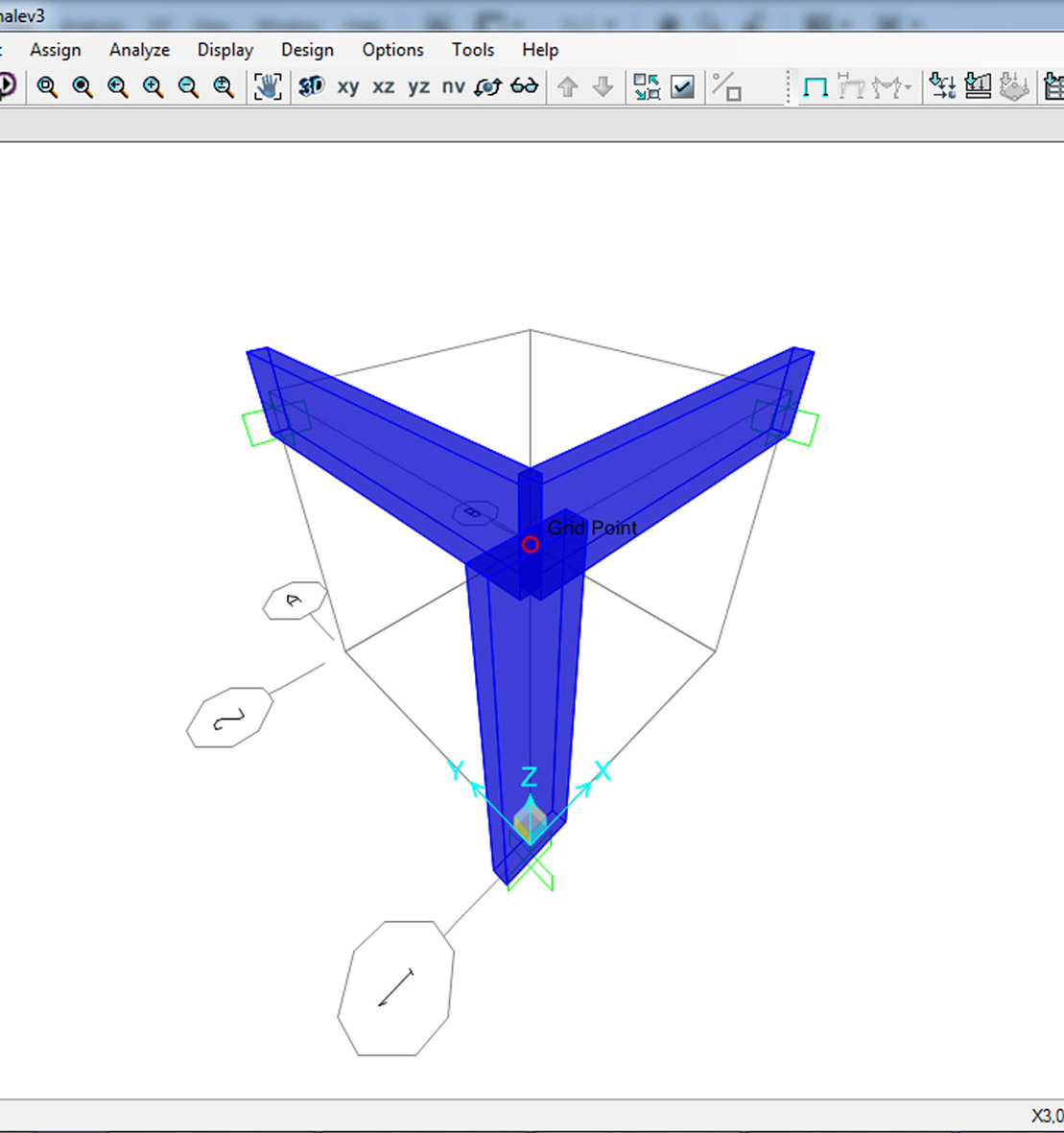
Deformed shape _ Deformata

 

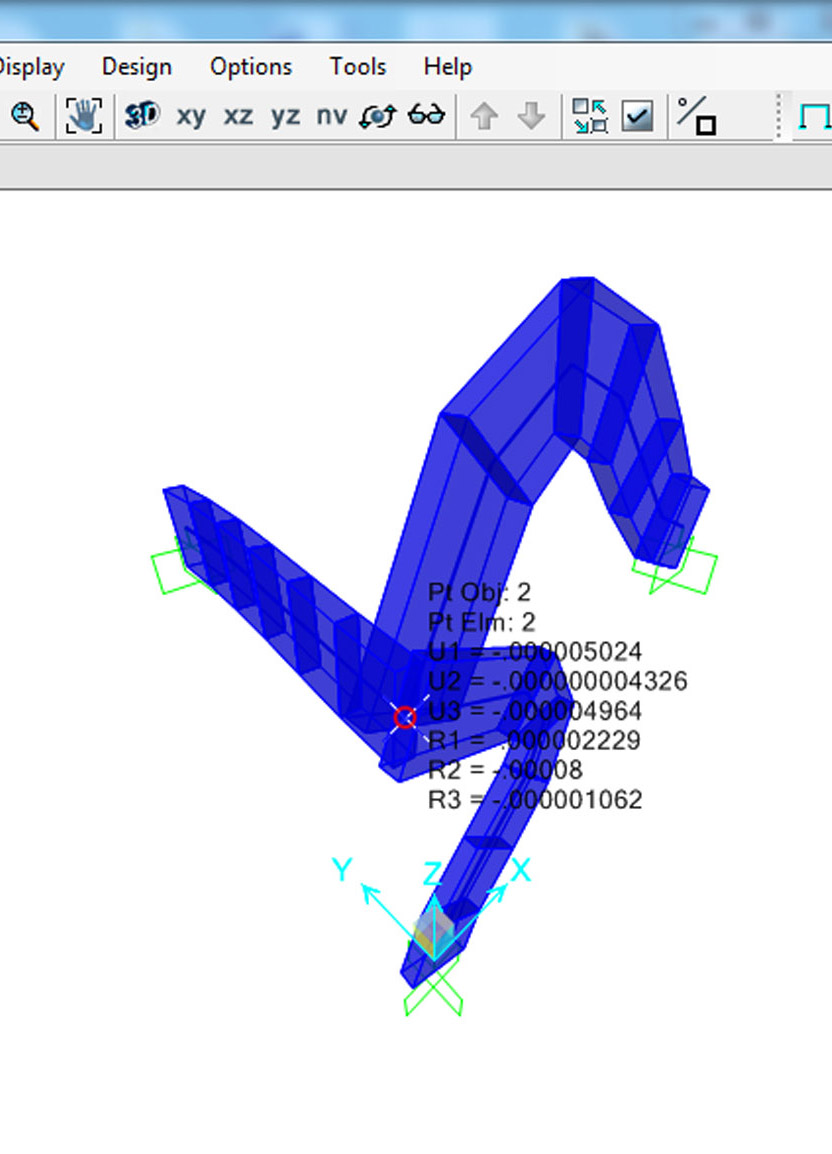
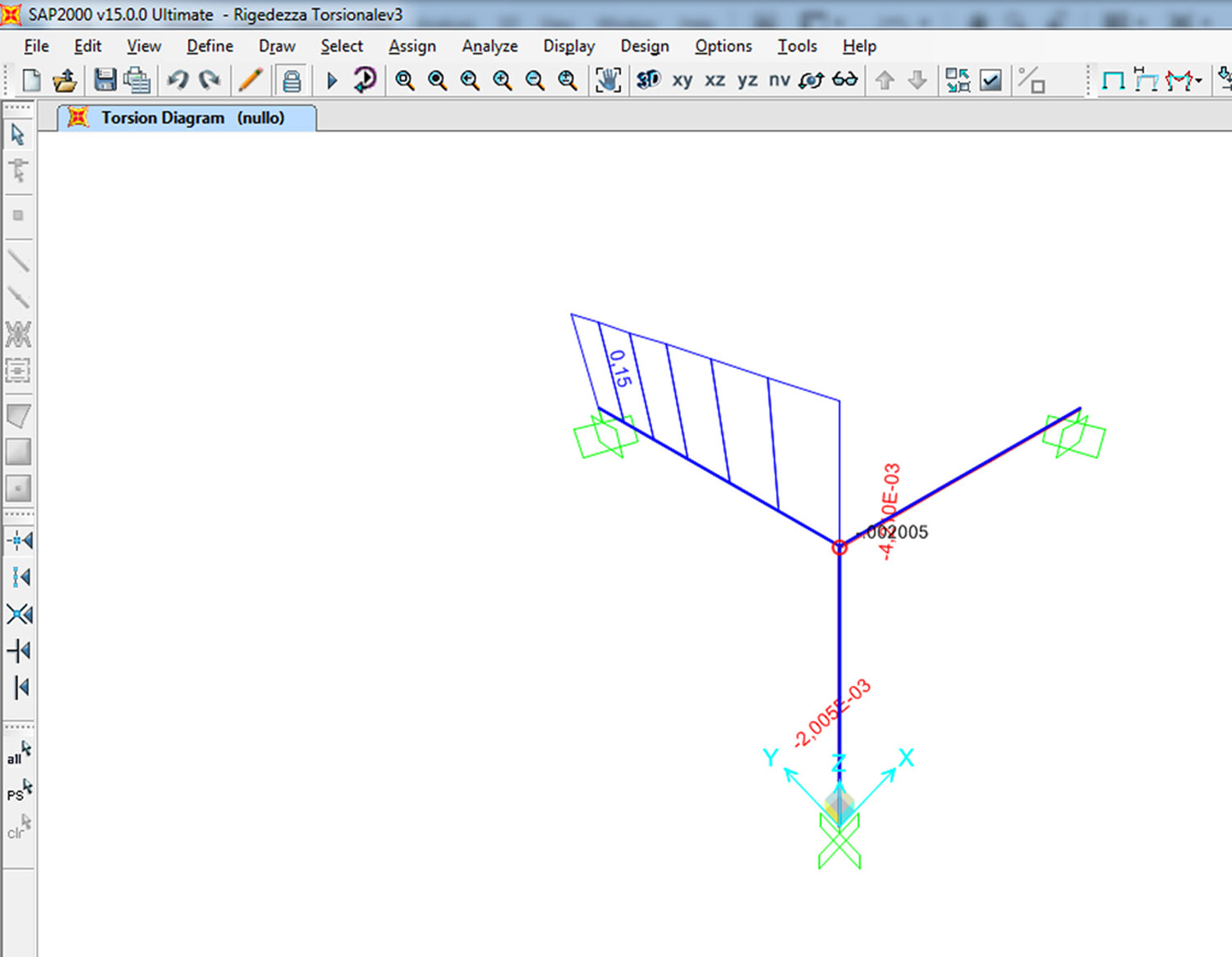
Cambio la sezione della trave BE ed analizzo i risultati

sezione CIRCOLARE  d = 36cm

Q= 30kN  Ql²/2 = 15kNm

E= 21 10⁶ kN/m²

I =bh³/12 = 0.15*(0.67)³/12 = 0.0037 m⁴

G =10.000 N/mm² = 10⁷ kN/m²

dati in SAP2000 “material property data”. G ha un nuovo valore cioè 8750000 kN/m²

L = trave BD = 3m; pilastro BC = 3m; trave BE = 1m;

 

Jt= Ip (momento polare d’inerzia) = π R⁴/2 = π (0.18)⁴/2 = 0.00164 m⁴

Cerco ϕ:

Equazione di Equilibrio al nodo:

RA = (8 EI/L + GJt/L )

RA = 8 (21 10⁶ * 0.0037)/3 + (8750000* 0.00164 /3) ϕ

RA = (207200 + 4783,33) = 211983,33 kN/m

ϕA = 15/211983,33 =0, 00007076

Mf (pilastro BC) =Mf (trave BD)= 4EI/L1 ϕ  con L=3m

(4*21 10⁶ * 0.0037/3)* 0, 00007076= 7.33 kN/m

Mt (trave BE)= GJt/L ϕcon L=3m 

(8750000* 0.00164 /3)* 0, 00007076= 0,338 kN/m

M1+M2+M3 = Ql²/2

7.33 +7.33 + 0,338 = 15 kN/m

Torno su SAP2000 e rinserisco i valori:

 

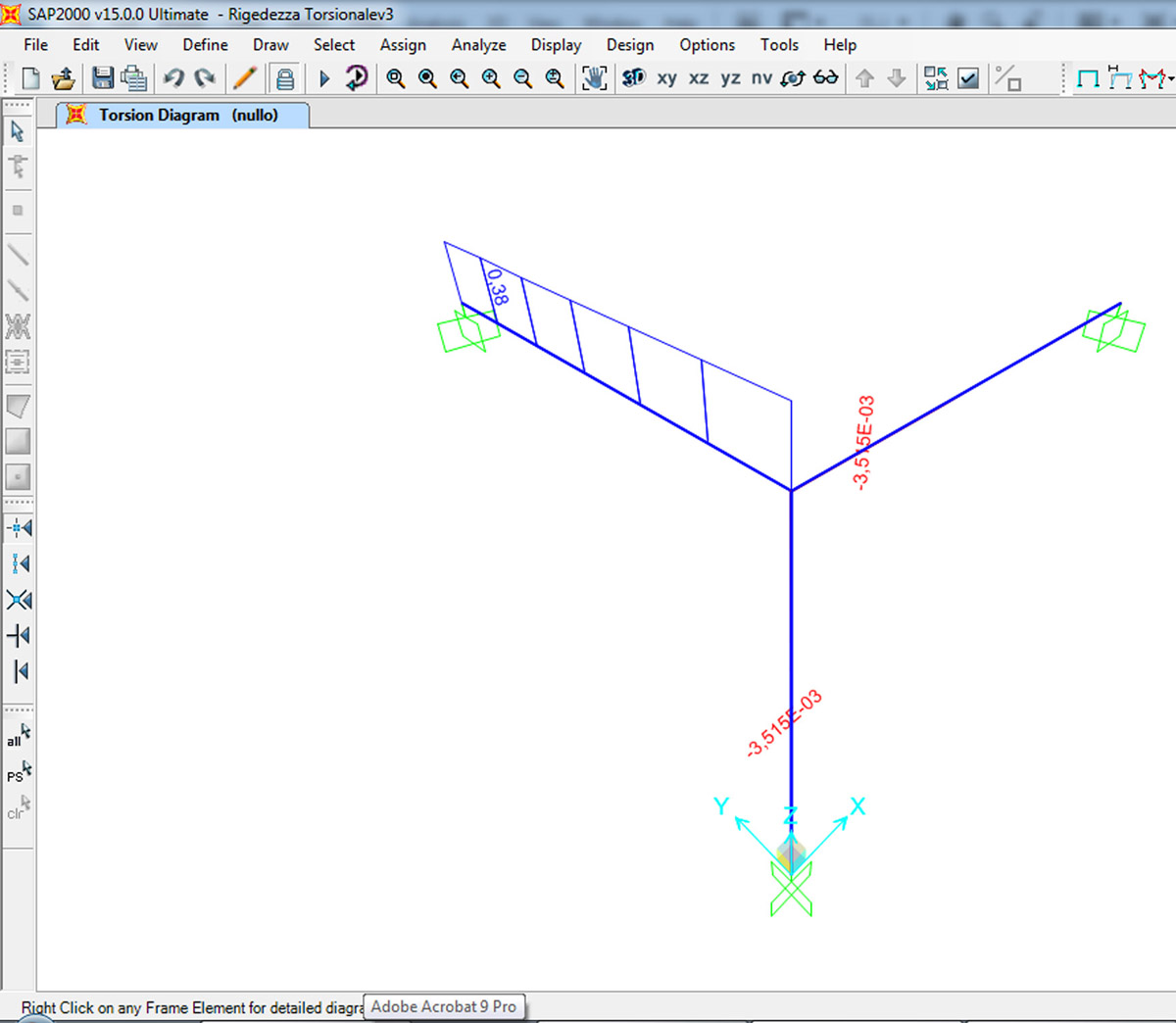
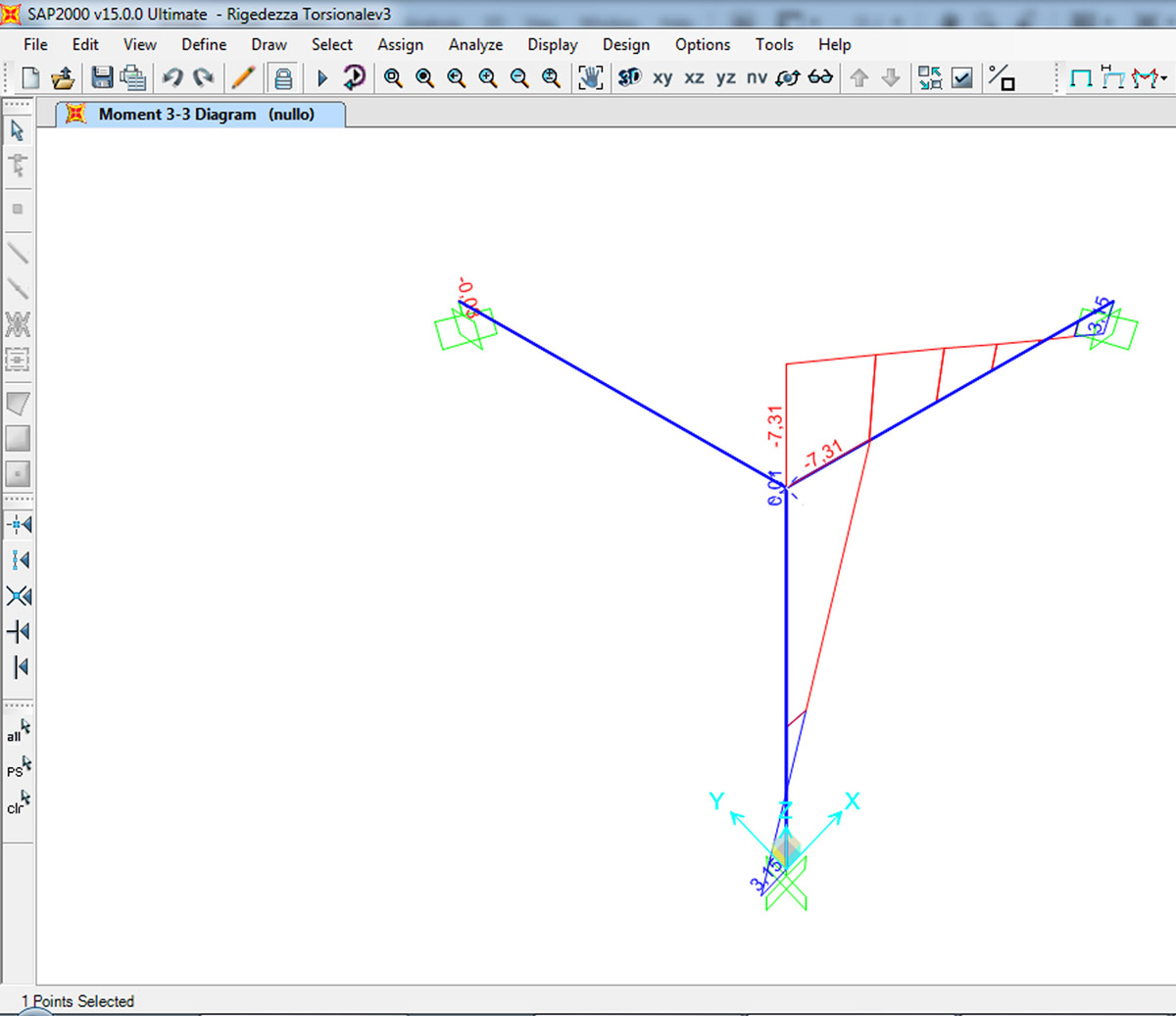
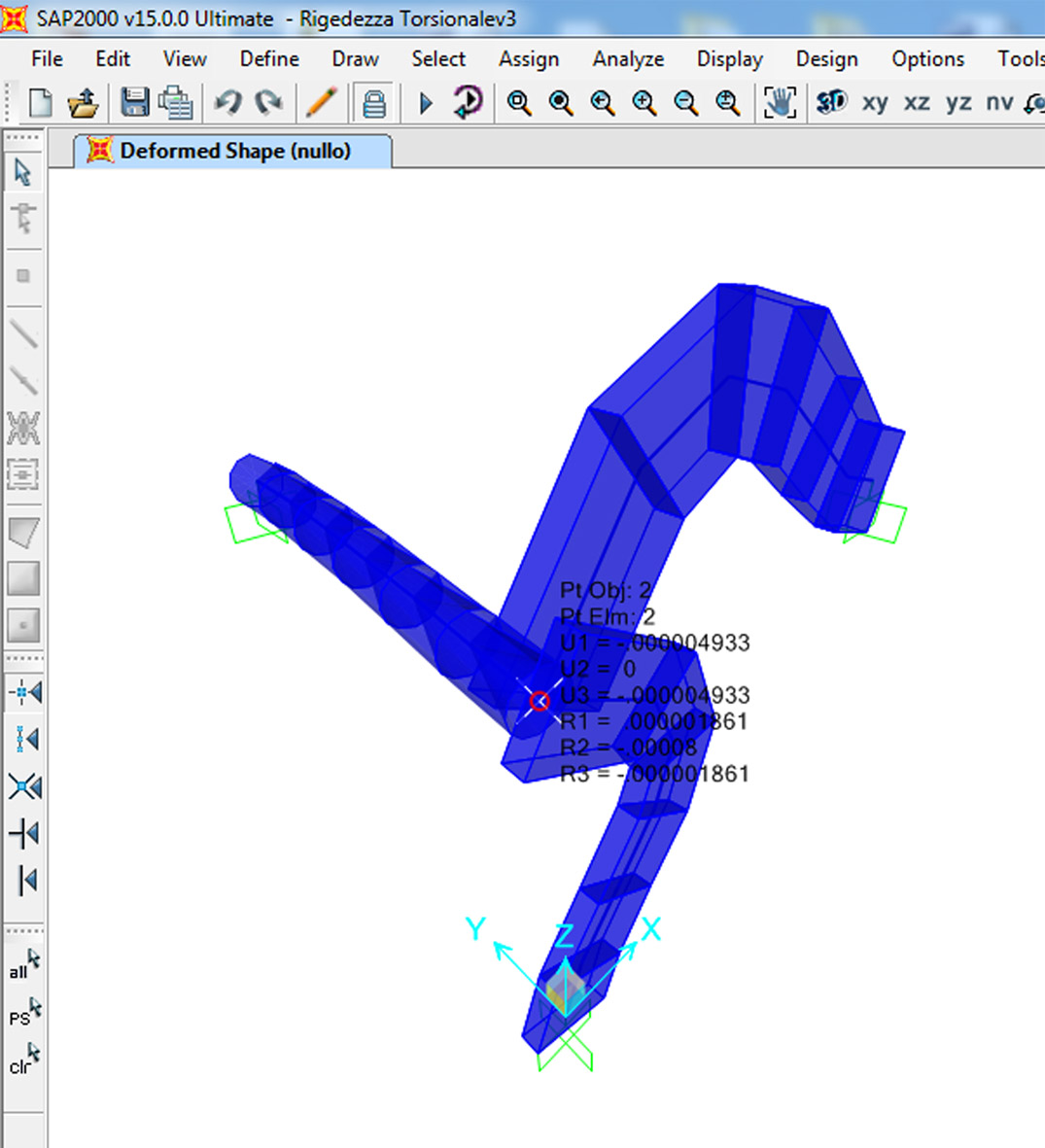
ACCIAIO

sezione APERTA

HEB 200 mm x 200 mm 

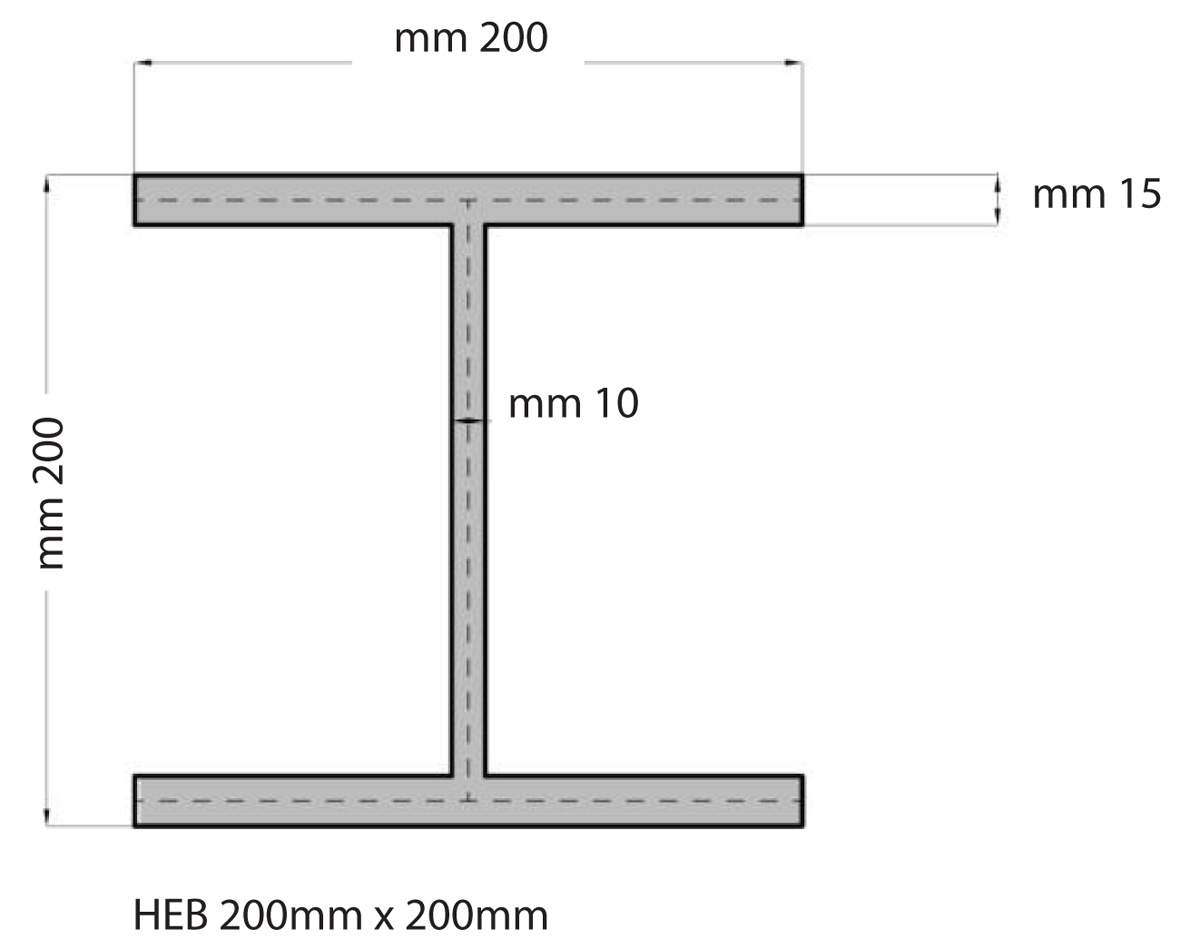
Q = 30kN/mq  Ql²/2 = 15kN/mq

E= 208 10⁶ kN/mq

I =5,544 10⁻⁵ m⁴

G = 80 10⁶ kN/mq

L = trave BD = 3m; pilastro BC = 3m; trave BE = 1m;

Jt1= C2*a*b³ = (0.333)(20)(1.5)³= 22,47 cm⁴   C2= a/b

Jt2= C2*a*b³ = (0.333)(17)(1)³= 5,66 cm⁴

Jt TOT = 22,47 + 22,47 + 5,66 = 50.6 cm⁴ = 50.6 10⁻⁸ m⁴

cerco ϕ:

Equazione di Equilibrio al nodo:

RA = (8 EI/L + GJt/L )

RA = 8 (208 10⁶ * 5,544 10⁻⁵)/3 + (80 10⁶ * 50.6 10⁻⁸ /3) ϕ

RA = (30750,72 + 13.49) = 30764,21 kN/m

ϕA = 15/30764,21 = 0, 0004875

Mf (pilastro BC) =Mf (trave BD) = 4EI/L1 ϕ  con L=3m

(4*208 10⁶ * 5,544 10⁻⁵/3)* 0, 0004875= 7.49 kN/m

 

Mt (trave BE) = GJt/L ϕcon L=3m

(80 10⁶ * 50.6 10⁻⁸ /3)* 0, 0004875 = 0,006578 kN/m

M1+M2+M3 = Ql²/2

7.49 +7.49 + 0,006578 = 15 kN/m

 

inseriamo i dati in SAP2000

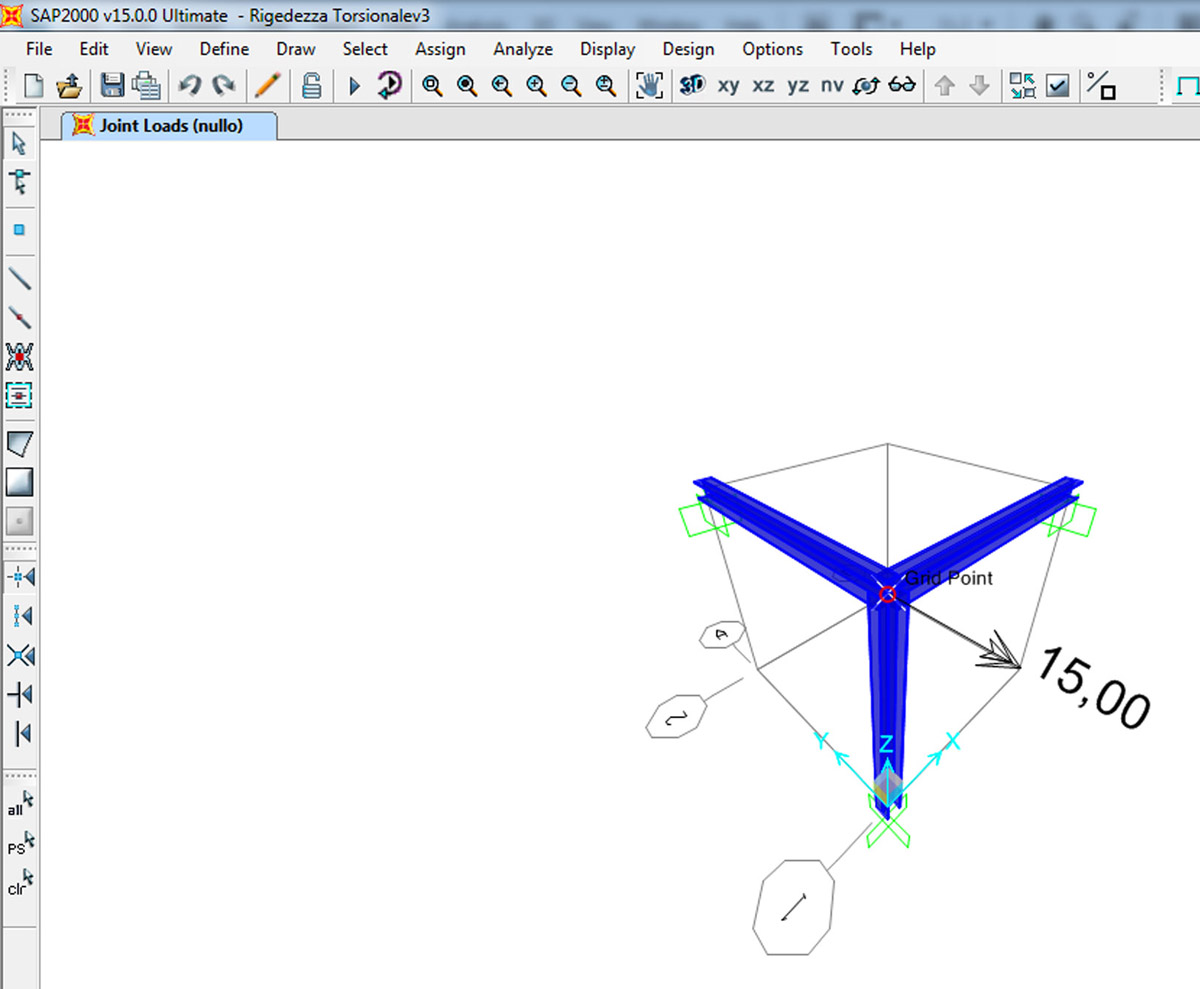
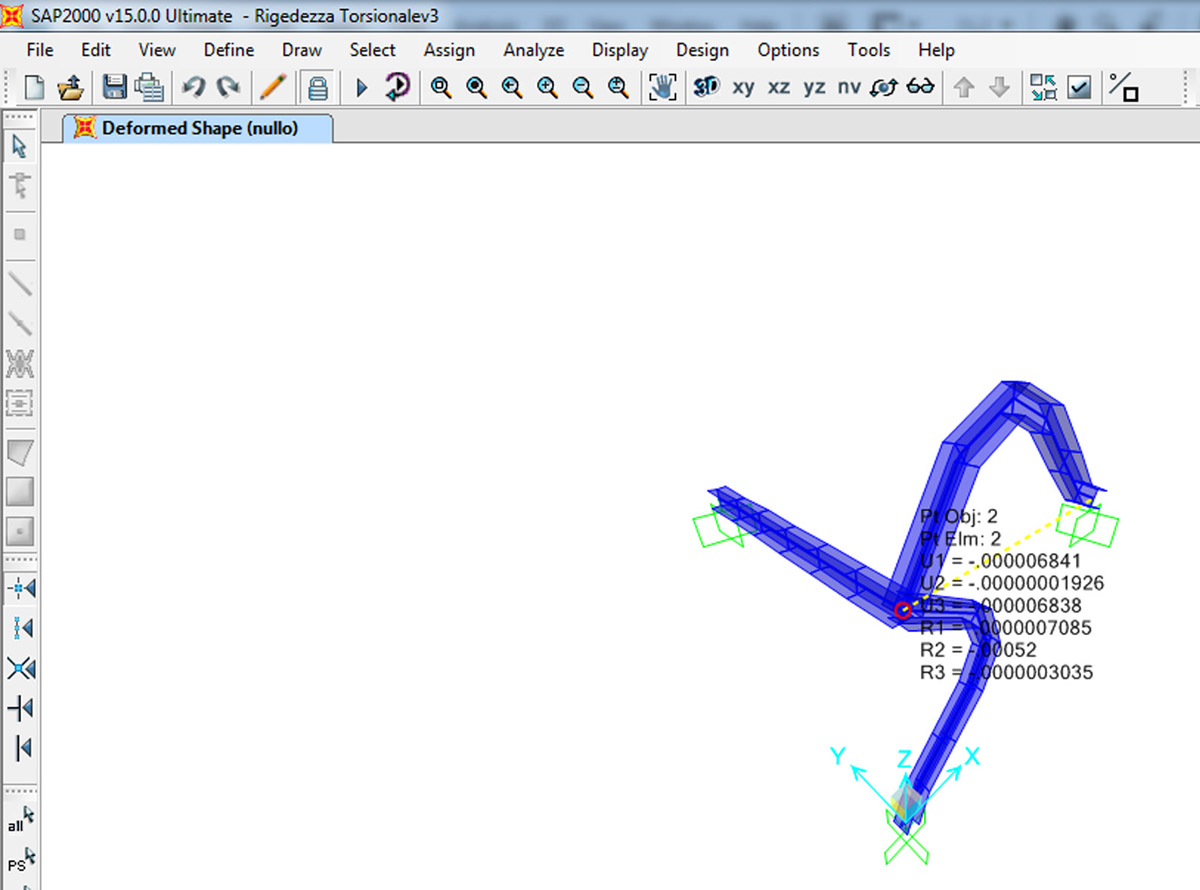
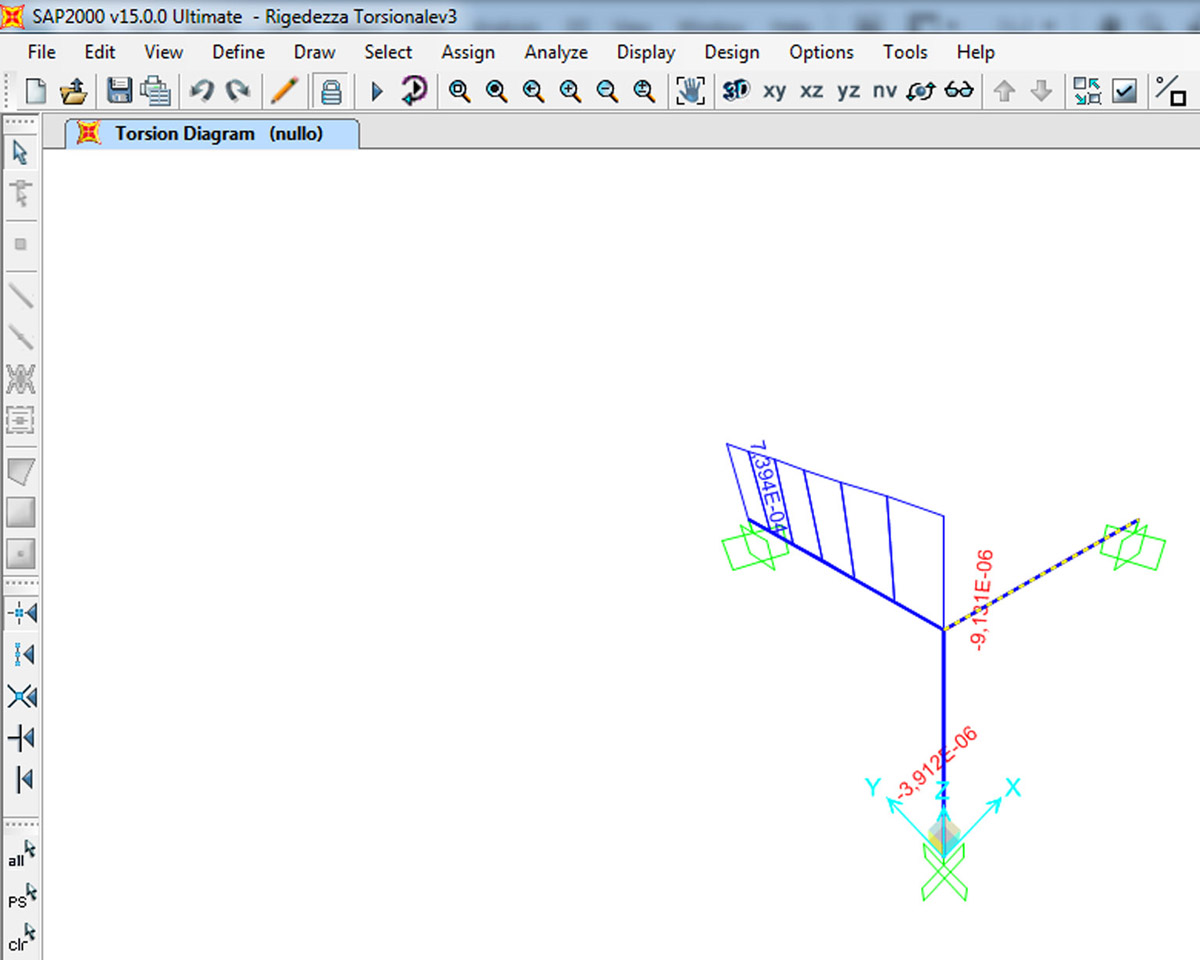
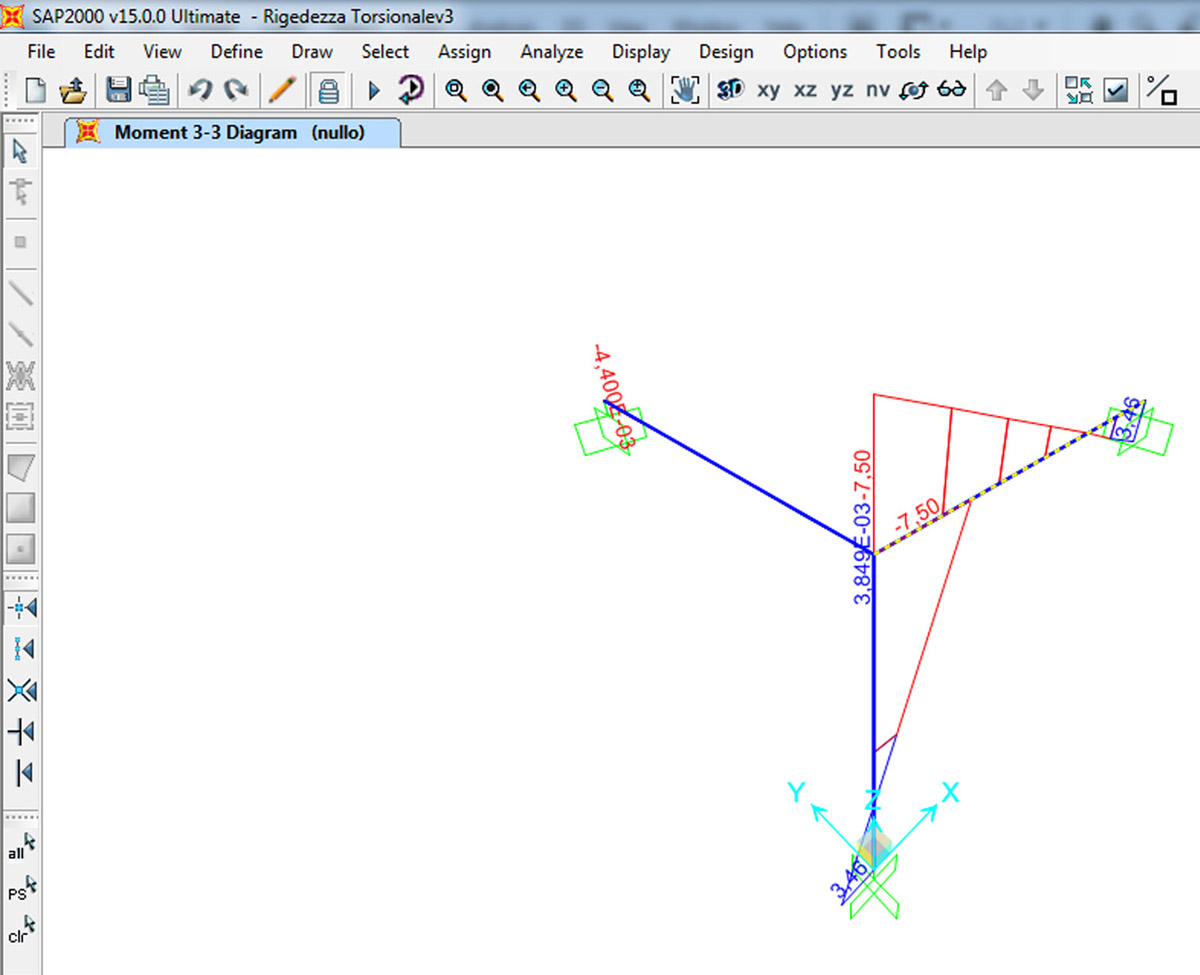
Cambio la sezione della trave BE ed analizzo i risultati

sezione SCATOLARE

HEB 200 mm x 200 mm

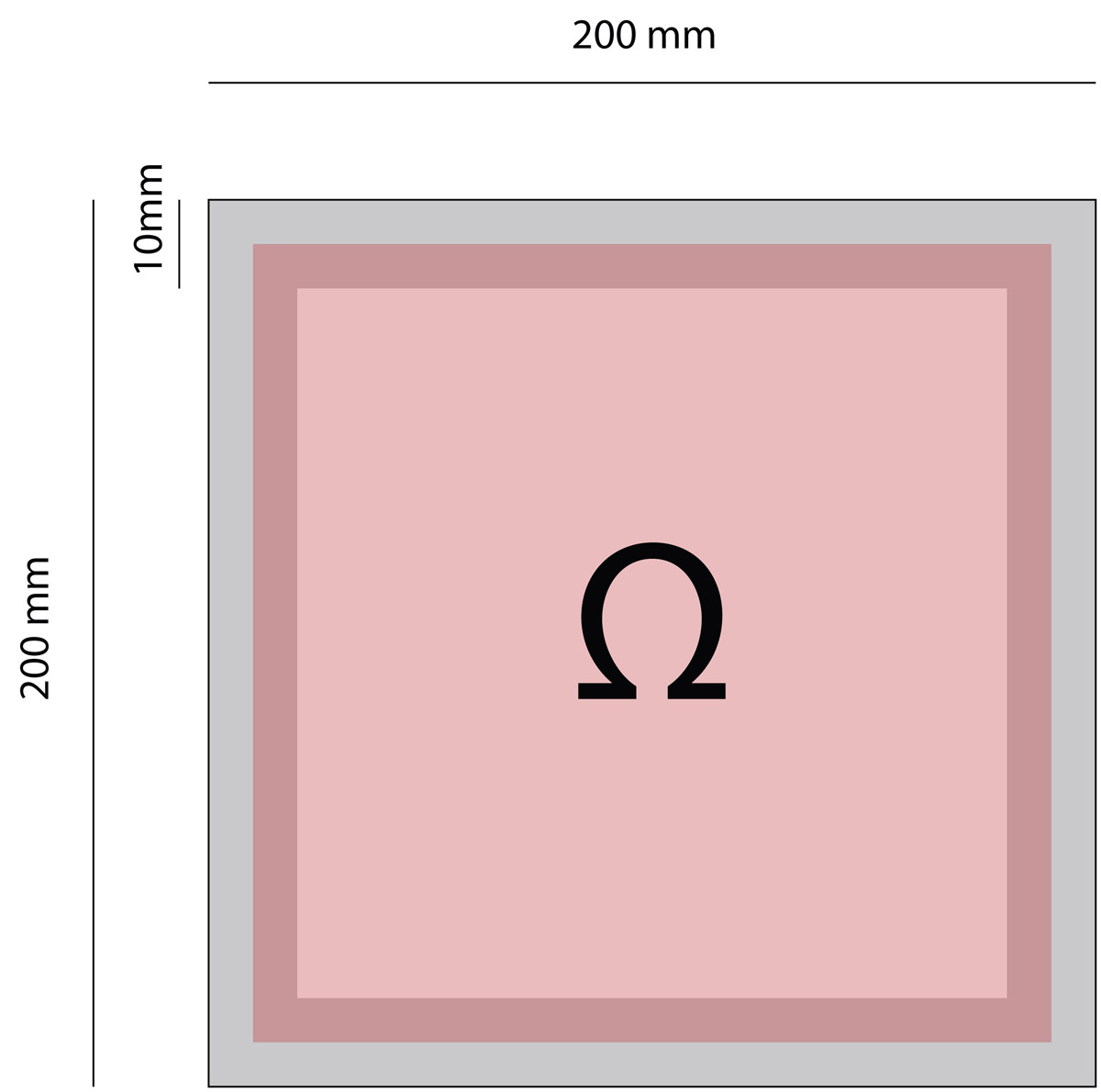
Q=30kN/mq  Ql²/2 = 15kN/mq

E = 208 10⁶ kN/mq

I = 5,544 10⁻⁵ m⁴

G = 80 10⁶ kN/mq

L = trave BD = 3m; pilastro BC = 3m; trave BE = 1m;

Jt = 4Ω²t/Lm

4(20*20) ² (1)/19*4

640000/76 = 0,00008421 m4

cerco ϕ:

Equazione di Equilibrio al nodo:

RA = (8 EI/L + GJt/L )

RA = 8 (208 10⁶ * 5,544 10⁻⁵)/3 + (80 10⁶ * 0,00011875/3) ϕ

RA = (30750,72 + 3166,66) = 33917,38 kN/m

ϕA = 15/33917,38 = 0, 0004422

Mf (pilastro BC) =Mf (trave BD) = 4EI/L1 ϕ  con L=3m

(4*208 10⁶ * 5,544 10⁻⁵/3)* 0, 0004422= 6.79 kNm

Mt (trave BE) = GJt/L ϕcon L=3m

(80 10⁶ * 0,00011875 /3)* 0, 0004422= 1,40 kNm

M1+M2+M3 = Ql²/2

6.79 +6.79 + 1,40= 15 kNm

inseriamo i dati in SAP2000

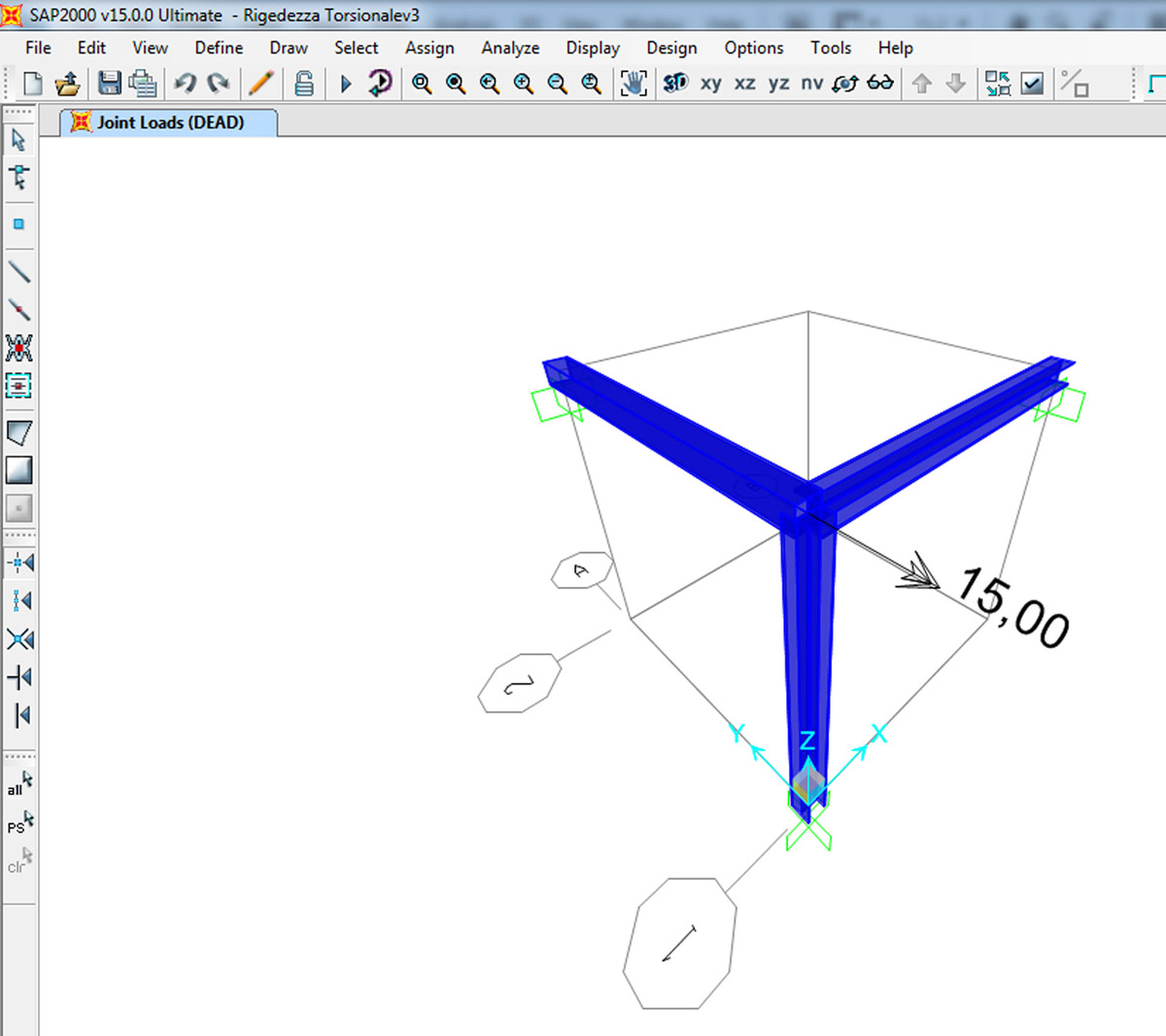
CONCLUSIONE

Osserviamo la tabella. Nel  CLS  sezione circolare piena la rigidezza della trave BE (quella soggetta a torsione), è maggiore rispetto alla sezione rettangolare.

Nella sezione circolare piena il Jt momento d’inerzia torsionale è più alto rispetto a quello nell’altra sezione.

Nell’acciaio la sezione chiusa scatolare della trave BE ha una rigidezza maggiore rispetto alla stessa rigidezza nella sezione HEB, la sua rotazione R2 ha il valore più piccolo tra tutte le sezioni. Inoltre notiamo, che l’acciaio offre una maggiore resistenza torsionale rispetto a quelle in cls armato perchè il modulo di elasticità tangenziale (G) è superiore.

La rigidezza delle aste sarà data dal momento flettente o il momento torsionale diviso la rotazione k=M/o  kN rad