In questo esercizio studieremo il comportamento di due travi perpendicolari tra di loro , le quali collaborano tra di loro per garantire un miglior equilibrio alla struttura.
SCHEMA DI RIFERIMENTO
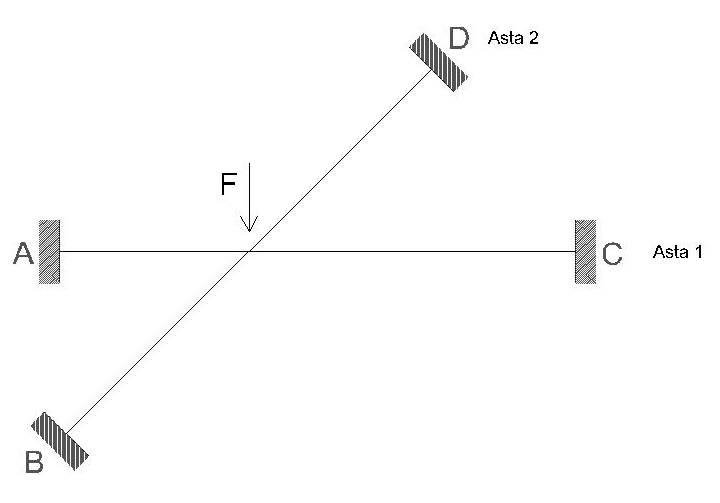
DEFORMATA
Lungo l'asta 2 avendo la forza che cade perfettamente al centro si avrà come detto precedentemento solo abbassamento, sull'asta 1 invece, abbiamo in y anche la rotazione poichè la forza non cade perfettamente al centro, ma a 1/3L .
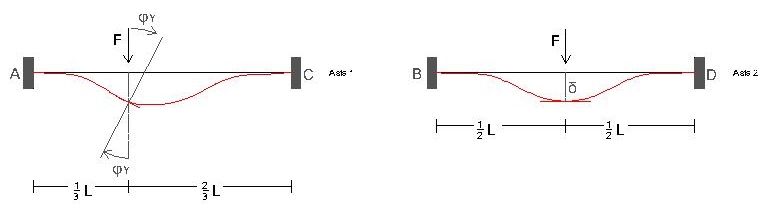
Dunque per quanto riguarda gli spostamenti sappiamo che ux = 0 , uy = 0 e uz = δ ; per quanto riguarda le rotazioni abbiamo solo φY.
Le incognite che ci rimangono sono dunque due : δ e φY.
δ lo troviamo facendo l'equazione all'equilibrio contro la traslazione verticale Σ Fz = 0
φY lo troviamo facendo l'equazione all'equilibrio contro la rotazione My = 0
Studiamo ogni trave singolarmente facendo agire prima solo δ e poi solo la rotazione φY.
Facciamo agire solo δ
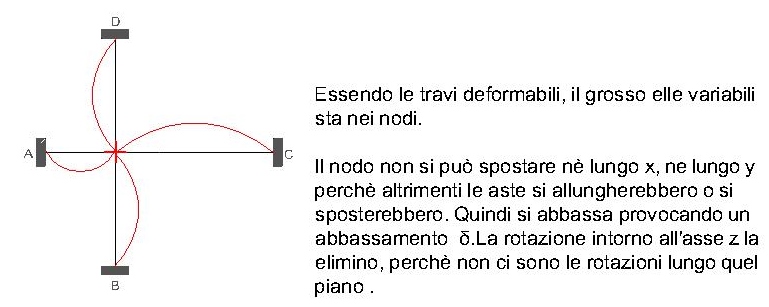
Essendo le travi deformabili, il grosso elle variabili sta nei nodi.
Il nodo non si può spostare nè lungo x, ne lungo y perchè altrimenti le aste si allungherebbero o si sposterebbero. Quindi si abbassa provocando un abbassamento δ.
La rotazione intorno all'asse z la elimino, perchè non ci sono le rotazioni lungo quel piano .Sull'aste 2, la rotazione in y invece c'è, visto che F non cadendo al centro fa ruotare l'asta.
Essendo le travi deformabili, il grosso elle variabili sta nei nodi.
Il nodo non si può spostare nè lungo x, ne lungo y perchè altrimenti le aste si allungherebbero o si sposterebbero. Quindi si abbassa provocando un abbassamento δ.
La rotazione intorno all'asse z la elimino, perchè non ci sono le rotazioni lungo quel piano .Sull'aste 2, la rotazione in y invece c'è, visto che F non cadendo al centro fa ruotare l'asta.
Essendo le travi deformabili, il grosso elle variabili sta nei nodi.
Il nodo non si può spostare nè lungo x, ne lungo y perchè altrimenti le aste si allungherebbero o si sposterebbero. Quindi si abbassa provocando un abbassamento δ.
La rotazione intorno all'asse z la elimino, perchè non ci sono le rotazioni lungo quel piano .Sull'aste 2, la rotazione in y invece c'è, visto che F non cadendo al centro fa ruotare l'asta.
Essendo le travi deformabili, il grosso elle variabili sta nei nodi.
Il nodo non si può spostare nè lungo x, ne lungo y perchè altrimenti le aste si allungherebbero o si sposterebbero. Quindi si abbassa provocando un abbassamento δ.
La rotazione intorno all'asse z la elimino, perchè non ci sono le rotazioni lungo quel piano .Sull'aste 2, la rotazione in y invece c'è, visto che F non cadendo al centro fa ruotare l'asta.
Essendo le travi deformabili, il grosso elle variabili sta nei nodi.
Il nodo non si può spostare nè lungo x, ne lungo y perchè altrimenti le aste si allungherebbero o si sposterebbero. Quindi si abbassa provocando un abbassamento δ.
La rotazione intorno all'asse z la elimino, perchè non ci sono le rotazioni lungo quel piano .Sull'aste 2, la rotazione in y invece c'è, visto che F non cadendo al centro fa ruotare l'ast
Facciamo agire solo φY
Sull'asse B-D la rotazione provoca rotazione torsionale concentrata , poichè tutto ciò che è flessionale in un piano retto , diventa torsionale in un piano perpendicolare.
Vediamo ora tutte le forze che arrivano al nodo
Equilibrio di bilancio al nodo contro la traslazione lungo l'asse z
Equazioni di bilancio della traslazione
Equilibrio di bilancio al nodo contro la rotazione lungo l'asse Y
Equazione di bilancio dei momenti
Metto in evidenza δ e φY
φY (12EI/L + 6EI/L + 4GJt/L) + δ ( -54EI/L2 +27/2 EI/L2) = 0
φY (18EI/L + 4GJt/L) + δEI/L2 ( -54 +27/2) = 0
EJ/L [ φY (18+ 4GJt/L) + δ/L ( -81/2)] = 0
Chiamo α = GJt/ EI
φY = (18+ 4α) - 81/2 (δ/L) = 0
δ/L = 2/81(18 + 4α) φY = (36/81 + 8/81α) φY = (36 + 8α)/81φY
δ/L = (36 + 8α)/81φY
Altra equazione :
F - (192EI/L3) δ - (324EI/L3) δ - 81/2(EI/L3) δ - 27/2 ( EI/L2) φY + (54EI/L2) φY = 0
Moltiplico tutto per FL2/EI
FL2/EI - 192 δ/L - 324 δ/L - 81/2 δ/L - 27/2 φY + 54 φY = 0
Posso sommare e ottengo
FL2/EI - 516 δ/L - 81/2 δ/L + (- 27/2 φY + 54 ) φY = 0
FL2/EI - δ/L*(516+81/2) + 81/2 φY = 0
FL2/EI - δ/L*(1113/2) + 81/2 φY = 0
Vado ora a sostituire δ/L con l'equazione prima ottenuta
FL2/EI - 1113/2*[(36+8α)/81]φY+ 81/2 φY = 0
FL2/EI - 371/27*(18+4α)φY+ 81/2 φY = 0
FL2/EI = 371/27*(18+4α)φY+ 81/2 φY = 0
Metto φY in evidenza
φY[371/27*18 -81/2 + 371/27 * 4α ] = 0
φY[1241/6 + 1484/27 α ] = 0
FL2/EI = φY[1241/6 + 1484/27 α ]
φY = FL2/EI [1241/6 + 1484/27 α ]
Abbiamo così ottenuto φY e δ
Definiamo ora una sezione inserendo dei valori noti per trovare i valori incogniti della rotazione e dello spostamento .
Supponiamo di realizzare una struttura in cls , in cui entrambe le aste abbiano la seguente sezione :
supponiamo di avere una luce di 8m e una forza applicata pari a 40kN
Sappiamo che :
Jt ( coefficiente di resistenza a torsione)
c2 è tabelleto in funzione di a/b . In questo caso vale a/b = 0.67/0.15= 4,46 →c2 = 0,291
Jt = c2ab3 = (0,291) 0,67 * (0,15)³ = 0,000658 m3
E (modulo di elasticità) = 21000000 kN/m2
I (momento di inerzia) = bh3/12 = (0,15 * 0,673) /12 = 0,003759 m4
G ( modulo di elasticità tangenziale) = 10000000 kN/m2
Andiamo ora a sostituire i valori noti nell'equazioni prima trovate
Ricordiamo che :
δ/L = (36 + 8α)/81φY
φY = FL2/EI [1241/6 + 1484/27 α ]
α = GJt/EI = 10000000 * 0,000658 / 21000000 * 0,003759 = 0,083355
φY = 40 * 64 / 21000000 * 0,003759 [ (1241/6 + 1484/27) * 0,08355] = 0,0001534
δ/L = [(36 + 8 * 0,08355) / 81) * 0,0001534 = 0,0000808
δ = 8 * 0,0000808 = 0,000646
VERIFICA SAP
Disegno la struttura grazie all'aiuto della griglia. Assegno i vincoli e la forza esterna, e cambio i valori del modulo di elasticità E e del modulo di elasticità tangenziale G.
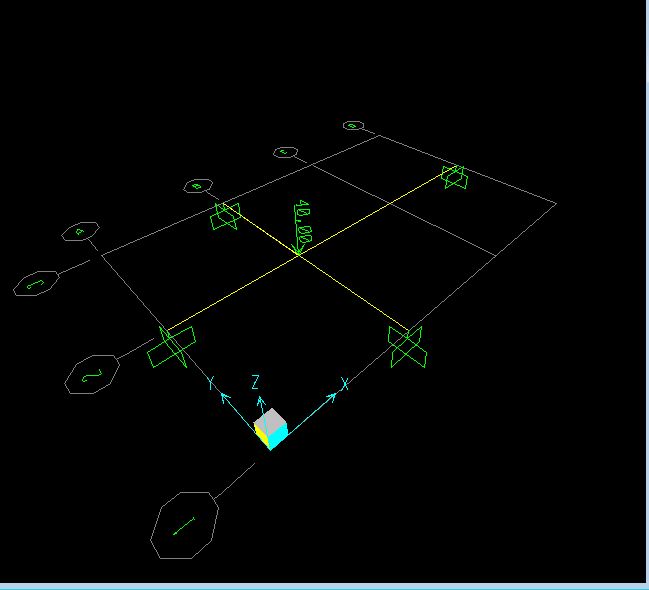
Assegno poi ad entrambe le travi la sezione scelta e faccio partire l'analisi.
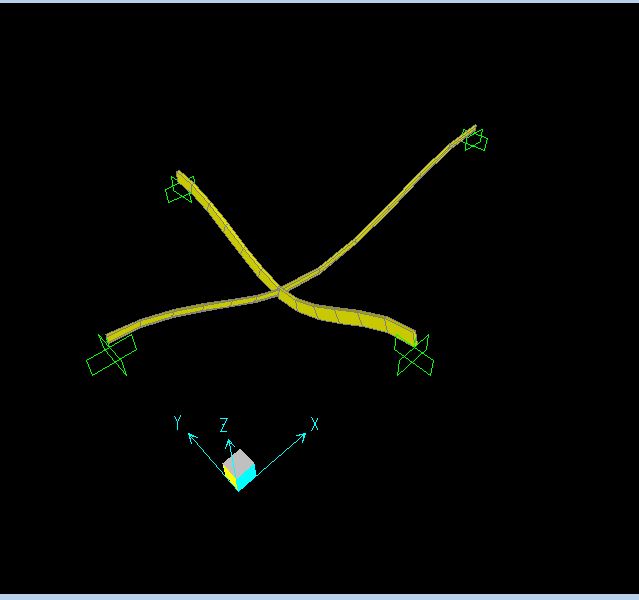
Leggiamo ora i risultati ottenuti.
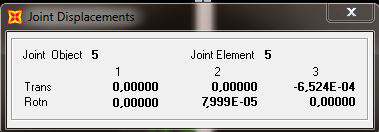
Abbiamo che Ux e Uy sono uguali a zero, mentre Uz = 0,0006524. Mentre per quanto riguarda la rotazione abbiamo un valore corrispondente a = 0,00008.
I valori trovati manualmente corrispondo, se non per un minimo scarto, a quelli trovati in sap.
Equilibrio di bilancio al nodo contro la traslazione lungo l'asse z
Equilibrio di bilancio al nodo contro la traslazione lungo l'asse z
Commenti recenti