Esercitazione

Analizziamo il comportamento di un impalcato sollecitato da forze esterne orizzontali e il comportamento dei controventi nel rispondere a tali sollecitazioni.

I controventi vengono rappresentati come delle molle, in quanto rappresentano dei vincoli elastici, cioè in grado di rispondere alle forze esterne subendo una deformazione reversibile.

La capacità di queste molle di rispondere alle forze esterne sarà strettamente collegata alla loro rigidezza k e alla loro distanza dal centro delle rigidezze, unico punto in cui la risultante delle forze esterne applicate avrà momento pari a zero e dunque rotazione nulla.

Dunque una volta determinate le caratteristiche dimensionali e tipologiche dell’ impalcato e il materiale dei suoi elementi, attraverso un file excel si calcolerà il centro delle rigidezze.

Scelgliamo di analizzare il seguente impalcato in calcestruzzo:

fig.1

L’impalcato ha i seguenti controventi:

fig.2

Dove:

d₂V= 9,00 mt

d₃V= 14,00 mt

d₄V= 19,00 mt

d₂O= 5,00 mt

d₃​O= 14,00 mt

Si tratta di un TELAIO SHEAR TYPE, infinitamente rigido, con rigidezza pari a 

K_t = 12 EI / h³

H PILASTRI: 4,00 m

PILASTRI IN CEMENTO ARMATO -> MODULO DI YOUNG : E= 21000 Nmm

SEZIONE PILASTRI:  30 x 50 cm

A seconda dell’ orditura del telaio avremo i pilastri orientati in 2 diversi modi e di conseguenza con diversi MOMENTI DI INERZIA.

 PILASTRI 7-8-9-10                PILASTRI 1-2-3-4-5-6

fig.3

Prima di procedere con i calcoli su excel definiamo i telai, rispettivamente al piano cui appartengono. Si faccia riferimento alla fig.2 .

TELAIO VERTICALE_piano Y-Z                                         TELAIO ORIZZONTALE_piano X-Z     TELAIO 1 : PILASTRI 1-5                                                        TELAIO 5 : PILASTRI 1-2-3-4

TELAIO 2 : PILASTRI 2-6                                                        TELAIO 6 : PILASTRI 5-6-7-8

TELAIO 3 : PILASTRI 9-7-3                                                    TELAIO 7 : PILASTRI 9-10

TELAIO 4 : PILASTRI 10-8-4                                                  

STEP 1 Calcolo delle RIGIDEZZE TRASLANTI dei controventi dell’edificio.

Inseriamo nelle celle i dati relativi al nostro progetto. La rigidezza traslante dei controventi presi in analisi è data dalla somma delle rigidezze di ciascun pilastro.

STEP 2     Tabella sinottica dei controventi e delle loro distanze dell’origine

Ci permette di raccogliere dati sulle rigidezze traslanti prima ottenute e sulle loro distanze rispetto al centro 0, le quali dipendono dagli interassi e dalle luci tra i pilastri. 

STEP 3 Calcolo del CENTRO DELLE MASSE:

Al fine di determinare il baricentro della struttura, occore suddividere la stessa in aree:

Dove XG e Y_G sono le coordinate del punto G, centro di massa della struttura.

A1 tot = 95 mq

A2 tot = 45 mq

A tot   = 95 + 45 = 140 mq

STEP 4  Calcolo del CENTRO DI RIGIDEZZE e delle RIGIDEZZE GLOBALI:

Calcolando la rigidezza totale delle molle, quindi la capacità dei controventi di contrastare le forze agenti in direzione perpendicolare al telaio, troviamo la rigidezza totale orizzontale e la rigidezza totale verticale. Le sommiamo rispettivamente e facciamo la media ponderata.

Il centro delle rigidezze lo troviamo calcolando, per ogni molla, il prodotto della sua rigidezza per la sua distanza dal punto 0, origine degli assi. Sommiamo rispettivamente i prodotti ottenuti e li dividiamo per la rigidezza globale, dato ora noto.

Avremo  X_CDR e  Y_CDR, coordinate del centro di rigidezza globale.

La RIGIDEZZA TORSIONALE TOTALE K  è data dalla sommatoria dei prodotti delle rigidezze traslanti di ciascun telaio per la distanza al quadrato di ognuno di essi rispetto a C, centro delle rigidezze.

STEP 5 Analisi dei carichi sismici:

Consideriamo il carico del solaio in c.a. analizzato nella precedente esercitazione. Moltiplichiamo il suo valore per il coefficiente di contemporaneità, al fine di trovare i pesi sismici. I pesi sismici vengono moltiplicati inoltre per il coefficiente di intensità sismica. In questo modo potremmo risalire al valore della forza sismica agente sui telai. Occorre chiarire che tale valore rimane aleatorio, per questo motivo il coefficiente di intensità sismica si presenta elevato.

STEP 6 e 7: Ripartizione della forza sismica lungo X e Y

La forza sismica si ripartisce nelle due direzioni. Sappiamo che sio verificherà una rotazione in quanto il centro delle rigidezze e il centro delle masse non coincidono. Il momento torcente è dal tal calcolo Forzaxbraccio, dove il braccio è paari alla differenza tra le rispettive coordinate del centro delle masse e del centro delle rigidezze.

Troviamo la traslazione orizzontale Ux dividendo la forza simica per la resistenza globale orizzontale e la traslazione verticale Uy dividendo la forza sismica per la resistenza globale verticale.

Calcoliamo la rotazione dividendo il momento torcente (su X o su y) per la rigidezza torsionale totale Kφ.

Per capire quanta forza sismica si ripartisce su ciascuna molla, occorre moltiplicare la rigidezza della molla, per la somma tra lo spostamento (u) ed il prodotto tra rotazione φ e distanza dal centro delle rigidezze.

La reazione di ciascuna molla viene calcolata semplicemente moltiplicando la resistenza della molla cui si è interessati conoscere la reazione, per la traslazione che ad essa è perpendicolare (u oppure v).

Verifichiamo che l' analisi effettuata risponda correttamente se inserita in SAP. 

Vincoliamo la struttura al terreno meidante incastro:

Selezionando tutti i nodi dell' impalcato, applicando Diaphram, conferiamo una rigidezza tale al telaio, da avere solo traslazioni.

Assegnamo la sezione ai pilastri, considerando l' orientamento degli stessi come da progetto:

Con lo stesso metodo, assegnamo la sezione alle travi, impostando un momento d' inerzia tale che venga simulato il modello di telaio shear type, infinitamente rigido:

Applichiamo la Forza sul centro di rigidezza e analizziamo:

La struttura trasla, ma non ruota.

In questa esercitazione verifichiamo, sulle tipologie di solai già analizzati nella seconda esercitazione, l’altezza della trave nel caso di uno sbalzo.

Rispetto all’esercitazione precedente di una trave doppiamente appoggiata, nel caso della trave incastrata e con un estremo libero, una mensola, il momento flettente M è uguale a ql²/2 .

Inoltre verificheremo l’altezza di trave calcolata in base alla resistenza a flessione in base alla sua deformabilità.

I parametri che inseriremo saranno:

H_d , l’altezza ingegnerizzata, arrotonda al valore di altezza trovata con il calcolo al maggiore e più vicino multiplo di 5.

Di nuovo la verifica aggiungendo il peso proprio della trave al carico q_s.

Il momento di inerzia I_x = b * h³ / 12

Lo spostamento v =  q l⁴ / 8 E I_x

La verifica alla deformabilità richiede che il rapporto tra lo spostamento e la luce sia  l / v_max > 250 , ossia l’entità dello spostamento all’estremo libero sia minore di 1/250 della lunghezza dello sbalzo.

I carichi considerati sono ripresi dall’analisi della seconda esercitazione.

SOLAIO CON TECNOLOGIA IN CALCESTRUZZO ARMATO

SOLAIO CON TECNOLOGIA IN ACCIAIO

SOLAIO CON TECNOLOGIA IN LEGNO

In conclusione vediamo come a causa della grande deformabilità delle mensole l’altezza della trave debba essere incrementata in tutti gli esempi visti.

Lo scopo di questa esercitazione è dimensionare la trave più sollecitata su tre casi di studio di solai con tre tecnologie diverse. Ho scelto di analizzare un solaio in latero-cemento con trave in calcestruzzo armato, un solaio con profili in acciaio e lamiera grecata e un solaio in legno lamellare.

Il calcolo, effettuato tramite una tabella excel considera i carichi strutturali, permanenti e accidentali del solaio, il momendo flettente che ne deriva e le resistenze caratteristiche del materiale. In seguito verifica il dimensionamento aggiungendo il peso proprio della trave principale trovata al carico strutturale.

Prendiamo in considerazione un impalcato tipo di misure 6m x 4m, comune per le tre tecnologie, con area di interesse di 24 m².

SOLAIO IN LATERO CEMENTO

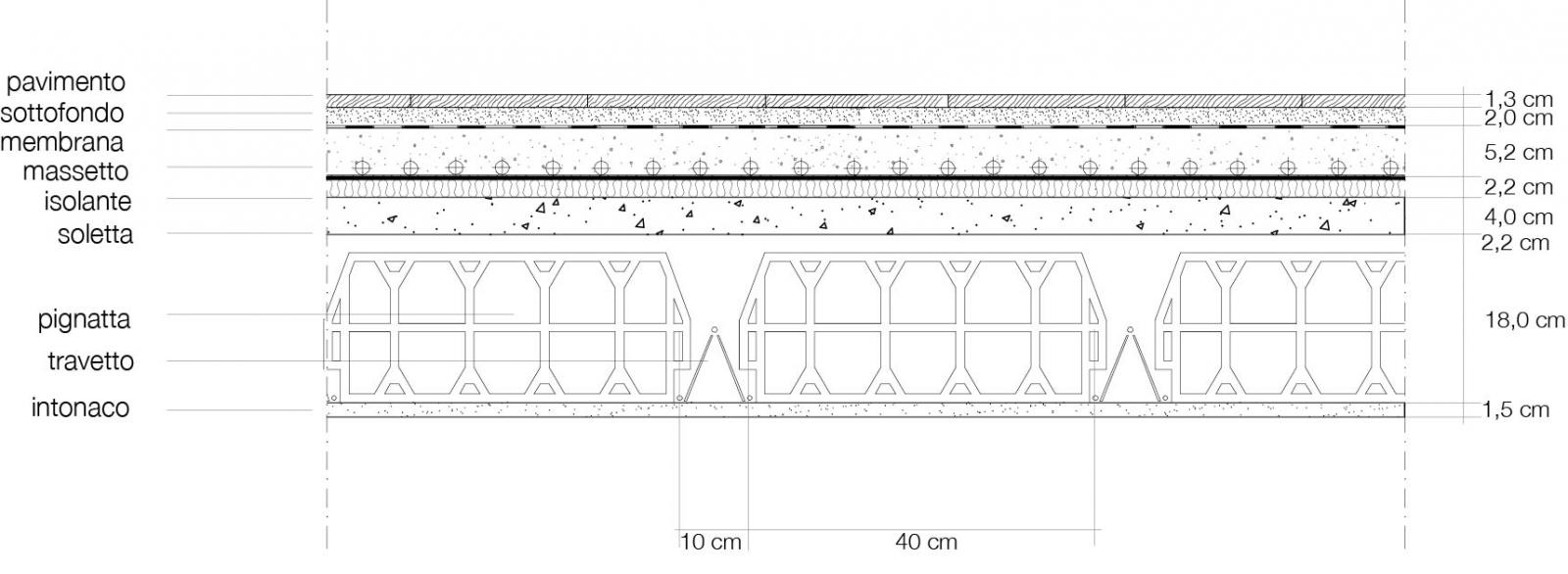
Carico strutturale

Strato strutturale in latero-cemento sp. 0,22 m interasse travetti 0,5 m

pignatte 2x dim. 0,18x0,40x1m /1m² x γ 5 kN/m³ = 0,72 kN/m²

travetti 2x dim.  0,10x0,18x1m  /1m² γ 25 kN/m³ = 0,9 kN/m²

soletta sp. 0,04 m γ 25 kN/m³ = 1 kN/m²

q_s = (0,72+0,9+1) kN/m² = 2,62 kN/m²

Carico permanente

Parquet di rovere naturale: essenza dura sp: 0,013 m γ 7 kN/m³ = 0,091 kN/m²

Sottofondo di sabbia e cemento sp. 0,02 m γ 18 kN/m³ = 0,36 kN/m²

Membrana in polietilene sp. 0,002 m γ 9 kN/m³ = 0,18 kN/m²

Massetto di integrazione impiantistica in Cls addittivato AT 30 sp. 0,052 m γ 18 kN/m³ = 0,936 kN/m²

Pannello isolante termoacustico in fibra di poliestere sp. 0,022 m γ 0,2 kN/m³ = 0,0044 kN/m²

Intonaco in calce-gesso sp. 0,015 m γ 15 kN/m³ = 0,225 kN/m²

tramezzi = 1 kN/m²

impianti = 0,5 kN/m²

q_p = (0,091+0,36+0,18+0,936+0,0044+0,225+1+0,5)kN/m² = 3,3 kN/m²

Carico accidentale

Categoria A, Ambienti ad uso residenziale

q_a = 2,00 kN/m²

Il carico totale q è uguale all’interasse per a somma del carico strutturale permanente e accidentale moltiplicati per dei coefficient di sicurezza : q= i* [ (qs+qp)*1,3 + (qa)*1,5 ]

Ora possiamo trovare il momento M, che sappiamo essere ql²/8 per una trave doppiamente appoggiata.

Inseriamo f_y  limite di snervamento dell’acciaio da armature e R_ck resistenza a compressione del calcestruzzo su provino cilindrico a 28 giorni per calcolare rispettivamente il sigma ammissibile dell’armatura in ferro e l sigma ammissibile del calcestruzzo.

Con questi valori e ipotizziando una base della trave di 20 cm viene calcolato un primo valore di altezza della trave, a cui va aggiunto delta, altezza del copriferro.

Verifica al peso proprio della trave

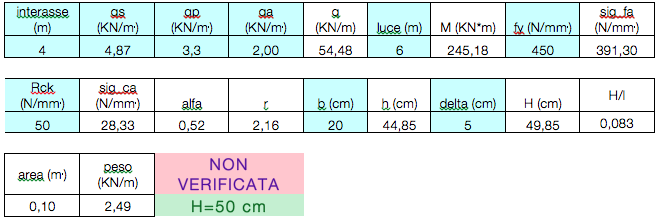
Notiamo che il peso proprio della trave di calcestruzzo influisce in modo importante sul calcolo e ci costringe a scegliere una sezione maggiore.

SOLAIO IN ACCIAIO

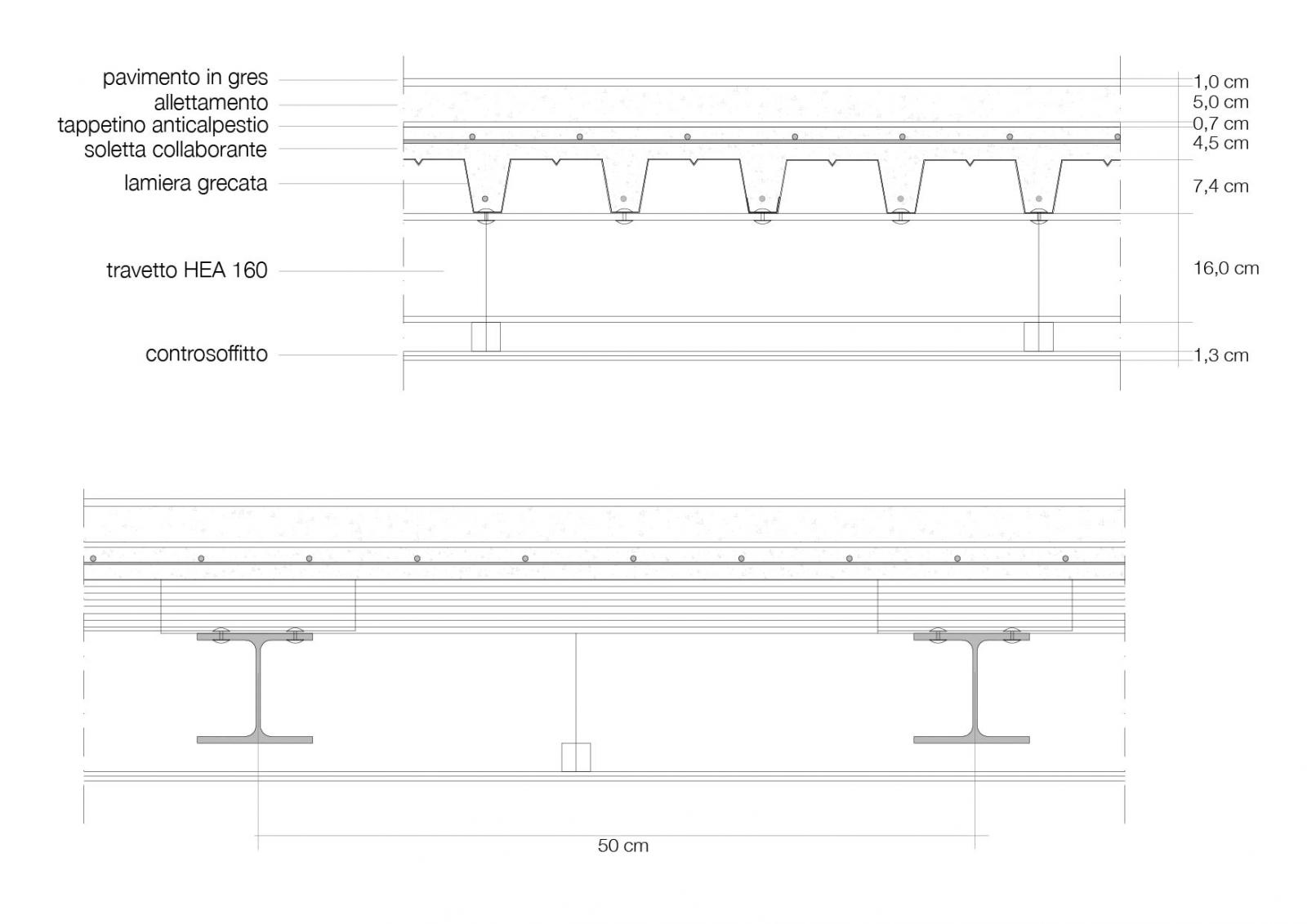
Carico strutturale

travetto HEA 160 = 0,304 kN/m²

lamiera gracata sp. 0,012 m = 0,165 kN/m²

soletta collaborante sp. 0,045  γ 25kN/m³ = 1,125 kN/m²

completamento gracata 5* (0,064m+0,034m)*0,074m /2 *1m * γ 25kN/m³ = 0,45 kN/m²

q_s = (0,304+0,165+1,125+0,45) kN/ m² = 2,044 kN/ m²

Carico permanente

massetto di allettamento in sabbia e cemento sp. 0,05 m * γ 18 kN/m³ = 0,9 kN/m²

tappetino anticalpestio sp.0,007 m * γ 0,9 kN/m³ = 0,0063 kN/m²

pavimento gres sp.0,01 m * γ 20 kN/m³ = 0,2 kN/m²

controsoffitto in cartongesso sp. 0,013 m * γ 9 kN/m³ = 0,117 kN/m²

tramezzi = 1 kN/m²

impianti = 0,5 kN/m²

q_p = (0,9+0,0063+0,2+0,117+1+0,5) kN/m² = 2,73 kN/m²

Carico accidentale

Categoria B2 uffici aperti al pubblico

q_a =  3,00 kN/m²

In questo caso usiamo f_y,k tensione di snervamento caratteristica dell’acciaio per la classe Fe 430/S275 per trovare il sigma ammissibile e la resistenza W_x  che comparata con i moduli di resistenza di un profilario ci porta a scegliere un’IPE 360.

Verifica peso proprio della trave  q=0,571 kN/m

La sezione trovata è verificata.

SOLAIO IN LEGNO

Carico strutturale

travetti legno lamellare interasse 0,50 m 2x dim. 0,22*0,06 m * γ 5 kN/m³ = 0,132 kN/m²

Rivestimento portante di pannelli OSB sp. 0,022 m * γ 5,8 kN/m³ = 0,128 kN/m²

q_s = (0,132+0,128) kN/m² = 0,26 kN/m²

Carico permanente

massetto sabbia cemento sp. 0,04 m * γ 18 kN/m³ = 0,72 kN/m²

pavimento legno sp. 0,013 m * γ 7 kN/m³ = 0,091 kN/m²

isolante lana minerale sp. 0,10 m * γ 1,2 kN/m³ = 0,12 kN/m²

listelli in legno interasse 0,25 m 4* dim. 0,04*0,02 m * γ 7 kN/m³ = 0,0224 kN/m²

barriera al vapore sp. 0,00022 m * γ 5 kN/m³ = 0,0011 kN/m²

lastra in cartongesso sp. 0,012 m * γ 9 kN/m³ = 0,108 kN/m²

tramezzi = 1 kN/m²

impianti = 0,5 kN/m²

q_p = (0,72+0,091+0,12+0,0224+0,0011+0,108+1+0,5) kN/m² = 2,5625 kN/m²

Carico accidentale

Categoria A ambienti ad uso residenziale

q_a =  2,00 kN/m² 

Prendiamo f_m,k ,resistenza a flessione per legno lamellare di conifera e k_mod, coefficiente che tiene conto dell’invecchiamento del legno.

Verifica al peso proprio della trave principale q=0,675 kN/m

Anche in questo caso dobbiamo scegliere una sezione con un'altezza maggiore.

Prendiamo in considerazione una maglia strutturale con delle travi a sbalzo che aggettano di 3 metri e hanno un'area d'influenza con interasse 6 metri. Utilizziamo gli stessi solai della seconda esercitazione nelle 3 diverse tecnologie (calcestruzzo armato, legno e acciaio).

Nel dimensionare le travi prenderemo in considerazione il valore L/vmax che per essere soddisfatto dovrà essere maggiore di 250.

Solaio in legno

Qs= 0,36   Qp=2,4   Qa=2,00

Per necessità di deformabilità ho aumentato la sezione della trave fino a (35 x 55)cm.

L/vmax=291,00 VERIFICATO

Solaio in Cls

Qs=3,45   Qp=3,3   Qa=2,00

Anche in questo caso l'altezza della trave è stata aumentata fino ad avere una sezione di (30 x 48,25)cm.

L/vmax=253,69 VERIFICATO

Solaio in acciaio

Qs=2,71   Qp=2,05   Qa=2,00

In questo caso osserviamo il modulo d'inerzia Wx che ci porta ad avere una IPE 360 con un Wx pari a 904,00.

L/vmax=304,98 VERIFICATO