Esercitazione

La struttura che ci troviamo a dover risolvere è una trave su più appoggi iperstatica, il metodo di risoluzione più adatto a questo tipo di trave è il MEDOTO DELLE FORZE, dove le incognite sono le FORZE, e verranno trovate attraverso le EQUAZIONI DI COMPATIBILITA' CINEMATICA.
Il metodo delle forze ci consente di risolvere strutture iperstatiche riconducendole a sistemi isostatici equivalenti dove per ciascun GRADO DI IPERSTATICITA’ corrisponde una REZIONE VINCOLARE INCOGNITA.

Nel caso preso in esame sostituiamo i tre carrelli esterni con delle cerniere interne aggiungendo le reazioni vincolari rimosse, cioè la rotazione a destra e a sinistra del nodo. Quindi la struttura isostatica di riferimento sarà composta da una serie di travi doppiamente appoggiate con l'aggiunta di coppie di momenti in corrispondenza dei punti B, C, D.
Nella strruttura iperstatica non avviene nessuna rotazione nei suddetti punti, quindi per ognuna delle cerniere inserite il DELTA delle rotazioni è uguale a 0. Inoltre dobbiamo trovare le reazioni vincolari incognite X1 X2 X3 relative ai tre vincoli interni, poichèla struttura è simmetrca sappiamo che X1 = X3 quindi d’ora in poi utilizzeremo solo X1 e X2. Avremo due schemi che andremo a sommare con il principio della sovrapposizione degli effetti.

Le equazioni di compatibilità cinematica in grado di ripristinare il vincolo iperstatico sono:

Aiutandoci con gli schemi notevoli troviamo le rotazioni di ciascun tratto della trave

Mettendole a sistema possiamo così ottenere i valori di X₁ eX₂ (X₁ = X₃)

Dopo aver trovato i valori delle incognite iperstatiche possiamo trovarci le reazioni vincolari con il metodo della sovrapposizione degli effetti, per il quale le reazioni finali sono la somma delle reazioni dovute al carico q e alle forze iperstatiche trovate. Le reazioni vincolari vanno determinate per ciascuna delle quattro campate della struttura isostatica di riferimento e vanno sommate quelle che si trovano sullo stesso vincolo.

Ora possiamo procedere col calcolarci il taglio ed il momento effettuando sezioni nelle varie campate e determinandone il valore per ognuna.

TAGLIO

Primo tratto

Secondo tratto

Terzo tratto

MOMENTO

Primo tratto

Secondo tratto

L'esercizio consiste in una struttura 3 volte iperstatica. Per risoleverla la trasfomo in un sistema isostatico trasformando i carrelli B-C-D in cerniere interne, dividendo cosi la struttura in 4 corpi separati. Inoltre applico dei momenti flettenti X1, X2 e X3 in modo da ripristinare la rigidità della trave.

Trovo il valore dei tre momenti X₁,X₂ e X₃ (data la simmetria della struttura X₁ = X₃):

Sappiamo che ΔφB=ΔφD=0 e ΔφC=0

Uguaglio valori della rotazione di sinistra con quelli di destra e ricaviamo X1 e X2.

Dopo aver trovato le 2 incognite mi calcolo le reazioni vincolari:

                          +  

                          =

Infine disegno i diagrammi del taglio e del Momento trovando i valori nei diversi punti.

Taglio

Momento 

Con il METODO DELLE FORZE è possibile risolvere le strutture iperstatiche riconducendole a sistemi isostatici equivalenti. Per farlo dobbiamo rispettare la condizione di COMPATIBILITA’ CINEMATICA ovvero la congruenza degli spostamenti e delle rotazioni in ciascuna delle strutture isostatiche di rifermento.

Analizzeremo ora una TRAVE CONTINUA SU PIU’ APPOGGI.

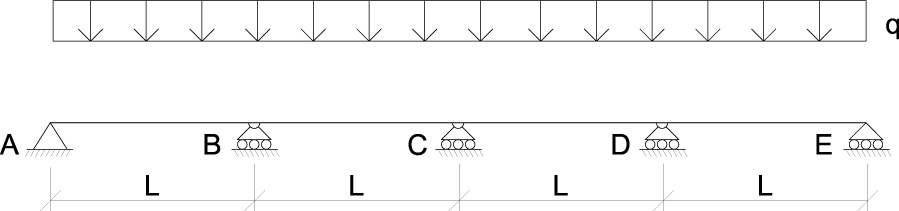
 Analizzando la struttura abbiamo:

GDL = 3

GDV = 2 + 1 + 1 + 1 + 1 = 6

Ci sono 3 INCOGNITE IPERSTATICHE. Dobbiamo quindi impostare una struttura isostatica equivalente in cui per ciascun GRADO DI IPERSTATICITA’ corrisponda una REZIONE VINCOLARE INCOGNITA in modo da avere una struttura corrispondente a quella iperstatica.

Possiamo quindi sostituire le 3 cerniere esterne delle campate centrali con delle cerniere interne permettendo la rotazione a destra e a sinistra di ciascuna cerniera. Poiché nella struttura iperstatica non avviene nessuna rotazione sappiamo che per ognuna delle cerniere inserite il DELTA delle rotazioni è uguale a 0. Inoltre dobbiamo inserire le reazioni vincolari vincolari incognite ottenendo X₁ X₂ X₃, per il principio di simmetria sappiamo che X₁ = X₃ quindi d’ora in poi utilizzeremo solo X₁ eX₂.

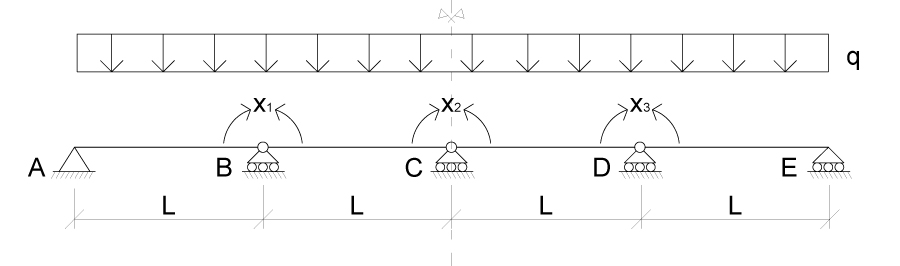
Una volta inserite le reazioni incognite, dobbiamo scrivere le equazioni di compatibilità cinematica in grado di ripristinare il vincolo iperstatico, dato che abbiamo sostituito un grado di iperstaticità con una reazione incognita.

∆φ_B= φ_Bs- φ_Bd =0

∆φ_C= φ_Cs- φ_Cd =0

∆φ_D= φ_Ds- φ_Dd =0

Per il principio di simmetria abbiamo :

φ_Ds= - φ_Bd

φ_Dd= - φ_Bs

Ora dobbiamo sostituire nelle equazioni di compatibilità cinematica i rispettivi valori dati dalle rotazioni in ciascuna cerniera.

Mettendole a sistema possiamo così ottenere i valori di X₁eX₂ ricordandoci che X₁ = X₃.

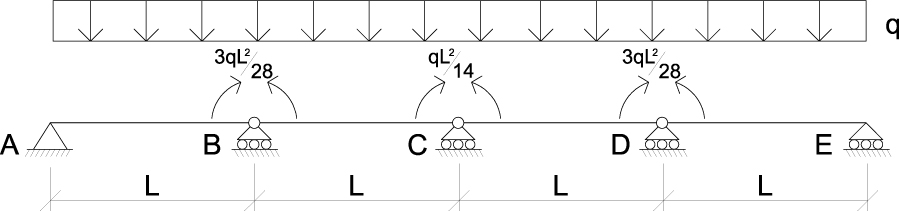
Ora che le incognite X₁ eX₂ sono note possiamo applicare il PRINCIPIO DI SOVRAPPOSIZIONE DEGLI EFFETTI secondo cui l’azione delle forze sulla struttura è uguale alla somma dell’effetto di ciascuna forza.

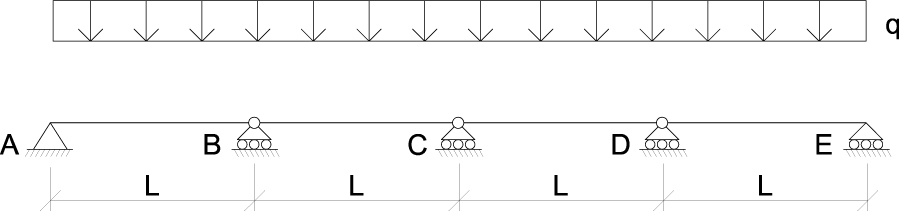
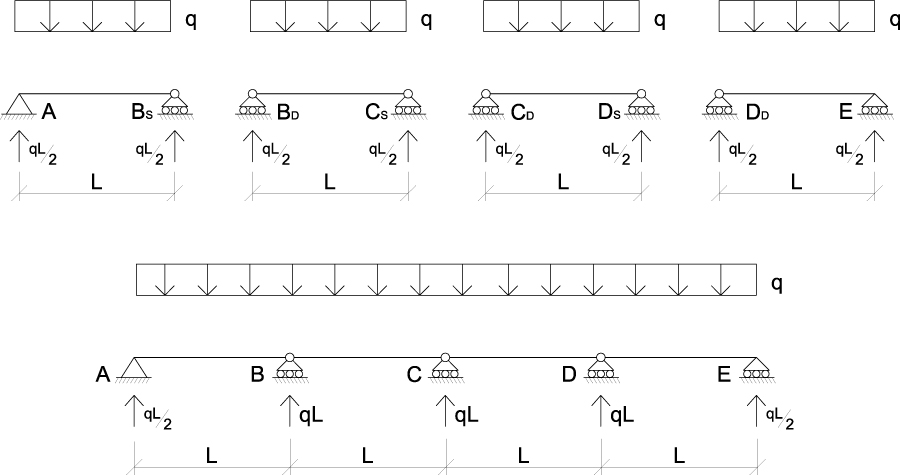
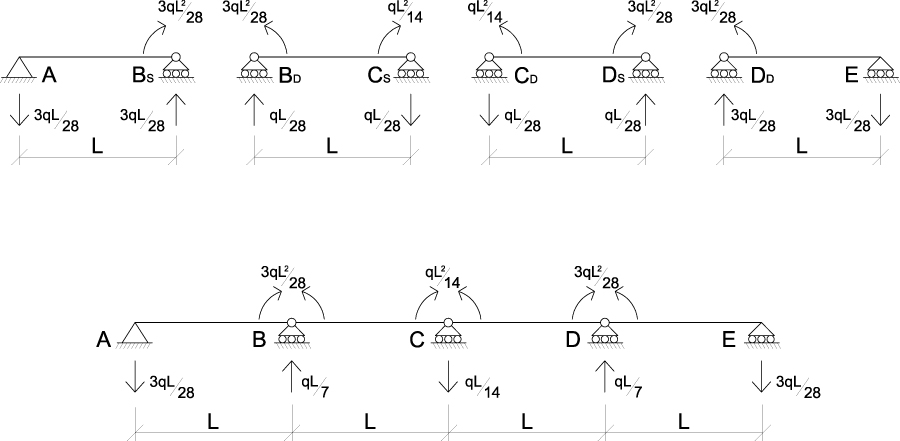
Analizziamo quindi la struttura isostatica equivalente una volta sotto l’effetto del CARICO q e una volta sotto l’effetto delle REAZIONI VINCOLARI X; ricordandoci di determinare le razioni vincolari per ciascuna campata (dato che la struttura è assimilabile a 4 travi doppiamente appoggiate) e sommando quindi quelle che insistono sullo stesso vincolo.

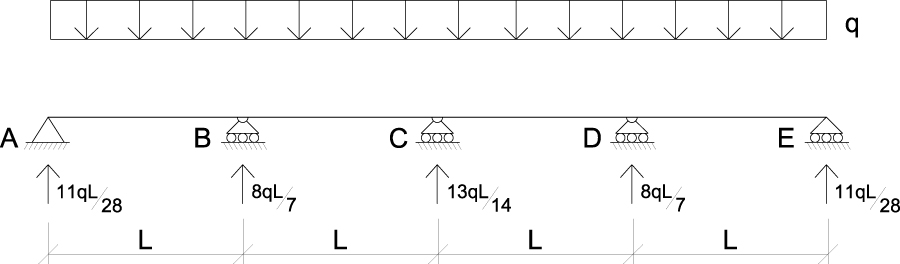
Rimane ora da determinare il diagramma del taglio e del momento.

TAGLIO

Primo tratto

secondo tratto 

terzo tratto

MOMENTO

Primo tratto

secondo tratto