Esercitazione

Importo in SAP il modello 3d creato con autocad e salvato in dxf, settando l'unità in (KN,m,C), ed impostando il layer utilizzato in autocad.

Annullo possibili margini d'errore che possono avvenire nel trasferimento di dati tra i 2 programmi. (edit-points--merge joints-merge tolerance- assegno un valore di 0.01.

Assegno i vincoli (in questo caso 1 cerniera e 2 carrelli): seleziono i nodi. poi Assign-joint restraint e scelgo il tipo di vincolo.

ESERCITAZIONE n.3

Dimensionamento di una trave in legno:

1-      Compongo una porzione di solaio:

2-      Definisco il dimensionamento del solaio:

-          Interasse tra le travi = 3m

-          Base di una trave (larghezza) = b = 0.30m

-          Interasse tra i travetti = 0.50m

-          Ipotizzo la composizione del solaio:

1-      Travetti in legno (conifera):

Dimensioni 8cm x 10cm

γ  = 5 KN/mc

2-      Tavolato (conifera):

h= 3cm

γ  = 5 KN/mc

3-      Sottofondo: sabbia e cemento

 h= 3cm

γ  = 18 KN/mc

4-      Isolante termico: fibra di legno

h = 2cm

γ  = 0.24 KN/mc

5-      Lastra di fibro-gesso

h = 3cm

γ  = 0.14 KN/mc

6-      Pavimento in ceramica

h = 1.5cm

γ  = 20 KN/mc

3-      Calcolo i carichi strutturali: qs

Questi sono costituiti dalle somme dei pesi degli elementi che compongono la struttura portante del solaio.

Calcolo i pesi di tutti gli elementi strutturali che compongono il solaio considerando una sezione dello stesso di dimensioni 1m X 1m:

-          Ps1 = γ x V = 5KN/mc x 0.08mc = 0.045 KN/mq ; essendo 2 I travetti : 0.045x2 = 0.09 KN/mq

-          Ps2 = 5KN/mc x  0.03mc = 0.18 KN/mq

Totale dei carichi strutturali = Ps1 + Ps2 = 0.27 KN/mq

4-      Calcolo i carchi portati: qp

Questi sono costituiti dalle somme dei pesi degli elementi che compongono il solaio con l’ aggiunta del peso degli eventuali impianti cosi come dei tramezzi.

Perciò considero:

Psi = 0.5KN/mq per gli impianti

Pst = 1    KN/mq per i tramezzi

Calcolo i pesi di tutti gli elementi che compongono il solaio considerando una sezione dello stesso di dimensioni 1m X 1m:

-          Ps3 = 18KN/mc x 0.03mc = 0.9 KN/mq

-          Ps4 = 0.24KN/mc x 0.02mc = 0.0048 KN/mq

-          Ps5 = 0.14KN/mc x 0.03mc = 0.0042 KN/mq

-          Ps6 = 20KN/mc x 0.015mc = 0.3 KN/mq

Totale dei carichi portati = Ps3+Ps4+Ps5+Ps6 = 2.7 KN/mq

5-      Calcolo i carichi accidentali : qa

Questi sono considerati sovraccarichi accidentali ed hanno valori regolati da una normativa.

Per questo esercizi ipotizzo edifici di categoria A e cioè Ambienti ad Uso Residenziale con

Ps = 2 KN/mq

6-      Trovati quindi tutti i carichi che insistono sulla sezione considerata inserisco gli stessi in una apposita tabella excell

In cui:

-           M è dato da =E3*F3^2/8

-          Fm,k è il valore della resistenza a flessione del legno lamellare di classe GL 24c

-          Sig am è dato da =I3*H3/1,45

-          h è dato da =( 6*G3*1000/(K3*J3))^0,5

ANALISI DEI CARICHI E DIMENSIONAMENTO DI UNA TRAVE

DESTINAZIONE D'USO

uffici non aperti al pubblico 

TRAVE PIU' SOLLECITATA

AREA D'INFLUENZA

STRATIGRAFIA SOLAIO

1)pavimento

2)allettamento (2 cm)

3)massetto cementizio (10 cm)

4)tavolato (4cm)

5)travicelli (10 x 10)

6)trave

ANALISI DEI CARICHI

-CARICHI STRUTTURALI qs

Travicelli

P = γ * V γ travicelli = 6 KN V = 0,1 * 0,1 * 1 = 0,01 m³

P = 6 KN/m³ * 0,01 m³ = 0,06 KN/mq mq perchè il carico agisce su un'area

Su 1 mq ci sono due travetti quindi 0,06 * 2 = 0,12 KN/mq

Tavolato

γ = 6 KN/ m³ V = 0,2 * 0,04 * 1 = 0,008 m³

P = 6 * 0,008 = 0,048 KN/mq

In 1 mq ci sono 5 tavole quindi 5 * 0,008 = 0,24 KN/mq

qs = 0,12 + 0,24 = 0,36 KN/mq

-CARICHI PERMANENTI qp

Massetto cementizio

γ = 18 KN/m³ V = 1 * 1 * 0,1 = 0,1 m³

P = 18 * 0,1 = 1,8 KN/mq

Allettamento

γ = 21 KN/m³ V = 1 * 0,02 * 1 = 0,02 m³

P = 21 * 0,02 = 0,42 KN/mq

Pavimento in mattonelle di granito

γ = 27 KN/m³ V = 0,2 * 0,2 * 0,01 = 0,0004 m³

P = 27 * 0,0004 = 0,0108 Kn/mq

il peso complessivo delle mattonelle che agisce su 1 mq = 0,0108 * 1 * 1 = 0,0108 KN/mq

Incidenza dei tramezzi

1 KN/mq

Impianti

0,5 KN/mq

qp = 1,8 + 0,42 + 0,0108 = 2,23 KN/mq

-CARICHI ACCIDENTALI qa = 2 KN/mq ( data dalla normativa )

DIMENSIONAMENTO CON LA TABELLA DI EXCEL

Avendo deciso di avere la base della trave di 30 cm e la luce della trave più sollecitata di 6 m, risulta dall'analisi dei carichi che per sorreggere i carichi provenienti dal solaio devo avere una trave alta 49,96 cm.

Questo tipo di dimensionamento ci permette di calcolare l'altezza di una trave per volta, quindi noi andremo a calcolare sempre i carichi che agiscono sulla trave più sollecitata (ci accorgiamo che una trave è più sollecitata rispetto ad un'altra osservando l'orditura del solai, quindi i carichi agiranno in maggior modo sulla trave perpendicolare all'orditura dei solai).

DIMENSIONAMENTO DI UN SOLAIO IN LEGNO

      In rosso è evidenziata la trave la quale si è scelta per effettuare il dimensionamento

sezione del solaio in legno

dobbiamo calcolarci l'altezza h della trave , mentre sono definiti i valori della base, del momento massimo e della resisenza di progetto fd 

La resistenza di progetto è fd= Kmod * fmk / γm

dove: 

Kmod (coefficiente che dipende dalla durata del carico e dall’umidità) = 0,6

fmK ( caratteristica resistenza a flessione) = 36 N/mmq

γm(coefficiente di sicurezza relativo al materiale) = 1,45

dove σmax= (Mmax/ Ix) * ymax = M/W

(W) è il modulo di resistenza a flessione che dipende dalle caratteristiche geometriche della sezione. In questo caso la trave ha sezione rettangolare, per cui (ymax = h/2), quindi avrò:

Ix = bh³/12

W= Ix/ymax

W= bh²/6 

quindi ymax/Ix = Wx è il modulo di resistenza a flessione della sezione   →   σmax= Mmax/(bh²/6)

da quest'ultima ci ricaviamo l'altezza  h = rad(6q/8b fd) * l

ANALISI DEI CARICHI

definiamo una base b= 30 cm 

 CARICHI STRUTTURALI qs

Trave = 1,00 m x 050 m x 0,30 m x 430 Kg/m³  = 0,65 KN/m²

Travicelli (abete)= 2 x 1,00 m x 0,10 m x 0,10 m x 600 Kg/m³ = 0,12 KN/m²

Tavolato  (abete) = 1,00 m x 1,00 m x 0,03 m x 600 Kg/m³ = 0,18 KN/m²

totale =      0,95 KN/m²

CARICHI PERMANENTI qp

Massetto = 1,00 x 1,00 m x 0,05 m x 1900 Kg/m³ = 0,95  KN/m²

Allettamento= 1,00 x 1,00 m x 0,03 m x 1800 Kg/m³ = 0,54  KN/m²

Pavimento = 1,00 m x 1,00 m x 0,01 m x 400 Kg/m³ = 0,40  KN/m²

Incidenza tramezzi = 1,00  KN/m²

Incidenza impianti = 0,50 KN/m²   

totale = 2,99  KN/m²

CARICO ACCIDENTALE qa

Locali d’abitazione = 2  KN/m²

 Totale dei carichi  = 5,94  KN/m²

qtot[Kn/m] = (qs+ qp+ qa) * i = 5,94 * 5 = 29,7 KN/m²

Insiriamo ora nella tabella excell i valori ricavati e ci troviamo l'altezza della trave 

L'altezza risulta essere circa 45 cm.

DIMENSIONAMENTO DI UN SOLAIO IN CALCESTRUZZO 

SEZIONE DEL SOLAIO

carico permanente q = 38 KN/m²

M = ql²/8 ( trave appoggiata appoggiata)

Imponiamo che fd= σmax = α * Rck/γm

dove:

Rck = resistenza caratteristica calcestruzzo = 30 N/mm²

E' stato scelto un calcestruzzo ordinario di classe C 25/30

α = coeff. riduttivo per la resistenza a lunga durata = 0,85

γm = coeff. riduttivo parziale di sicurezza relativo al cls = 1,5

σfa = fy/γs

dove:

fy = tensione di snervamento delle barre di acciaio = 450 N/mm²

γs = coeff. di sicurezza relativo all’acciao = 1,15

L'altezza di una sezione rettangolare è data da H = hu + δ

hu= r * rad(Mmax/b)

δ è distanza dal centro dei tondini al lembo inferiore della trave (5 cm)

ANALISI DEI CARICI

Carichi strutturali qs

Soletta = 1,00m x 1,00m x 0,04m x 2500Kg/m²   =  1KN/m²

Nervature = 2 x 0,1m x 0,2m x 1,00m x 2500 Kg/m²   = 1 KN/m²

Forati = 2 x 0,4 mx 0,2m x 1,00m x 800Kg/m²= 128    = 1,28 KN/m²

Totale = 3,28 KN/m²

Carichi permanenti qp

Intonaco = 1,00m x 1,00m x 30m = 0,30   KN/m²

Massetto = 1,00 mx 1,00m x 0,03m x 1900Kg/m²   =0, 57 KN/m²

Pavimento =   1,00mx 1,00m x 40m  =  0,40 KN/m²   

Incidenza tramezzi = 1  KN/m²  

Incidenza impianti = 0,50 KN/m²  

totale = 2,77

CARICO ACCIDENTALE qa

Locali d’abitazione = 2  KN/m²

Totale dei carichi  = 8,05  KN/m²

Inseriamo i valori nella tabella excel

L'altezza risulta essere circa 55 cm.

 Il metodo della linea elastica serve per risolvere l'equilibrio di strutture sia iperstatiche che isostatiche; consentendoci di determinare le reazioni vincolari, i diagrammi delle sollecitazioni , gli spostamenti e le deformazioni.              

Richiamiamo di seguito tutte le equazioni del modello di trave di bernoulli, distinguendole in tre gruppi in base al loro diverso significato fisico.

• EQUAZIONI DI BILANCIO esprimono il legame tra carichi esterni e sollecitazioni 

dN/ds + q1 = 0

dT/ds + q2 = 0

dM/ds + T = 0

• EQUAZIONI DI CONGRUENZA esprinono il legame tra deformazioni e spostamenti

E =    du/ds

y = dv/ds - φ = 0

X = dφ/ds

dove E = deformazione assiale

       y = scorrimento angolare

       X = curvatura

• LEGAME COSTITUTIVO ELASTICO esprimono il legame tra la deformazione e la sollecitazione

N = EA * E 

M = EI * X

Analizziamo il problema flessionale e prendiamo in considerazione le seguenti grandezze

v ; Y ; T ; M ; x

quindi non prendendo in considerazione le equazioni che riguardano lo sforzo normale, le equazioni che definiscono il problema flessionale sono :

dT/ds + q₂ = 0

dM/ds  + T = 0

M = EI * X

X = dφ/ds

φ= dv/ds

Prendiamo in considerazione l'equazione ( dM / ds ) + T = 0 e ci ricaviamo T = - dM / ds e sostituiamo la T in

( dT/ds ) + q₂ = 0

avremo che d/ds ( -dM/ds) + q₂ = 0 ⇒ -d²M/ds² + q₂ = 0 

X = dφ/ds - d/ds(dv/ds) = d²v/ds^{2 =} d²v/ds²

andiamo ora a sostituire φ= dv/ds in X= dφ/ds

avremo che X = dφ/ds - d/ds(dv/ds) = d²v/ds^{2 =} d²v/ds²

ci rimane solo l'equazione M = EIx

Sostituiamo la x e avremo che M = EI (d²v)/ds

sostituiamo poi l'equazione ricavata nell'equazione  -d²M/ds² + q₂ = 0 

si avrà che :

 d²/ds² ( EI * d²v/ds²) = q₂

portiamo EI al di fuori della derivata e avremo che 

EI d⁴v/ds⁴ = q₂  EQUAZIONE DIFFERENZIALE DELLA LINEA ELASTICA

L'equazione della linea elastica mette in relazione i carichi agenti sulla trave con gli spostamenti da essi prodotti , integrando quattro volte otteniamo la funzione spostamento

d⁴v/ds = q₂/EI

d³v/ds = q₂/EIs + c₁

d²v/ds = q²/EI * s²/2 + c₁s + c₂   (3)

dv/ds = q₂/EI + s³/6 + c₁ * s²/2 + c₂s + c₃   (2)

v(s) = q₂/EI * s⁴/24 + c₁*s³/6 + c₂ s_2/2 + c₃s + c_{4    spostamento}  (1)

Abbiamo così ottenuto quattro equazioni che dipendono dai vincoli quindi andiamo a sostituire le equazioni al bordo

Nell'incastro v(0) = 0 

Andando a sostituire nella 1 la condizione al bordo v(0) = 0 si ottiene v(s=0) = 0 --> C4 = 0

 φ(0) = 0

Sostituendo nella 2 si ottiene 

φ (s=0) --> c3=0

Nell'appoggio

v(l) = 0

sostituiamo nella 1 avremo che :

v(s=l)= 0 ⇒ - q₂l⁴/24EI + c₁l³/6 + c₂l²/2 = 0  (4)

Nel carrello il momento vale zero M (l) = 0

sostituendo nella 3 avremo che :

M(s=l) = 0 ⇒ -q₂l²/2EI + c₁l + c₂ = 0 

ci ricaviamo c_{2 =} q₂l²/2EI - c₁l    (5)

sostituiamo c₂ nella 4 

- q₂l⁴/24EI + c₁l³/6 + (q₂l²/2EI - c₁l ) * l²/2 = 0

- q₂l⁴/24EI + c₁l³/6 q₂l⁴/4EI - c₁l³/2 = 0

5q₂l⁴/24EI -1/3 l³ c₁ = 0

c₁ = 5/8 q₂l/EI

Andiamo a sostituire c₁ nella (5) e ricaviamo c₂

c₂ = -q₂l²/8EI

Abbiamo così trovato le quattro costanti di integrazione , ora dobbiamo calcolare l'abbassamento massimo . Sappiamo che y= dv/ds, ossia che la rotazione è la derivata dello spostamento . Quindi nel punto in cui la rotazione è nulla lo spostamento sarà massimo

φ = dv/ds = q₂/EI + s³/6 + c₁ * s²/2 + c₂s + c₃

Andiamo a sostituire nell'equazione scritta le costanti trovate 

φ (s) = - q₂/EI + s³/6 + 5/8 q₂l/EI s²/2 - q₂l²/8EI + 0 

poniamola uguale a zero 

φ (s) = - q₂/EI + s³/6 + 5/8 q₂l/EI s²/2 - q₂l²/8EI = 0

che possiamo scrivere come

q/2EI s * ( - s₂/3 + 5/8 ls - l²/4) = 0 

Questa equazione ha tre soluzioni. Una è data da s=0 ed altre due le troveremo svolgendo l'equazione di secondo grado 

1.  - s₂/3 + 5/8 ls - l²/4 = 0 
2.    s₂/3 + 5/8 ls - l²/4) = 0 

Poniamo 1/3 = A   -5/8 l = B  ⇒ As² - Bs - l₂/4 = 0 

Risolvendo con la formula del delta otteniamo due valori :

1.  1,3 l  ( soluzione non accettabile perchè s < l )
2. 0,57 l 

I punti di massimo della funzione spostamento si trovano uno a zero e l'altro a 0,57 l. Per ricavarci l'abbassamento massimo basta sostituire la s nell'equazione 4.

Adesso calcoliamo il momento M

Ms = -q/2 s₂ + 5/8 qls - ql²/8

Ora dobbiamo calcolare il punto in cui si annulla la derivata del momento M'(s)

M ( s=0) = -ql²/8

M ( s=l) = -ql²/2 + 5/8 ql² - ql²/8 = 0 

DIAGRAMMA DEL MOMENTO

Adesso calcoliamo il taglio 

T(s) = -dM/ds = - M'(s)

- M'(s) = T(s) = qs - 5/8 ql

T ( s=l) = ql - 5/8ql = 3/8 ql

DIAGRAMMA DEL TAGLIO

RISOLUZIONE SAP

Ho riprodotto la struttura in SAP disegnandola di lunghezza l = 2 e con un carico distribuito pari a q = 40 kN

1.    Divido ( con il comando Point ) la struttura in due parti, posizionando il punto ad una distanza di 0,57 dal punto zero e con asse y = z = 0 dato che dal calcolo a mano abbiamo visto che l'ammassamento massimo avviene in questo punto

L'analisi è stata fatta su due sezioni differenti , una rettangolare in acciaio cavo 

e l'altra in cemento armato 

DEFORMATA

REAZIONI VINCOLARI

DIAGRAMMA DEL TAGLIO

DIAGRAMMA DEL MOMENTO

SEZIONE IN CEMENTO

REAZIONI VINCOLARI

DIAGRAMMA DEL TAGLIO

DIAGRAMMA DEL MOMENTO

Dimensionamento travi principali e secondarie appartenenti a una struttura di destinazione residenziale con pianta:

E con solaio di sezione:

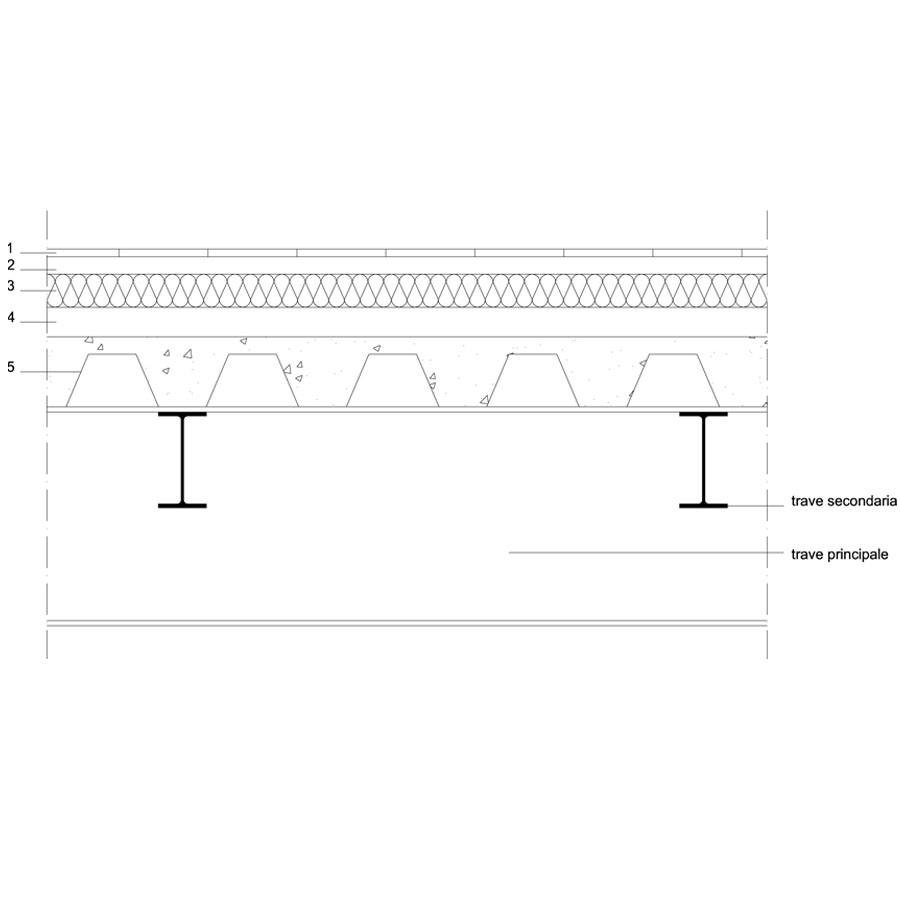
1_ pavimento in parquet di legno d’acero (15mm): 8KN/m³

2_ malta di sottofondo (20mm): 20KN/m³

3_ isolante (30mm): 3KN/m³

4_ massetto (30mm): 20KN/m³

5_ getto in cls e lamiera grecata: 2,5KN/m³

_ tramezzi e impianti: 1,5KN/m²

Acciaio Fe360/S235        f_y,k=235N/mm²

SCELTA DELLE TRAVI SECONDARIE

Per la scelta del profilato ottimale destinato a fungere da TRAVE SECONDARIA, è necessario valutare quale sia l’entità dei carichi agenti sulla struttura, il momento massimo M, la tensione ammissibile σ_amm, e quindi, grazie a questi ultimi due dati, valutare il minimo modulo di resistenza a flessione W_x=M/σ_amm

il profilato scelto avrà W_{x maggiore o uguale a quello ottenuto.}

1_ CALCOLO DEI CARICHI AGENTI:

a)         Carichi accidentali q_a,

b)        Carichi permanenti q_p,

c)         Carichi strutturali q_s.

a)         I CARICHI ACCIDENTALI dipendono dalla destinazione d’uso del fabbricato e vengono dettati dalla normativa.

Per la destinazione abitativa si considera:

CARICO ACCIDENTALE q_a 2KN/m² che moltiplicato per un coefficiente di sicurezza di valore 1,5 adimensionale:

q_a=3KN/m².

a)         I CARICHI PERMANENTI comprendono:

pavimento in parquet di legno d’acero: 8KN/m³ x 0.015m=0,12KN/m²

malta di sottofondo: 20KN/m³ x 0,02m=0,4KN/m²

isolante: 3KN/m³ x 0,03m=0,09KN/m²

massetto: 20KN/m³ x 0,03m=0,6KN/m²

tramezzi e impianti: 1,5 KN/m²

il carico permanente totale, moltiplicato per un coefficiente di sicurezza di valore 1,3 adimensionale:

q_p=3,523KN/m²

a)         I CARICHI STRUTTURALI comprendono la lamiera grecata e la gettata di cls, di peso totale q_s=2,5KN/m², che moltiplicato per un coefficiente di sicurezza di valore 1,5 adimensionale:

q_s=3,75KN/m²

IL CARICO LINEARE si ottiene moltiplicando il carico totale per l'interasse i_ts delle travi secondarie:

q=(q_p+q_a+q_s) x i_{ts= (}3,523KN/m² + 3KN/m² + 3,75KN/m²) x 1m= 10,273KN/m

2_ CALCOLO DEL MOMENTO AGENTE

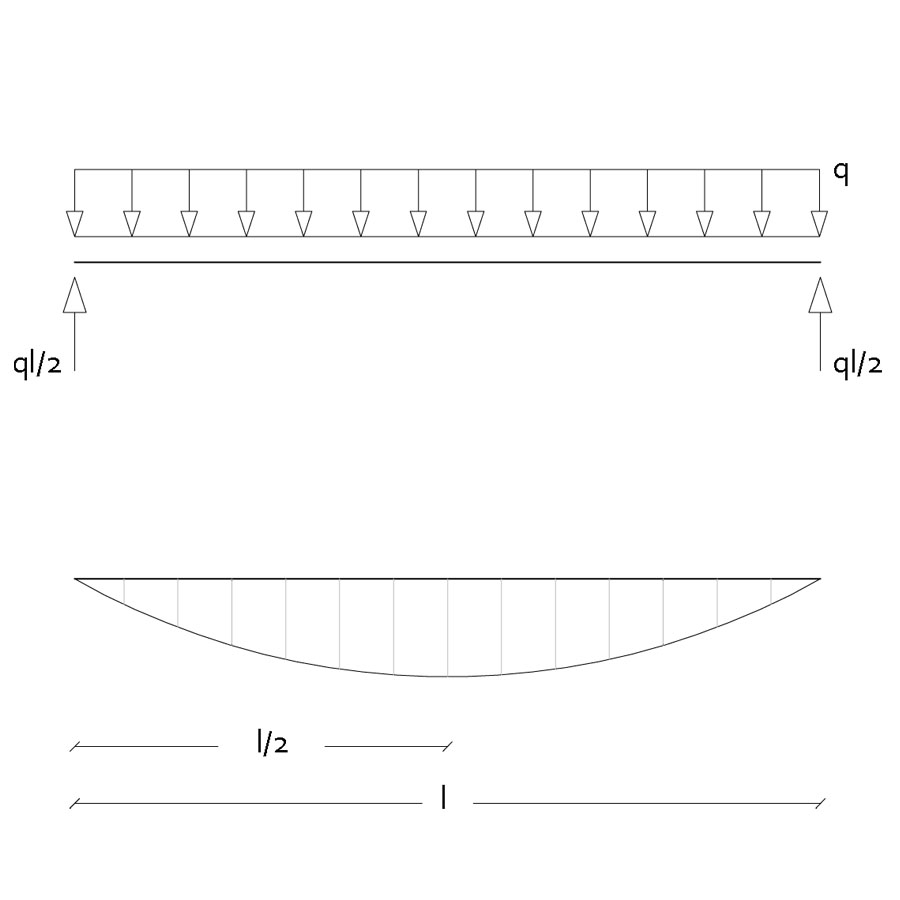
Considerando la trave appoggiata agli estremi su vincoli cerniera e carrello, di reazione vincolare di pari intensità ql/2, il momento massimo M lungo la sezione l/2 è:

M=ql²/8=10,273KN/m x (6m)²/8 = 46,2285 KNxm

3_ LA TENSIONE AMMISSIBILE σ_amm

La tensione ammissibile coincide con il valore della massima tensione di snervamento legata alla classe di resistenza dell’acciaio scelto, ridotta da un coefficiente di sicurezza di valore adimensionale 1.15; in questo caso per Fe360/S235:

σ_amm = f_y,k / 1.15 = 235 N/mm² / 1.15 = 204,35N/mm²

4_ MODULO DI RESISTENZA A FLESSIONE  W_x

Grazie ai valori di σ_amm e M è possibile valutare il modulo di resistenza a flessione (moltiplicando per 1000 per effettuare la conversione in cm³⁾:

W_x=M/σ_amm= 46,2285 KNxm / 204,35 N/mm² x 1000= 226,22 cm³

5_ LA SCELTA DEL PROFILATO

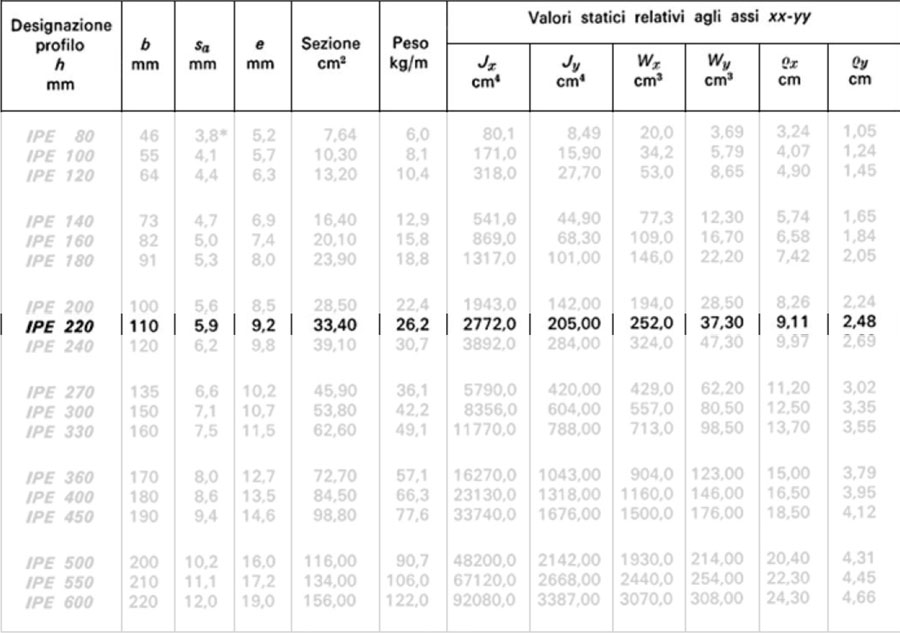
La scelta del profilato si effettua osservando i valori di W_x e scegliendo quello uguale o superiore al valore minimo trovato con i calcoli precedenti. In questo caso si sceglierà il Wx=252,0cm^₃ del profilo IPE220.

Grazie a un foglio di calcolo Excel è possibile tabellare questi risultati:

6_ VERIFICA DELLA TRAVE SECONDARIA SCELTA

Per verificare che la trave scelta sostenga anche il suo peso si ripetono i calcoli precedentemente svolti aggiungendo al carico strutturale q_s il peso proprio della trave.

Per l’IPE 220 il peso proprio è 26,2 Kg/m che convertito in KN e considerato al m² equivale a 0,26KN/m².

q_s=(2,5KN/m²+0,26KN/m²)x 1,5=4,14 KN/m²

Grazie al foglio di calcolo precedentemente impostato si ottengono i nuovi valori di momento, tensione ammissibile e quindi modulo di resistenza a flessione. Quest’ultimo è comunque inferiore a quello dell’IPE 220 scelto, quindi adatto.

SCELTA DELLE TRAVI PRINCIPALI

Esattamente come per il ragionamento seguito per le travi secondarie, il procedimento di calcolo porta a valutare il modulo di resistenza a flessione W_x di una trave di luce l=8m, interasse i_tp=6m, e carico strutturale q_s comprendente il peso delle travi secondarie al m².

q_s=(2,5KN/m²+0,26KN/m²)x 1,5= 4,14 KN/m².

Il foglio di calcolo Excel mostra un modulo di resistenza a flessione minimo pari a W_x=2504,67cm³, per questo valore è quindi necessaria una trave IPE 600 con W_x=3070,00cm³.

VERIFICA DEL PROFILO IPE SCELTO PER LE TRAVI PRINCIPALI

A questo punto è possibile verificare se la trave principale è in grado di sostenere anche il peso proprio; per l’IPE 600 il peso proprio è 122Kg/m che convertito in KN e considerato al m² equivale a 1,22KN/m²; acquisito nel valore del carico strutturale:

q_s=(2,5KN/m²+1,22KN/m²)x1,5=5,58KN/m²

Il calcolo del modulo di resistenza elastico W_x=2842,92cm³<W_x,IPE600=3070,00cm³ quindi il profilo è sufficiente.

Voglio Dimensionare le travi in acciaio di un solaio per un' abitazione privata.

Luce delle travi : L = 5 m

Interasse i = 4 m

A) CARICHI STRUTTURALI

4 rete elettrosaldata (0,3 kN/m2) > 0,3 kN/m2

5 lamiera grecata e soletta in CLS (2,50KN/m2) > 2,50 kN/m2

Totale carichi strutturali = 2,8 kN/m2

B) CARICHI PERMANENTI

Pavimento in parquet (6 kN/m3) s= 2 cm > 6x0,02 = 0,12 kN/m2

Strato di allettamento in malta di calce (18 kN/m3)  s = 3 cm  > 18x0,03 = 0,54 kN/m2

Massetto in CLS (20 kN/m3) s= 5 cm > 20x0,05 = 1,00 kN/m2

Tramezzi (considerati carichi distribuiti secondo nuova NTC) = 1,00 kN/m2
 

Totale carichi permanenti =  2,66  kN/m2

C) CARICHI VARIABILI

Destinazione d'uso: Residenziale = 2,00  kN/m2

Totale carichi = 7,46 kN/m2

Analisi dei carichi sulle travi portanti

Carico agente sulla trave : q = qs + qp + qa  x Area d'influenza

La trave B hanno un area di influenza uguale a 2 m > 7,46x2 = 14,92 kN/m

Le travi A,C hanno un area di influenza uguale a 4 m > 7,46x4 = 29,84 kN/m

Progetto a momento flettente una trave doppiamente appoggiata > M = ql2/8

il momento massimo si ha in mezzeria = 2,5 m

Trave B > 29,84x2,52/8 = 23,31 kN/m

Travi A,C > 14,92x2,52/8 = 11,65 kN/m

Scelgo delle travi in Acciaio S275 

Tramite l'inserimento dei dati trovati il foglio excel mi calcola il valore del modulo di resistenza Wx con cui potrò scegliere dal profilario le trave IPE necessarie.

Trave B > Wx = 390 cm3, per ragioni di sicurezza, vado a scegliere una IPE 270 con Wx = 429 cm3 

Trave A,C > Wx = 194 cm3, per ragioni di sicurezza, vado a scegliere una IPE 220 con Wx = 252 cm3 

Voglio Dimensionare le travi in CLS armato di una copertura non praticabile.

Luce delle travi : L = 5 m

Interasse i = 4 m

A) CARICHI STRUTTURALI

Travetti in c.a. (25 kN/m3)   s=2, n=2 > 25x2x0,12x0,10 = 0,6 kN/m2

Caldana superiore (25 kN/m3)  s= 4 > 25x0,04x1,00 = 1,00 kN/m2

Pignatte in laterizio (5,5 kN/m3) s=2, n=2 > 5,5x2x0,12x0.40  = 0,53 kN/m2

Totale carichi strutturali =  2,15 kN/m2

B) CARICHI PERMANENTI

Massetto (19 kN/m3) s= 4 cm > 19x0,04x1,00 = 0,76 kN/m2

Intonaco (2.0 kN/m3) s= 1,5 cm > 2x0,15x1,00x2 = 0,3 kN/m2

Impermeabilizzazione  (0,3 kn/m2) > 0,3 kN/m2

Tegole (0,5 kN/m2) > 0,5 kN/m2

Totale carichi permanenti =  1,9  kN/m2

C) CARICHI VARIABILI

Destinazione d'uso: Copertura non praticabile + Carico neve = 1,00  kN/m2

In questo esercizio andremo a trasformare i carichi caratteristici in carichi di progetto, aumentati dai coefficienti di sicurezza prescritti dalle NUOVE NORME TECNICHE del 2008. 

Carichi strutturali di progetto = 1.3 x g1k = 1.3 x 2.15 = 2.80 kN/m2 

Carichi permanenti di progetto = 1.5 x g2k = 1.5 x 1.90 = 2.85 kN/m2 

Carico variabile di progetto = 1.5 x qk = 1.5 x 1.00 = 1.50 kN/m2

Totale carichi di progetto = 7,15 kN/m2

Analisi dei carichi sulle travi portanti

Carico agente sulla trave : q = qs + qp + qa  x Area d'influenza

Tra le tre travi andrò a calcolare solo i valori di progetto di quella mediana, in quanto sollecitata da carico maggiore.

Trave B =  4 m > 7,15x4 = 28,60 kN/m

Progetto a momento flettente una trave appoggiata > M = ql2/8

il momento massimo si ha in mezzeria > 2,5 m

M > 28,60x2,52/8 = 22,35 kN/m

Scelgo un calcestruzzo con classe di resistenza 25/30, un'acciaio B450C con fy = 450 MPa e un'altezza di 15 cm, in quanto il carico da sostenere non è eccessivo.

Inserisco di nuovo i dati nel foglio di calcolo e ottengo un'altezza di 22,61 cm che vado ad aumentare a 25 cm.

·         Dimensionamento solaio:

_trave principale luce = 8 m, interasse = 6 m

_trave secondaria luce = 6 m, interasse = 1m

·         Elementi sezione stratigrafica solaio:

1_ pavimento (15mm), peso s. 6,5 kN/m³

2_ malta (20mm), peso s. 20 kN/m³

3_ isolante (33mm), peso s. 3kN/m³

4_ massetto (30 mm) peso s. 20 kN/m³

5_ lamiera grecata + getto di completamento in cls (0,8mm), peso s. 2,5 kN/m²

·         Dalla tabella comparativa degli acciai scelgo la classe Fe 360/S235.

TRAVE SECONDARIA:

Per prima cosa calcolo i carichi permanenti (q_p), carichi strutturali (q_s) e carichi accidentali (q_a):

-       carichi permanentiq_p

1_ pavimento in teak 6,5 kN/m³ * 0,015 m = 0,0975 kN/m²

2_ malta 20 kN/m³ * 0,020 m = 0,4 kN/m²

3_ isolante 3 kN/m³ * 0,03 m = 0,09 kN/m²

4_ massetto 20 kN/m³ * 0,03 = 0,6 kN/m²

Totale q_p  = 1,1875 kN/m²

È necessario moltiplicare il totale dei carichi permanenti per un coefficiente di sicurezza (valore tabellato).

1,1875 kN/m² * 1,5 = 1,78 kN/m²

-       carichi strutturaliq_s

1_ lamiera gracata + getto di completamento in cls 2,5 kN/m²

È necessario moltiplicare il totale dei carichi strutturali per un coefficiente di sicurezza.

2,5 kN/m² * 1,3 = 3,25 kN/m²

-       carichi accidentaliq_a – il peso dei carichi accidentali è un valore tabellato in base alla destinazione d’uso dell’edificio che si sta progettando. Nel nostro caso utilizziamo il valore relativo alla destinazione d’uso abitativa = 2kN/m^2.

2kN/m² * 1,5 = 3,00 kN/m²

Totale carichi = (q_p+ q_s+ q_a)*(i)

                      = (1,78 + 3,25 + 3,00)*1 = 8,03 kN/m²

È necessario moltiplicare il totale dei carichi accidentali per un coefficiente di sicurezza.

Dopo aver calcolato tutti i carichi, inserisco i risultati nel foglio di calcolo Excel che calcola il momento M = 36,135 kN*m.

Considerando una trave l doppiamente appoggiata su carrello e cerniera, su cui vi è un carico distribuito, le reazioni vincolari saranno uguali a ql/2, quindi il momento massimo è ql²/8.

Poi calcolo la tensione ammissibile s_amm= fy, k/1,15 dove con fy, k indico la classe dell’acciaio scelto.

Conoscendo i valori M e s_amm posso calcolare W_x = M/s_amm.

W_x = 176,83

Questo numero deve essere inferiore ai valori di W tabellati relativi ai profili standard.

In questo caso il valore ottenuto ci impone di utilizzare una trave IPE 200.

TRAVE PRINCIPALE:

Per il calcolo relativo alla trave principale eseguiamo esattamente lo stesso procedimento, considerando però una trave di luce = 8 e i = 6. Inoltre il carico strutturale comprenderà il peso delle travi secondarie.

Q_p = 1,78 kN/m²

Q_a = 3,00 kN/m²

Q_s = 3,25 kN/m² + 0,224 kN/m² = 3,47 kN/m²

Il nuovo valore di W_x = 1937,85 cm³ che ci impone di utilizzare una trave IPE 550. 

VERIFICA TRAVE PRINCIPALE:

Per verificare se la trave è in grado di reggere anche il suo stesso peso è necessario sommare il valore del peso specifico relativo alla trave IPE 550 (106,0 kg/m) nel calcolo dei carichi strutturali:

Q_s = 3,47 kN/m² + 1,06 kN/m² = 4,53 kN/m²

W_x = 2186,84 cm³

L’IPE 550 ha valore W_x = 2440,0. Il valore  ottenuto dai calcoli deve essere inferiore a quello tabellato, quindi il profilo IPE 550 è sufficiente per sopportare i carichi pervisti.

La struttura presa in questione presenta una trave più soggetta delle altre al momento flettente M, prendiamo in questione proprio questa trave al fine di calcolarne l’altezza della sezione. Essa presenta un’area di influenza di 4 x 5 m.
Supponiamo che la struttura sia in pioppo, un legno povero che presenta però delle buone caratteristiche di resistenza

Il primo passo consiste nella definizione della stratigrafia del solaio, il quale presenta una struttura primaria che non consideriamo al momento (visto che la stiamo per calcolare) ed una secondaria costituita dai travetti, ai quali diamo una dimensione di 80 x 100 cm.

Ho eseguito manualmente i calcoli per poi verificarli sul foglio excel in fase finale. Andando per ordine possiamo calcolare prima i CARICHI PERMANENTI NON STRUTTURALI (qp).

Pavimento parquet in rovere (1)
Peso specifico = 7 kN/m³
Volume = 0,015 x 1 x 1 = 0,015 m³
Peso al m² = 7 x 0,015 = 0,1 kN/m²

Massetto in cls alleggerito (2)
Peso specifico = 4,7 kN/m³
Volume = 0,04 x 1 x 1 = 0,04 m³
Peso al m² = 4,7 x 0,04 = 0,2 kN/m²

Isolamento in fibra di legno (3)
Peso specifico = 2,1 kN/m³
Volume = 0,05 x 1 x 1 = 0,05 m³
Peso al m² = 2,1 x 0,05 = 0,1 kN/m²

Incidenza impianti = 1 kN/m²

Incidenza tramezzi = 1 kN/m²

Muro di tamponamento  = 2 kN/m²

Totale qp = 4,4 kN/m²

Ora calcoliamo i CARICHI STRUTTURALI (qs)

Caldana (4)
Peso specifico = 18 kN/m³
Volume = 0,05 x 1 x 1 = 0,05 m³
Peso al m² = 18 x 0,05 = 0,9 kN/m²

Tavolato in pioppo (5)
Peso specifico = 5 kN/m³
Volume = 0,035 x 1 x 1 = 0,035 m³
Peso al m² = 5 x 0,035 = 0,175 kN/m²

Travetti in pioppo (6)
Peso specifico = 5 kN/m³
Volume = 0,08 x 0,1 x 1 = 0,008m³
Peso al m² = 5 x 0,08 x 0,1 x 2 = 0,08 kN/m²(moltiplichiamo per due perché consideriamo la presenza di 2 travetti ogni metro)

Totale qs = 1,15 kN/m²

CARICHI ACCIDENTALI (qa), cioè quelli dipendenti dalla destinazione d’uso dell’ambiente. Nel nostro caso, come progettiamo la struttura per un uso residenziale.

Totale qa = 2 kN/m² (da normativa)

TOTALE CARICHI
qs + qp + qa = 1,15 + 4,4 + 2 =7,55 kN/m²

Ora possiamo calcolare il valore del carico distribuito agente sulla trave presa in esame, moltiplicando la somma dei carichi per il valore i, cioè l’ampiezza dell’area di influenza degli stessi carichi sulla trave.

Calcoliamo il momento massimo che insiste sulla trave, valutata come una trave appoggiata con un carico distribuito. L è la luce della trave, che utilizziamo come seconda dimensione dell’area di influenza.

Calcoliamo la resistenza di progetto (fd)considerando il coefficiente di degrado nel tempo  kmod, esso  tiene conto della durata del carico e della classe di servizio (deve essere sempre <1), il coefficiente di sicurezza ɣm e la fmk, cioè la resistenza caratteristica.

Ora possiamo procedere con il dimensionamento della trave secondo la teoria flessionale di Navier, considerando che 

Abbiamo ora la formula per ottenere h. Scegliamo arbitrariamente una b = 20 cm

Si presenta quindi una trave di legno di 20 x 55 cm, inserendo i dati all’interno della tabella di excel possiamo verificare che i calcoli sono giusti.

A questo punto dobbiamo considerare il peso proprio della trave, il quale va sommato al totale dei carichi strutturali qs ed andrà ad aumentare l’altezza totale della trave.

Trave in pioppo
Peso specifico = 5 kN/m³
Volume = 0,2 x 0,55 x 1 = 0,11m³
Peso al m² = 5 x 0,11 = 0,55 kN/m²

Totale qs = 1,15 + 0,55 =1,7 kN/m²

Come previsto l’altezza della trave è aumentata, aumentando per eccesso le dimensioni della trave possiamo ottenere la sezione di 20 x 60 cm.