Esercitazione

Commerzbank Tower - Foster & Partners

In questo nuovo post continuiamo il discorso sulle travi Vierendeel, occupandoci in questo caso di un modello che preveda gli estremi incastrati ad ambo i lati. E' la scelta progettuale adottata tra gli altri da Foster & Partners per il progetto della Commerzbank Tower a Francoforte (1994-1997), la cui soluzione strutturale prevede una coppia di montanti verticali all’interno di ognuna delle strutture d’angolo, ai quali sono collegate travi Vierendeel da otto piani, che sorreggono i solai degli uffici da angolo ad angolo. Sicuramente una scelta audace ed onerosa, che permette però di avere diversi vantaggi, tra cui, ad esempio, la possibilità di fruire di un open space privo di pilastri all'interno degli uffici.

Vediamo quindi in sintesi come si comporta meccanicamente la trave doppiamente incastrata:

Si nota subito come nel nostro caso la trave sia perfettamente simmetrica attorno al montante verticale 1. Conosciamo inoltre, come segnalato nel precedente post, i valori del taglio e del momento e l'analisi della deformata di una trave doppiamente incastrata, che costituisce il singolo elemento della trave Vierendeel:

Dallo schema della deformata della singola trave possiamo facilmente ricavare la deformata di tutta la Vierendeel:

Per quanto riguarda il valore del taglio sui traversi, possiamo utilizzare il metodo empirico adottato anche con la precedente trave. Occorre però precisare come si ripartisce la forza F sul pilastro 1, che risulta essere il nostro asse di simmetria:

Una volta capito ciò, si può procedere con il calcolo dei valori del taglio agenti sui traversi, semplicente dividendo la forza agente su ogni tratto orizzontale per 2 e assegnandone una metà a ciascuno di essi:

Verifichiamo la correttezza del procedimento ancora una volta scrivendo l'equilibrio alla traslazione verticale, e sostituendo il valore nell'equazione del taglio derivante dallo schema notevole della trave doppiamente incastrata. Scriviamo solo i primi 3, perchè, essendo la struttura simmetrica, sarà sufficiente specchiarli per ottenere i rimanenti:

Passiamo ora ai momenti dei traversi. Come nel caso precedente, conoscendo i punti di nullo, sarà sufficiente moltiplicare il valore del taglio ottenuto per il braccio. Questo è il diagramma:

Per conoscere invece i valori dei momenti sui montanti, abbiamo bisogno di scrivere l'equilibrio ai nodi. Ancora una volta, data la simmetria della struttura, sarà sufficiente analizzare solo i primi 3:

Non ci rimane che trovare i valori delle forze taglianti dei montanti (sommando la coppia dei momenti agenti sul montante e dividendoli per la luce su cui lavorano) e diagrammarli:

 

Verifichiamo infine su SAP2000 di non aver commesso errori:

Taglio

Momento

Deformata

Es5 -Trave Vierendeel-

La trave Vierendeelha lo stesso comportamento di un telaio “shear-type” solo che è ruotato di 90 gradi. La trave è infinitamente resistente a flessione, mentre i pilastri  per effetto delle forze esterne traslano di una quantità δ ma senza deformarsi. 

 

Per risolvere la trave occorre risolvere ogni tratto verticale considerandolo come se fosse una trave doppiamente appoggiata.

Trave iperstatica  soggetta ad un cedimento vincolare δ,  si hanno i seguenti valori notevoli del momento e del taglio.

M= 6EI/l²*δ     T= 12 EI/l³*δ

 

Si trovano i valore di ogni asta orizzontale

 1.      F = 2T  → F = 24 EI/l³δ1  

         δ1= Fl³/24 EI

 T = 12 EI/l³*δ1  

M = 6 EI/l²*δ1

T = 12 EI/l³*(Fl³/24 EI) = F/2

M = 6 EI/l²*(Fl³/24 EI)  = Fl/4

 

2.      F + F/2 + F/2= 2T  → 2F = 24 EI/l³*δ2   

        δ2= Fl³/12 EI

T = 12 EI/l³*δ2

M = 6 EI/l²*δ2

T = 12 EI/l³*(Fl³/12 EI) = F

M = 6 EI/l²*(Fl³/12 EI)  = Fl/2

 

3.      F + F + F= 2T  → 3F = 24 EI/l³*δ3 

         δ3= Fl³/8 EI

T = 12 EI/l³*δ3

M = 6 EI/l²*δ3

T =12 EI/l³*(Fl³/8 EI) = 3/2F

M =6 EI/l²*(Fl³/8 EI) = 3/4 Fl

 

4.      F + 3/2F + 3/2F= 2T  → 4F = 24 EI/l³*δ4 

         δ4= Fl³/6 EI

T = 12 EI/l³ δ3

M = 6 EI/l²*δ4

T = 12 EI/l³ * (Fl³/6 EI) = 2F

M = 6 EI/l²*(Fl³/6 EI)=  Fl

 

5.      F + 2F + 2F= 2T  → 5F = 24 EI/l³*δ5  

        δ5= 5 Fl³/ 24EI

T = 12 EI/l³*δ2

M = 6 EI/l²*δ2

T = 12 EI/l³*(5 Fl³/24 EI) = 5/2F

M = 6 EI/l²*(5 Fl³/24 EI) = 5/4Fl

 

6.      F + 5/2F + 5/2F= 2T  → 6F = 24 EI/l³*δ6   

         δ1= Fl³/4 EI

T = 12 EI/l³*δ1

M = 6 EI/l²*δ6

T = 12 EI/l³*(Fl³/4 EI) = 3F

M = 6 EI/l²*(Fl³/4 EI)=3/2 Fl

• Distribuzione delle forze orizzontale

• Diagramma del Taglio dei traversi

 

 

 

 

• Diagramma del Momento dei traversi

• Ora si deve trovare i momenti degli elementi verticali, per trovarli basta fare l’equilibrio di ogni nodo

1

 

2

 

3

FL/2 + FL/4 =5/4 FL

4

3FL/4 + FL =7/4 FL

5

FL + 5Fl/4 =9/4 FL

6

5FL/4 + 3Fl/2 =11/4 FL

 

Posso trovare i valori dei tagli, calcolando l'equilibrio di ciascuna asta verticale:

1

2

3

 

(5FL/4+5FL/4) /2L= 5FL

 

4

(7FL/4+7FL/4) /2L=7FL

 

5

(9FL74+9FL/4) /2L=9FL

 

6

(11FL/4+11FL/4) /2L=11FL

 

• Diagramma taglio ritti

 

• Diagramma momento ritti

 

 

 

Si può facilmente determinare lo sforzo normale sui traversi, poiché è pari al taglio dei ritti che si trasmettono ai traversi e diventano sforzo normale.

 

 

Verifica con sap dove si deve cambiare il Modulo Elastico per rendere la struttura infinitivamente rigida.

Deformata

 

Diagramma del taglio

 

Diagramma del momento

 

 

 

 

 

Villa Chardonne

Nel corso degli ultimi 30 anni diversi architetti, in linea con la loro più o meno velata adesione al movimento De Stijl e alle correnti da esso derivate, hanno costruito il loro successo e la loro affermazione in campo architettonico, grazie alla progettazione di architetture che ricorrono sistematicamente a sbalzi più o meno azzardati. Si è assistito quindi alla massiccia implementazione nelle nuove architetture di quei sistemi strutturali che, fino ad allora, erano una prerogativa esclusiva di ponti di notevole luce. In questa ottica, giocò un ruolo fondamentale la trave ideata dall'ingegnere belga Jules Arthur Vierendeel che la brevettò alla fine del 1800.

Essa consiste in un telaio a più campate costituito da travi continue alla testa ed ai piedi, e da una serie di montanti verticali che, dal punto di vista geometrico, la rendono assimiliabile ad una trave reticolare dalla quale vengono rimosse le aste diagonali; tale assenza comporterebbe la labilità del sistema ai carichi orizzontali nel caso di nodi che non impediscono le rotazioni (ad es. cerniere). Per rendere stabile questa trave, dunque, è necessario che i nodi siano rigidi, con conseguente trasmissione di momento flettente sulle aste; è proprio questa la differenza sostanziale tra travi reticolari e Vierendeel: le prime sono composte da elementi sottoposti a sollecitazioni di sola trazione o compressione, mentre nelle seconde le aste sono inflesse.

In questa esercitazione, quindi, vedremo qual è il comportamento di queste travi dal punto di vista meccanico. Nello specifico prendiamo in esame una trave Vierendeel con gli estremi di sinistra incastrati ad un supporto e quelli di destra liberi, come potrebbero essere ad esempio quelle adottate in Villa Chardonne di cui sopra:

Come detto in precedenza, questa trave, per l'enorme rigidezza dei montanti verticali, può essere assimilata ad un telaio SHEAR TYPE disposto orizzontalmente, e, come quest'ultimo, fa riferimento agli schemi notevoli della trave doppiamente incastrata, sia per quanto riguarda l'analisi della deformata sia per i valori del momento flettente e del taglio:

Dall'analisi della deformata della singola trave possiamo ricavare la deformata di tutta la trave Vierendeel:

Inoltre, in una Vierendeel costituita dallo stesso materiale e da traversi uguali (che hanno quindi la stessa rigidezza), possiamo rapidamente calcolare i valori del taglio di ogni traverso, semplicemente ripartendo in 2 la forza che agisce su ogni campata e assegnandola ai traversi in questione:

Verichiamo che il metodo utilizzato è corretto analizzando ogni singolo nodo e scrivendo l'equilibrio alla traslazione verticale, sostituendo poi ogni volta il valore del taglio trovato dentro l'equazione precedentemente ottenuta dallo schema notevole:

Lo schema della deformata ci da un'ulteriore informazione: nel punto di flesso sappiamo che la curvatura è 0. Quindi anche il momento, come riportato dallo schema notevole, è nullo nel punto medio del traverso. Per conoscere il valore massimo del momento, quindi, sarà sufficiente moltiplicare il valore del taglio di ogni campata per la metà del traverso (che nel nostro caso è L/2). Avremo quindi il seguente diagramma dei momenti:

Conoscendo i valori del momento sui traversi, possiamo trovare tramite l'equilibrio dei nodi i rispettivi valori dei momenti sui montanti verticali. Non sarebbe possibile ricavarli tramite l'equazione del momento del modello della trave di Bernoulli (M=EIX), in quanto, a causa dell'estrema rigidezza dei montanti (EI=infinito), avremmo un'equazione indeterminata. I momenti risultano essere quindi:

Una volta ottenuti i valori dei momenti sarà sufficiente bilanciare i montanti verticali con una coppia di forze taglianti, il cui valore è sempre ricavabile tramite questo semplice metodo:

Analizzando quindi ogni singolo nodo, avremo i seguenti valori per il taglio:

Grazie ai valori del taglio appena trovati, sappiamo anche quanto vale lo sforzo normale sui traversi, in quanto secondo il principio dell'equilibrio dei nodi ciò che è taglio diventa sforzo normale e viceversa. Il diagramma sarà perciò questo:

Come si nota dal diagramma, i traversi orizzontali sono tesi, mentre quelli inferiori sono compressi.

Ora non ci rimane che verificare la bontà del metodo utilizzato, disegnando su SAP2000 la nostra trave Vierendeel e ricordandoci di modificare il modulo elastico (E) del materiale che utilizzeremo per i pilastri verticali, assegnandogli un valore molto alto. Di seguito riporto i diagrammi di sforzo normale, taglio e momento e l'analisi della deformata:

SFORZO NORMALE

TAGLIO

MOMENTO FLETTENTE

DEFORMATA

Esercizio 1 : TRAVE VIERENDEEL

 SCHEMA DI CALCOLO

                    

Riferendoci allo schema notevole riportato di seguito, conoscendo il valore di δ possiamo determinare il valore delle caratteristiche di sollecitazione e delle rigidezze dei traversi :

Determiniamo il valore del taglio e del momento nei vari tratti della struttura :

           

DIAGRAMMA DEL TAGLIO        

                                        

DIAGRAMMA MOMENTO

                                    

EQUILIBRIO AI NODI -MOMENTO -

         

EQUILIBRIO SULLE ASTE RIGIDE - TAGLIO -

            

DIAGRAMMA DEL TAGLIO

                   

DIAGRAMMA DEL MOMENTO

                       

 

VERIFICA SAP2000

DIAGRAMMA TAGLIO

            

DIAGRAMMA MOMENTO

                   

Esercizio 2 : TRAVE DOPPIAMENTE INCASTRATA

SCHEMA DI CALCOLO

                     

La trave è simmetrica e simmetricamente caricata, quindi ne basta studiare metà. In corrispondenza della simmetria la forza F  diverrà F/2.

Determiniamo il valore del taglio e del momento nei vari tratti della struttura :

                                           

DIAGRAMMA DEL TAGLIO

                                           

DIAGRAMMA DEL MOMENTO

                              

EQUILIBRIO AI NODI -MOMENTO -

             

EQUILIBRIO SULLE ASTE RIGIDE - TAGLIO -

                

DIAGRAMMA DEL TAGLIO

                    

DIAGRAMMA DEL MOMENTO

                    

VERIFICA SAP2000

DIAGRAMMA SFORZO ASSIALE

                        

DIAGRAMMA DEL TAGLIO

                          

DIAGRAMMA DEL MOMENTO

                             

 

 

 

 

                          

 

 

Per risolvere una struttura reticolare dobbiamo definire tutte le sollecitazioni delle aste, composte di sole tensioni assiali di compressione e trazione.

 

1. Disegno il modello di trave reticolare spaziale in Autocad o Rhino. 

    (composto esclusivamente da linee e non su livello 0)

    (reticolo di lunghezza 3L, larghezza 2L e altezza L)

 

2. Esporto il modello in DFX (versione 2004) o IGES/IGS.

3. Importo creando un nuovo documento in SAP 2000  (import information-->unità di misura: Kn,m,C) (Dxf import, frames-->seleziono il layer)

4. Imposto opzioni grafiche (sfondo bianco, colore delle aste, delle forze ecc)   (Options>Color>Display)

5. Imposto la tolleranza

   (Selezioni tutto, Edit>Edit Point>Merge joints>Merge tollerance>0,01 m)

6. Attivo le etichette sulle aste

   (View>Set display>Options>Frame/Cables/Tendons>Lables)

 

7. Impongo 3 vincoli , 2 carrelli e una cerniera.

    (Assign>Joint>Restraint. non devono essere allineati, in tal caso la trave non riuscirebbe ad essere in piano)

 

8. Definisco il materiale-->sezione tubolare in acciaio A992fy50 (di default)

    (Define>Section propreties>Frame sections>Add new propreties>Section name:"tubolare")

    Outside diameter:0,1m       Wall thickness: 0,004 m

9. Assegno il materiale alle aste.

   (Selezioni tutto, Assign>Frame>Frame sections>"tubolare">ok)

10. Definisco un pattern con fattore di moltiplicazione 0 per azzerare la massa delle aste.    

  (Define>Load pattern>"peso nullo", Self Weight Multiplier=0)

11. Assegno un carico di -40KN (negativa perchè verso il basso) dopo aver selezionato il pattern "peso nullo"

    (Selezioni i nodi superiori, Assign>Joint loads>Forces, Force Global z = -40 Kn)

12. Assegno il rilascio. I nodi devono essere riconosciuti come cerniere interne e non come nodi indeformabili, ovvero le aste non devono essere soggette a momento.

    (Seleziono tutto, Assing>Frames, spunto la casella Start/End di Moment 3-3)

    

13. Calcolo la deformata del sistema

 

14. Osservo il diagramma dello sforzo assiale.

     (Show forces/stresses/>frames/cables>Axial forces)

      

15. Valori tabellati

     (Display>Show tables>Analysis results)

      

16. Valori di tensione. Otteniamo i valori di ogni forza agente su ciascuna asta. Per capire se le aste sono puntoni (negativo) o tiranti (positivo) dobbiamo guardare la voce "P-KN". 

       Calcolo la tenzione σ = N/A . 

 

 

VERIFICA SU SAP 2000

1. Apro Sap 2000, imposto le unità di misura Kn,m,C

2. Seleziono l'opzione Grid Only

    (NUMBER OF GRID LINES-->X DIRECTION: 2 e Y,Z DIRECTION: 1

   GRID SPACING-->X DIRECTION: 1, ovvero la lunghezza della trave)

3. Imposto opzioni grafiche (sfondo bianco, colore della trave, delle forze ecc)

    (Options>Color>Display)

4. Disegno la trave con lo strumento Draw Frame, da A a B.

5. Assegno un incastro all'estremo A e un carrello all'estremo B.

   (Assign>Joint>Restraints)

6. Disegno un punto (Draw Special Joint) a distanza 0,57l (0,57 m per me da inserire nella casella Offset X dopo aver cliccato sull'origine) che dovrebbe coincidere con il punto di spostamento massimo della trave deformata.

 

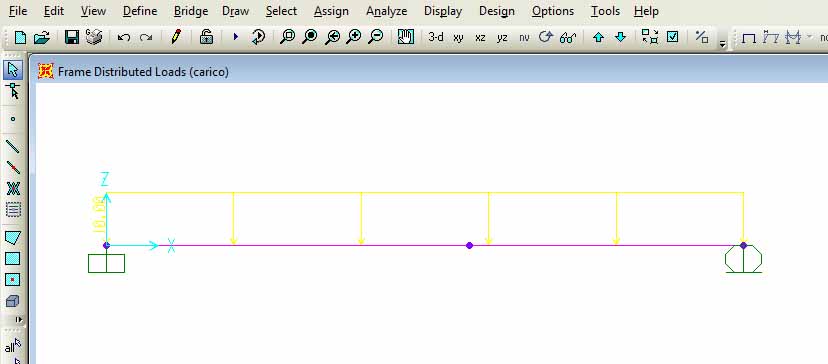
7. Definisco un pattern con fattore di moltiplicazione 1 per azzerare la massa della trave.    

  (Define>Load pattern>"carico", Self Weight Multiplier=1)

8. Assegno un carico di 10KN dopo aver selezionato il pattern "carico"

 (Seleziono l'asta, Assign>Frame loads>Distributed, Uniform Load:10Kn. Mi assicuro che sia spuntata la voce Gravity nelle opzioni di direzione)

9. Definisco il materiale-->sezione tubolare in acciaio A992fy50 (di default)

    (Define>Section propreties>Frame sections>Add new propreties>Section name:"FSE52")

    Outside depth:0,2 m        Outside width: 0,1 m     Flange thickness:0,005 m  

    Web thickness:0,005 m

11. Controllo i valori di I: 1,522 10^-5 m⁴

                              E: 1,999 10⁸  Kn/ m²       

10. Assegno il materiale alle aste.

      (Selezioni tutto, Assign>Frame>Frame sections>"FSE52">ok)

12. Calcolo la deformata del sistema. Ad occhio possiamo constatare come il punto calcolato manualmente coincida con quello calcolato da SAP.

      Spostando il mause sopra al punto individuato osserviamo le coordinate U1, U2, U3.

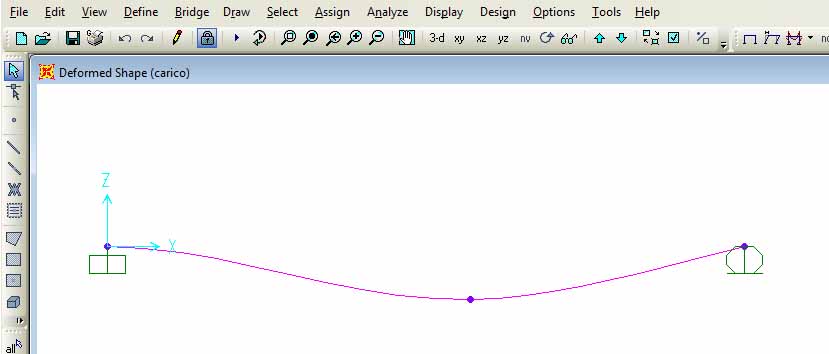
         Ci interessano il valori di U3= -0,0000277

                                             R2= -0,000007627

13. Osserviamo che l'ordinata del punto calcolato manualmente si avvicina in maniera ragionevole al calcolo fatto manualmente di 2 10^-5 m.

14. Osserviamo che la rotazione in R2 non è pari a 0. Ciò significa che il punto scelto in 0,57 m è un approssimazione accettabile del punto di spostamento massimo, ma che si discosta                   leggermente in quanto non rappresenta il punto di minimo della deformata.

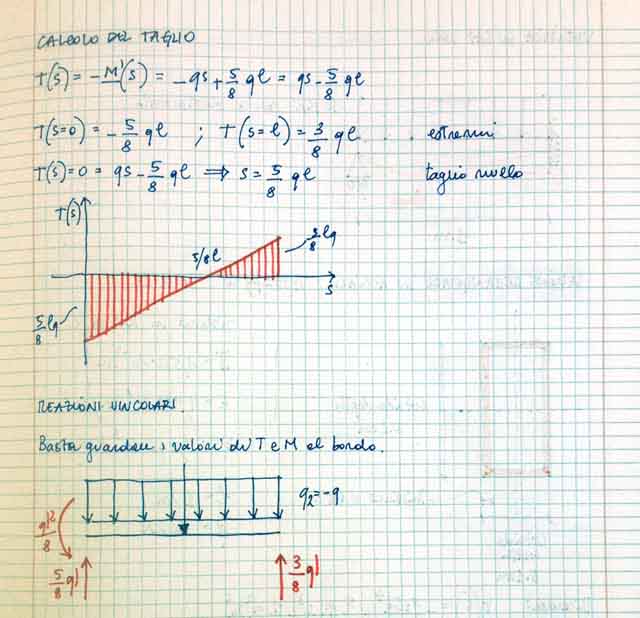
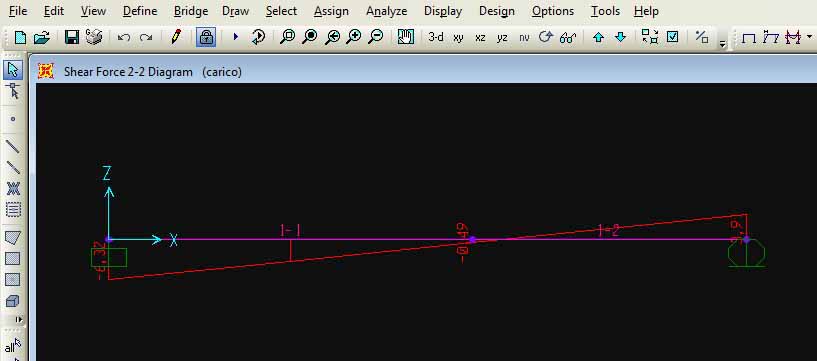
15. Confronto del Taglio (SHEAR 2-2)

       Taglio massimo su Sap: 3,9 Kn

       Taglio massimo calcolato manualmente: 3 ql/ 8  = 3,7Kn

       Taglio minimo su Sap: -6,32Kn

       Taglio minimo calcolato manualmente: -5ql/8 = -6,2Kn    

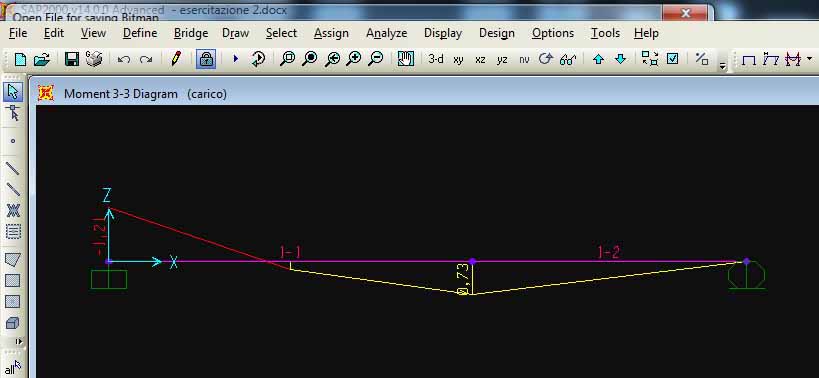
16. Confronto del Momento  (MOMENT 3-3)

       Momento massimo su Sap: -1,21Kn

       Momento massimo calcolato manualmente: -ql² / 8 = -1,25Kn

       Momento minimo su Sap: 0,73Kn

       Momento minimo calcolato manualmente: 9ql²/128   = 0,70Kn