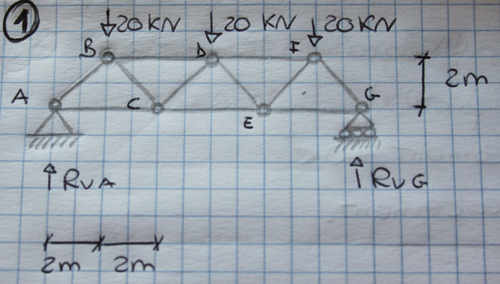
La travatura reticolare è una particolare tipologia strutturale in cui tutti gli elementi che compongono la struttura sono tratti lineari (puntoni o tiranti) collegati da due cerniere. In questo caso ci troviamo di fronte ad una configurazione simmetrica, sia nella disposizione delle aste che nella ripartizione dei carichi nei nodi superiori.
Il primo passo nel calcolo di questa struttura è la verifica dell'isostaticità (una situazione in cui il numero dei gradi di libertà della struttura sia pari al numero dei vincoli applicati su questa). Per verificare che la struttura sia isostatica possiamo utilizzare due metodi:
1. L=V (numero gradi di libertà=numero gradi di vincolo)
V = Ve + Vi =>33
L= 3 x numero corpi =>33
2. Ve + a = 2 nodi (vincoli esterni+n°aste=n°nodi x 2)
3 + 11 = 2 x 7 => 33
Da queste uguaglianze si deduce che la struttura si trova in una condizione di isostaticità.
Il secondo passo è il calcolo delle reazioni vincolari. La reazione vincolare orizzontale nel nodo A risulta pari a 0 (in quanto unica forza orizzontale all’interno della struttura, non bilanciata, quindi, da altre forze) mentre le due reazioni verticali nei nodi A e G, trovandosi in una condizione di simmetria, si ripartiscono equamente il carico applicato sui nodi superiori, bilanciando, quindi, la forza esterna pari a 60 KN.
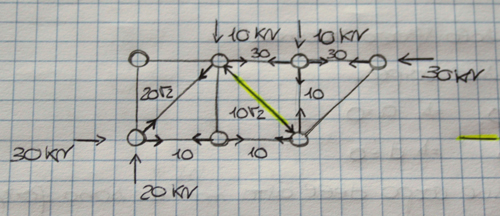
In questo caso abbiamo risolto la struttura utilizzando il metodo di Ritter, sezionando idealmente la trave in due parti, andando a tagliare tre aste non convergenti nello stesso punto.

Scegliamo arbitrariamente la porzione di struttura sulla sinistra. Attraverso questa sezione possiamo mettere in evidenza gli sforzi normali delle singole aste sezionate. Il verso ipotizzato è “uscente”: ciò equivale a dire che secondo la nostra ipotesi, e secondo le convenzioni riguardo la direzione positiva o negativa dello sforzo normale, le aste sono sottoposte a sforzo di trazione.
Attraverso l’equilibrio dei momenti intorno al nodo C ricaviamo il valore dello sforzo normale dell’asta 1.
(20x2)-(30x4)-(N1x2)=0
40-120-2N1=0
2N1=40-120
N1=-40
Quindi il verso ipotizzato non è esatto: l’asta, sottoposta a sforzo di compressione, è un puntone. Attraverso l’equilibrio dei momenti intorno al nodo B ricaviamo lo sforzo normale N3.
-30x2+N3x2=0
N3=30
Il verso ipotizzato è corretto: l’asta è un tirante.
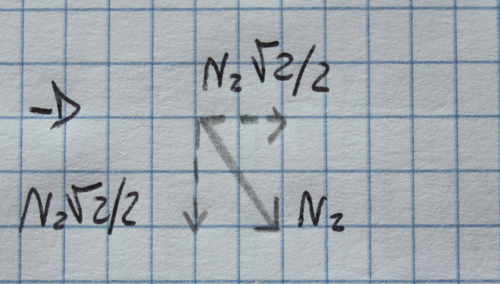
L’asta BC è inclinata di 45°: per calcolare il valore dello sforzo normale N2 devo, quindi, scomporre la forza in una componente verticale e una orizzontale. Tramite l’equilibrio delle forze verticali posso calcolarmi l’unica incognita all’interno di questa sezione, ovvero N2.
30-20-N2√2/2=0
N2 =10√2
Il verso ipotizzato è corretto: l’asta è un tirante.
In questo modo, attraverso altri tagli e tramite gli sforzi normali delle aste ricavati in precedenza, possiamo risolvere l’intera struttura, verificando se le singole aste sono sottoposte a sforzi di trazione o compressione.
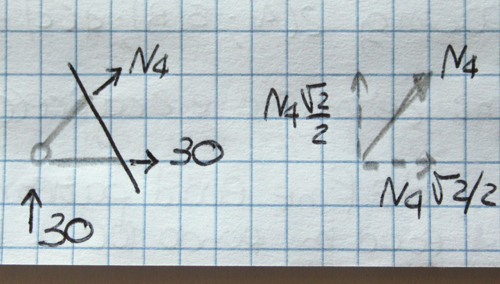
30+N4√2/2=0
N4√2/2=-30
N4=-30√2/2
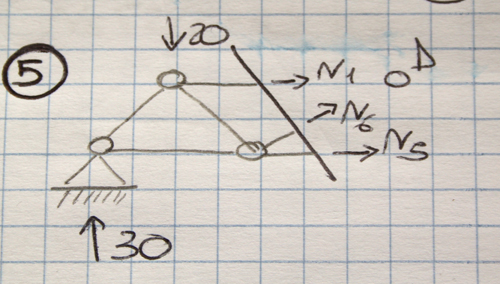
(N5x2)+(20x4)-(30x6)=0
2N5+80-180=0
2N5-100=0
N5=50
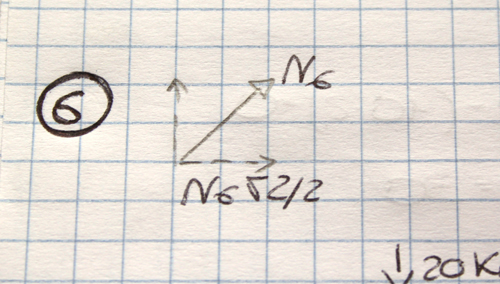
N6√2/2+30-20=0
N6=-10√2
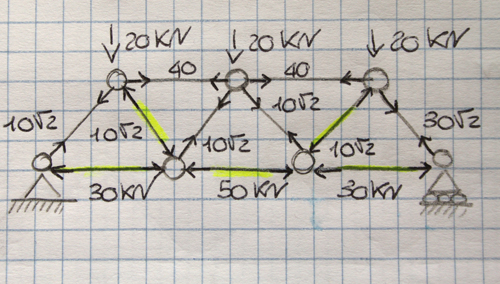
(Le aste evidenziate in giallo corrispondono alle aste tese)
Verifica della struttura con il software di calcolo SAP 2000
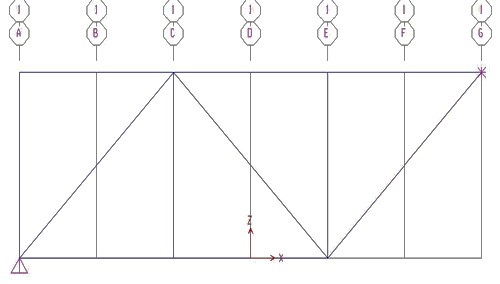
A partire dalla griglia disegno la struttura reticolare, i vincoli esterni e definisco i carichi che gravano sui nodi B,D,F.
Mi assicuro che le aste siano soggette soltanto a sforzo normale, ponendo pari a zero il momento sia all'inizio che alla fine di ogni singola asta.
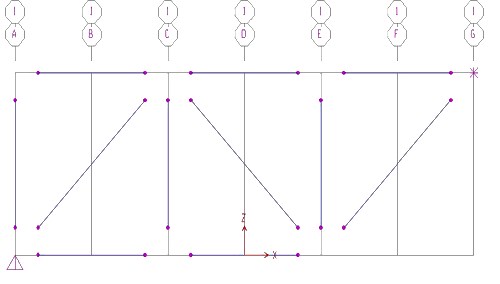
Ottengo così il valore delle reazioni vincolari e la deformazione della struttura dovuta ai carichi esterni.
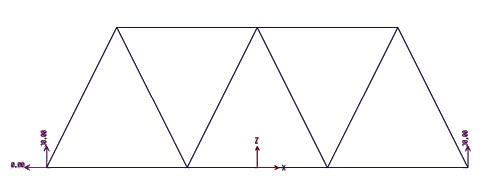
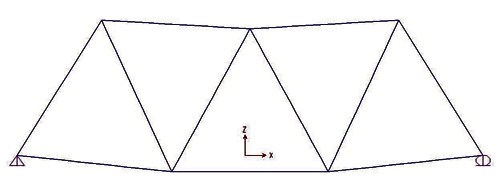
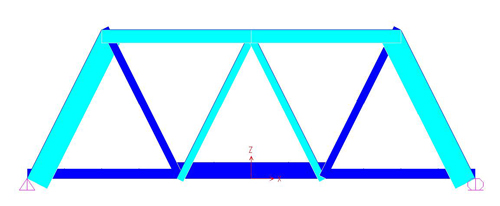
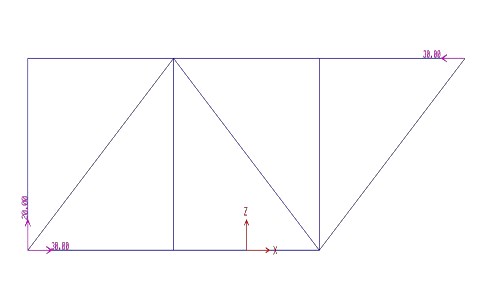
Attraverso l'analisi di SAP ottengo anche il diagramma degli sforzi assiali (in blu le aste tese) con i relativi valori.
Seconda esercitazione-travatura reticolare asimmetrica
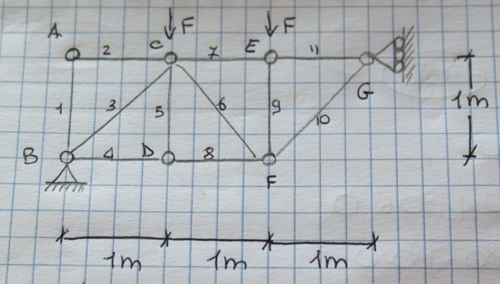
In questo esercizio ci troviamo di fronte ad una struttura reticolare asimmetrica. In questo caso, quindi, non possiamo risolvere soltanto metà configurazione e avvalerci delle proprietà della simmetria per la restante parte.
Partiamo dalla verifica dell'isostaticità:
Ve + a=2 x n°nodi
3 + 11=2 x 7
14=14
La struttura è isostatica.
Calcoliamo ora le reazioni vincolari.
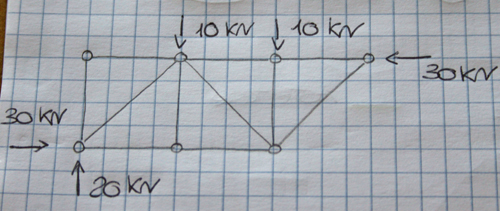
Per risolvere questa struttura utilizziamo il metodo dell'equilibrio ai nodi, attraverso il quale isoliamo un nodo della struttura reticolare calcolando il valore dello sforzo assiale che arriva sulla cerniera attraverso il solo equilibrio delle forze orizzontali e verticali.
Partiamo dal nodo A nel quale convergono visibilmente due aste scariche (AB e AF) in quanto non è presente una reazione vincolare o un carico esterno: dall'equilibrio delle forze orizzontali e verticali risulterà quindi che
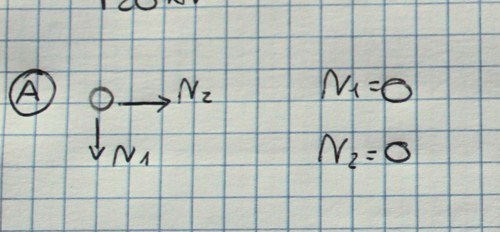
Grazie al valore dello sforzo N1 possiamo calcolare il valore delle incognite sul nodo B che, altrimenti, risulterebbero maggiori rispetto al numero di equazioni a disposizione.
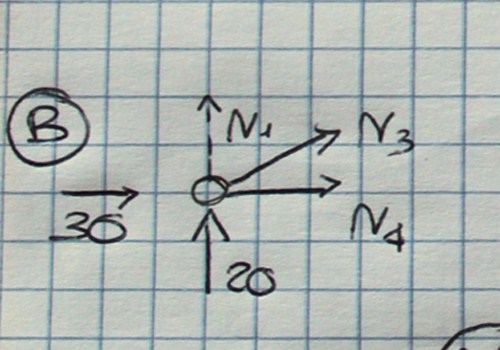
20+N3√2/2=0
N3=-20√2
30+N3√2/2+N4=0
30-(20√2x√2/2)+N4=0
N4=-10
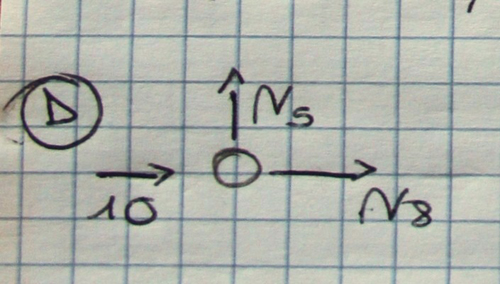
10+N8=0
N8=-10
N5=0
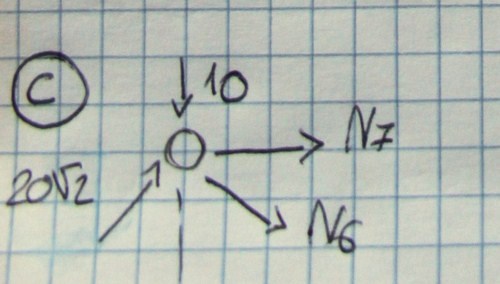
10+N6√2/2-(20√2x√2/2)=0
10+N6√2/2-20=0
N6=10√2
N7+N6√2/2-(20√2x√2/2)=0
N7+(10√2x√2/2)+20=0
N7=-30
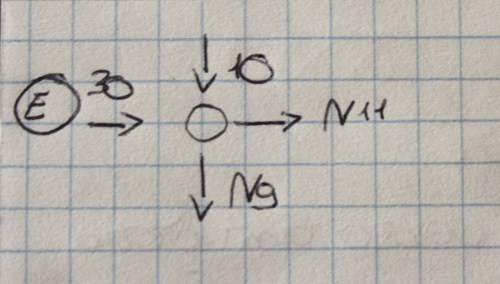
N9=-10
N11=-30
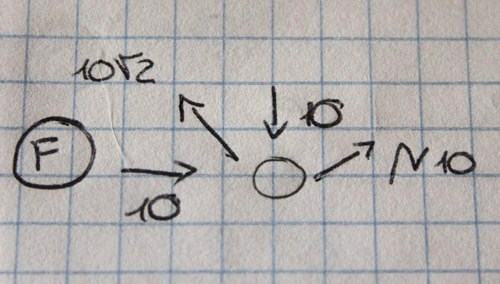
N10√2/2+10-(10√2x√2/2)=0
N10√2/2=10-10
N10=0
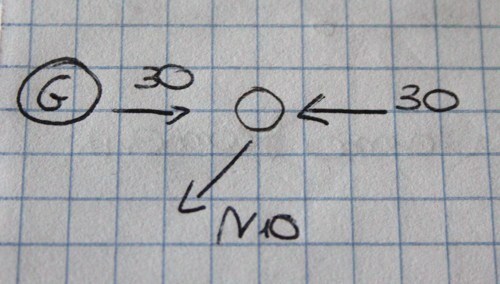
N10√2/2=0
(Le aste evidenziate in giallo corrispondono alle aste tese)
Verifica della struttura con il software di calcolo SAP 2000
A partire dalla griglia disegno la struttura reticolare, i vincoli esterni e definisco i carichi che gravano sui nodi C,E.
Mi assicuro che le aste siano soggette soltanto a sforzo normale, ponendo pari a zero il momento sia all'inizio che alla fine di ogni singola asta.
Ottengo così il valore delle reazioni vincolari e la deformazione della struttura dovuta ai carichi esterni.
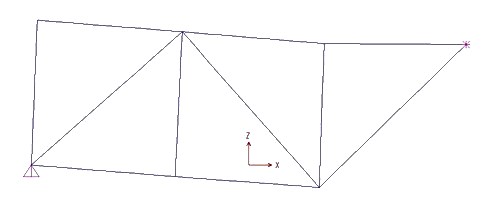
Attraverso l'analisi di SAP ottengo anche il diagramma degli sforzi assiali (in blu le aste tese) con i relativi valori.
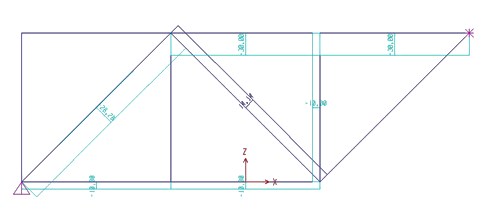
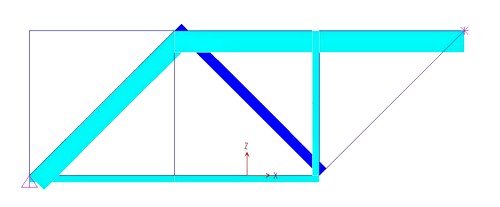
Terza esercitazione:
arco a tre cerniere con carico distribuito laterale
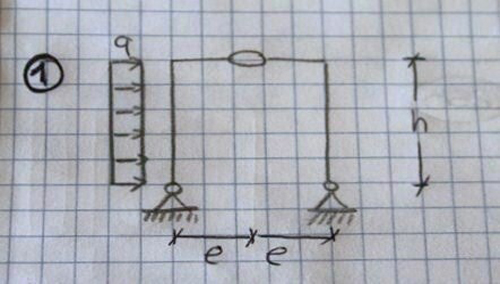
La struttura in questione è un portale: due corpi incernierati a terra e collegati da una cerniera interna. La configurazione non è simmetrica in quanto è presente lateralmente un carico distribuito pari a q. Anche in questo caso il primo passo è il calcolo delle reazioni vincolari: dividiamo la struttura in due corpi.
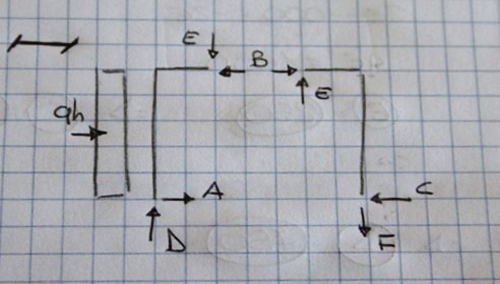
Dall'equilbrio dei momenti intorno alle due cerniere esterne e dall'equilibrio delle due traslazioni ottengo il valore delle singole forze

Le forze orizzontali bloccate dalle due cerniere esterne sono pari a 3qh/4 e qh/4 e possiedono lo stesso verso in quanto vanno a contrastare insieme il carico distribuito esterno pari a qh.
Attraverso i valori ottenuti e tramite i diagrammi di N,T,M andiamo a visualizzare lo sforzo della struttura.
Diagramma sforzo normale

Possiamo vedere come l'andamento dello sforzo normale sia costante in tutta la struttura in quanto in ogni punto sono assenti carichi concentrati q1 paralleli agli assi. Il valore dello sforzo normale assume valori positivi se agli estremi dell'asta è presente uno sforzo di trazione e negativi se, al contrario, è presente uno sforzo di compressione.
Diagramma sforzo di taglio
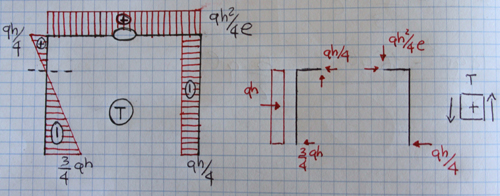
Nel primo tratto verticale lo sforzo di Taglio assume un andamento lineare per la presenza di un carico distribuito q2 perpendicolare all'asse, con estremi negativi e positivi pari al valore e al verso delle forze orizzontali. Nei tratti rimanenti i diagrammi sono costanti (per la presenza di sole forze concentrate), positivi o negativi in base alla direzione delle forze orizzontali alle estremità del tratto considerato.
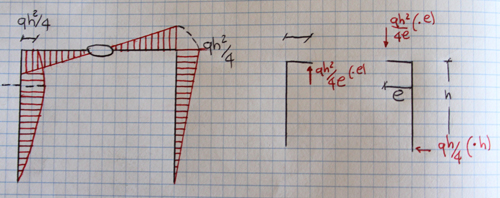
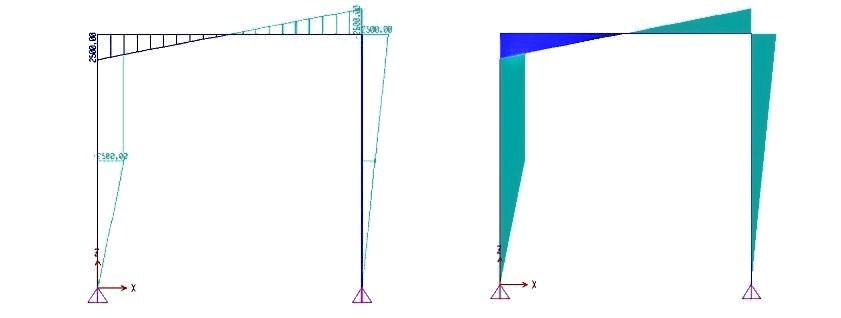
Nel primo tratto verticale il diagramma del momento è parabolico e presenta un punto di massimo proprio dove si annulla il diagramma del taglio. Nei tratti rimanenti, il diagramma è lineare.
Verifica della struttura con il software di calcolo SAP 2000
Deformazione struttura sotto il carico distribuito q
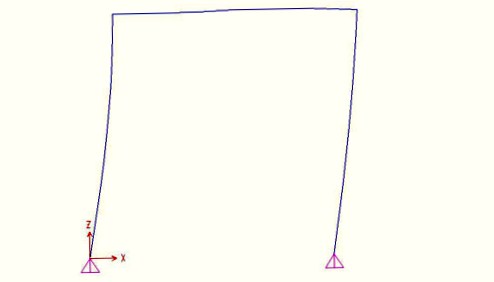
Diagramma sforzi assiali
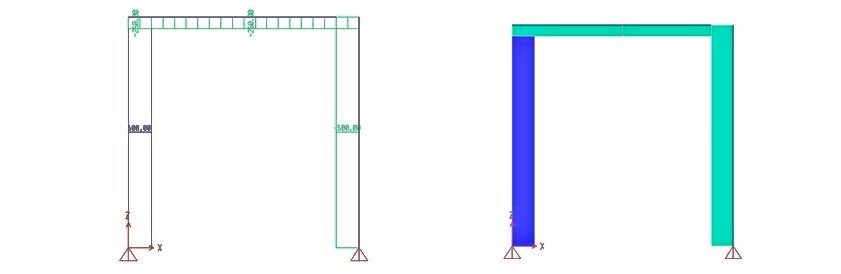
Diagramma sforzi di Taglio
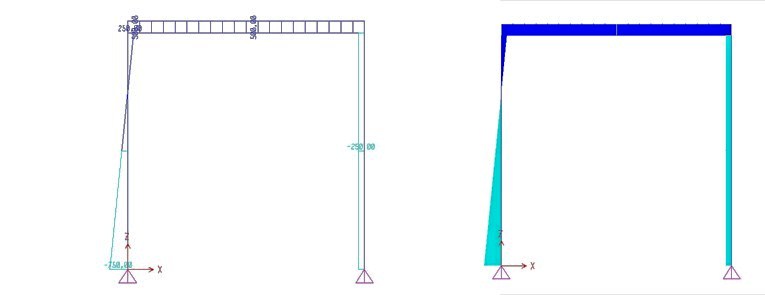
Diagramma Momenti
Quarta esercitazione:
arco a tre cerniere con carico centrale
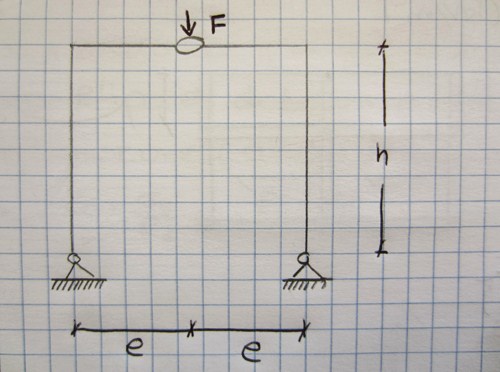
La configurazione di questo portale è simmetrica: l'unica forza presente è il carico puntuale F disposto esattamente sull'asse di simmetria della struttura (in corrispondenza della cerniera interna). Da questa conformazione possiamo dedurre che le reazioni vincolari orizzontali delle cerniere a terra saranno uguali ma di verso opposto, mentre, al contrario quelle verticali avranno stesso modulo e verso (pari a metà della forza concentrata superiore). Dall'equilibrio dei momenti intorno alla cerniera otteniamo le reazioni orizzontali:
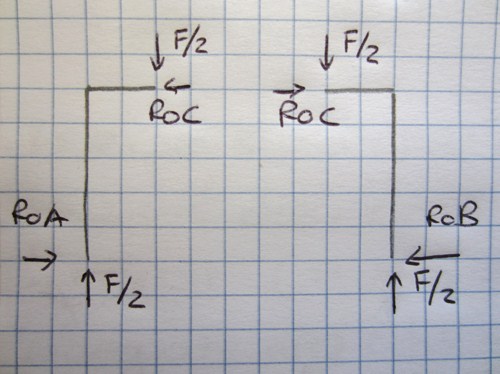
RoC h-F/2 l=0 => RoC=Fl/2h
RoA=RoC=RoB=Fl/2h
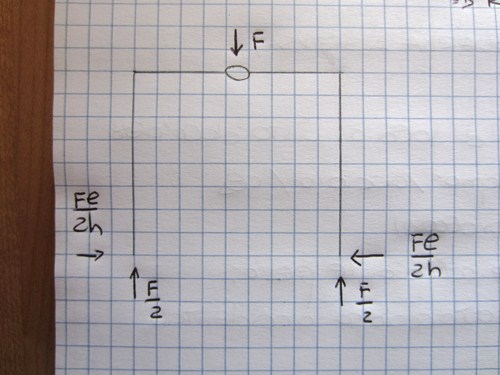
Attraverso i valori ottenuti e tramite i diagrammi di N,T,M andiamo a visualizzare lo sforzo della struttura.
Diagramma sforzo normale
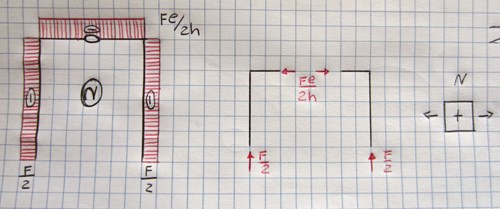
Possiamo vedere come l'andamento dello sforzo normale sia costante in tutta la struttura in quanto in ogni punto sono assenti carichi concentrati q1 paralleli agli assi. Il valore dello sforzo normale assume per ogni tratto della struttura valori negativi in quanto agli estremi di ogni asta è presente una forza di compressione.
Diagramma sforzo di taglio
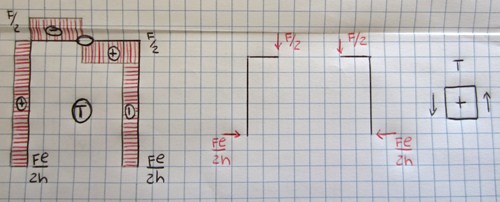
Nel primo tratto verticale lo sforzo di Taglio assume un andamento costante per la presenza del solo carico concentrato Fl/2h (positivo secondo la convenzione stabilita). Stessa situazione nel tratto verticale sulla destra, anche se in qesto caso la forza Fl/2h fa assumere all'asta uno sforzo di taglio negativo pari al valore della stessa forza. Nel tratto orizzontale possiamo vedere un salto nel diagramma del taglio, in corrispondenza della forza esterna, pari al valore della forza F.
Diagramma Momento
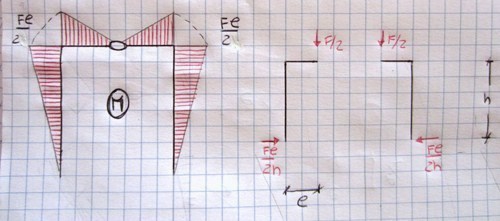
Il momento assume un andamento lineare in tutti i tratti del portale (il diagramma del taglio è infatti costante per tutti i punti), annullandosi in corrispondenza delle cerniere esterne e della cerniera interna.
Verifica della struttura con il software di calcolo SAP 2000
Deformazione struttura sotto il carico concentrato centrale F
Diagramma sforzi assiali
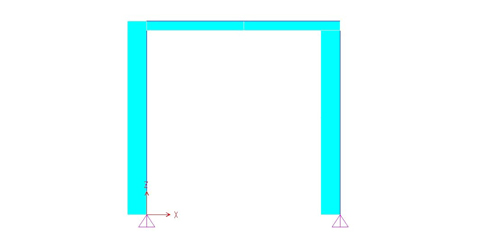
Diagramma sforzi di Taglio
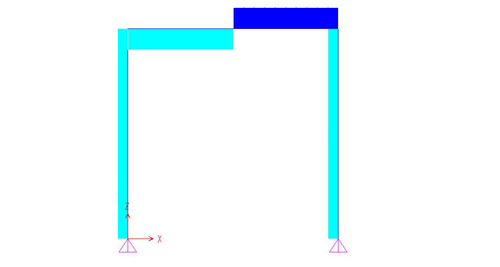
Diagramma Momento
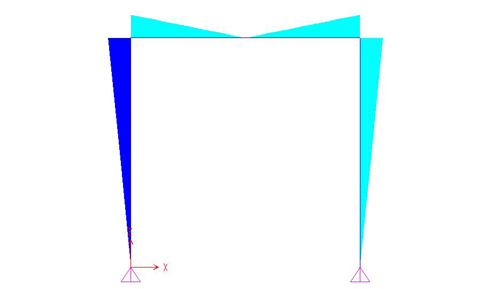
Quarta esercitazione:
arco a tre cerniere con carichi concentrati laterali
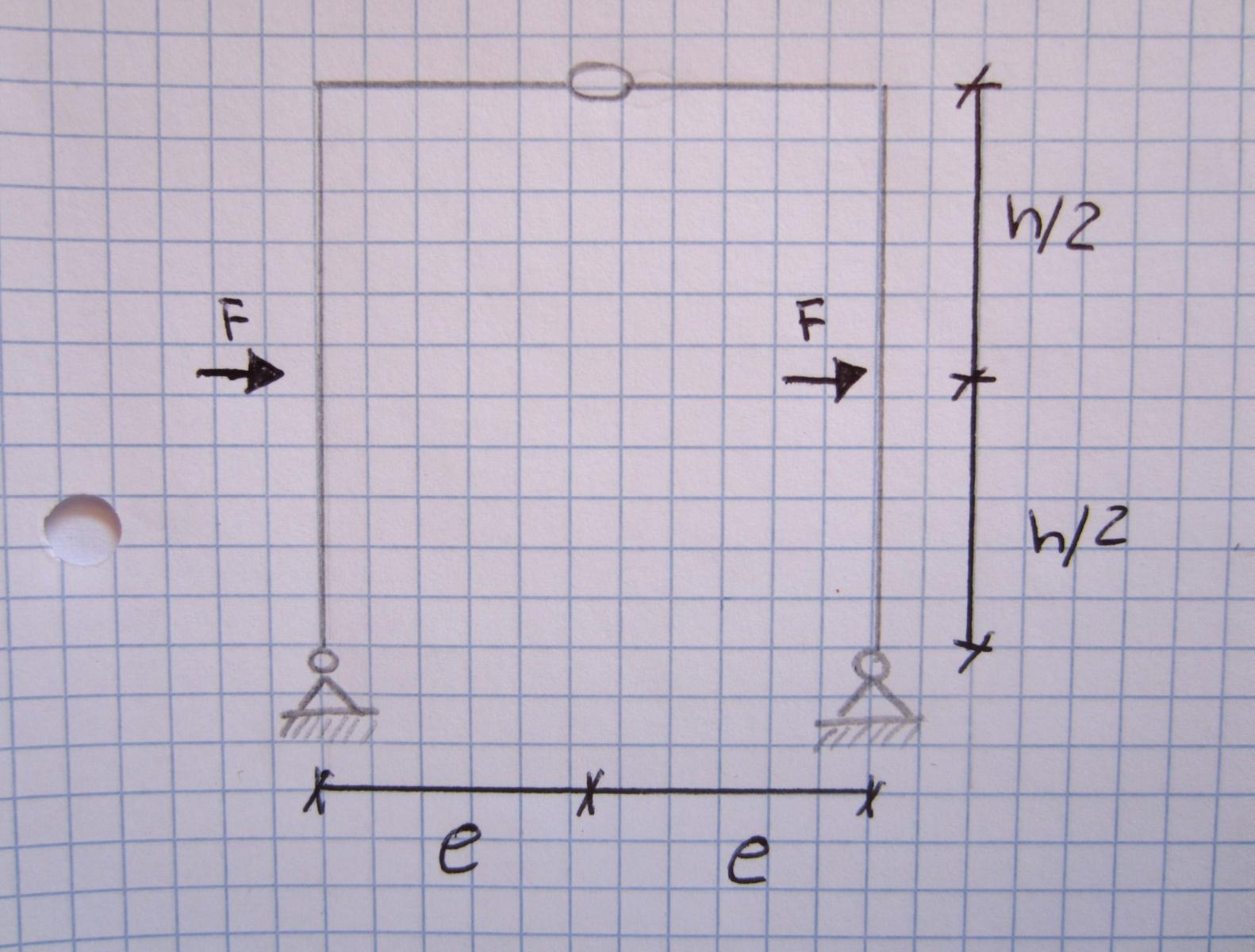
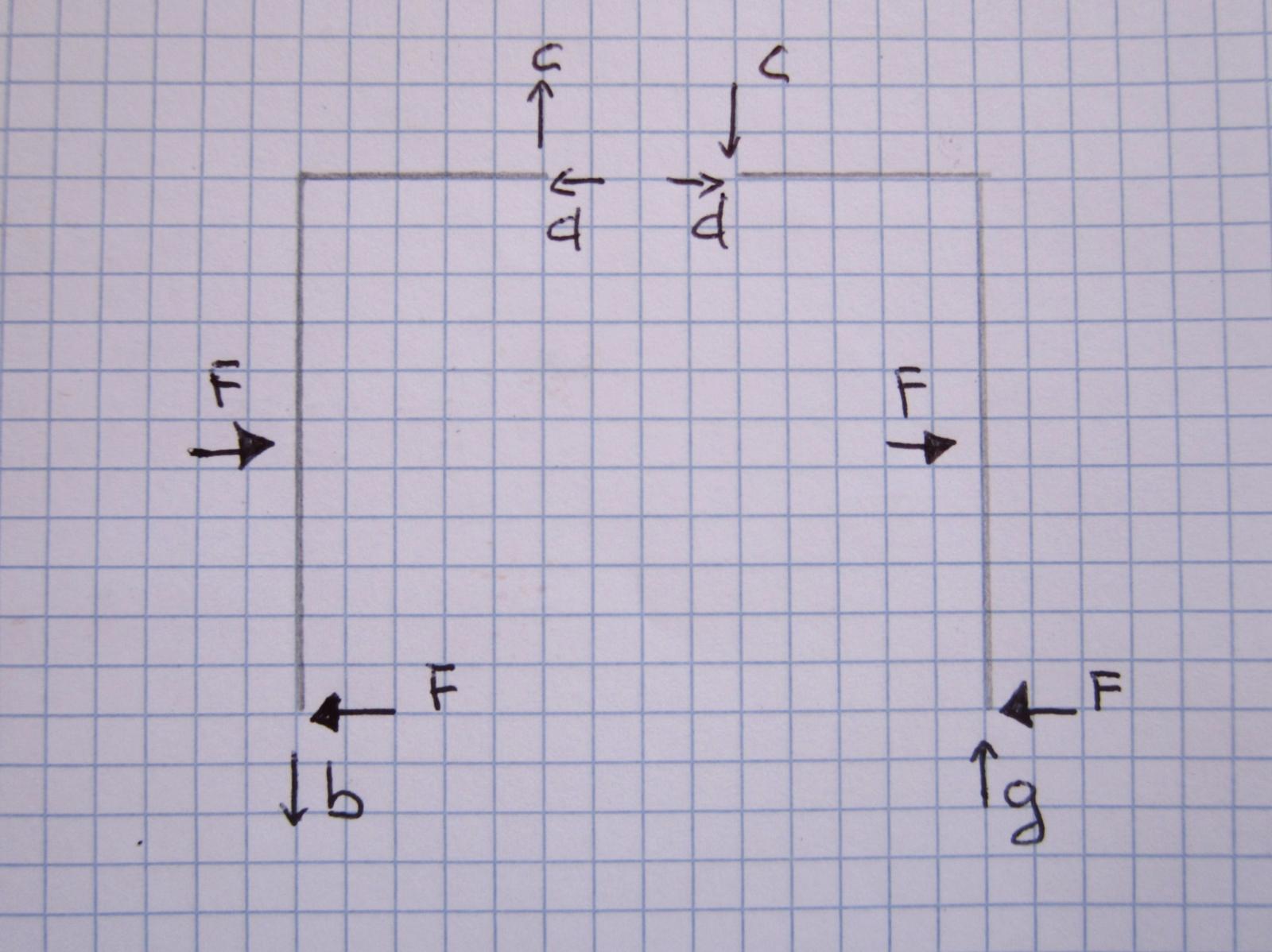
Le uniche forze presenti su questo portale sono i carichi puntuali F disposti ad h/2 rispetto all'altezza del portale. Da questa conformazione possiamo dedurre che le reazioni vincolari orizzontali delle cerniere a terra avranno un valore pari a F ma di verso opposto rispetto al carico esterno, mentre quelle verticali sicuramente andranno a bilanciare il momento Fh/2 prodotto dalle forze orizzontali. Dall'equilibrio dei momenti intorno alla cerniera otteniamo le reazioni verticali:
-cl-dh-Fh/2=0 (corpo a destra)
-cl+dh-Fh/2=0 (corpo a sinistra)
Dalla seconda equazione mi ricavo il valore di d:
d=(cl+Fh/2) x 1/h
sostituisco il valore trovato nella prima equazione:
-cl-(cl/h+F/2) x h - fh/2 = 0
=> c (= b = g) = - Fh/2l
Attraverso i valori ottenuti e tramite i diagrammi di N,T,M andiamo a visualizzare lo sforzo della struttura.
Diagramma sforzo normale
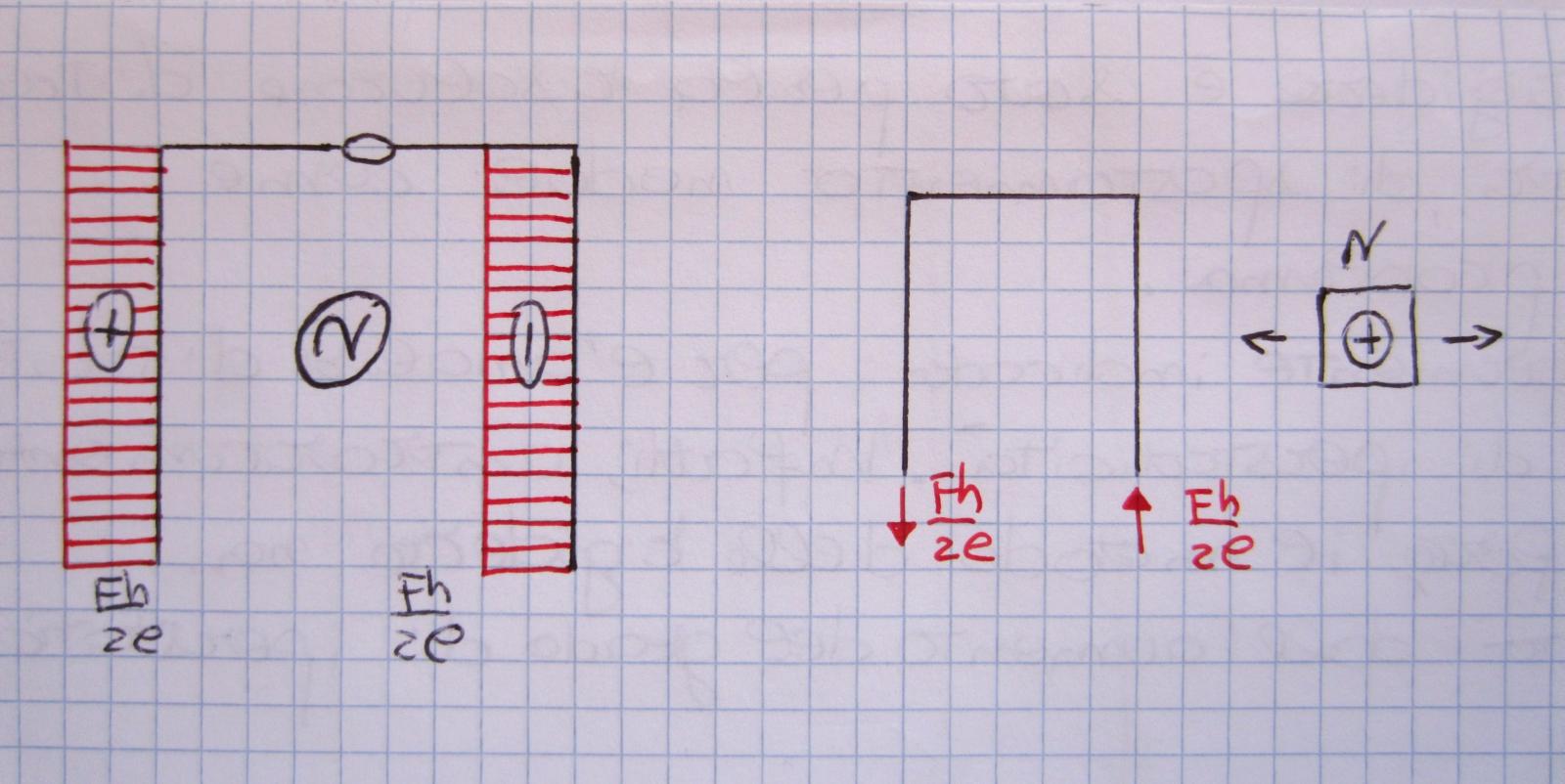
Possiamo vedere come l'andamento dello sforzo normale sia costante in tutta la struttura in quanto in ogni punto sono assenti carichi concentrati q1 paralleli agli assi. Il valore dello sforzo normale assume per ogni tratto a sinistra un valore positivo in quanto agli estremi dell’ asta è presente una forza di trazione, e negativo a destra, in quanto è presente uno sforzo di compressione.
Diagramma sforzo di taglio
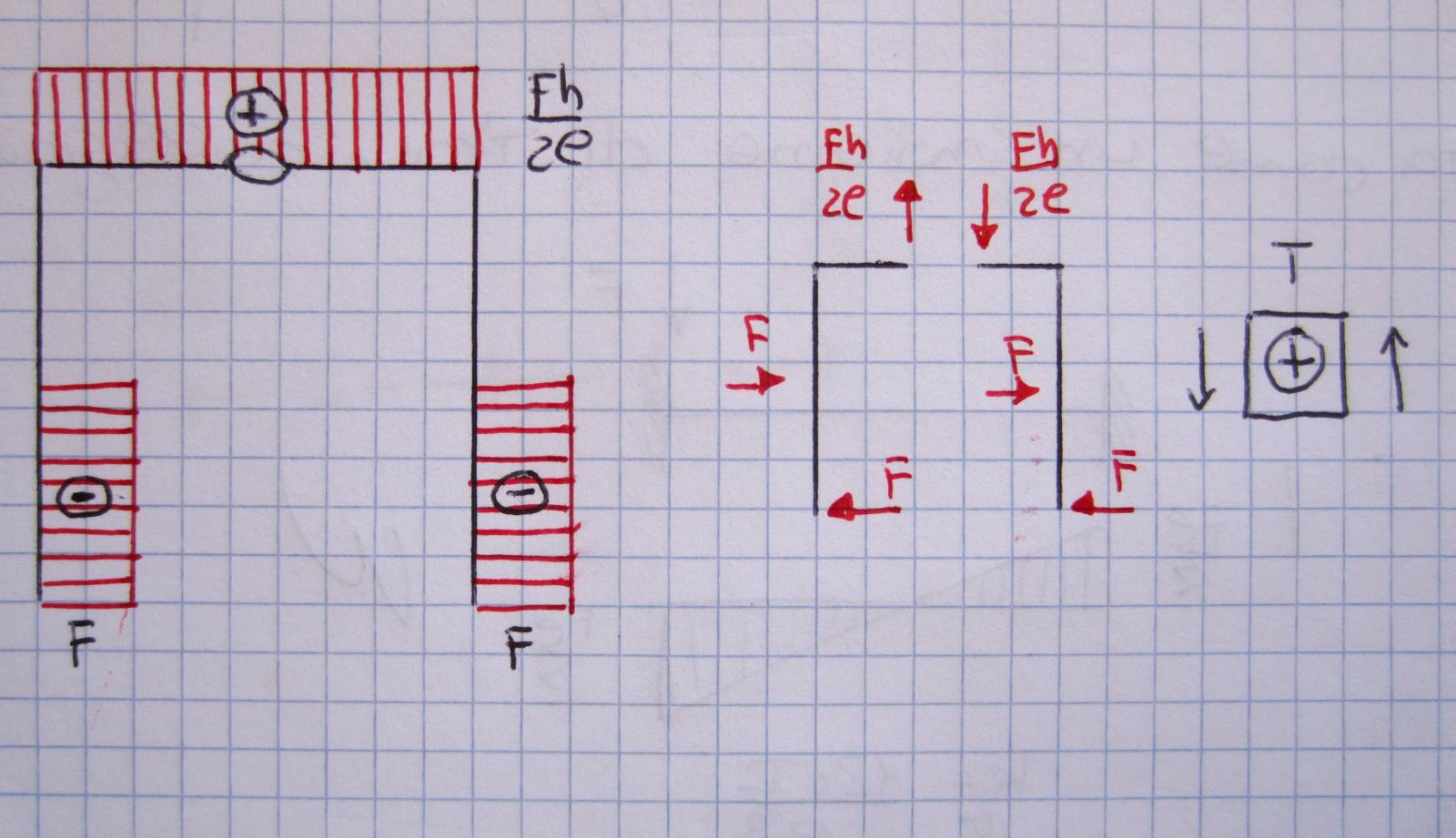
Nei primi tratti verticali lo sforzo di Taglio assume un andamento costante per la presenza delle sole forze concentrate F (negativo secondo la convenzione stabilita). Nel secondo tratto, in assenza di carichi, non c'è sforzo di Taglio. Nel tratto orizzontale il diagramma è costante e positivo e pari al valore della forza verticale della cerniera interna.
Diagramma momento
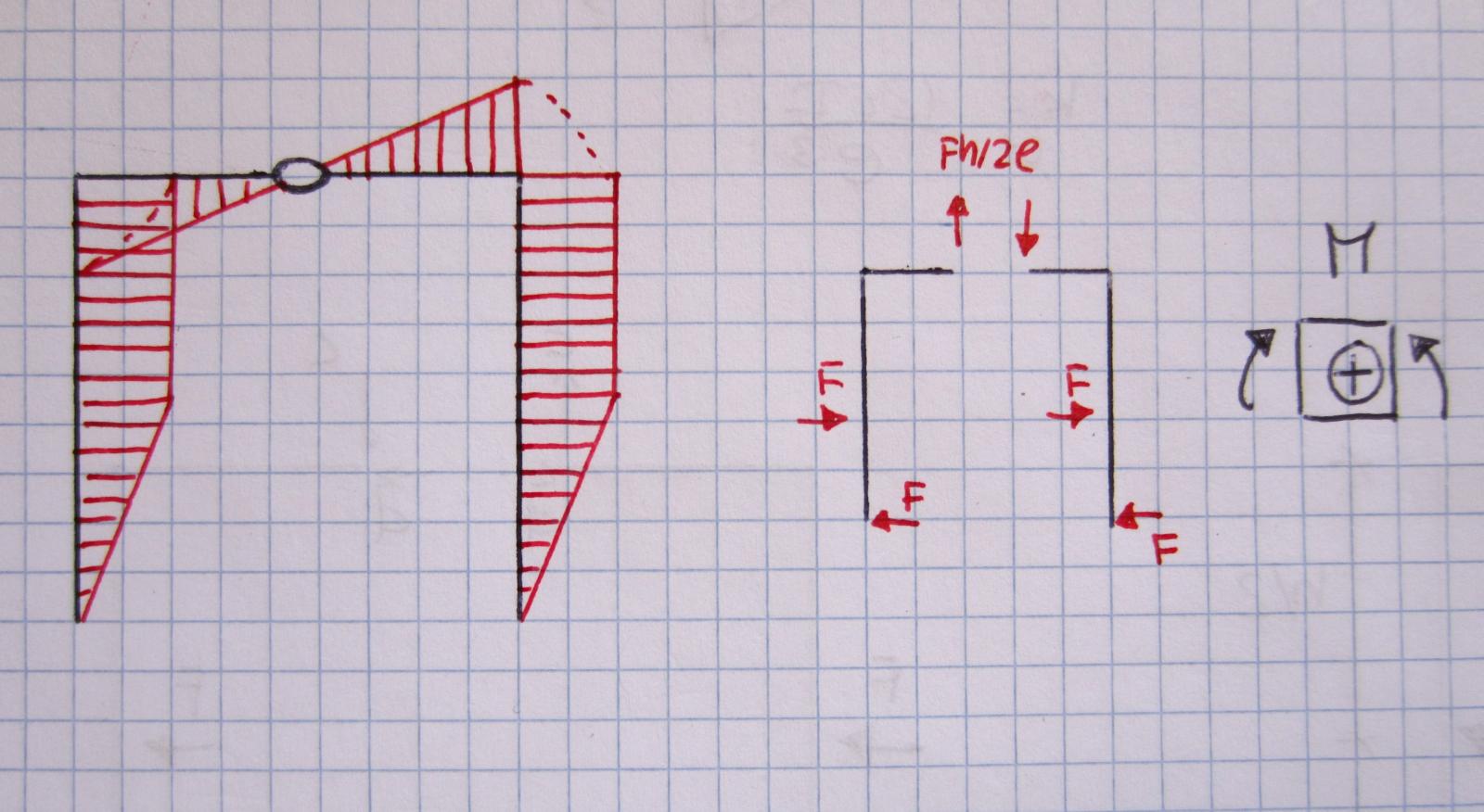
Il momento assume un andamento lineare in tutti i tratti del portale (dove il diagramma del Taglio è costante) tranne per il secondo tratto verticale dove il taglio è pari a 0.
Verifica della struttura con il software di calcolo SAP 2000
Deformazione struttura
.jpg)
Diagramma sforzi assiali
_0.jpg)
Diagramma sforzi di Taglio
_1.jpg)
Diagramma Momento
.jpg)
Quinta esercitazione:
dimensionamento di una trave
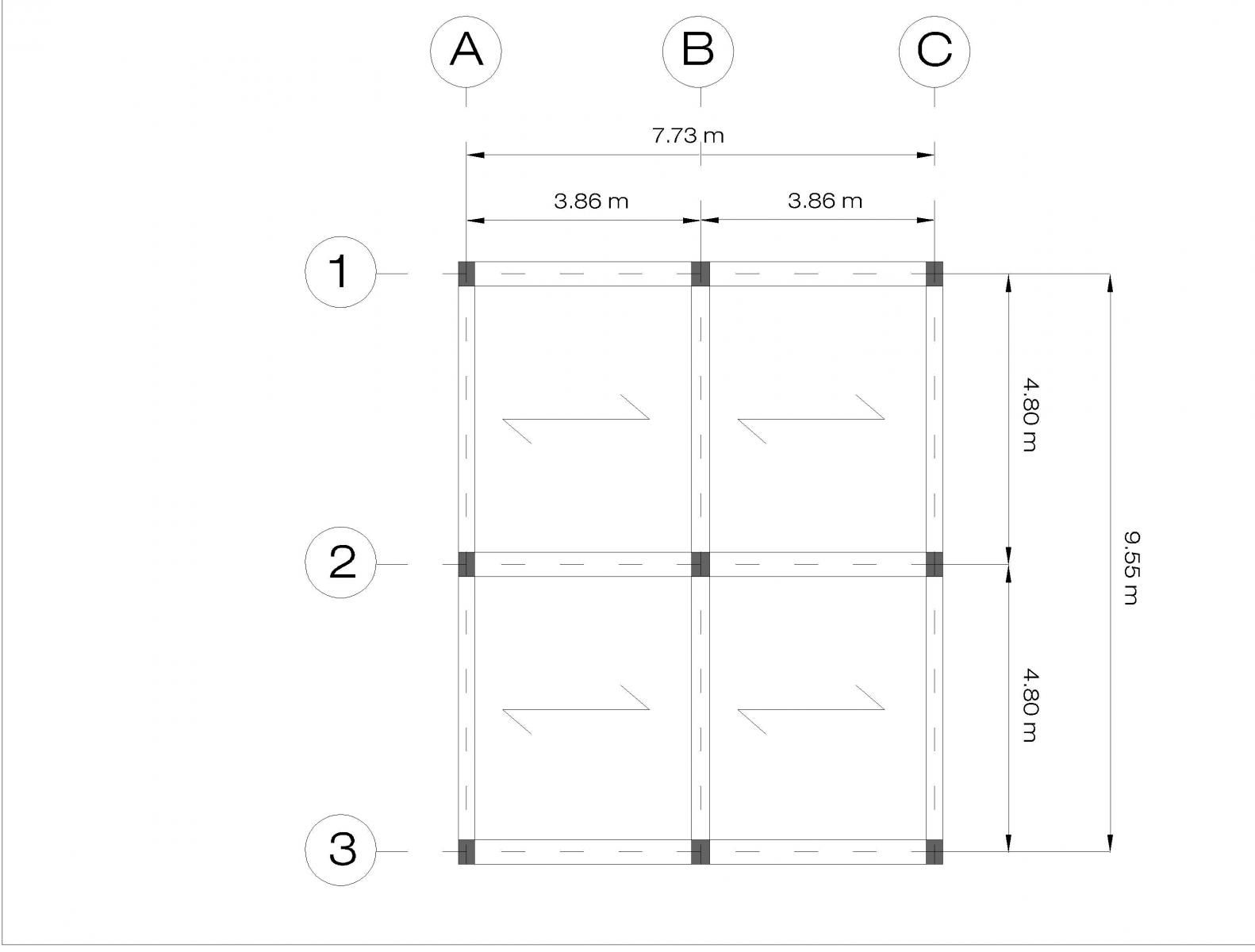
Per questo esercizio ho scelto di esaminare la struttura di due appartamenti simmetrici, all'interno di un complesso residenziale, studiata per il Laboratorio di Progettazione 3 (triennale): la pianta si riferisce al piano terra. Nella progettazione fatta in passato era stata ipotizzata un'orditura nella stessa direzione per tutta la lunghezza dell'impalcato, con un solaio in c.a.
L'esercizio prevede il dimensionamento di una trave della struttura ipotizzando l'uso di tre differenti tipologie strutturali: legno, acciaio e c.a.
La trave che andrò a dimensionare è quella compresa tra i pilastri B1-B2, con una luce pari a 4.80 m, un interasse di 3.86 m (1.93 m + 1.93 m) e un'area d'influenza di circa 18.53 mq (3.86 m x 4.8 m).
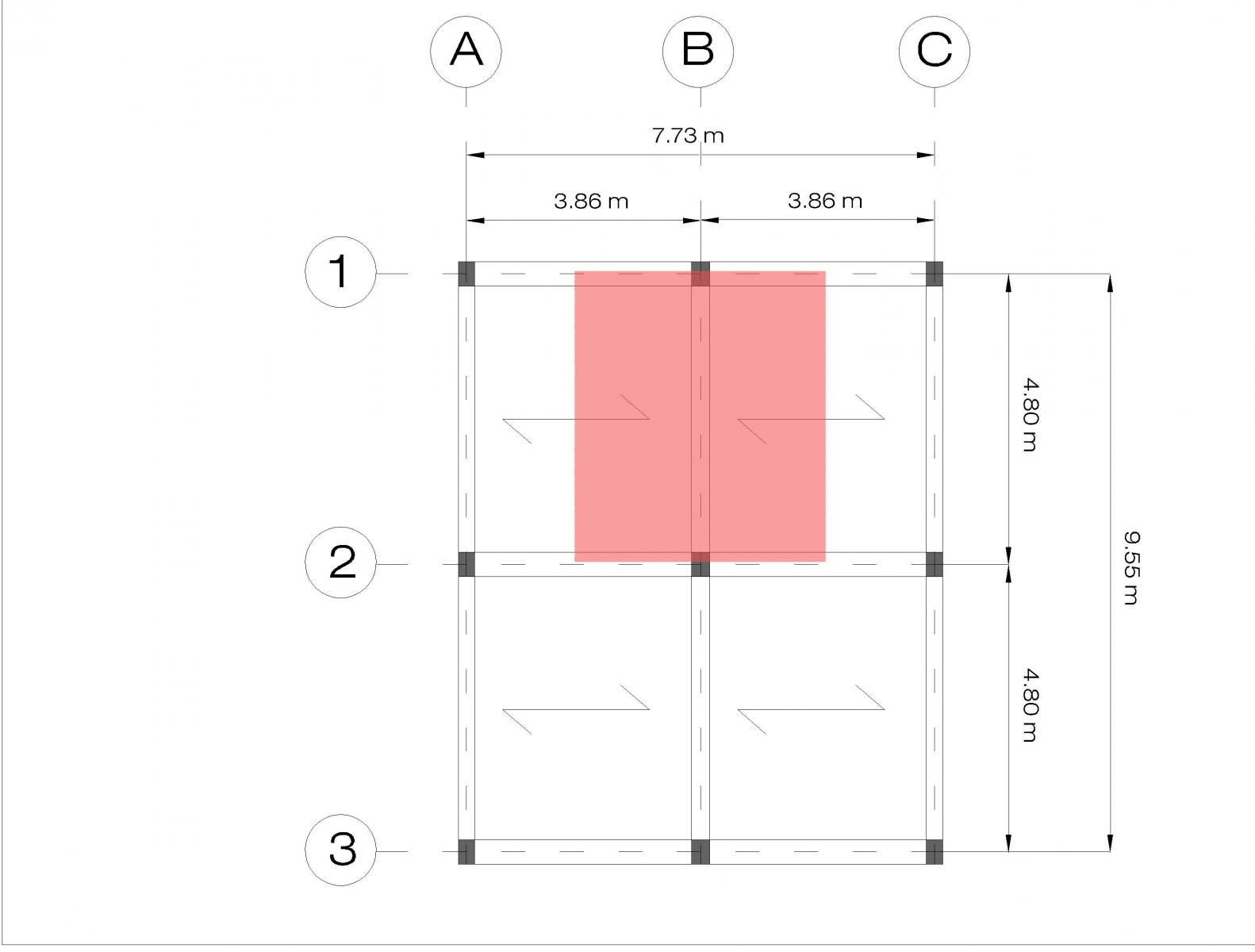
Per poter effettuare il dimensionamento e inserire nel foglio di calcolo excel i valori noti, dobbiamo prima calcolarci il peso totale dei carichi che gravano sulla struttura, distinguendoli in tre classi:
1. Qs = pesi propri dei materiali strutturali
2. Qp = carichi permanenti non strutturali (carico non removibile durante il normale esercizio della costruzione, relativo a tamponature esterne, massetti, isolamenti, pavimenti, rivestimenti, intonaci, impianti e altro)
3. Qa = carichi accidentali (carichi legati alla destinazione d'uso dell'opera)
Dalla Normativa (d.m. 14.01.2008) possiamo ricavare i valori dei carichi d'esercizio in base alla categoria dell'edificio: in particolare per gli ambienti ad uso residenziale si adotta un valore di carico accidentale pari a 2 KN/mq.

1. LEGNO
Per poter effettuare il dimensionamento della trave dobbiamo prima di tutto sommare le tre classi di carico, inserendo all'interno dei carichi strutturali, anche il peso dei travetti.
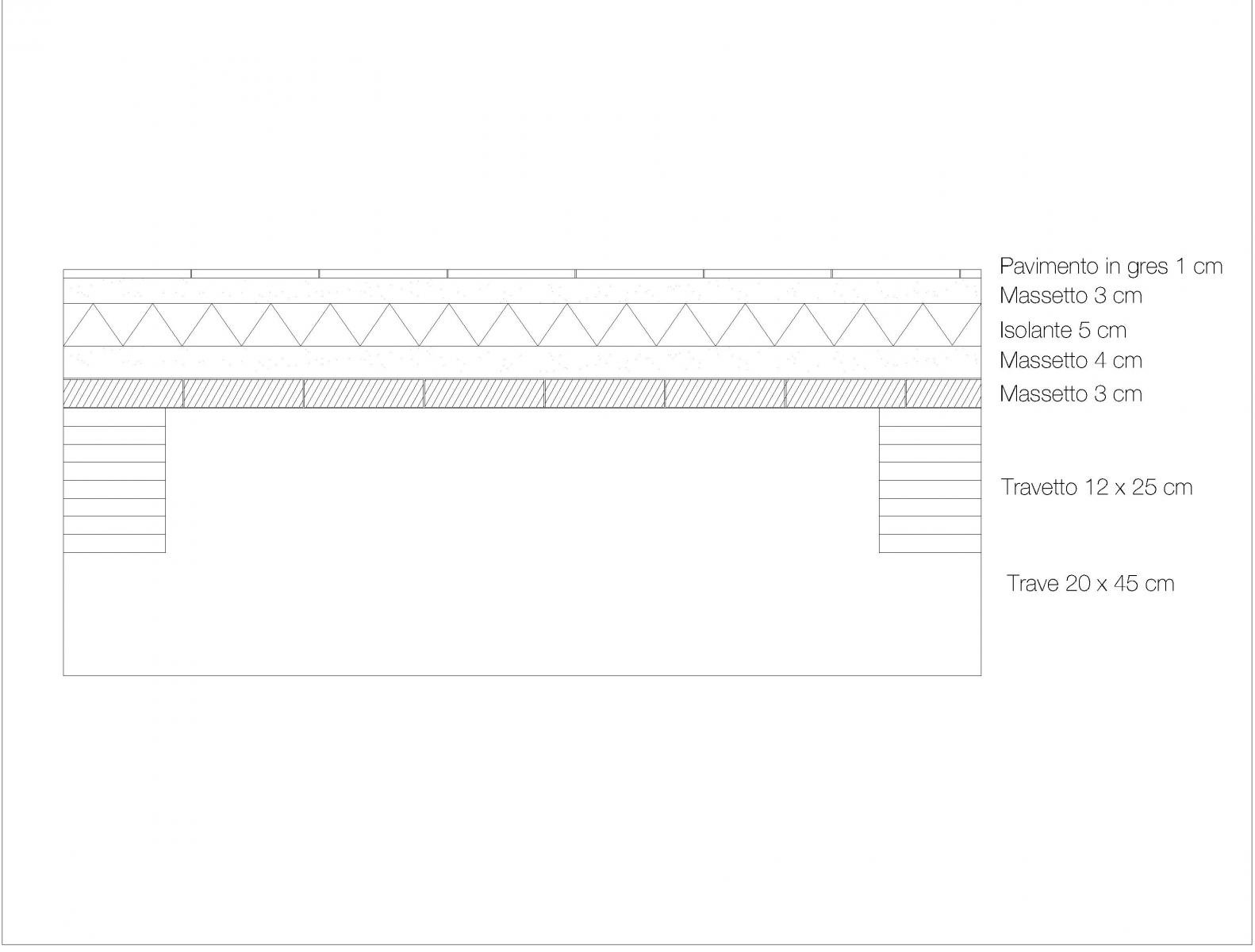
1.1 Progetto Travetti
Luce = 3.86 m; Interasse = 1 m
1.1.1 Calcolo dei carichi:
In questo passaggio vado a calcolarmi il peso di ogni singolo elemento che compone la stratigrafia del solaio e che incide direttamente sul travetto, attraverso il prodotto tra lo spessore dell'elemento (m) e il proprio peso specifico (KN/mc), considerando un'area di 1 mq. Divido sempre i carichi nelle tre categorie.
Assito in legno: 6 KN/mc (peso specifico) x 0.035 m (spessore) = 0.21 KN/mq
-
Qp (carico permanente non strutturale):
Pavimento in gres: 0.01 m (spessore) = 0.2 KN/mq
Malta in cls alleggerito: 20 KN/mc x 0.03 m = 0.6 KN/mq
Isolante (lana di vetro): 0.6 KN/mc x 0.05 m = 0.03 KN/mq
Massetto: 22 KN/mc x 0.04 m = 0.88 KN/mq
Impianti: 0.5 KN/mq
=> 0.2 + 0.6 + 0.03 + 0.88 + 0.5 = 2.21 KN/mq
-
Qa (carico accidentale): 2 KN/mq
1.1.2 Inserimento dati nel foglio excel:
Attraverso l'inserimento dei dati noti all'interno del foglio di calcolo excel ricavo le dimensioni del travetto. Prima di tutto vado a calcolare il carico totale a metro lineare (q = KN/m) che grava sull'elemento strutturale, sommando tutti i carichi (qa + qp + qs) e moltiplicando la somma per l'interasse dei travetti:
(0.21 KN/mq + 2.21 KN/mq + 2 KN/mq) x 1m = 4.42 KN/m
Questo dimensionamento è applicabile a tutte quelle travi che hanno come schema statico di riferimento una trave doppiamente appoggiata con M=ql^2/8.Una volta calcolato il carico totale a metro lineare vado a impostare la luce del travetto, pari a 3.86 m, così da calcolare il Momento massimo agente:
M = ql2/8 = 4.42 x (3.86)2/8 = 8.23 KN*m
Avendo scelto come classe di legno la GL28h, inserisco all'interno del foglio excel la tensione di snervamento corrispondente (28 N/mmq) e il Kmod, un coefficiente correttivo caratteristico del legno che tiene conto dell'effetto, sui parametri di resistenza, sia della durata del carico sia dell'umidità della struttura (stesso effetto del coefficiente γm, ovvero quello di diminuire il valore della resistenza)

Ottengo così una tensione di progetto fD pari a 9.66 N/mmq
Ipotizzo, quindi, una dimensione per la base del travetto (12 cm), così da calcolarmi l'altezza:
h= (6 x M x 1000 / b x fD) ^ 0,5 = 20.65 cm
Approssimando per eccesso i valori ottenuti ottengo un travetto di dimensioni 12x25 cm.

Per verificare il risultato ottenuto, sommando al carico strutturale il carico dei travetti, inserisco nuovamente i dati nel foglio di calcolo excel:
Qtr al metro lineare = A x γ = 0.12 m x 0.25 m x 6 KN/mc = 0.18 KN/m
Qtr al metro quadro = qtr/interasse = 0.18 KN/m /1m = 0.18 KN/mq
=> Qs = 0.21 KN/mq + 0.18 KN/mq = 0.39 KN/mq

Il dimensionamento è verificato anche con h = 21,06 cm, in quanto l'altezza precedentemente ipotizzata era pari a 25 cm
=> Travetto GL28h 12 x 25 cm
1.2 Progetto Trave
Luce = 4.8 m; Interasse = 3.86 m
1.2.1 Calcolo dei carichi:
-
Qs (carico strutturale) : 0.39 KN/mq (assito in legno + travetti)
-
Qp (carico permanente non strutturale): 2.21 KN/mq
-
Qa (carico accidentale): 2 KN/mq
1.2.2 Inserimento dati nel foglio excel:
Somma carichi:
(0.39 KN/mq + 2.21 KN/mq + 2 KN/mq) x 3.86 m = 17.756 KN/m
Calcolo Momento massimo agente:
M = ql^2/8 = 17.756 x (4.8)2/8 = 51.13728 KN*m
Calcolo tensione di progetto fD:
fD = Kmod*fmk/γm = 9.66 N/mmq
Calcolo altezza trave h (ipotizzando una base di 20 cm):
h= (6 x M x 1000 / b x fD) ^ 0,5 = 39.86 cm
Approssimando per eccesso i valori ottenuti ottengo una trave di dimensioni 20 x 40 cm.

Per verificare il risultato ottenuto, sommando al carico strutturale anche il carico della trave stessa, inserisco nuovamente i dati nel foglio di calcolo excel.
Qtr al metro lineare = A x γ = 0.20 m x 0.40 m x 6 KN/mc = 0.48 KN/m
Qtr al metro quadro = qtr/interasse = 0.48 KN/m /3.86m = 0.124 KN/mq
=> Qs = 0.39 KN/mq + 0.124 KN/mq = 0.514 KN/mq

Il dimensionamento non risulta verificato poichè mantenendo una base pari a 20 cm l'altezzza nuova (che considera all'interno dei carichi anche il peso della trave) risulta pari a 40.39 cm.
=> Trave GL28h 20 x 45 cm
2. ACCIAIO
Per il dimensionamento della trave in acciaio applico inizialmente lo stesso procedimento effettuato per il solaio in legno: sommatoria dei carichi, calcolo del momento massimo agente, calcolo tensione di progetto fD, pertendo, anche in questo caso, dal progetto dei travetti.
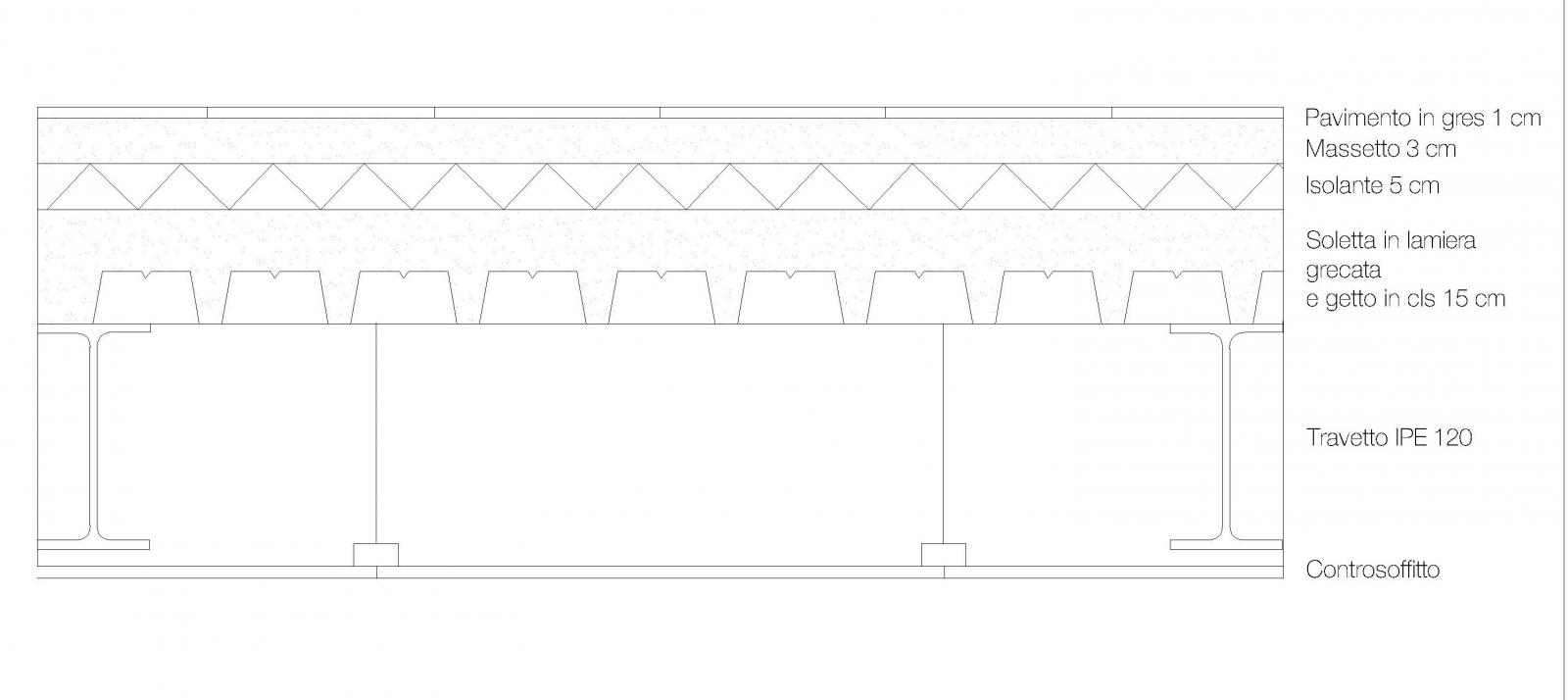
2.1 Progetto Travetti
Luce = 3.86 m; Interasse = 1 m
2.1.1 Calcolo dei carichi:
In questo passaggio vado a calcolarmi il peso di ogni singolo elemento che compone la stratigrafia del solaio e che incide direttamente sul travetto, attraverso il prodotto tra lo spessore dell'elemento (m) e il proprio peso specifico (KN/mc), considerando un'area di 1 mq. Divido sempre i carichi nelle tre categorie.
Soletta in lamiera grecata e getto in cls ( lamiera di tipo A75/P600, con un'altezza di 75mm e una altezza totale della soletta di 15cm) = 2.50 KN/mq
-
Qp (carico permanente non strutturale):
Pavimento in gres: 0.01 m (spessore) = 0.2 KN/mq
Malta in cls alleggerito: 20 KN/mc x 0.03 m = 0.6 KN/mq
Isolante (lana di vetro): 0.6 KN/mc x 0.05 m = 0.03 KN/mq
Pannelli in cartongesso: 0.1 KN/mq
Impianti: 0.5 KN/mq
=> 0.2 + 0.6 + 0.03 + 0.1 + 0.5 = 1.43 KN/mq
-
Qa (carico accidentale): 2 KN/mq
2.1.2 Inserimento dati nel foglio excel:
Attraverso l'inserimento dei dati noti all'interno del foglio di calcolo excel ricavo le dimensioni del travetto. Prima di tutto vado a calcolare il carico totale a metro lineare (q = KN/m) che grava sull'elemento strutturale, sommando tutti i carichi (qa + qp + qs) e moltiplicando la somma per l'interasse dei travetti:
(2.50 KN/mq +1.43 KN/mq + 2 KN/mq) x 1m = 5.93 KN/m
Una volta calcolato il carico totale a metro lineare vado a impostare la luce del travetto, pari a 3.86 m, così da calcolare il Momento massimo agente:
M = ql2/8 = 5.93 x (3.86)2/8 = 11.04 KN*m
Avendo scelto come classe di acciaio la Fe360S235, inserisco all'interno del foglio excel la tensione di snervamento corrispondente (235 N/mmq), così da calcolare la tensione di design fD:
fD = fyk/1.05 = 223.81 N/mmq
Dai calcoli effettuati ottengo un Modulo di resistenza a flessione Wx pari a 49.35 cm^3; ricerco quindi nelle tabelle il profilo con il modulo di resistenza immediatamente superiore:
=> Profilo IPE 120 (Wx = 53 cm^3)

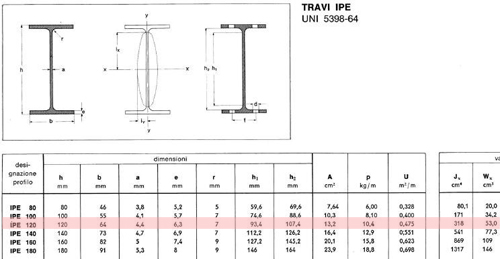
Per verificare il risultato ottenuto, sommando al carico strutturale il carico dei travetti, inserisco nuovamente i dati in excel:
Peso travetto (tabella) = 10.4 Kg/m = 0.104 KN/m
Qtr al metro quadro = 0.104 KN/m /interasse = 0.104 KN/m /1 m = 0.104 KN/mq
Qs = 2.50 KN/mq + 0.104 KN/mq = 2.604 KN/mq

Il dimensionamento è verificato anche questa volta in quanto Wx = 50.21 cm^3
=> Travetto IPE 120 (Wx = 53 cm^3) (12cm x 6.4 cm)
2.2 Progetto Trave
Luce = 4.8 m; Interasse = 3.86 m
2.2.1 Calcolo dei carichi:
-
Qs (carico strutturale) =
carico soletta + travetti = 2.50 KN/mq +0.104 KN/mq = 2.604 KN/mq
-
Qp (carico permanente non strutturale) =
Pavimento in gres: 0.01 m (spessore) = 0.2 KN/mq
Malta in cls alleggerito: 20 KN/mc x 0.03 m = 0.6 KN/mq
Isolante (lana di vetro): 0.6 KN/mc x 0.05 m = 0.03 KN/mq
Pannelli in cartongesso: 0.1 KN/mq
Impianti: 0.5 KN/mq
=> 0.2 + 0.6 + 0.03 + 0.1 + 0.5 = 1.43 KN/mq
-
Qa (carico accidentale): 2 KN/mq
2.2.2Inserimento dei dati all'interno del foglio excel:
Somma carichi:
(2.604 KN/mq + 1.43 KN/mq + 2 KN/mq) x 3.86 m = 23.29 KN/m
Calcolo Momento massimo agente:
M = ql^2/8 = 23.29 x (4.8)2/8 =67.07 KN*m
Calcolo tensione di progetto fD:
fD = fγk/1.05 = 223.81 N/mmq
Dai calcoli effettuati ottengo un Modulo di resistenza a flessione Wx pari a 299.71 cm^3; ricerco quindi nelle tabelle il profilo con il modulo di resistenza immediatamente superiore
=> Profilo IPE 240 (Wx = 324 cm^3)

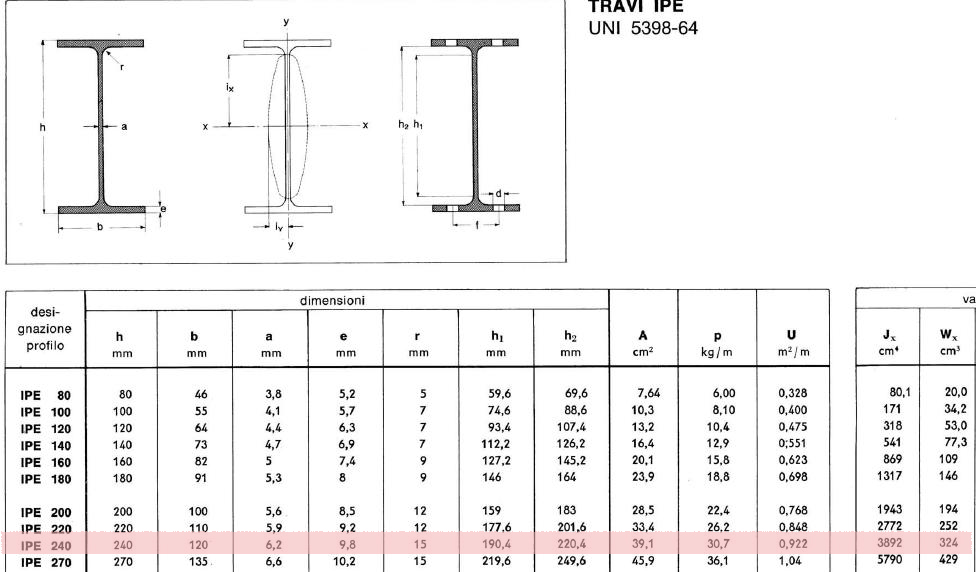
Per calcolare il risulatato ottenuto , sommando al carico strutturale il carico dei travetti, inserisco nuovamente i dati nel foglio di calcolo excel:
Peso trave (tabella) = 30.7 Kg/m = 0.307 KN/m
Qtr al metro quadro = 0.307 KN/m /interasse = 0.307 KN/m /3.86 m = 0.026 KN/mq
Qs = 2.604 KN/mq + 0.026 KN/mq =2.63 KN/mq

Il dimensionamento è verificato anche questa volta in quanto Wx = 301.01 cm^3
=> Trave IPE 240 (Wx = 324 cm^3)(24 cm x 12 cm)
3. CLS ARMATO
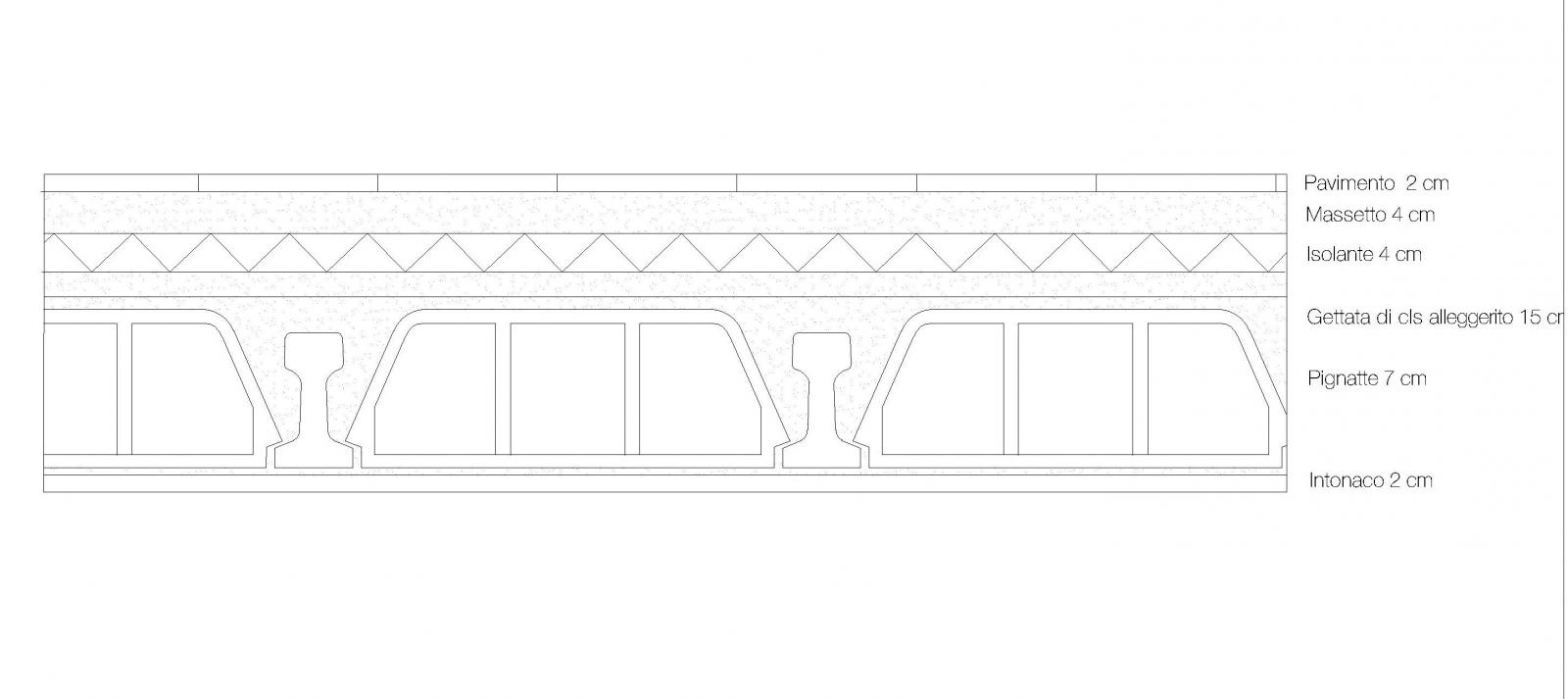
Luce = 4.8 m; Interasse = 3.86 m
3.1.Calcolo dei carichi:
Solaio in laterocemento con travetti armati= 2.65 KN/mq
-
Qp (carico permanente non strutturale):
Pavimento : 0.01 m (spessore) = 0.2 KN/mq
Malta in cls alleggerito: 20 KN/mc x 0.03 m = 0.6 KN/mq
Isolante (lana di vetro): 0.6 KN/mc x 0.05 m = 0.03 KN/mq
Intonaco (2 cm): 0.3 KN/mq
Impianti: 0.5 KN/mq
=> 0.2 + 0.6 + 0.03 + 0.3 + 0.5 = 1.63 KN/mq
-
Qa (carico accidentale) = 2 KN/mq
3.2.Inserimento dei dati all'interno del foglio excel:
Somma carichi:
(2.65 KN/mq + 1.63 KN/mq + 2 KN/mq) x 3.86 m = 26.32 KN/m
Calcolo Momento massimo agente:
M = ql^2/8 = 26.32 x (4.8)2/8 = 75.80 KN*m
Inseriamo il valore della tensione di snervamento in base al tipo di acciaio adottato, in questo caso B450C, l'unico ammesso in zona sismica, con un fyk = 450 MPa.
Ricavo poi il valore della tensione di snervamento fD pari al rapporto tra fyk e il coefficiente di sicurezza utilizzato per le barre di acciaio, pari a 1.15.
fD = fyk/1.15 = 450/1.15 = 391.3 N/mmq
La fck rappresenta invece il valore caratteristico della resistenza a compressione del calcestruzzo, misurata su provini cilindrici, in base al tipo di calcestruzzo scelto.
C 40/50 => 40 N/mmq
Ponendo la base della trave pari a 30 cm, ottengo dal calcolo del dimensionamento un'altezza pari a 23.68, anche se sommando i 5 cm di copriferro l'altezza totale H della sezione arriva a misurare 28.68 cm. Arrotondo le dimensioni scegliendo una trave di 30 cm x 35 cm (evitando una sezione quadrata).
La classe di resistenza utilizzata per il cls è la C40/50, mentre per l'acciaio la B450C (normativa per zona sismica).
Sapendo che il Peso lineare P = 2.15 KN/m (determinato dal foglio excel), vado a sommarlo al carico totale Q (26.32 KN/mq + 2.15 KN/mq) => Q = 28.47 KN/m da
cui un H = 29.40 cm (entro le dimensioni calcolate). Il dimensionamento risulta corretto.


Sesta esercitazione:
Struttura reticolare spaziale
Le reticolari spaziali sono strutture rigide costruite per mezzo di incastri e secondo opportuni schemi geometrici (principalmente di tipo piramidale), consentendo la realizzazione di ampie campate nonostante il numero limitato di supporti.
Dopo aver disegnato la struttura in autocad possiamo importarla nel software di calcolo Sap 2000 per analizzarla.
Disegniamo quindi la struttura reticolare in autocad, uno schema realizzato a partire da una base quadrata, composta da tiranti, puntoni e diagonali, partendo dalla sua unità per realizzare poi una serie: assegnate le unità di misura in metri, attraverso una polilinea (e partendo dalle coordinate dello 0 assoluto 0,0,0 per facilitare l'esportazione su Sap) costruiamo un quadrato di 2m x 2m, lasciando uno dei quattro lati aperto per evitare di incollare più linee sullo stesso lato durante la serie
Per costruire la reticolare è necessario passare da una vista bidimensionale ad una tridimensionale

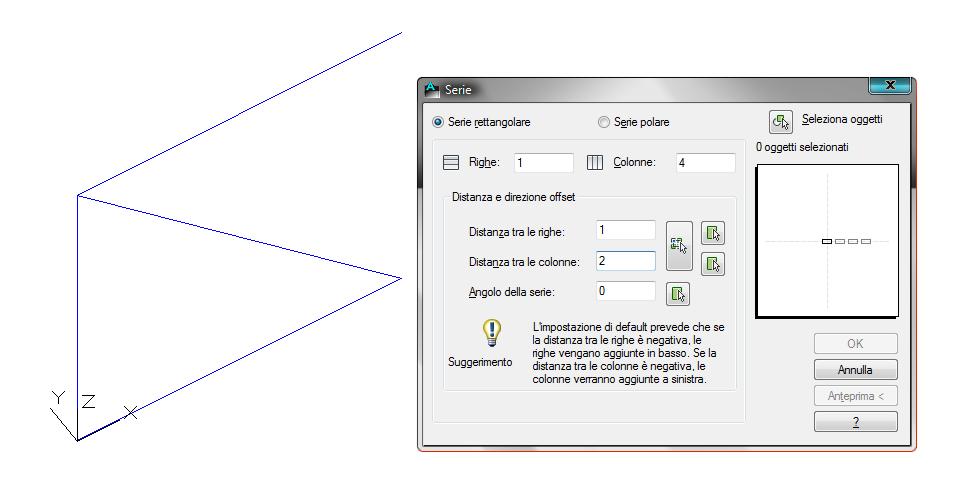
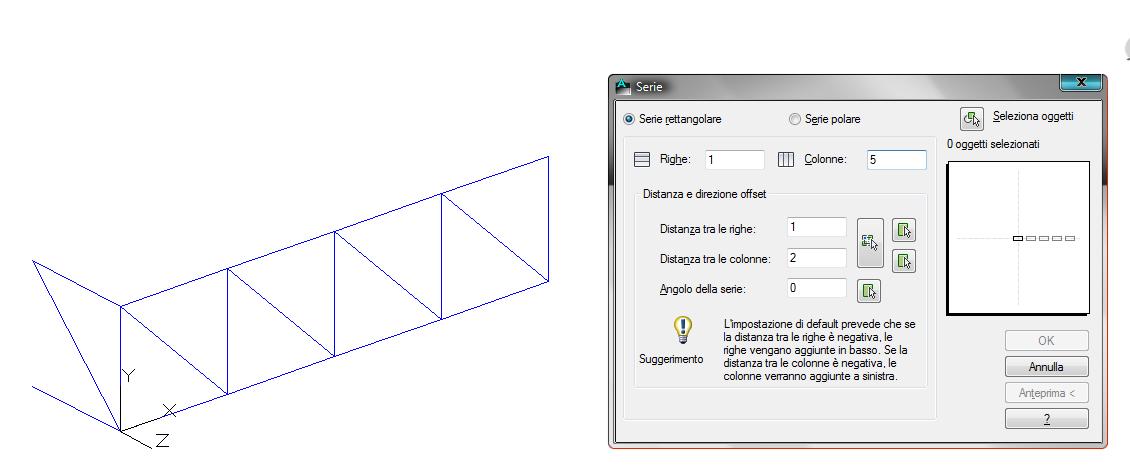
Cambiamo nuovamente vista e ruotiamo la figura disegnata nello spazio tridimensionale: a questo punto siamo in grado si disegnare nello spazio i moduli mancanti della reticolare. Selezioniamo le quattro aste e utilizziamo il comando "serie "(array), che ci permetterà di disegnare copie multiple della nostra unità di base attraverso una serie rettangolare. Per disegnare la nostra struttura occorre realizzare quattro copie lungo l'asse x: diciamo quindi ad arrey di realizzare quattro colonne distati 2 m l'una dall'altra (misura pari alla larghezza della nostra unità)
Chiudiamo ora la figura attraverso l'ultima asta verticale della serie
Nello stesso modo in cui abbiamo disegnato le quattro colonne lungo l'asse X disegniamo l'unità base (quadrato con diagonale, aperto sul quarto lato) lungo l'asse perpendicolare, facendo attenzione a non duplicare le aste verticali già disegnate nella prima serie. Inoltre, per disegnare le altre maglie della faccia laterale, bisogna cambiare il sistema di riferimento UCS poichè il piano su cui possiamo disegnare è quello xy.
Utilizziamo nuovamente il comando array per completare le aste mancanti
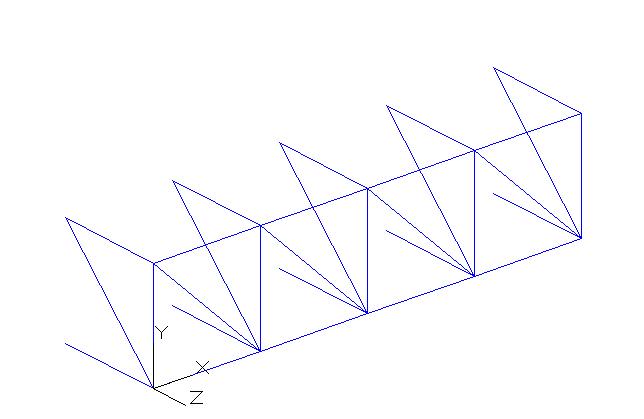
Completiamo ora la prima campata disegnando le aste oblique superiori e inferiori, lasciando ancora una volta il quarto lato aperto per poter effettuare una nuova serie (quella definitiva)
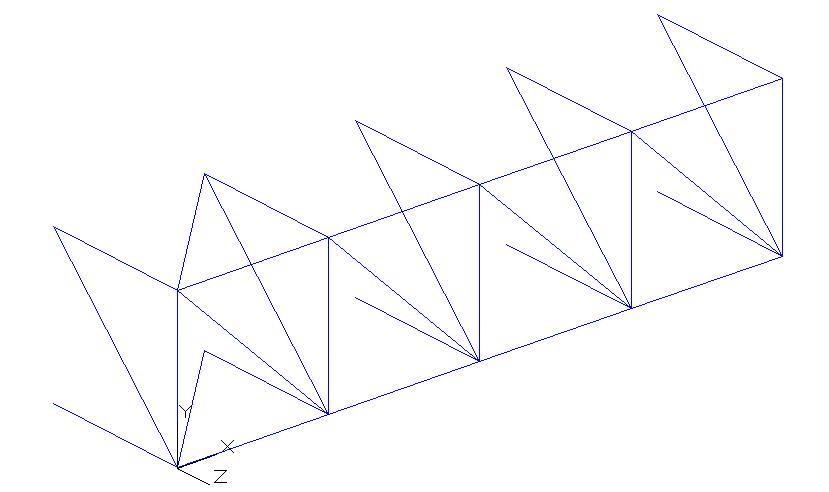
Completiamo quindi la struttura riprendendo ancora una volta il comando array che ci permetterà di disegnare copie multiple della nostra "riga" di base attraverso una serie rettangolare. Per disegnare la nostra struttura occorre realizzare sette copie lungo l'asse x: diciamo quindi ad arrey di realizzare sette colonne distati 2 m l'una dall'altra (misura pari alla larghezza della nostra unità)
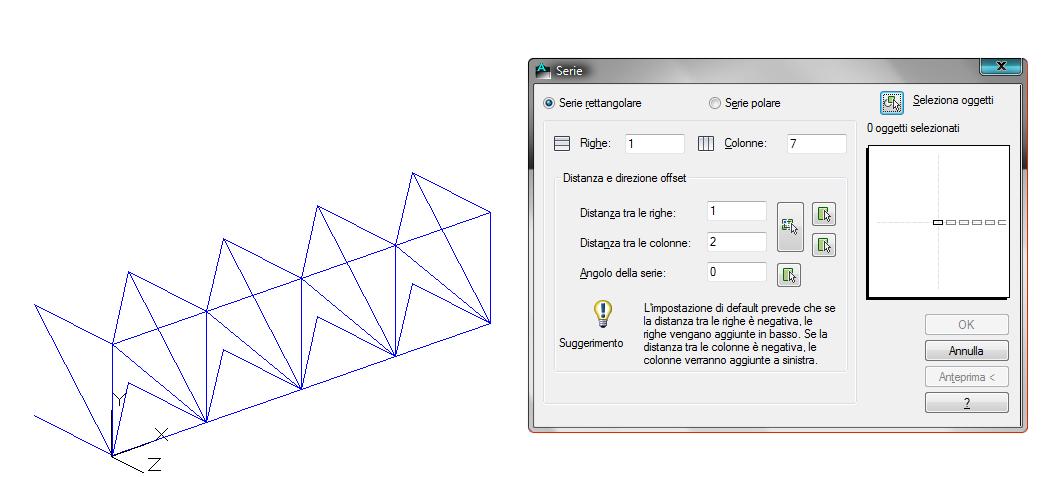
Otteniamo la reticolare, composta da quattro campate lungo l'asse Z e sette campate lungo l'asse X
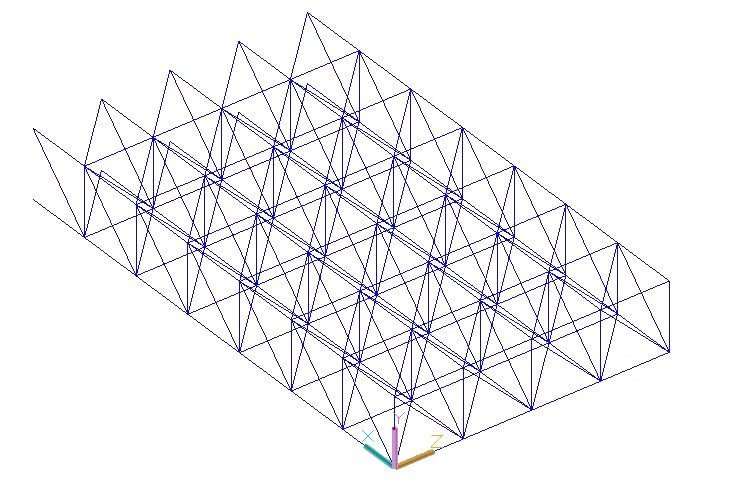
La struttura disegnata presenta una campata in più (sette invece di sei) in quanto risulta più semplice eliminare le aste della settima campata piuttosto che andare a disegnare le aste mancanti
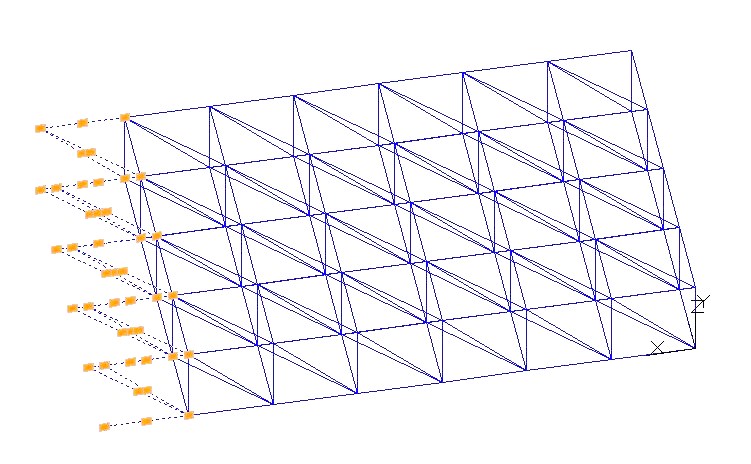
Eliminiamo quindi le aste dell'ultima campata così da ottenere la struttura definitiva (quattro campate x sei campate). Prima di passare su Sap, attraverso il comando "esplodi", separiamo le polilinee in modo da creare aste singole (processo necessario per il calcolo su Sap).
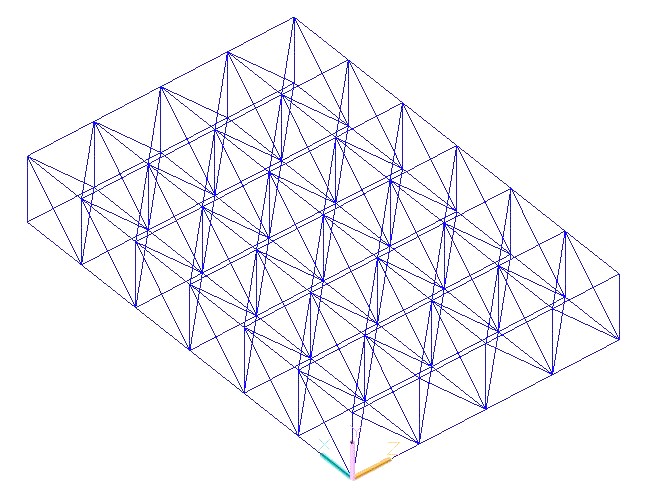
Salviamo la struttura e importiamo il modello in formato .dxf Autocad 2000 sul software di calcolo SAP 2000. Impostiamo le unità di misura (KN, m, C) e attraverso il comando "import" inseriamo il modello .dxf di Autocad. Selezionando i quattro nodi alle estremità della struttura reticolare possiamo assegnare i vincoli (quattro cerniere esterne)
Seleziono i nodi => assign => joint => restraints => translation 1 e 2 (ovvero impedisce la traslazione verticale e orizzontale)
Essendo una struttura reticolare mi assicuro che le aste siano soggette soltanto a sforzo normale, ponendo pari a zero il momento sia all'inizio che alla fine di ogni singola asta, andando a creare cerniere interne di collegamento
Seleziono i nodi => assign => frame => releases/partial fixity => moment 2-2 e moment 3-3 start-end
Prima di analizzare la struttura definisco e assegno alle aste una sezione e un materiale: in questo caso acciaio e sezione tubolare. Inoltre definisco un nuovo carico concentrato, pari a 40 KN (in questo caso -40, in quanto in direzione opposta a quella dell'asse verticale Z), assegnandolo ai soli nodi superiori. Una volta assegnati i carichi possiamo lanciare l'analisi, limitandola alle sole forze concentrate inserite nell'ultimo passaggio.
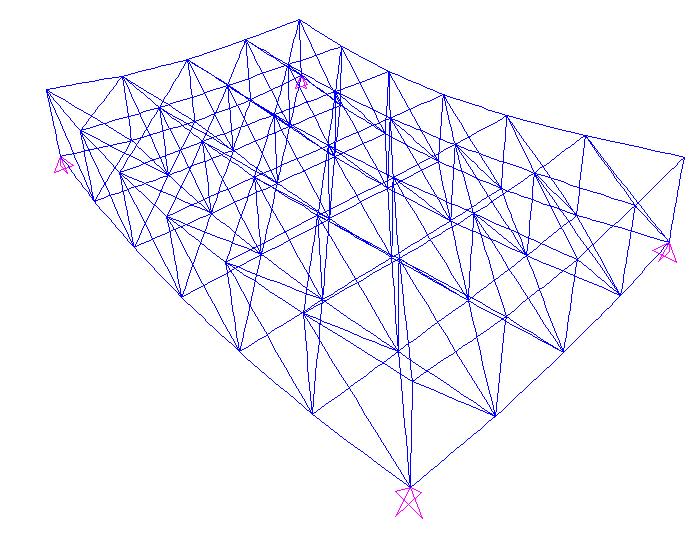
Ottengo la struttura reticolare spaziale deformata sotto l'azione dei carichi esterni: le aste sono sollecitate solamente a sforzo assiale (i diagrammi del momento e del taglio sono infatti pari a zero). Dalla vista 3d possiamo vedere come varia lo sforzo assiale nelle aste della struttura
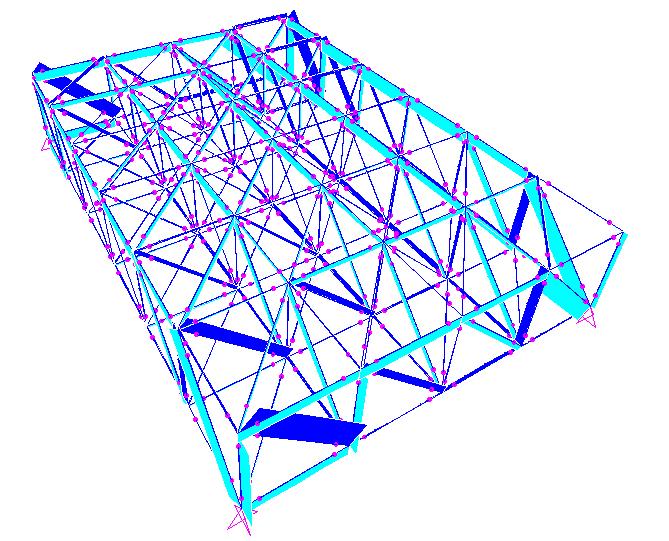
Variazione dello sforzo normale nel piano YZ
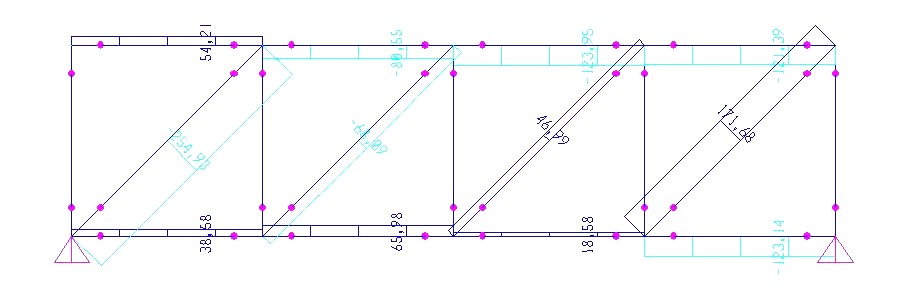
Per visualizzare i risultati dello sforzo normale sulle aste
Display => Show table => analysis results => element output
Otteniamo così lo sforzo normale di ogni singola asta
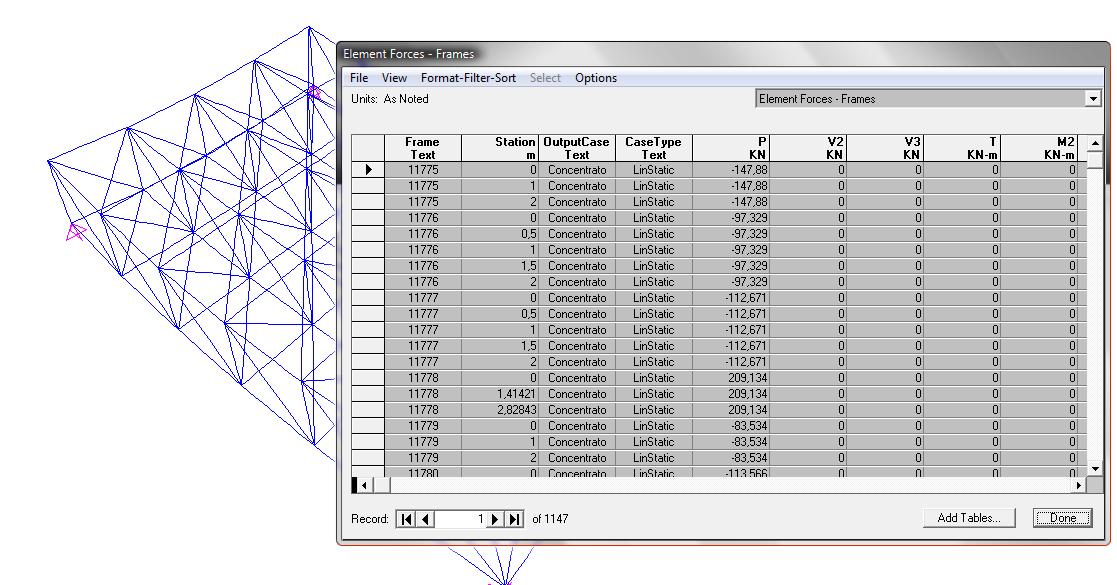
dopo aver esportato la tabella su excel (così da poter ordinare in maniera più veloce i valori, dal più grande al più piccolo o viceversa) possiamo individuare facilmente l'asta maggiormente sollecitata a trazione e a compressione
File => Export all tables => to excel
Progetto asta maggiormente sollecitata a trazione
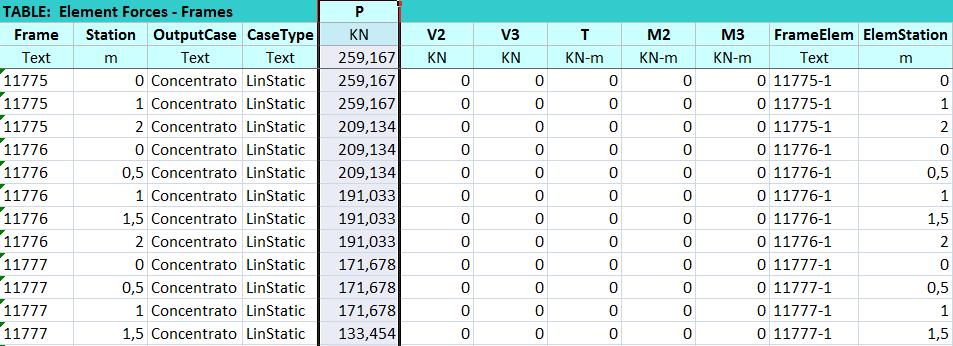
All' asta maggiormente sollecitata a trazione corrisponde uno sforzo assiale N = 259,167 KN. Mi calcolo quindi l'area minima che resiste a trazione tramite la formula
fD = N/A => A = N/fD
Scegliendo un acciaio Fe360S235 posso calcolarmi la tensione di progetto
fD = fyk/1.05 = 223.81 N/mmq
A = N/fd = 259167 N / 223.81 N/mmq = 1157.9 mm2 = 11.58 cm2
Avendo calcolato l'area minima necessaria vado a scegliere le sezioni disponibili per i tubolari e scelgo il profilo con l'area immediatamente superiore a 11.58 cm2

Scelgo il profilato con una sezione pari a 12.5 cm2.
Verifica asta maggiormente sollecitata a trazione
Per quanto riguarda l'asta tesa posso effettuare una verifica a resistenza del profilo scelto: la sezione risulta verificata se il risultato del quoziente tra lo sforzo normale e l'area del nuovo profilo risulta essere inferiore o al limite uguale a fD.
259167 N / 1250 mmq = 207.3 N/mmq < 223.81N/mmq
Il profilo scelto è verificato.
Progetto asta maggiormente sollecitata a compressione
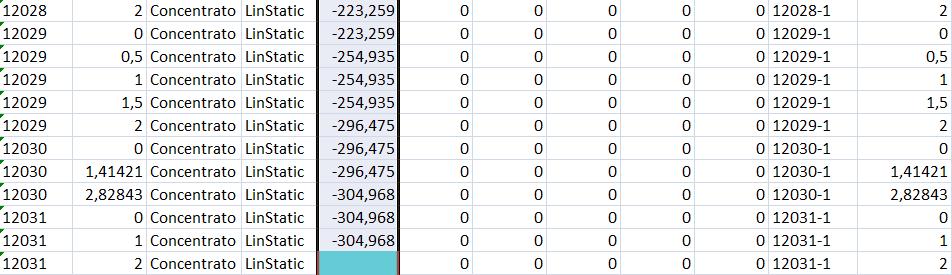
All' asta maggiormente sollecitata a compressione corrisponde uno sforzo assiale N = 304.968 KN. Mi calcolo quindi l'area minima che resiste a trazione tramite la formula
fD = N/A => A = N/fD
Scegliendo un acciaio Fe360S235 posso calcolarmi la tensione di progetto
fD = fyk/1.05 = 223.81 N/mmq
A = N/fd = 304968 N / 223.81 N/mmq = 1362.6 mm2 = 13.62 cm2
Avendo calcolato l'area minima necessaria vado a scegliere le sezioni disponibili per i tubolari e scelgo il profilo con l'area immediatamente superiore a 13.62 cm2
Scelgo il profilato con una sezione pari a 13.9 cm2.
Verifica asta maggiormente sollecitata a compressione
Per quanto riguarda l'asta compressa posso effettuare tre tipi di verifica del profilo scelto: verifica a resistenza, a stabilità e a snellezza. L'asta compressa è infatti soggetta al cosiddetto "carico assiale di punta" (o carico critico euleriano), un improvviso collasso di un membro strutturale soggetto ad intensi sforzi di compressione: una struttura snella (Valore elevato del rapporto h/l), ricevendo sollecitazioni di questo tipo, tende ad incurvarsi fino al punto di rottura
Verifica a resistenza:
la sezione risulta verificata se il risultato del quoziente tra lo sforzo normale e l'area del nuovo profilo risulta essere inferiore o al limite uguale a fD.
304968 N / 1390 mmq = 219.4 N/mmq < 223.81N/mmq
Il profilo scelto risulta verificato a resistenza.
Verifica a snellezza:
La snellezza dell'asta è definita dalla formula
λ = l0 /ρ
con l0 lunghezza libera d'inflessione (distanza tra due punti di flesso successivi della deformata flessionale) e ρ il raggio d'inerzia della sezione retta nel piano di inflessione. La normativa impone limiti alla snellezza massima negli elementi in cui possa essere presente uno sforzo normale di compressione:
λmax ≤ 200 per le membrature principali
λmax ≤ 250 per le membrature secondarie
Lo schema dell'asta incernierata porta ad avere un valore di lo= l, mentre il raggio d'inerzia (desumibile dalle tabelle) è pari a 3,9 cm.
=> λ = l0 /ρ = 1 x 282 cm/3,9 cm = 72.3 < 200
Il profilo scelto risulta verificato a snellezza.
Verifica a stabilità:
Uno degli aspetti principali da tenere presente nella progettazione delle strutture in acciaio è quello legato ai problemi di stabilità dell'equilibrio. L'elevata resistenza dell'acciaio consente infatti, a parità di sollecitazioni, di adottare per gli elementi strutturali sezioni molto ridotte: la snellezza può quindi portare a situazioni di instabilità.
Nd ≤Nbrd
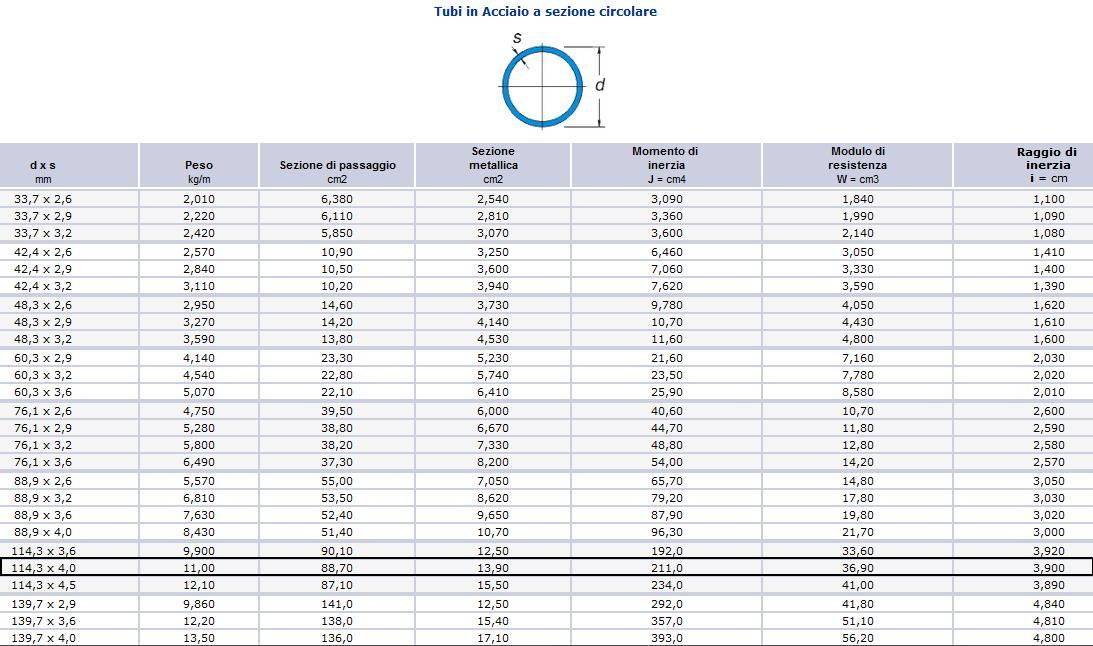
Per prima cosa mi calcolo il carico critico euleriano, ovvero il più piccolo valore del carico assiale per il quale la trave caricata di punta può assumere una configurazione di equlibrio diversa dalla configurazione "indeformata".
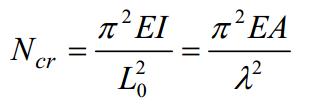
E = 210000 N/mmq
I = 211 cm4 = 2110000 mm4
Lo = 282 cm = 2820 mm
=> Ncr = (3.14)2 x 210000 N/mm2 x 2110000 mm4 / (2820 mm)2 = 549367 N = 549 KN
Ora la snellezza adimensionale:
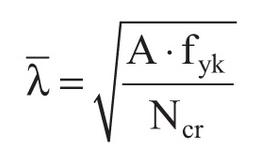
A = 13.9 cm2 = 1390 mm2
fyk = 235 N/mmq
Ncr = 549367 N
=> √1390 mm2 x 235 N/mm2 / 549367 N = 0.77
Il coefficiente χ, che dipende dal tipo di sezione e dal tipo di acciaio impiegato: si desume, in funzione di appropriati valori della snellezza adimensionale, dalla seguente formula:

dove Φ = 0.5 [1 + α (λ - 0.2) + λ2 ], mentre α è il fattore di imperfezione (ricavabile dalle tabelle della normativa)
=> Φ = 0.5[1 + 0.21 ( 0.77 - 0.2) + (0.77)2] = 0.8563
=> X = 1 / 0.8563 + √(0.8563)2 - (0.77)2 = 0.815<1
Infine, Nbrd
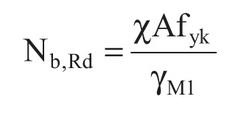
X = 0.815
A = 13.9 cm2 = 1390 mm2
=> Nbrd = 0.815 x 1390 mm2 x 235 N/mm2 / 1.05 = 253542 N = 253 KN < 549 KN
Il profilo scelto risulta verificato a compressione.
Settima esercitazione:
Ripartizione forze sismiche
(Svolto con Yanbin Zhu, Andrea Muglia, Flavia Valdarnini)
Questa esercitazione ci permetterà di calcolare come, in presenza di forze sismiche, debbano essere disposti i controventi all'interno di una struttura: i controventi sono infatti dei particolari vincoli che impediscono alla struttura di effettuare uno spostamento o una rotazione dovuta ad una forza orizzontale.
Chiamiamo Centro di Massa il punto in cui si considera concentrata la forza derivante dall'azione sismica: planimetricamente la posizione del baricentro dipende dalla forma geometrica dell'impalcato e viene determinata con i metodi forniti dalla geometria delle masse.
Si definisce invece Centro elastico dell'impalcato il baricentro delle rigidezze degli elementi resistenti verticali che si oppongono all'azione sismica orizzontale: di conseguenza, il baricentro delle rigidezze deve essere determinato attraverso la rigidezza dei telai.
Se il Centro di Massa e il Centro delle Rigidezze coincidono, il movimento teorico del piano indotto dal sisma sarà di pura traslazione.
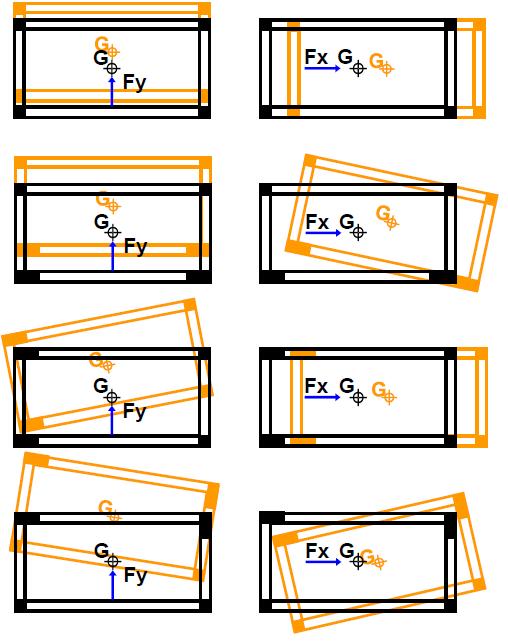
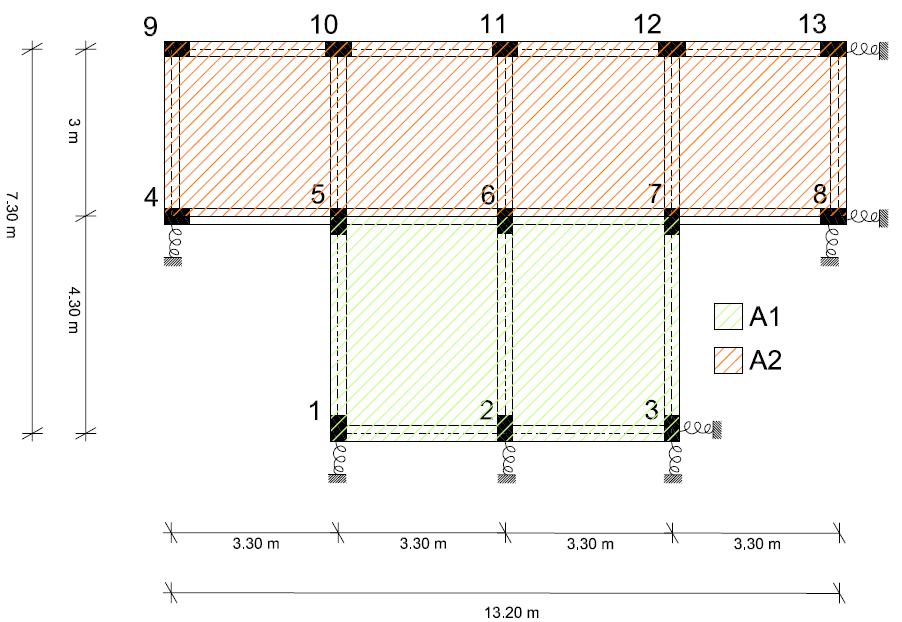
L'impalcato in esame è una struttura simmetrica composta da cinque controventi verticali e tre controventi orizzontali.
.jpg)
La prima ipotesi da fare è che questa struttura sia composta da telai Shear Type, ovvero un telaio con nodi ad incastro e con una trave considerata infinitamente rigida flessionalmente rispetto ai pilastri (che non si deformano né a compressione né a trazione o, comunque, in maniera trascurabile).
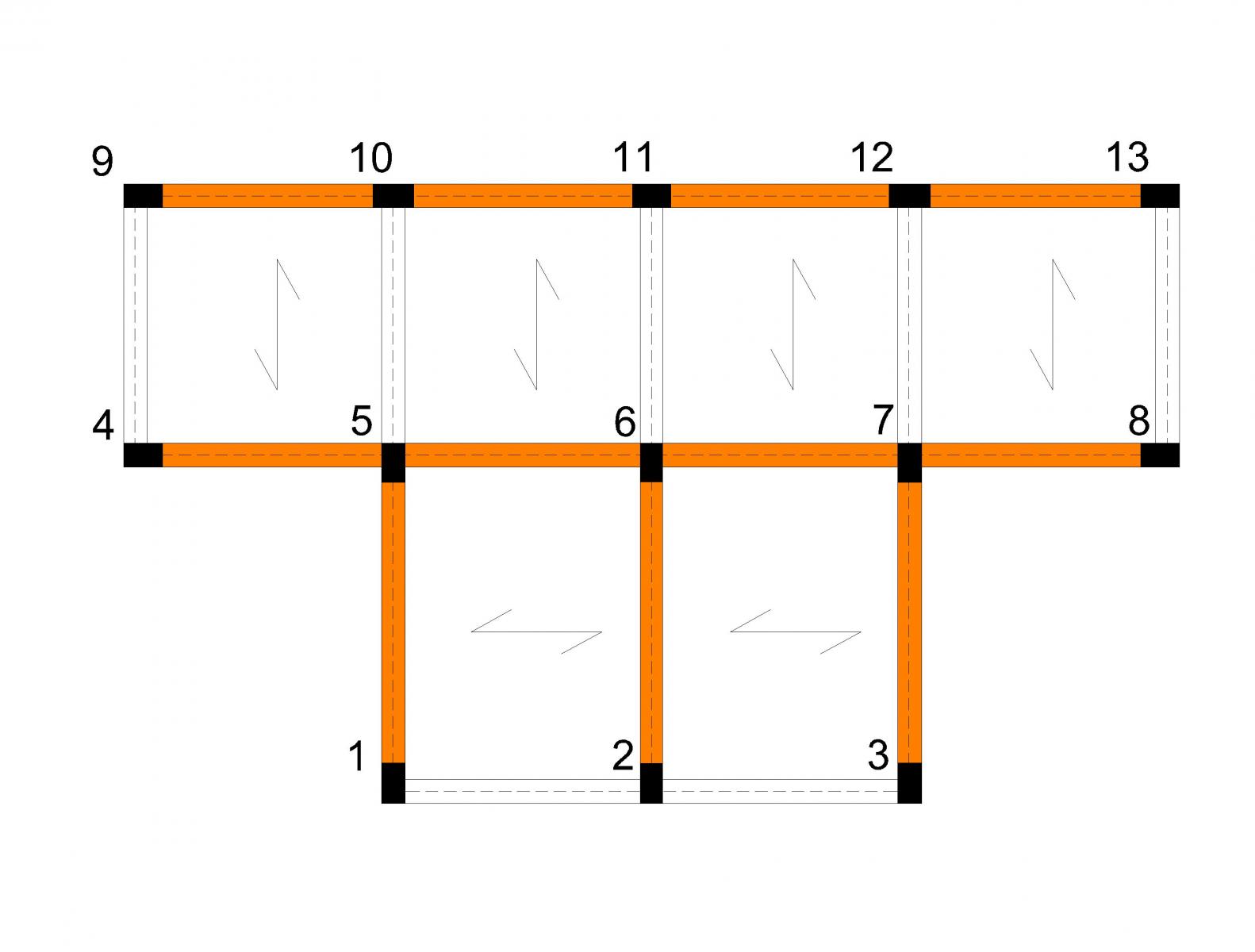
Le travi arancioni sono quelle che portano il solaio. In questo passaggio cerchiamo di capire se l'orientamento dei 13 pilastri (30x50 cm) risulta corretto. Partendo dal calcolo dei differenti momenti d'Inerzia (lungo gli assi x e y) di una sezione rettangolare e ricordando che i pilastri che portano il solaio si inflettono maggiormente (avremo bisogno, quindi, di un maggiore momento d'inerzia nella direzione in cui questi pilastri collegano le travi portanti), disponiamo i pilastri in base alla tessitura del solaio. Nei punti in cui si incontrano tre travi portanti, in questo caso i pilastri 5,6,7, i pilastri sono orientati nella direzione della trave portante più lunga.
Prima ipotesi: impalcato in c.a.
Esaminando la struttura con la prima tecnologia (c.a.) andiamo a scrivere alcuni dati che andranno inseriti successivamente nella tabella.
-
Ix = 1/12 x b x h3 = 1/12 x 50 x 303 = 112500 cm4
-
Iy = 1/12 x h3 x b = 1/12 x 30 x 503 = 312500 cm4
-
E = 21000 N/mmq
-
h = 4m
I controventi, avendo un comportamento elastico, possono essere paragonati a delle molle: la legge di Hooke, F = Ks, afferma che l'allungamento di un corpo elastico è direttamente proporzionale alla forza ad esso applicata. Nel nostro caso K rappresenta la rigidezza del controvento.
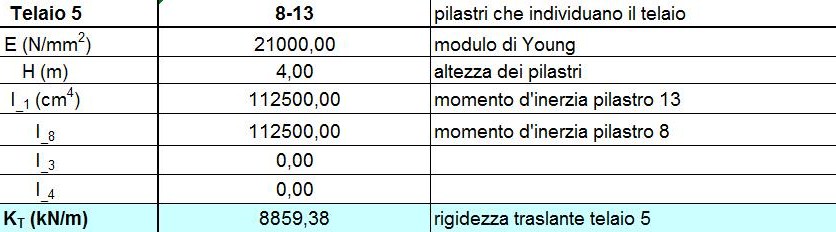
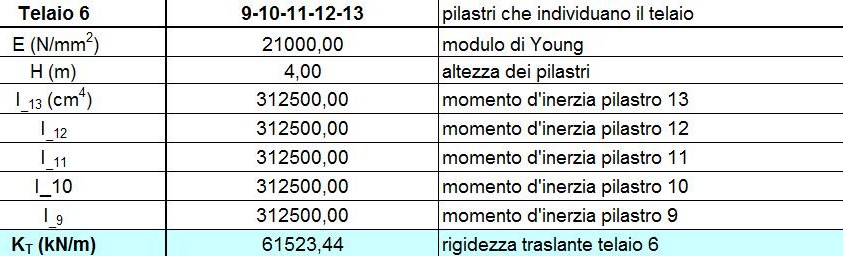
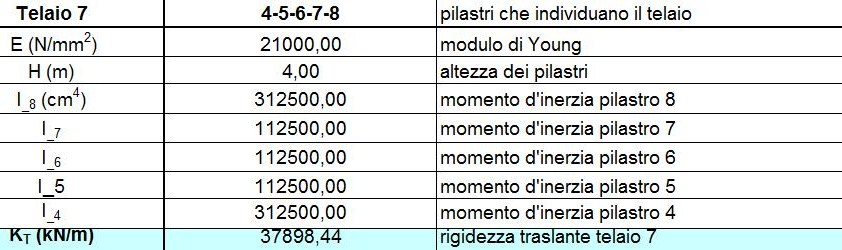
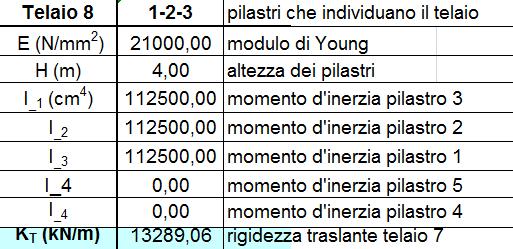
Step 1: calcolo delle rigidezze traslanti dei controventi dell'edificio
Tramite questo passaggio calcoliamo le rigidezze traslanti di ogni singolo controvento




Step 2: tabella sinottica controventi e distanze
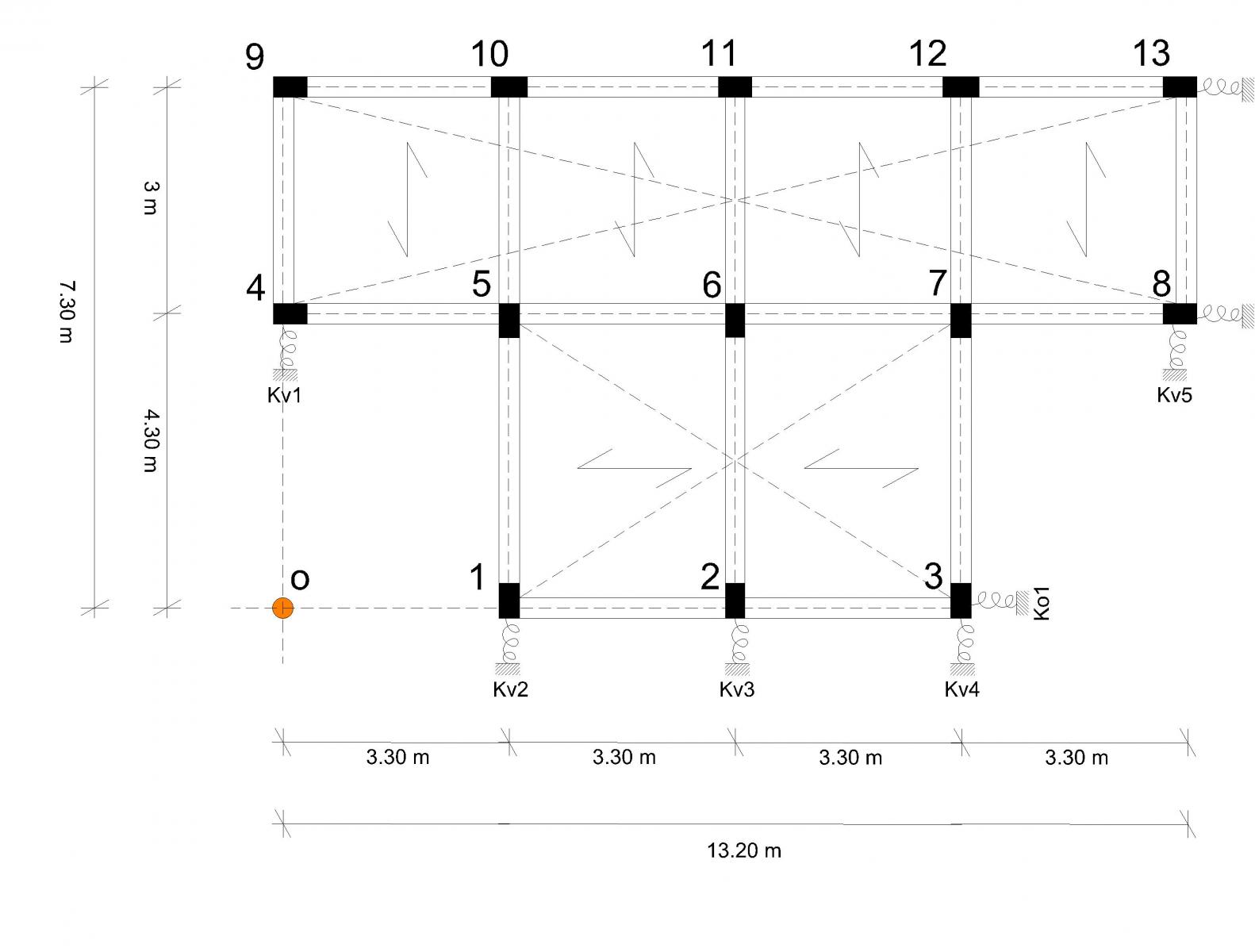
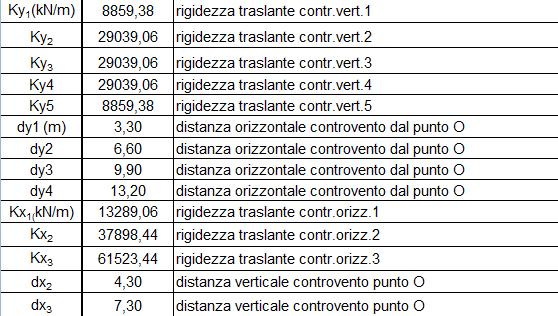
Calcoliamo ora le ditanze verticali (dv) e orizzontali (do) dei controventi rispetto al punto scelto O, origine del nostro sistema di riferimento.
Step 3: calcolo del centro di massa
Per calcolare il centro di massa G, punto in cui risulta applicata la forza sismica, dividiamo la struttura in due grandi rettangoli, di area 28.38 m2 e 39.60 m2. Inseriamo nella tabella le coordinate X e Y dei baricentri delle due aree, andando così a calcolarci l'area totale e, soprattutto, le coordinate X e Y del centro d'area dell'intero impalcato tramite la formula:
Xg = A1 x Xg1 + A2 x Xg2 / A1+A2
Yg = A1 x Yg1 + A2 x Yg2 / A1+A2

Step 4: calcolo del centro di rigidezze e delle rigidezze globali
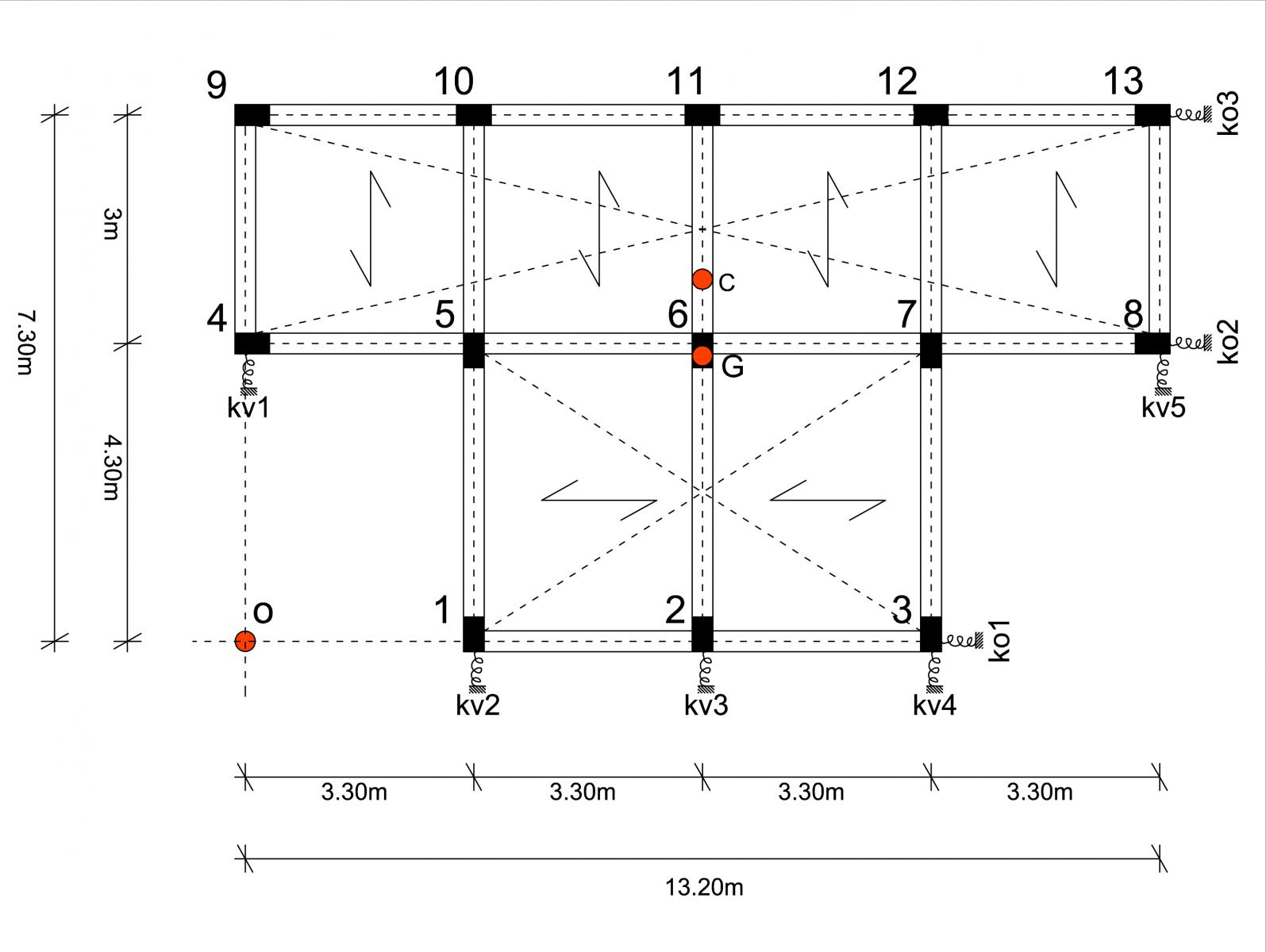
In questo passaggio tramite il foglio di calcolo Excel ci calcoliamo il centro delle rigidezze.
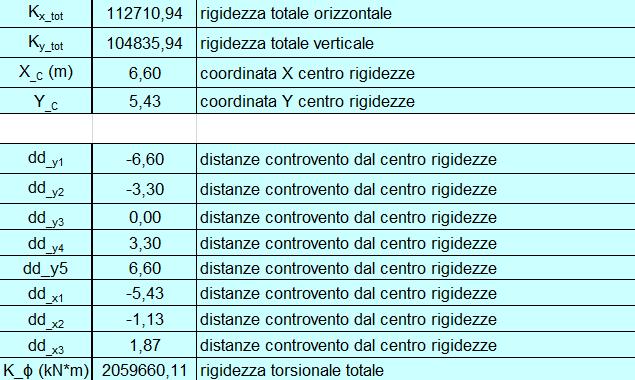
-
Vengono sommate separatemente le rigidezze dei controventi verticali e orizzontali
-
Si calcola la coordinata Xc del centro delle rigidezze tramite la formula:
Kv2 x dv2 + Kv3 x dv3 + Kv4 x dv4 + Kv5 x dv5/ Kv tot
-
Si calcola la coordinata Yc del centro delle rigidezze tramite la formula:
K02 x d02 + K03 x d03 + K04 x d04 + K05 x d05/ K0 tot
-
Si calcolano le distanze di ogni controvento dal centro delle rigidezze.
-
Si calcola la rigidezza torsionale totale tramite il prodotto tra la sommatoria delle rigidezze e la distanza al quadrato di ogni rigidezza.
KΦ= Σi Ki x ddi2
Step 5: analisi dei carichi sismici
Inseriamo nella tabella il valore dei carichi, dividendoli in strutturali, permanenti, accidentali e li moltiplichiamo per l'area totale dell'impalcato, calcolandoci così il carico permanente totale e il carico accidentale totale.
Il totale delle due classi di carico viene poi moltiplicato per un coefficiente di contemporaneità y (pari a 0.8): si ottiene il valore del peso sismico.
A sua volta il peso sismico viene moltiplicato ad un coefficiente di intensità sismica: nella struttura in analisi la Forza sismica orizzontale è pari a 38.07 KN.
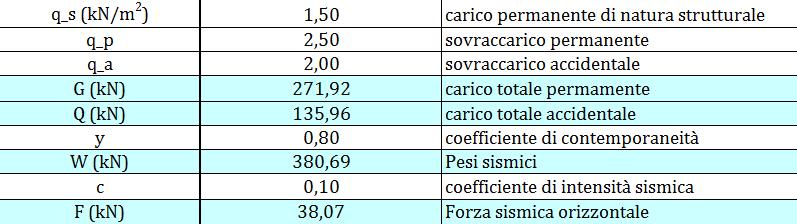
Step 6-7: ripartizione forza sismica lungo x e lungo y
Tramite questo ultimo passaggio verifichiamo la risposta della struttura alla forza sismica esterna lungo due direzioni perpendicolari tra loro, ovvero come si ripartisce la forza F, disposta lungo l'asse X o Y alternativamente, lungo i controventi della struttura.
Dallo schema precedente possiamo vedere come, lungo l'asse Y, il centro di massa e il centro delle rigidezze coincidano: di conseguenza, alla presenza di una forza sismica verticale l'impalcato è soggetto a traslazione.
Nel caso opposto, invece, la presenza di un braccio che separa i due centri farà ruotare in maniera antioraria l'intero impalcato: come si può vedere dal disegno sottostante, la forza sollecitante Fi (sisma) e la forza resistente V trovano condizione di equilibrio solo tramite un momento torcente M.
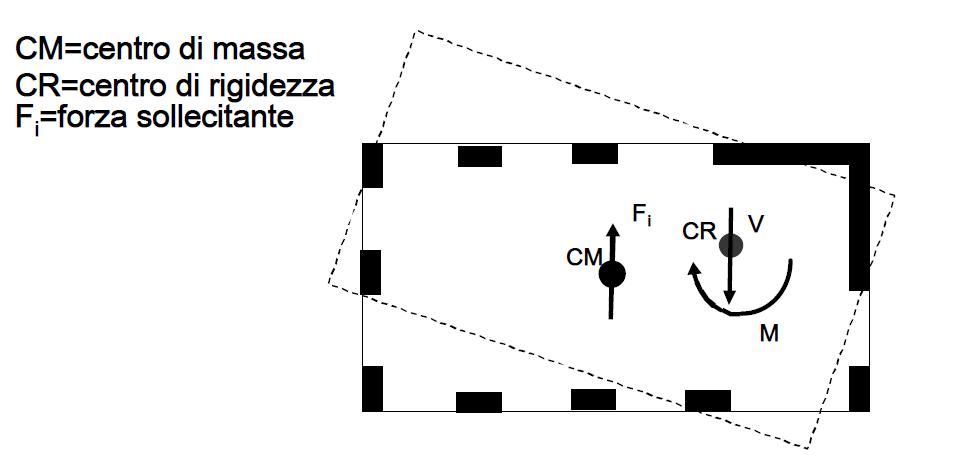
Esempio di un centro di massa e di rigidezze non coincidenti ( immagini tratte dal dipartimento di Ing. Strutturale e Geotecnica di Verbania).

Il Momento torcente viene calcolato tramite il prodotto della forza sismica F e della distanza tra i due baricentri (Forza x Braccio).
La traslazione si calcola, invece, dividendo la forza sismica per la rigidezza totale, mentre la rotazione dell'impalcato si ottiene dividendo la Forza F per la rigidezza torsionale totale, calcolata in precedenza.
Tramite i valori della traslazione e della rotazione dell'impalcato possiamo calcolare la forza sismica che si riprtisce su ogni controvento su entrambe le direzioni X e Y.

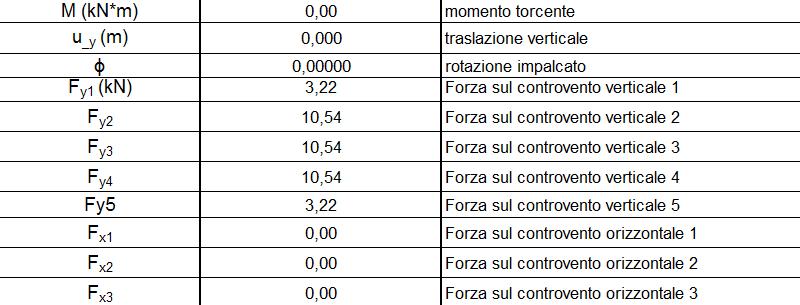
Commenti recenti