ESERCITAZIONE 2 - reticolare spaziale
RETICOLARE SPAZIALE
Ipotizzando uno schema semplice, un solaio piano basato su un telaio a cubi controventati, utilizziamo il software SAP2000 per ottenere informazioni sulle sollecitazioni a cui sarebbe sottoposta la struttura (e per imparare a sfruttare il software per configurazioni più complesse).
Lo studio delle strutture reticolari attraverso questo strumento è particolarmente utile perchè permette di avere informazioni su ogni singolo componente di telai composti da un grande numero elementi.
L’uso combinato di questo software e di un foglio di calcolo dove verranno inseriti i valori ottenuti, manipolati tramite le equazioni della meccanica, ci permette di dimensionare ed ingegnerizzare i profili da utilizzare per la struttura.
Iniziamo con la parte inerente al sofware.
Partiamo scegliendo lo schema base che utilizzeremo per la parte di modellazione e impostiamo le unità di misura. Nel nostro caso GRID ONLY e kN,m,C.
Una volta selezionata si aprirà un menù di interfaccia che ci permette di impostare le caratteristiche geometriche e dimensionali della griglia di riferimento che utilizzeremo per modellare il nostro solaio
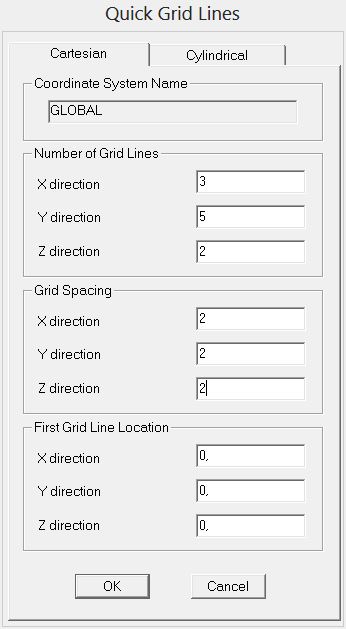
Per questo semplice esempio impostiamo una griglia con 3 linee sull’asse X, 5 sull’asse y e 2 sull’asse z (ipotizzando che sia una struttura ad un solo livello). La distanza su tutti e tre gli assi è di 2m.
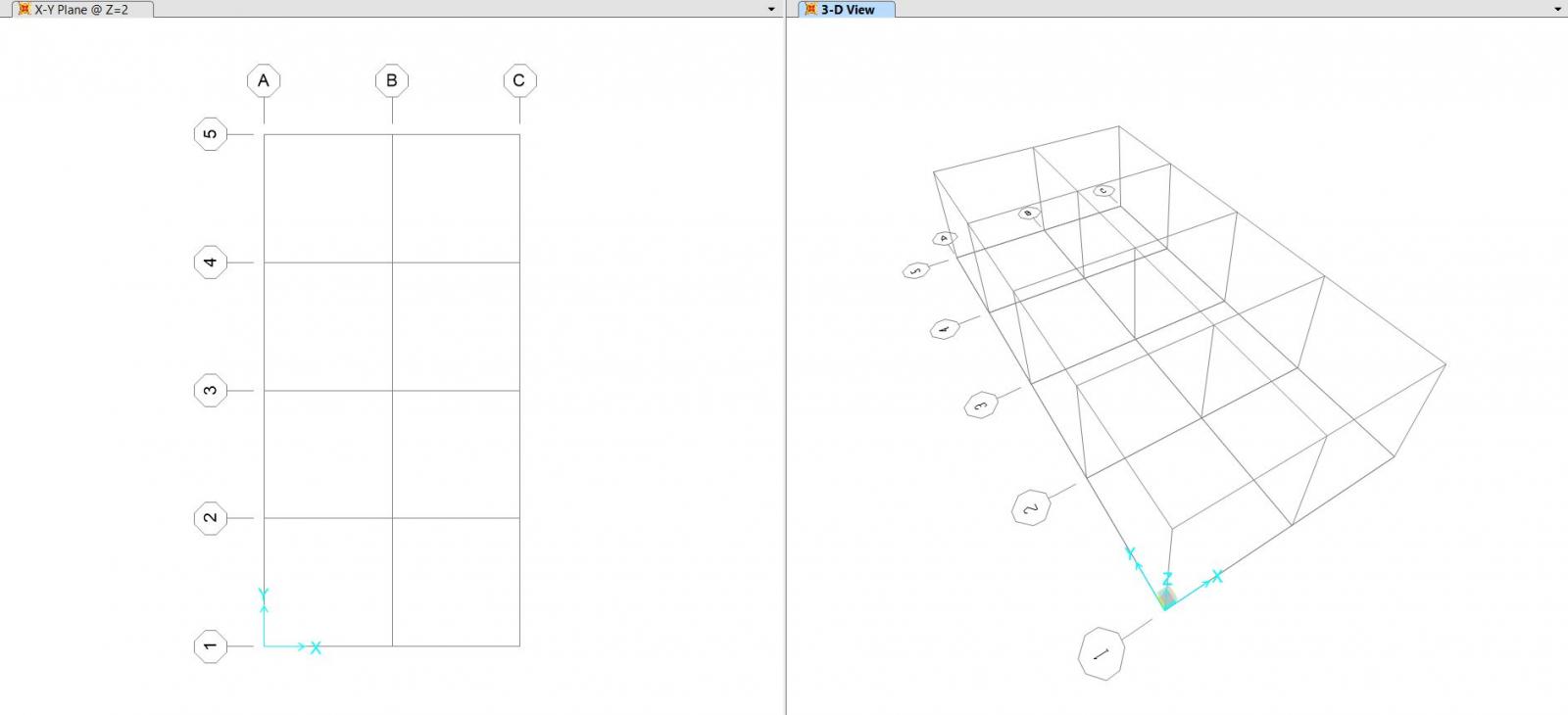
Il software ci mostra una vista bidimensionale e una tridimensionale della griglia che possiamo ora utilizzare come base di modellazione della nostra struttura.
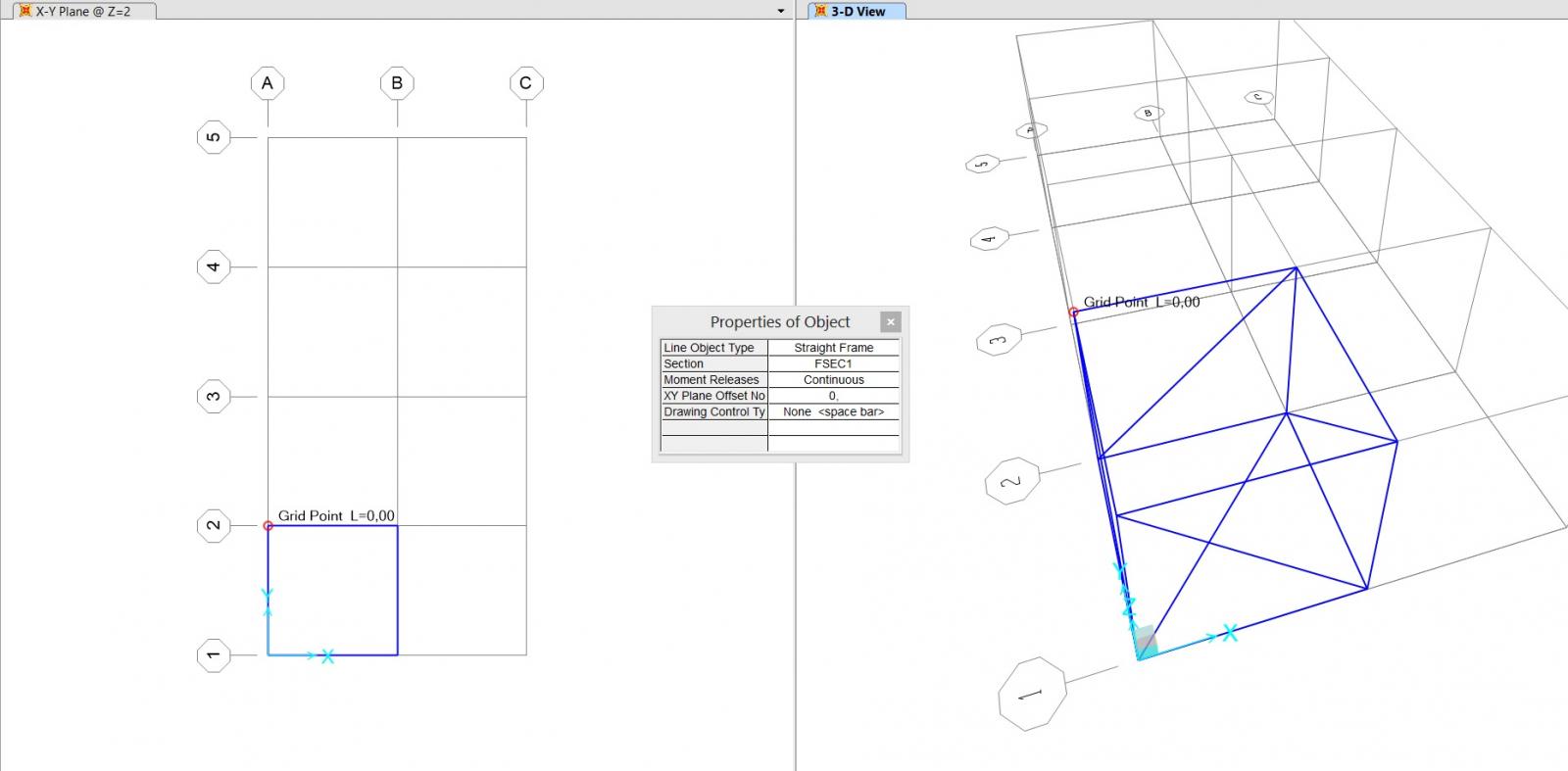
utilizzando lo strumento di disegno draw frame/cable impostiamo il primo elemento del telaio:
un cubo con tutti i lati controventati da un elemento diagonale.
per terminare la struttura utilizziamo lo strumento copia e incolla per replicare l’elemento base il numero delle volte necessario a riempire tutti i campi della griglia
sull’asse X
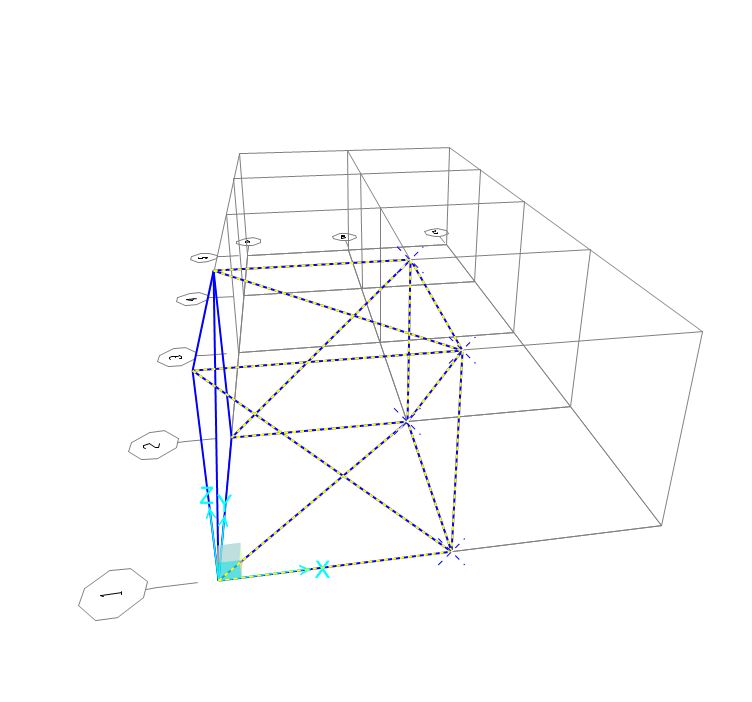
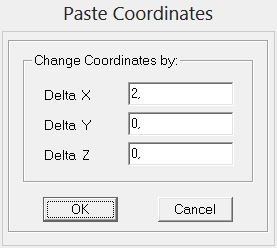
seleziono gli elementi da copiare e imposto l’offset rispetto al punto d’origine (in questo caso 2m).
Ripeto rispetto ad y.
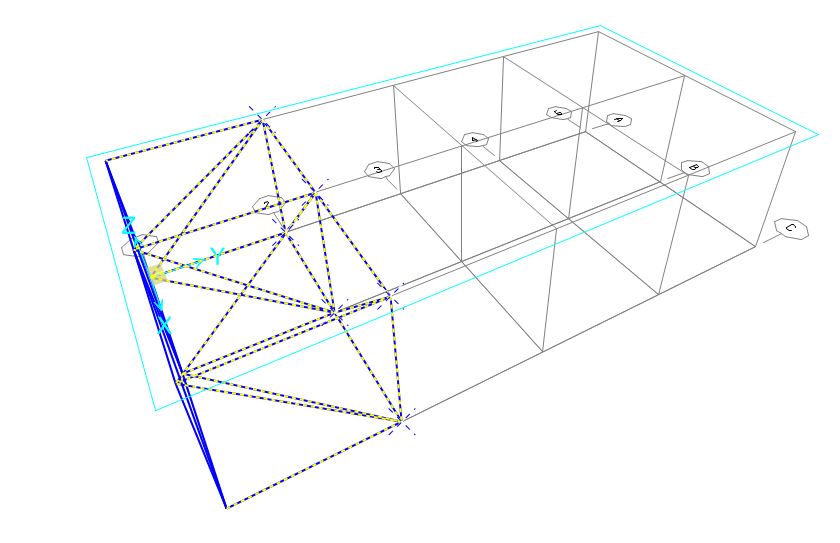
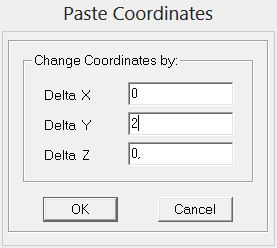
Otteniamo così la struttura completa.
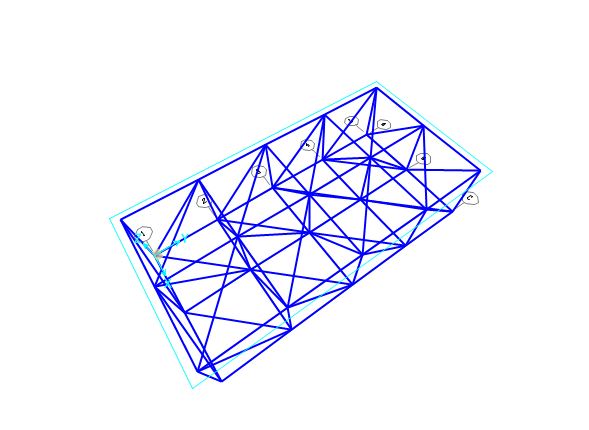
Per verificare che non ci siano sovrapposizioni, o meglio elementi duplicati, utilizzo il comando MERGE DUPLICATES
Come sappiamo tutte le aste di una struttura reticolare lavorano trasmettendo solo le sollecitazioni assiali, ed i nodi sono a tutti gli effetti cerniere interne.
Di conseguenza utilizziamo il comando FRAME RELEASES/PARTIAL FIXITY, impostando che tutte le aste della struttura non trasmettano momento.
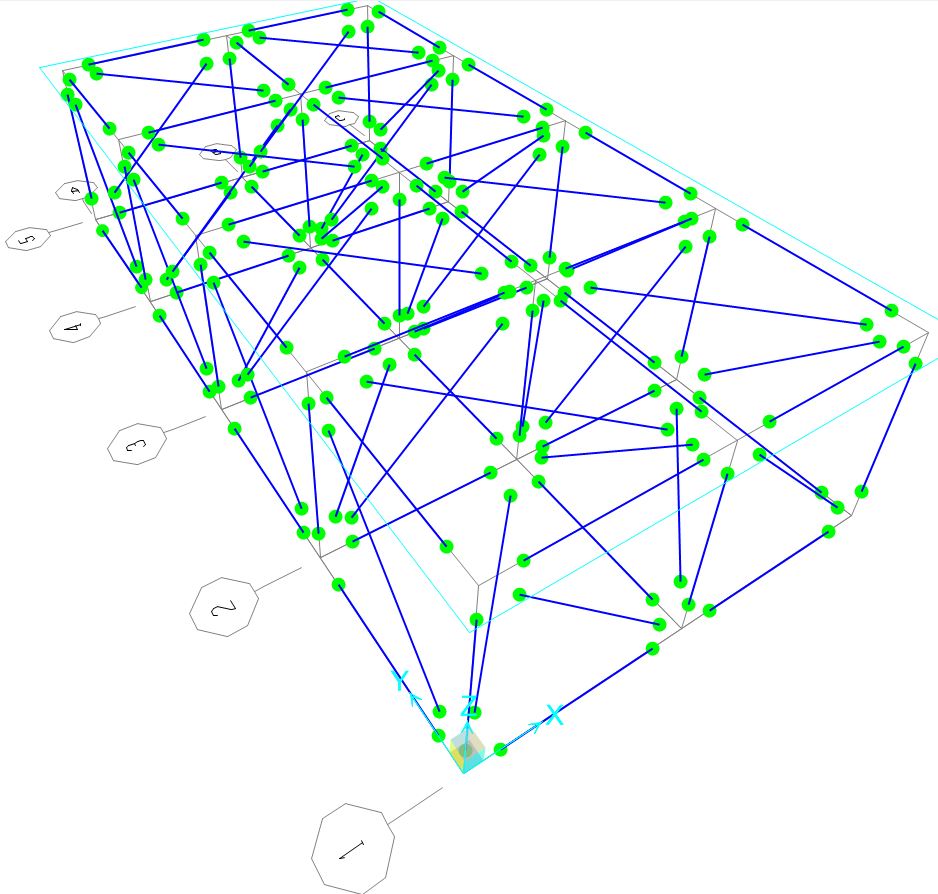
Il prossimo passo sarà definire la sezione e le caratteristiche meccaniche dei profili che compongono la struttura.
Selezionando il comando Frame section dal menù a tendina Define ci apparirà questa finestra di dialogo
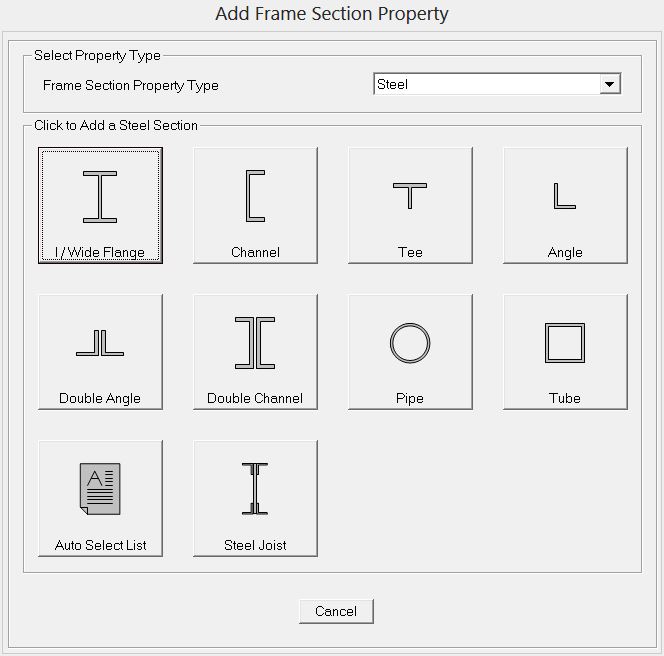
Scegliamo un profilo a sezione circolare cava Pipe e il materiale (steel).
nella finestra successiva potremo definire le caratteristiche del nostro profilato
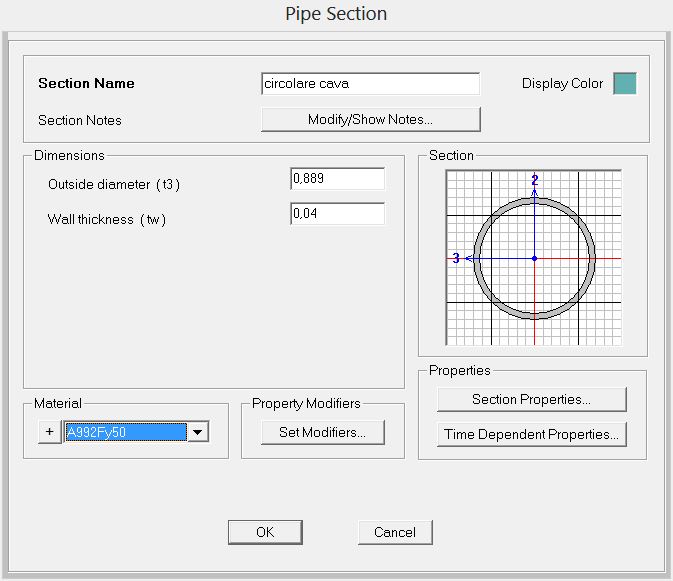
Attribuiamo un nome alla nuova sezione e una volta impostate le dimensioni e la classe di resistenza dell’acciaio (nel nostro caso quella si default: A992Fy50) possiamo assegnarla agli elementi moedellati.
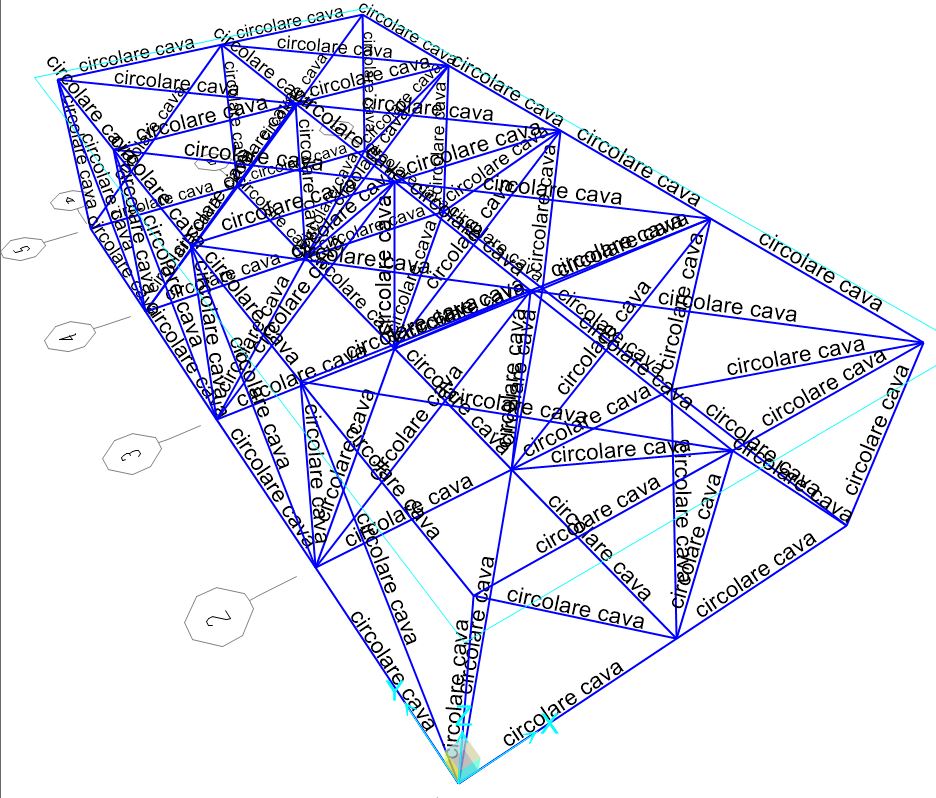
Avremo conferma del buon esito dell’operazione dalla presenza del nome assegnato lungo la linea che rappresenta l’asta.
Dobbiamo ora definire i vincoli esterni della struttura: selezioniamo i quattro vertici esterni e impostiamo le equazioni cinematiche dei vincoli. Nel nostro caso imposteremo quattro cerniere che come sappiamo bloccano le traslazioni sulle tre direzioni ma consentono le rotazioni.
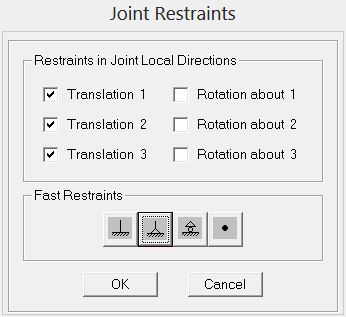
Ora dobbiamo definire il carico a cui è sottoposta la struttura, impostando una forza f
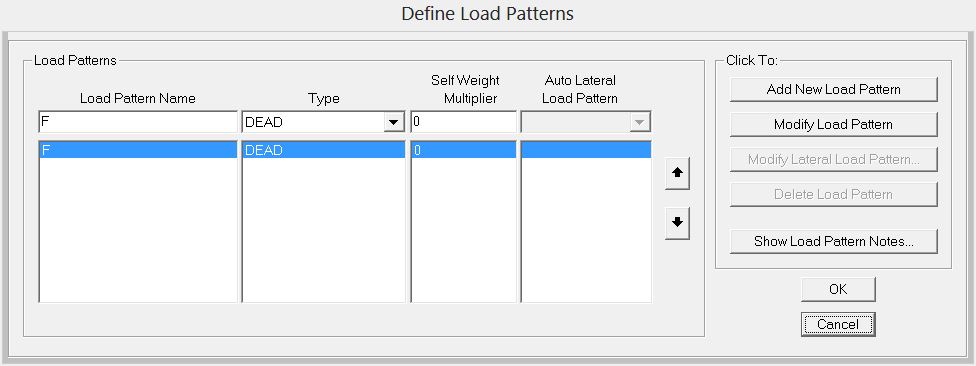
dopodichè assegnamo un valore in kN alla forza: in questo caso 100 kN, con il segno meno perchè rivolta verso il basso
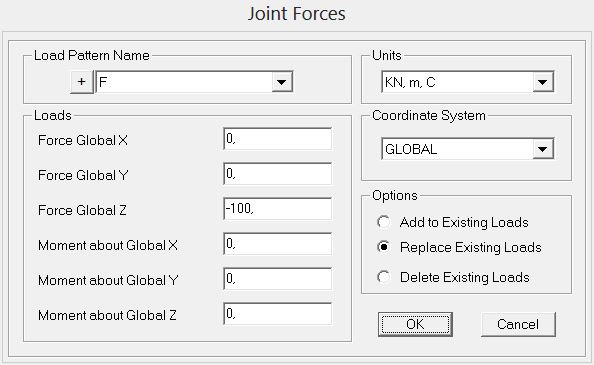
assegniamo quindi il carico ai nodi
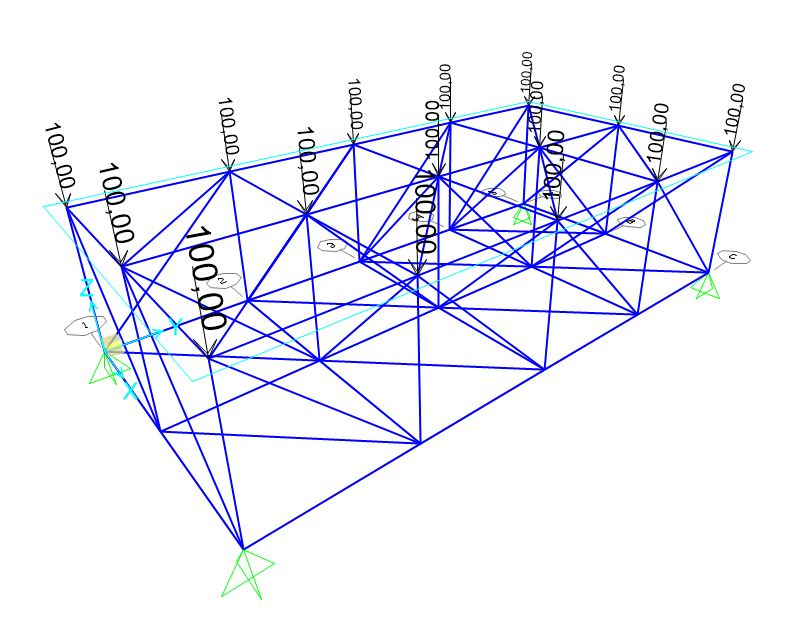
Dopo aver impostato tutti gli aspetti della rappresentazione virtuale della nostra struttura reticolare, possiamo finalmente avviare l’analisi simulata tramite il software.
La prima cosa che otteniamo dall’analisi del software è la simulazione delle deformazioni della struttura.
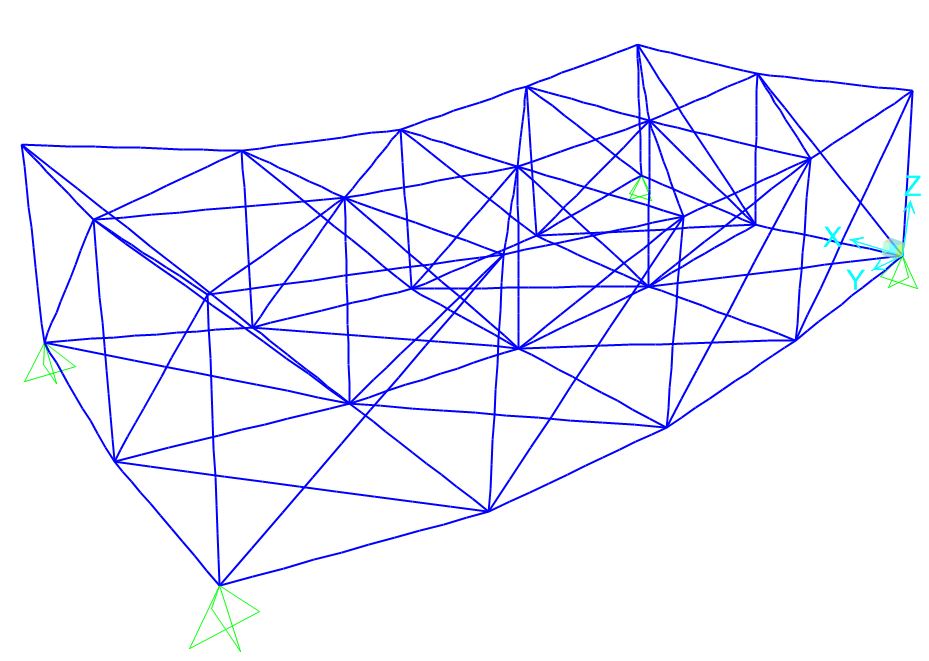
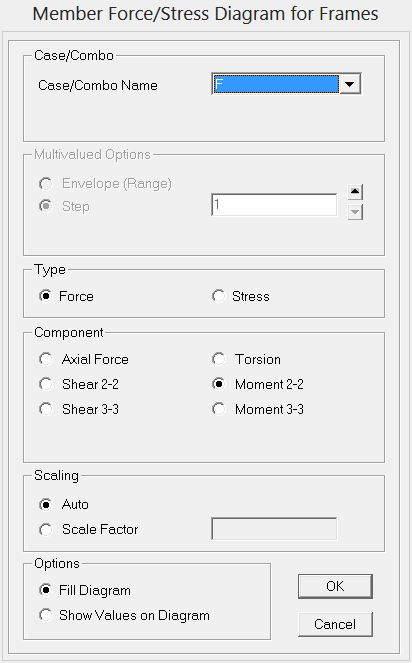
Richiedendo quindi di visualizzare i grafici delle sollecitazioni assiali otteniamo una simulazione grafica che le rappresenta.
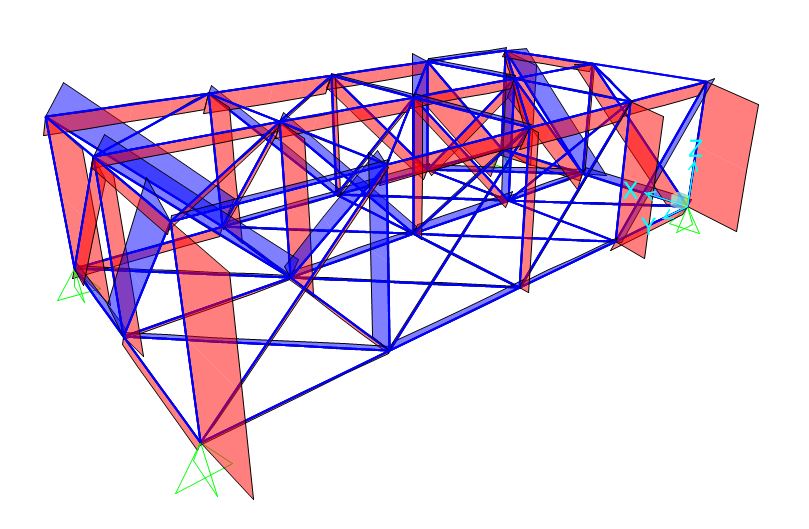
con in rosso le aste compresse ed in blu le aste tese.
Per verificare di non aver commesso errori proviamo ad analizzare la struttura osservando le altre sollecitazioni interne, che come sappiamo devono risultare nulle.
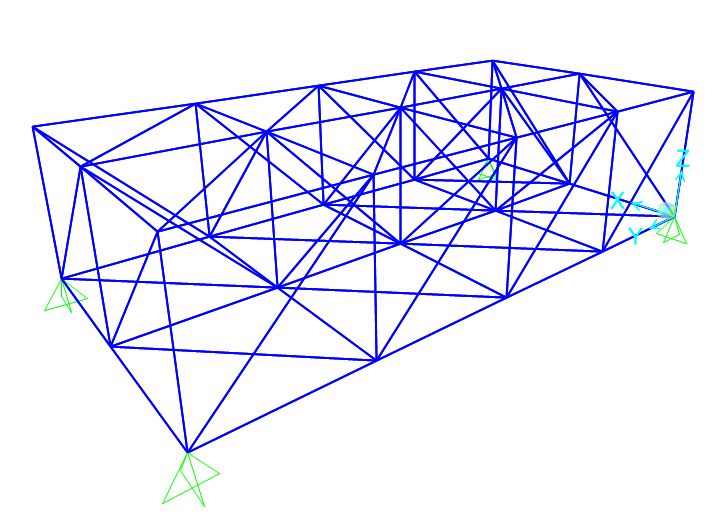
Possiamo adesso esportare i dati ottenuti dall’analisi.
Il software genera una serie di tabelle che contengono i valori numerici estratti dalla simulazione.
Quelli utili al nostro scopo sono nella sezione Element Forces - Frames
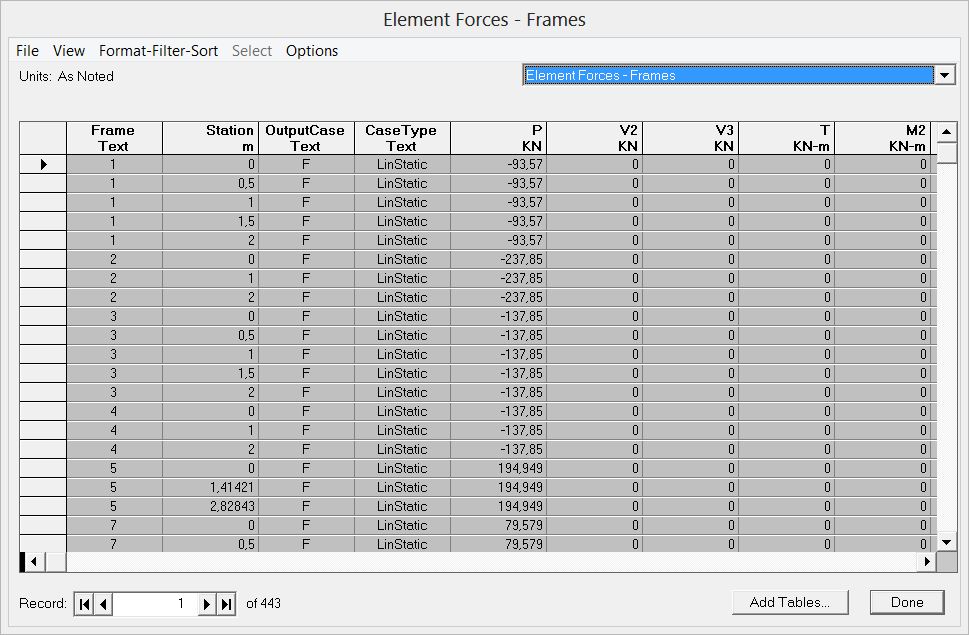
Come abbiamo detto utilizzeremo questi dati per dimensionare e successivamente ingegnerizzare le sezioni delle nostre aste, utilizzando un foglio di calcolo excel.
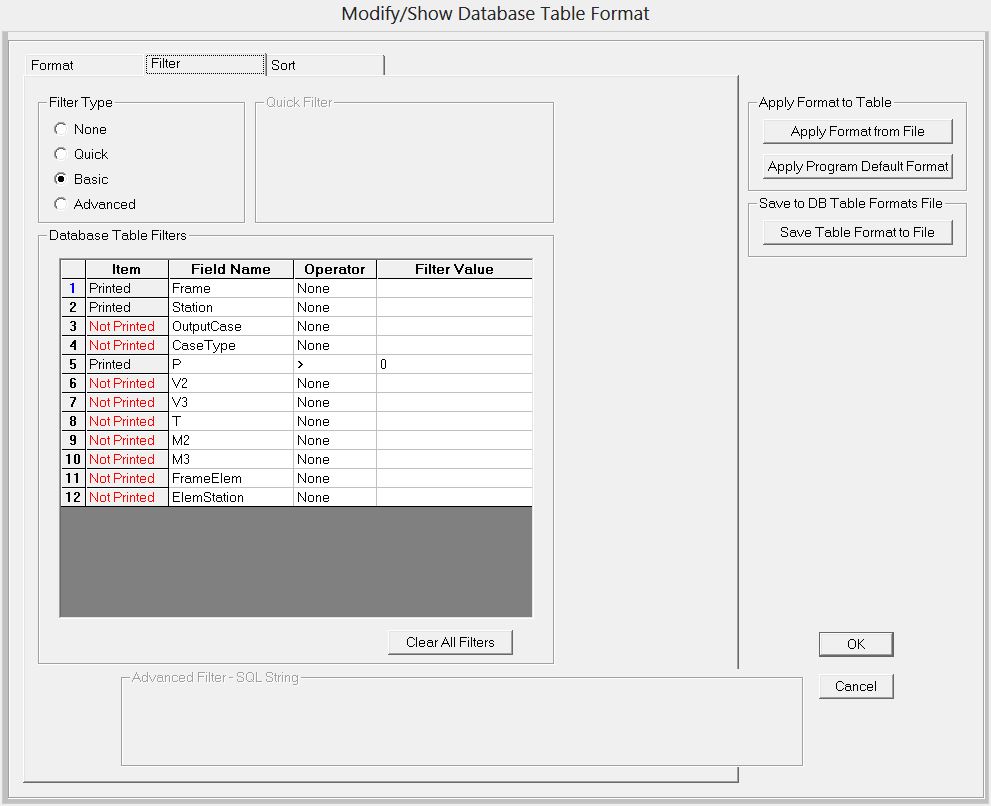
Al fine di rendere manipolabili i dati è necessario organizzarli utilizzando gli strumenti di filtro.
per prima cosa eliminiamo i campi che non ci sono utili, e filtriamo in base al valore di P
(sollecitazione)>0 in modo da poter ottenere una tabella che mostri solo le aste tese
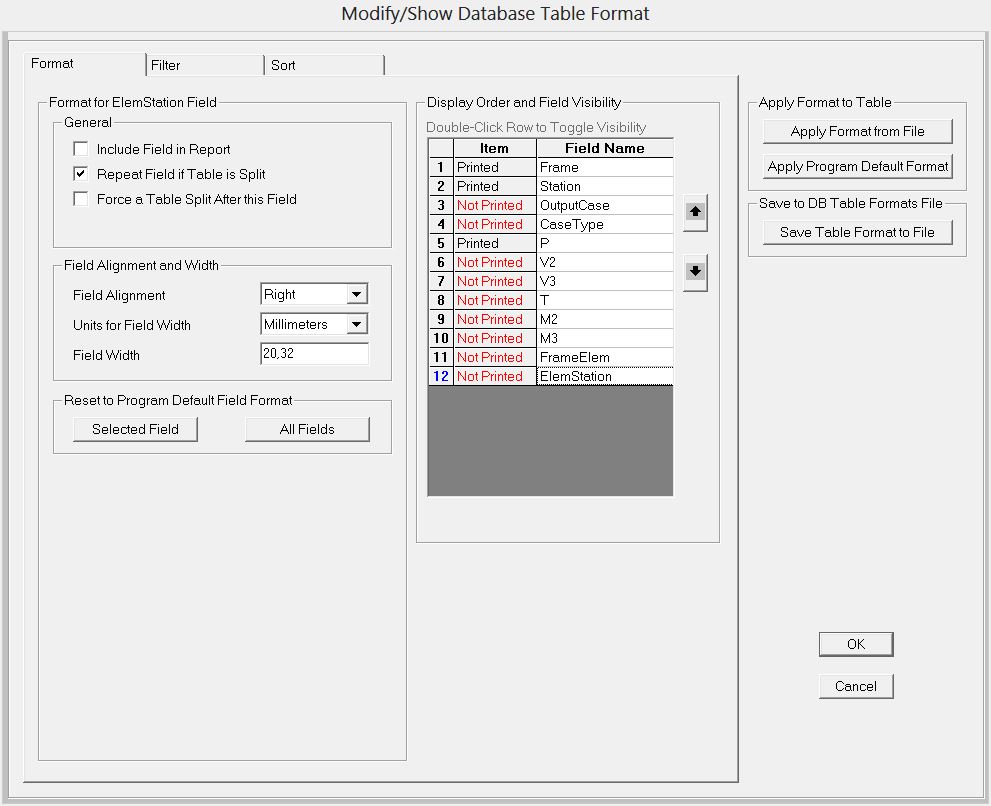
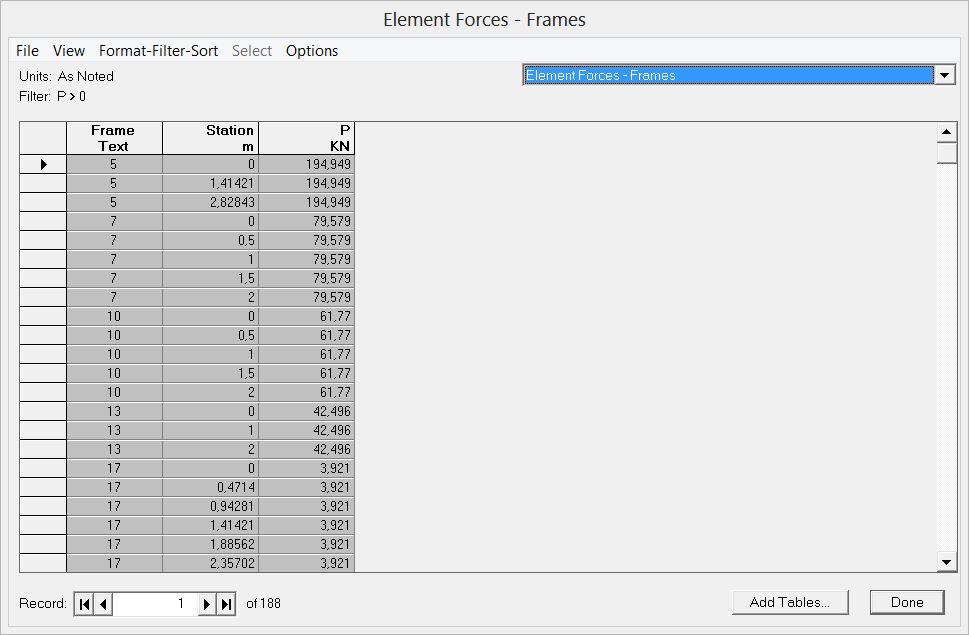
Possiamo ora esportare questi dati all’interno di un file excel per manipolarli.
Una volta esportati i dati possiamo ripetere le operazioni di “pulizia” della tabella includendo solo le aste compresse, P<=0.
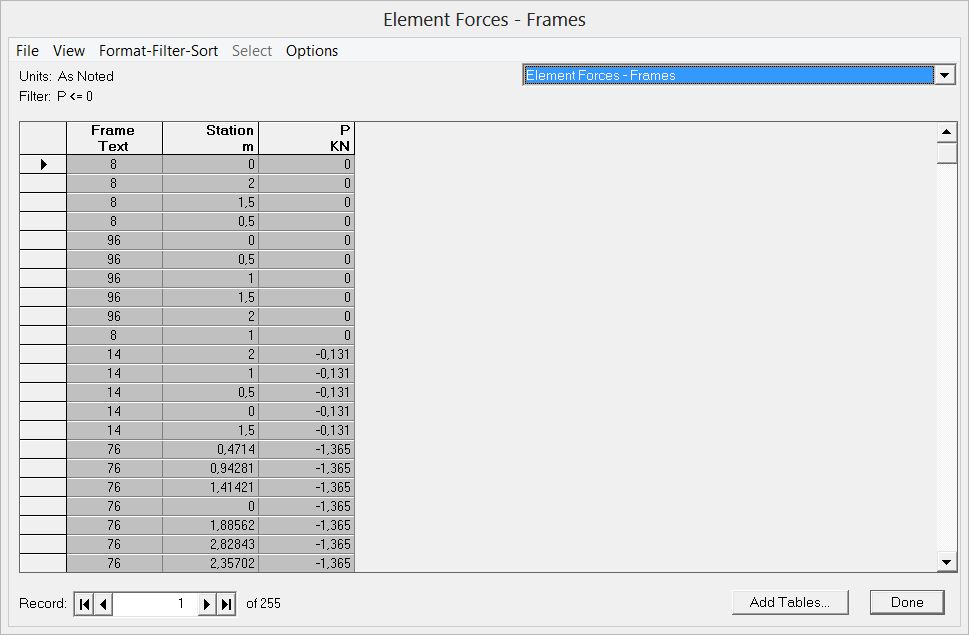
Una volta esportati anche questi valori possiamo iniziare a manipolare i dati nel foglio di calcolo excel.
Noteremo che per tutt le aste, numerate con un numero progressivo casuale attribuito dal software, avremo nel foglio excel dei valori attibuiti a diverse lunghezze intermedie. Questo ovviamente accade perchè le sollecitazioni potrebbero avere in un’accezione più generale una andamento variabile in funzione della sezione dell’asta presa in considerazione. Nel nostro caso questa suddivisione ci è utile solamente per individuare la differenza tra le aste che rappresentano i lati del quadrato e le diagonali (che saranno più lunghe data la formula
D = Lrad2), visto che le sollecitazioni hanno un andamento costante lungo tutto l’elemento. Questa differenziazione sarà ovviamente utile per il calcolo della snellezza massima dell’elemento.
Evidenziamo quindi in rosso le diagonali ed eliminiamo le righe con le sezioni intermedie che non ci sono più utili, ottenedo queste tabelle ordinate in base all’andamento crescente delle sollecitazioni.
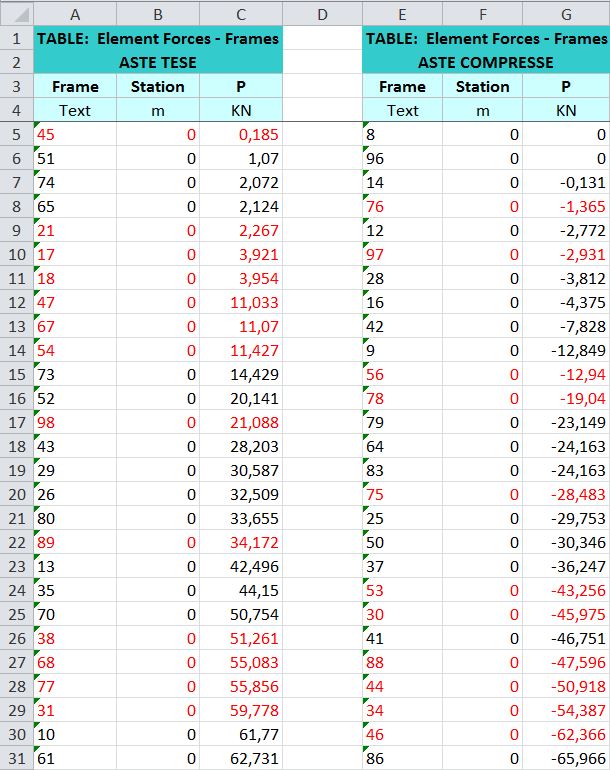
Possiamo inserire questi valori opportunamente organizzati e filtrati all’interno del foglio di calcolo per il dimensionamento.
Come prima cosa notiamo che il foglio di calcolo è diviso in due cartelle, una per le aste tese e un aper le compresse. Questo perchè come già detto per le aste compresse dovremo verificare anche la snellezza massima per evitare il verificarsi di fenomeni di instabilità.
Le aste tese vanno dimensionate solamente tenendo in considerazione la resistenza del materiale, o meglio la tensione  che può sopportare il materiale.
che può sopportare il materiale.
Dovremo quindi calcolare la tensione ammissibile sigma max con la funzione sigma max = fd = fyk/gamma
otterremo quindi la tensione di progetto che determierà di conseguenza l’area minima del profilo da selezionare secondo la formula  .
.
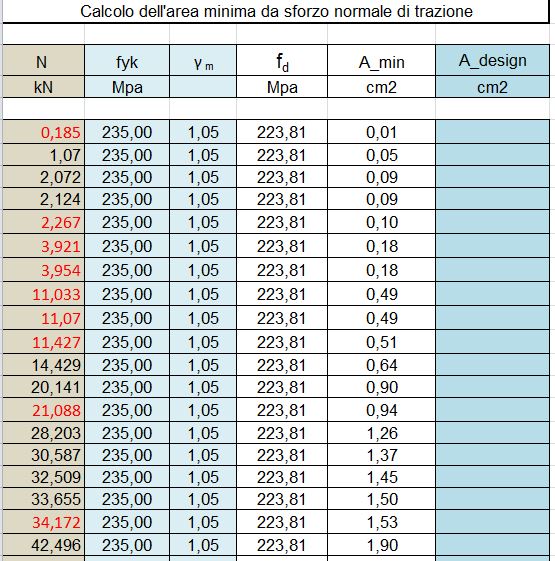
sceglieremo ora un profilo che soddisfi le necessità per l’asta più sollecitata. Teoricamente potremmo assegnare un profilo differente per ogni asta, diciamo che solitamente si tende ad utilizzare un unico profilo per semplicità.
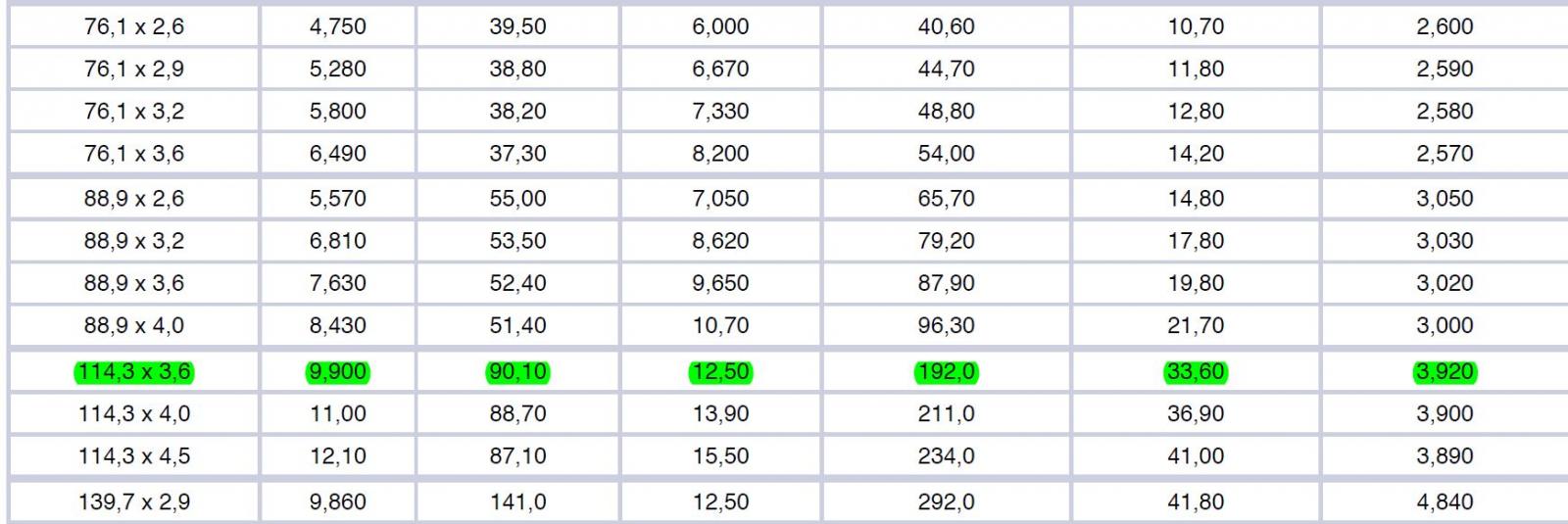
dobbiamo quindi consultare un catalogo di profili e scegliere quello che soddisfi le nostre necessità.
la tensione massima è 212,313 kN con una conseguente area minima (selezionando un acciaio 235Mpa) di 9,49 cm2 .
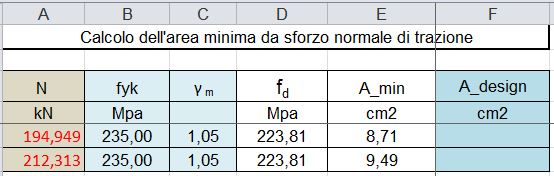
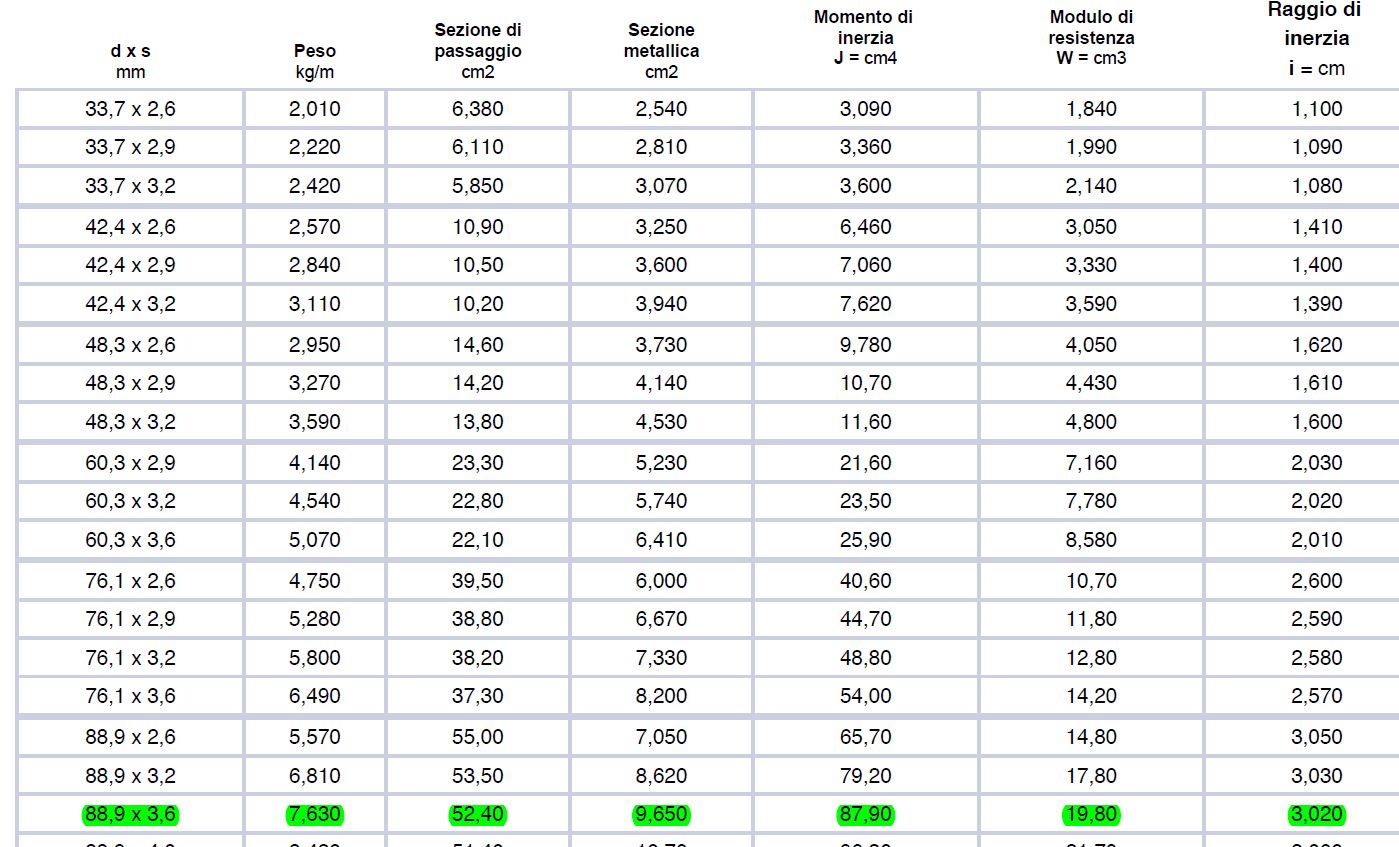
selezioniamo quindi un profilo con diametro 88,9mm che avrà un’area di 9,65cm2
Per la scelta del profilo adatto per le aste sottoposte a compressione il foglio di calcolo è leggermente più complesso, data la necessità di dimensionare gli elementi anche tenendo conto dei fenomeni di instabilità euleriana.
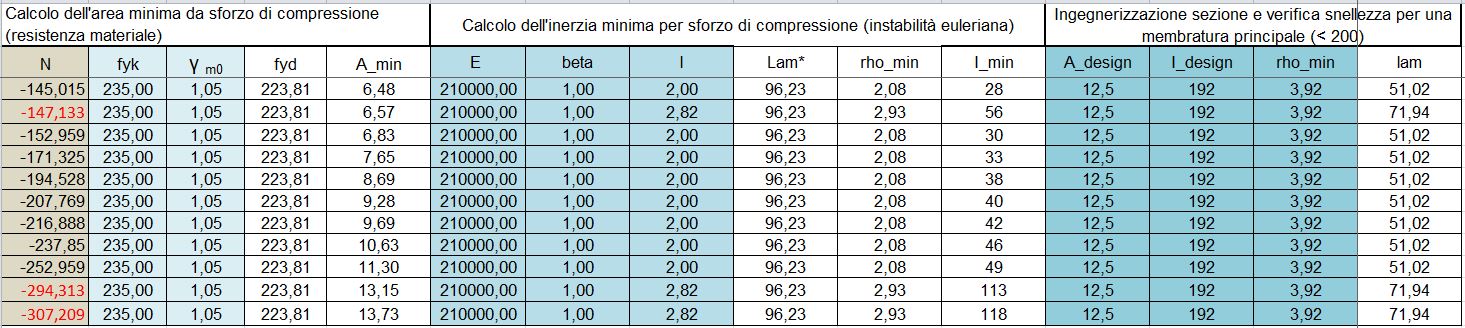
Dopo aver effettuato il procedimento base per la verifica della resistenza del materiale dobbiamo passare al calcolo dell’inerzia minima che come sappiamo ha un ruolo fondamentale nell’evitare il verificarsi delle instabilità. Per effettuare questo calcolo sarà necessario prendere in considerazione anche il modulo di elasticità del materiale E e la tipologia di vincolo dell’elemento che sarà rappresentata da un valore del coefficiente beta necessario per il calcolo della lunghezza di libera inflessione l0 .
Questi valori ci permetteranno di calcolare il valore di snellezza massimo ammisisbile lambda, il raggio d’inerzia minimo e l’inerzia minima della sezione (rhomin e Imin).
Impositiamo E = 210000 Mpa (acciaio 235), beta= 1 (cerniera/cerniera) e la lunghezza (2m per il lati e 2,82m per le diagonali).
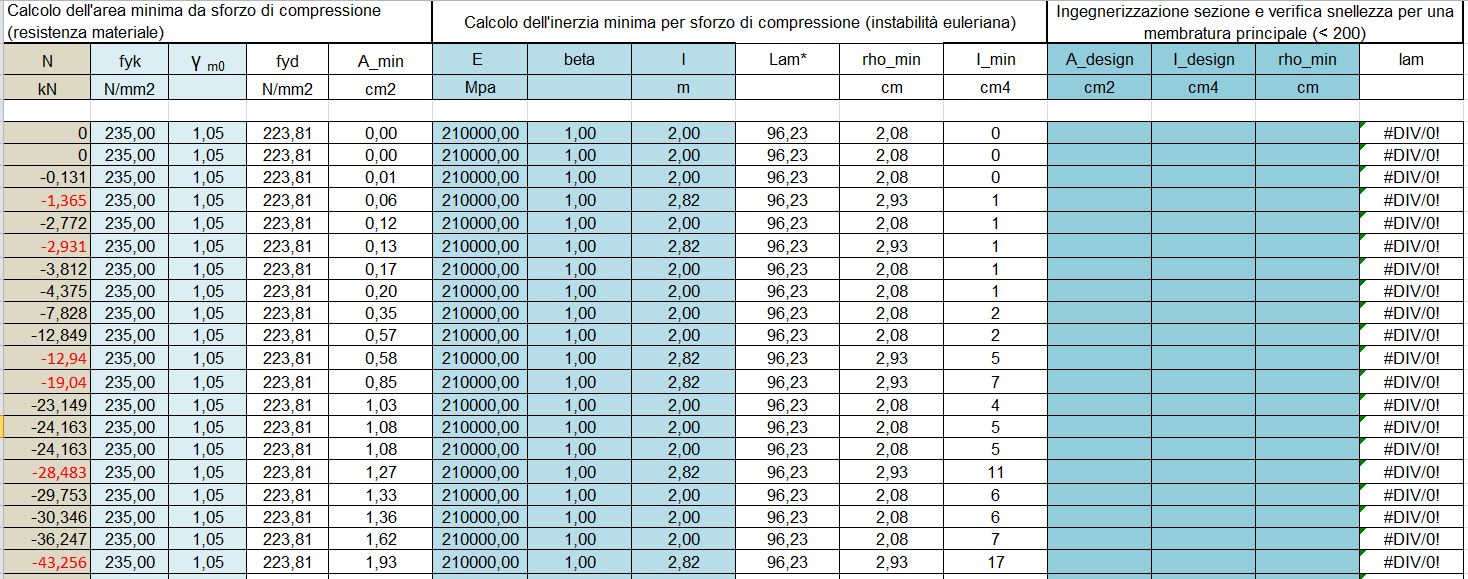
anche in questo caso ipotizziamo una sola sezione dimesionata in base all’asta maggiormente sollecitata.
In questo caso oltre all’area minima dobbiamo scegliere una sezione che abbia un valore sufficiente di momento di inerzia e di raggio di inerzia minimo
una volta inseriti i valori delle aste ingegnerizzate dobbiamo verificare che il valore di snellezza rientri in quelli ammessi dalla normativa
Commenti recenti