Dimensionamento di massima di un pilastro di un edificio nelle tre tecnologie (legno, acciaio, cemento armato)
L’ obiettivo della quarta esercitazione è quello dimensionare la sezione di un pilastro nelle tre tecnologie, Legno, Acciaio e Cemento armato.
VERIFICA
Ho bisogno di fare alcune considerazioni in quanto prendo come modello fisco matematico di un pilastro un asta soggetta a sforzo normale di compressione centrato: i carichi compiendo continuamente LAVORO (che è la Forza per lo spostamento del punto di applicazione per la direzione dello spostamento) e comprimendo dunque l’asta possono provocare due crisi, la rottura del materiale (1) e due fenomeni detti fenomeni di instabilità euleriana quali la flesso-torsione e il carico di punta (2).

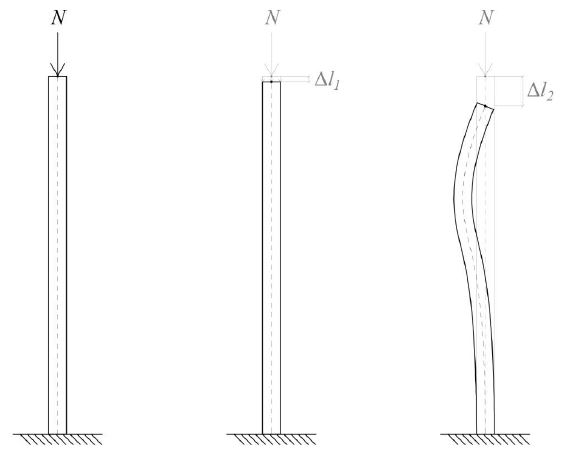
In figura Δl1<Δl2 perché abbiamo disegnato un’asta snella la cui rigidezza assiale è molto superiore a quella flessionale. In tal caso anche L1<L2 e dunque più l’asta è snella e più ci sarà possibilità che il fenomeno di instabilità si inneschi. La forza di compressione che che porta ad innescare il carico di porta è uguale a :
NcritE = ∏2EImin / l02 in cui
E= è il modulo di elasticità del materiale
Imin= è il momento di inerzia minimo della sezione, cioè la sua resistenza Imin= A x ρ2min
ρmin = è il raggio di inerzia minimo cioè come è distribuita l’area rispetto il suo asse baricentrico
l0 = è la luce libera di inflessione, ossia la distanza tra due flessi l0= β x l e dipende dalla luce dell’asta
l=lunghezza asta
β= coefficiente adimensionale che riflette l’influenza dei vincoli, cioè cambia a secondo il modo in cui il pilastro è agganciato alla trave.
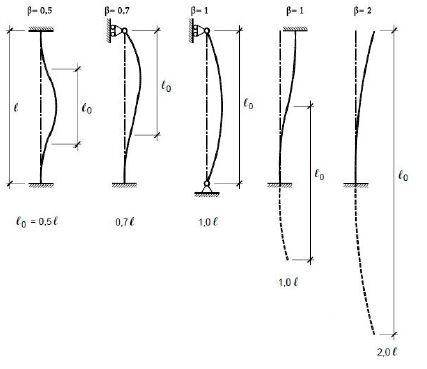
Per poter procedere al dimensionamento del mio pilastro devo verificare entrambe i fenomeni 1 e 2 dunque controllo che la tensione σ = N /A sia
1- σ ≤ fcd
2- σ ≤ σcrit
σcrit = Ncrit /A= ∏2EImin / l02 A , divide per A e ho che NCRIT = ∏2EImin / l02 = ∏2EAρmin/l02
So che la snellezza λ= ρmin / l0 quindi sostituisco λ nell’equazione :
NCRIT = ∏2EA/ λ2 Deduco dunque che un asta più ha il valore della snellezza elevato minire è il carico critico.
Invece la tensione critica σcrit= Ncrit /A= ∏2E/ λ2
PROGETTO
Quando un asta è compressa come in questo caso abbiamo bisogno di un AREA e di un MOMENTO DI INERZIA minimo della sezione medesima. Area e momento di inerzia sono variabili che NON dipendono tra loro.
L’ Area della sezione me la ricavo uguagliando la tensione massima sulle sezioni (che ho messo in relazione con la tensione critica ricavata precedentemente σmax = σcrit ) σcrit alla resistenza di progetto a compressione del materiale preso in esame fcd .Quest’area è da intendersi come il minimo valore che deve avere l’area della sezione per evitare lo schiacciamento del materiale.
σcrit = fcd Ncrit /A = fcd Amin = Ncrit / fcd
uguagliando il la tensione critica con la resistenza di progetto ho effettuato una operazione DANNOSA poiché ho detto che io voglio che quando la tensione è tale da raggiungere la rottura del materiale contemporaneamente va in carico di punta.
Quindi dovrò cambiare la relazione tra questi due fattori:
se fcd > σcrit il pilastro andrebbe in carico di punta e successivamente si romperebbe per schiacciamento del materiale; questa scelta progettuale potrebbe venire intrapresa solo quando si ha conoscenza di quanto accade nella fase post-critica del fenomeno di instabili ma nel nostro caso non la sapremmo gestire.
se fcd < σcrit il materiale si rompe prima che il profilo ha il tempi di andare in carico di punta; questa relazione la PREFERIAMO alle due precedenti dal momento che sappiamo controllarla.
Quindi sostituisco : fcd < ∏2E/ λ2 , metto in evidenza la snellezza λ2 < ∏2E / fcd
λ max = ∏ √E/fcd
λ max è la massima snellezza possibile che la trave compressa deve avere affinchè l’instabilità non si inneschi prima dello schiacciamento.
Da questo valore di λ max possiamo ottenere una indicazione sul valore minimo del raggio di inerzia minimo che la sezione deve avere. Ricordando che la snellezza è uguale a λ= ρmin / l0,
ρmin= l0 /λ max una volta travato ρmin sappiamo anche che Imin= A ρmin2 quindi da qui mi ricavo
ρmin2= Imin/A dunque ρmin=√Imin/A
Da quest’ultima equazione posso ricavare un importante dato che mi serve per calcolare l’Area minima quale la base:
ρmin=√1/12hb2/hb −› ρmin=√b2/12 −› ρmin=b/√12 −› bmin= ρmin 2√3
infine troverò hmin=b/A e ingenierizzo il tutto.
DIMENSIONAMENTO E INGENIERIZZAZIONE PILASTRO
Con l’ausilio di un foglio Excel vado ora a dimensionarmi la sezione del pilastro ed a ingenierizzarla conoscendo ora come trovare l’area minima e il momento di inerzia che mi servivano per dimensionare questo elemento strutturale soggetto a compressione nelle tre diverse tecnologie.
Disegno una pianta di carpenteria, individuo il pilastro più sollecitato che sarà quello centrale e inquadro la sua area di influenza. Considero quindi la pianta di carpenteria del piano terra, poiché è quello più compressa dovendo supportare i carichi dei piani superiori, di un edificio tipo di 4 piani.
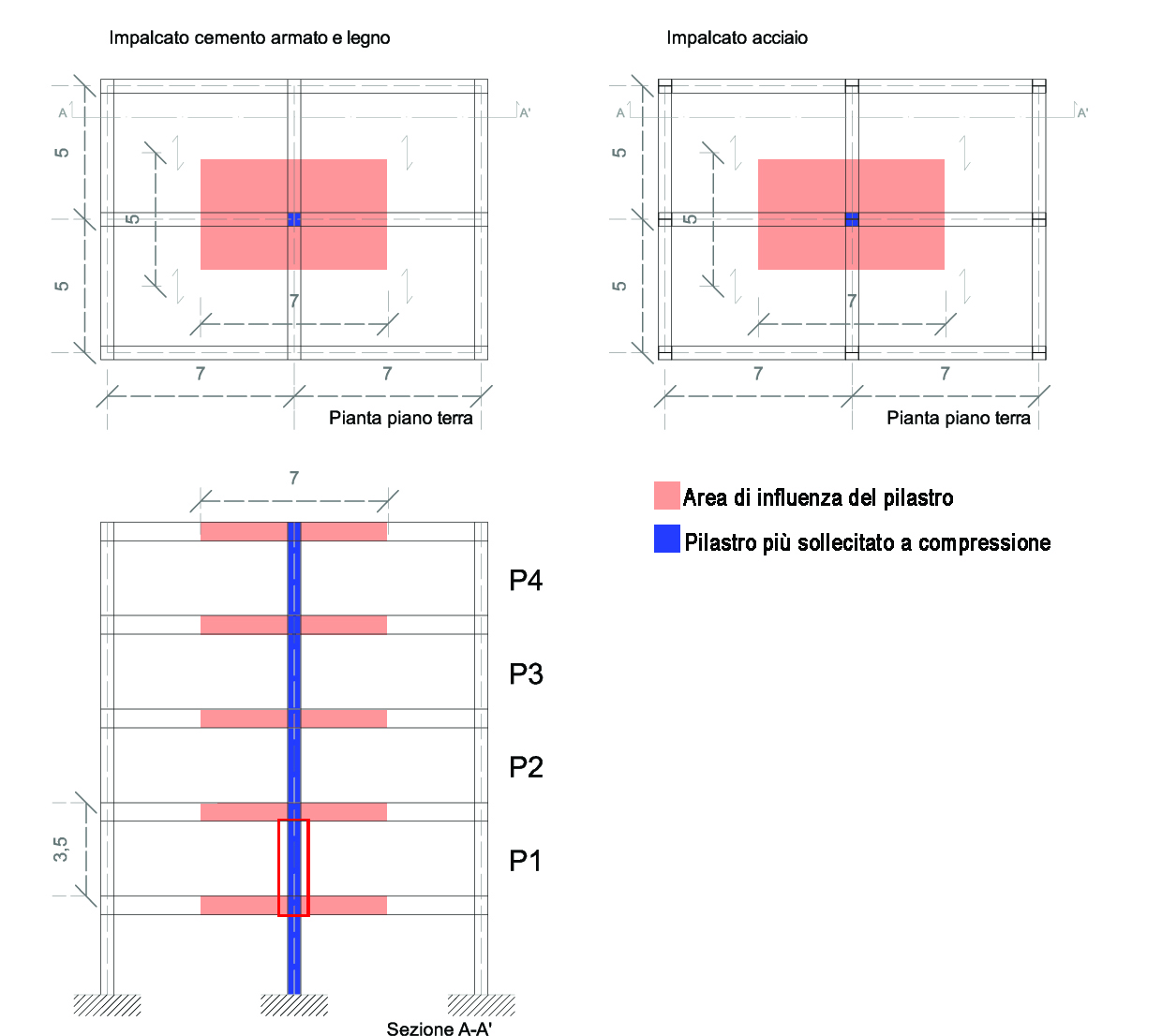
NB: Alcuni dei dati che andrò a mettere nel foglio Excel saranno presi dalle esercitazioni precedenti pubblicate sul mio blog come ad esempio i carichi strutturali come anche la stratigrafia dei solai delle tre tecnologie prese in considerazione.
LEGNO
Per poter compilare il mio foglio di lavoro Excel e trovare come fine ultimo la dimensione della sezione del pilastro ho bisogno di alcuni dati, che andrò ad inserire in 4 step.

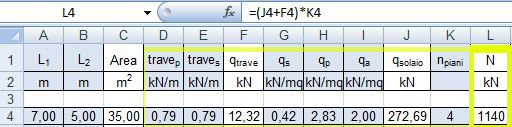
1 AREA DI INFLUENZA
In cui L1 e L2 sono le due luci della pianta
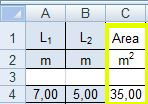
2 SFORZO NORMALE DI COMPRESSIONE N
Per trovare N vado a prendere alcuni dati dai miei esercizi precedenti e mi trovo il carico dovuto al peso proprio delle travi qtrave che si calcola area di sezione x peso specifico del materiale x lunghezza della trave nell’area di influenza del pilastro x il numero delle travi che confluiscono nel nodo.
Trave principale = (0.35 x 0.55)m2 x 4.10 KN/m3 =0.79 KN/m
Trave secondaria= (0.35 x 0.55)m2 x 4.10 KN/m3=0.79 KN/m
Qtrave=(0.79x7)x1.3 + (0.79x5) x1.3 = 12.32 KN
Carichi strutturali qs = 0.42KN/m2
Carichi permanenti qp= 2.83 KN/m2
Carichi accidentali qa= 2 KN/m2
Qsolaio: calcolo il carico dovuto al solaio allo SLU (stato limite ultimo) sommo i 3 carichi qs, qp e qa moltiplicandoli per i coefficienti di sicurezza e tutto moltiplicato per l’area di influenza
Qsolaio = (0.42x1.3 + 2.83x1.5 + 2x1.5) x 35 = 272.69 KN
Numero piani= 4
N= la forza di compressione N è dovuto al carico delle travi più il carico del solaio per il numero di piani.
N= (12.32 + 272.69) x 4 = 1140 KN
3 AREA MINIMA NECESSARIA
Avendo trovato il valore dello sforzo normale di compressione posso trovare ora l’area minima affinchè il materiale non entri in crisi.
Ho scelto un legno lamellare incollato GL28h il mio coefficiente parziale di sicurezza γm=1.45.
Kmod: è un coefficiente che riduce i valori della resistenza che tiene conto della durata del carico e delle condizioni di umidità e cambia a seconda del materiale prescelto , nel mio caso: classe di servizio 2, classe di durata del carico media =0.80. Fc0,k è la resistenza a flessione caratteristica del legno = 28 Mpa
Con questi coefficienti mi ricavo la tensione ammissibile di progetto a compressione: Fc0d= Kmod x Fc0,k / γm = 15.45 MPa
Amin= N/ Fc0d=738 cm2

4 RAGGIO DI INERZIA MINIMO AREA DI DESIGN E INERZIA DI DESIGN
Grazie al raggio di inerzia minima e al fatto che la sezione del pilastro è rettangolare e piena posso trovarmi la base minima della sezione del pilastro.
E= modulo di elasticità 8800Mpa
β = 1 il pilastro è vincolato a terra tramite un incastro e nel nodo trave pilastro tramite una cerniera/carrello
l= altezza del pilastro 3.5m
Con le formule che abbiamo dimostrato prima il foglio di Excel mi calcola: λ max = ∏ √E/fcd ρmin= l0 /λ max
bmin= ρmin 2√3=16.18cm ingenierizzo a b=30cm
hmin=b/Amin =24.60 cm ingenierizzo a h=50cm
Una volta che ho base e altezza ingenierizzate della sezione del pilastro trovo l’area di design e il momento di inerzia di design
Adesign= bxh = 1500 cm2 Idesign= hxb3/12 =112500cm4
La sezione del pilastro più sollecitato è di 30cmx50cm ed è VERIFICATA avendo Adesign>Amin ed essendo h>b!

CEMENTO ARMATO
Per dimensionare la sezione del pilastro in cemento armato procedo come fatto per il legno dal momento che entrambe hanno sezione piena rettangolare dunque posso trovare la base minima della sezione tramite il raggio di inerzia e secondo perché nonostante siano composti da due materiali, (in entrambe gli elementi strutturali c’è dell’acciaio) li tratto come materiali omogenei essendo molto reagenti a compressione. Unica differenza, nel C.A. ci sarà un quinto step che tiene conto del fatto che il pilastro in cemento armato è soggetto a presso-flessione e non a solo sforzo di compressione.
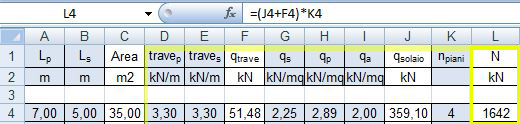
1 AREA DI INFLUENZA
In cui L1 e L2 sono le due luci della pianta

2 SFORZO NORMALE DI COMPRESSIONE N
Per trovare N vado a prendere alcuni dati dai miei esercizi precedenti e mi trovo il carico dovuto al peso proprio delle travi qtrave che si calcola area di sezione x peso specifico del materiale x lunghezza della trave nell’area di influenza del pilastro x il numero delle travi che confluiscono nel nodo.
Trave principale = (0.30 x 0.50)m2 x 22 KN/m3 =3.3 KN/m
Trave secondaria= (0.30 x 0.50)m2 x 22 KN/m3=3.3 KN/m
Qtrave=(3.3x7)x1.3 + (3.3x5) x1.3 = 51.48 KN
Carichi strutturali qs = 2.25KN/m2
Carichi permanenti qp= 2.89 KN/m2
Carichi accidentali qa= 2 KN/m2
Qsolaio: calcolo il carico dovuto al solaio allo SLU (stato limite ultimo) sommo i 3 carichi qs, qp e qa moltiplicandoli per i coefficienti di sicurezza e tutto moltiplicato per l’area di influenza Qsolaio = (2.25x1.3 + 2.89x1.5 + 2x1.5) x 35 = 359.10 KN
Numero piani= 4
N= la forza di compressione N è dovuto al carico delle travi Qtrave più il carico del solaio Qsolaio per il numero di piani.
N= (54.48 + 359.10) x 4 = 1642 KN
3 AREA MINIMA NECESSARIA
Avendo trovato il valore dello sforzo normale di compressione posso trovare ora l’area minima affinchè il materiale non entri in crisi.
fck è la resistenza caratteristica a compressione del calcestruzzo data dal tipo di cls scelto in questo caso 50 N/mm2. αcc è un coefficiente riduttivo pari a 0.85 e γc è il coefficiente di sicurezza per il cls pari a 1.5 .
Con questi coefficienti mi ricavo la tensione ammissibile di progetto a compressione : Fcd= αcc (fck/ γc) = 0.85(50/1.5)= 28.03 MPa
Amin= N/ Fcd=579.6 cm2 avendo ipotizzato una sezione quadrata per il pilastro mi posso trovare intanto un ipotetica bmin= √ Amin=24.1 cm

4 RAGGIO DI INERZIA MINIMO AREA DI DESIGN E INERZIA DI DESIGN
Grazie al raggio di inerzia minima e al fatto che la sezione del pilastro è rettangolare e piena posso trovarmi la base minima della sezione del pilastro.
E= modulo di elasticità 21000Mpa
β = 1 il pilastro è vincolato a terra tramite un incastro e nel nodo trave pilastro tramite sempre un incastro.
l= altezza del pilastro 3.5m
Con le formule che abbiamo dimostrato prima il foglio di Excel mi calcola: λ max = ∏ √E/fcd ρmin= l0 /λ max
bmin= ρmin 2√3=14.18cm ingenierizzo a b=50cm
hmin=b/Amin =16.56 cm ingenierizzo a h=50cm
Una volta che ho base e altezza ingenierizzate della sezione del pilastro trovo l’area di design e il momento di inerzia di design
Adesign= bxh = 2500 cm2 Idesign= hxb3/12 =520833cm4
La sezione del pilastro più sollecitato è di 50cmx50cm ed è VERIFICATA avendo Adesign>Amin ed essendo h≥b!

5 VERIFICA A PRESSO-FLESSIONE
Il pilastro essendo collegato alla trave con un incastro, in quel nodo trasmette un momento il quale potrebbe sottoporre il pilastro alla presso-flessione.
Per far si chè il pilastro non sia soggetto a presso flessione la tensione massima deve essere minore uguale alla tensione di progetto σmax ≤ fcd
- mi calcolo l’inerzia massima Imax= hxb3/12 =520833cm4
- calcolo il modulo di resistenza a flessione per le sezioni rettangolari
Wmax= bxh2/6=20833.33 cm3
- calcolo il carico distribuito sulla trave qt= qsolaio x Ls =51.30 KN/m
- calcolo il momento in testa al pilastro che è collegato alla trave
Mt= qt x L12 /12 = 209.48 KNxm
- infine trovo la tensione massima la quale deve essere minore di quella di progetto:
σmax=(N/A) +(Mt/Wmax) x 1000 =16.62 Mpa
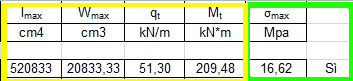
VERIFICATA σmax ≤ fcd 16.62 < 28.3 Mpa
ACCIAIO
Per dimensionare un pilastro in acciaio con una sezione HEA si procede inizialmente come per il legno e per il c.a. in questo caso però non ho necessità di ricavarmi la base ma una volta trovato il raggio di inerzia mi calcolo l’inerzia minima e dopo di che posso andare sulle tabelle dei profilati e scegliere quello che ha l’inerzia maggiore di quella da me ottenuta.
1 AREA DI INFLUENZA
In cui L1 e L2 sono le due luci della pianta

2 SFORZO NORMALE DI COMPRESSIONE N
Per trovare N vado a prendere alcuni dati dai miei esercizi precedenti e mi trovo il carico dovuto al peso proprio delle travi qtrave che si calcola area di sezione x peso specifico del materiale x lunghezza della trave nell’area di influenza del pilastro x il numero delle travi che confluiscono nel nodo.
La trave che avevo dimensionato nell’esercitazione precedente è un IPE 360 e nella tabella ho preso il suo peso proprio che è uguale a 57,1 kg/m che trasformo in KN/m dividendo per 100
Trave principale = 0.57 KN/m
Trave secondaria= 0.57 KN/m
Qtrave=(0.57x7)x1.3 + (0.57x5) x1.3 = 8.89 KN
Carichi strutturali qs = 1.87 KN/m2
Carichi permanenti qp= 2.50 KN/m2
Carichi accidentali qa= 2 KN/m2
Qsolaio: calcolo il carico dovuto al solaio allo SLU (stato limite ultimo) sommo i 3 carichi qs, qp e qa moltiplicandoli per i coefficienti di sicurezza e tutto moltiplicato per l’area di influenza Qsolaio = (1.87x1.3 + 2.50x1.5 + 2x1.5) x 35 = 321.34 KN
Numero piani= 4
N= la forza di compressione N è dovuto al carico delle travi Qtrave più il carico del solaio Qsolaio per il numero di piani.
N= (8.89 + 321.34) x 4 = 1321 KN
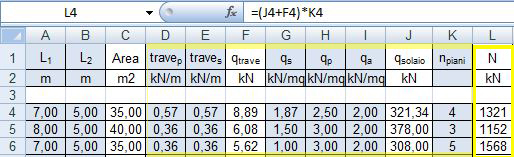
3 AREA MINIMA NECESSARIA
Avendo trovato il valore dello sforzo normale di compressione posso trovare ora l’area minima affinchè il materiale non entri in crisi.
fyK è valore caratteristico di snervamento per l’acciaio che mi individua la classe di resistenza del materiale , in questo caso scelgo un acciaio medio (classe Fe430/s275) di resistenza 275 Nmm2.
γm coefficienti di sicurezza per la resistenza delle membrature e la stabilità pari a 1.05 .
Con questi coefficienti mi ricavo la tensione ammissibile di progetto a compressione: Fyd= fyk/ γm = 275/1.05)= 261.90 MPa
Amin= N/ Fyd=50.4 cm2

4 RAGGIO DI INERZIA MINIMO AREA DI DESIGN E INERZIA DI DESIGN
Trovo l’ Inerzia minima per poter cercare il mio profilato sulla tabella non prima di aver trovato dei valori importanti quali la snellezza e il raggio di inerzia.
E= modulo di elasticità 21000Mpa
β = 1 il pilastro è incernierato sia a terra che nel nodo trave pilastro.
l= altezza del pilastro 3.5m
Con le formule che abbiamo dimostrato prima il foglio di Excel mi calcola:
λ max = ∏ √E/fcd ρmin= l0 /λ max Imin= A x ρmin2=3123 cm4
Una volta che ho l’inerzia minima vado sulle tabelle dei profilati HEA e scelgo il profilato che abbia un Inerzia maggiore dell’ inerzia minima.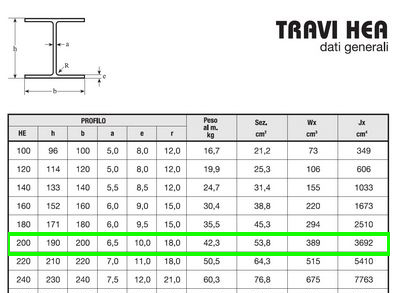
Una volta scelto il profilato ho l’area di design e il momento di inerzia di design.
Adesign= 53.8 cm2 Idesig=3692cm4 ρdesign=8.28 cm
Il profilato adatto per il pilastro è un HEA 200 VERIFICATO avendo Adesign>Amin

Commenti recenti