SdC(b) (LM PA)

 

In questa esercitazione,  procederemo al dimensionamento a flessione della trave più sollecitata in un solaio scelto arbitrariamente. Effettueremo l’analisi  ripetendo l’operazione per un solaio in legno, uno in calcestruzzo armato ed uno acciaio.

La trave soggetta a maggior carico, e di conseguenza al maggior momento flettente, è quella evidenziata in rosso, in quanto la sua area d’influenza è pari a 6m x 4m = 24mq, ossia il  prodotto della luce per l’interasse.

Analizziamo ora il carico distribuito (KN/mq) dei vari tipi di materiali che compongono  ciascuna tipologia di solaio, ricordando che nel caso il materiale sia distribuito su tutta la superficie analizzata (1mq) avremo:

·        ( peso specifico x volume ) /superficie analizzata = carico distribuito

Nel caso in cui sia presente invece una sezione che si ripete ad un determinato interasse:

·        [ peso specifico x volume x ( lunghezza analizzata/interasse) ] / superficie analizzata = carico distribuito

Calcoleremo i diversi carichi distribuiti (q) in base alla loro classificazione:

qs = Carico degli elementi strutturali.

qp = Carico permanente degli altri elementi presenti nel solaio con funzione non strutturale, a cui va aggiunto il carico dato dai tramezzi (1KN/mq) e quello dato dagli impianti (0,5 KN/mq).

qa = Carico accidentale, dato da normativa tecnica in base allo destinazione d’uso degli ambienti, per la destinazione residenziale è pari a 2 KN/mq.

 

Solaio in legno

Carichi strutturali (qs)                                                                                                 

_travetti in legno di conifere    

 [6 KN/mc x 0.15 m x 0.15 m x 1m x (1m/0,5)]/ 1mq = 0.27 KN/mq

_tavolato in legno di conifere

(6 KN/mc x 0,035 m x 1m x 1m)/ 1mq = 0.21 KN/mq

TOT.  =  0.48 KN/mq

 

Carichi permanenti (qp) 

_caldana in malta di cemento

(21 KN/mc x 0,040 m x 1m x 1m)/ 1mq = 0.84 KN/mq

_isolante in fibra di legno

(9 KN/mc x 0,040 m x 1m x 1m)/ 1mq = 0.36 KN/mq

_sottofondo in malta di calce

(18 KN/mc x 0,030 m x 1m x 1m)/ 1mq = 0.54 KN/mq

_tavolato in legno di quercia

(8 KN/mc x 0,025 m x 1m x 1m)/ 1mq = 0.20 KN/mq

_incidenza tramezzi  =      1 KN/mq

_incidenza impianti =   0.5 KN/mq

 TOT.  =  3.44 KN/mq        

     

Carichi accidentali (qa)

_Ambiente ad uso residenziale (Normativa)

TOT. = 2 KN/mq                                                                       

 

Inseriamo ora i valori ottenuti nel foglio di calcolo per dimensionare la trave.

Per prima cosa scriviamo l’interasse dell’area d’influenza della trave (4m) e i diversi carichi calcolati precedentemente per ottenere q (KN/m):

                                                          q = (1.3 x qs + 1.3 x qp + 1.5 qa) x interasse

dove i carichi strutturali, permanenti e accidentali vengono ognuno moltiplicati per un coefficiente di sicurezza.

Attraverso la luce possiamo ottenere il momento, che è pari  qL²/8 (in quanto il sistema è equivalente ad una trave doppiamente appoggiata).

Passiamo successivamente alle caratteristiche del materiale per ottenere la tensione sig_am;  questa dipende dal tipo di legno scelto (legno lamellare GL24h) ed è data dal prodotto del coefficiente riduttivo kmod  (0.80) che tiene conto della durata del carico e della classe di servizio del progetto e della resistenza a flessione caratteristica fm,k, che viene ulteriormente ridotta dal coefficiente parziale di sicurezza γ che nel legno lamellare è pari a 1.45.

Per concludere inseriamo il valore della base che ipotizziamo per la nostra trave, in questo caso 30 cm e attraverso la formula di Navier otteniamo una trave con altezza pari a 46.92 cm, perciò per approssimazione scegliamo di utilizzare una sezione 30 x 50 cm.

Verifichiamo ora se la trave resiste al peso proprio ovvero se aggiungendo il suo carico al qs precedentemente ottenuto, l’altezza della trave risultante sia inferiore da quella da noi scelta.

Per farlo dobbiamo moltiplicare il peso specifico (KN/mc) del materiale scelto, in questo caso sempre legno di conifere) per lasezione della trave in modo da ottenere il carico della trave a metro lineare, ricordandoci di dividerlo per l’interasse del solaio dato:

q_trave = (6 KN/mc x 0.30 m x 0.5 m) / 4 m = 0.225 KN/mq

qs + q_trave  =  (0.48 + 0.225) KN/mq = 0.705 KN/mq

Avendo scelta una sezione  30 x 50 la trave è verificata.

 

Solaio in C.A.

Carichi strutturali (qs)                                                                                               

_travetti in C.A.

 [25 KN/mc x 0.10 m x 0.12 m x 1m x (1m/0,5)]/ 1mq = 0.6 KN/mq

_caldana in malta di cemento

(21 KN/mc x 0,040 m x 1m x 1m)/ 1mq = 0.84 KN/mq

TOT.  =  1.44 KN/mq

 

Carichi permanenti (qp) 

_pignatte

(5.5 KN/mc x 0,4 m X 0.12 m x 1m x (1m/0,5)]/ 1mq = 0.528 KN/mq

_isolante in fibra di legno

(9 KN/mc x 0,040 m x 1m x 1m)/ 1mq = 0.36 KN/mq

_sottofondo in malta di calce

(18 KN/mc x 0,030 m x 1m x 1m)/ 1mq = 0.54 KN/mq

_Pavimento parquet in legno

(8 KN/mc x 0,02 m x 1m x 1m)/ 1mq = 0.16 KN/mq

_intonaco di calce

(11.5 KN/mc x 0,015 m x 1m x 1m)/ 1mq = 0.1725 KN/mq

_incidenza tramezzi  =      1 KN/mq

_incidenza impianti =   0.5 KN/mq

 TOT.  =  3.260 KN/mq    

 

Carichi accidentali (qa)

Ambiente ad uso residenziale (Normativa)

TOT. = 2 KN/mq                                                                       

Come per il caso in legno, inseriamo ora i valori ottenuti nel foglio di calcolo per dimensionare la trave.

Scriviamo l’interasse dell’area d’influenza della trave (4m) e i diversi carichi calcolati precedentemente per ottenere q,il carico al metro lineare.

q = (1.3 x qs + 1.3 x qp + 1.5 qa) x interasse

dove, ricordiamo, che i carichi strutturali, permanenti e accidentali vengono ognuno moltiplicati per un coefficiente di sicurezza.

Attraverso la luce possiamo ottenere il momento, che è pari  qL²/8 (in quanto il sistema è equivalente ad una trave doppiamente appoggiata).

Passiamo successivamente alle caratteristiche del materiale per trovare le tensioni sig_fa e sig_ca.

Per quanto riguarda i ferri di armatura che devono resistere a trazione, la tensione sig_fa è data dal rapporto tra la resistenza caratteristica di snervamento dell’acciaio  fy e il coefficiente parziale di sicurezza γ pari a 1,5. Sceglieremo una classe di resistenza B450A, con limite di snervamento ≥ 450 Mpa.

Sig_fa = (fk / γ )

Per il calcestruzzo avremo invece una tensione sig_ca data dalla resistenza caratteristica cubica a compressione Rck, (in questo caso 50 avendo scelto un calcestruzzo con classe di resistenza C 40/50)  moltiplicata per un coefficiente riduttivo αcc  pari a 0,85 e poi divisa per un coefficiente parziale di sicurezza γ che anche per il cls vale  1,5.

Sig_ca = (Rck x αcc)/γ

Possiamo trovare ora l’altezza della trave. Per farlo dobbiamo calcolare il coefficiente di omogeinizzazione n che tiene conto che la sezione in cls armato non è omogenea ma composta da 2 materiali: il calcestruzzo che resiste a compressione e l’acciaio che resiste a trazione. Questo valore è dato dal rapporto dei due moduli elastici (n = Efe / Eca ) ma si assume pari a 15 a vantaggio della sicurezza. Ci serve per ottenere il valore alfa.

Fissiamo una base di 30 cm e calcoliamo infine l’altezza utile h, cioè la sezione reagente in calcestruzzo, a cui aggiungiamo un delta (dato dal copriferro) pari a 5 cm. Otteniamo l’altezza finale della trave, pari a 34,94 che porteremo a 35 cm. Avremo quindi una sezione finale pari a 30 x 35 cm.

Verifichiamo ora se la trave resiste al peso proprio ovvero se aggiungendo il suo carico al qs precedentemente ottenuto, l’altezza della trave risultante sia inferiore da quella da noi scelta.

Per farlo dobbiamo moltiplicare il peso specifico (KN/mc) del materiale per la sezione della trave in modo da ottenere il carico della trave a metro lineare, ricordandoci di dividerlo per l’interasse del solaio dato:

q_trave = (25 KN/mc x 0.30 m x 0.35 m) / 4 m = 0.656 KN/mq

qs + q_trave  =  (1.44 + 0.656) KN/mq = 2.096 KN/mq

Avendo scelto una sezione in C.A. 30x35cm la trave non è verificata

Procediamo nuovamente al calcolo del peso proprio della trave ipotizzando una sezione in C.A. 30x40cm, questa volta la trave è VERIFICATA.

 

Solaio in Acciaio

 

Carichi strutturali (qs)                                                                                                 

_travetti Ipe 140

 [0.129 KN/m x  1m x (1m/0,5)]/ 1mq = 0.258 KN/mq

_caldana in malta di cemento + lamiera grecata tipo SOLAC (da scheda tecnica)

1.7 KN/mq

TOT.  =  1.958 KN/mq

 

Carichi permanenti (qp) 

_sottofondo in malta di calce

(18 KN/mc x 0,030 m x 1m x 1m)/ 1mq = 0.54 KN/mq

_Pavimento parquet in legno

(8 KN/mc x 0,02 m x 1m x 1m)/ 1mq = 0.16 KN/mq

_incidenza tramezzi  =      1 KN/mq

_incidenza impianti =   0.5 KN/mq

 TOT.  =  2.2 KN/mq    

        

Carichi accidentali (qa)

Ambiente ad uso residenziale (Normativa)

TOT. = 2 KN/mq

 

Possiamo calcolare il carico q al metro lineare                                                                      

_qtot (Kn/m)= (1.3 x qs + 1,3 x qp + 1,5 x qa) x 4 = 33.62 KN/m

Dopo aver inserito la luce per ottenere il momento, sempre pari qL²/8 , vediamo ora come calcolare il profilo di trave da utilizzare.

Nel caso dell’acciaio il valore della resistenza caratteristica  fy,k, dipende dal tipo di acciaio scelto (nel nostro caso abbiamo usato un acciaio di classe Fe 430/S275 con resistenza caratteristica di snervamento pari a 275 Mpa).

La tensione sig_am è uguale a quella caratteristica fy,k divisa per il  coefficiente di sicurezza γ, pari a 1,15.

sig_am = (fm,k / γ) = 239,13 N/mm²

L’ultimo passaggio consiste nello scegliere un profilo IPE che abbia un modulo di resistenza W_x  (valore tabellato) maggiore di quello che si ottiene dalla tabella grazie alla formula di Navier. Scegliamo il valore immediatamente superiore a 632,70 cm³, quindi Wx= 713 cm³  relativo ad una IPE 360.

Verifichiamo se la trave resiste al peso proprio ovvero se aggiungendo il carico della trave al q_s che abbiamo precedentemente ottenuto il modulo di resistenza della trave risultante sia inferiore da quello da noi scelto.

Dividiamo il peso lineare (KN/ml) del profilo per l’interasse del solaio dato.

 Q_{trave al mq} = peso lineare / INTERASSE e lo sommiamo al  q_sprecedente.

0,491 KN/mq /4m = 0,123 kN/mq

Avendo scelto una profilo IPE 330 (Wx = 713 cm³) la trave è VERIFICATA.

 

 

 

 

 

 

 

In questa esercitazione ho sperimentato la progettazione e, quindi, il processo di dimensionamento di una trave portatrice di tre tipi di solaio (calcestruzzo, acciaio e legno), mantenendo fissa la luce della trave e quindi facendo riferimento ad una stessa carpenteria per ognuno dei casi di studio.

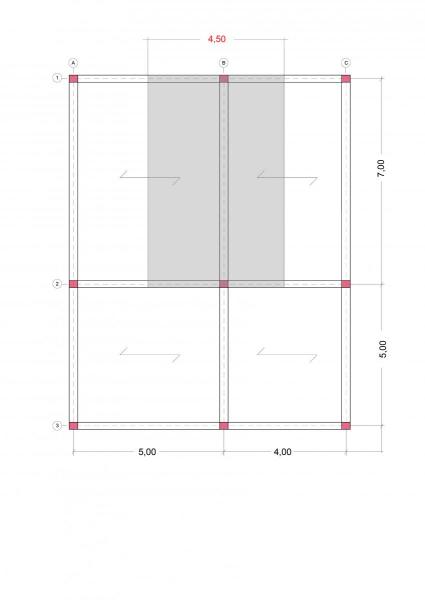
La carpenteria scelta è la seguente:

In basso ho evidenziato quella che è l’area su cui insiste la porzione di solaio gravante sulla trave principale B, che risulta essere la più sollecitata dell’intera struttura, andando essa a coprire un interasse i= 4,5 metri. Questa sarà quindi la trave di progetto in quando il suo dimensionamento andrebbe bene, cioè, sarebbe verificato anche per le altre travi principali che supportano un carico minore.

 

SOLAIO CEMENTO ARMATO

La prima tipologia di solaio presa in esame è stata quella di un solaio di interpiano in CLS.

Riporto in basso la stratigrafia del solaio scelto con la relativa legenda:

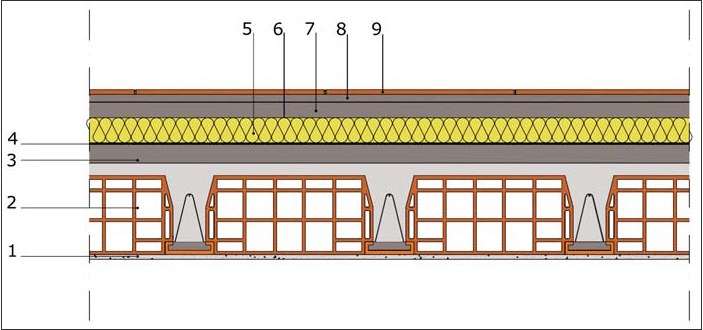
1. Strato di rivestimento in intonaco di calce-cemento, sp. 15 mm

2. Struttura portante in laterocemento a travetti e blocchi interposti, sp. 250+40 mm di getto di completamento

3. Massetto di pendenza in cls alleggerito con argilla espansa, sp. 40 mm

4. Strato di barriera al vapore (non la terrò in conto ai fini dei calcoli)

5. Pannello isolante, sp. 80 mm

6. Membrana impermeabilizzante (non la terrò in conto ai fini dei calcoli)

7. Strato di ripartizione in calcestruzzo, sp. 50 mm

8. Malta di sottofondo, sp. 20mm

9. Pavimentazione in laterizio, sp.15 mm

 

Per prima cosa ho dovuto calcolarmi manualmente il valore della azioni agenti sull’area di influenza, calcolando quindi il peso su superficie unitaria di ognuno degli strati componenti il solaio (P/s= Volume x peso specifico del materiale/superficie)

• azioni pemanenti strutturali qs (carichi che sono presenti e costanti durante il tempo di vita, o gran parte di essa, di una data struttura)

qs:       caldana: (0,04*1,00*1,00) mc/mq * 25 kN/mc= 1,00 kN/mq

             travetti 2*(0,12*0,25*1,00) mc/mq * 25 kN/mc= 1,50 kN/mq

             blocchi laterizio 2*(0,38*0,25*1,00) mc/mq * 5,5 kN/mc= 1,04 kN/mq

qs tot= (1,00+1,50+1,04)= 3,54 kN/mq

• azioni permanenti non strutturali qp (carichi portati dovuti a tutti quegli elementi che pur essendo parte integrante della struttura non hanno funzione strutturale, come tramezzi, arredi fissi, bagni, pavimenti etc…)

qp:       massetto cls alleggerito (0,04*1,00*1,00)mc/mq * 18 kN/mc= 0,72 kN/mq

             isolante (0,08*1,00*1,00) mc/mq * 0,5 kN/mc= 0,04 kN/mq

             strato di ripartizione cls (0,05*1,00*1,00) mc/mq *24 kN/mc= 1,2 kN/mq

             malta di sottofondo (0,02*1,00*1,00) mc/mq * 21 kN/mc= 0,42 kN/mq

            intonaco 0,3 kN/mq

            impianti 0,5 kN/mq

            tramezzi 1,00 kN/mq

qp tot= (0,72+0,04+1,2+0,42+0,34+0,3+0,5+1,00)= 4,52 kN/mq

(i valori del carico dovuto alla presenza di impianti e tramezzi sono tabellati dalla normativa)

• azioni variabili qa (tutti i carichi dovuti alla presenza di oggetti che non costituiscono parte integrante della costruzione, comprese le persone che la occupano, essi possono variare nel tempo)

qa:  3,00 kN/mq à valore tabellato da normativa, dipendente dalla destinazione d’uso dell’ambiente architettonico preso in esame, in questo caso ho scelto di immaginare il solaio come interpiano di un edificio per uffici aperti al pubblico.

A questo punto ho dovuto combinare le azioni allo stato limite ultimo (stato il cui superamento comprometterebbe in modo rilevante la capacità portante della struttura), moltiplicando ogni carico per il suo coefficiente di sicurezza gamma, (costante che mi permette di ampliare il valore di carico considerato, assicurandomi un margine di sicurezza maggiore di quello effettivo della struttura progettata) ed infine sommando tra loro i tre carichi. La formula generale di combinazione dei carichi riportata su normativa è la seguente:

                                                             Fd = γgGk +γpPk +γqQlk + ∑n i=2 γq (ψ0i⋅Qik)

Gk, Pk e Qlk sono rispettivamente i nostri carichi qs, qp e qa

 γg, γp γq sono i coefficienti di sicurezza associati ad ogni tipo di azione (rispettivamente 1,3, 1,3 e 1,5)

∑n i=2 γq (ψ0i⋅Qik) questo termine fa riferimento a valori caratteristici di altri carichi che sono scalati con i rispettivi coefficienti di combinazione che tengono in conto la probabilità delle azioni di verificarsi contemporaneamente. ( Non verranno da me considerati).

Grazie al foglio excel ho potuto combinare i carichi e moltiplicarli per l’interasse i=4,50 m, ottenendo il mio carico lineare q (kN/m). (Più precisamente si moltiplica la somma dei carichi amplificati con i loro coefficienti di sicurezza per l’area di influenza (ixl) ottenendo il carico complessivo e, poi, lo si divide per la luce l coperta dalla trave considerata, ottenendo così il carico lineare).

 

A questo punto mi interessa capire quanto vale il momento flettente massimo. Nel mio caso considero la trave come trave appoggiata, il cui momento massimo sarà in mezzeria è sarà uguale a Mmax= ql^2/8 .

(il calcolo è stato svolto automaticamente da excel una volta inseriti i dati dei carichi, interasse e luce).

Quindi, ho scelto un tipo di acciaio per le armature e riportato nella casella fyk, la tensione allo snervamento dei tondini di acciaio di tipo B450 fyd=450 Mpa. Excel mi ha calcolato automaticamente la tensione ammissibile (tensione di progetto) Fyd=Fyk/γm0 = 391,3 Mpa.

In base poi, alla classe di resistenza C32/40 di cls scelta ho riportato i valori di Rck (resistenza  a compressione cubica del cls) e automaticamente ho avuto la resistenza fcd= 0,85Rck/γm0 = 22,67 Mpa.

Fissando, infine, la base di sezione b= 30 cm, excel ha riportato nelle caselle successive del foglio il valore dell’altezza utile h di sezione pari a  55,59 cm ed, avendo scelto un copri ferro di 3,00 cm, un valore di H totale pari a 58,59 cm. Ho scelto allora una trave di sezione 30x60 cm.

Ora ho verificato la trave, tenendo conto del suo peso proprio, peso strutturale (Ptrave= Asezione*l*peso specifico/l= AREA DI SEZIONE*PESO SPECIFICO DEL CLS), peso che vado ad aggiungere al carico q (kN/mq) moltiplicando anch’esso per il coefficiente di sicurezza 1,3 assegnato ai carichi strutturali. 

Così facendo, ottengo un valore di Momento massimo differente, conseguentemente un’altezza utile più alta rispetto alla precedente, pari a 57,59 cm. La mia altezza totale H diventa allora di 60,90 cm.

La sezione che avevo scelto in precedenza non verifica il carico totale comprensivo del peso proprio della trave. Ne scelgo una di sezione 30x65.

Ora, a seguito di questo primo calcolo, ho voluto rendermi conto di cosa succedesse nel caso di dimensionamento di un solaio di copertura. I solai di copertura “pesano” meno di quelli di interpiano, perché su di loro non gravano i carichi accidentali dovuti a persone, gruppi di persone, tramezzi, etc… Quindi, in generale, il dimensionamento di una trave di interpiano dovrebbe in casi standard verificare ampliamente il dimensionamento di una trave di copertura, meno “caricata” di una di un interpiano generico.

Ho quindi ipotizzato un solaio di copertura sempre in laterocemento con lo stesso pacchetto strutturale di quello di interpiano, di questo tipo:

 

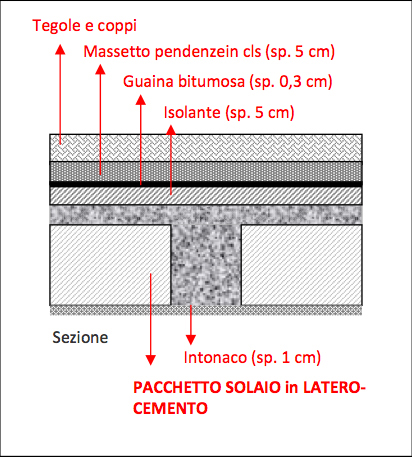
Oltre al pacchetto strutturale base, gli altri strati sono da aggiungere come carichi al qp calcolato precedentemente (meno tramezzi e impianti), qs rimarrà uguale e qa sarà pari a 1,00 kN/mq in quanto considererò una copertura non praticabile, tenendo conto in modo generico di un eventuale carico neve.

 

qs tot:      3,54 kN/mq

 

qp:      isolante  (0,05*1,00*1,00) mc/mq * 0,5 kN/mc= 0,025 kN/mq

           guaina: 0,10 kN/mq

           massetto pendenze (0,05*1,00*1,00)mc/mq * 18 kN/mc= 0,9 mq

           tegole 0,6 kN/mq

           intonaco 0,3 kN/mq

 

qp tot: 1,925 kN/mq

qa tot: 1,00 kN/mq

 

A questo punto il procedimento è lo stesso: ho inserito nel foglio excel tutti i dati e ho ricavato la mia altezza utile h= 42,14 cm, la mia altezza totale H= 45.14 cm. La sezione della trave è stata ingegnerizzata come 30x50 cm. Quella di interpiano era di 30x65, quindi può benissimo essere utilizzata anche per sorreggere il solaio di copertura.

Ho, per una sicurezza maggiore, svolto il calcolo di verifica della trave tenendo conto del suo peso proprio. 

La H= 47,47 cm, quindi la sezione scelta di 30x50 cm risulta corretta e comunque verificata dalla sezione della trave di interpiano.

 

SOLAIO ACCIAIO

Il medesimo ragionamento fatto per progettare la trave in cls, con qualche differenza dovuta a caratteristiche di materiale e normativa, è stato effettuato per dimensionare la trave in acciaio di un solaio interpiano.

In basso riporto la stratigrafia del solaio scelto con materiali e spessori:

 

 

 

Ho calcolato i carichi qs, qp e qa:

 

qs:     lamiera grecata 0,10 kN/mq

         

          soletta in cls  (0,12*1,00*1,00)mc/mq * 25 kN/mc= 3 kN/mq

 

          travetti IPE 140 2*(0,12kN/mq)= 0,24 kN/mq

  

qs tot= (0,1+3,00+0,24)= 3, 46 kN/mq

 

qp:     pavimento parquet    (0,018*1,00*1,00) mc/mq * 7,06 kN/mc= 1,27 kN/mq

          

           massetto   (0,05*1,00*1,00)mc/mq *18 kN/mc=0,9 kN/mq

 

           controsoffitto in cartongesso   (0,015*1,00*1,00)mc/mq*13 kN/mc= 0,19 kN/mq

 

qp tot= (1,27+0,9+0,19)= 2,36 kN/mq

 

qa= 3,00 kN/mq (uffici aperti al pubblico)

Inseriti tutti questi valori su excel ho potuto prender nota di quello che fosse il Momento massimo sempre considerando la mia trave come trave appoggiata e quindi mantenendo la formula M= ql^2/8. A questo punto ho scelto il tipo di acciaio S275 e inserito nella tabella il valore fyk=275 Mpa. Excel mi ha calcolato la sigma ammissibile= 239,13 Mpa e conseguentemente il valore del modulo di resistenza Wx= 1390,74 cmc.

A questo punto ho scelto sul profilario delle travi IPE una sezione avente un modulo di resistenza Wx maggiore o pari a quello ottenutoà ho scelto la trave IPE450 con Wx=1500 cmc.

Ho voluto allora verificarla in due modi: il primo più immediato, inserendo come avevo fatto nel caso del cls il peso proprio della trave all’interno del carico q e verificando che il modulo Wx ottenuto fosse ancora inferiore a quello della IPE450 scelta. Il modulo Wx è risultato pari a 1416,05  e dunque con questo metodo la trave è stata verificata.

Il secondo metodo ha previsto la verifica tramite la seguente disuguaglianza:

 

Sigmax<sigamm     con sigma ammissibile= 239,13 Mpa.

 

So che:

Sigmax= Mmax/Wx -->338,621*10^3*10^3 N*mm/1500 * 10^3mmc=225,74 Mpa<239,13Mpa.

La trave risulta verificata!

(Il valore del momento era quello ottenuto una volta aggiunto il peso proprio della trave al carico q totale).

Ora, per fare un ulteriore piccolo esperimento ho cambiato il tipo di acciaio, scegliendone uno meno resistente, un Fe360/S235, dunque ho modificato nella tabella il valore di fyk inserendovi 235 Mpa. Ho ottenuto un modulo di resistenza Wx= 1627,47cmc. Ho scelto allora una trave IPE500 con Wx=1930cmc. Ho verificato la trave tenendo conto del suo peso proprio, ottenendo un Wx=1600 cmc. Quindi, essa risultava ancora verificata.

Inoltre ho verificato che la Sigmax fosse minore della Sigammissibile.

339,576*10^3 * 10^3 N*mm/1600*10^ 3mmc= 175,94 Mpa<204,35 Mpa.

 

SOLAIO LEGNO

Questo è il tipo di solaio scelto per dimensionare la trave in legno lamellare di tipo GL32c.

   

 

Gli strati partendo dall’alto verso il basso prevedono i seguenti materiali:

 

-Pavimentazione in parquet

 

-massetto cls alleggerito 0,03 m

 

-pavimento radiante (che considererò come peso permanente di impianti)

 

-isolante acustico

 

-massetto isolante cls alleggerito

 

-doppio assito incrociato 0,07 m

 

-travetti

 

Per fare un progetto più accurato, ho voluto dimensionare anche i travetti, perché anch’essi possono considerarsi come elementi strutturali e allora posso comunque progettarli come ho fatto fino ad ora con le travi. Ho calcolato il carico gravante su di essi, tenendo presente che l’interasse del travetto più carico è i=1,00 m e la luce l=5,00 m.

 

qs:      doppio assito 2*(0,35*1,00*1,00)mc/mq * 6kN/mc= 0,42 kN/mq

 

qs tot: 0,42 kN/mq

 

qp:      parquet 0,2 kN/mq

           

            massetto (0,03*1,00*1,00)mc/mq*18kN/mc= 0,54 kN/mq

 

            isolante 0,64 kN/mq

   

            massetto 0,5 kN/mq

 

            impianti 0,5 kN/mq

 

            tramezzi 1,00 kN/mq

 

qp tot: 3,6 kN/mq       

 

qa: 2,00 kN/mq (in questo caso, diversamente dai due precedenti, ho scelto di analizzare un solaio per una civile abitazione, ho preso allora questo valore tabellato da normativa).

Tutti questi dati li ho inseriti in excel ed ho ottenuto il valore di q e del momento massimo M. A questo punto, in base al tipo di legno scelto (GL32c) ho dovuto inserire il valore della resistenza caratteristica fm,k=32 Mpa e poi il valore di kmod (coefficiente che tiene conto della durata del legno nel tempo, cioè del carico dovuto all’umidità e della struttura)=0,8 (media durata). A questo punto excel mi ha calcolato la Sigma ammissibile=17,66 Mpa.

Conseguentemente ho ottenuto il valore di H=24,13 cm, fissata una base b=15 cm.

Ho scelto una sezione di 15x25cm. Ora, tenendo conto del peso del travetto ho rifatto il calcolo e verificato che la sezione scelta fosse corretta e così è stato. (Il peso=Area sezione travetto* peso specifico=0,22 kN/m da aggiungere a q). H=24,56<25.

Inoltre, so che la Sigmamax=Mmax/Wx e che Wx=bh^2/6. Ricavo quindi dalla formula inversa h= (6*Mmax/b*Sigma)^0,5= (6*26,62*10^3*10^3N*mm/150mm*17,66N/mmq)=24,55 cm. La trave è verificata.

 

A questo punto ho dimensionato la trave principale, aggiungendo al carico qs precedentemente calcolato il peso dei travetti progettati. Qp e qa sono rimasti invariati.

 

qs tot:       0,42+ (0,15*0,25)*2*7,65 kN/mq= 0,99 --> 1,00 kN/mq

 

qp tot: 3,6 kN/mq

 

qa: 2,00 kN/mq

Inserendo tutti i valori su excel, ho ottenuto un’altezza h=52,95 cm con una base fissata b=30 cm. Ho scelto una sezione di 30x55 cm. A questo punto ho voluto verificarla tenendo conto del suo peso proprio (p =1,37 kN/m), aggiungendolo al carico totale q (kN/m) e verificando che l’altezza fosse minore di 55 cm. Inoltre, Sigmax=Mmax/Wx-->h=(6*Mmax/b*Sigma)^0,5= (6* 258,475*10^3*10^3 N*mm/300mm*17,66N/mmq= 54,1 cm. La trave risulta verificata con entrambi i metodi.

                          SOLAIO IN ACCIAO

1-pavimento di parquet in Rovere (spessore:2,5cm)

2-massetto (spessore:6cm9

3-rete elettrosaldata (spessore:6mm9

4-lamiera grecata tipo HiBond A55/P600(spessore:8mm x 20cm x 20cm)+ soletta(spessore:10cm)

5-trave IPE 240

Definizione dei carichi

qs=travi,travetti,lamiera grecata ,soletta

qp=pavimento in parquet,massetto,rete elettrosaldata,impianti,tramezzi

qa=2KN/mq

Dimensionamento travetti(luce:3m,interasse:1m);area di influenza: 3mq

                   calcolo qs

-lamiera grecata (spessore:8mm)

                            Peso al mq=0,104KN/mq

-Soletta in cemento (spessore:10cm)

                                Peso specifico: 21KN/mc

                         Volume al mq: 0,1mx1mx1m=0,1mc

                           Peso al mq: 0,1mx21KN/mc=2,19KN/mq

 

                  qs=2,19KN/mq

                                         calcolo qp

-Pavimento in parquet di Rovere (spessore:2,5cm)

                                 Peso specifico:7,2KN/mc

                           Volume al mq: 0,025mx1mx1m=0,025mc

                             Peso al mq: 0,025mx7,2KN/mc=0,18KN/mq

-Massetto (spessore:6cm)

                          Peso specifico:20KN/mc

                       Volume al mq: 0,06mx1mx1m=0,06mc

                           Peso al mq: 0,06mx20KN/mc=1,2KN/mq

-Rete elettrosaldata 820/2 AD(DIAM.8MM;20CMX20CM)      

              

                                 Peso al mq=0,04KN/mq

-Incidenza Impianti: 0,5KN/mq

-Incidenza Tramezzi: 1KN/mq

                                 qp=1,42+0,5+1=2,92KN/mq

                                      calcolo totale

(qs+qp+qa)xinterasse=(2,19+2,92+2)KN/mqx1m=7,11KN/m

Scelgo di utilizzare un acciaio con valore di snervamento fy,k = 235 N/mmq (classe Fe 360/S235)e, inserendo i dati nel foglio excel, ottengo un Modulo di Resistenza Wx (Momento max/ tensione di progetto) pari a 62,8 cm.

Calcolo del momento massimo

M=qxl^2/8=7,11x(3,8x3,8)/8=12,83KNm

Calcolo della tensione di progetto sig.am

fy,k/1,45=204,35N/mmq

Modulo di resistenza

Wx=Mx1000/Sig.am=62,8cmc

-Attraverso il risultato ottenuto si puo scegliere un travetto IPE 140(14cm x7,3cm) con Wx=77,3cmc e peso pari a 0,129KN/m

                     Verifica

Per effettuare la verifica devo sommare al qs iniziale il peso relativo ai travetti:

-Nuovo calcolo aggiungendo il peso dei travetti al metro lineare totale

peso travetto al mq=(0,129KN/mq)/1m=0,129KN/mq

                      qs=(2,19+0,129)KN/mq= 2,32KN/mq

-Anche aggiungendo il peso dei travetti ottengo un risultato inferiore al Wx trovato in precedente;la trave IPE 124 è ugualmente verificata (63,95<77,3cmc)

Dimensionamento trave (luce =4m; interasse = 3,8 m; area di influenza = 15,2 mq):

Il dimensionamento della trave avviene utilizzando i valori di carico trovati in precedenza, comprensivi del peso relativo ai travetti; devo però cambiare l'interasse e la luce della trave.

calcolo strutturale qs

° lamiera grecata=0,0915KN/mq

°soletta=2,1KN/mq

°travetti IPE 140= 0,129KN/mq

                     Totale=2,32KN/mq

sovraccarivo permanente qp

2,92KN/mq

sovraccarivo accidentale qa

2KN/mq

                            foglio excel(trave)

-calcolo del carico totale a metro lineare:

(qs+qp+qa)x i=(2,32+2,92+2)x3,8=27,51KN/m

-calcolo del momento massimo

M=qxl^2/8=27,51x(4x4)/8=55,02KN/m

-calcolo della tensione di progetto sigam

fy,k/1,15=235/1,15=204,35N/mmq

-calcolo del modulo di resistenza

Wx=Mx1000/Sigam=269,27cmc

-Attraverso il risultato ottenuto si puo scegliere una trave  IPE 240(24cm x 12cm) con Wx=324cmc e peso pare a 0,3KN/m

 verifica

Per effettuare la verifica devo sommare al qs iniziale il peso relativo ai trave:

peso trave al mq=0,3KN/m/3,8m(interasse)=0,078KN/mq

                      qs=(2,32+0,078)=2,39KN/mq

-anche aggiungendo il peso della trave ottengo un risultato inferiore al Wx trovato in precedente ,la trave IPE 240 è ugualmente verificata(271,81<324cmc)

 

                                      SOLAIO IN CLS

1-pavimento in parquet di Rovere(spessore:2,5cm)

2-malta di cemento(spessore:15cm)

3-massetto in cls (spessore:4cm)

4-soletta (spessore:5cm)

5-pignata in laterizio (spessore:20cm)

6-intonaco (spessore:15cm)

Definizione dei carichi

qs=solaio in laterocemento

qp=pavimento in parquet di rovere,malta di cemento,massetto,intonaco,impianti,tramezzi

qa=2KN/mq

                     Calcolo qs

-Solaio in laterocemento(20cm blocco + 5cm soletta)

                     qs=3,17KN/mq (valore tabellato)

                        Calcolo qp

-Pavimento in parquet di Rovere (spessore:2,5cm)

peso specifico:7,2KN/mc

volume al mq:0,025mx1mx1m=0,025mc

peso al mq=0,025mx7,2KN/mq=0,18KN/mq

-malta di cemento (spessore:15cm)

peso specifico:21KN/mc

volume al mq:0,015mx1mx1m=0,015mc

peso al mq=0,015mx21KN/mq=0,31KN/mq

-massetto in cls (spessore:4cm)

peso specifico:20KN/mc

volume al mq:0,04mx1mx1m=0,04mc

peso al mq=0,04mx20KN/mq=0,8KN/mq

-intonaco (spessore:15cm)

peso specifico:10KN/mc

volume al mq:0,015mx1mx1m=0,015mc

peso al mq=0,015mx10KN/mq=0,15KN/mq

-incidenza impianti: 0,5KN/mq

-incidenza tramezzi: 1KN/mq

                          qp=(0,18+0,31+0,8+0,15+0,5+1)KN/mq=2,94KN/mq

Calcolo del carico totale a metro lineare

             (qs+qp+qa)xi=(3,17+2,94+2)KN/mqx3m=24,33KN/m

Calcolo del momento massimo

                   M=qxl^2/8=24,33x(4mx4m)/8=48,66KNm

Calcolo della tensione di progetto Sig.fa

              fy/1,15=450/1,15=391,30N/mmq

-Acciaio B450C

il valore di progetto della tensione dell'acciaio sarà pari al valore massimo della tensione fy diviso il coefficiente di sicurezza 1,15

Calcolo della tensione di progetto Sig.ca

            Rck/1,5=40/1,5=26,67N/mmq

-Calcestruzzo C40/50

il valore di progetto della tensione del calcestruzzo sarà pari alla resistenza cilindrica Rck diviso il coefficiente di sicurezza 1,5.

Calcolo della sezione della trave

stabilendo una sezione di base pari a 20cm ottengo un'altezza utile pari a 20,84cm,l'atezza utile corrisponde alla distanza tralembo compresso del calcestruzzo e l'armatura tesa.per trovare l'altezza totale della sezione(H) si sommerà l'altezza utile e copriferro(delta:5cm)--->25,84cm

-Quindi scelgo una sezione di trave 20cm x30cm

verifica

per effettuare la verifica devo sommare al qs iniziale il peso relativo della trave

peso specifico: 24KN/mc  (trave in c.a)

volume della trave:0,2x0,3x3=0,18mc

peso della trave=0,18mc x 24KN/mc=4,32kN/mq

il peso della trave distribuito sull'area d'influenza =4,32KN/mq/12mq=0,36KN/mq

                      qs=(3,17+0,36)=3,53KN/mq

Carico totale

q=(3,53+2,94+2)KN/mq x 3m=25,41KN/m

-Anche sommando il carico della trave,la sezione ipotizzata (20cmx30cm) viene ugualmente verificata (28,89<30cm).

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

                                        

1- solaio in legno:

2- solaio in acciaio

solaio in cls armato:

 

 

 

 

 

 

                                     SOLAIO IN LEGNO

                                La geometria e lo schema strutturale

Nel solaio la orditura principale è costituita da una trave 23x25 cm e la secondaria è costituita da travetti 9x11 cm poggianti da un lato sulla muratura e dall’altro sulla trave principale. La pavimentazione è costituita da un massetto e da tavelle in cotto. Superiormente è appoggiato un ulteriore pavimento in parquet sostenuto da un’orditura di travetti di interasse di 61 cm appoggiati a pilastrini in mattoni di interasse 66 cm.

Destinazione d'uso:

Categoria A(Ambienti ad uso residenziale)

Definizione dei carichi:

Carichi strutturali: Travi, Travetti(orditura secondaria),Tavolato

Carichi permanenti: pavimento di parquet,travetto,muricci in mattoni pieni,tavella in cotto,sottofondo,impianti,tramezzi

Carico accidentale: 2KN/mq

 

Dimensionamento travetti (luce = 3,8 m; interasse = 1m; area di influenza = 3,8 mq):

                           Calcolo qs

-Tavolato in legno di abete (spessore:2,5cm)

                           Peso specifico:4,5KN/mc

                       Volume al mq: 0,025mx1mx1m=0,025mc

                        Peso al mq: 0,025mx4,5KN/mc=0,11KN/mq

                         qs=0,11KN/mq

                                       Calcolo qp

-Pavimento in parquet di Rovere (spessore:2,5cm)

                                Peso specifico:7,2KN/mc

                             Volume al mq: 0,025mx1mx1m=0,025mc

                                 Peso al mq: 0,025mx7,2KN/mc=0,18KN/mq

-Travetto in legno lamellare (classe di resistenza GL24h,dim:13x8cm)

                         Peso specifico:3,73KN/mc

                         Volume al mq: (0,13x0,08)mx1mx1m=0,01mc

                            Peso al mq: 0,01mx3,73KN/mc=0,038KN/mq

-Pilastrino in mattoni (altezza:12,5cm)

                        Peso specifico:6,4KN/mc

                               Volume al mq: 0,125mx1mx1m=0,125mc

                                Peso al mq: 0,125mx6,4KN/mc=0,8KN/mq

-Tavella in cotto(spessore:3cm)

                           Peso specifico:0,28KN/mc

                                  Volume al mq: 0,03mx1mx1m=0,03mc

                                Peso al mq: 0,03mx0,28KN/mc=0,0084KN/mq

-Massetto alleggerito(spessore:8,5cm)

                                 Peso specifico:4,71KN/mc

                                     Volume al mq: 0,085mx1mx1m=0,085mc

                                      Peso al mq: 0,085mx4,71KN/mc=0,4KN/mq

-Incidenza Impianti: 0,5KN/mq

-Incidenza Tramezzi: 1KN/mq

                              qp=0,18+0,038+0,8+0,0084+0,4+0,5+1=2,92

                                           qp=2,92KN/mq

                                                   Calcolo Totale:

                                  (qs+qp+qa)xinterasse=(0,11+2,92+2)KN/mqx1m=5,03KN/m

                             Scelgo di utilizzare un travetto in legno lamellare di tipo GL 28h (resistenza a flessione fm,k = 28 N/mmq):

 

 

 

Il valore di Kmod relativo alla durata del materiale (legno lamellare) viene ricavato dalla tabella e fissato a 0,6:

                             Calcolo del momento massimo

                            M=qxl^2/8=5,03x(3,8x3,8)/8=9,07KNm

                             Calcolo della tensione di progetto sig.am

                                       fm,k=28N/mmq ;kmod= 0,6

                                 fm,k x kmod/1,45=28x0,6/1,45=11,59N/mmq

Calcolo dell'altezza del travetto stabilendo una base di 9cm

h=(6xMx1000)/bxSigam)^0,5=15,33cm

Inserendo pure i dati nel foglio excel ,scegliendo una base per il travetto di 20 cm, ottenendo un'altezza minima per la sezione di 15,33 cm:

Attraverso il risultato ottenuto si può scegliere un travetto di sezione 20cmx20cm

                         Verifica

Per effettuare la verifica devo sommare al qs iniziale il peso relativo ai travetti:

                   Peso specifico:4,5KN/mc

                         Volume travetto al mq: (0,2x0,2)mx1mx1m=0,04mc

                           Peso travetto al mq: 0,04mx4,5KN/mc=0,18KN/mq

                            qs=(0,11+0,18)KN/mq=0,29

                                          qs=0,29KN/mq

 

-Anche aggiungendo il peso dei travetti ottengo un risultato inferiore,la sezione è verificata (15,60<20).

                 

                    Dimensionamento trave (luce = 5,5 m; interasse = 3,8 m; area di influenza = 20,9 mq):

Il dimensionamento della trave avviene utilizzando i valori di carico trovati in precedenza, comprensivi del peso relativo ai travetti; devo però cambiare l'interasse e la luce della trave e scegliere un legno con maggiore resistenza a flessione; in questo caso opto per un legno lamellare di tipo GL 36c (resistenza a flessione fm,k = 36 N/mmq).

Inserisco i dati nel foglio excel e scelgo una base per la trave di 23 cm, ottenendo un'altezza minima per la sezione di 36,21 cm:           

                        

Scelgo quindi di utilizzare un travetto di sezione 23 cm x 40 cm.

                             Verifica:

 

Per effettuare la verifica devo sommare al qs iniziale il peso relativo alla trave:

 

Peso Specifico = 4,5 KN/mc

Volume trave = 0,23 m x 0,40m x 5,5m = 0,506 mc

Peso trave = 0,506 mc x 4,5 KN/mc =2,27 KN/mq

Peso trave distribuito sull'area di influenza = 2,27 KN/mq / 20,9 mq = 0,108 KN/mq

 

qs = (0,29 + 0,108) KN/mq = 0,398 KN/mq

 

                                              

 

 

 

 

Poiché l'altezza minima è pari a 36,58 cm la sezione è verificata (36,58 cm < 40 cm).

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

  

Dimensionamento della trave più sollecitata del solaio in figura. L'operazione verrà eseguita per il dimensionamento di una trave in cls armato, in acciaio e in legno.

Prendo in considerazione il solaio in figura, la trave più sollecitata è quella in evidenza poichè l'area di influenza è maggiore rispetto alle altre ed è pari a 4m x 6m = 24m² 

Per il calcolo ci aiuteremo con un foglio Excel preimpostato.

SOLAIO IN CALCESTRUZZO

Il primo passo è fare l'analisi dei carichi strutturali qs, i carichi permanenti qp e i carichi accidentali qa.

Analisi dei carichi strutturali qs

Pignatte

(0,20m x 0,40m x 1m)/m² x 11KN/m³ x 2 = 1,76KN/m²

Calcestruzzo armato

(0,086m³/m²) x 25KN/m³ = 2,15KN/m²

TOTALE= 1,76KN/m² + 2,15KN/m² = 3,91 Kn/m²

Analisi dei carichi permanenti qp

Intonaco

(0,015m x 1m x 1m)/m² x 18 KN/m³ = 0,27 KN/m²

Massetto

(0,04m x 1m x 1m)/m² x 18KN/m³ = 0,72 KN/m²

Allettamento

(0,03m x 1m x 1m)/m² x 20 KN/m³ = 0,6 KN/m²

Pavimento (granito)

(0,02m x 1m x 1m)/m² x 27Kn/m³ = 0,54 KN/m²

Totale = 0,27 KN/m² + 0,72 KN/m² + 0,6 KN/m² + 0,54 KN/m²

Si aggiungono ai carichi permanenti, i carichi dati dalla normativa, dei tramezzi (1KN/m²) e degli impianti (0,5KN/m²)

TOTALE= 2,13 KN/m² + 1KN/m² + 0,5KN/m² = 3,63 KN/m²

Analisi dei carichi accidentali qa

Ambiente ad uso residenziale (Normativa)

TOTALE = 2KN/m²

Dopo aver fatto i calcoli inseriamo nella tabella i carichi strutturali qs, i carichi permanenti qp e i carichi accidentali qa. La tabella moltiplicherà tali valori per un coefficiente di sicurezza di 1,3 per i qs e i qp e 1,5 per i qa. La trave presa in considerazione è una trave appoggiata quindi il momento è pari a M= ql²/8. Per le armature scelgo una resistenza caratteristica fyk=450 MPa mentre per il cls prendo C 40/50 con resistenza caratteristica a compressione Rck=50Mpa. Quindi con una base b=30cm, avrò un'altezza H=40,50cm. Ingegnerizziamo quindi la sezione portandola ad un'altezza H=45cm.

In questo calcolo non abbiamo tenuto conto del peso proprio della trave. Dobbiamo quindi inserire il peso proprio della trave nella tabella excel, per verificare che la trave che abbiamo dimensionato con sezione di 45cmx30cm vada bene.

Sia p il carico proprio della trave.

p = (0,30m x 0,45m x 1m)/m x 25KN/m³ = 3,375 Kn/m

Il carico dovrà essere inserito nella casella q della tabella excell moltiplicato per il fattore di sicurezza 1,3. Se la nuova H sarà minore di 45cm allora il dimensionamento è stato fatto correttamente.

La sezione precedentemente dimensionata risulta verificata.

SOLAIO IN ACCIAIO

Analisi dei carichi strutturali qs

Travi secondarie (IPE 180)

(0,00239m² x 1m)/m² x 78,50 KN/m³ x 2 = 0,38KN/m²

Lamiera grecata

0,10 KN/m²

Getto in cls

(0,09m² x 1m)/m² x 24KN/m² = 2,16KN/m²

TOTALE= 0,38KN/m² + 0,10 KN/m² + 2,16 KN/m² = 2,64KN/m²

Analisi dei carichi permanenti qp

Strato in cls alleggerito

(0,08m x 1m x 1m)/m² x 18KN/m³ = 1,44 KN/m²

Pavimento (granito)

(0,02m x 1m x 1m)/m² x 27KN/m³ = 0,54 KN/m²

Si aggiungono ai carichi permanenti, i carichi dati dalla normativa, dei tramezzi (1KN/m²) e degli impianti (0,5KN/m²)

TOTALE= 1,44 KN/m² + 0,54KN/m² + 1KN/m² + 0,5KN/m² = 3,48 KN/m²

Analisi dei carichi accidentali qa

Ambiente ad uso residenziale (Normativa)

TOTALE = 2KN/m²

Inseriamo i carichi nella tabella excel, come fatto precedentemente.

Per dimensionare la trave è necessario confrontare il modulo di resistenza Wx dato dalla tabella Excel con i moduli di resistenza dati dal profilario.

Possiamo quindi prendere come trave una IPE 400 con Wx=1160cm³.

Inseriamo il peso proprio p della trave nella tabella Excel.

p= (0.00845m² x 1m)/m x 78,50 KN/m³=0,67 KN/m

La sezione precedentemente dimensionata risulta verificata.

SOLAIO IN LEGNO

Analisi dei carichi strutturali qs

Travetto

(0,09m x 0,11m x 1m)/m² x 8KN/m³ x 4 = 0,317 Kn/ m²

TOTALE= 0,317 Kn/ m²

Analisi dei carichi permanenti qp

Parquet-Rovere

(0,025m x 1m x 1m)/m² x 7,2 KN/m³ = 0,18 KN/m²

Travetto Parquet

(0,13m x 0,08m x 1m)/m² x 6 KN/m³ x 3= 0,1872 KN/m²

Pilastrini in mattoni

(0,125m x 0,25m x 1m)/m² x 18KN/m³ x 12= 0,5625 KN/m²

Tavella in cotto

(0,03m x 1m x 1m)/m² x 18KN/m³= 0,54 KN/m²

Massetto

(0,085m x 1m x 1m)/m² x 20KN/m³ = 1,7 KN/m²

Tavolato in pioppo

(0,025m x 1m x 1m)/m² x 7KN/m³ = 0,175 KN/m²

Si aggiungono ai carichi permanenti, i carichi dati dalla normativa, dei tramezzi (1KN/m²) e degli impianti (0,5KN/m²)

TOTALE= (0,18 + 0,1872 + 0,5625 + 0,54 + 1,7 +0,175 + 1 + 0,5) KN/m² = 4,85 KN/m²

Analisi dei carichi accidentali qa

Ambiente ad uso residenziale (Normativa)

TOTALE = 2KN/m²

Dopo aver inserito i carichi nella tabella Excel, scegliamo il legno GL 24h con resitenza a flessione fm,k = 24MPa, si troverà quindi la sigma ammissibile. Impostando la base b=30cm si troverà l'altezza H= 51,40cm.

Si prenderà quindi una sezione pari a 30cmx55cm e si calcolerà il peso proprio p della trave.

p= (0,30m x 0,55m x 1m)/m x 7KN/m³= 1,155 KN/m

La sezione precedentemente dimensionata risulta verificata.