Blog

 

Esercitazione_5

trave VIERENDEEL (metodo delle rigidezze)

 

1_

tipologia di esercizio

L’esercizio inquadra una struttura composta a telaio che usa lo schema del telaio Shear Type, questo tipo di analisi da come si potrà vedere, definirà valori del momento flettente molto minori rispetto al telaio con travi deformabili incernierate.

Come si potrà vedere successivamente la caratteristica principale del telaio Shear Type è quella di presentare una trave infinitamente rigida, la quale ha una rigidezza flessionale che ne impedisce la deformazione. I pilastri sono invece considerati deformabili, trascurandone però l’allungamento (il che avrebbe potuto generare una rotazione rigida della trave).

Fatta questa premessa sul sistema, si può comprendere come l’unico movimento che questo elemento può fare sia quello di traslare orizzontalmente.

 

2_

analisi tramite l’integrazione della linea elastica

Si procede quindi con l’analisi dello spostamento δ ipotizzando un cedimento vincolare elastico in uno dei due estremi e analizzando la curvatura (in una struttura iperstatica un cedimento provoca una curvatura e di conseguenza una tensione) ed il momento flettente (analizzando la deformata e definendone il punto di flesso, possiamo dire che in quel punto il grafico del momento si annullerà).

Si procede quindi all’applicazione del metodo della linea elastica:

 

 

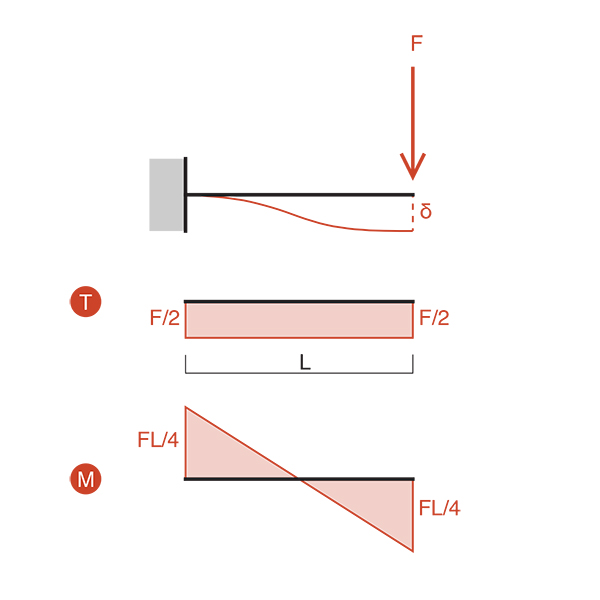
vs= (C₁*s³/6) + (C₂*s²/2) + (C₃*s) + C₄

φ(s)= (C₁*s²/2) + (C₂*s) + C₃

 

 

3_

analisi della deformata

Successivamente definisco le condizioni al bordo:

 

 

_estremo sinistro - incastro: s= 0

In questo punto  lo spostamento verticale e la rotazione della sezione della trave risultano essere pari a zero, quindi abbiamo:

v(0)= 0

φ(0)= 0

 

Sostituendo le due condizioni risultanti nelle rispettive equazioni, derivate sempre dall’integrazione dell’equazione della linea elastica per lo spostamento verticale a cui facciamo riferimento (q(s)= (d⁴v/ds⁴)*E*J) si può constatare che C₃ e C₄ sono nulle.

 

v(0)= 0 ⇒ C₄= 0

φ(0)= 0 ⇒ C₃*s = 0

 

_estremo destro - incastro: s= L

In questo punto  lo spostamento verticale e la rotazione della sezione della trave risultano essere pari a zero, quindi abbiamo:

v(L)= 0

φ(L)= 0

 

Sostituendo le due condizioni risultanti nelle rispettive equazioni, derivate sempre dall’integrazione dell’equazione della linea elastica per lo spostamento verticale a cui facciamo riferimento (q(s)= (d⁴v/ds⁴)*E*J) si può constatare che C₃ e C₄ sono nulle.

 

v(L) = -δ ⇒ C₂= -((6/L²)*δ)

φ(L) = 0 ⇒ C₁= ((12/L³)* δ)

 

4_

equazione di spostamento e rotazione

Sostituendo i valori definiti dall’analisi delle condizioni al bordo della trave possiamo definire le equazioni di spostamento e rotazione:

 

vs= (C₁*s³/6) + (C₂*s²/2) + (C₃*s) + C₄

⇒ C₁= ((12/L³)* δ) ⎫

⎬ ⇒ vs= (((12/L³)* δ)*s³/6) - (((6/L²)*δ)*s²/2)

⇒ C₂= -((6/L²)*δ) ⎭

 

φ(s)= (C₁*s²/2) + (C₂*s) + C₃

⇒ C₁= ((12/L³)* δ) ⎫

⎬ ⇒ φ(s)= (((12/L³)* δ)*s²/2) + (((6/L²)*δ)*s) + C₃

⇒ C₂= -((6/L²)*δ) ⎭

 

Si procede derivando l’equazione della rotazione per ottenere la curvatura, ricavandoci il momento flettente e derivando l’equazione del momento flettente ricavandoci il valore del taglio:

 

φ(s)’= χ ⇒ χ= (((12/L³)* δ)* s) - ((6/L²)*δ)

M= E*J*χ ⇒ M= (E*J)*((((12/L³)* δ)* s) - ((6/L²)*δ))

T= -Ms‘ ⇒ T= -((E*J)*(12/L³)* δ)

 

5_

calcolo dello spostamento e della rigidezza

Attraverso l’equilibrio alla traslazione orizzontale si arriva a definire la relazione che lega lo spostamento δ con lo sforzo di taglio a cui sono soggetti i pilastri. Infatti questi sono legati da una proporzionalità diretta tramite un fattore k definito come rigidezza del pilastro.

 

F= 2T ⇒ F= (2* (E*J)*(12/L³)* δ)

F= ((E*J)*(24/L³)* δ) ⇒ δ= ((F*L³)/(24*E*J))

⇒ k= ((24*E*J)/L³)

 

6_

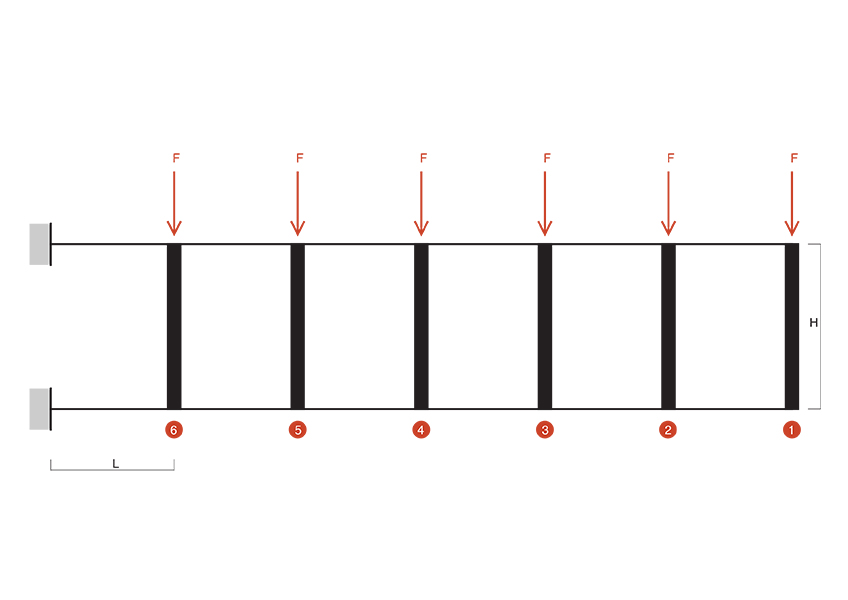
analisi della trave Vierendeel

 

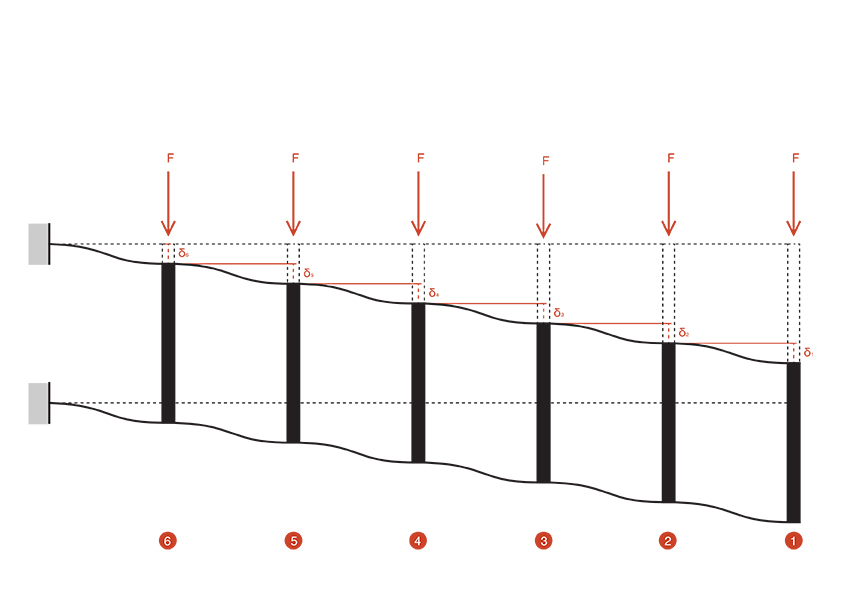
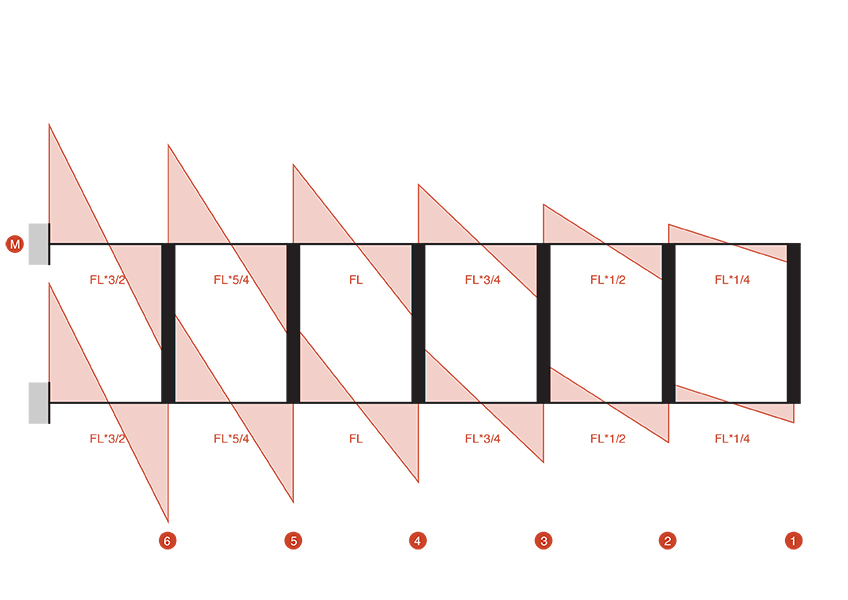
Dall’analisi della deformata della singola trave possiamo ricavare la deformata completa della trave Vierendeel:

 

Passiamo al calcolo del taglio utilizzando l’equilibrio delle forze orizzontali, il quale risulta essere costante nei ritti. Dalla precedente analisi si è quindi capito che la forza agente si ripartisce in maniera proporzionale alla rigidezza e alla luce. Presentando quindi i ritti le stesse caratteristiche in quanto: lunghezza, materiale, sezione; da queste premesse si può capire che quest’ultimi avranno la stessa rigidezza, quindi su ognuno di loro insisterà metà della forza agente.

 

Nodo_1

F= 2T

F= (2* (E*J)*(12/H³)* δ1)

δ1= (F*H³) / ((1/24)*(E*J)) ⇒ T= F*1/2

 

Nodo_2

F= T

F= ((E*J)*(12/H³)* δ2)

δ2= (F*H³) / ((1/12)*(E*J)) ⇒ T= F

 

Nodo_3

F= 2/3*T

F= ((2/3)* (E*J)*(12/H³)* δ3)

δ3= (F*H³) / ((1/8)*(E*J)) ⇒ T= F*3/2

 

Nodo_4

F= 1/2*T

F= ((1/2)* (E*J)*(12/H³)* δ4)

δ4= (F*H³) / ((1/6)*(E*J)) ⇒ T= F*2

 

Nodo_5

F= 2/5*T

F= ((2/5)* (E*J)*(12/H³)* δ5)

δ5= (F*H³) / ((5/24)*(E*J)) ⇒ T= F*5/2

 

Nodo_6

F= 1/3*T

F= ((1/3)* (E*J)*(12/H³)* δ5)

δ5= (F*H³) / ((1/4)*(E*J)) ⇒ T= F*3

 

 

 

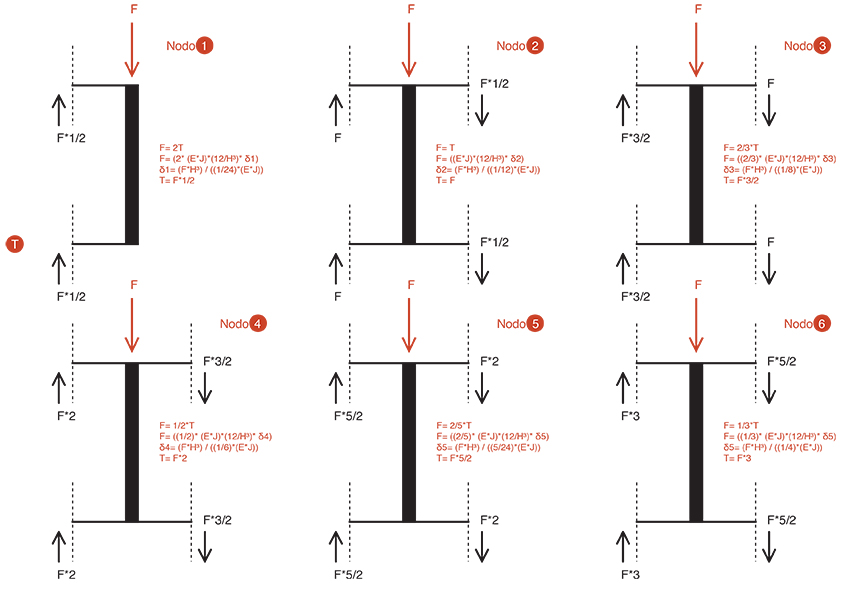
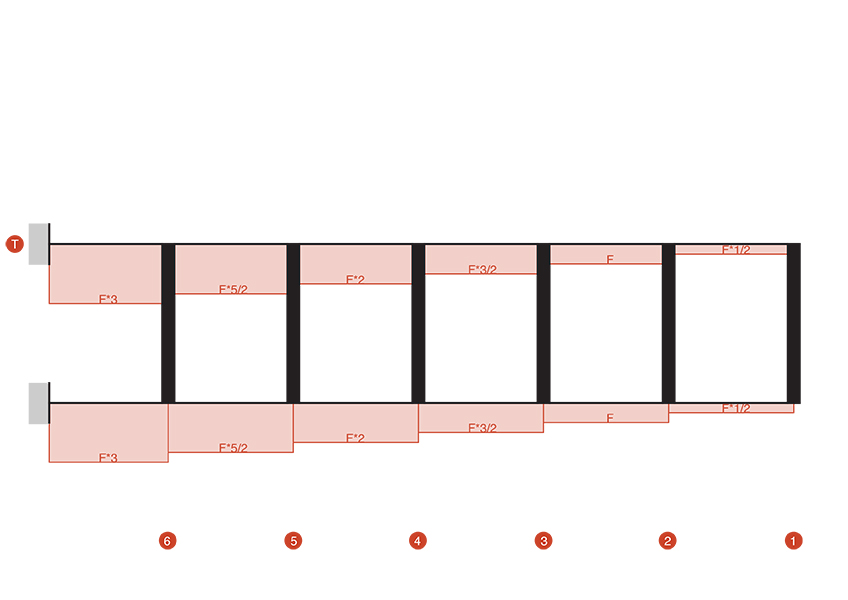
Passiamo al calcolo del momento flettente, sapendo da considerazioni precedenti che la legge del momento avrà un nullo in L*1/2 ci serve un solo altro valore noto per tracciare il diagramma del momento. Questo valore verrà identificato dal momento con polo in L*1/2.

 

Nodo_1

M1= ((F*1/2) * (L*1/2)) ⇒ M1= FL*1/4

 

Nodo_2

M2= (F * (L*1/2)) ⇒ M1= FL*1/2

 

Nodo_3

M3= ((F*3/2) * (L*1/2)) ⇒ M1= FL*3/4

 

Nodo_4

M4= ((F*2) * (L*1/2)) ⇒ M1= FL

 

Nodo_5

M5= ((F*5/2) * (L*1/2)) ⇒ M1= FL*5/4

 

Nodo_6

M6= ((F*3) * (L*1/2)) ⇒ M1= FL*3/2

 

 

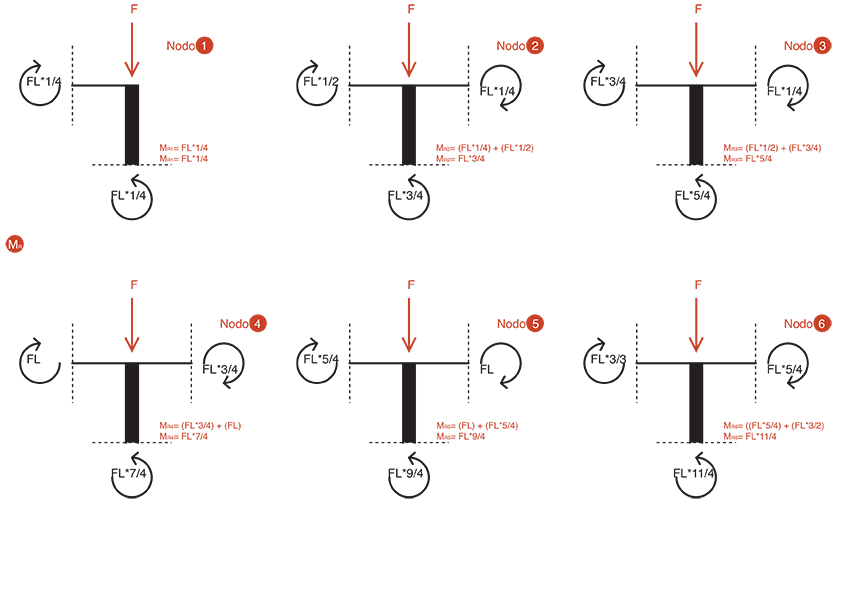
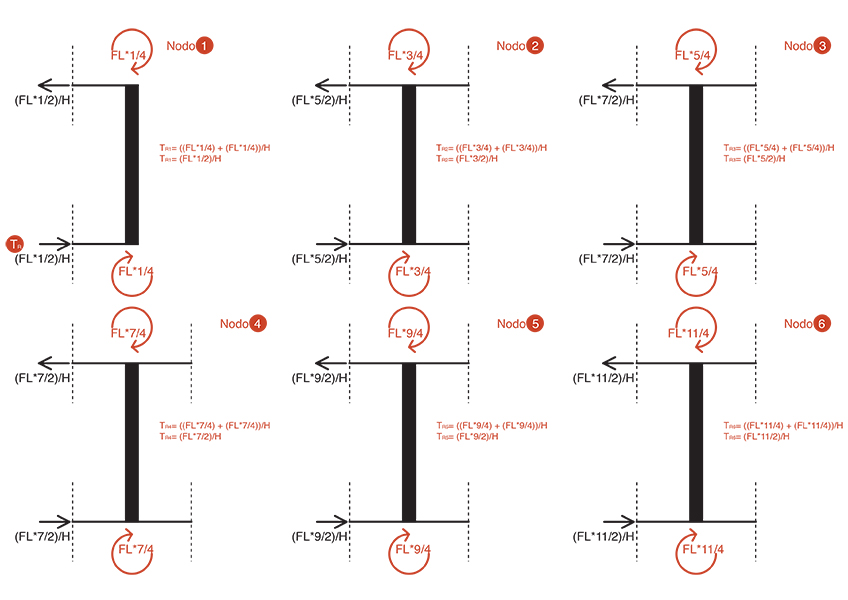
Passiamo al calcolo del momento flettente sui ritti, facendo l’equilibrio dei momenti del nodo.

 

Nodo_1

MR1= FL*1/4 ⇒ MR1= FL*1/4

 

Nodo_2

MR2= (FL*1/4) + (FL*1/2) ⇒ MR2= FL*3/4

 

Nodo_3

MR3= (FL*1/2) + (FL*3/4) ⇒ MR3= FL*5/4

 

Nodo_4

MR4= (FL*3/4) + (FL) ⇒ MR4= FL*7/4

 

Nodo_5

MR5= (FL) + (FL*5/4) ⇒ MR5= FL*9/4

 

Nodo_6

MR6= ((FL*5/4) + (FL*3/2) ⇒ MR6= FL*11/4

 

 

 

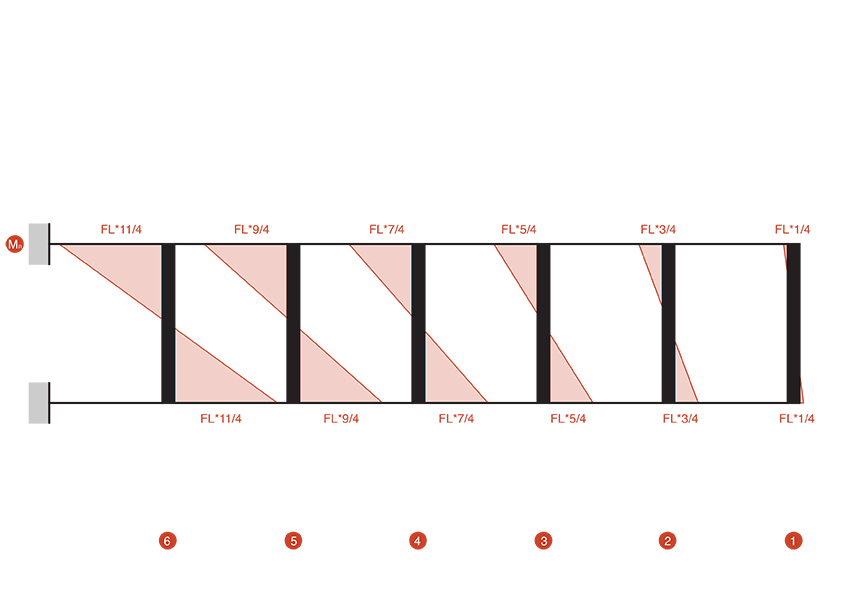
Passiamo al calcolo del taglio sui ritti, avendo i momenti flettenti agli estremi del ritto concordi li possiamo sommare e dividere il risultato per la luce del ritto, definendo così il valore del taglio.

 

Nodo_1

TR1= ((FL*1/4) + (FL*1/4))/H ⇒ TR1= (FL*1/2)/H

 

Nodo_2

TR2= ((FL*3/4) + (FL*3/4))/H ⇒ TR2= (FL*3/2)/H

 

Nodo_3

TR3= ((FL*5/4) + (FL*5/4))/H ⇒ TR3= (FL*5/2)/H

 

Nodo_4

TR4= ((FL*7/4) + (FL*7/4))/H ⇒ TR4= (FL*7/2)/H

 

 

Nodo_5

TR5= ((FL*9/4) + (FL*9/4))/H ⇒ TR5= (FL*9/2)/H

 

Nodo_6

TR6= ((FL*11/4) + (FL*11/4))/H ⇒ TR6= (FL*11/2)/H

 

 

 

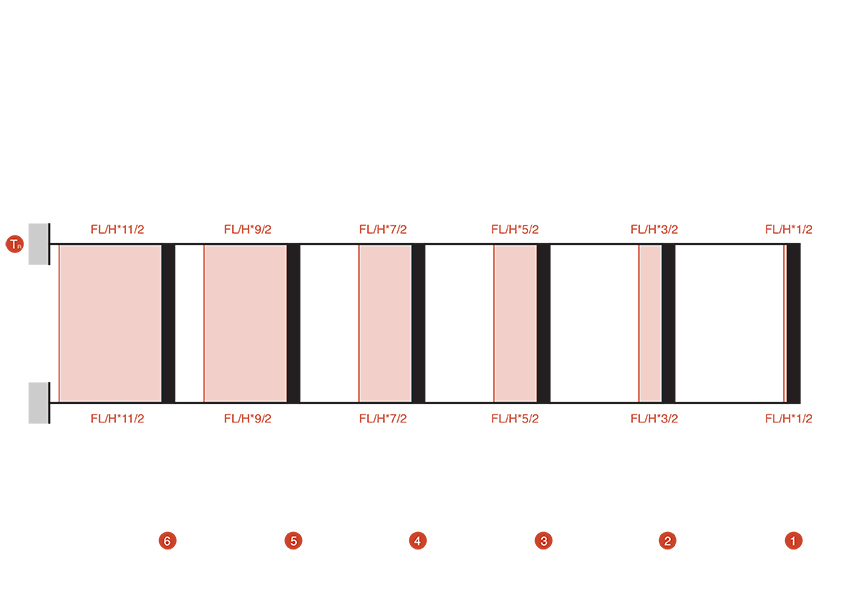
Passiamo al calcolo della normale sui traversi, sapendo che essendo tratti ortogonali ai ritti, lo sforzo di taglio di quest’ultimi si trasmette come sforzo normale nei traversi.

 

Nodo_1

⇒ NR1= (FL*1/2)/H

 

Nodo_2

⇒ NR2= (FL*3/2)/H

 

Nodo_3

⇒ NR3= (FL*5/2)/H

 

Nodo_4

⇒ NR4= (FL*7/2)/H

 

Nodo_5

⇒ NR5= (FL*9/2)/H

 

Nodo_6

⇒ NR6= (FL*11/2)/H

 

 

 

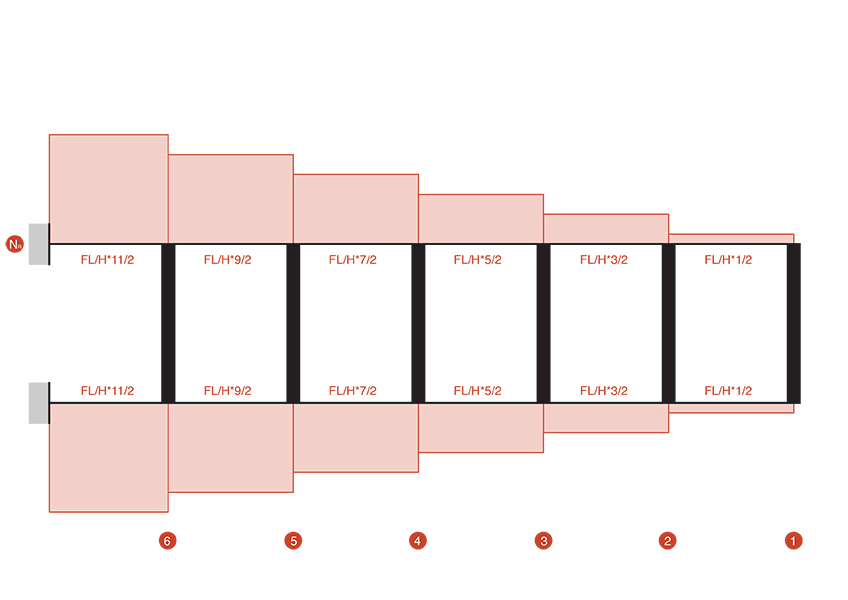
Passiamo al calcolo dello spostamento della trave Vierendeel, avendo definito che tutti i ritti della struttura hanno una rigidezza pari a 12*E*J/L³. Per definire lo spostamento utilizzeremo  l’equilibrio alla traslazione orizzontale della trave.

 

Nodo_1

F/2 = T = ((12*E*J)/L³)*δ1 ⇒ δ1= (F*L³) / (1/24*E*J)

 

Nodo_2

F = T = ((12*E*J)/L³)*δ2 ⇒ δ2= (F*L³) / (1/12*E*J)

 

Nodo_3

F*3/2 = T = ((12*E*J)/L³)*δ3 ⇒ δ3= (F*L³) / (1/8*E*J)

 

Nodo_4

F*2 = T = ((12*E*J)/L³)*δ4 ⇒ δ4= (F*L³) / (1/6*E*J)

 

Nodo_5

F*5/2 = T = ((12*E*J)/L³)*δ5 ⇒ δ5= (F*L³) / (1/24*E*J)

 

Nodo_6

F*3 = T = ((12*E*J)/L³)*δ6 ⇒ δ6= (F*L³) / (1/4*(E*J)

 

Commerzbank Tower - Foster & Partners

In questo nuovo post continuiamo il discorso sulle travi Vierendeel, occupandoci in questo caso di un modello che preveda gli estremi incastrati ad ambo i lati. E' la scelta progettuale adottata tra gli altri da Foster & Partners per il progetto della Commerzbank Tower a Francoforte (1994-1997), la cui soluzione strutturale prevede una coppia di montanti verticali all’interno di ognuna delle strutture d’angolo, ai quali sono collegate travi Vierendeel da otto piani, che sorreggono i solai degli uffici da angolo ad angolo. Sicuramente una scelta audace ed onerosa, che permette però di avere diversi vantaggi, tra cui, ad esempio, la possibilità di fruire di un open space privo di pilastri all'interno degli uffici.

Vediamo quindi in sintesi come si comporta meccanicamente la trave doppiamente incastrata:

Si nota subito come nel nostro caso la trave sia perfettamente simmetrica attorno al montante verticale 1. Conosciamo inoltre, come segnalato nel precedente post, i valori del taglio e del momento e l'analisi della deformata di una trave doppiamente incastrata, che costituisce il singolo elemento della trave Vierendeel:

Dallo schema della deformata della singola trave possiamo facilmente ricavare la deformata di tutta la Vierendeel:

Per quanto riguarda il valore del taglio sui traversi, possiamo utilizzare il metodo empirico adottato anche con la precedente trave. Occorre però precisare come si ripartisce la forza F sul pilastro 1, che risulta essere il nostro asse di simmetria:

Una volta capito ciò, si può procedere con il calcolo dei valori del taglio agenti sui traversi, semplicente dividendo la forza agente su ogni tratto orizzontale per 2 e assegnandone una metà a ciascuno di essi:

Verifichiamo la correttezza del procedimento ancora una volta scrivendo l'equilibrio alla traslazione verticale, e sostituendo il valore nell'equazione del taglio derivante dallo schema notevole della trave doppiamente incastrata. Scriviamo solo i primi 3, perchè, essendo la struttura simmetrica, sarà sufficiente specchiarli per ottenere i rimanenti:

Passiamo ora ai momenti dei traversi. Come nel caso precedente, conoscendo i punti di nullo, sarà sufficiente moltiplicare il valore del taglio ottenuto per il braccio. Questo è il diagramma:

Per conoscere invece i valori dei momenti sui montanti, abbiamo bisogno di scrivere l'equilibrio ai nodi. Ancora una volta, data la simmetria della struttura, sarà sufficiente analizzare solo i primi 3:

Non ci rimane che trovare i valori delle forze taglianti dei montanti (sommando la coppia dei momenti agenti sul montante e dividendoli per la luce su cui lavorano) e diagrammarli:

 

Verifichiamo infine su SAP2000 di non aver commesso errori:

Taglio

Momento

Deformata

Es5 -Trave Vierendeel-

La trave Vierendeelha lo stesso comportamento di un telaio “shear-type” solo che è ruotato di 90 gradi. La trave è infinitamente resistente a flessione, mentre i pilastri  per effetto delle forze esterne traslano di una quantità δ ma senza deformarsi. 

 

Per risolvere la trave occorre risolvere ogni tratto verticale considerandolo come se fosse una trave doppiamente appoggiata.

Trave iperstatica  soggetta ad un cedimento vincolare δ,  si hanno i seguenti valori notevoli del momento e del taglio.

M= 6EI/l²*δ     T= 12 EI/l³*δ

 

Si trovano i valore di ogni asta orizzontale

 1.      F = 2T  → F = 24 EI/l³δ1  

         δ1= Fl³/24 EI

 T = 12 EI/l³*δ1  

M = 6 EI/l²*δ1

T = 12 EI/l³*(Fl³/24 EI) = F/2

M = 6 EI/l²*(Fl³/24 EI)  = Fl/4

 

2.      F + F/2 + F/2= 2T  → 2F = 24 EI/l³*δ2   

        δ2= Fl³/12 EI

T = 12 EI/l³*δ2

M = 6 EI/l²*δ2

T = 12 EI/l³*(Fl³/12 EI) = F

M = 6 EI/l²*(Fl³/12 EI)  = Fl/2

 

3.      F + F + F= 2T  → 3F = 24 EI/l³*δ3 

         δ3= Fl³/8 EI

T = 12 EI/l³*δ3

M = 6 EI/l²*δ3

T =12 EI/l³*(Fl³/8 EI) = 3/2F

M =6 EI/l²*(Fl³/8 EI) = 3/4 Fl

 

4.      F + 3/2F + 3/2F= 2T  → 4F = 24 EI/l³*δ4 

         δ4= Fl³/6 EI

T = 12 EI/l³ δ3

M = 6 EI/l²*δ4

T = 12 EI/l³ * (Fl³/6 EI) = 2F

M = 6 EI/l²*(Fl³/6 EI)=  Fl

 

5.      F + 2F + 2F= 2T  → 5F = 24 EI/l³*δ5  

        δ5= 5 Fl³/ 24EI

T = 12 EI/l³*δ2

M = 6 EI/l²*δ2

T = 12 EI/l³*(5 Fl³/24 EI) = 5/2F

M = 6 EI/l²*(5 Fl³/24 EI) = 5/4Fl

 

6.      F + 5/2F + 5/2F= 2T  → 6F = 24 EI/l³*δ6   

         δ1= Fl³/4 EI

T = 12 EI/l³*δ1

M = 6 EI/l²*δ6

T = 12 EI/l³*(Fl³/4 EI) = 3F

M = 6 EI/l²*(Fl³/4 EI)=3/2 Fl

• Distribuzione delle forze orizzontale

• Diagramma del Taglio dei traversi

 

 

 

 

• Diagramma del Momento dei traversi

• Ora si deve trovare i momenti degli elementi verticali, per trovarli basta fare l’equilibrio di ogni nodo

1

 

2

 

3

FL/2 + FL/4 =5/4 FL

4

3FL/4 + FL =7/4 FL

5

FL + 5Fl/4 =9/4 FL

6

5FL/4 + 3Fl/2 =11/4 FL

 

Posso trovare i valori dei tagli, calcolando l'equilibrio di ciascuna asta verticale:

1

2

3

 

(5FL/4+5FL/4) /2L= 5FL

 

4

(7FL/4+7FL/4) /2L=7FL

 

5

(9FL74+9FL/4) /2L=9FL

 

6

(11FL/4+11FL/4) /2L=11FL

 

• Diagramma taglio ritti

 

• Diagramma momento ritti

 

 

 

Si può facilmente determinare lo sforzo normale sui traversi, poiché è pari al taglio dei ritti che si trasmettono ai traversi e diventano sforzo normale.

 

 

Verifica con sap dove si deve cambiare il Modulo Elastico per rendere la struttura infinitivamente rigida.

Deformata

 

Diagramma del taglio

 

Diagramma del momento