Blog

metodo di integrazione della linea elastica

Inviato da Morena.Mimmi il Mer, 24/04/2013 - 11:50

SdC(b) (LM PA)

Esercitazione

travatura reticolare 3D

Inviato da Morena.Mimmi il Mer, 24/04/2013 - 11:21

SdC(b) (LM PA)

Esercitazione

travatura reticolare piana

Inviato da Morena.Mimmi il Mer, 24/04/2013 - 10:57

SdC(b) (LM PA)

Esercitazione

TRAVATURE RETICOLARI PIANE TABELLE.pdf

METODO DELLE FORZE

Inviato da francesca.marino il Lun, 22/04/2013 - 20:47

La struttura che ci troviamo a dover risolvere è una trave su più appoggi iperstatica, il metodo di risoluzione più adatto a questo tipo di trave è il MEDOTO DELLE FORZE, dove le incognite sono le FORZE, e verranno trovate attraverso le EQUAZIONI DI COMPATIBILITA' CINEMATICA.
Il metodo delle forze ci consente di risolvere strutture iperstatiche riconducendole a sistemi isostatici equivalenti dove per ciascun GRADO DI IPERSTATICITA’ corrisponde una REZIONE VINCOLARE INCOGNITA.

Nel caso preso in esame sostituiamo i tre carrelli esterni con delle cerniere interne aggiungendo le reazioni vincolari rimosse, cioè la rotazione a destra e a sinistra del nodo. Quindi la struttura isostatica di riferimento sarà composta da una serie di travi doppiamente appoggiate con l'aggiunta di coppie di momenti in corrispondenza dei punti B, C, D.
Nella strruttura iperstatica non avviene nessuna rotazione nei suddetti punti, quindi per ognuna delle cerniere inserite il DELTA delle rotazioni è uguale a 0. Inoltre dobbiamo trovare le reazioni vincolari incognite X1 X2 X3 relative ai tre vincoli interni, poichèla struttura è simmetrca sappiamo che X1 = X3 quindi d’ora in poi utilizzeremo solo X1 e X2. Avremo due schemi che andremo a sommare con il principio della sovrapposizione degli effetti.

Le equazioni di compatibilità cinematica in grado di ripristinare il vincolo iperstatico sono:

$\varphi _{BS}=\varphi _{BD}$ $\varphi _{CS}=\varphi _{CD}$ $\varphi _{DS}=\varphi _{DD}$

Aiutandoci con gli schemi notevoli troviamo le rotazioni di ciascun tratto della trave

$\varphi _{BS}=\frac{ql^{3}}{24EI}-\frac{X_{1}l}{3EI}$

$\varphi _{BD}=-\frac{ql^{3}}{24EI}+\frac{X_{1}l}{3EI}+\frac{X_{2}l}{6EI}$

$\frac{ql^{3}}{24EI}-\frac{X_{1}l}{3EI}=-\frac{ql^{3}}{24EI}+\frac{X_{1}l}{3EI}+\frac{X_{2}l}{6EI}$

$\frac{2ql^{3}}{24EI}-\frac{2X_{1}l}{3EI}=\frac{X_{2}l}{6EI}$

$\frac{ql^{2}}{12EI}-\frac{2X_{1}}{3}=\frac{X_{2}}{6}$

$X_{2}=\frac{ql^{2}}{2}-4X_{1}$

$\varphi _{CS}=\frac{ql^{3}}{24EI}-\frac{X_{2}l}{3EI}-\frac{X_{1}l}{6EI}$

$\varphi _{CD}=-\frac{ql^{3}}{24EI}+\frac{X_{2}l}{3EI}+\frac{X_{1}l}{6EI}$

$\frac{ql^{3}}{24EI}-\frac{X_{2}l}{3EI}-\frac{X_{1}l}{6EI}=-\frac{ql^{3}}{24EI}+\frac{X_{2}l}{3EI}+\frac{X_{1}l}{6EI}$

$\frac{2ql^{3}}{24}-\frac{2X_{2}l}{3EI}=\frac{2X_{1}l}{6EI}$

$X_{1}=\frac{ql^{2}}{4}-2X_{2}$

Mettendole a sistema possiamo così ottenere i valori di X₁ eX₂(X₁ = X₃)

$\left\{\begin{matrix}X_{1}=\frac{ql^{2}}{4}-2x_{2} & & \\ X_{2}=\frac{ql^{2}}{2}-4x_{1} & & \end{matrix}\right.$

$X_{2}=\frac{ql^{2}}{2}-4\left ( \frac{ql^{2}}{4}-2X_{2} \right )=\frac{ql^{2}}{2}-ql^{2}+8X_{2}$

$7X_{2}=-\frac{ql^{2}}{14}$

$X_{2}=\frac{ql^{2}}{14}$

$X_{1}=\frac{ql^{2}}{4}-2\frac{ql^{2}}{14}=\frac{7ql^{2}-4ql^{2}}{28}=\frac{3}{28}ql^{2}$

Dopo aver trovato i valori delle incognite iperstatiche possiamo trovarci le reazioni vincolari con il metodo della sovrapposizione degli effetti, per il quale le reazioni finali sono la somma delle reazioni dovute al carico q e alle forze iperstatiche trovate. Le reazioni vincolari vanno determinate per ciascuna delle quattro campate della struttura isostatica di riferimento e vanno sommate quelle che si trovano sullo stesso vincolo.

Ora possiamo procedere col calcolarci il taglio ed il momento effettuando sezioni nelle varie campate e determinandone il valore per ognuna.

TAGLIO

Primo tratto

$T\left ( s \right )=-\frac{11}{28}ql+qs$

$T\left ( s=0 \right )=-\frac{11}{28}ql$

$T\left ( s=l \right )=-\frac{11}{28}ql+ql=\frac{17}{28}ql$

Secondo tratto

$T(s)=-\frac{11}{28}ql-\frac{8}{7}ql+qs$

$T(s=l)=-\frac{11}{28}ql-\frac{8}{7}ql+ql=-\frac{15}{28}ql$

$T(s=2l)=-\frac{11}{28}ql-\frac{8}{7}ql+2ql=\frac{13}{28}ql$

Terzo tratto

$T(s)=-\frac{11}{28}ql-\frac{8}{7}ql-\frac{13}{14}ql+qs$

$T(s=2l)=-\frac{11}{28}ql-\frac{8}{7}ql-\frac{13}{14}ql+2ql=-\frac{13}{28}ql$

MOMENTO

Primo tratto

$M\left ( s \right )=-\frac{qs^{2}}{2}+\frac{11}{28}qls$

$M\left ( s=0 \right )=0$

$M\left ( s=l \right )=-\frac{qs^{2}}{2}+\frac{11}{28}ql^{2}=-\frac{3}{28}ql^{2}$

$Mmax\rightarrow T=0\rightarrow s=\frac{11}{28}l$

$M\left ( s=\frac{11}{28}l \right )=-\frac{q\left ( \frac{11}{28}l \right )^{2}}{2}+\frac{11}{28}ql\left ( \frac{11}{28}l \right )$

$M\left ( s=\frac{11}{28}l \right )=-\frac{121}{784}ql^{2}\frac{1}{2}+\frac{121}{754}ql^{2}=\frac{121}{1568}ql^{2}$

Secondo tratto

$M\left ( s \right )=-\frac{qs^{2}}{2}+\frac{11}{28}qls+\frac{8}{7}ql\left ( s-l \right )$

$M\left ( s=2l \right )=-2ql^{2}+\frac{11}{28}2ql^{2}+\frac{8}{7}ql^{2}=-2ql^{2}+\frac{11}{14}ql^{2}+\frac{8}{7}ql^{2}=-\frac{ql^{2}}{14}$

$Mmax\rightarrow T=0\rightarrow s=\frac{15}{28}l+l$

$M\left ( s=\frac{43}{28}l \right )=\frac{q\left ( \frac{43}{28}l \right )^{2}}{2}+\frac{11}{28}ql\left ( \frac{43}{28}l \right )+\frac{8}{7}ql\left ( \frac{15}{28}l \right )$

$M\left ( s=\frac{43}{28}l \right )=\frac{1849}{784}ql^{2}\frac{1}{2}+\frac{473}{784}ql^{2}+\frac{120}{196}ql^{2}=\frac{57}{1568}ql^{2}$

SdC(b) (LM PA)

Esercitazione

Metodo delle forze per la risoluzione di un sistema iperstatico

Inviato da federica.murtas il Lun, 22/04/2013 - 19:47

SdC(b) (LM PA)

Esercitazione

esercitazione 4_metodo delle forze

Inviato da Mauro.Rocchi il Lun, 22/04/2013 - 17:04

L'esercizio consiste in una struttura 3 volte iperstatica. Per risoleverla la trasfomo in un sistema isostatico trasformando i carrelli B-C-D in cerniere interne, dividendo cosi la struttura in 4 corpi separati. Inoltre applico dei momenti flettenti X1, X2 e X3 in modo da ripristinare la rigidità della trave.

Trovo il valore dei tre momenti X₁,X₂ e X₃(data la simmetria della struttura X₁ = X₃):

Sappiamo che ΔφB=ΔφD=0 e ΔφC=0

Uguaglio valori della rotazione di sinistra con quelli di destra e ricaviamo X1 e X2.

Dopo aver trovato le 2 incognite mi calcolo le reazioni vincolari:

Infine disegno i diagrammi del taglio e del Momento trovando i valori nei diversi punti.

Taglio

Momento

SdC(b) (LM PA)

Esercitazione

ESERCITAZIONE 4_METODO DELLE FORZE

Inviato da lorenzo.procaccini il Lun, 22/04/2013 - 15:19

Con il METODO DELLE FORZE è possibile risolvere le strutture iperstatiche riconducendole a sistemi isostatici equivalenti. Per farlo dobbiamo rispettare la condizione di COMPATIBILITA’ CINEMATICA ovvero la congruenza degli spostamenti e delle rotazioni in ciascuna delle strutture isostatiche di rifermento.

Analizzeremo ora una TRAVE CONTINUA SU PIU’ APPOGGI.

Analizzando la struttura abbiamo:

GDL = 3

GDV = 2 + 1 + 1 + 1 + 1 = 6

Ci sono 3 INCOGNITE IPERSTATICHE. Dobbiamo quindi impostare una struttura isostatica equivalente in cui per ciascun GRADO DI IPERSTATICITA’ corrisponda una REZIONE VINCOLARE INCOGNITA in modo da avere una struttura corrispondente a quella iperstatica.

Possiamo quindi sostituire le 3 cerniere esterne delle campate centrali con delle cerniere interne permettendo la rotazione a destra e a sinistra di ciascuna cerniera. Poiché nella struttura iperstatica non avviene nessuna rotazione sappiamo che per ognuna delle cerniere inserite il DELTA delle rotazioni è uguale a 0. Inoltre dobbiamo inserire le reazioni vincolari vincolari incognite ottenendo X₁ X₂ X₃, per il principio di simmetria sappiamo che X₁ = X₃ quindi d’ora in poi utilizzeremo solo X₁ eX₂.

Una volta inserite le reazioni incognite, dobbiamo scrivere le equazioni di compatibilità cinematica in grado di ripristinare il vincolo iperstatico, dato che abbiamo sostituito un grado di iperstaticità con una reazione incognita.

∆φ_B= φ_Bs- φ_Bd=0

∆φ_C= φ_Cs- φ_Cd=0

∆φ_D= φ_Ds- φ_Dd=0

Per il principio di simmetria abbiamo :

φ_Ds= - φ_Bd

φ_Dd= - φ_Bs

Ora dobbiamo sostituire nelle equazioni di compatibilità cinematica i rispettivi valori dati dalle rotazioni in ciascuna cerniera.

$\varphi _{BS}=\frac{ql^{3}}{24EI}-\frac{X_{1}l}{3EI}$

$\varphi _{BD}=-\frac{ql^{3}}{24EI}+\frac{X_{1}l}{3EI}+\frac{X_{2}l}{6EI}$

$\frac{ql^{3}}{24EI}-\frac{X_{1}l}{3EI}=-\frac{ql^{3}}{24EI}+\frac{X_{1}l}{3EI}+\frac{X_{2}l}{6EI}$

$\frac{2ql^{3}}{24EI}-\frac{2X_{1}l}{3EI}=\frac{X_{2}l}{6EI}$

$\frac{ql^{2}}{12EI}-\frac{2X_{1}}{3}=\frac{X_{2}}{6}$

$X_{2}=\frac{ql^{2}}{2}-4X_{1}$

$\varphi _{CS}=\frac{ql^{3}}{24EI}-\frac{X_{2}l}{3EI}-\frac{X_{1}l}{6EI}$

$\varphi _{CD}=-\frac{ql^{3}}{24EI}+\frac{X_{2}l}{3EI}+\frac{X_{1}l}{6EI}$

$\frac{ql^{3}}{24EI}-\frac{X_{2}l}{3EI}-\frac{X_{1}l}{6EI}=-\frac{ql^{3}}{24EI}+\frac{X_{2}l}{3EI}+\frac{X_{1}l}{6EI}$

$\frac{2ql^{3}}{24}-\frac{2X_{2}l}{3EI}=\frac{2X_{1}l}{6EI}$

$X_{1}=\frac{ql^{2}}{4}-2X_{2}$

Mettendole a sistema possiamo così ottenere i valori di X₁eX₂ricordandoci che X₁ = X₃.

$\left\{\begin{matrix}X_{1}=\frac{ql^{2}}{4}-2x_{2} & & \\ X_{2}=\frac{ql^{2}}{2}-4x_{1} & & \end{matrix}\right.$

$X_{2}=\frac{ql^{2}}{2}-4\left ( \frac{ql^{2}}{4}-2X_{2} \right )=\frac{ql^{2}}{2}-ql^{2}+8X_{2}$

$7X_{2}=-\frac{ql^{2}}{14}$

$X_{2}=\frac{ql^{2}}{14}$

$X_{1}=\frac{ql^{2}}{4}-2\frac{ql^{2}}{14}=\frac{7ql^{2}-4ql^{2}}{28}=\frac{3}{28}ql^{2}$

Ora che le incognite X₁ eX₂sono note possiamo applicare il PRINCIPIO DI SOVRAPPOSIZIONE DEGLI EFFETTI secondo cui l’azione delle forze sulla struttura è uguale alla somma dell’effetto di ciascuna forza.

Analizziamo quindi la struttura isostatica equivalente una volta sotto l’effetto del CARICO q e una volta sotto l’effetto delle REAZIONI VINCOLARI X; ricordandoci di determinare le razioni vincolari per ciascuna campata (dato che la struttura è assimilabile a 4 travi doppiamente appoggiate) e sommando quindi quelle che insistono sullo stesso vincolo.

Rimane ora da determinare il diagramma del taglio e del momento.

TAGLIO

Primo tratto

$T\left ( s \right )=-\frac{11}{28}ql+qs$

$T\left ( s=0 \right )=-\frac{11}{28}ql$

$T\left ( s=l \right )=-\frac{11}{28}ql+ql=\frac{17}{28}ql$

secondo tratto

$T(s=l)=-\frac{11}{28}ql-\frac{8}{7}ql+ql=-\frac{15}{28}ql$

$T(s=2l)=-\frac{11}{28}ql-\frac{8}{7}ql+2ql=\frac{13}{28}ql$

terzo tratto

$T(s)=-\frac{11}{28}ql-\frac{8}{7}ql-\frac{13}{14}ql+qs$

$T(s=2l)=-\frac{11}{28}ql-\frac{8}{7}ql-\frac{13}{14}ql+2ql=-\frac{13}{28}ql$

MOMENTO

Primo tratto

$M\left ( s \right )=-\frac{qs^{2}}{2}+\frac{11}{28}qls$

$M\left ( s=0 \right )=0$

$M\left ( s=l \right )=-\frac{qs^{2}}{2}+\frac{11}{28}ql^{2}=-\frac{3}{28}ql^{2}$

$Mmax\rightarrow T=0\rightarrow s=\frac{11}{28}l$

$M\left ( s=\frac{11}{28}l \right )=-\frac{q\left ( \frac{11}{28}l \right )^{2}}{2}+\frac{11}{28}ql\left ( \frac{11}{28}l \right )$

$M\left ( s=\frac{11}{28}l \right )=-\frac{121}{784}ql^{2}\frac{1}{2}+\frac{121}{754}ql^{2}=\frac{121}{1568}ql^{2}$

secondo tratto

$M\left ( s \right )=-\frac{qs^{2}}{2}+\frac{11}{28}qls+\frac{8}{7}ql\left ( s-l \right )$

$M\left ( s=2l \right )=-2ql^{2}+\frac{11}{28}2ql^{2}+\frac{8}{7}ql^{2}=-2ql^{2}+\frac{11}{14}ql^{2}+\frac{8}{7}ql^{2}=-\frac{ql^{2}}{14}$

$Mmax\rightarrow T=0\rightarrow s=\frac{15}{28}l+l$

$M\left ( s=\frac{43}{28}l \right )=\frac{q\left ( \frac{43}{28}l \right )^{2}}{2}+\frac{11}{28}ql\left ( \frac{43}{28}l \right )+\frac{8}{7}ql\left ( \frac{15}{28}l \right )$

$M\left ( s=\frac{43}{28}l \right )=\frac{1849}{784}ql^{2}\frac{1}{2}+\frac{473}{784}ql^{2}+\frac{120}{196}ql^{2}=\frac{57}{1568}ql^{2}$

SdC(b) (LM PA)

Esercitazione

ESERCITAZIONE SUL METODO DELLE FORZE

Inviato da aleandro.masi il Lun, 22/04/2013 - 01:14

ESERCIZIO SUL METODO DELLE FORZE

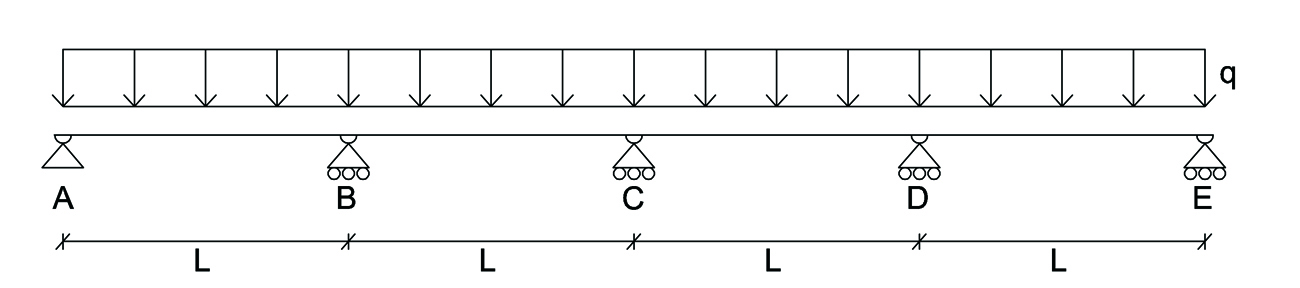
La struttura è IPERSTATICA 3 volte perché GDL=3 NGV=6.

Consideriamo una struttura isostatica, realizzata trasformando i vincoli esterni in vincoli interni, ristabilendo però le condizioni di vincolo della prima struttura ( i momenti x1, x2 ).

ΔφB = 0 => φBS - φBD = 0

ΔφC = 0 => φCS - φCD = 0

ΔφD = 0 => φDS - φDD = 0

N.B. La struttura è simmetrica, quindi basterà studiare metà struttura.

Devo considerare la struttura tratto per tratto.

Avrò

φBS = ql³/24EI -X1l/3EI

φBD = X1l/3EI - ql³/24EI + X2l/6EI

φCS = ql³/24EI – X2l/3EI – X1l/6EI

φBD = - ql³/24EI + X2l/3EI + X1l/6EI

Scrivo queste equazioni nella forma φBS - φBD = 0 e φCS - φCD = 0 mettendole a sistema per trovare i valori di X1 e X2

ql³/24EI -X1l/3EI - X1l/3EI + ql³/24EI – X2l/6EI = 0

ql³/24EI – X2l/3EI – X1l/6EI + ql³/24EI - X2l/3EI – X1l/6EI = 0

X2 = 1/14 ql²

X1 = 3/28 ql²

Studio le reazioni vincolari dovute al carico ripartito

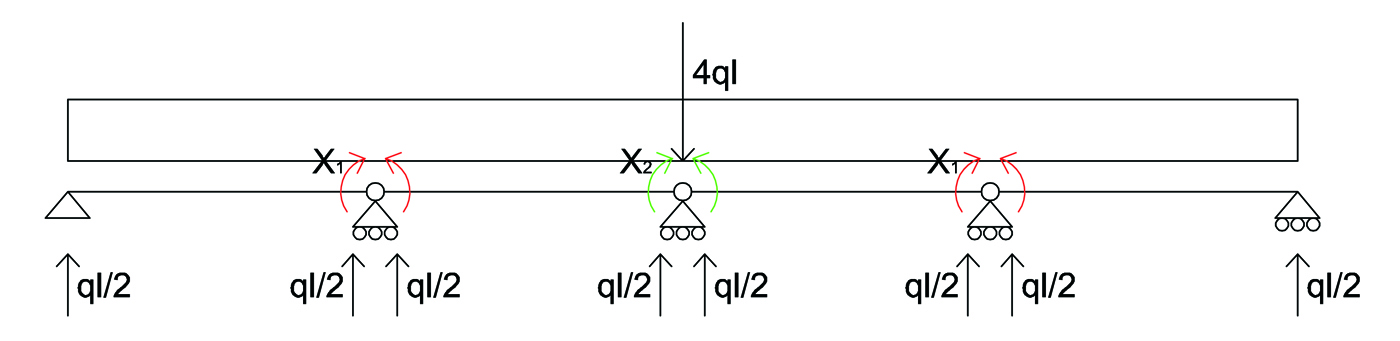
Considerando i tratti come strutture indipendenti, per oppormi a 4ql, dovrò avere, per l'equilibrio su ogni tratto, delle forze opposte con un valore di ql/2.

Posso scrivere il grafico di prima come:

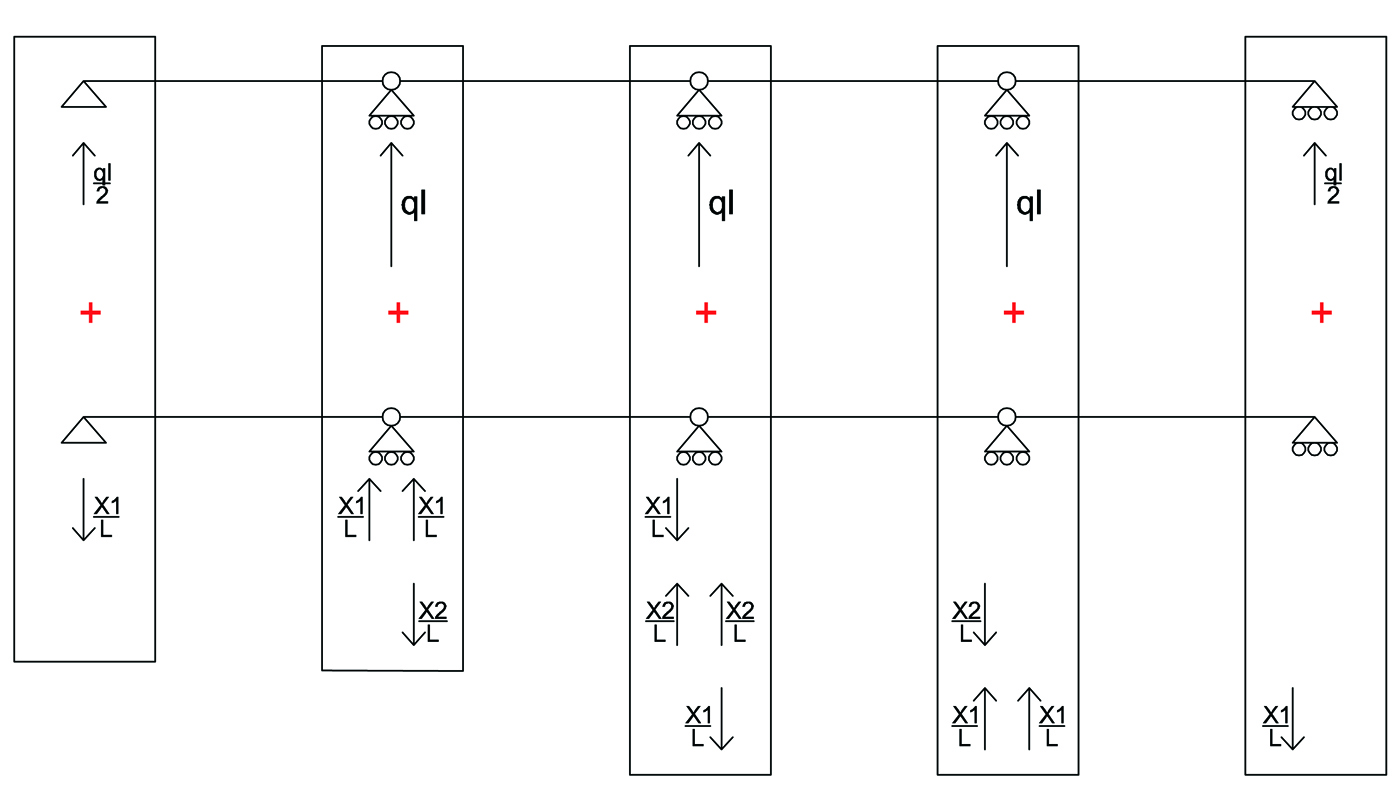
sommando, per il PRINCIPIO DI SOVRAPPOSIZIONE DEGLI EFFETTI i contributi del carico ripartito e delle reazioni che vado a considerare per mettere in equilibrio i singoli tratti e che derivano dall'effetto dei momenti nei nodi.

In A - X1/l + ql/2

In B X1/l + X1/l - X2/l + ql = 2 X1/l - X2/l + ql

In C - X1/l + X2/l + X2/l - X1/l + ql = - 2X1/l + 2 X2/l + ql

In D - X2/l + X1/l + X1/l + ql = - X2/l + 2X1/l + ql

In E - X1/l + ql/2

sostituendo i valori di X1 e X2 avrò

In A 11/28 ql

In B 8/7 ql

In C 13/14 ql

In D 8/7 ql

In E 11/28 ql

Le reazioni vincolari finali saranno

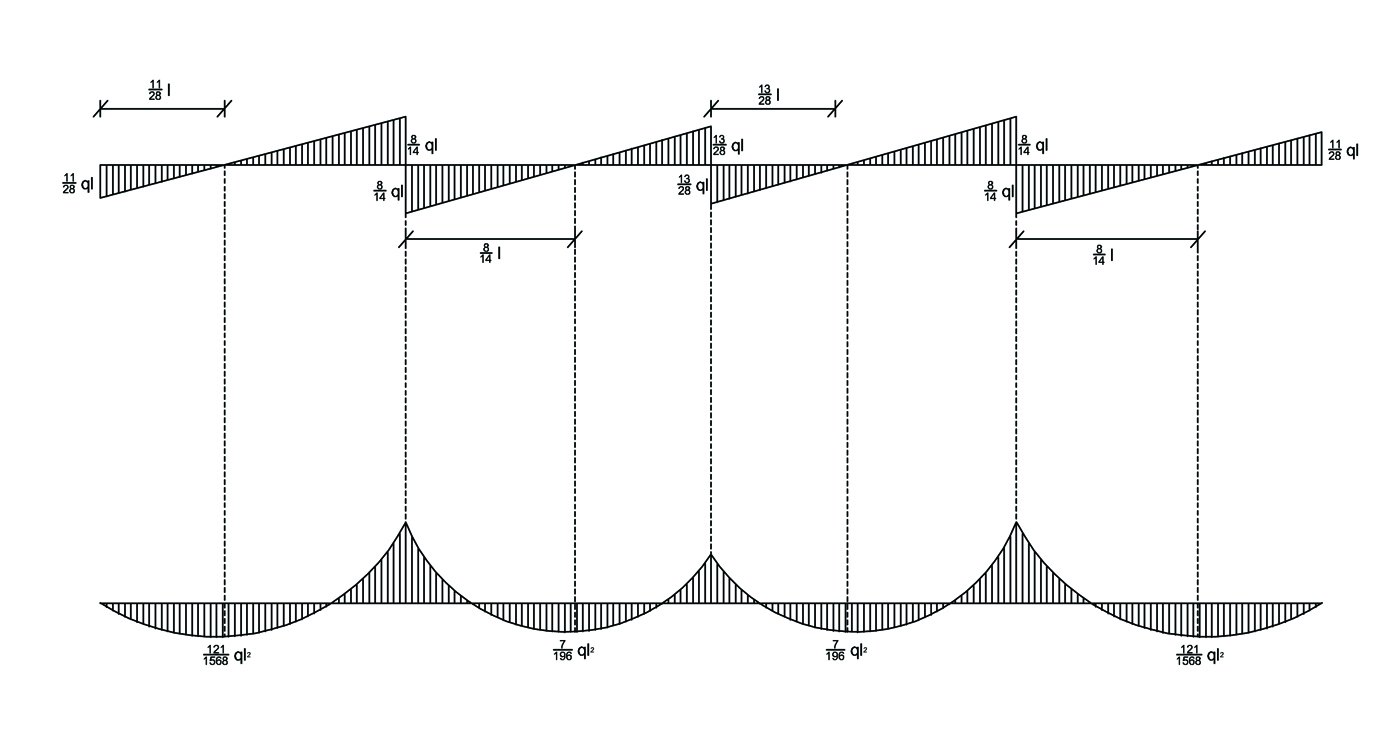
Disegno i diagrammi delle sollecitazioni

TAGLIO e MOMENTO

SdC(b) (LM PA)

Esercitazione

Esercitazione: metodo delle forze per la risoluzione di una struttura iperstatica

Inviato da valerio.sorgini il Dom, 21/04/2013 - 21:10

Il sistema in esame risulta essere tre volte iperstatico.

Per la sua risoluzine applico il metodo delle forze: definisco in primis tre reazioni vincolari (in numero pari al grado di iperstaticità della trave analizzata) che sono quelle della rotazione delle tre cerniere interne, notando subito che il sistema risulta essere simmetrico, e che si tratta di una trave doppiamente appoggiata. Chiamerò le incognite iperstatiche X1 e X2, disegnandole nella struttura iperstatica di riferimento.

Devo quindi determinare il valore delle incognite iperstatiche, studiando i nodi in successione, tratto per tratto, valutando sia l’effetto cinematico provocato dal carico distribuito sulla struttura (densità di carico), sia l’effetto dovuto all’incognita iperstatica (equazioni di compatibilità cinematica).Questo vuol dire che la differenza della rotazione di sinistra e di destra, ovvero la rotazione relativa, deve essere pari a zero.

Metto a sistema le equazioni :

Si determinano dunque le reazioni vincolari con la sovrapposizione degli effetti:

Disegno infine i diagrammi di taglio e momento:

SdC(b) (LM PA)

Esercitazione

Esercitazione 4 -Metodo delle forze-

Inviato da alessandro.mast... il Dom, 21/04/2013 - 13:37

Esercitazione 4 -Metodo delle forze-

Trave tre volte iperstatica NGL=3 NGV=6

La struttura è 3 volte iperstatica. Per risolvere la struttura con il metodo delle forze trasformo la struttura iniziale in una struttura isostatica di riferimento. Trasformo le cerniere in B,C,D in cerniere interne applicando dei momenti X1,X2 in A e B, essendo la trave simmetrica nel punto C posso applicare X1. Si eliminano cosi i 3 gradi di vincoli.

Sistema equivalente isostatico

1. Equazioni di compatibilità Cinematica

· ΔφB=0 φBs – φBd=0

φBs= ql³/24EI – X1L/3EI

φBd= -ql³/24EI + X1L/3EI + X2L/6EI

· ΔφC=0 φCs – φCd=0

φCs= ql³/24EI – X2L/3EI - X1L/6EI

φCd= -ql³/24EI + X2L/3EI + X1L/6EI

· ΔφD=ΔφB

2. Trovare X1 E X2

φBs – φBd=0

ql³/24EI - X1L/3EI+ ql³/24EI - X1L/3EI - X2L/6EI=0

2ql³/24EI - 2X1L/3EI - X2L/6EI=0

X2/2 = -2X1 + ql²/4

X2 = -4X1 + ql²/2

φCs – φCd=0

ql³/24EI – X2L/3EI - X1L/6EI+ ql³/24EI - X2L/3EI - X1L/6EI=0

2ql³/24EI – 2X2L/3EI - 2X1L/6EI=0

-X1/2 = X2 - ql²/8

X1 = - 2X2 - ql²/4

X1=3/28 ql²

X2=1/14 ql²

2. Reazioni

Reazioni dovute al carico

Reazioni dovute ai momenti X1 e X2

Somma delle reazioni dei momenti

Trovare le reazione finali dovute alla somma tra le reazione del carico e dei momenti

Diagramma del taglio e del momento

SdC(b) (LM PA)

Esercitazione

Menu principale

Commenti recenti

Blog

metodo di integrazione della linea elastica

travatura reticolare 3D

travatura reticolare piana

METODO DELLE FORZE

Metodo delle forze per la risoluzione di un sistema iperstatico

esercitazione 4_metodo delle forze

ESERCITAZIONE 4_METODO DELLE FORZE

ESERCITAZIONE SUL METODO DELLE FORZE

Esercitazione: metodo delle forze per la risoluzione di una struttura iperstatica

Esercitazione 4 -Metodo delle forze-

Pagine

Menu principale

Tu sei qui

Commenti recenti

Maschera di ricerca

Blog

Pagine