Il Metodo delle Forze, che ha una profonda parentela con il Principio dei Lavori Virtuali, è uno dei possibili metodi per la risoluzione di strutture iperstatiche e consiste primariamente nel porre come incognite del problema alcune reazioni vincolari, il cui numero è pari al grado di iperstaticità della struttura in esame.
Definite queste incognite in modo opportuno, ossia senza “labilizzare” la struttura di partenza, il metodo procede, tramite una sistematica applicazione del principio di sovrapposizione degli effetti, nella determinazione delle equazioni che ci consentono di determinare il valore delle suddette incognite. Queste equazioni sono di compatibilità cinematica: difatti, la scelta di rappresentare qualche grado di vincolo tramite la reazione (forza o coppia) corrispondente, elevandola al rango di incognita, equivale all'eliminazione di alcuni vincoli cinematici, che devono essere ripristinati in termini di equazioni, affinché il sistema isostatico che si sta studiando corrisponda al sistema iperstatico di partenza.
Prendiamo quindi una struttura iperstatica, nel nostro caso 3 volte, ed applichiamo il Metodo delle Forze per determinare gli sforzi di Momento, Taglio e Normale.
1) scelta di una struttura isostatica di riferimento e individuazione delle incognite iperstatiche
La struttura isostatica scelta è una trave appoggiata e le incognite iperstatiche sono i momenti applicati sulle cerniere non passanti nei punti B,C,D.
2) scrittura delle equazioni di compatibilità cinematica che ripristinino i vincoli cinematici soppressi dalla trasformazione del vincolo cinematico in forza (reazione vincolare)
Per simmetria abbiamo X1 = X3 ; imponiamo poi che:
Scomponiamo la struttura in quattro travi appoggiate e ne studiamo gli effetti separatamente del carico ripartito e del momento applicato, troviamo le equazioni delle rotazioni e, infine, determiniamo le incognite:
per simmetria abbiamo che:
3) la risoluzione del sistema di equazioni per la determinazione delle incognite iperstatiche
sostituisco il valore di X1:
Avendo trovato le 3 incognite ho tutte le forze agenti sulla struttura e posso trovare le reazioni vincolari e disegnare i diagrammi di TAGLIO e MOMENTO
4) la sistematica applicazione del principio di sovrapposizione degli effetti per la determinazione delle azioni di contatto sulla struttura iperstatica
Divido la struttura in una successione di travi appoggiate:
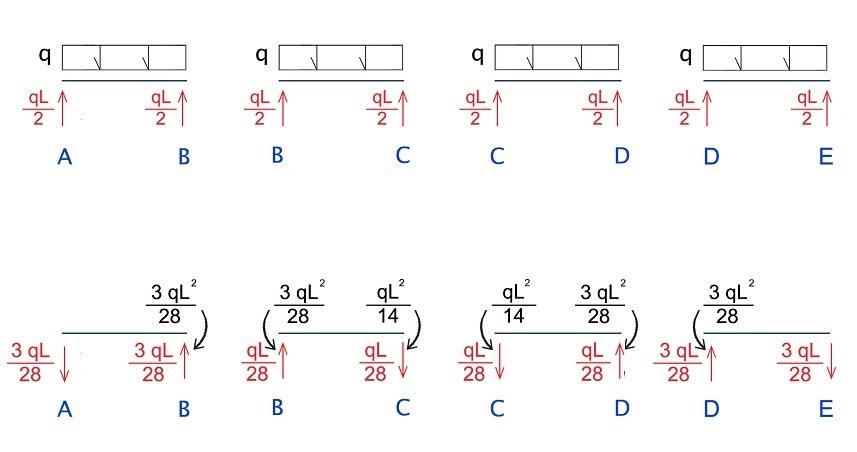
L'orientamento delle coppie è dato per equilibrare l'azione dei MOMENTI introdotti in precedenza. Sommo facendo un passo alla volta:
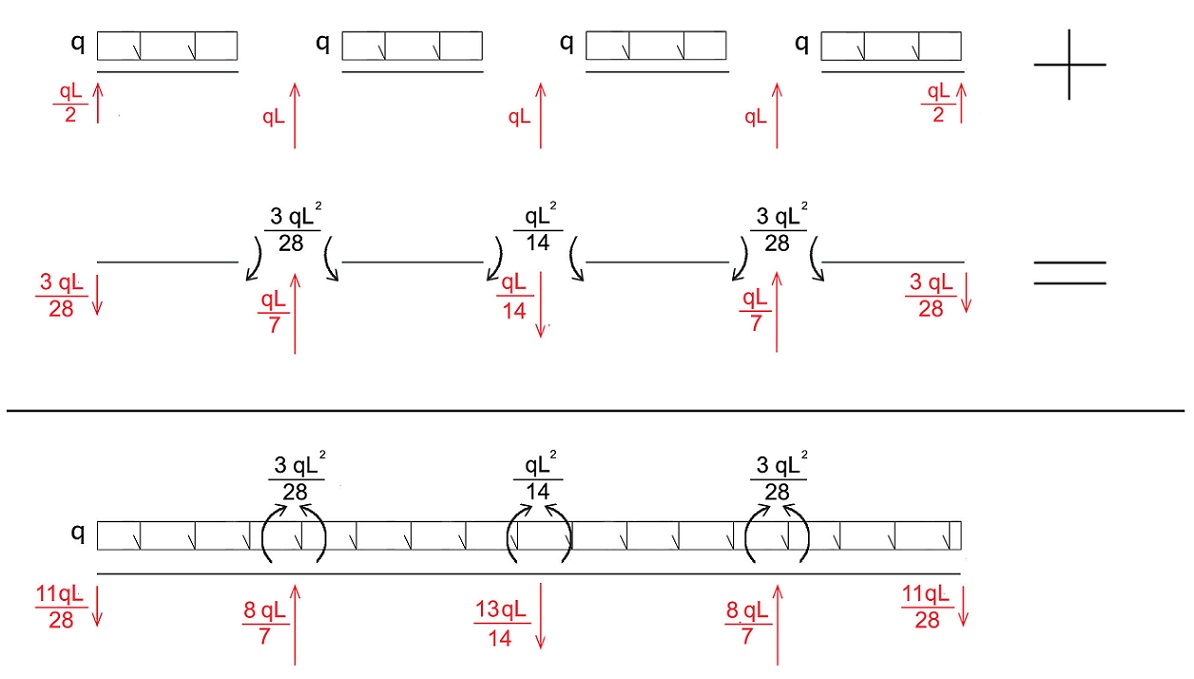
Avendo un carico distribuito so già che il diagramma del MOMENTO sarà descritto da una funzione parabolica e, conseguentemente, quello del TAGLIO da una lineare. Posso anche già dire che in presenza delle forze puntuali il diagramma del TAGLIO avrà una discontinuità (SALTO), e che dove il taglio si annulla il MOMENTO avrà la tangente orizzontale (MASSIMO o MINIMO).
Posso quindi fare un primo disegno QUALITATIVO del momento mentre del taglio so già i valori (REAZIONI VINCOLARI):
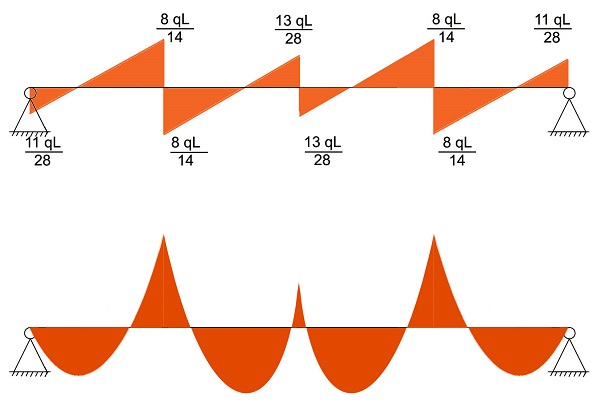
Per torvare i valori dei momenti faccio i tagli e sfrutto la simmetria:
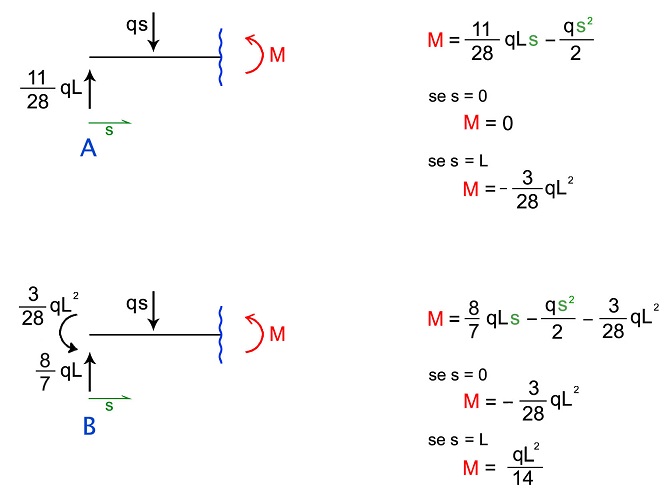
Commenti recenti