Blog

Esercitazione Trave Reticolare

Inviato da matteo.polci il Gio, 04/04/2013 - 22:53

SdC(b) (LM PA)

Esercitazione

EsercitazioneTRAVERETICOLARE.pdf

Esercitazione reticolare.jpg

tabella excell es trave reticolare.pdf

Esercitazione 1_ Trave reticolare 2D e 3D

Inviato da paola.lenzonimilli il Gio, 04/04/2013 - 22:50

SdC(b) (LM PA)

Esercitazione

Struttura reticolare 3d_Tabelle.xls

esercitazione struttura reticolare

Inviato da ilaria.verrengia il Gio, 04/04/2013 - 22:20

SdC(b) (LM PA)

Esercitazione

EsercitazioneTRAVERETICOLARE.pdf

tabella excell es trave reticolare.pdf

esercitazione struttura reticolare

Inviato da ilaria.verrengia il Gio, 04/04/2013 - 22:19

tabella excell es trave reticolare.pdf

EsercitazioneTRAVERETICOLARE.pdf

Esercitazione sulla Trave Reticolare Piana

Inviato da letizia.gagliardi il Gio, 04/04/2013 - 21:45

LA TRAVE RETICOLARE

Le strutture reticolari sono strutture che hanno il vantaggio di essere leggere e utilizzabili per grandi luci. Sono costituite da aste, che possono essere tese (tiranti) oppure compresse (puntoni) collegate tra loro tramite cerniere interne, i nodi. La struttura presenta un corrente superiore, uno inferiore, aste diagonali e montanti verticali. E' composta da una serie di trinagoli e risulta isostatica in quanto i gradi di libertà sono uguali ai gradi di vincolo. Per calcolare il grado di vincolo di ogni asta utilizzo la seguente formula:2(n – 1) dove n = numero di aste che confluiscono nel nodo.

Solitamente nelle strutture reticolari il corrente superiore è teso, quello inferiore compresso e i montanti quasi sempre compressi. Dopo aver trovato le reazioni vincolari, due sono i metodi per analizzare una struttura reticolare:

METODO DEI NODI e METODO DELLE SEZIONI DI RITTER

Per quanto riguarda il METODO DEI NODI è fodamentale capire l'ordine con cui si decide di risolvere la struttura. Generalmente si sceglie il nodo con 2 aste e 1 forza applicata e di seguito si risolvono gli altri nodi. E' necessario fare l'equilibrio al nodo considerando anche il contributo orizzantale o verticale dato dalla scomposizione delle aste inclinate.

esempio

Per quanto riguarda invece il METODO DELLE SEZIONI DI RITTER si sceglie di dividere via via la struttura con una sezione di ritter appunto, ovvero tagliando 3 aste convergenti nello stesso nodo. In tal modo avremo 3 equazioni in 3 incognite che saranno gli sforzi normali delle aste tagliate. La regola consiste nello scrivere le equazioni di equilibrio a rotazione, cambiando ogni volta il polo. Inizialmente nell'equazione di equilibrio del momento viene scelto il punto di incontro di 2 delle 3 aste in modo da avere una sola forza incognita. Successivamente sposto il polo e trovo la seconda incognita e infine per la terza posso applicare l'equazione alla traslazione verticale o orizzontale nel nodo. Qualora il risultato delle incognite sia positivo allora l'asta sarà un tirante, negativo sarà un puntone.

SdC(b) (LM PA)

Esercitazione

esercizio trave reticolare piana su sap.pdf

LINEA ELASTICA

Inviato da francesca.marino il Gio, 04/04/2013 - 21:41

L'esercitazione ci richiede di risolvere una struttura iperstatica con il metodo della linea elastica e verificare i dati ottenuti con Sap.

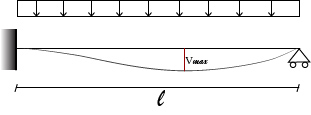
Calcolare il valore dell'abbassamento massimo V ed il punto in cui si trova sulla seguente trave iperstatica.

Abbiamo a nostra disposizione 8 equazioni con 8 incognite, tra cui equazioni di bilancio, equazioni delle deformate, e legame costitutivo elastico.

$\left\{\begin{matrix}N'+q_{1}=0 & & \\ T'+q_{2}=0 & & \\ M'+T=0 & & \end{matrix}\right.$ $\left\{\begin{matrix}\varepsilon=u' & & \\ \varphi =v' & & \\ \chi =\varphi ' & & \end{matrix}\right.$ $\left\{\begin{matrix}N=EA\varepsilon & & \\ M=EI\chi & & \end{matrix}\right.$

considerando solo l'abbassamento V possiamo combinare le varie equazioni:

$\frac{dT}{ds}+q_{2}=0$ $T=-\frac{dM}{ds}$

$\frac{d}{ds}\left ( -\frac{dM}{ds} \right )+q_{2}=0$ $-\frac{d^{2}M}{ds^{2}}+q_{2}=0$ $\frac{d^{2}M}{ds^{2}}=q_{2}$

$\chi =\frac{d\varphi }{ds}$ $\varphi =\frac{dv}{ds}$

$\chi =\frac{d}{ds}\left ( \frac{dv}{ds} \right )=\frac{d^{2}v}{ds^{2}}$ $M=EI\chi =EI\frac{d^{2}v}{ds^{2}}$

$\frac{d^{2}}{ds^{2}}\left ( EI\frac{d^{2}v}{ds^{2}} \right )=q_{2}$

consideriamo EI=costante

$EI\frac{d^{4}v}{ds^{4}}=q_{2}$ $\frac{d^{4}v}{ds^{4}}=\frac{q_{2}}{EI}$ EQUAZIONE DELLA LINEA ELASTICA

Per trovare il valore di V(s) integriamo 4 volte l'equazione ottenuta

$\frac{d^{3}v}{ds^{3}}=\frac{q_{2}}{EI}s+C_{1}$

$\frac{d^{2}v}{ds^{2}}=\frac{q_{2}}{EI}\frac{s^{2}}{2}+C_{1}s+C_{2}$

$\frac{dv}{ds}=\frac{q_{2}}{EI}\frac{s^{3}}{6}+C_{1}\frac{s^{2}}{2}+C_{2}s+C_{3}$

$v\left ( s \right )=\frac{q_{2}}{EI}\frac{s^{4}}{24}+C_{1}\frac{s^{3}}{6}+C_{2}\frac{s^{2}}{2}+C_{3}s+C_{4}$

Si ottengono cosi quattro costanti che dipendono dai vincoli, andando ad applicare le condizioni ai bordi possiamo trovarci il valore di ognuna.

Nell'incastro s=0 abbiamo ABBASSAMENTO e ROTAZIONE nulli

v(0)=0 sostituendo nell'equazione v(s) otteniamo

$C_{4}=0$

$\varphi \left ( 0 \right )=0$ $\varphi$ è la derivata prima dell'abbassamento, sostituendo in dv/ds otteniamo

$C_{3}=0$

Nel carrello S=l non c'è ABBASSAMENTO ed ha MOMENTO nullo

v(l)=0 sostituendo in v(s)

$v\left ( l \right )=-\frac{ql^{4}}{24EI}+C_{1}\frac{l^{3}}{6}+C_{2}\frac{l^{2}}{2}=0$

il carico diventa negativo per la convenzione dei segni

$M\left ( l \right )=0$ $M=\frac{d^{2}v}{ds^{2}}$

$M\left (l \right )=-\frac{ql^{2}}{2EI}+C_{1}l+C_{2}=0$

$C_{2}=\frac{q_{2}l^{2}}{2EI}-C_{1}l$ sostituendo nel'abbassamento v(l)

$-\frac{q_{2}l^{4}}{24EI}+C_{1}\frac{l^{3}}{6}+\left ( \frac{q_{2}l^{2}}{2EI}-C_{1}l \right )\frac{l^{2}}{2}=0$

$-\frac{q_{2}l^{4}}{24EI}+C_{1}\frac{l^{3}}{6}+ \frac{q_{2}l^{4}}{4EI}-C_{1} \frac{l^{3}}{2}=0$

$-\frac{q_{2}l^{4}+6q_{2}l^{4}}{24EI}+C_{1}\frac{l^{3}-3C_{1}l^{3}}{6}=0$

$\frac{5q_{2}l^{4}}{24EI}-\frac{C_{1}l^{3}}{3}=0$

$C_{1}=\frac{5q_{2}l^{4}}{24EI}*\frac{3}{l^{3}}=\frac{5}{8}\frac{q_{2}l}{EI}$

$C_{2}=\frac{q_{2}l^{2}}{2EI}-\left ( \frac{5q_{2}l}{8EI} \right )l=\frac{4q_{2}l^{2}-5q_{2}l^{2}}{8EI}=-\frac{q_{2}l^{2}}{8EI}$

Trovate le costanti possiamo trovare l'abbassamento massimo richiesto dal problema. Siccome la rotazione è la derivata dello spostamento, in corrispondenza della rotazione nulla abbiamo l'abbassamento massimo

$\varphi =\frac{dv}{ds}=-\frac{q_{2}s^{3}}{6EI}+C_{1}\frac{s^{2}}{2}+_{2}s+C_{3}$

$\varphi =-\frac{q_{2}s^{3}}{6EI}+\frac{5q_{2}ls^{2}}{16EI}-\frac{q_{2}l^{2}s}{8EI}=0$

$\varphi =s\left ( -\frac{q_{2}s^{2}}{6EI}+\frac{5q_{2}ls}{16EI}-\frac{q_{2}l^{2}}{8EI} \right )$

Affinchè la rotazione sia nulla avremo

$s=0$

$s=\left ( \frac{5q_{2}l^{2}}{16EI}\pm \sqrt{\frac{25q_{2}^{2}l^{2}}{256E^{2}I^{2}}-4\frac{q{_{2}}^{2}l^{2}}{48E^{2}I^{2}}} \right )*\frac{3EI}{q_{2}}$

$S=0,57$

$v\left ( 0,57 \right )=\frac{q_{2}\left ( 0,57 \right )^{4}}{24EI}+\frac{5q_{2}l\left ( 0,57 \right )^{3}}{48EI}-\frac{q_{2}l\left ( 0,57 \right )^{2}}{16EI}=-\frac{0,25q_{2}l^{2}}{48EI}$

$l=1\rightarrow v\left ( 0,57 \right )=-0,00536\frac{q_{2}}{EI}$

Considerando il valore di v(s) possiamo determinare il momento ed il taglio per ogni sezione $M=EI\frac{d^{2}v}{ds^{2}}=-\frac{q_{2}s^{2}}{2}+\frac{5q_{2}l}{8}s-\frac{q_{2}l^{2}}{8}$

$M\left ( 0 \right )=-\frac{q_{2}l^{2}}{8}$ $M\left ( l \right )=-\frac{q_{2}s^{2}}{2}+\frac{5q_{2}l}{8}s-\frac{q_{2}l^{2}}{8}$

Il momento è nullo nei punti

$s_{1}=0$

$s_{2}=\frac{l}{4}$

$T=-M\left ( s \right )=q_{2}s-\frac{5q_{2}l}{8}$

$T\left ( 0 \right )=-\frac{5q_{2}l}{8}$ $T\left ( l \right )=q_{2}l-\frac{5q_{2}l}{8}=\frac{3}{8}q_{2}l$

Il taglio è nullo nel punti

$T\left ( \frac{5}{8}l \right )=0$

RISOLUZIONE IN SAP

Apriamo un nuovo file di tipo grid, con unità di misura kn, m, C, e GRIGLIA x=2 , Y= 1, Z=1 e spaziatura 1. Disegnare la struttura sulla griglia e posizionare un punto a 0.57, dato che dal calcolo a mano abbiamo visto che l’abbassamento massimo avviene in questo punto della struttura.

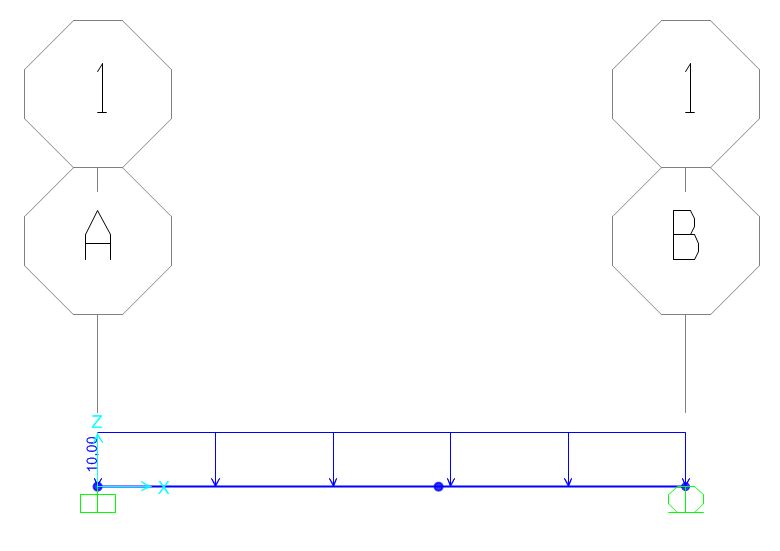
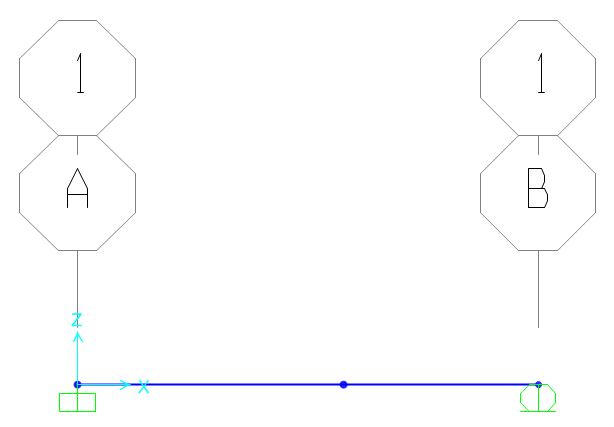
L'analisi è stata fatta su due sezioni differenti, una rettangolare in acciaio cavo di dimensoni 40x30x2, e l'altra in cemento armato.

I risultati della sezioni in acciaio

DEFORMATA

REAZIONI VINCOLARI

DIAGRAMMA DEL TAGLIO

DIAGRAMMA DEL MOMENTO

I risultati della sezioni in cemento

DEFORMATA

REAZIONI VINCOLARI

DIAGRAMMA DEL TAGLIO

DIAGRAMMA DEL MOMENTO

In allegato ci saranno le tabelle dei risultati per entrambe le sezioni.

SdC(b) (LM PA)

Esercitazione

ACCIAIO.pdf

CA.pdf

trave reticolare piana

Inviato da francesca.secci il Gio, 04/04/2013 - 21:32

trave reticolare3d

Inviato da francesca.secci il Gio, 04/04/2013 - 21:27

trav3d2.jpg

trave3d ten.pdf

esercizio linea elastica

Inviato da francesca.secci il Gio, 04/04/2013 - 21:19

ESERCITAZIONE 2 - Linea Elastica

Inviato da lavinia.sabatini il Gio, 04/04/2013 - 21:08

Nella progettazione delle opere di architettura è importante saper valutare spostamenti e deformazioni, in modo da poterne verificare, oltre che la resistenza, anche la funzionalità.

Abbiamo una trave iperstatica, così definita perchè il numero dei vincoli è maggiore dei gradi di libertà, e ne vogliamo determinare il massimo spostamento, nel punto C. La mia ultima incognita è quindi v_(s), e la calcolo attraverso il metodo dell'integrazione della linea elastica, una curva che rappresenta la forma assunta dall’asse della trave a deformazione avvenuta.