Blog

Risoluzione di una struttura iperstatica

Per risolvere questo tipo di trave andiamo ad analizzare i tre gruppi di equazioni della trave di Eulero Bernoulli (equazioni di equilibrio, legami costitutivi, equazioni di compatibilità)

Potremmo escludere da questi tre gruppi tutte le equazioni contenenti i termini  u, N e ε (poichè non abbiamo uno spostamento orizzontale) ed accorpare le rimanenti equazioni in un unico sistema

Ora vado ad unire T'+q2=0 con M'+T=0 :           -[(d²M)/(dS²)]+q2=0
Posso unire anche anche χ = ϕ’ con ϕ = v’ :       χ= d²v/dS²

Grazie all’ultima componente del sistema (M = E I χ) potrò formulare un unica equazione che contiene tutte le altre:    EI*(d⁴v/dS⁴)=q2

Ora vado a derivare l’equazione differenziale imponendo il termine q2 come costante

Ora posso ottenere il valore dello spostamento (v) andando a ricavare le incognite c.
Le incognite possono essere ricavate ponendo il valore di s=l e s=0

Ottenuto il sistema vado a ricavare le uniche incognite rimaste (c1;c2)

Conoscendo ora tutte le incognite (c1;c2;c3;c4) posso sostituirle in v(s) per trovare il valore di s

Il primo risultato che troviamo è s=0 per gli altri due risultati applichiamo la formula risolutiva delle equazioni di secondo grado ottenendo i due risultati:

s = +0,57 l     s = +1,513 l

Di questi due valori prenderemo solo il primo (s= +0,57 l) poichè la trave ha una lunghezza:  0 < l < 1

A questo punto inserisco il vaore di s in v(s) =>   v(0,57) ed ottengo la distanza s in cui il momento è massimo:

s = 0,57

Risoluzione della struttura in SAP 2000

Per prima cosa disegno la struttura, definisco l'unità di misura (KN,m,C), ed assegno i carichi

Poi assegno un carico distribuito di 10 N/m su tutta la struttura

Associo alla trave un profilo rettangolare in calcestruzzo (Assign->Frame->Frame Sections)

Questo profilo (probabilmente eccessivo) determina una deformata in cui l'inflessione è così impercettibile che il software non la mostra

Ripeto il passaggio precedente associando alla struttura un profilo tubolare in acciaio

Avvio il calcolo della struttura (Run Analysis)

Dal diagramma del monmento posso verificare che il momento massimo (0,67) si trova esattamente ad una distanza pari a 0,57

 La Cacciata di Adamo ed Eva dal Giardino del Paradiso - Alexandre Cabanel

Chissà a che livelli arrivò la frustrazione di Adamo ed Eva nell'ascoltare la sentenza di Dio, riguardante il loro definitivo allontanamento dal Paradiso Terrestre. Allora erano forse inconsapevoli del fatto che, a causa di quel gesto di superbia, avevano perduto per sempre i doni preternaturali, i quali, tra le altre cose, li mettevano al riparo da ignoranza e inettitudine. Sicuramente non immaginavano di aver abbandonato, col loro atto, una parte del genere umano alle frustrazioni causate dal burrascoso rapporto con la meccanica e la statica. Diverse generazioni di studenti di architettura hanno convissuto con lo spauracchio degli esami di queste due discipline. Spauracchio che puntualmente si acuiva nel momento in cui venivano pronunciate due parole: LINEA ELASTICA.

Nonostante il senso di inquietudine che ancora mi pervade, proverò in questo post a spiegare come affrontare un sistema iperstatico, tramite l'utilizzo, appunto, dell'equazione della linea elastica. Iniziamo.

Questo era il sistema iperstatico assegnato, in cui dovevamo trovare il valore dello spostamento verticale v e ricavare un disegno della deformata, da verificare poi in SAP2000.

Scriviamo innanzitutto le equazioni relative al modello della trave di Bernoulli.

Equazioni differenziali di bilancio:

Equazioni del legame costitutivo:

Equazioni di congruenza:

Eliminiamo dal sistema le equazioni relative allo sforzo normale, dato che non prendiamo in considerazione l'analisi della deformata assiale, e mettiamo a sistema le rimanenti:

Partiamo dalla 2° equazione:

Sostituendo nella precedente:

Imponiamo che q2 sia costante, e,integrando 4 volte l'equazione differenziale ottenuta qui sopra, possiamo ricavare l'equazione esplicitata in v(s), che ci permetterà poi di ricavare tutte le altre incognite:

Scriviamo quindi le condizioni al bordo nei punti s=0 e s=L, per trovare i valori delle varie costanti c.

Per s=0:

Per la condizione s=L, mettiamo a sistema le 2 equazioni:

Sapendo che lo spostamento v ha un massimo o un minimo dove la pendenza della tangente alla deformata è nulla, poniamo l'equazione della rotazione pari a 0, per trovare un valore accettabile di s:

Supponiamo inoltre che la sezione della trave sia costante e dello stesso materiale, cosicchè possiamo sostituire ad I la formula del momento di inerzia di una sezione generica:

Consideriamo solo s=0,57, in quanto s<1, e lo andiamo a sostituire nell'equazione differenziale precedente per trovare v(s):

Disegniamo i diagrammi del taglio e del momento, da confrontare poi con quelli di SAP2000, impostando q₂=-q e calcolando i relativi valori:

Per le condizioni al bordo, M è nullo in:

Troviamo anche i valori del taglio, sapendo che esso è la derivata del momento, consapevoli del fatto che nel punto in cui il taglio è nullo, il momento è invece massimo:

Dopo la parte dei calcoli manuali (poco piacevole, a dir la verità), portiamo il tutto su SAP2000, verificando di non aver sbagliato nulla.

Apriamo innanzitutto un nuovo file basato su griglia e andiamo nella vista 2D xz. Tramite lo strumento POINT inseriamo un punto in corrispondenza del vmax che usciva fuori dai precedenti calcoli (0,57L), e, grazie allo snap dei 3 punti, disegniamo la nostra trave (DRAW-FRAME):

Ora assegniamo una sezione generica IPE alla trave in acciaio (DEFINE-SECTION PROPERTIES-FRAME SECTIONS):

Dopo  aver assegnato i vincoli e rimosso l'analisi del carico proprio della struttura, come al solito, impostiamo la densità di carico q₂ per la trave:

Ora non ci resta che avviare l'analisi della deformata, ricordandoci prima di rimuovere dall'analisi il MODAL:

In ultimo, lasciamo che SAP2000 ci calcoli i diagrammi del momento flettente e del taglio, per verificare di averli disegnati correttamente in precedenza:

Milstein Hall at Cornell University - OMA

 

Inauguro il blog con una fotografia della Milstein Hall, progettata dalla sezione newyorkese dello studio OMA, che, rimanendo sempre fedele alla metafisica progettuale del suo fondatore (Rem Koolhaas), ha incentrato la progettazione dell'edificio su mastodontiche travi reticolari.

Cercherò quindi in questo primo post di spiegare come è possibile calcolare le sollecitazioni a cui è soggetta una trave di questo tipo, dapprima secondo il metodo manuale delle sezioni di Ritter, e poi verificando il tutto su SAP2000. Iniziamo.

Prendiamo come esempio questo semplice sistema isostatico di trave reticolare:

 

 

Essendo una struttura simmetrica caricata uniformemente, procediamo sezionando la trave in due punti e nel nodo 1, così da avere tutte le informazioni necessarie (gli sforzi normali delle aste) per studiare l’intero comportamento della struttura. Affinché una sezione di Ritter sia valida, occorre sezionare al massimo 3 aste per volta.

Inoltre, essendo la trave reticolare in questione assimilabile ad una trave doppiamente appoggiata, conosciamo già le reazioni vincolari nel nodo 1 e 7:

Si inizia dalla sezione AA':

Per trovare N₂₃  invece dobbiamo scomporre la forza e trovare l'equilibrio alla traslazione verticale:

 

Passiamo alla sezione BB':

Scomponiamo N₃₄ ,come fatto in precedenza, e troviamo l'equilibrio alla traslazione orizzontale:

 

Infine analizziamo il nodo 1, per trovare il valore dello sforzo normale dell'asta N₁₂, facendo l'equilibrio alla traslazione verticale:

 

I valori degli sforzi normali dell’intera trave risultano essere quindi:

dove i valori negativi rappresentano dei puntoni, mentre i positivi dei tiranti.

 

Ora non rimane che verificare l’analisi della deformata su SAP2000 e ricavare le tabelle di tutte le aste che compongono la trave reticolare.

Per prima cosa disegno su SAP2000 la trave precedentemente studiata, applicando un carrello e una cerniera come vincoli della trave e scegliendo il numero dei correnti e delle aste diagonali:

Assegniamo, quindi, alle aste la sezione relativa, scegliendo, in questo caso, dei tubolari d’acciaio uguali per tutti gli elementi (DEFINE-SECTION-PROPERTIES-FRAME SECTION):

Comunichiamo a SAP2000, inoltre, che le aste sono collegate da cerniere interne, proprio perché, come sappiamo, non ci interessa che nei nodi di una qualsiasi trave reticolare venga impedita la rotazione (nelle reticolari spaziali questo è sottolineato dalla presenza nei nodi di una “pallina” in acciaio):

Non ci resta che aggiungere i carichi puntuali sui nodi della struttura (seleziono i nodi, poi ASSIGN-JOINT LOADS-FORCES), dopo aver precedentemente rimosso il carico proprio della struttura, al fine di analizzare solo la sollecitazione dei carichi esterni (DEFINE-LOAD PATTERNS):

Verifichiamo in ultimo lo schema della deformata (RUN) e il diagramma delle sforzo normale:

SAP2000 ci conferma quindi quanto calcolato a mano, con la sola presenza di sforzi assiali.

Risoluzione di una Trave reticolare con il metodo di Ritter

Per risolvere questa trave reticolare posso utilizzare il metodo di Ritter che prevede l'analisi dello sforzo normale di tre aste tagliate da una sezione 

           

Utilizzo il punto 5 come centro di rotazione di N46:             - N46*l - 9/2 F *2l + F*l + F*2l = 0          N46 = - 6 F

Utilizzo il punto 4 come centro di rotazione di N35               + N35*l - 9/2 F*l + F*l = 0                       N35 = 7/2 F

L'asta obliqua è inclinata di 45° rispetto alla trave e al montante quindi dovrò utilizzare il seno o il coseno di 45 ( √2/2) 
 
N45 * √2 /2 + 7/2 F - 6F     N45 = 5 √2 /2 F

Con lo stesso metodo trovo le sezioni delle aste di metà trave (l’altra metà sarà simmetrica)

- N24*l - 9/2 F*l + F*l = 0                        N24 = - 7/2 F
+ N13*l = 0                                              N13 = 0 (asta scarica)
+ N23√2 /2 - 7/2 F = 0                             N23 = 7 √2 /2 F
- N68*l - 9/2 F*3l + F*6l = 0                     N68 = - 15/2 F
+ N57*l - 9/2 F*2l + F*3l = 0                    N57 = 6 F
+ N67√2 /2 - 15/2 F + 6 F = 0                  N67 = 3 √2 /2 F
- N810*l - 9/2 F*4l + F*10l = 0                 N810 = - 8 F
+ N79*l - 9/2 F*3l + F*6l = 0                    N79 = 15/2 F
+ N89 √2 /2 + 15/2 F - 8 F = 0                  N89 = √ 2 /2 F

Per i montanti verticali eseguo sempre una sezione di Ritter su tre aste per ricavarne la normale

+ N12 + F + 7  2 /2 *  2 /2 F = 0                             N12 = - 9/2 F
+ N34 - F + 9/2 F = 0                                              N34 = - 7/2 F
+ N56 - 2F + 9/2 F = 0                                            N56 = - 5/2 F
+ N78 - 3 F + 9/2 F = 0                                           N78 = - 3/2 F
+ N910 + F  = 0                                                      N910 = - F 

A questo punto ho tutti gli sforzi normali di metà trave che si ripeteranno simmetricamente sulla seconda metà consentendomi di disegnare il diagramma dello sforzo normale di tutta la trave reticolare

Ho assegnato alla lunghezza delle aste l = 1m e alla forza applicata sui nodi F = 100 N

Risoluzione della struttura in SAP 2000

Stabilisco l’unità di misura (KN,m,C), disegno la trave ed associo il peso proprio della struttura pari a 0 (Define -> Load Patterns)

 

Ora inserisco i due vincoli ai vertici della struttura (Assign -> Joint -> Restraints) ed inserirsco le cerniere interne alle aste assegnando un rilascio (Assign -> Frame -> Releases/Partial Fixity)   

Devo assegnare un profilo alle varie aste quindi scelgo un tubolare in acciaio (Define -> Section Properties -> Frame Sections) definendone il diametro e lo spessore. Dopo aver definito il profilo posso associarlo alle aste della struttura reticolare (Assign -> Frame -> Frame Sections)

A questo punto vado ad inserire le mie forze di F = 100 N applicate sui nodi nella parte alta della trave (Assing -> Joint Loads -> Forces). Le forze dovranno riportare segno negativo poichè orientate verso in basso con verso opposto alla Z del sistema di riferimento

      

La mia struttura a questo punto ha sia vincoli che forze applicate e può essere calcolata (Run Analysis). Visto che è una struttura reticolare avrà solo sforzi normali che posso visualizzare nel diagramma della normale (Show Forces/Stresses ->Frames/Cables -> Axial Force)   

Ora vado a visualizzare le tabelle relative al calcolo della struttura (Display -> Show Tables -> [Joint Output; Element Output; Structure Output] -> Element Forces/Frames) poi esporto la tabella in Excel (File -> Export Current Table -> To Excel) la pulisco dai valori nulli di taglio e momento lasciando solo gli sforzi normali (KN), l'area della sezione del tubolare (mm2) ed il valore di sigma (Mpa)

 

 

 

 

 

 

 

 

 

 

 

 

Come "ripasso" (ma anche no...) del metodo della Linea Elastica o degli spostamenti, in aula si è svolto un piccolo esercizio su una trave iperstatica: i fini erano e sono quelli di ricavare tramite le equazioni di LEGAME, CONGRUENZA, ed EQUILIBRIO, e successivamente con una serie di integrazioni, l'equazione lineare differenziale della linea elastica, un "passpartout" della statica/meccanica/scienza delle costruzioni. Come vedrete, tramite questa "semplice" equazione, si è in grado, procedendo a ritroso, e con occhi sempre vigili, ricavarsi ogni condizione utile alla risoluzione del problema (controllare con esagerata minuzia sempre i segni che entrano in gioco, altrimenti alla fine ci si trova non poco incasinati, sfociando in deliri numerici supportati da una quantità di alcol non indifferente per alleviare la sofferenza. Quindi, SVEGLI! ).

PS: Per una più accurata e valida spiegazione teorica, si rimanda alla onnipresente sezione "downloads" di questo sito. ).

Di seguito, gli svolgimenti in pulito e quasi leggibili dell'esercizio svolto manualmente (notate che ficata i colori! )

Nell'ultima delle precedente immagini allegate, per arrivare ad una soluzione numerica, utilizzando il nostro migliore amico SAP2000, si è scelto ed impostato alla trave un materiale ed una sezione, in modo da utilizzare lo stesso modulo elastico E e lo stesso momento d'inerzia I per il confronto manuale/digitale. Grazie alla nostra nuova "fiamma" (equazione linea elastica), sono stato in grado in pochissimo tempo di ricavarmi il punto dove lo spostamento è massimo, e il valore di quest'ultimo. In seguito, ma solo per compiacere la mia bravura (o culo... ) ho confrontato il valore da me ottenuto con quello di SAP (mi raccomando, una volta disegnata la trave di una lunghezza di vostra scelta, ponete anche UN PUNTO alla distanza trovata precedente manualmente dove lo spostamento dovrebbe essere massimo, altrimenti non riuscirete a visualizzare i valori a video se non tramite le criptiche tabelle!), e tadaaaa!!! I risultati sono più o meno gli stessi!!! (più o meno perchè nel calcolo manuale ho approssimato i valori che ottenevo a 6 cifre dopo la virgola, mentre SAP, che è più bravo, li calcola tutti, portandosi dietro un errore sempre minore). Come vedrete dalle immagini seguenti (dove sono riassunti i passaggi prinncipali ed esaurienti, lo scarto è stato soltanto di 1mm, su 5 cm! Non male!!

PS: lo spostamento verticale che ci interessa, SAP lo chiama U3...  Ma poi, perchè?? Non era più facile, se proprio volesse utilizzare la U, segnare l'asse di riferimento, come Z e non un numero???).

PPS: allego anche i diagrammi del momento e del taglio ricavati da SAP, ce li dà senza alcuna fatica!! (chiaramente un minino di consapevolezza c'è, e vi assicuro che sono giusti... ).

A voi, posteri, l'ardua sentenza! 

PS: certo, ad occhio e croce si vede come lo spostamento sia alquanto esagerato, e quindi forse, ma dico forse, la sezione non sia affatto adeguata al carico scelto. Ma questa è un altra storia .

 

Esercitazione_2

trave reticolare spaziale (risoluzione tramite software SAP2000)

 

La modellazione viene effettuata per comodità e necessità di accuratezza su RHINOCEROS, avendo l’accortezza di non disegnare in layer 0 e di non usare polilinee (dato che dovranno risultare aste separate). 

Il file viene quindi salvato in IGES per poter essere importato in SAP.

Tale operazione avviene con il comando FILE > IMPORT > IGES.IGS FILE.

 

 

IGES.IGS FILE > BROWSE > “RETICOLARE” > RATIONAL B-SPLINE ENTITY > 

IMPORT

Le unità di misure vengono impostate kN, m, °C.

 

 

 

 

 

Dato che l’importazione potrebbe avvenire generando qualche errore nei punti di nodo fra le varie aste, si può impostare una tolleranza di approssimazione che si ritenga accettabile tramite il comando EDIT > EDIT POINT > MERGE JOINTS > MERGE TOLERANCE > 0,01. Questo comando fa sì che due estremi di aste che distino meno di questa misura vengano considerate unite.

 

 

 

Assegniamo quindi tre vincoli (per rendere la struttura isostatica) nella parte bassa della trave con il comando ASSIGN > JOINT > RESTRAINTS.

 

 

 

 

 

 

 

 

 

Si procede assegnando l’acciaio come materiale e definendone il tipo per definire un modulo elastico E. Si sceglie inoltre la forma della sezione (tubolare pipe). DEFINE > SECTION PROPERTIES > FRAME SECTIONS.

 

 

 

 

 

Si procede con l’assegnazione dei carichi con il comando ASSIGN > JOINT LOADS > FORCES, trattandosi di un’idealizzazione per la quale i carichi sono concentrati tutti nei nodi.

 

 

 

N.B. In questo tipo di esercizi, impostiamo l’analisi in modo che non consideri il peso proprio della struttura (che costituirebbe un carico distribuito su travi che si deve considerare scariche). 

Ciò viene fatto creando un nuovo LOAD PATTERN che abbia 0 come coefficiente di moltiplicazione del carico SELF WEIGHT MULTIPLER.

 

 

 

 

 

 

Dato che in una struttura reticolare tutti i vincoli interni sono cerniere, dobbiamo fare un’operazione di rilascio del momento ASSIGN > FRAME > RELEASE > MOMENT 3-3(MAJOR) > START 0 – END 0.

Possiamo ora avviare l’analisi. Il software mostra per prima cosa l’andamento della deformata.

Si può richiedere al programma di analizzare gli sforzi assiali (unici presenti) con il comando SHOW FORCES/STRESSES > FRAME/CABLES > AXIAL FORCE

 

 

 

 

 

 

 

 

N.B. si possono anche analizzare gli sforzi a cui sono sottoposti i nodi dando il comando SHOW FORCES/STRESSES > JOINTS.

 

 

 

 

 

 

 

Il comando DISPLAY > SHOW TABLES > JOINT REACTION ci mostra una tabella contenente tutti i valori delle reazioni vincolari, mentre ELEMENT FORCES - FRAMES mostra la tabella dei valori dello sforzo normale.

 

 

N.B. Nella tabella ci sono aste che sono soggette a sforzo normale negativo (compresse) e aste con sforzo normale positivo (tese). Risulta così semplice la individuazione rispettivamente di puntoni e tiranti della struttura. 

 

 

 

Asta	N	A	σ
Text	KN	m2	N/mm²
1	-17,36	0,01	-2,13
2	-42,59	0,01	-5,22
3	37,35	0,01	4,57
4	12,08	0,01	1,48
5	11,49	0,01	1,41
6	-11,99	0,01	-1,47
7	48,03	0,01	5,88
8	149,09	0,01	18,26
9	304,81	0,01	37,34
10	-260,88	0,01	-31,95
11	-56,86	0,01	-6,96
12	56,28	0,01	6,89
13	152,06	0,01	18,6
14	302,55	0,01	37,06
15	-263,14	0,01	-32,23
16	-65,11	0,01	-7,98
17	-67,52	0,01	-8,27
18	-173,93	0,01	-21,30
19	-253,93	0,01	-31,10
20	146,07	0,01	17,89
21	6,04	0,01	0,74
22	-73,96	0,01	-9,06
23	-145,42	0,01	-18
24	-255,53	0,01	-31,30
25	80,20	0,01	9,82
26	0,20	0,01	0,02
27	19,23	0,01	2,36
28	13,94	0,01	1,71
29	84,37	0,01	10,33
30	-121,55	0,01	-14,89
31	-182,42	0,01	-22,34
32	-189,01	0,01	-23,15
34	-0,78	0,01	-0,10
35	85,56	0,01	10,48
36	-54,31	0,01	-6,65
37	128,32	0,01	15,7
38	-79,97	0,01	-9,80
39	136,19	0,01	16,68
40	-196,60	0,01	-24,08
41	141,79	0,01	17,37
42	-72,75	0,01	-8,91
43	-185,07	0,01	-22,67
44	104,01	0,01	12,74
45	-47,18	0,01	-5,78
46	-119,52	0,01	-14,6
47	95,82	0,01	11,74
48	-0,89	0,01	-0,108
49	38,90	0,01	4,76
50	-94,41	0,01	-11,56
51	-37,50	0,01	-4,59
52	-35,56	0,01	-4,36
53	135,92	0,01	16,65
54	182,61	0,01	22,37
55	173,69	0,01	21,28
56	1,48	0,01	0,18
57	-32,94	0,01	-4,04
58	-103,60	0,01	-12,69
59	-40,28	0,01	-4,93
60	-98,93	0,01	-12,12
61	-124,33	0,01	-15,23
62	58,86	0,01	7,21
63	182,58	0,01	22,36
64	54,07	0,01	6,62
65	-130,50	0,01	-16,0
66	184,00	0,01	22,54
67	-129,54	0,01	-15,87
68	-49,13	0,01	-6,02
69	134,55	0,01	16,48
70	-94,37	0,01	-11,56
71	-38,75	0,01	-4,75
72	1,48	0,01	0,181
73	-84,89	0,01	-10,40
74	2,97	0,01	0,36
75	90,88	0,01	11,13

 

Esercitazione_1

trave iperstatica (risoluzione tramite la linea elastica)

 

struttura

 

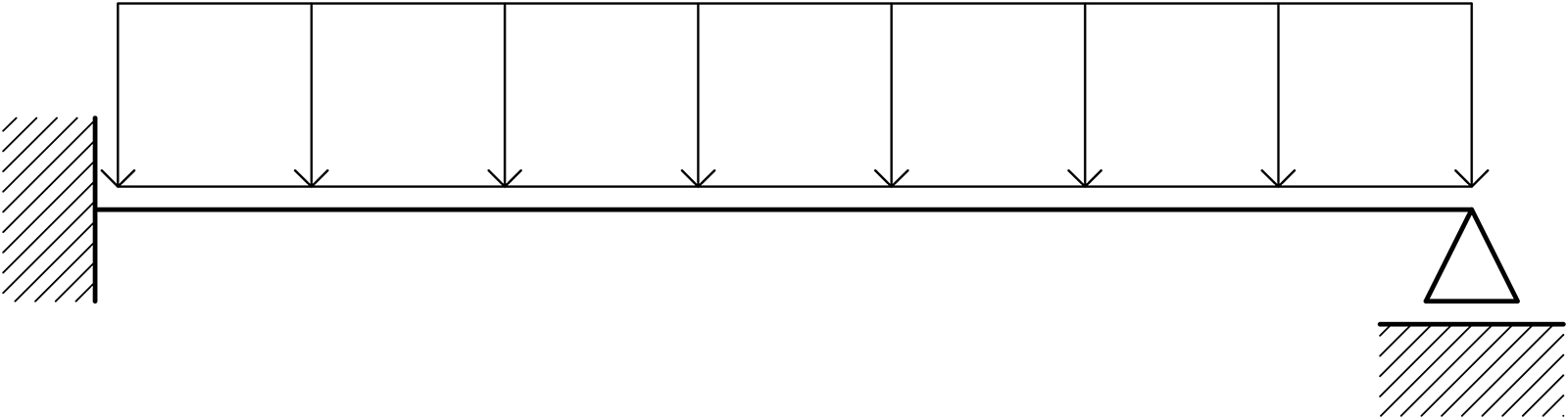
Il sistema proposto risulta essere un sistema iperstatico, quindi per poterlo risolvere si ricorre al metodo d’integrazione della linea elastica (adottando per la trave il modello di Eulero-Bernoulli), il quale ci permette di individuare l’incognita richiesta, ovvero lo spostamento verticale massimo_vs  della deformata.

 

1_

Si procede quindi con l’analisi delle 8 equazioni fondamentali (3 equazioni di EQUILIBRIO, 3 equazioni di DEFORMAZIONE e 2 equazioni COSTITUTIVE); le equazioni successivamente verranno usate per indagare due aspetti fondamentali dello spostamento della deformata della trave, in quanto definiscono sia lo spostamento assiale (definito dallo sforzo normale) che quello trasversale (definito dallo sforzo di taglio e momento flettente).

Le 8 equazioni fondamentali quindi vengono divise in due sistemi:

us

⎧(dN/ds) + q₁=0

⎨N=E*A*ε

⎩ε=(du/ds)

vs

⎧(dT/ds) + q₂=0

⎢(dM/ds) + T=0

⎨M=E*J*χ

⎢ χ=(dφ/ds)

⎩φ=(dv/ds)

Quindi per rispondere alle richieste avanzate nell’esercizio verrano utilizzate solamente le 5 equazioni che descrivono il comportamento dello spostamento verticale_vs  della deformata.

 

2_

Si nota che questo è un sistema di 5 equazioni in 5 incognite. Siamo quindi in grado di dedurle tutte, esprimendole come progressive derivate della legge dello spostamento verticale_vs.

Quindi si procede con l’analisi delle condizioni al bordo; per poter risolvere l’equazione dello spostamento verticale_vs  necessitiamo di 4 equazioni aventi risultati noti poiché l’equazione suddetta presenta 4 incognite, che si presentano sotto costanti di integrazione C₁, C₂, C₃ e C₄ (derivanti dalle 4 integrazioni fatte per la determinazione della stessa).

 

vs= (q₂*s⁴/24*E*J) + (C₁*s³/6) + (C₂*s²/2) + (C₃*s) + C₄

 

A questa equazione si giunge integrando quattro volte l’equazione che descrive il carico, ovvero:

 

q(s)= (d⁴v/ds⁴)*E*J

 

Si suppone quindi che il carico sia descritto da una legge costante, fatto che ci fa dedurre che la legge dello spostamento verticale_vs sia un polinomio del tipo:

 

 p(x)= a₀ + a₁*x + a₂*x² + a₃*x³ + a⁴*x₄

 

Inoltre si è ipotizzato che il prodotto E*J sia costante lungo lo sviluppo assiale della trave_s, ovvero che le sezioni mantengano costanti le loro dimensione, forma e materiale. Grazie a questa ipotesi si è potuto estrapolare dall’integrazione il prodotto suddetto considerandolo come una costante, e quindi semplificando l’integrazione.

 

3_

Nel caso specifico dell’esercizio:

 

deformata

 

 

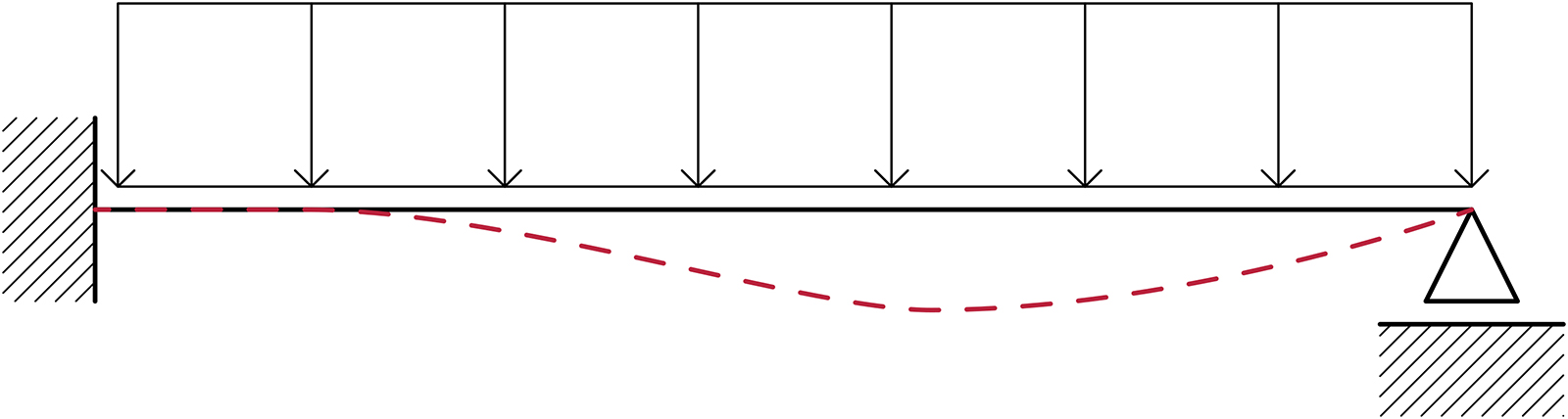
_estremo sinistro - incastro: s= 0

In questo punto  lo spostamento verticale e la rotazione della sezione della trave risultano essere pari a zero, quindi abbiamo:

v(0)= 0

φ(0)= 0

 

Sostituendo le due condizioni risultanti nelle rispettive equazioni, derivate sempre dall’integrazione dell’equazione della linea elastica per lo spostamento verticale a cui facciamo riferimento (q(s)= (d⁴v/ds⁴)*E*J) si può constatare che C₃ e C₄ sono nulle.

 

v(0)= 0 ⇒ C₄= 0

φ(0)= 0 ⇒ C₃*s = 0

 

_estremo destro - carrello orizzontale: s= L

In questo punto lo spostamento verticale risulta essere pari a zero, mentre la rotazione della sezione risulta essere diversa da zero ed ignota. Si necessita, quindi, di un ulteriore equazione nota e prendiamo in considerazione quella del momento che in prossimità della cerniera del carrello orizzontale deve essere uguale a zero.

v(L)= 0

φ(L)≠ 0 ⇒ M(L)= E*J*χ= E*J*(d²v/ds₂)= 0

 

Sostituendo le due condizioni risultanti nelle rispettive equazioni, derivate sempre dall’integrazione dell’equazione della linea elastica per lo spostamento verticale a cui facciamo riferimento (q(s)= (d⁴v/ds⁴)*E*J) ricavandoci C₁ e C₂.

 

 

v(L)= 0 ⇒

φ(L)= 0 ⇒ M(L)= E*J*χ= E*J*(d²v/ds₂)= 0 ⇒ ⎰(q₂*s²/2*E*J) + (C₁*L) + C₂

⇒ ⎱(q₂*s⁴/24*E*J) + (C₁*L³/6) + (C₂*L²/2)= 0

⇒ ⎰ C₁= -(5*q*L)/(8*E*J)

⇒ ⎱ C₂= (q*L)/(8*E*J)

Le due equazioni relative al bordo L, messe a sistema, ci permettono di calcolare le costanti C₁ e C₂.

 

4_

Successivamente si procede con la definizione dell’ultimo dato incognito presente nell’equazione dello spostamento verticale_vs, senza il quale non risulta possibile determinare l’abbassamento verticale: si tratta quindi del valore da assegnare alla variabile s all’interno dell’equazione dello spostamento verticale. Sapendo che all’abbassamento verticale massimo corrisponde un valore nullo della derivata della funzione che approssima la deformata della trave, si può dedurre che per la sua risoluzione bisogna derivare la funzione vs e trovare i valori di s per i quali la derivata si annulla.

 

v’s= φ=(dv/ds)= (q₂*s³/6*E*J) + (C₁*s²/2) + (C₂*s)= 0

 

Risolvendo questa equazione di terzo grado (mettendo in evidenza la s  per trovare la prima soluzione, ottenendo di conseguenza un’equazione di secondo grado) ottenendo 3 valori di s per i quali la derivata è nulla, ma solo 2 sono da prendere in considerazione (in quanto uno si riferisce ad un valore di s maggiore di L):

 

v’s= φ=(dv/ds)= (q₂*s³/6*E*J) + ((-(5*q*L)/(8*E*J))*s²/2) + (((q*L)/(8*E*J))*s)= 0

⇒ s= 0

⇒ s₁= (15*L/16) - ((√33)*L/16)

⇒ s₂= (15*L/16) + ((√33)*L/16) ⇒ s₂= 0,578*L

5_

Successivamente si procede con il calcolo dello spostamento verticale. Sostituiamo il valore di s₂ e C₁ e C₂ all’interno dell’equazione dello spostamento verticale_vs.

 

v’s= (q₂*s⁴/24*E*J) + (C₁*s³/6) + (C₂*s²/2)

 

⇒ v’s= (q₂*(0,578*L )⁴/24*E*J) + ((-(5*q*L)/(8*E*J))*(0,578*L)³/6) + (((q*L)/(8*E*J))*(0,578*L)²/2)

Il risultato dello dello spostamento verticale_vs  sarà in funzione di q/E*J. Per avere un risultato esclusivamente numerico basterà assegnare un valore numerico al carico q, scegliere il materiale per avere un modulo elastico E e la sezione della trave per avere il momento d’inerzia J.

 

6_

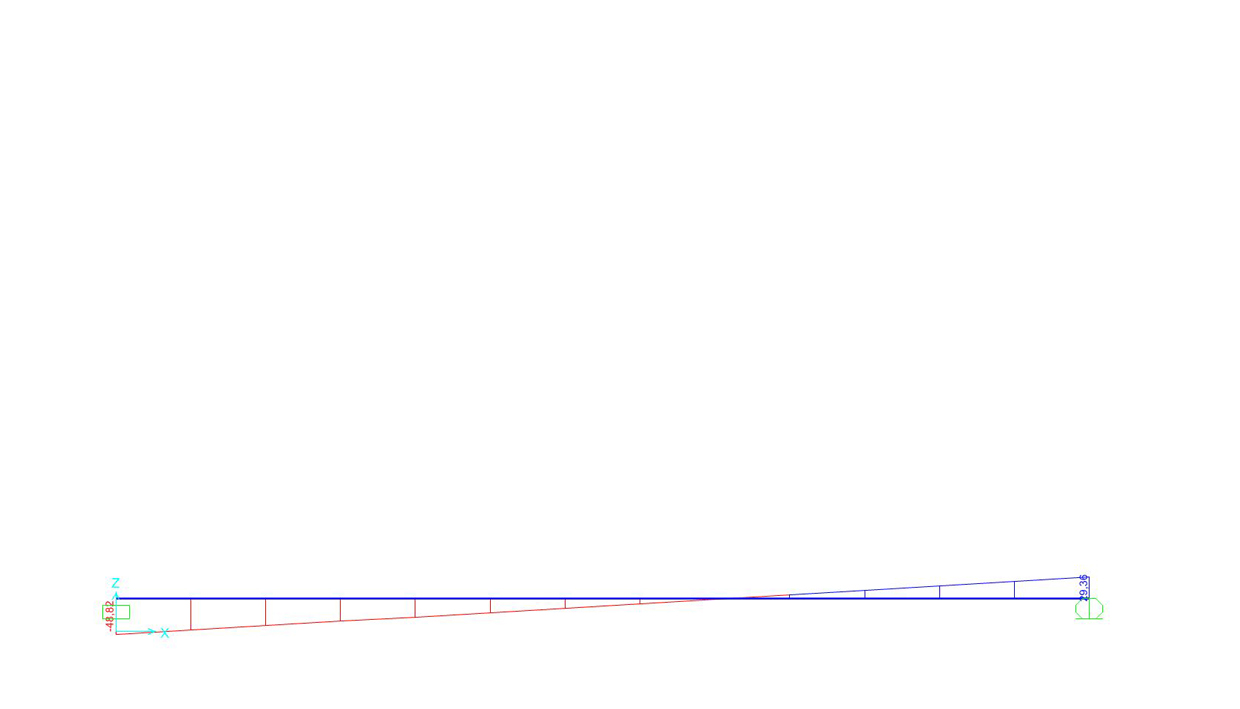
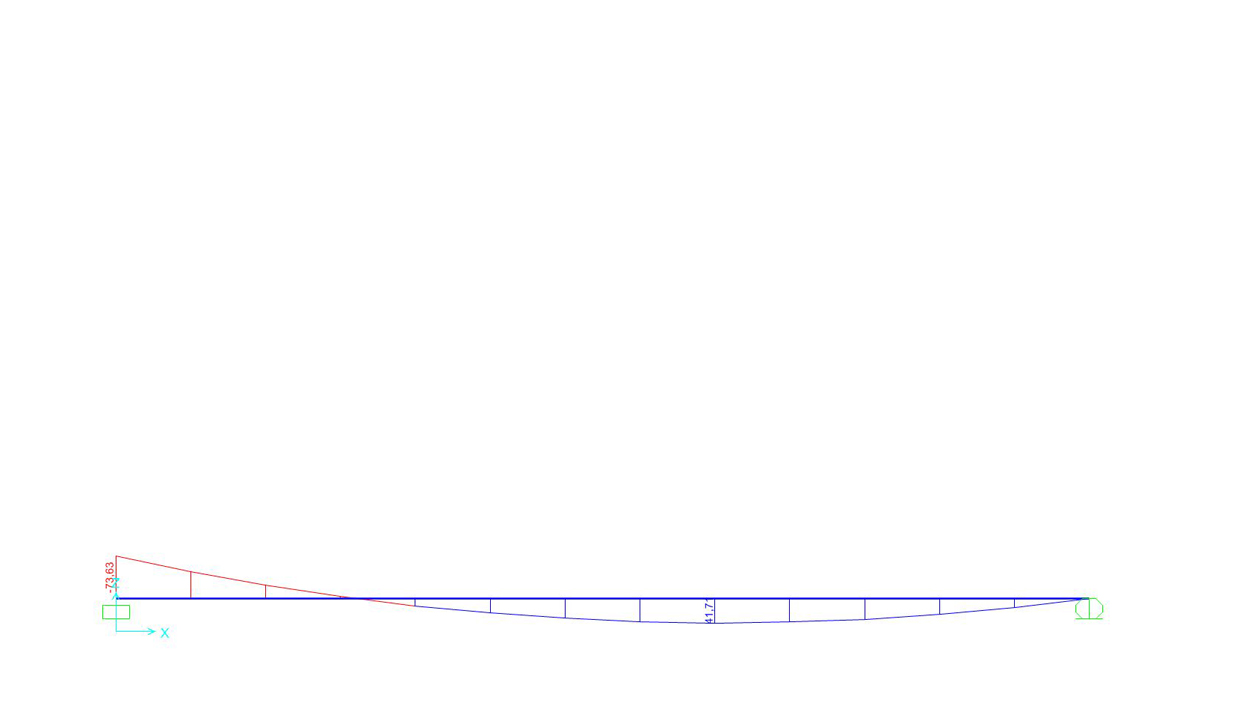
L’ultimo passo consiste nel diagrammare il Taglio ed il Momento. Per il primo possiamo affermare che l’andamento è lineare e abbiamo un taglio negativo massimo in prossimità dell’incastro e uno positivo massimo nel carrello orizzontale. L’intersezione con l’asse della trave corrisponde a s= 0,578*L. Il momento, di conseguenza, avrà andamento parabolico, con un massimo positivo nell’incastro, curvatura verso il basso e valore zero nel carrello; ad s= 0,578*L corrisponde un momento negativo massimo.

 

 

 

 

 

 

 

 

 

 

 

 

grafici qualitativi di TAGLIO e MOMENTO

 

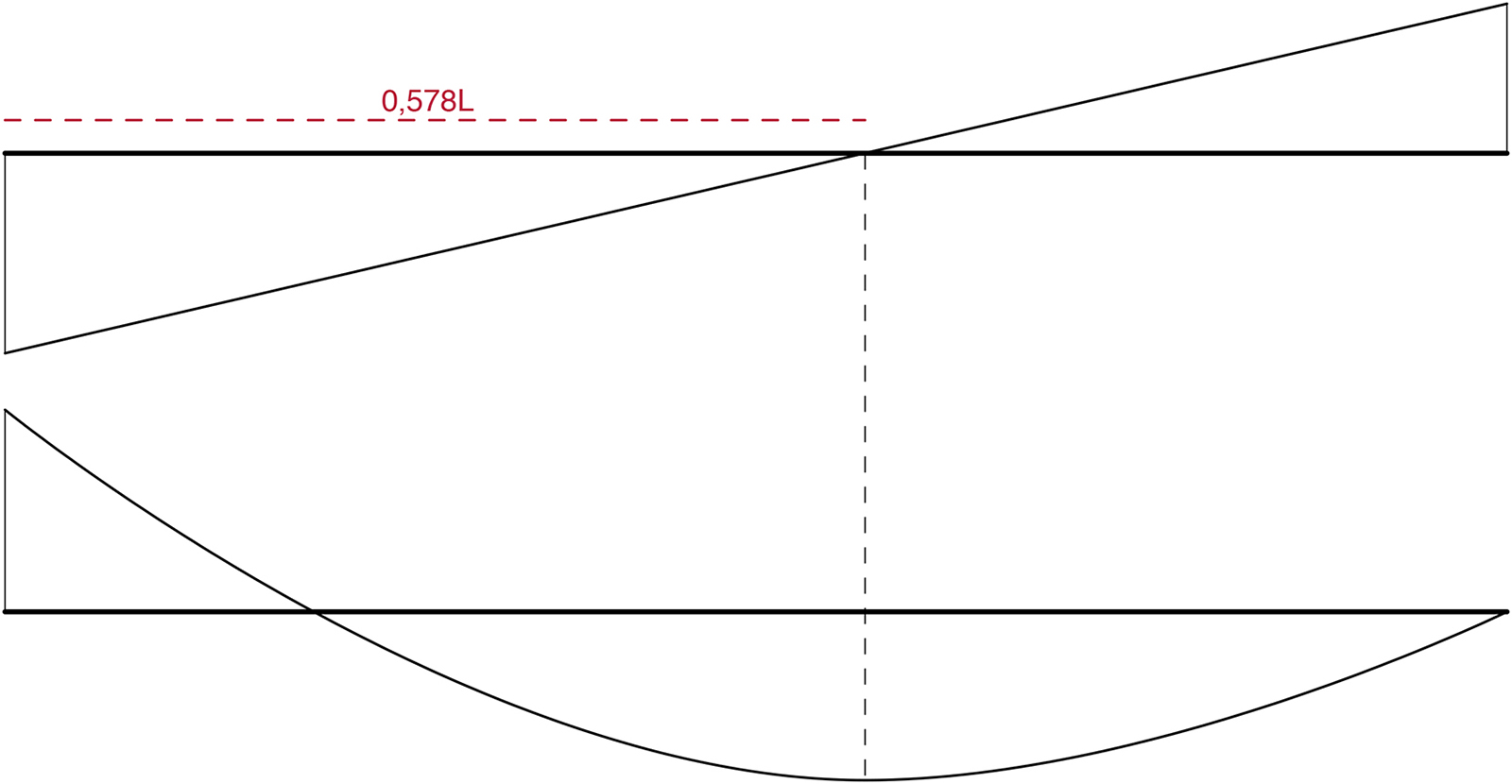
I diagrammi delle sollecitazioni della struttura iperstatica possono essere visti come somma di due diagrammi di due struttura isostatiche.

 

7_

Succesivamente attraverso l’uso del software SAP2000 verrà assegnato un materiale (E), una dimensione ed una forma (J).

 

creare un nuovo file con una griglia utile al disegno dell’asta:

FILE > NEW MODEL >

 

 

 

 

 

 

 

 

 

 

QUICK GRID LINES > impostare 2 assi sull’asse x, 1 sull’asse y e 1 sull’asse z > impostare come GRID SPACING la dimensione che vorremo dare alla lunghezza della trave

 

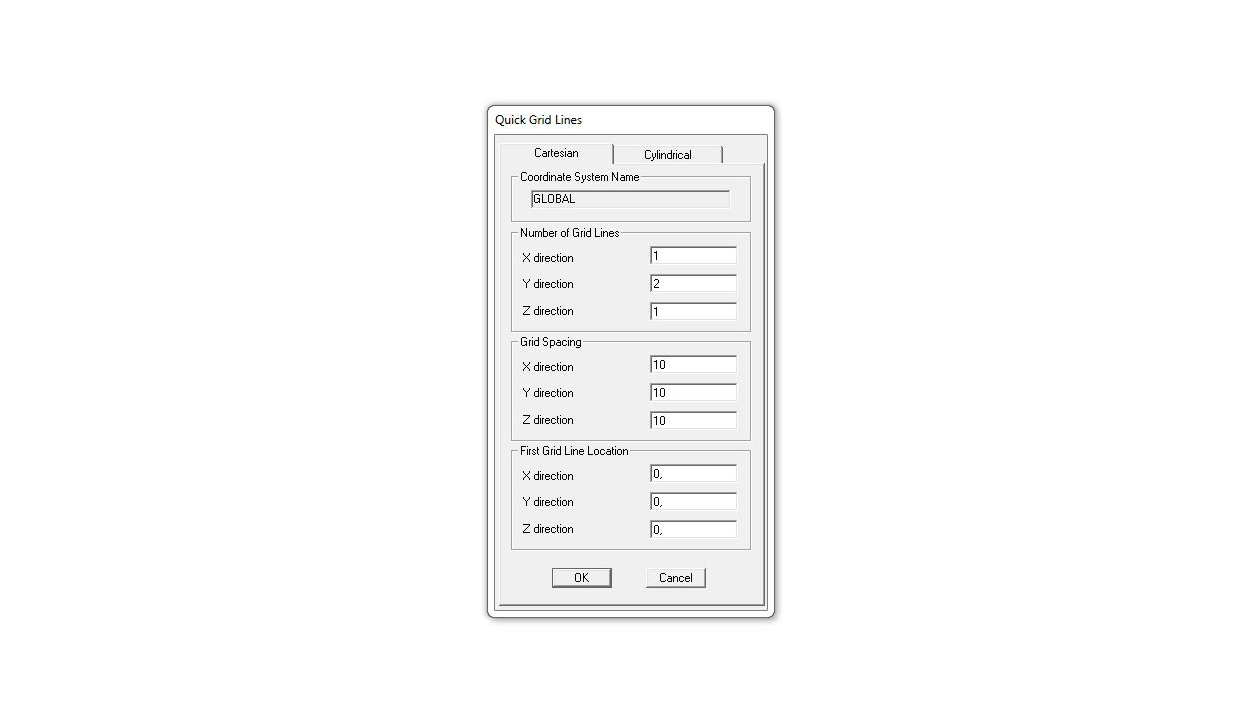
le impostazioni date alla griglia dovrebbero produrre una condizione analoga alla seguente:

 

 

 

 

 

 

 

 

disegnare un’asta seguendo la spaziatura della griglia preimpostata.

 

 

 

 

assegnare i vincoli: 

selezionare il punto > ASSIGN > JOINT RESTRAINTS > spuntare le sollecitazioni che il vincolo da posizionare trattiene

 

 

 

 

 

 

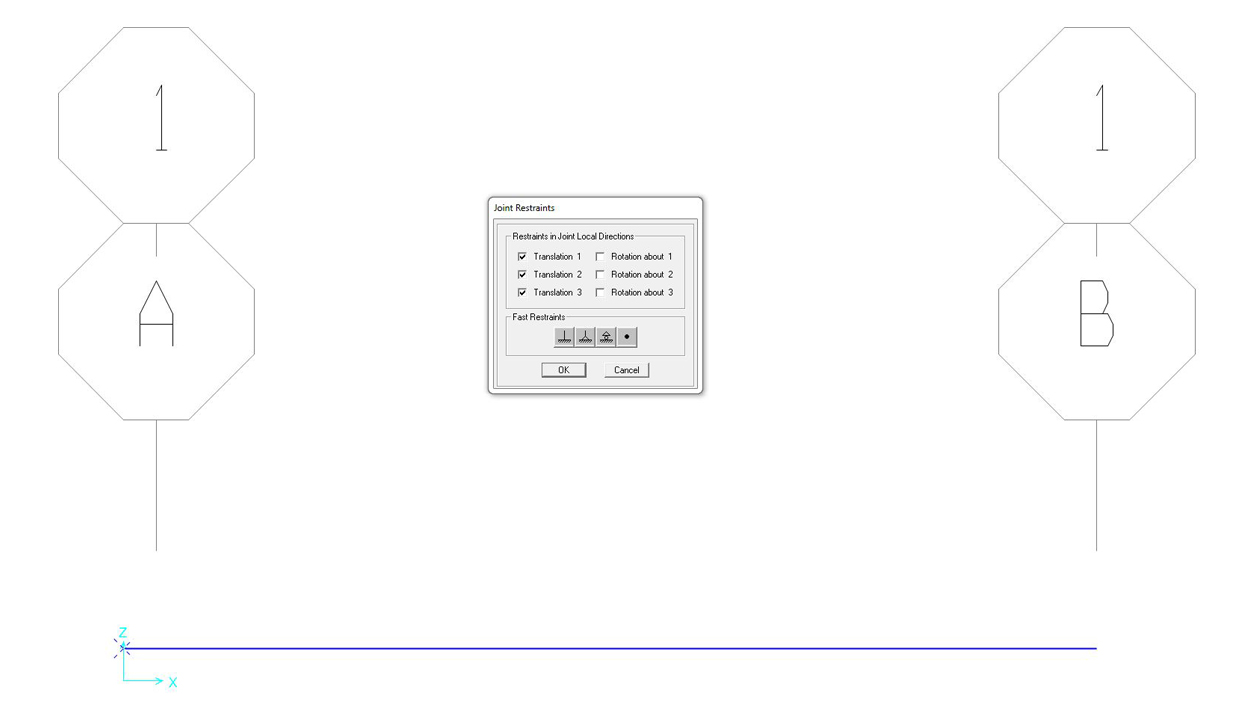
assegnare un incastro a sinistra ed un carrello a destra

 

 

 

 

assegnare il carico uniformemente distribuito:

selezionare l’asta  > ASSIGN > FRAME LOADS > DISTRIBUTED > impostare l’unità di misura voluta (nel nostro caso N, m, °C) > nella casella UNIFORM scrivere (ad esempio) -10 KN

 

 

 

 

 

 

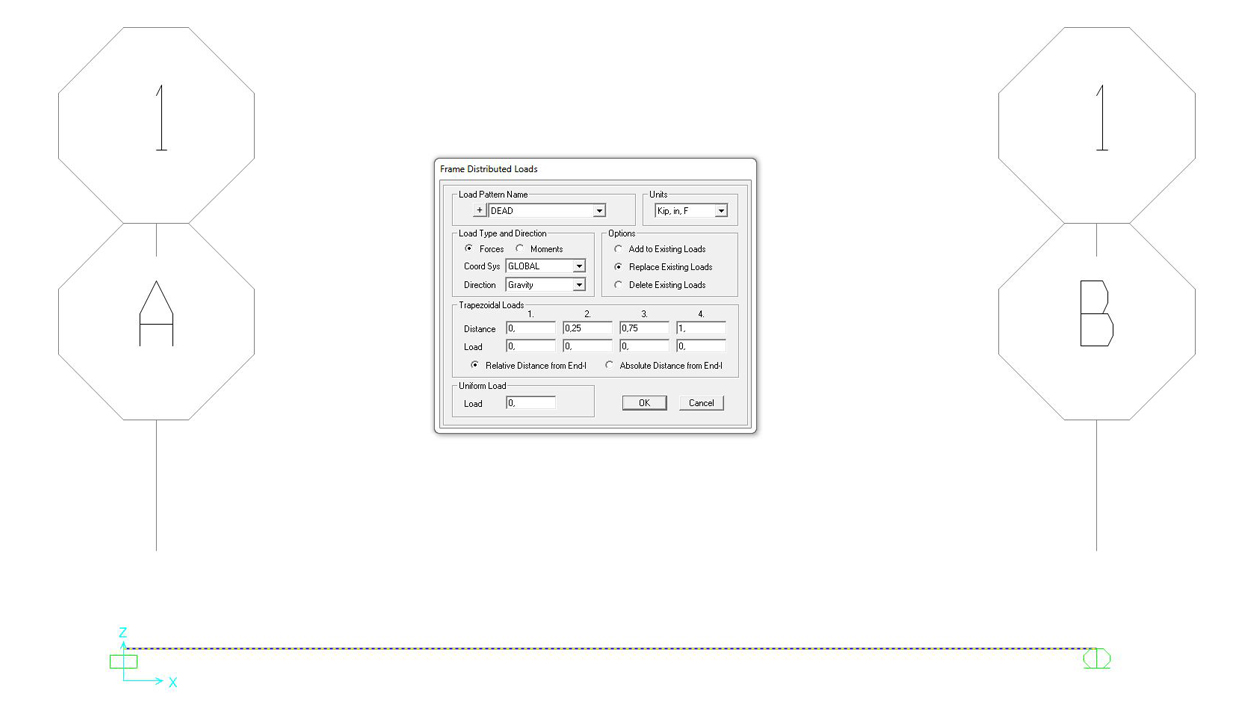
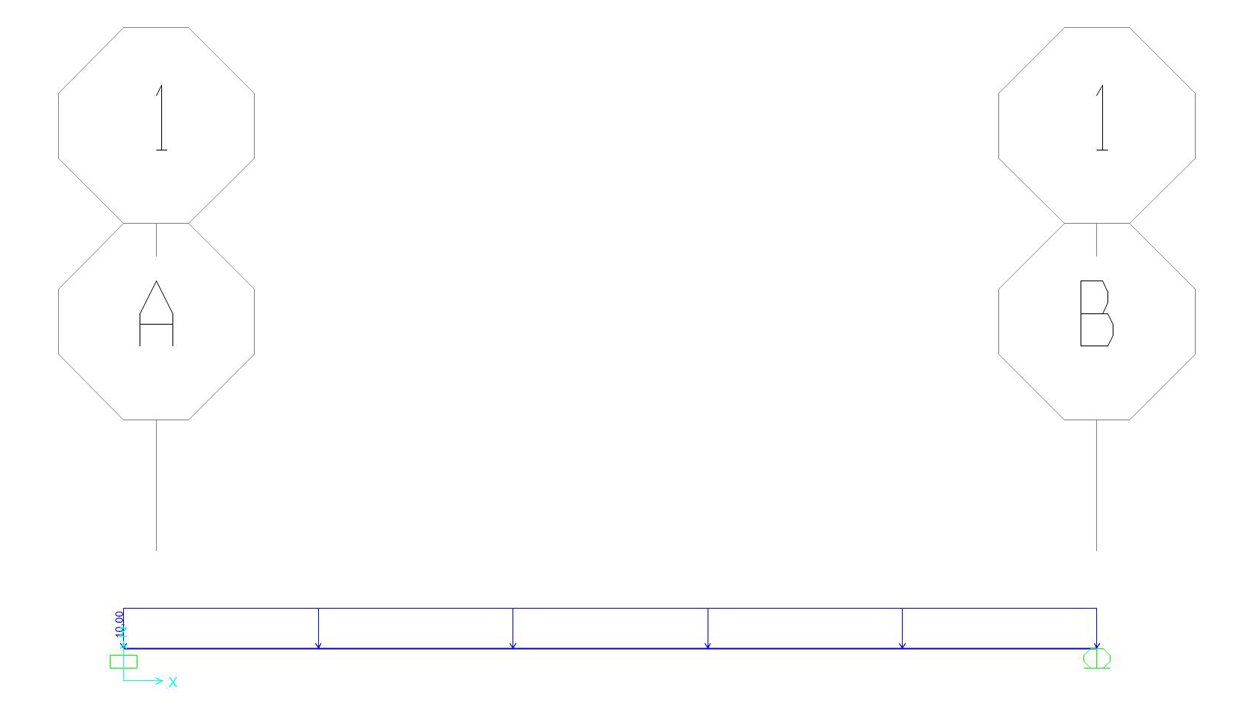
rendere visibile il carico impostato:

DISPLAY > VIEW LOADS

 

 

 

 

eliminare il contributo del peso proprio della struttura dall’analisi:

DEFINE > LOAD PATTERNS > SELF WEIGHT MULTIPLER = 0 > nominare il load pattern “peso_nullo” > ADD NEW LOAD PATTERN

 

 

 

 

 

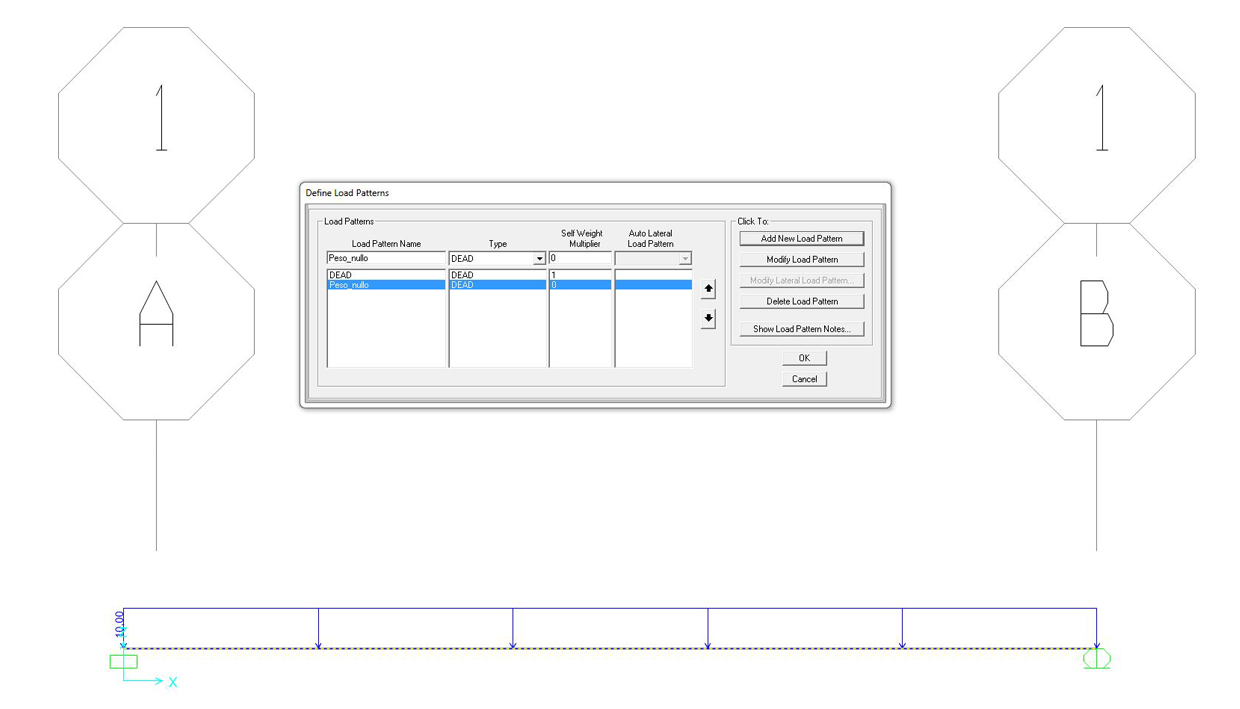
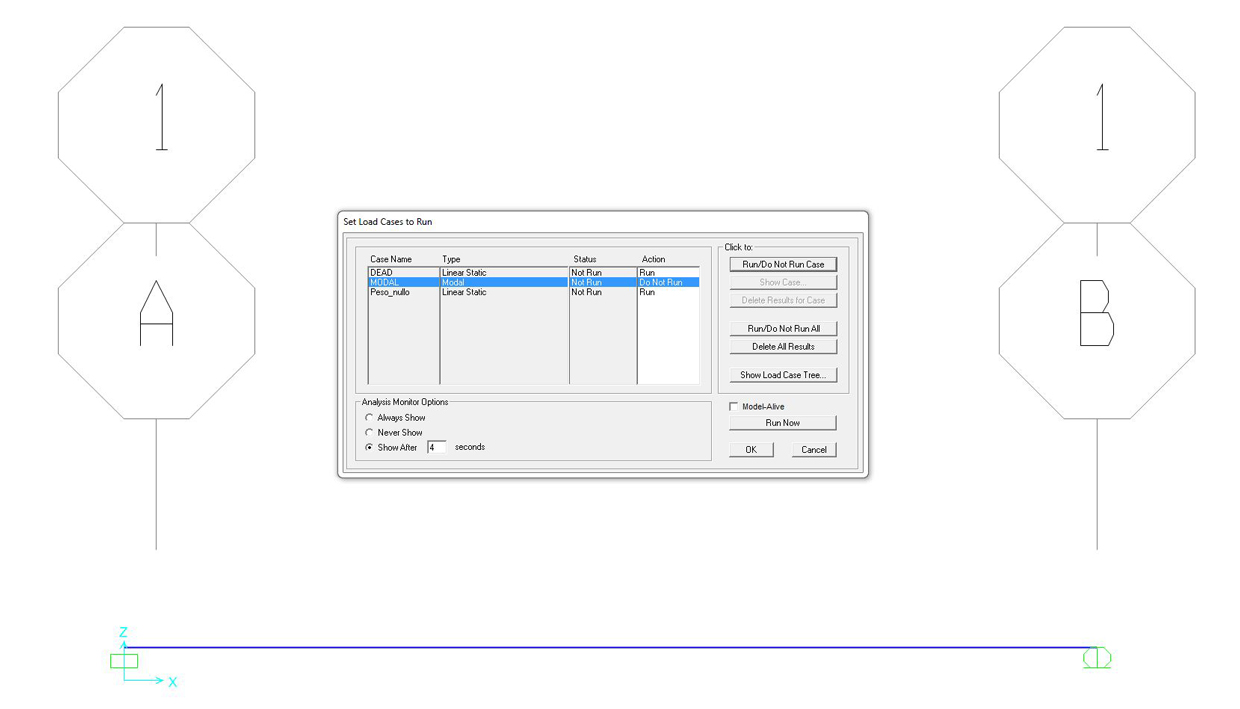
eliminare MODAL dall’analisi:

selezionare il load pattern MODAL > se nella colonna ACTION c’è RUN, premere il pulsante RUN/DO NOT RUN CASE per disattivare l’analisi

 

 

 

visualizzare la curva della deformata e confrontarla qualitativamente con quella ipotizzata:

RUN ANALYSIS 

 

 

 

 

 

 

visualizzare le reazioni vincolari:

RUN ANALYSIS > JOINT REACTIONS 

 

 

 

 

 

visualizzare il grafico del taglio e confrontarlo qualitativamente con quello ipotizzato:

RUN ANALYSIS  > SHEAR 2-2

 

 

 

 

 

visualizzare il grafico del momento e confrontarlo qualitativamente con quello ipotizzato:

RUN ANALYSIS > MOMENT 3-3 > spuntare START e END

 

 

 

 

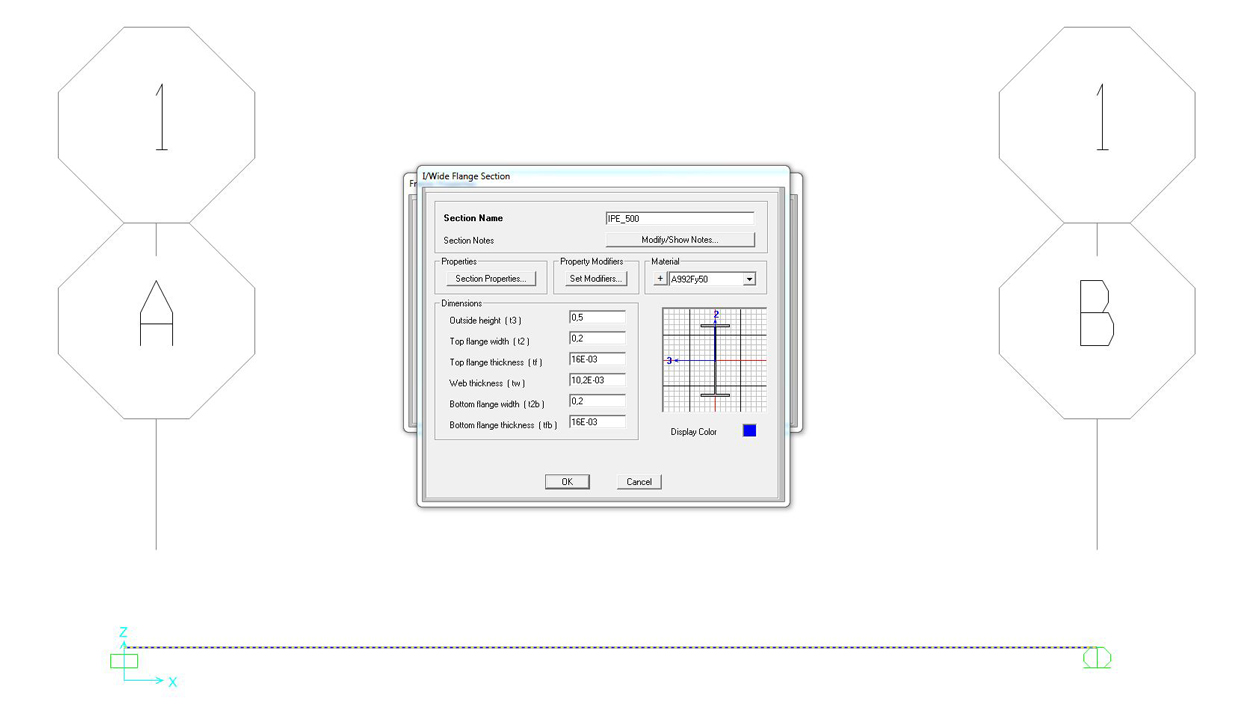
impostare il materiale, la forma e la dimensione della sezione:

ASSIGN > FRAME > FRAME SECTION > (nel nostro caso) impostare acciaio a doppia T > impostare le misure desiderate (nel nostro caso quelle di una IPE500) > rinominare la sezione

 

 

 

 

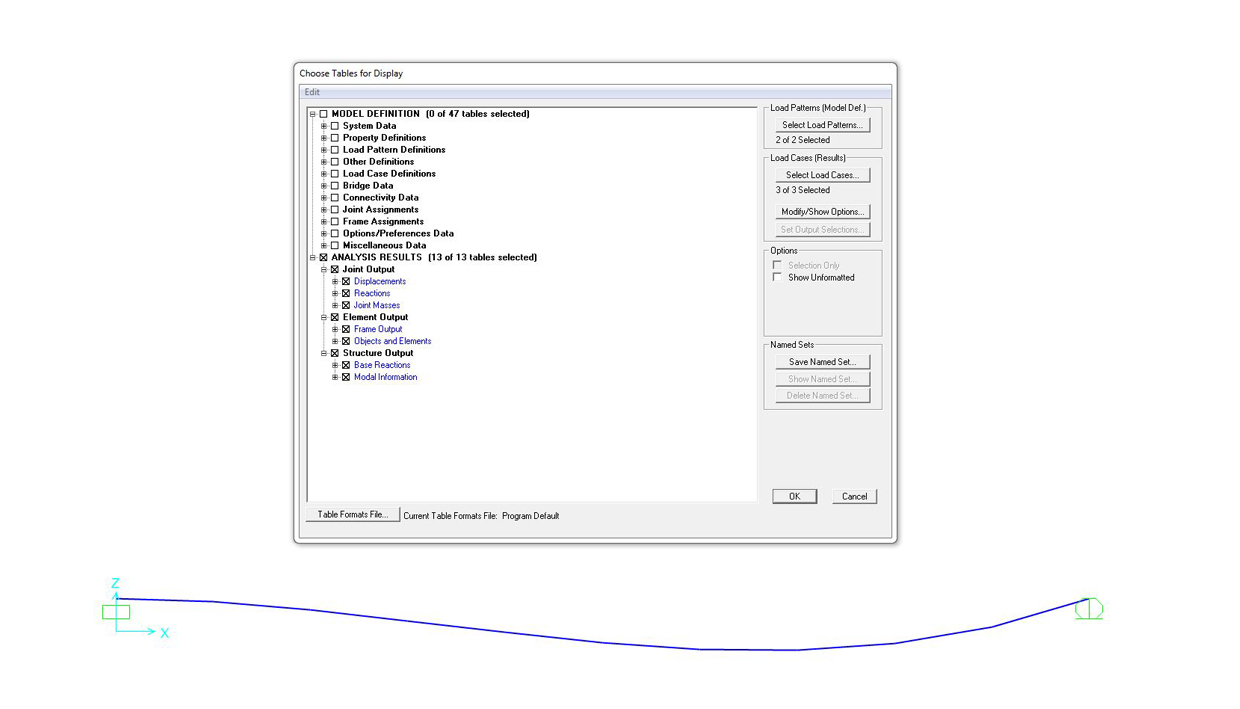
visualizzare le tabelle relative ai dati dell’analisi:

DISPLAY > SHOW TABLES > spuntare la parte ANALYSIS RESULTS 

 

 

 

 

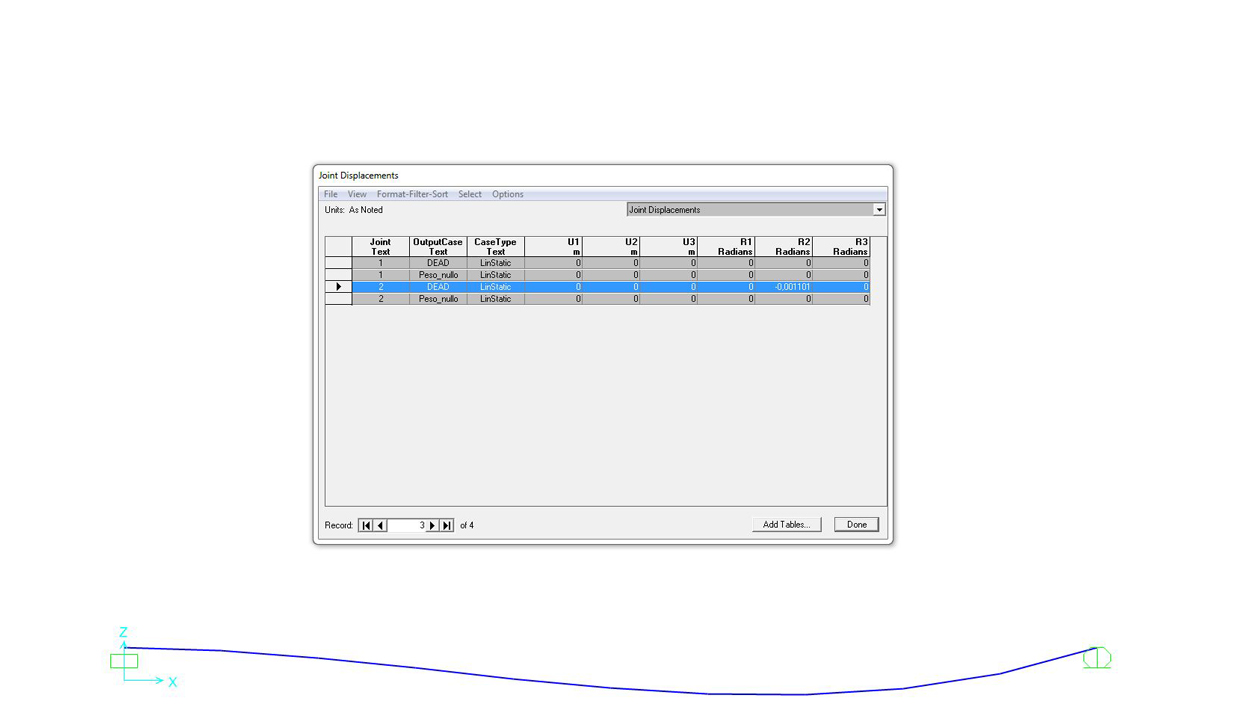
visualizzare gli spostamenti dovuti alle deformazioni per confrontare quello verticale con quello ottenuto nell’esercizio:

dal menù a tendina scegliere JOINT DISPLACEMENT > trovare il dato in R2

 

 

 

 

 

esportare i dati in formato EXCEL per organizzarli:

finestra delle tabelle > FILE > EXPORT > EXCEL FILE > SAVE

 

 

stazioni di record	sollecitazione di TAGLIO	sollecitazione di MOMENTO
0	-47,192	-70,7434
0,58225	-41,37	-44,9609
1,16449	-35,547	-22,5686
1,74674	-29,725	-3,5664
2,32898	-23,902	12,0457
2,91123	-18,08	24,2677
3,49348	-12,257	33,0996
4,07572	-6,435	38,5414
4,65797	-0,613	40,5931
5,24022	5,21	39,2547
5,82246	11,032	34,5262
6,40471	16,855	26,4076
6,98695	22,677	14,8988
7,5692	28,5	1,004*E-15

 

 

 

VINCOLI	REAZIONI VINCOLARI	REAZIONI VINCOLARI
	TAGLIO	MOMENTO
incastro	47,192	-70,7434
cerniera	28,5	0