Portale di Meccanica

Lo scopo di questa esercitazione è dimensionare la trave più sollecitata su tre casi di studio di solai con tre tecnologie diverse. Ho scelto di analizzare un solaio in latero-cemento con trave in calcestruzzo armato, un solaio con profili in acciaio e lamiera grecata e un solaio in legno lamellare.

Il calcolo, effettuato tramite una tabella excel considera i carichi strutturali, permanenti e accidentali del solaio, il momendo flettente che ne deriva e le resistenze caratteristiche del materiale. In seguito verifica il dimensionamento aggiungendo il peso proprio della trave principale trovata al carico strutturale.

Prendiamo in considerazione un impalcato tipo di misure 6m x 4m, comune per le tre tecnologie, con area di interesse di 24 m².

SOLAIO IN LATERO CEMENTO

Carico strutturale

Strato strutturale in latero-cemento sp. 0,22 m interasse travetti 0,5 m

pignatte 2x dim. 0,18x0,40x1m /1m² x γ 5 kN/m³ = 0,72 kN/m²

travetti 2x dim.  0,10x0,18x1m  /1m² γ 25 kN/m³ = 0,9 kN/m²

soletta sp. 0,04 m γ 25 kN/m³ = 1 kN/m²

q_s = (0,72+0,9+1) kN/m² = 2,62 kN/m²

 

Carico permanente

Parquet di rovere naturale: essenza dura sp: 0,013 m γ 7 kN/m³ = 0,091 kN/m²

Sottofondo di sabbia e cemento sp. 0,02 m γ 18 kN/m³ = 0,36 kN/m²

Membrana in polietilene sp. 0,002 m γ 9 kN/m³ = 0,18 kN/m²

Massetto di integrazione impiantistica in Cls addittivato AT 30 sp. 0,052 m γ 18 kN/m³ = 0,936 kN/m²

Pannello isolante termoacustico in fibra di poliestere sp. 0,022 m γ 0,2 kN/m³ = 0,0044 kN/m²

Intonaco in calce-gesso sp. 0,015 m γ 15 kN/m³ = 0,225 kN/m²

tramezzi = 1 kN/m²

impianti = 0,5 kN/m²

q_p = (0,091+0,36+0,18+0,936+0,0044+0,225+1+0,5)kN/m² = 3,3 kN/m²

 

Carico accidentale

Categoria A, Ambienti ad uso residenziale

q_a = 2,00 kN/m²

Il carico totale q è uguale all’interasse per a somma del carico strutturale permanente e accidentale moltiplicati per dei coefficient di sicurezza : q= i* [ (qs+qp)*1,3 + (qa)*1,5 ]

 

Ora possiamo trovare il momento M, che sappiamo essere ql²/8 per una trave doppiamente appoggiata.

Inseriamo f_y  limite di snervamento dell’acciaio da armature e R_ck resistenza a compressione del calcestruzzo su provino cilindrico a 28 giorni per calcolare rispettivamente il sigma ammissibile dell’armatura in ferro e l sigma ammissibile del calcestruzzo.

Con questi valori e ipotizziando una base della trave di 20 cm viene calcolato un primo valore di altezza della trave, a cui va aggiunto delta, altezza del copriferro.

Verifica al peso proprio della trave

Notiamo che il peso proprio della trave di calcestruzzo influisce in modo importante sul calcolo e ci costringe a scegliere una sezione maggiore.

 

SOLAIO IN ACCIAIO

 

Carico strutturale

travetto HEA 160 = 0,304 kN/m²

lamiera gracata sp. 0,012 m = 0,165 kN/m²

soletta collaborante sp. 0,045  γ 25kN/m³ = 1,125 kN/m²

completamento gracata 5* (0,064m+0,034m)*0,074m /2 *1m * γ 25kN/m³ = 0,45 kN/m²

q_s = (0,304+0,165+1,125+0,45) kN/ m² = 2,044 kN/ m²

 

Carico permanente

massetto di allettamento in sabbia e cemento sp. 0,05 m * γ 18 kN/m³ = 0,9 kN/m²

tappetino anticalpestio sp.0,007 m * γ 0,9 kN/m³ = 0,0063 kN/m²

pavimento gres sp.0,01 m * γ 20 kN/m³ = 0,2 kN/m²

controsoffitto in cartongesso sp. 0,013 m * γ 9 kN/m³ = 0,117 kN/m²

tramezzi = 1 kN/m²

impianti = 0,5 kN/m²

q_p = (0,9+0,0063+0,2+0,117+1+0,5) kN/m² = 2,73 kN/m²

 

Carico accidentale

Categoria B2 uffici aperti al pubblico

q_a =  3,00 kN/m²

In questo caso usiamo f_y,k tensione di snervamento caratteristica dell’acciaio per la classe Fe 430/S275 per trovare il sigma ammissibile e la resistenza W_x  che comparata con i moduli di resistenza di un profilario ci porta a scegliere un’IPE 360.

Verifica peso proprio della trave  q=0,571 kN/m

La sezione trovata è verificata.

 

SOLAIO IN LEGNO

Carico strutturale

travetti legno lamellare interasse 0,50 m 2x dim. 0,22*0,06 m * γ 5 kN/m³ = 0,132 kN/m²

Rivestimento portante di pannelli OSB sp. 0,022 m * γ 5,8 kN/m³ = 0,128 kN/m²

q_s = (0,132+0,128) kN/m² = 0,26 kN/m²

 

Carico permanente

massetto sabbia cemento sp. 0,04 m * γ 18 kN/m³ = 0,72 kN/m²

pavimento legno sp. 0,013 m * γ 7 kN/m³ = 0,091 kN/m²

isolante lana minerale sp. 0,10 m * γ 1,2 kN/m³ = 0,12 kN/m²

listelli in legno interasse 0,25 m 4* dim. 0,04*0,02 m * γ 7 kN/m³ = 0,0224 kN/m²

barriera al vapore sp. 0,00022 m * γ 5 kN/m³ = 0,0011 kN/m²

lastra in cartongesso sp. 0,012 m * γ 9 kN/m³ = 0,108 kN/m²

tramezzi = 1 kN/m²

impianti = 0,5 kN/m²

q_p = (0,72+0,091+0,12+0,0224+0,0011+0,108+1+0,5) kN/m² = 2,5625 kN/m²

 

Carico accidentale

Categoria A ambienti ad uso residenziale

q_a =  2,00 kN/m² 

Prendiamo f_m,k ,resistenza a flessione per legno lamellare di conifera e k_mod, coefficiente che tiene conto dell’invecchiamento del legno.

Verifica al peso proprio della trave principale q=0,675 kN/m

Anche in questo caso dobbiamo scegliere una sezione con un'altezza maggiore.

Prendiamo in considerazione una maglia strutturale con delle travi a sbalzo che aggettano di 3 metri e hanno un'area d'influenza con interasse 6 metri. Utilizziamo gli stessi solai della seconda esercitazione nelle 3 diverse tecnologie (calcestruzzo armato, legno e acciaio).

Nel dimensionare le travi prenderemo in considerazione il valore L/vmax che per essere soddisfatto dovrà essere maggiore di 250.

Solaio in legno

 

Qs= 0,36   Qp=2,4   Qa=2,00

Per necessità di deformabilità ho aumentato la sezione della trave fino a (35 x 55)cm.

L/vmax=291,00 VERIFICATO

Solaio in Cls

Qs=3,45   Qp=3,3   Qa=2,00

Anche in questo caso l'altezza della trave è stata aumentata fino ad avere una sezione di (30 x 48,25)cm.

L/vmax=253,69 VERIFICATO

Solaio in acciaio

Qs=2,71   Qp=2,05   Qa=2,00

In questo caso osserviamo il modulo d'inerzia Wx che ci porta ad avere una IPE 360 con un Wx pari a 904,00.

L/vmax=304,98 VERIFICATO

In questa esercitazione si analizzerà la deformabilità di una trave a sbalzo in tre diversi materiali, in calcestruzzo armato, in legno e in acciaio. Si studia il telaio mostrato in figura sottostante, con interasse pari a 3 m e luce dello sbalzo pari a 3 m, in cui viene evidenziata la trave maggiormente sollecitata.

                                    Fig. 1

Per calcolare la deformabilità di una trave a sbalzo, come è stato fatto nell’esercitazione precedente della trave appoggiata, prima di tutto è necessario calcolare i carichi agenti su di essa.

 

SOLAIO IN CLS

                                    Fig. 2

In seguito vengono riportate le tabelle dei carichi permanenti strutturali e non, già ricavati nella seconda esercitazione.

Carichi strutturali qs=    2.13    Kn/ m²

Carichi permanenti qp=  1.5   KN/m²

Carichi accidentali qa=    2    KN/m²

Quindi è possibile inserire i risultati ottenuti nel foglio di calcolo. E' inoltre necessario inserire il valore pari 450 MPa per la resistenza caratteristica delle armature e scegliendo una classe C 40/50 per il cls si definisce anche la resistenza caratteristica a compressione pari a 50 Mpa.

Infine si sceglie la base della trave pari a 30 cm e si ottine l'altezza.

L'altezza della trave risulta essere pari a 28.73 cm questo valore viene arrotondato a 35 cm. Conoscendo le dimensioni della base e dell'altezza si può ottenere il peso proprio della trave e aggiungendolo ai carichi si dimostra se l/Vmax>250 è verificata, ovvero se la trave sopporta anche il peso proprio.

Peso trave P= (0.30 m x 0.35 m x 1 m ) x 25KN/m³ = 2.625 KN/m

l/Vmax>250 è verificata poiché l/Vmax =341 e si ha uno spostamento Vmax pari a 0.88 cm.

 

SOLAIO IN LEGNO

Fig. 3

In seguito vengono riportate le tabelle dei carichi permanenti strutturali e non, già ricavati nella seconda esercitazione.

Carichi strutturali qs=    1.2    Kn/ m²

Carichi permanenti qp=  1.5   KN/m²

Carichi accidentali qa=    2    KN/m²

Quindi è possibile inserire i risultati ottenuti nel foglio di calcolo. Si è scelto un legno lamellare GL 24h con resistenza a flessione fm,k = 24MPa e la base della trave pari a 30cm.

Considerando la base della trave pari a 30 cm si ottiene un'altezza pari a 36.4 cm che si arrotonda a 40 cm. Conoscendo le dimensioni della base e dell'altezza si può ottenere il peso proprio della trave e aggiungendolo ai carichi si dimostra se l/Vmax>250 è verificata, ovvero se la trave sopporta anche il peso proprio.

Peso trave P= (0.30 m x 0.40 m x 1 m ) x 7 KN/m³ = 0.84 KN/m

l/Vmax>250 è verificata poiché l/Vmax =265 e si ha uno spostamento Vmax pari a 1.13 cm.

 

SOLAIO IN ACCIAIO

In seguito vengono riportate le tabelle dei carichi permanenti strutturali e non, già ricavati nella seconda esercitazione.

Carichi strutturali qs=    1    Kn/ m²

Carichi permanenti qp=  1   KN/m²

Carichi accidentali qa=    2   KN/m²

Per dimensionare una trave in acciaio, una volta che si conosce la Wx è possibile ricavare la sezione dal profilario.

Quindi si sceglie una IPE 220 con una Wx=252 cm³ e Ix= 9110 cm⁴ .

Conoscendo le dimensioni della base e dell'altezza si può ottenere il peso proprio della trave e aggiungendolo ai carichi si dimostra se l/Vmax>250 è verificata, ovvero se la trave sopporta anche il peso proprio.

P= (0.0033 m² x 1m)/m x 78,50 KN/m³= 0.259 KN/m

l/Vmax>250 è verificata poiché l/Vmax =374 e si ha uno spostamento Vmax pari a 0.8 cm.

In tutte le tecnologie considerate nel caso in cui la verifica non fosse stata soddisfatta si sarebbe dovuta modificare la sezione oppure la luce.

 

 

 

Individuo nel solaio la trave a sbalzo più sollecitata e la relativa area di influenza.

Utilizziamo gli stessi esempi di solai della seconda esercitazione e procediamo con il dimensionamento della trave. Affinchè il calcolo sia verificato è necessario che l'abbassamento (Vmax) dell'estremo della trave non superi 1/250 della luce. Questo rapporto è indicato sul foglio excel tramite questa formula L/Vmax > 250

SOLAIO IN LEGNO

Qs = 0,42 Kn/mq         Qp = 1,72 Kn/mq        Qa = 2,00 Kn/mq

Inseriamo i dati nel foglio di calcolo excel 

Un primo calcolo ci ha portato ad avere una trave di sezione 25 cm x 43,43 cm; scegliamo una trave di sezione 25 cm x 45 cm, ma, dato che il rapporto L/Vmax è minore di 250 (quindi non verificato), siamo costretti ad aumentare l'altezza della trave portandola a 50 cm.

Utilizzando una trave di sezione 25 cm x 50 cm il rapporto L/Vmax > 250 è verificato.

SOLAIO IN CLS

Qs = 1,8 Kn/mq        Qp = 2,4 Kn/mq        Qa = 2,00 Kn/mq

Un primo calcolo ci ha portato ad avere una trave di sezione 25 cm x 37,79 cm (32,79 cm + 5 cm di copriferro); scegliamo una trave di sezione 25 cm x 40 cm, ma, dato che il rapporto L/Vmax è minore di 250 (quindi non verificato), siamo costretti ad aumentare l'altezza della trave portandola a 45 cm.

Utilizzando una trave di sezione 25 cm x 45 cm il rapporto L/Vmax > 250 è verificato.

SOLAIO IN ACCIAIO

Qs = 2,50 Kn/mq        Qp = 1,04 Kn/mq        Qa = 2,00 Kn/mq

Un primo calcolo ci ha portato ad avere una trave che abbia Wx superiore a 669,62 cm3; scegliamo una trave IPE 330 (Wx 713,00 cm3 e Ix 11770 cm4), ma, dato che il rapporto L/Vmax è minore di 250 (quindi non verificato), siamo costretti a scegliere un profilo che abbia un momento d'inerzia Ix maggiore: IPE 360, Ix 16270 cm4.

Utilizzando una trave IPE 360 il rapporto L/Vmax > 250 è verificato.

In questa esercitazione,  procederemo al dimensionamento della trave a sbalzo più sollecitata in un solaio scelto arbitrariamente. Effettueremo l’analisi  ripetendo l’operazione per un solaio in legno, uno in calcestruzzo armato ed uno acciaio, utilizzando le stesse misure e tipologie costruttive del solaio ( legno, C.A., acciaio) analizzate per il precedente dimensionamento della trave doppiamente appoggiata.

La trave a sbalzo soggetta a maggior carico, e di conseguenza al maggior momento flettente, è quella evidenziata in rosso, in quanto la sua area d’influenza è pari a 3m x 6m = 18mq, ossia il  prodotto della luce per l’interasse.

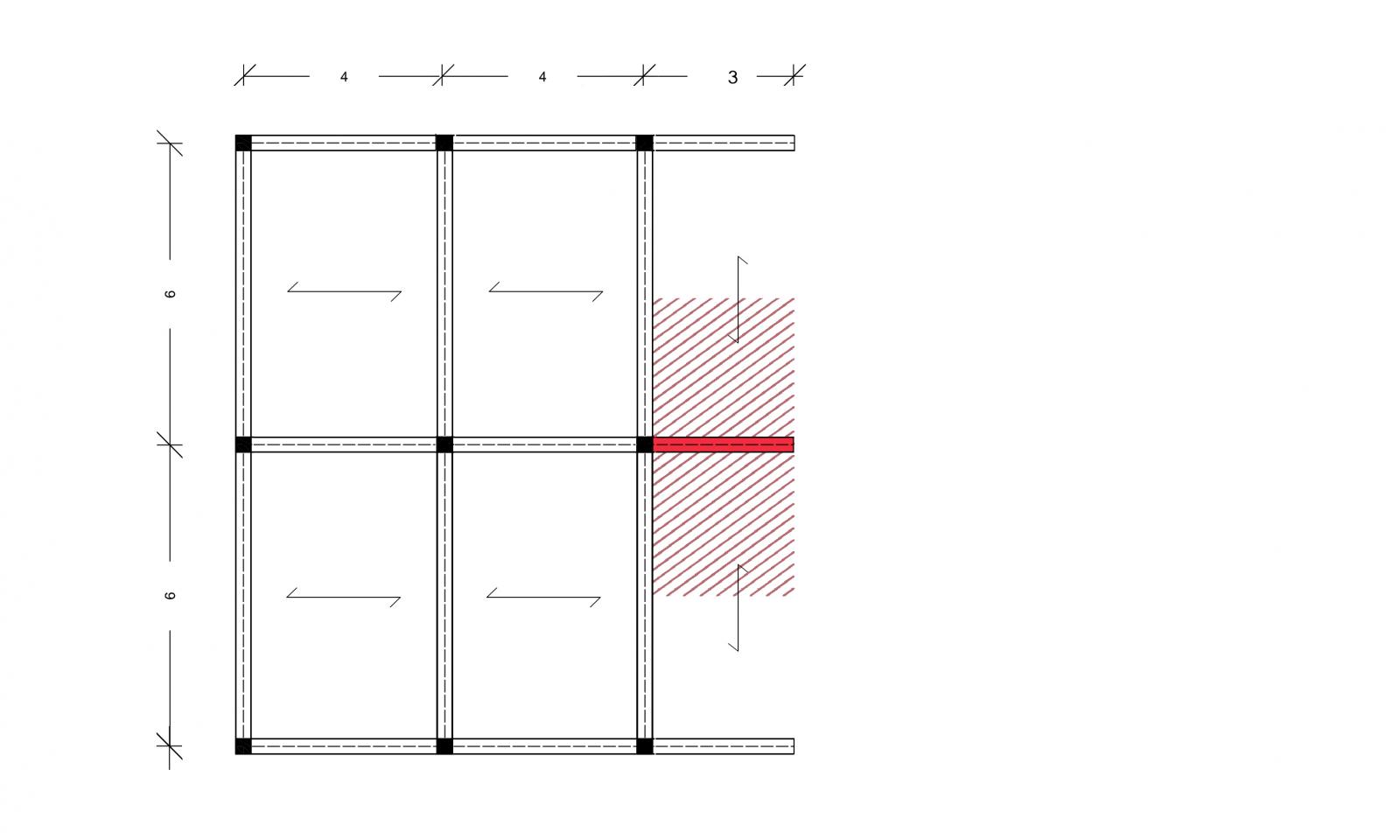
Analizziamo ora il carico distribuito (KN/mq) dei vari tipi di materiali che compongono  ciascuna tipologia di solaio, ricordando che nel caso il materiale sia distribuito su tutta la superficie analizzata (1mq) avremo:

• ( peso specifico x volume ) /superficie analizzata = carico distribuito

Nel caso in cui sia presente invece una sezione che si ripete ad un determinato interasse:

• [ peso specifico x volume x ( lunghezza analizzata/interasse) ] / superficie analizzata = carico distribuito

Calcoleremo i diversi carichi distribuiti (q) in base alla loro classificazione:

qs = Carico degli elementi strutturali.

qp = Carico permanente degli altri elementi presenti nel solaio con funzione non strutturale, a cui va aggiunto il carico dato dai tramezzi (1KN/mq) e quello dato dagli impianti (0,5 KN/mq).

qa = Carico accidentale, dato da normativa tecnica in base allo destinazione d’uso degli ambienti, per la destinazione residenziale è pari a 2 KN/mq.

 

Solaio in legno

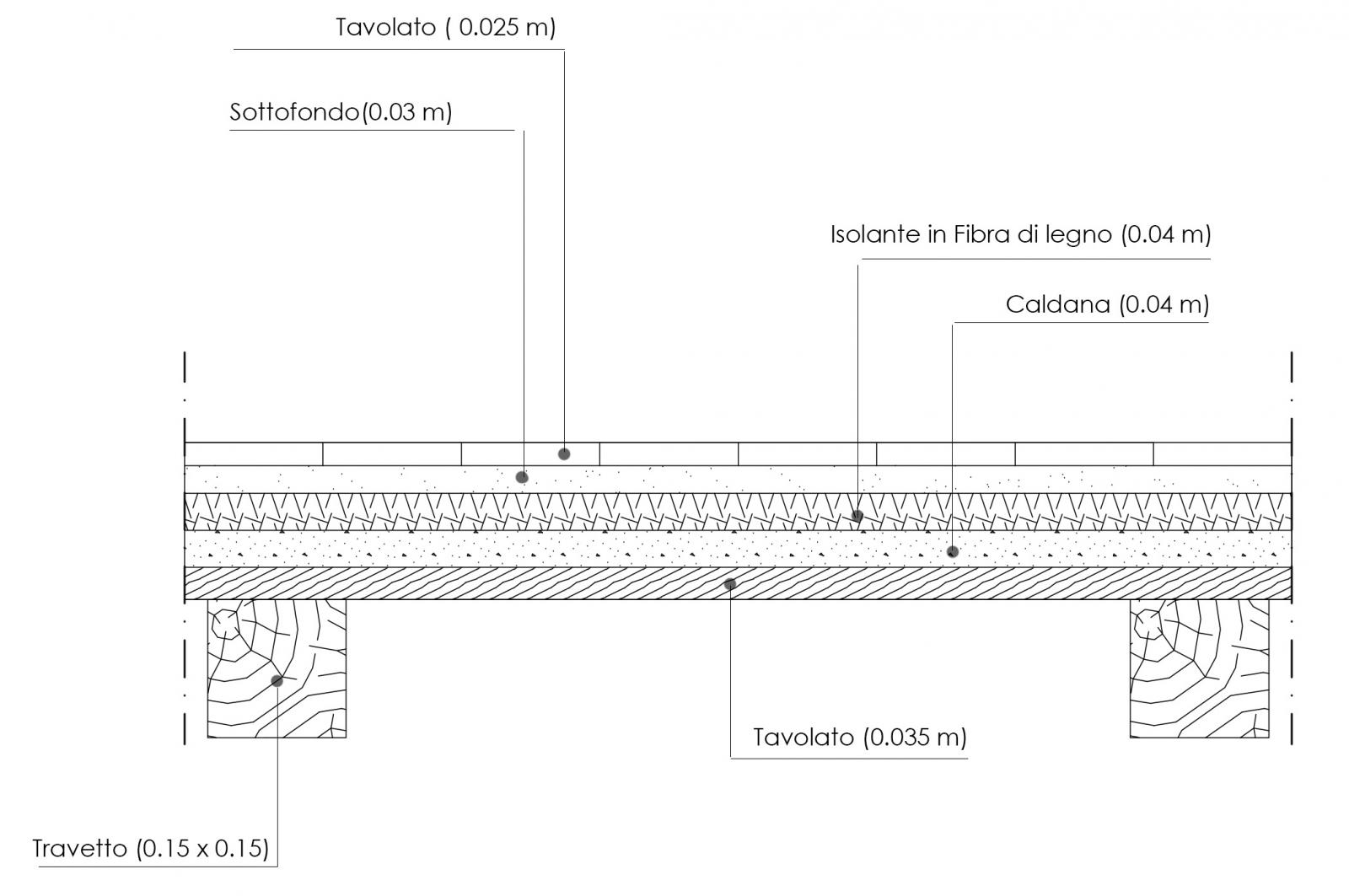
Carichi strutturali (qs)                                                                                                

_travetti in legno di conifere    

 [6 KN/mc x 0.15 m x 0.15 m x 1m x (1m/0,5)]/ 1mq = 0.27 KN/mq

_tavolato in legno di conifere

(6 KN/mc x 0,035 m x 1m x 1m)/ 1mq = 0.21 KN/mq

TOT.  =  0.48 KN/mq

 

Carichi permanenti (qp) 

_caldana in malta di cemento

(21 KN/mc x 0,040 m x 1m x 1m)/ 1mq = 0.84 KN/mq

_isolante in fibra di legno

(9 KN/mc x 0,040 m x 1m x 1m)/ 1mq = 0.36 KN/mq

_sottofondo in malta di calce

(18 KN/mc x 0,030 m x 1m x 1m)/ 1mq = 0.54 KN/mq

_tavolato in legno di quercia

(8 KN/mc x 0,025 m x 1m x 1m)/ 1mq = 0.20 KN/mq

_incidenza tramezzi  =      1 KN/mq

_incidenza impianti =   0.5 KN/mq

 TOT.  =  3.44 KN/mq             

 

Carichi accidentali (qa)

Ambiente ad uso residenziale (Normativa)

TOT. = 2 KN/mq                                                                       

Inseriamo ora i valori ottenuti nel foglio di calcolo per dimensionare la trave.

Per prima cosa scriviamo l’interasse dell’area d’influenza della trave (6m) e i diversi carichi calcolati precedentemente per ottenere q:

q = (1.3 x qs + 1.3 x qp + 1.5 qa) x interasse

dove i carichi strutturali, permanenti e accidentali vengono ognuno moltiplicati per un coefficiente di sicurezza.

Attraverso la luce possiamo ottenere il momento, che in questo caso è pari  qL²/2.

Passiamo successivamente alle caratteristiche del materiale per ottenere la tensione sig_{_}d, data dal prodotto del coefficiente riduttivo kmod  (0.80), che tiene conto della durata del carico e della classe di servizio del progetto, per la resistenza a flessione caratteristica fm,k , che dipende dal tipo di legno scelto (in questo caso un legno lamellare GL24h), ulteriormente ridotta dal coefficiente parziale di sicurezza γ che nel legno lamellare è pari a 1.45.

Inseriamo il valore della base che ipotizziamo per la nostra trave, in questo caso 30 cm e attraverso la formula di Navier otteniamo una trave con altezza pari a 57.46cm, perciò per approssimazione scegliamo di utilizzare una sezione ingegnierizzata 30 x 60 cm.

 

Inseriamo il valore della base che ipotizziamo per la nostra trave, in questo caso 30 cm e attraverso la formula di Navier otteniamo una trave con altezza pari a 57.46cm, perciò per approssimazione scegliamo di utilizzare una sezione 30 x 60 cm.

Passiamo ora all’analisi e alla verifica a deformabilità della trave. Il valore dell’abbassamento v_max nell’estremo non vincolato è pari a ql⁴/8EI_x.

Esso dipende essenzialmente da due valori: il modulo di Young e il momento di inerzia della sezione stessa. Il primo dipende dalla tipologia di materiale scelto. In questo caso, la trave scelta di legno lamellare classe GL 24 h ha un valore di E= 11600 N/mm². Invece, il valore I_x, modulo di inerzia della sezione è calcolato con la formula bh³/12, in quanto si tratta di una sezione rettangolare.

Per verificare che l’abbassamento sia realmente accettabile da parte della struttura, è necessario che il rapporto tra v_max/ l ≤ 1/250. Nella tabella questo rapporto è invertito, perciò l’abbassamento è accettabile se l/ v_max ≥ 250. In questo caso il rapporto l/ v_max = 382,08 quindi la struttura è verificata.

Verifichiamo ora se aggiungendo il peso proprio della trave al qs precedentemente ottenuto, cambia in maniera significativa lo spostamento v_max.

Per farlo dobbiamo moltiplicare il peso specifico (KN/mc) del materiale scelto, in questo caso sempre legno di conifere) per la sezione della trave in modo da ottenere il carico della trave a metro lineare, ricordandoci di dividerlo per l’interasse del solaio dato:

q_trave = (6 KN/mc x 0.3 m x 0.6 m) / 6 m = 0.18 KN/mq

qs + q_trave  =  (0.48 + 0.18) KN/mq = 0.66 KN/mq

Il contributo dato dal peso proprio della trave è minimo, e porta ad uno spostamento v_max pari a  0,81 cm.

La struttura è comunque  verificata ( l/ v_max ≥ 250) e la trave è quindi  in grado di sopportare uno sbalzo di 3m.

 

Solaio in C.A.

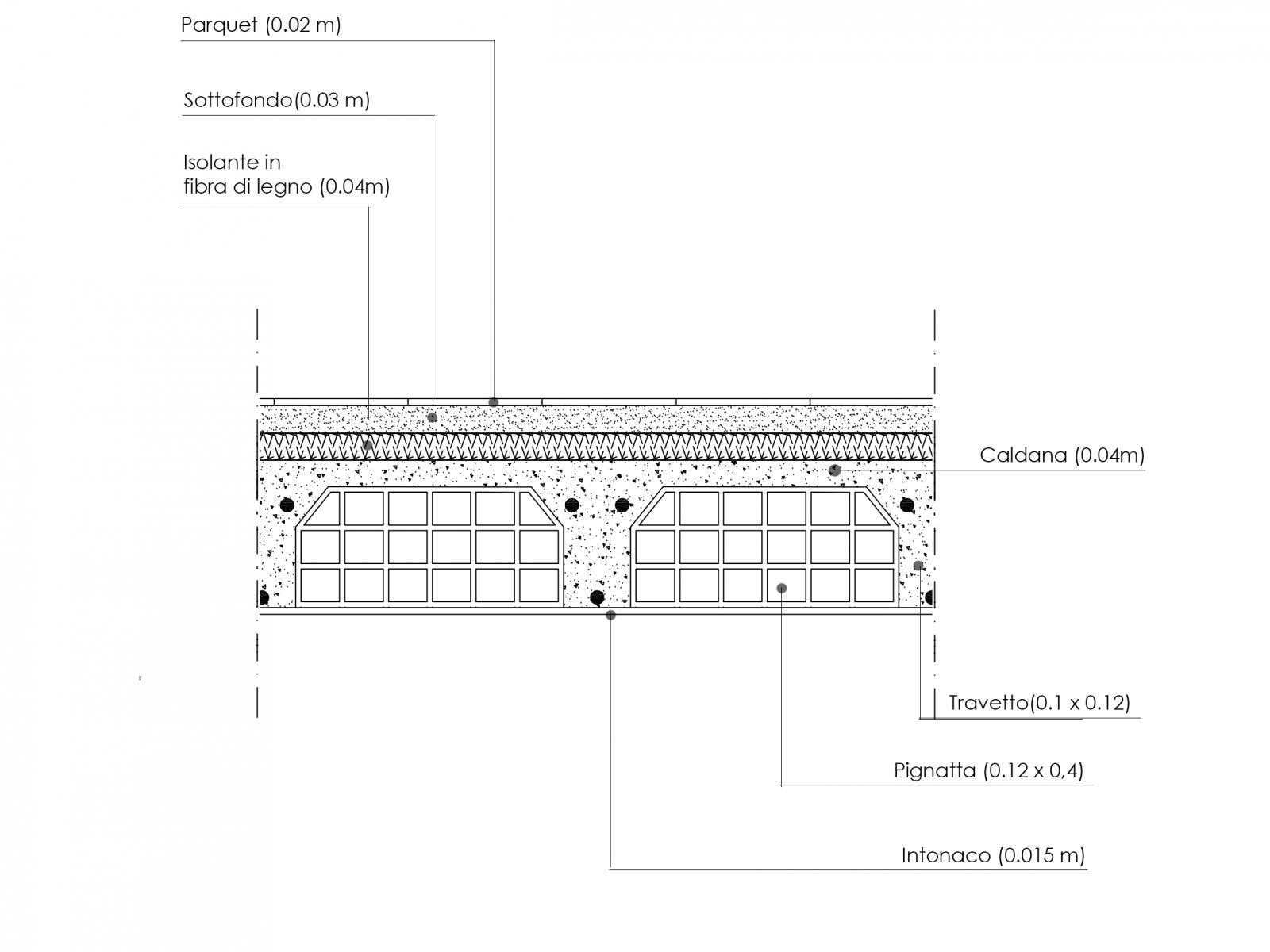
Carichi strutturali (qs)                                                                                                

_travetti in C.A.

 [25 KN/mc x 0.10 m x 0.12 m x 1m x (1m/0,5)]/ 1mq = 0.6 KN/mq

_caldana in malta di cemento

(21 KN/mc x 0,040 m x 1m x 1m)/ 1mq = 0.84 KN/mq

TOT.  =  1.44 KN/mq

 

Carichi permanenti (qp) 

_pignatte

(5.5 KN/mc x 0,4 m X 0.12 m x 1m x (1m/0,5)]/ 1mq = 0.528 KN/mq

_isolante in fibra di legno

(9 KN/mc x 0,040 m x 1m x 1m)/ 1mq = 0.36 KN/mq

_sottofondo in malta di calce

(18 KN/mc x 0,030 m x 1m x 1m)/ 1mq = 0.54 KN/mq

_Pavimento parquet in legno

(8 KN/mc x 0,02 m x 1m x 1m)/ 1mq = 0.16 KN/mq

_intonaco di calce

(11.5 KN/mc x 0,015 m x 1m x 1m)/ 1mq = 0.1725 KN/mq

 

_incidenza tramezzi  =      1 KN/mq

_incidenza impianti =   0.5 KN/mq

 TOT.  =  3.260 KN/mq    

        

Carichi accidentali (qa)

Ambiente ad uso residenziale (Normativa)

TOT. = 2 KN/mq                                                                       

Come per il caso in legno, inseriamo ora i valori ottenuti nel foglio di calcolo per dimensionare la trave.

Scriviamo l’interasse dell’area d’influenza della trave (6m) e i diversi carichi calcolati precedentemente per ottenere q, il carico al metro lineare.

q = (1.3 x qs + 1.3 x qp + 1.5 qa) x interasse

dove, ricordiamo, che i carichi strutturali, permanenti e accidentali vengono ognuno moltiplicati per un coefficiente di sicurezza.

Attraverso la luce possiamo ottenere il momento, che è pari  qL²/2.

Passiamo successivamente alle caratteristiche del materiale per trovare le tensioni sig_fa e sig_ca.

Per quanto riguarda i ferri di armatura che devono resistere a trazione, la tensione sig_fa è data dal rapporto tra la resistenza caratteristica di snervamento dell’acciaio  fy e il coefficiente parziale di sicurezza γ pari a 1,5. Sceglieremo una classe di resistenza B450A, con limite di snervamento ≥ 450 Mpa.

Sig_fa = (fk / γ )

Per il calcestruzzo avremo invece una tensione sig_ca data dalla resistenza caratteristica cilindrica a compressione Rck, (in questo caso 50 avendo scelto un calcestruzzo con classe di resistenza C 40/50)  moltiplicata per un coefficiente riduttivo αcc  pari a 0,85 e poi divisa per un coefficiente parziale di sicurezza γ che anche per il cls vale  1,5.

Sig_ca = (Rck * αcc)/ γ

Possiamo trovare ora l’altezza della trave. Per farlo dobbiamo calcolare il coefficiente di omogeinizzazione n che tiene conto che la sezione in cls armato non è omogenea ma composta da 2 materiali: il calcestruzzo che resiste a compressione e l’acciaio che resiste a trazione. Questo valore è dato dal rapporto dei due moduli elastici (n = Efe / Eca ) ma si assume pari a 15 a vantaggio della sicurezza. Ci serve per ottenere il valore alfa.

Fissiamo una base di 25 cm e calcoliamo infine l’altezza utile h, cioè la sezione reagente in calcestruzzo, a cui aggiungiamo un delta (dato dal copriferro) pari a 5 cm. Otteniamo l’altezza finale della trave, pari a 44,94 cm che porteremo a 45 cm. Avremo quindi una sezione finale pari a 25 x 45 cm.

Dall’altezza della trave è possibile ricavare  sia l’area della sezione, che il peso lineare in KN/m, che poi viene sommato per ottenere il carico q definitivo 43,01 KN/m.

Passiamo ora all’analisi e alla verifica a deformabilità della trave. Il valore dell’abbassamento v_max nell’estremo non vincolato è pari a ql⁴/8EI_x.

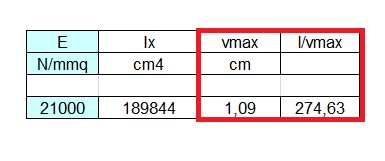
Il valore di E è pari a 21000 N/mm², mentre il modulo d’inerzia I_x anche questa volta viene calcolato con la formula bh³/12, e vale 189844 cm⁴.

Otteniamo un valore v_max  pari a 1,09 cm . Per verificare che l’abbassamento sia realmente accettabile da parte della struttura, è necessario che il rapporto l/ v_max ≥ 250. In questo caso il rapporto l/ v_max = 274,63 quindi la struttura è verificata.

Solaio in Acciaio

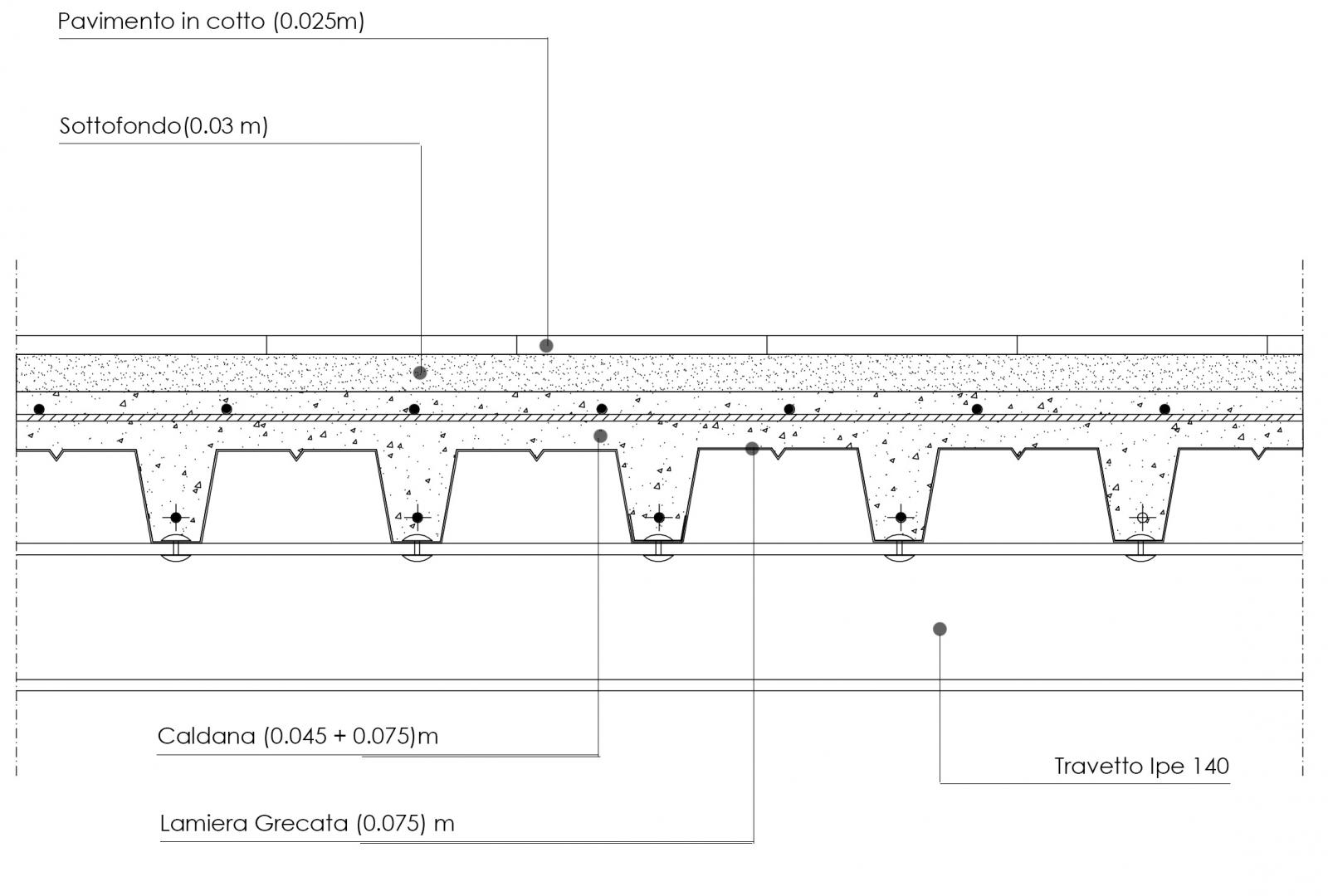
Carichi strutturali (qs)                                                                                                

_travetti IPE 140

 [0.129 KN/m x  1m x (1m/0,5)]/ 1mq = 0.258 KN/mq

_caldana in malta di cemento + lamiera grecata tipo SOLAC (da scheda tecnica)

1.7 KN/mq

TOT.  =  1.958 KN/mq

 

Carichi permanenti (qp) 

_sottofondo in malta di calce

(18 KN/mc x 0,030 m x 1m x 1m)/ 1mq = 0.54 KN/mq

_Pavimento parquet in legno

(8 KN/mc x 0,02 m x 1m x 1m)/ 1mq = 0.16 KN/mq

_incidenza tramezzi  =      1 KN/mq

_incidenza impianti =   0.5 KN/mq

 TOT.  =  2.2 KN/mq    

        

Carichi accidentali (qa)

Ambiente ad uso residenziale (Normativa)

TOT. = 2 KN/mq 

Dopo aver inserito la luce per ottenere il momento, sempre pari qL²/2, vediamo ora come calcolare il profilo di trave da utilizzare.

Nel caso dell’acciaio il valore della resistenza caratteristica  fy,k, dipende dal tipo di acciaio scelto (nel nostro caso abbiamo usato un acciaio di classe Fe 430/S275 con resistenza caratteristica di snervamento pari a 275 Mpa).

La tensione sig_am è uguale a quella caratteristica fy,k divisa per il  coefficiente di sicurezza γ, pari a 1,15.

sig_am = (fm,k / γ) = 239,13 N/mm²

L’ultimo passaggio consiste nello scegliere un profilo IPE che abbia un modulo di resistenza W_x  (valore tabellato) maggiore di quello che si ottiene dalla tabella grazie alla formula di Navier. Scegliamo il valore immediatamente superiore a 949,05 cm³, quindi Wx= 1160 cm³  relativo ad una IPE 400.

Passiamo ora all’analisi e alla verifica a deformabilità della trave. Il valore dell’abbassamento v_max nell’estremo non vincolato è pari a ql⁴/8EI_x.

Il valore di E è pari a 210000 N/mm², mentre il modulo d’inerzia I_x  vale 23130 cm⁴.

Otteniamo un valore v_max  pari a 1,19 cm . Per verificare che l’abbassamento sia realmente accettabile da parte della struttura, è necessario che il rapporto l/ v_max ≥ 250. In questo caso il rapporto l/ v_max = 252,22 quindi la struttura è verificata.

 

 

Obiettivo di questa esercitazione è il dimensionamento di una trave a sbalzo utilizzando i tre solai analizzati (legno, acciaio, calcestruzzo) nella seconda esercitazione

Ho disegnato per prima cosa la carpenteria del solaio

Inserisco all'interno del foglio excell i dati relativi a luce e interasse della trave e riporto i carichi strutturali, i carichi permanenti e i carichi accidentali calcolati in precedenza per i tre differenti tipi di solaio

Nei tre casi il rapporto tra luce della trave e abbassamento deve essere maggiore o uguale a 250

 

LEGNO

Riportando i dati all'interno del foglio excell trovo, partendo da una base di 20 cm, un'altezza minima di 24,36 cm che ingegnerizzata diventa di 30 cm.

Il rapporto l/vmax è 274,85 quindi la sezione è verificata

 

ACCIAIO

Il profilo necessario a soddisfare i dati ottenuti dal foglio excell è un IPE 200 con Wx=194 cm^3, Ix=1943 cm^4 e peso di 0,22 KN/m

Il rapporto l/vmax è 318,77 quindi la sezione è verificata

 

CALCESTRUZZO

Partendo sempre da una base di 20 cm, scelgo una sezione ingegnerizzata di 20x30

Il rapporto l/vmax è 601,91 quindi la sezione è verificata