SdC(b) (LM PA)

1. ANALISI DEI CARICHI

1.1 CARICO DEL SOLAIO

Individuo i valori del peso specifico di ogni materiale (gamma) --> [kN/m3]

Calcolo il peso al mq degli elementi, suddividendo tra carico strutturale (qs) e carico permanente portato (qp)

                  qx [kN/mq] = [(V [m3] / 1 mq) * gamma + ... ] * (1/i)                      

in cui V= volume elemento calcolato rispetto all’interasse (in questo caso 0,5 m) = spessore*interasse*1m; gamma= peso specifico; i= interasse.

Calcolo i carichi al metro lineare

                                   Qs [kN/m] = qs*Li

                                   Qp [kN/m] =(qp + incidenza tramezzi + incidenza impianti )*Li

in cui Li= lunghezza dell’area di influenza (indicata in figura); varia a seconda della trave considerata

incidenza tramezzi =  1 kN/mq; incidenza impianti= 0,5 kN/mq

Calcolo la combinazione di carico frequente per un edificio di civile abitazione

                                   qu [kN/m] = Qs*gamma qs+Qp*gamma qp+Qk1*gamma qk1+ Qk2*gamma qk2* psi 02 + ...

in cui Qk= (carico accidentale da NTC, per civile abitazione=2kN/mq -->sto considerando il carico di persone come carico accidentale dominante)

1. PESO PROPRIO della TRAVE

* da aggiungere dopo averla dimensionata ma prima di dimensionare il pilastro

2. PREDIMENSIONAMENTO DELLA TRAVE PRINCIPALE Più SOLLECITATA (trave 2) --> flessione pura

Per fare un predimensionamento della trave in c.a. ho utilizzato la formula per il dimensionamento “a braccio”

Impongo b = 20 cm e ho che h = l/12 = 41,66666        con l = 500 cm

                                 Ingegnerizzo la sezione --> b = 20    h = 42

3. PREDIMENSIONAMENTO PILASTRO Più SOLLECITATO (pilastro C3) --> presso-flessione         sezione quadrata

Calcolo il peso proprio della trave e lo sommo a qu à ottengo qu’

Calcolo le sollecitazioni all’incastro

                                   Mmax [kN*m] = P1*(a/2) – P2* (b/2)

                                   N max [kN] = qu’ * Li’

In cui Li’= lunghezza di influenza del pilastro C3; a= campata CD/2; b=campata BC/2

Calcolo l’inerzia minima

                                   J minima [cm3] = [Ned * (lo)^2] / [(pigreco^2)*Ec*gamma]           =261,71 cm3

In cui Ec [kN/cm2] = modulo elastico = 22000*(fcm/10)^0,3;  fcm=fck+8; fck=30MPa;    gamma=coef. maggiorativo (>1); lo= lunghezza libera di inflessione = L*beta -->con beta= 0,7 (varia a seconda dei vincoli alle estremità)

Calcolo l’area minima

                                   A minima [cm2] = Ned/sigma,cd = Nmax/fcd             = 55,78 cm2

Calcolo il raggio di inerzia minore minimo

                                   ro min [cm] = radice di [J min / Amin]           =2,166 cm

Sapendo che     ro x= ro y   per sezione quadrata (h=b);  e che quindi       ro=h/radice di 12       calcolo il lato della sezione

                                   h= b= ro* radice di 12         =7,5 cm  --> con questo valore il pilastro non risulta verificato a instabilità e inoltre non rispetta il limite sull’area minima imposto dalla NTC...                   quindi scelgo un pilastro 25x25

3.1 VERIFICO LA SNELLEZZA DEL PILASTRO

Calcolo il nuovo ro considerando la sezione 25x25

                                   lambda [adim] = lo/ro minore          =117,6    ok perché <=200

4. VERIFICA SU SAP

Dall’analisi su SAP del telaio in cemento armato, come già evidenziato nel caso dell’acciaio, ho riscontrato il primo errore nell’aver dimensionato il pilastro senza tener conto del peso dei solai di tutti i piani e del peso proprio del pilastro stesso. 

Ho notato che il pilastro D subisce una notevole deformazione il che mi porta a pensare di doverlo riprogettare tenendo conto delle reciproche influenze tra N,T ed M.

Inoltre ho notato che il momento massimo del tratto di trave CD, che è risultato effettivamente il più sollecitato, non è in mezzeria ma nell’appoggio C.

Dunque alle analisi con SAP sono emersi errori importanti che prevedrebbero la riprogettazione complessiva del telaio sia per quanto riguarda le travi che per i pilastri. Ho capito l’importanza di utilizzare in parallelo i calcoli a mano (EXCEL) e il programma di analisi strutturale per poter confrontarne i risultati in corso d’opera e prevenire errori (gravi) come quelli che ho riscontrato in questa prima esercitazione.

1. ANALISI DEI CARICHI

1.1 CARICO DEL SOLAIO

Individuo i valori del peso specifico di ogni materiale (gamma) à [kN/m3]

Calcolo il peso al mq degli elementi, suddividendo tra carico strutturale (qs) e carico permanente portato (qp)

                  qx [kN/mq] = [(V [m3] / 1 mq) * gamma + ... ] * (1/i)                      

in cui V= volume elemento calcolato rispetto all’interasse (in questo caso 0,25m) = spessore*interasse*1m; gamma= peso specifico; i= interasse.

Calcolo i carichi al metro lineare

                                   Qs [kN/m] = qs*Li

                                   Qp [kN/m] =(qp + incidenza tramezzi + incidenza impianti )*Li

in cui Li= lunghezza dell’area di influenza (indicata in figura); varia a seconda della trave considerata

incidenza tramezzi =  1 kN/mq; incidenza impianti= 0,5 kN/mq

Calcolo la combinazione di carico frequente per un edificio di civile abitazione

                                   qu [kN/m] = Qs*gamma qs+Qp*gamma qp+Qk1*gamma qk1+ Qk2*gamma qk2* psi 02 + ...

in cui Qk= (carico accidentale da NTC, per civile abitazione=2kN/mq àsto considerando il carico di persone come carico accidentale dominante)

1.2 PESO PROPRIO della TRAVE

* da aggiungere dopo averla dimensionata ma prima di dimensionare il pilastro

2. PREDIMENSIONAMENTO DELLA TRAVE PRINCIPALE Più SOLLECITATA (trave 2) --> flessione pura

Calcolo delle sollecitazioni in mezzeria

(tralascio in questo momento il contributo del taglio, che però potrebbe contribuire a ridurre la resistenza della trave influenzando il momento!!)

                  Mmax [kN*m] = qu*(L^2)/8

In cui Mmax= momento in mezzeria e L= campata CD

Calcolo il modulo di resistenza a flessione

Dalla formula di Navier so che         sigma(y) = (Mx / Ix)* y         --> sigma max= (Mx/Ix)*ymax         --> Ix/ymax = Wx

                 Wx [cm^3] = Mmax/sigma max = Mmax/ fd = b*(h^2)/6

In cui sigma max= fd per imposizione di progetto; fd preso da catalogo= 28 MPa.

Ipotizzo b= 20cm             -->         h [cm] = radice di [(6Wx)/b] =30 cm                arrotondo per eccesso

Dal catalogo (es. Rubner) scelgo una trave con Amin = b*h 

                                   scelgo trave 20x32                

3. PREDIMENSIONAMENTO PILASTRO Più SOLLECITATO (pilastro C3) --> presso-flessione             sezione quadrata

Calcolo il peso proprio della trave e lo sommo a qu à ottengo qu’

Calcolo le sollecitazioni all’incastro

                                   Mmax [kN*m] = P1*(a/2) – P2* (b/2)

                                   N max [kN] = qu’ * Li’

In cui Li’= lunghezza di influenza del pilastro C3; a= campata CD/2; b=campata BC/2

Calcolo l’inerzia minima

                                   J minima [cm3] = [Ned * (lo)^2]/[(pigreco^2)*El*gamma]

In cui El [kN/cm2] = modulo elastico = 102 kN/cm2 (da catalogo); gamma = coef. maggiorativo (>1); lo= lunghezza libera di inflessione = L*beta -->con beta= 0,7 (varia a seconda dei vincoli alle estremità)

Calcolo l’area minima

                                   A minima [cm2] = Ned/sigma = Nmax/fd

Calcolo il raggio di inerzia minore minimo

                                   ro min [cm] = radice di [J min / Amin]

Sapendo che        ro x= ro y per sezione quadrata (h=b)              e che quindi           ro=h/radice di 12

...calcolo il lato della sezione

                                   h= b= ro* radice di 12                  arrotondo per eccesso e scelgo la sezione definitiva dal catalogo

Scelgo pilastro 40x40

3.1 VERIFICO LA SNELLEZZA DEL PILASTRO

Calcolo il nuovo ro considerando la sezione 40x40

                                   lambda [adim] = lo/ro minore          ok se <=200

1. ANALISI DEI CARICHI

1.1 CARICO DEL SOLAIO

Individuo i valori del peso specifico di ogni materiale (gamma) à [kN/m3]

Calcolo il peso al mq degli elementi, suddividendo tra carico strutturale (qs) e carico permanente portato (qp)

                  qx [kN/mq] = [(V [m3] / 1 mq) * gamma + ... ] * (1/i)                      

in cui V= volume elemento calcolato rispetto all’interasse (in questo caso 0,5 m) = spessore*0,5*1m; gamma= peso specifico; i= interasse.

Per il calcolo del cls di completamento ho arrotondato considerando lo spessore pari a 5 cm.

Per il travetto (IPE 140) ho preso dal sagomario il peso in kg/m

                  Peso IPE140 = 12,9 Kg/m *1m                            Volume IPE140 = area*1m =0,001643 [m3]

                  Peso specifico = peso / volume = 12,9 Kg / 0,001643 m3 = 129*10^(-3) [kN] /0,001643 [m3] =78,51 kN/m3

Calcolo i carichi al metro lineare

                                   Qs [kN/m] = qs*Li

                                   Qp [kN/m] =(qp + incidenza tramezzi + incidenza impianti )*Li

in cui Li= lunghezza dell’area di influenza (indicata in figura); varia a seconda della trave considerata

incidenza tramezzi =  1 kN/mq; incidenza impianti= 0,5 kN/mq

Calcolo la combinazione di carico frequente per un edificio di civile abitazione

                                   qu [kN/m] = Qs*gamma qs+Qp*gamma qp+Qk1*gamma qk1+ Qk2*gamma qk2* psi 02 + ...

in cui Qk= (carico accidentale da NTC, per civile abitazione=2kN/mq àsto considerando il carico di persone come carico accidentale dominante)

1.2 PESO PROPRIO della TRAVE

* da aggiungere dopo averla dimensionata ma prima di dimensionare il pilastro

2. PREDIMENSIONAMENTO DELLA TRAVE PRINCIPALE Più SOLLECITATA (trave 2) à flessione pura           S450

Calcolo delle sollecitazioni in mezzeria

(tralascio in questo momento il contributo del taglio, che però potrebbe contribuire a ridurre la resistenza della trave influenzando il momento!!)

                  Mmax [kN*m] = qu*(L^2)/8

In cui Mmax= momento in mezzeria e L= campata CD

Calcolo il modulo di resistenza a flessione                    (hp. sezione in classe 1: no instabilità flesso-torsionale)

Dalla formula di Navier so che         sigma(y) = (Mx / Ix)* y          à sigma max= (Mx/Ix)*ymax             à Ix/ymax = Wx

                 Wx [cm^3] = Mmax/sigma max = Mmax/ fyd

In cui sigma max= fyd per imposizione di progetto; fyd= resistenza di progetto = fyk/gamma à gamma =1,05 coef. di sicurezza: riduce la resistenza caratteristica del materiale (fyk).

Arrotondo per eccesso e scelgo dal sagomario una trave con Wx >= a quello ottenuto.

                  Scelgo trave          IPE 600 

3. PREDIMENSIONAMENTO PILASTRO Più SOLLECITATO (pilastro C3) à presso-flessione                               HEA

Calcolo il peso proprio della trave e lo sommo a qu à ottengo qu’

Calcolo le sollecitazioni all’incastro

                                   Mmax [kN*m] = P1*(a/2) – P2* (b/2)

                                   N max [kN] = qu’ * Li’

In cui Li’= lunghezza di influenza del pilastro C3; a= campata CD/2; b=campata BC/2

Calcolo l’area minima

                                   A minima [cm2] = Ned/(fyd*Xo)

In cui Xo= X di primo tentativo <1 à coef. che tiene conto preventivamente della possibile insorgenza di instabilità.

Scelgo dal catalogo un profilato con sezione di area >= a quella ottenuta

Scelgo    HEA100

3.1 VERIFICO LA SNELLEZZA DEL PILASTRO

Ottengo il ro min dai dati nel sagomario                         

ro minore= 2,51 cm

                                   lambda [adim] = lo/ro min = 400*0,7/2,51=111,55                       ok se <=200

in cui lo=L*beta con beta=0,7 (varia a seconda dei vincoli agli estremi)

4. VERIFICA SU SAP

! Dall’analisi su SAP è evidente come il progetto del pilastro non sia adatto a sostenere il carico che arriva al piano terra, infatti nel predimensionamento ho considerato solo il peso di un solaio invece di moltiplicare il peso qu’ per il numero di piani del telaio E aggiungere inoltre il peso proprio del pilastro!!

Questo stesso errore/incompiutezza è ripetuto per tutti i telai (c.a. e legno); è necessario quindi riprogettare il pilastro tenendo conto dell’aumento dei carichi mano a mano che si scende verso le fondazioni.

Oltre a questo ho notato che il progetto del pilastro e della trave che ho eseguito con EXCEL (che sono quindi il pilastro e la trave dell’ultimo piano) sono da rivedere, essendo le sollecitazioni di SAP leggermente maggiori di quelle ottenute su EXCEL.

Dimensionamento di una struttura a telaio in cemento armato, acciaio e legno.

Per ogni tecnologia si considera la stessa struttura, geometricamente simmetrica e con luci piuttosto ridotte, cosi’ da avere anche un confronto piu’ visibile ed immediato.

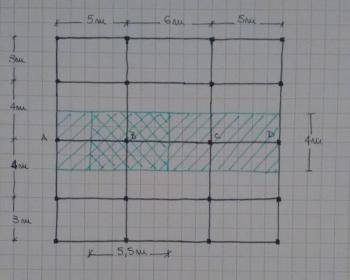
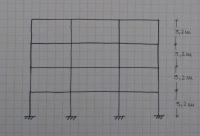
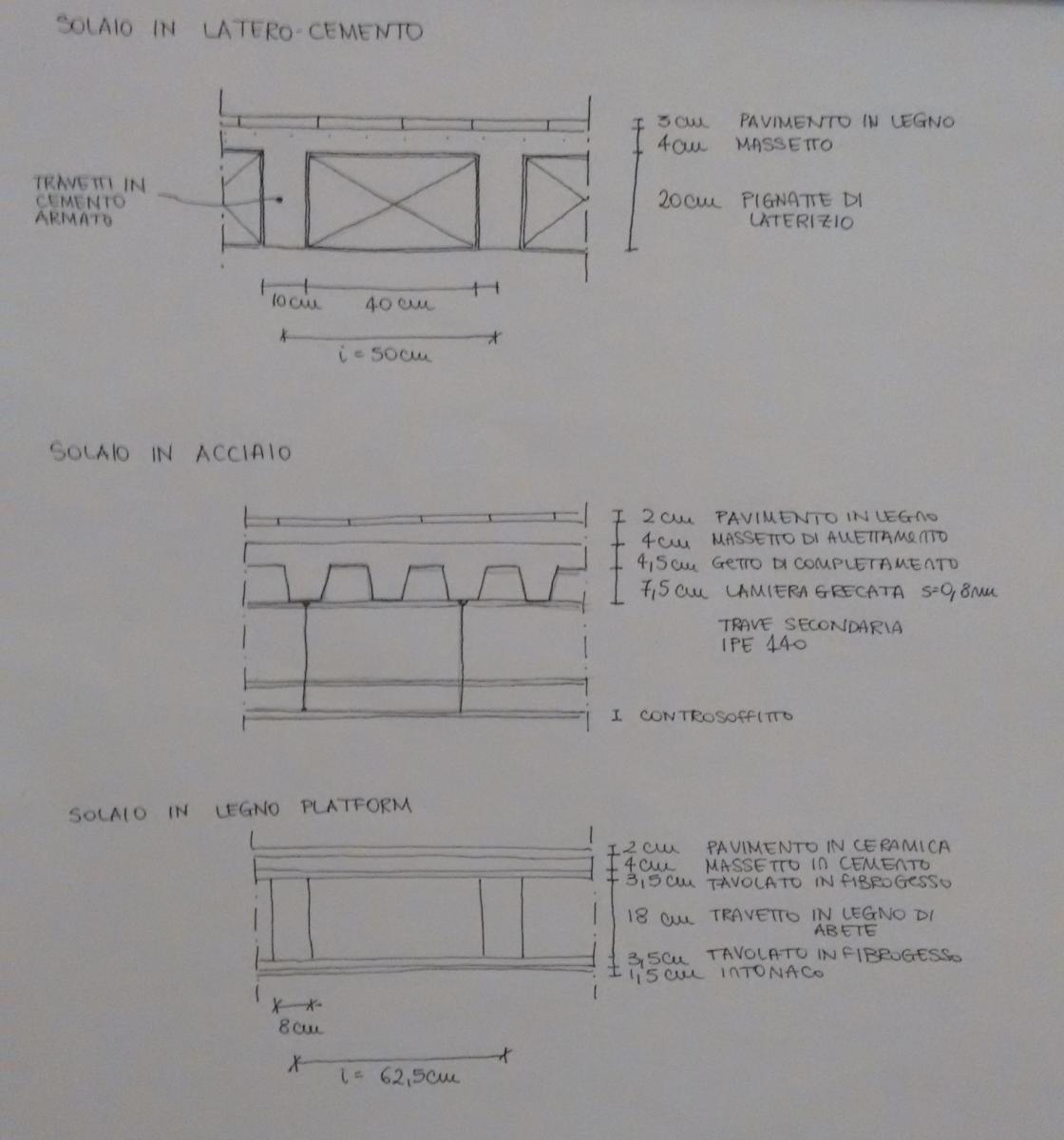
Una volta scelte le stratigrafie per i diversi solai, si procede calcolando i carichi strutturali (travetti, getti di completamento), sovraccarichi permanenti (getti di allettamento, pavimenti, intonaco, controsoffitti, incidenze di impianti e tramezzi) ed accindentali (pari a 2 kN da normativa, poiche’ si tratta di una struttura residenziale) di ogni solaio per dimensionare le travi.

Struttura in cemento armato.

Per dimensionare la trave maggiormente sollecitata (BC) si fa una verifica a flessione utilizzando il foglio Excel e considerando la trave come doppiamente appoggiata, percio’ il momento massimo sara’ ql²/8 in cui importante e’ il ruolo della luce, oltre che il valore di carico.

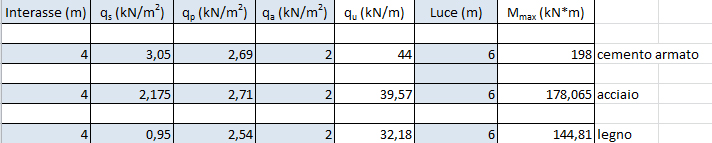
Avendo un Mmax= 203,36 kNm e utilizzando un calcestruzzo di classe 25/30 e’ possibile dimensionare la trave 30x55 cm, cosi' da avere una altezza di trave maggiore della base garantendo un migliore momento di inerzia della trave stessa.

Per dimensionare i pilastri si prende di riferimento il pilastro piu’ sollecitato a sforzo normale, ovvero il pilastro con una maggiore area di influenza, e si utilizza il modello di pilastrata poiche’ scendendo verso il piano terra il pilastro dovra’ sopportare uno sforzo di compressione sempre maggiore. Lo sforzo normale di un piano e’ pari a 281,18 kN e per il valore di Nmax al piano terra si deve moltiplicare  lo sforzo normale di un piano per il numero di piani della struttura.

Una volta ottenuto Nmax= 1124,75 kN, scelto il cls di classe 25/30, considerato l’altezza del pilastro di 3,2 e le condizioni di vincolo pari a 2, e’ possibile calcolare le dimensioni minime del pilastro e scegliere una sezione di 25x30 cm.

A questo punto si modella un telaio piano su SAP che si sviluppa dal piano terra (in cui ai pilastri si assegna un vincolo di incastro) all’ultimo piano di copertura, assegnando alla struttura il materiale cemento armato e le relative sezioni. Dopo aver assegnato ad ogni piano i carichi distribuiti e al pilastro esterno di sinistra il carico distribuito del vento si possono analizzare le deformate della struttura e i valori dei momenti e degli sforzi assiali, per verificare se il dimensionamento effettuato e’ corretto.

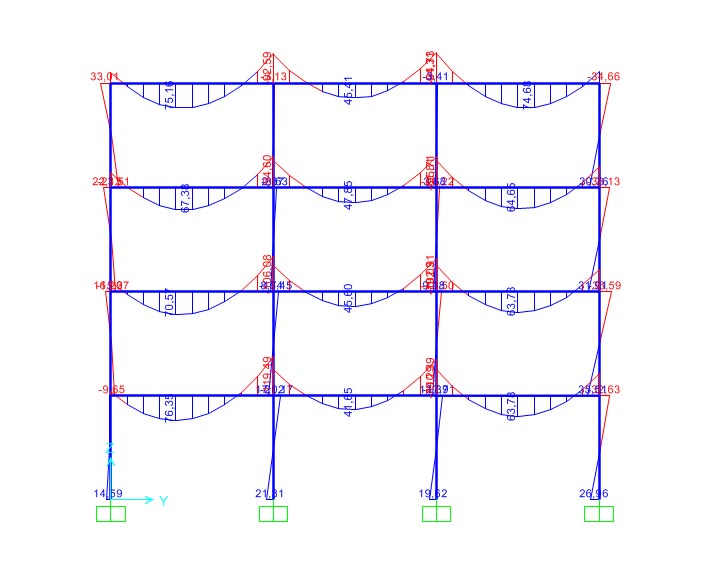
Partendo dalla trave, si nota che Mmax= 119,49 kNm calcolato in SAP e’ inferiore, percio’ la trave e’ stata sovradimensionata e, utilizzando il foglio excel, si ridimensiona la trave con una sezione di 30x45 cm.

Dopo aver corretto le dimesioni della trave su SAP e aver analizzato nuovamente i momenti, si puo’ dire che la nuova trave e’ corretta poiche’ Mmax e’ 120,29 kN, quindi piu’ grande del momento flettente usato per il dimensionamento.

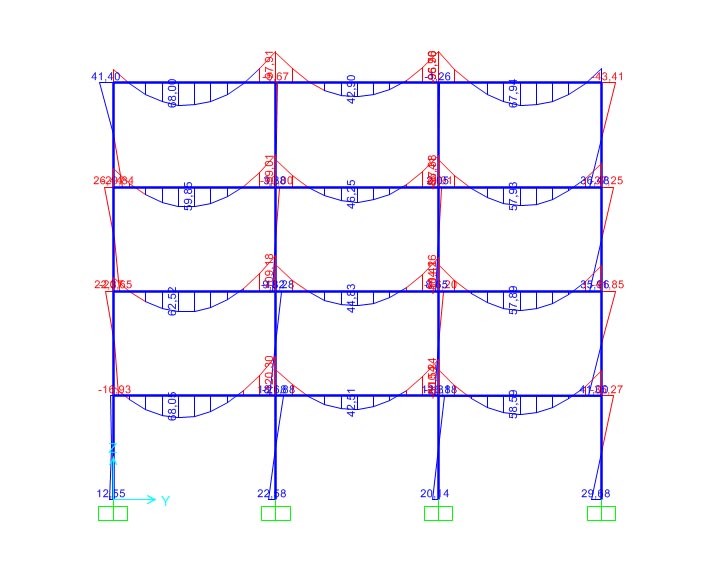
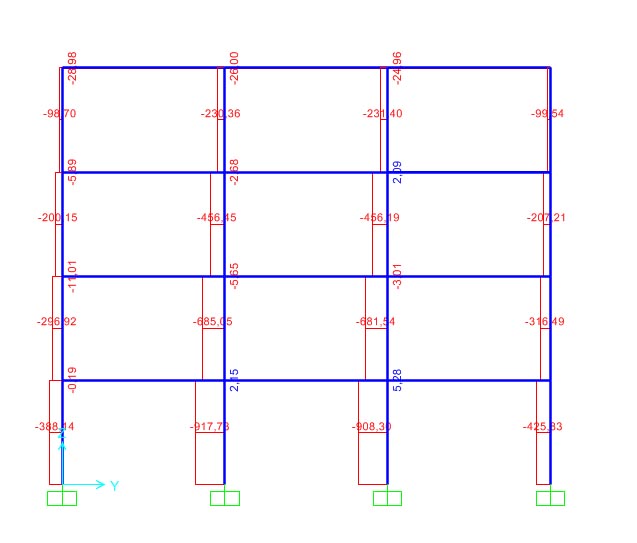
Gli sforzi di compressione dei pilastri calcolati in SAP sono invece inferiori a quelli di design, ma la sezione va verificata anche a pressoflessione. Si calcolano le tensioni σ=(N/A)+(M/W) dei pilastri B, C e D, ma il loro valore e’ maggiore della tensione di progetto Fcd= 17 Mpa percio’ e’ necessario aumentare le dimensioni dei pilastri. Aumentando l’area del pilastro e il suo modulo di resistenza a flessione si migliorano le prestazioni del pilastro, e optando per 30x30 cm e’ verificata la sezione.

Struttura in acciaio

Per dimensionare la trave (BC) e il pilastro maggiormente sollecitati si procede come per il telaio in cemento armato, con l’unica differenza che le caratteristiche geometriche e di resistenza della sezione sono fornite da tabellari di profilati.

Avendo un Mmax= 178,05 kNm e utilizzando un acciaio di classe S275 si ottiene un modulo di resistenza a flessione minimo Wxmin= 679,9 cm³ e si sceglie una trave IPE 330 con Wx= 713,1 cm^{3 _,} poiche’ la resistenza a flessione deve essere necessariamente maggiore.

Per dimensionare i pilastri si prende di riferimento il pilastro piu’ sollecitato a sforzo normale, ovvero il pilastro con una maggiore area di influenza, e si utilizza il modello di pilastrata poiche’ scendendo verso il piano terra il pilastro dovra’ sopportare uno sforzo di compressione sempre maggiore.

Lo sforzo normale di un piano e’ pari a 892,23 kN e per il valore di Nmax al piano terra si deve moltiplicare  lo sforzo normale di un piano per il numero di piani della struttura. Una volta ottenuto Nmax= 1039,25 kN, scelto l’acciaio S275, considerato l’altezza del pilastro di 3,2 e le condizioni di vincolo pari a 2, e’ possibile calcolare le dimensioni minime del pilastro e scegliere il profilo HEA 160.

A questo punto si modella un telaio piano su SAP che si sviluppa dal piano terra (in cui ai pilastri si assegna un vincolo di incastro) all’ultimo piano di copertura, assegnando alla struttura il materiale acciaio e le relative sezioni. Dopo aver assegnato ad ogni piano i carichi distribuiti e al pilastro esterno di sinistra il carico distribuito del vento si possono analizzare le deformate della struttura e i valori dei momenti e degli sforzi assiali, per verificare se il dimensionamento effettuato e’ corretto.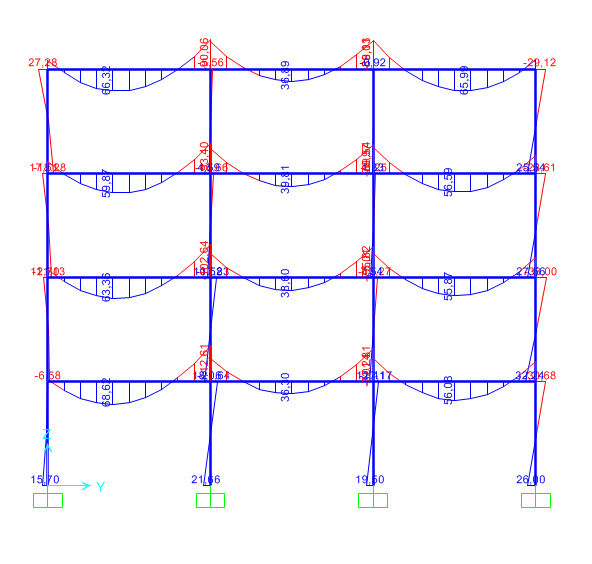

Partendo dalla trave, si nota che Mmax= 112,6 kNm calcolato in SAP e’ inferiore, percio’ la trave e’ stata sovradimensionata e, utilizzando il foglio excel, si ridimensiona la trave scegliendo un profilo IPE 300.

Dopo aver corretto le dimesioni della trave su SAP e aver analizzato nuovamente i momenti, si puo’ dire che la nuova trave e’ corretta poiche’ Mmax e’ piu’ piccolo del momento flettente usato per il dimensionamento.

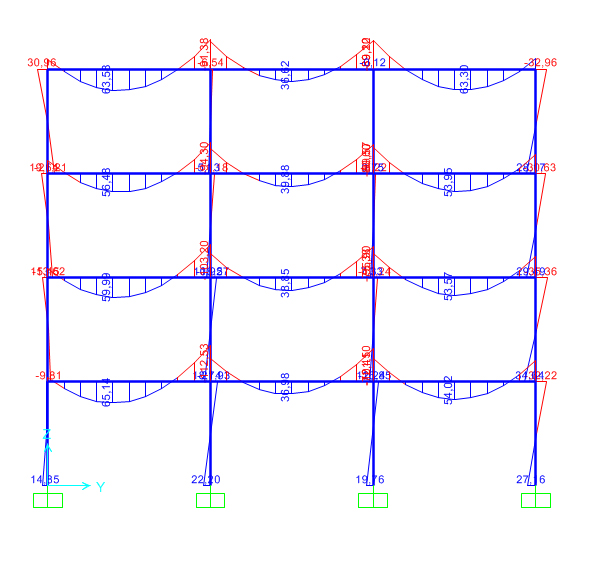
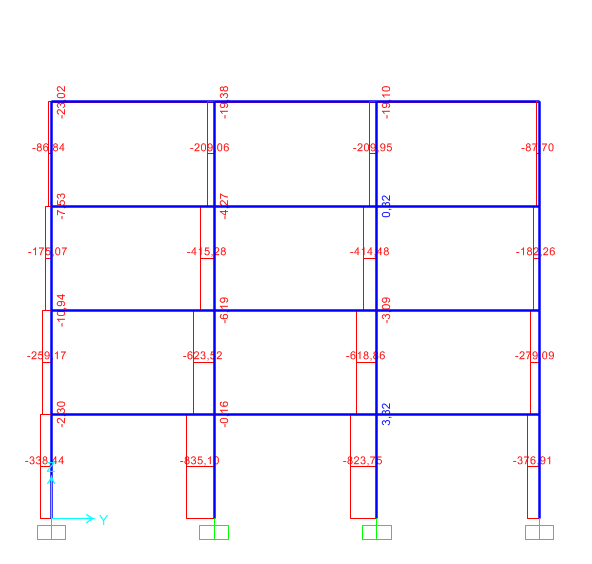
Gli sforzi di compressione dei pilastri calcolati in SAP sono invece inferiori a quelli di design, ma la sezione va verificata anche a pressoflessione. Si calcolano le tensioni σ=(N/A)+(M/W) dei pilastri ma il valore di  e’ maggiore della tensione di progetto Fyd= 261,9  Mpa percio’ e’ necessario aumentare le dimensioni dei pilastri scegliendo un HEA 180.

Struttura in legno.

Per dimensionare la trave maggiormente sollecitata (BC) si fa una verifica a flessione utilizzando il foglio Excel e considerando la trave come doppiamente appoggiata, percio’ il momento massimo sara’ ql²/8 in cui importante e’ il ruolo della luce, oltre che il valore di carico.

Avendo un Mmax= 144,81kNm e utilizzando un legno di abete di classe C24  e’ possibile dimensionare la trave 30x50 cm.

Per dimensionare i pilastri si prende di riferimento il pilastro piu’ sollecitato a sforzo normale, ovvero il pilastro con una maggiore area di influenza, e si utilizza il modello di pilastrata poiche’ scendendo verso il piano terra il pilastro dovra’ sopportare uno sforzo di compressione sempre maggiore.

Lo sforzo normale di un piano e’ pari a 185,54 kN e per il valore di Nmax al piano terra si deve moltiplicare  lo sforzo normale di un piano per il numero di piani della struttura. Una volta ottenuto Nmax= 742,16 kN, scelto illegno di abete classe C24, considerato l’altezza del pilastro di 3,2 e le condizioni di vincolo pari a 2, e’ possibile calcolare le dimensioni minime del pilastro e scegliere una sezione di 30x30 cm.

A questo punto si modella un telaio piano su SAP che si sviluppa dal piano terra (in cui ai pilastri si assegna un vincolo di incastro) all’ultimo piano di copertura, assegnando alla struttura il materiale legno di abete e le relative sezioni. Dopo aver assegnato ad ogni piano i carichi distribuiti e al pilastro esterno di sinistra il carico distribuito del vento si possono analizzare le deformate della struttura e i valori dei momenti e degli sforzi assiali, per verificare se il dimensionamento effettuato e’ corretto.

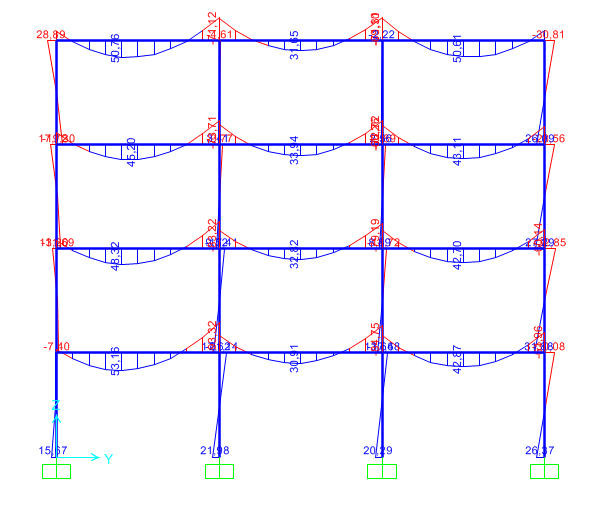
Partendo dalla trave, si nota che Mmax= 93,32 kNm calcolato in SAP e’ inferiore, percio’ la trave e’ stata sovradimensionata e, utilizzando il foglio excel, si ridimensiona la trave con una sezione di 30x40 cm.

Dopo aver corretto le dimesioni della trave su SAP e aver analizzato nuovamente i momenti, si puo’ dire che la nuova trave e’ corretta poiche’ Mmax e’ piu’ piccolo del momento flettente usato per il dimensionamento.

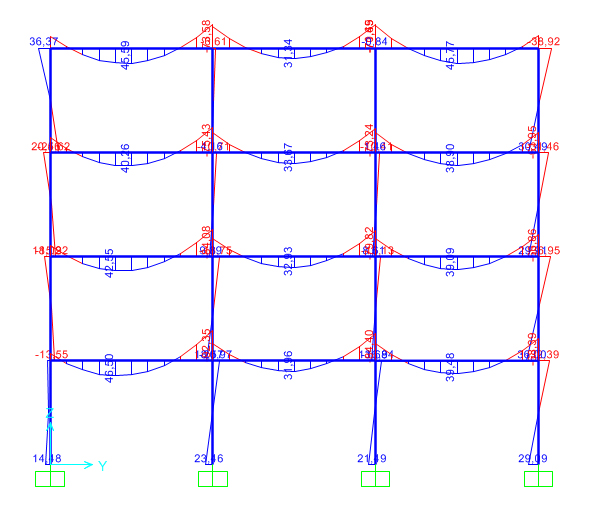
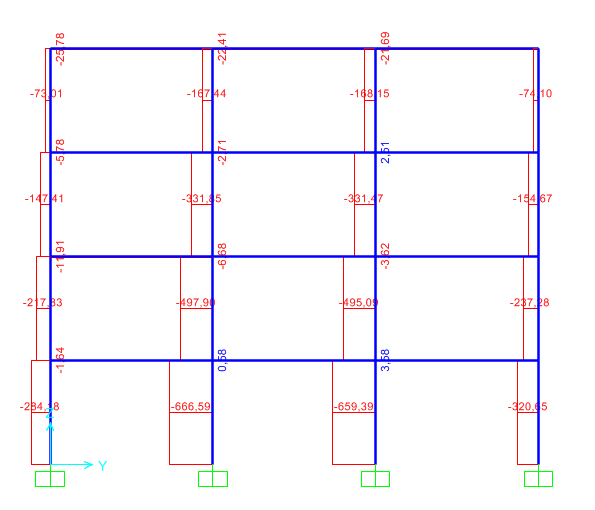
Gli sforzi di compressione dei pilastri calcolati in SAP sono invece inferiori a quelli di design, ma la sezione va verificata anche a pressoflessione. Si calcolano le tensioni σ=(N/A)+(M/W) dei pilastri e si considerano verificati poiche’  il valore delle tensioni e’ minore della tensione di progetto Fmd= 13,24 Mpa.

Lavoro svolto da Burattini Paolo e Cavuoti Matteo.

TELAIO DI ACCIAIO

1)

Disegno il telaio della mia struttura, che avrà una luce massima di 8 m e un'altezza di tre piani.

Scelgo la tecnologia del solaio, composta da travetti in travi di acciaio IPE140, sormontati da una pacchetto composto da una lamiera gregata e da una soletta. Il carico strutturale sarà calcolato dal prodotto tra volume e peso specifico dei materiali del solaio a metro quadro. 2)

                     qs=(V1* γ1 + ... + Vn* γn)*1/i 

Il carico permanente sarà calcolat con lo stesso criterio, considerando la pavimentazione del solaio, isolante, massetto, pavimentazione, a cui saranno aggiunti i carichi di 1kN/m2 per i tramezzi, e di 0,5 kN/m2 per gli impianti.

Il dato del carico accidentale lo leggo sempre nella normativa vigente, e nel nostro caso è pari a 2 kN/m2

Posso trovare il qu, dalla seguente somma

                     qu=(1,3*qs+1,5*qp+1,5*qa)

il peso sarà maggiorato da coefficenti di sicurezza che mi obbligano ad aumentare il valore del mio peso considerato.

3) 

Il peso a metro quadro del solaio, mi serve nel predimensionamento della trave, in quanto questo, moltiplicato per l'interasse di interessa e poi spalmato per la lunghezza della trave mi fornisce il carico distribuito sulla mia trave.

Per cui la prima operazione da fare sarà quella di trovare q, espresso in kN/m. Per calcolare il Momento massimo della trave, che considero come se fosse una trave doppiamente appoggiata, applicherò la formula

                         M=(q*l2)/8 (kN*m)

Una volta trovato M max, per scegliere il profilo più adeguato da utilizzare per predimensionare la mia trave, utilizzerò la formula fd=M/W , dove fd, è la tensione di progetto che io scelgo dal materiale. Nello specifico fd si calcola conoscendo la tensione di snervamento dell’acciaio prescelto,considerando di un coefficiente parziale di sicurezza γs,  pari a 1,05.

                         fd=fk/1,05

In questo modo posso ricavare il modulo di resistenza a flessione

                         W=M/fd

scegliendo un W uguale o maggiore da una tabella di profilati IPE, avrò ottenuto un primo dimensionamento della mia trave.

4)

Il dimensionamento del pilastro parte da ragionamenti simili, in questo caso conosco già il peso del mio solaio e metro quadro, e devo fissare altri valori. Primo tra tutti l'area di influenza del solaio sul pilastro più sollecitato, che per l'appunto sarà quello su cui grava un'area di influenza maggiore. Avendo poi scelto una trave, aggiungo al peso qu, anche il peso lineare della trave scelta, moltiplicato per i metri degli interassi all'interno sempre dell'area di influenza interessata.

Ora, conoscendo anche il numero dei piani, posso calcolare lo sforzo N del pilastro più sollecitato con la seguente formula    

                       Nmax=((qu*Ainf)*qt)*np

Trovato lo sforzo normale, posso trovare una prima area minima con la seguente formula 

                       Amin=Nmax/fd

Tuttavia, l'area di questo pilastro terrebbe conto solo della compressione esercitata sul pilastro, e non della flessione a cui questo viene sottoposto con un carico verticale. Per non ovviare a questo problema, dovrò quindi tenere conto anche del carico critico Euleriano, e di conseguenza non avrò solo un'area minima, ma anche un'altro valore, cioè, quello del momento di inerzia minimo affinché la sezione del pilastro consenta a quest'ultimo di resistere a flessione.

Sapendo che la formula del momento di inerzia minimo è la seguente, posso calcolarlo, sapendo che y è un coefficiente di sicurezza, E il modulo elastico, e l0, la lunghezza libera di inflessione, che conosco conoscenso i vincoli agli estremi del mio pilastro.

                     Jmin > N*l0/γ*π^2*E

Altro valore da tenere in considerazione è il raggio di inerzia minimo che ricavo conoscendo l0 e la snellezza, in quanto la snellezza λ è il raggorto tra la lunghezza libera di inflessione e il raggio di inerzia minimo. E sapendo che la normativa mi impone di porre λ non minore di 200, scrivo:

                     imin > 200/l0

Dalla scelta del momento di inerzia minimo, scelgo nella tabella, il pilastro HEA con le caratteristiche corrispondenti ai tre valori minimi che devo soddisfare.

Il primo pilastro scelto, HEA140, tuttavia non soddisfa uno dei valori richiesti, come si vede nella figura 04.

Si passa alla scelta di un secondo pilastro, HEA200, che apparentemente soddisfa le nostre richieste prestazionali.

5)

Passo alla fase in cui devo verificare se effettivamente gli elementi strutturali predimensionati soddisfano o meno le reali richieste prestazionali.

per la trave utilizzo la formula 

                    σ=Mmax/W 

La trave è verificata se fd, cioè la tensione di progetto è maggiore della tensione trovata 

                    fd>σ

Nel nostro caso la trave è stata sovradimensionata, avendo considerato un momento massimo, quello della trave doppiamente appoggiata, di molto superiore al momento massimo reale trovato su sap, corrispondente al modello di una trave a doppio incastro.

La verifica per il pilastro utilizza invece la seguente formula dovendo tener conto sia dello sforzo normale sia della flessione

                   σ=(Nmax/Ad)+(Mmax/W)

Il pilastro preso in considerazione non soddisfa la verifica, in quanto  σ>>fd

Si cambiano quindi i paramenti presi in considerazione per il dimensionamento del pilastro, fino a trovare uno adeguato.