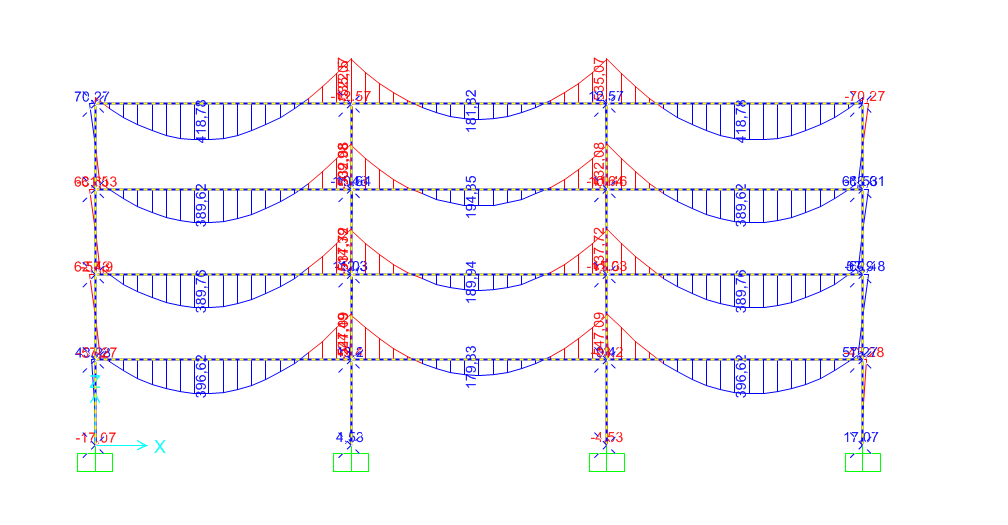
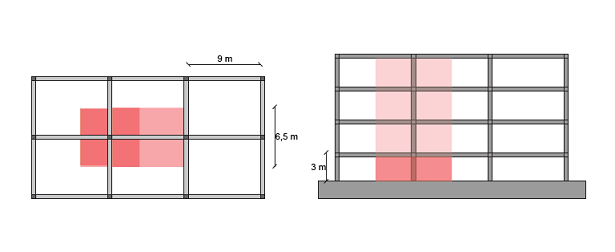
Si considera un edificio, con destinazione d’uso di tipo residenziale, composto da una struttura a telaio (ossia da elementi orizzontali, travi, e elementi verticali, pilastri). Dalla pianta di carpenteria si osserva la trave e il pilastro maggiormente sollecitati.
Il telaio verrà analizzato nelle tre tecnologie: CEMENTO ARMATO, ACCIAIO E LEGNO.
CEMENTO ARMATO
TRAVI
Il metodo di progetto utilizzato prevede di imporre che la tensione massima nella trave sia uguale alla tensione di progetto del materiale, definita dalla normativa.
Osservando la trave maggiormente sollecitata, la prima operazione da compiere è di mettere in evidenza la sua area di influenza e misurare il suo interasse.
Si analizzano i diversi carichi agenti sul solaio (kN/mq), al fine di determinare il carico di progetto sulla trave messa in evidenza (espresso come densità di carico lineare, kN/m).
I diversi carichi si suddividono in carichi strutturali (peso proprio di tutti gli elementi strutturali), carichi permanenti (elementi che non svolgono funzione strutturale) e carichi accidentali, (funzione aleatoria e legati alla funzione che svolgerà l’edificio) e sono regolati dalla normativa NTC2008.
Si calcola il peso al mq di ogni elemento tecnologico che compone il solaio
moltiplicando il peso specifico (kN/mc) per la quantità di volume del materiale contenuta in un mq (mc/mq).
CARICHI STRUTTURALI Qs
-Soletta 25 kN/mc * 0.04 mc/mq 1 kN/m2
-Travetto 25 kN/mc * 0.2 mc/mq 1 kN/m2
-Pignatta 11 kN/mc * 0.2 mc/mq 1.76 kN/m2
3.76 kN/m2
CARICHI PERMANENTI Qp
-Intonaco calcecemento 0.3 kN/mc * 0.015 mc/mq 0.04 kN/m2
-Allettamento 20 kN/mc * 0.02 mc/mq 0.4 kN/m2
-Massetto 18 kN/mc * 0.04 mc/mq 0.72 kN/m2
-Pavimento in parquet 7.5 kN/mc * 0.02 mc/mq 0.15 kN/m2
- incidenza Tramezzi 1 kN/m2
-incidenza impianti 0.5 kN/m2
2.81 kN/m2
CARICHI ACCIDENTALI Qa
-Destinazione d’uso: CIVILE ABITAZIONE (regolato dalla normativa) 2 kN/m2
La normativa impone che per il calcolo del carico totale a ml sulla trave, si debba moltiplicare i singoli carichi per dei coefficienti moltiplicativi ( COMBINAZIONE DI CARICO) e per l’interasse.
I coefficienti moltiplicativi sono riportati in funzione dello stato limite ultimo (SLU)
Qu= gG1 qs+gG2 qp+ gQ qa
Qu= 1,3* Qs + 1,5*Qp + 1,5*Qa (kN/m2)
QU= Qu * i
Si determina il Mmax agente sulla trave considerando per il calcolo il modello della trave appoggiata-appoggiata, il Mmax si trova in mezzeria e si calcola
Mmax= QU x l2 / 8
Per il dimensionamento della trave si impone che la tensione massima nella trave sia uguale alla tensione di progetto del materiale. Al fine del calcolo della tensione è necessario scegliere la resistenza caratteristica del materiale. Per il cemento armato, materiale non omogeneo in quanto composto da Acciaio di armatura e calcestruzzo, è necessario definire la resistenza caratteristica del calcestruzzo (fck) e dell’acciaio
d’armatura (fyk).
Dopo aver effettuato questa scelta, si definiscono le tensioni di progetto del calcestruzzo ( fcd ) e dell’acciaio di armatura ( fyd )
fcd = αcc fck / gc
αcc coefficiente riduttivo per le resistenze di lunga durata = 0,85
gc coefficiente parziale di sicurezza relativo al calcestruzzo = 1,5
fyd = fyk / gs
gs coefficiente riduttivo dell’acciaio d’armatura = 1,15
Una volta calcolate le tensioni di progetto si calcolano α e r, tramite i quali sarà possibile calcolare
l’ Hu. Si sceglie poi una base di design per la trave e si determina l’altezza utile della sezione della trave.
L’altezza minima della sezione sarà data dalla somma (regolarizzata) di H u con lo spessore del copriferro δ
(distanza tra il baricentro del tondino di armatura e il filo del calcestruzzo teso)
Si determina poi il peso Unitario della trave calcolando l’Area della trave per il peso specifico del cls.
La trave, ora dimensionata e con un proprio peso, incide direttamente sul Qtot (il peso unitario _considerevole per le travi in CA_ è moltiplicato per un coefficiente)
Per questo è necessario verificare se la sezione calcolata riesce a sostenere i carichi o se sarà opportuno ridimensionarla.
PILASTRI
Dimensionamento di un elemento strutturale verticale soggetto a sforzo normale di compressione, si deve definire un’ AREA DI PROGETTO e un MOMENTO DI INERZIA MINIMO DI PROGETTO, tenendo conto della possibilità della rottura del materiale per schiacciamento e della possibilità che si verifichi il fenomeno di instabilità euleriana (lo sbandamento laterale dell’elemento verticale).
Il pilastro maggiormente sollecitato si trova al piano terra in quanto sostiene tutto carico dei piani superiori.
Si calcola L’area di influenza del pilastro e al fine di ricavare lo SFORZO NORMALE di compressione N,
si determinano prima
-il carico che grava sul pilastro, dovuto al peso proprio delle travi che poggiano sulla testa del pilastro,
-il carico dovuto al solaio
-per il numero di piani dell’edificio.
Qtrave = 1,3 * Peso Unitario della trave * L della trave nell’area di influenza
N = (Qtrave + Qsolaio) * n° piani
Una volta calcolata la forza agente sul pilastro, è possibile dimensionare la sezione, partendo dalla resistenza del materiale per poi definire l’AREA MINIMA necessaria affinché il materiale non entri in crisi.
Fcd = Fck αα / gm gm 1,5 αα 0.85
Amin = N / Fcd
Si determina ora il RAGGIO MINIMO DI INERZIA MINIMO, parametro da cui si ricava (nel caso di sezioni rettangolari) la B min che deve avere la sezione. Saranno necessari i dati relativi
-E modulo di elasticità
-β(valore legato ai vincoli a cui è soggetto il pilastro)
-L altezza del pilastro
Da cui è possibile ricavare il massimo valore di SNELLEZZA λ max che può avere il pilastro e il MINIMO VALORE DEL RAGGIO DI INERZIA MINIMO r min , per determinare il valore minimo della Base.
λ max = p E / Fcd r min = l0 / λ max b= 2 3 r min
L’altra dimensione H verrà trovata dal rapporto dell’Area e la base
h= Amin / b
I valori dovranno poi essere sovradimensionati nell’atto dell’ingegnerizzazione ( Bdesign e Hdesign)
Si ricava infine l’AREAdesign e il MOMENTO DI INERZIAdesign Idesign = hb3/12
Per il cls sarà necessaria un’ulteriore verifica della sezione, in quanto il nodo tra trave e pilastro è un incastro, trasmette dunque Momento e sottopone in pilastro a presso-flessione. Per fare la verifica a presso-flessione si impone che la tensione massima sia minore della resistenza di progetto:
smax Fcd
La tensione può essere calcolata con le due sollecitazioni sul pilastro, ovvero N e M (trasmesso dalla trave)
smax = N/A + Mt/ Wmax Wmax modulo di resistenza a flessione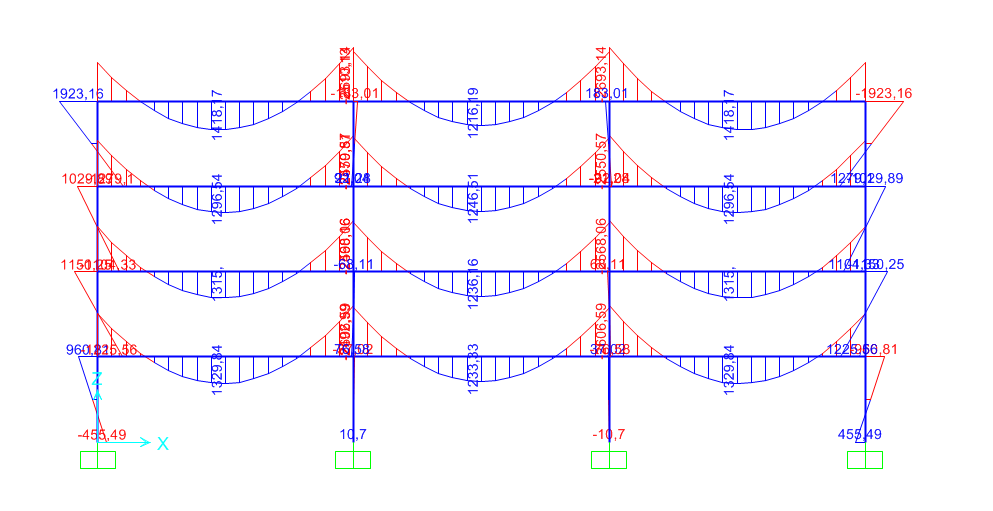
LEGNO
TRAVI
La prima operazione da compiere è di mettere in evidenza la sua area di influenza e misurare il suo interasse.
Si analizzano i diversi carichi agenti sul solaio (kN/mq), al fine di determinare il carico di progetto sulla trave messa in evidenza (espresso come densità di carico lineare, kN/m).
CARICHI STRUTTURALI Qs
-Tavolato di base 7.4 kN/mc * 0.03 mc/mq 0.22 kN/m2
-Travicello 7.4 kN/mc * 0.016 mc/mq 0.12 kN/m2
-Caldana Cls 2.3 kN/mc * 0.04 mc/mq 0.92 kN/m2
- Rete Elettrosaldata 0.053 kN/mc * 1 mc/mq 0.053 kN/m2
1.31 kN/m2
CARICHI PERMANENTI Qp
-Pavimento in parquet 7.2 kN/mc * 0.015 mc/mq 0.11 kN/m2
-isolamento acustico 0.05 kN/mc * 0.01 mc/mq 0.5 kN/m2
-Massetto sabbia e cemento 18 kN/mc * 0.04 mc/mq 0.72 kN/m2
- incidenza Tramezzi 1 kN/m2
-incidenza impianti 0.5 kN/m2
2.83 kN/m2
CARICHI ACCIDENTALI Qa
-Destinazione d’uso: CIVILE ABITAZIONE (regolato dalla normativa) 2 kN/m2
COMBINAZIONE DI CARICO
Qu= gG1 qs+gG2 qp+ gQ qa
Qu= 1,3* Qs + 1,5*Qp + 1,5*Qa (kN/m2)
QU= Qu * i
Si determina il Mmax agente sulla trave considerando per il calcolo il modello della trave appoggiata-appoggiata, il Mmax si trova in mezzeria e si calcola
Mmax= QU x l2 / 8
Nel dimensionamento di una trave in legno è necessario scegliere il tipo di legno da utilizzare, non riferendosi all’essenza del legno ma alla tecnologia e alla classe di resistenza a flessione, da cui si ricava la tensione di progetto calcolata secondo la norma.
fd = kmod * fmk / gm
Si è scelto il legno lamellare G 24 con
fmk 24 N/mm2 resistenza caratteristica
kmod 0.7 coefficiente diminutivo dei valori di resistenza del materiale, tiene conto dell’effetto della durata del carico e delle condizioni di umidità, e quindi delle condizioni climatiche in cui la struttura si trova ad operare (classe di servizio)
gm 1.45 coefficiente parziale di sicurezza relativo al materiale
E’ possibile dimensionare la sezione rettangolare scegliendo arbitrariamente una Base di progetto calcolando l’ Hmin , valore che andrà poi ingegnerizzato, valore subito superiore compatibile con i profili esistenti sul mercato.
Hmin = 
Mmax/b 6/ fd
PILASTRI
Si calcola L’area di influenza del pilastro e si inserisce l'area della trave precedentemente trovata, e assegnando il peso specifico del materiale (7.2 kN/m3) si calcola il peso delle travi.
Qtrave = 1,3 * Peso Unitario della trave * L della trave nell’area di influenza
N = (Qtrave + Qsolaio) * n° piani
Una volta calcolata la forza agente sul pilastro, è possibile dimensionare la sezione, partendo dalla resistenza a compressione parallela alle fibrature definita da tabellario Fc0k , k mod e gm
per definire la resistenza a compressione del pilastro e l’Area min. necessaria affinché il materiale non entri in crisi.
Fc0d = Fc0k * k mod / gm gm 1,45 k mod 0.8
Amin = N / Fc0k
Si determina ora il RAGGIO MINIMO DI INERZIA MINIMO, parametro da cui si ricava (nel caso di sezioni rettangolari) la B min che deve avere la sezione. Saranno necessari i dati relativi
-E modulo di elasticità
-β(valore legato ai vincoli a cui è soggetto il pilastro)
-L altezza del pilastro
Da cui è possibile ricavare il massimo valore di SNELLEZZA λ max che può avere il pilastro e il MINIMO VALORE DEL RAGGIO DI INERZIA MINIMO r min , per determinare il valore minimo della Base.
λ max = p 
E / Fc0d r min = l0 / λ max b= 2 3 r min
L’altra dimensione H verrà trovata dal rapporto dell’Area e la base
h= Amin / b
I valori dovranno poi essere sovradimensionati nell’atto dell’ingegnerizzazione ( Bdesign e Hdesign)
Si ricava infine l’AREAdesign e il MOMENTO DI INERZIAdesign
Idesign = hb3/12
Affinché la sezione sia verificata è necessario che Adesign > Amin
ACCIAIO
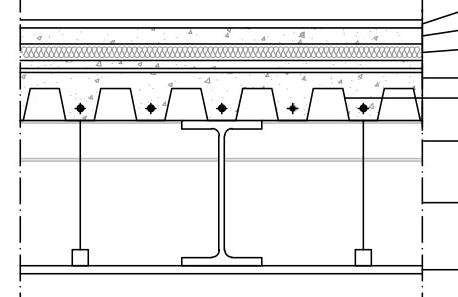
TRAVI
La prima operazione da compiere è di mettere in evidenza la sua area di influenza e misurare il suo interasse.
Si analizzano i diversi carichi agenti sul solaio (kN/mq), al fine di determinare il carico di progetto sulla trave messa in evidenza (espresso come densità di carico lineare, kN/m).
CARICHI STRUTTURALI Qs
-Trave IPE 100 78.5 kN/mc * 0.01 mc/mq 0.07 kN/m2
- Lamiera Grecata zincata 9.8 kN/mc * 0.016 mc/mq 0.16 kN/m2
-Getto di compl. in CA 25 kN/mc * 0.04 mc/mq 1 kN/m2
1.23 kN/m2
CARICHI PERMANENTI Qp
-Pavimento in gres p. 20 kN/mc * 0.02 mc/mq 0.4 kN/m2
-isolamento fibra legno 1.4 kN/mc * 0.04 mc/mq 0.56 kN/m2
-Massetto cls 18 kN/mc * 0.04 mc/mq 0.72 kN/m2
- Intonaco 3.9 kN/mc * 0.02 mc/mq 0.078 kN/m2
- incidenza Tramezzi 1 kN/m2
-incidenza impianti 0.5 kN/m2
3.25 kN/m2
CARICHI ACCIDENTALI Qa
-Destinazione d’uso: CIVILE ABITAZIONE (regolato dalla normativa) 2 kN/m2
COMBINAZIONE DI CARICO
Qu= gG1 qs+gG2 qp+ gQ qa
Qu= 1,3* Qs + 1,5*Qp + 1,5*Qa (kN/m2)
QU= Qu * i
Si determina il Mmax agente sulla trave considerando per il calcolo il modello della trave appoggiata-appoggiata, il Mmax si trova in mezzeria e si calcola
Mmax= QU x l2 / 8
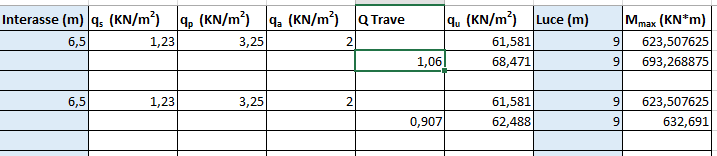
Dopo aver calcolato il Mmax è necessario scegliere il tipo di acciaio, andando ad individuare la tensione caratteristica di snervamento f y,k che individua la classe di resistenza del materiale.
fyd = fyk / gs Tensione di progetto
fyk 275 Mpa Tensione di snervamento caratteristica
gs 1.05 coefficiente parziale di sicurezza relativo al materiale
Per determinare la sezione della trave si deve determinare il modulo di resistenza a flessione minimo
Wx min = Mmax / fyd Modulo di resistenza a flessione
Il valore determinato è il valore minimo che la sezione deve avere affinché nessuna fibra superi la tensione di progetto. Questo valore andrà poi ingegnerizzato ( valore superiore al valore minimo e compatibile con i profili esistenti sul mercato.
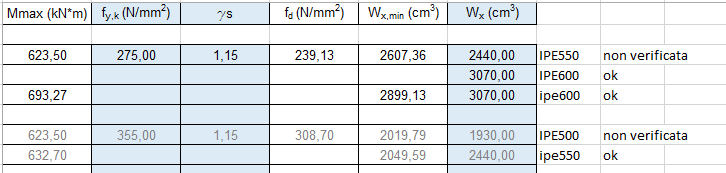
PILASTRI
Dimensionamento di un elemento strutturale verticale soggetto a sforzo normale di compressione, si deve definire quindi un’ AREA DI PROGETTO e un MOMENTO DI INERZIA MINIMO DI PROGETTO, tenendo conto della possibilità della rottura del materiale per schiacciamento e della possibilità che si verifichi il fenomeno di instabilità euleriana (lo sbandamento laterale dell’elemento verticale).
Il pilastro maggiormente sollecitato si trova al piano terra in quanto sostiene tutto carico dei piani superiori.
Si calcola L’area di influenza del pilastro, si inserisce l'area della trave precedentemente trovata, e assegnando il peso specifico del materiale si calcola il peso delle travi.
Qtrave = 1,3 * Peso Unitario della trave * L della trave nell’area di influenza
N = (Qtrave + Qsolaio) * n° piani
Una volta calcolata la forza agente sul pilastro, è possibile dimensionare la sezione, definendo
la resistenza a compressione del pilastro e l’Area min. necessaria affinché il materiale non collassi per schiacciamento-
FYd = Fcyk / gm gm 1,05
Amin = N / Fyd
Per il controllo del fenomeno dell’instabilità euleriana si determina il RAGGIO MINIMO DI INERZIA
MIN. r min , SNELLEZZA λ max che può avere il pilastro e il VALORE DI INERZIA MIN. I min
Saranno necessari i dati relativi
-E modulo di elasticità
-β(valore legato ai vincoli a cui è soggetto il pilastro)
-L altezza del pilastro
Da cui è possibile ricavare
λ max = p E / Fc0d r min = l0 / λ max
Imin = A * r min2
Con i valori trovati si deve scegliere dal formulario una sezione di progetto, facendo attenzione che l’
Adesign e Idesign siano maggiori di quelli calcolati.
E’ stata scelto un profilo HEA 220
Il diagramma dei momenti flettenti corrisponde a quello di una trave doppiamente incastrata. 
Estraggo dalle tabelle il valore del momento massimo che corrisponde a 260,58 kN·m e lo inserisco nella tebella per il dimensionamento corretto della sezione. Verifico, in questo caso che la sezione scelta è corretta. 
A questo punto esporto direttamente da sap una tabella excell che riassume tutti gli sforzi normali agenti sulle diverse aste.
DIAGRAMMI MOMENTO E SFORZO NORMALE LEGNO
DIAGRAMMA SOLLECITAZIONI TRAVE 
DIAGRAMMA SOLLECITAZIONI TRAVE 
Dopo avere trovato i rispettivi carichi passiamo su excel per poter calcolare e dimensionare i pilastri e travi a secondo della tecnologia.
al contrario delle strutture precendentemente studiate la trave in calcestruzzo non ha bisogno di due dimensioni diverse per le diverse misure della struttura
Attraverso questultimo calcolo vediamo che per avere un pilastro adatto alla struttura dobbiamo quasi quadruplicare hmin per far sia che sia verificato 
