SdC(b) (LM PA)

1. Costruisco su SAP 2000 una travatura reticolare spaziale di modulo 2,2 x 2,2 x 2,2.
   
   
2. Aggiungo una nuova sezione, in questo caso Tubolare Cava (PIPE), la quale sarà quella scelta per tutta la travatura reticolare.
3. Poichè il software riconosce i punti interni come degli incastri, devo assegnare le cerniere interne.
4. A questo punto ho bisogno di ricavare la forza concentrata da cui, poi, definirò un caso di carico nelle cerniere. Tenendo conto di determinati parametri, quali:
   - Numero piani: 5
   - Mq per piano: 116 mq
   - Peso proprio per piano per mq: 9,23 KN/m²
   - Peso per piano: (116 mq x 9,23 KN/m²) = 1072 KN
   - Peso totale piani: 5360 KN
   - Peso per nodo: (5360 KN / 35) = 153 KN dove 35 sta per il numero di nodi

   Sulla base del peso proprio della struttura pari a  148,46 KN, abbiamo ricalcolato il peso che insiste su ogni nodo e il peso totale della struttura:

   - Peso totale: (5360 KN + 148,46 KN) = 5508,46 KN
   - Peso per nodo: (5508,46 KN / 35) = 157,38 KN

5. Assegno le forze concentrate nei nodi strutturali.

6. Inserite tutte le forze necessarie per l'avvio dell'analisi, posso conoscere in che modo la mia struttura si è deformata, vedendo gli sforzi assiali lungo le aste reticolari.
   
   

7. Esportiamo su Excel la tabella con tutti i valori della struttura.

8. E' possibile dimensionare le aste più sollecitate

   ASTA COMPRESSA
   Prendiamo in considerazione alcuni fattori quali:

F_yk: Tensione caratteristica di snervamento dell’acciaio, che risulta, da normativa, pari a 235 N/mm² per quanto riguarda l'acciaio scelto.
Ɣs: Coefficiente parziale di sicurezza pari a 1,05.
β : Coefficiente di vincolo = 1 (in quanto l'asta è vincolata da 2 cerniere)
E: Modulo di elasticità dell'acciaio, pari a 210000 MPa
I: lunghezza delle aste, pari a 2,2 m

Da qui, ricaverò alcuni dati, quali:

f_yd = Tensione di progetto dell'acciaio = f_yk/ Ɣs = 235 MPa / 1,05 = 223,80 MPa
A_min = Area minima della sezione = N_max/f_yd = (418,349 KN / 235 MPa) * 10 = 18,692 cm²
λ= Coefficiente di snellezza massimo = π x √ (E/f_yd) = π x √ (210000 MPa / 223,80 MPa) = 96,23
ρ_min = Raggio di inerzia minimo = (β x I) / λ = (1 x 2,2 m) / 96,23 x 100 = 2,286 cm

Per trovare le sezioni delle aste, vado sulla tabella dei profilati e trovo i valori di A_design  e ρ_min, considerando che l'area di progetto deve essere appena superiore a quella calcolata precedentemente.
 

ASTA TESA
In questo caso, i passaggi sono abbreviati, dovendo individuare, allo stesso modo di prima, solo parametri quali:

f_yd = f_yk/ Ɣs = 235 MPa / 1,05 = 223,80 MPa
A_min = N_max/f_yd = (361,573 KN / 235 MPa) * 10 = 16,15 cm²

Una volta trovati i profili per le sezioni, si procede all'analisi su SAP, inserendo il profilato corretto. 

Consegna in gruppo : Pasqualino, Pellegrini, Rossi

1. Costruisco su SAP 2000 una travatura reticolare spaziale di modulo 2,2 x 2,2 x 2,2.
   
   
2. Aggiungo una nuova sezione, in questo caso Tubolare Cava (PIPE), la quale sarà quella scelta per tutta la travatura reticolare.
3. Poichè il software riconosce i punti interni come degli incastri, devo assegnare le cerniere interne.
4. A questo punto ho bisogno di ricavare la forza concentrata da cui, poi, definirò un caso di carico nelle cerniere. Tenendo conto di determinati parametri, quali:
   - Numero piani: 5
   - Mq per piano: 116 mq
   - Peso proprio per piano per mq: 9,23 KN/m²
   - Peso per piano: (116 mq x 9,23 KN/m²) = 1072 KN
   - Peso totale piani: 5360 KN
   - Peso per nodo: (5360 KN / 35) = 153 KN dove 35 sta per il numero di nodi

   Sulla base del peso proprio della struttura pari a  148,46 KN, abbiamo ricalcolato il peso che insiste su ogni nodo e il peso totale della struttura:

   - Peso totale: (5360 KN + 148,46 KN) = 5508,46 KN
   - Peso per nodo: (5508,46 KN / 35) = 157,38 KN

5. Assegno le forze concentrate nei nodi strutturali.
6. Inserite tutte le forze necessarie per l'avvio dell'analisi, posso conoscere in che modo la mia struttura si è deformata, vedendo gli sforzi assiali lungo le aste reticolari.
   
   
7. Esportiamo su Excel la tabella con tutti i valori della struttura
8. E' possibile dimensionare le aste più sollecitate

   ASTA COMPRESSA
   Prendiamo in considerazione alcuni fattori quali:

F_yk: Tensione caratteristica di snervamento dell’acciaio, che risulta, da normativa, pari a 235 N/mm² per quanto riguarda l'acciaio scelto.
Ɣs: Coefficiente parziale di sicurezza pari a 1,05.
β : Coefficiente di vincolo = 1 (in quanto l'asta è vincolata da 2 cerniere)
E: Modulo di elasticità dell'acciaio, pari a 210000 MPa
I: lunghezza delle aste, pari a 2,2 m

Da qui, ricaverò alcuni dati, quali:

f_yd = Tensione di progetto dell'acciaio = f_yk/ Ɣs = 235 MPa / 1,05 = 223,80 MPa
A_min = Area minima della sezione = N_max/f_yd = (418,349 KN / 235 MPa) * 10 = 18,692 cm²
λ= Coefficiente di snellezza massimo = π x √ (E/f_yd) = π x √ (210000 MPa / 223,80 MPa) = 96,23
ρ_min = Raggio di inerzia minimo = (β x I) / λ = (1 x 2,2 m) / 96,23 x 100 = 2,286 cm

Per trovare le sezioni delle aste, vado sulla tabella dei profilati e trovo i valori di A_design  e ρ_min, considerando che l'area di progetto deve essere appena superiore a quella calcolata precedentemente.

ASTA TESA
In questo caso, i passaggi sono abbreviati, dovendo individuare, allo stesso modo di prima, solo parametri quali:

f_yd = f_yk/ Ɣs = 235 MPa / 1,05 = 223,80 MPa
A_min = N_max/f_yd = (361,573 KN / 235 MPa) * 10 = 16,15 cm²

Una volta trovati i profili per le sezioni, si procede all'analisi su SAP, inserendo il profilato corretto

CONSEGNA IN GRUPPO: PELLEGRINI_ROSSI_PASQUALINO

Trave reticolare spaziale

Nella progettazione di una trave reticolare spaziale si inizia realizzando un modulo 3x3x3 che si ripete nelle direzioni X e Y.

In seguito si assegnano i vincoli, nei punti in cui la trave poggia sul pilastro inseriremo cerniere esterne, mentre i nodi devono essere delle cerniere interne per impedire il passaggio del momento. 

Poi si assegna la sezione in acciaio con profilato tubolare. 
Dopo aver stabilito la geometria della struttura si calcolano i carichi che gravano sulla reticolare spaziale:
il carico dato dal solaio in acciaio è q=8,65 kN/m²  
l’area di un singolo piano è A=30*12=360 m², quindi ogni piano ha un carico totale qᵤ=8.65*360=3114 kN
L’edificio si eleva per cinque piani, q=5*3114=15570 kN
Suddividendo il carico totale sui nodi avremo una forza concentrata in ogni nodo di Q= 15570/55=283 kN.

Successivamente si avvia l’analisi della struttura, ottenendo la deformata e i valori di sforzo normale, che vengono estratti in una tabella excel. 

Dalla tabella generale si estraggono i dati utili per il dimensionamento delle aste tese e di quelle compresse.

Per il dimensionamento delle aste tese trovo Amin=N/fyd e scelgo un profilo con area maggiore.
Nel dimensionamento delle aste compresse oltre all’area minima bisogna tener conto sia dell’inerzia che del raggio d’inerzia per evitare fenomeni di instabilità.

1. Costruisco su SAP 2000 una travatura reticolare spaziale di modulo 2,2 x 2,2 x 2,2.
   
   
    
2. Aggiungo una nuova sezione, in questo caso Tubolare Cava (PIPE), la quale sarà quella scelta per tutta la travatura reticolare.
    
3. Poichè il software riconosce i punti interni come degli incastri, devo assegnare le cerniere interne.
    
4. A questo punto ho bisogno di ricavare la forza concentrata da cui, poi, definirò un caso di carico nelle cerniere. Tenendo conto di determinati parametri, quali:
   - Numero piani: 5
   - Mq per piano: 116 mq
   - Peso proprio per piano per mq: 9,23 KN/m²
   - Peso per piano: (116 mq x 9,23 KN/m²) = 1072 KN
   - Peso totale piani: 5360 KN
   - Peso per nodo: (5360 KN / 35) = 153 KN dove 35 sta per il numero di nodi

   Sulla base del peso proprio della struttura pari a  148,46 KN, abbiamo ricalcolato il peso che insiste su ogni nodo e il peso totale della struttura:

   - Peso totale: (5360 KN + 148,46 KN) = 5508,46 KN
   - Peso per nodo: (5508,46 KN / 35) = 157,38 KN

5. Assegno le forze concentrate nei nodi strutturali.

6. Inserite tutte le forze necessarie per l'avvio dell'analisi, posso conoscere in che modo la mia struttura si è deformata, vedendo gli sforzi assiali lungo le aste reticolari.
   
   

7. Esportiamo su Excel la tabella con tutti i valori della struttura.

8. E' possibile dimensionare le aste più sollecitate

   ASTA COMPRESSA
   Prendiamo in considerazione alcuni fattori quali:

   F_yk: Tensione caratteristica di snervamento dell’acciaio, che risulta, da normativa, pari a 235 N/mm² per quanto riguarda l'acciaio scelto.
   Ɣs: Coefficiente parziale di sicurezza pari a 1,05.
   β : Coefficiente di vincolo = 1 (in quanto l'asta è vincolata da 2 cerniere)
   E: Modulo di elasticità dell'acciaio, pari a 210000 MPa
   I: lunghezza delle aste, pari a 2,2 m

   Da qui, ricaverò alcuni dati, quali:

   f_yd = Tensione di progetto dell'acciaio = f_yk/ Ɣs = 235 MPa / 1,05 = 223,80 MPa
   A_min = Area minima della sezione = N_max/f_yd = (418,349 KN / 235 MPa) * 10 = 18,692 cm²
   λ= Coefficiente di snellezza massimo = π x √ (E/f_yd) = π x √ (210000 MPa / 223,80 MPa) = 96,23
   ρ_min = Raggio di inerzia minimo = (β x I) / λ = (1 x 2,2 m) / 96,23 x 100 = 2,286 cm
   

   Per trovare le sezioni delle aste, vado sulla tabella dei profilati e trovo i valori di A_design  e ρ_min, considerando che l'area di progetto deve essere appena superiore a quella calcolata precedentemente.

   
   

   ASTA TESA
   In questo caso, i passaggi sono abbreviati, dovendo individuare, allo stesso modo di prima, solo parametri quali:

   f_yd = f_yk/ Ɣs = 235 MPa / 1,05 = 223,80 MPa
   A_min = N_max/f_yd = (361,573 KN / 235 MPa) * 10 = 16,15 cm²
   

   
   
   Una volta trovati i profili per le sezioni, si procede all'analisi su SAP, inserendo il profilato corretto. 

   Consegna in gruppo: Pasqualino Chiara, Pellegrini Davide, Rossi Andrea

Si procede al dimensionamento di un graticcio 12x18m, con modulo 1x1m.

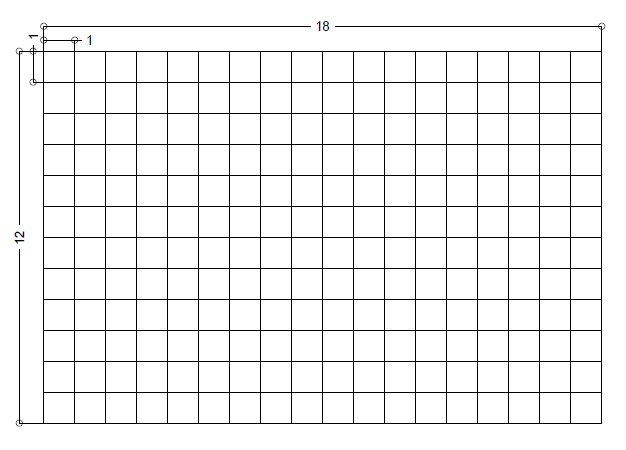
Si considera, per questa esercitazione, che non si conosce il posizionamento dei pilastri, ma si conosce il numero di piani che il graticcio deve sorreggere.

Per questo motivo si andranno ad applicare dei carichi distribuiti sulle travi.

Si sceglie il tipo di solaio da utilizzare e con il foglio excel si calcolano i carichi qp, qa e qs.

Il carico iniziale da applicare sulle travi è dato dai soli qp e qa in modo da progettare una sezione che sia in grado di sorreggere i carichi alla quale sarà sottoposta.

qp*1,5+qa*1,5= 11,778kN/m²

Per applicare il carico si tiene conto dell'area d'influenza di ogni trave, che ai bordi sarà dimezzata.

qu*Anf*n°piani=q1

Facendo l'analisi con SAP si avrà una deformata e delle sollecitazioni pari a quelle di una trave doppiamente incastrata, avendo vincolato solo i lati al bordo, quindi le sezioni più sollecitate saranno quelle all'estremità.

 Dalle tabelle di SAP si individua il valore massimo, che servirà per dimensionare la struttura.

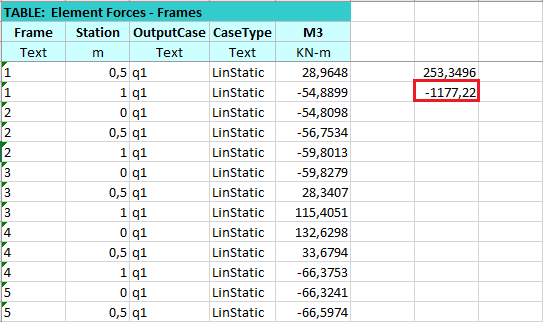
Si procede al dimensionamento, prendendo in considerazione sia il calcestruzzo sia i tondini d'armatura.

Il foglio troverà l'altezza utile, ed infine l'altezza minima della sezione.

La trave trovata ha una sezione di 30x80m.

Come conferma del giusto dimensionamento, si assegna su SAP la sezione appena ingegnerizzata e si verifica che sia in grado di sorreggere il proprio peso, oltre a quello dei carichi, applicando come carico qs, con il peso proprio. 

Si trova il momento massimo e si procede al nuovo dimensionamento.

La trave progettata in precedenza è in grado di sorreggere la struttura, ci si rende conto che è anche sovraddimensionata, quindi si può ridurre la sezione a 30x75m.

Per ultimo si procede alla verifica dell'SLE (stato limite d'esercizio).

L'abbassamento massimo non deve superare 1/200 della luce.

Vmax: -0,02253m

l/200: 0,055m

Vmax<l/200, la struttura è verificata.