SdC(b) (LM PA)

ESERCITAZIONE 3_Svolta con Alice Grondona

L’esercitazione svolta ha il compito di confrontare la posizione del centro di massa della struttura del progetto con quella del centro delle rigidezze, per verificare che la progettazione strutturale sia corretta in quanto questi due punti dovrebbero coincidere; la loro coincidenza garantisce alla struttura di non ruotare.

La struttura presa in esame è il seguente impalcato.

E’ un  telaio composto da pilastri e travi in cemento armato; le travi sono 40x30 cm, i pilastri sono di due tipi: 30x30cm e 30x60cm dove la luce è maggiore. La presenza del blocco  in cemento armato al piano terra è dovuta alla presenza di una seconda struttura ai piani superiori dove per il volume degli uffici si è utilizzata una reticolare spaziale; questa seconda struttura al piano terra è comunque collegata alla prima con giunti che non sono però strutturali.

Abbiamo modellato l’ impalcato su SAP attribuendo tutte le caratteristiche del caso; calcolato il centro delle masse suddividendo tutto in tre aree distinte:

A₁= 515 m²

A₂= 49 m²

A₃= 169 m²

E trovati i tre centri di ciascuna area di coordinate:

A¹ (15;9)

A² (33;15)

A³ (42;9)

Il centro delle masse avrà coordinate C (X;Y) con

X= (A₁X_A1+ A₂X_A2+ A₃X_A3)/(A₁+A₂+A₃)

Y= (A₁Y_A1+ A₂Y_A2+ A₃Y_A3)/(A₁+A₂+A₃).

Una volta trovato il centro delle masse lo disegno su Sap alla stessa quota delle travi.

Viene poi assegnato il vincolo interno DIAPHRAM, in modo che tutti i punti si muovano contemporaneamente e facciano parte dello stesso impalcato.

Si passa al calcolo del peso proprio della struttura su SAP che si ottiene dalle tabelle di valori ottenute dall'analisi; definiamo secondo la normativa il valore della forza sismica in funzione dell’ area di progettazione . Per Roma, essendo il rischio sismico basso, il valore equivale al 20% del peso proprio e lo calcoliamo.

Il valore trovato viene applicato come forza concentrata nel centro delle masse C, prima in direzione x e poi in direzione y.

Assegno una forza Fx al centro delle masse

Posso osservare come la struttura subisca non solo una traslazione ma anche una rotazione oraria.

Definisco ora la forza sismica lungo l'asse y come Fy

Osservo come anche in questo caso la struttura non solo subisca una traslazione lungo l'asse y ma anche una rotazione.

Possiamo dedurre che centro delle masse e centro delle rigidezze non coincidono dunque bisognerà ridisegnare l'impalcato.

L'esercitazione è stata in .jpeg perchè il blog non salva gli avanzamenti, ma solo una parte dell'esercitazione caricata.

Esercitazione svolta con Francesco Petrelli.

NOTA: Ho dovuto caricare l'esercitazione in formato jpeg, perché il blog non salva gli avanzamenti del lavoro, ma salva solo una parte dell'esercitazione caricata.

Esercitazione svolta con Susanna Terreri.

La terza esercitazione consiste nel trovare il centro delle rigidezze e verificare che coincida, o sia abbastanza vicino al centro delle masse, così da avere solo traslazione e non rotazione della struttura in caso di sisma.  

Consideriamo solo un piano dell'edificio. La nostra struttura ha un telaio in cemento armato di 6m per 5m.  

Una volta disegnata la griglia strutturale mettiamo i vincoli e assegniamo la sezione di travi e pilastri, infine inseriamo i setti (sempre in cemento armato) con i corpi scala.  

Troviamo il baricentro e assegniamo la condizione di corpo rigido ai punti che si trovano sulla quota delle travi (compreso il centro delle masse).

Avviamo l'analisi e ricaviamo il peso proprio della struttura, tramite le tabelle. Lo moltiplichiamo per 0,2 dato che Roma è a basso rischio sismico. 

Assegniamo un carico concentrato del valore trovato in direzione X e poi in direzione Y.  Infine avviamo l'analisi e verifichiamo che non ci sia una rotazione. In conclusione il nostro centro delle masse coincide con il centro delle rigidezze.  

L'esercitazione consiste nell'analisi del telaio di un piano tipo dell'edificio progettato, nell'individuazione del centro di massa e del centro delle rigidezze. Per una buona progettazione il centro di massa e quello delle rigidezze devono essere più vicini possibile, in modo che sotto azione di forze orizzontali si evitino  rotazioni e traslazioni dell'impalcato. Il fine dell'esercitazione è quello di garantire una resistenza strutturale dell'impalcato sottoposto all'azione di una forza sismica.

La struttura utilizzata per il progetto è una travatura reticolare spaziale, quindi sono stati rappresentati soltanto gli elementi strutturali, quali travi e setti murari.

Per determinare la posizione del centro di massa suddivido la struttura in tre rettangoli e vado a definire le coordinate x e y di ogni area.

C1_ (9-24)                    A1_ 864

C2_(9-6)                      A2_216

C3_(7,5-21)                 A3_630

Xc= (A1 X1+A2 X2+A3 X3) / (A1+A2+A3) = 8,44

Yc=(A1 Y1+A2 Y2+A3 Y3) / (A1+A2+A3) = 20,62            

Quindi le coordinate del centro di massa saranno:           X= (8,44 - 20,62)

Disegno quindi il centro di massa come un punto sulla pianta strutturale.

Disegnato il centro di massa assegno a tutti gli elementi la condizione di nodo rigido, questo affinché non si verifichino spostamenti e rotazioni relative.
Per calcolare il peso proprio dell'impalcato eseguo l'analisi considerando soltanto il peso proprio e verificando i valori sulle tabelle.

        Dalla tabella ricavo il peso proprio sommando tutti i valori della voce F3.

Il peso proprio dell'impalcato risulta   Pp= 4438,202 KN

La normativa mi fornisce il coefficiente di sicurezza da applicare alla struttura che è pari al 20% del peso dell'impalcato e che varia a seconda della zona in cui viene studiato il progetto.

quindi: 4438,202 x 0,2= 887,64              

Definisco ora idue casi di carico Fx ed Fy, ovvero le due componenti della forza orizzontale che andrò ad applicare nelle due differenti direzioni sul centro di massa. Una volta assegnati i carichi avvio l'analisi senza considerare il peso proprio e verifico la posizione del centro delle rigidezze.

   COMPONENTE X_         

COMPONENTE Y_

Dall'analisi risulta che il centro delle rigidezza non è coincidente con quello di massa.

Per un corretto comportamento dell'impalcato bisegerà far coincidere i due punti, effettuando delle modifiche sulla posizione degli elementi strutturali.

La terza esercitazione consiste nell’analisi di un telaio di un piano di un edificio, in questo caso il nostro, in particolare individuando il centro di massa e il centro delle rigidezze. Un buon progetto strutturale prevede che i due centri siano coincidenti o più vicini possibile in modo che, all'agire di forze orizzontali, vengano evitate rotazioni dell’impalcato.

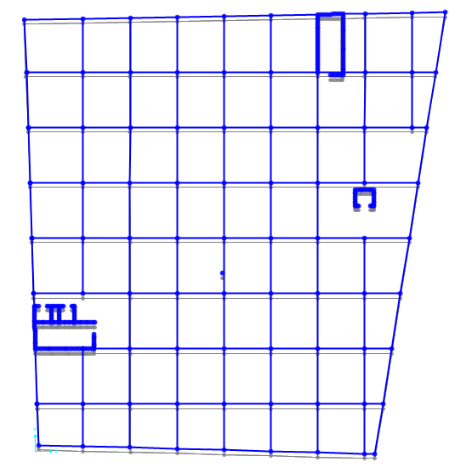
Per realizzare il piano tipo ho importato da autocad una griglia di riferimento in cui ho incluso gabbie ascensori e corpi scala.

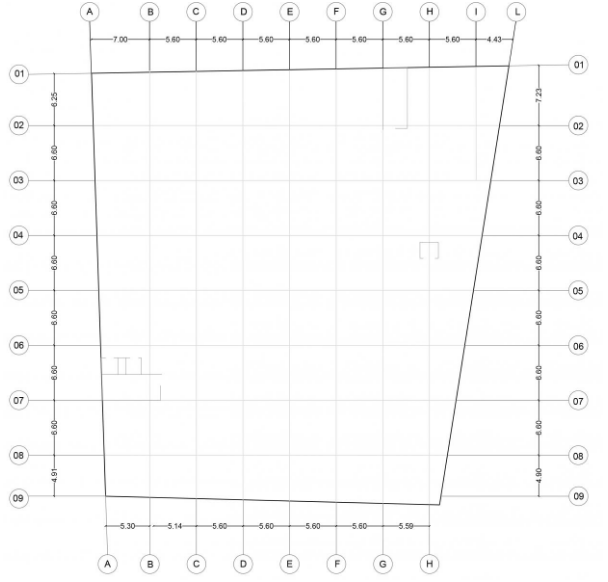
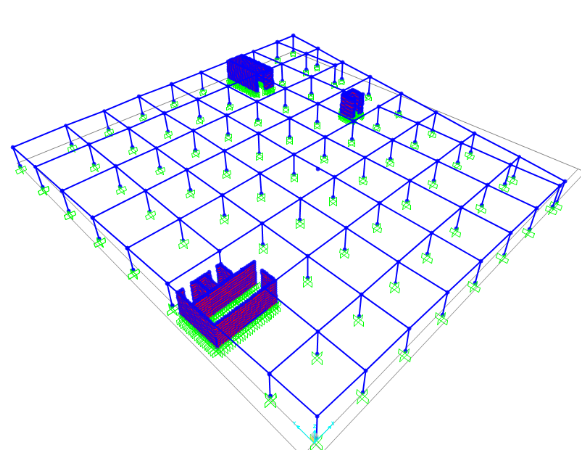
Realizzato un sistema di travi e pilastri, ho disegnato delle aree poligonali lì dove dovevo definire dei setti.  Alla base di ogni pilastro e di ogni punto appartenente ai setti ho posto un incastro.

Sezioni degli elementi in calcestruzzo :

• pilastri circolari → d = 60 cm
• travi → 70x45 cm
• setti → 30x30 cm

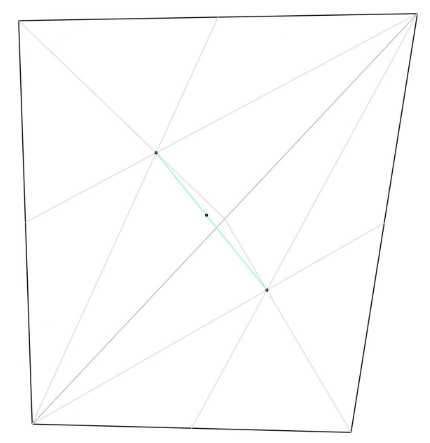
Per determinare il centro di massa (o centro d'area) ho suddiviso il trapezio in due triangoli, posizionando i due centri d’area nei baricentri. Ottenute le coordinate dei due centri ho trovato, tramite le formule seguenti, le coordinate del centro dell’intera figura:

                                                       G_x = (A₁x₁ + A₂x₂ ) / (A₁+A₂)

                                                       G_y = (A₁y₁ + A₂y₂) / (A₁+A₂)

Posizionato il centro di massa, al piano z=3, ho assegnato una condizione di vincolo interno Diaphragm per imporre la rigidezza del telaio, incluso il centro di massa che deve far parte dell’impalcato riproducendo la condizione di impalcato rigido.

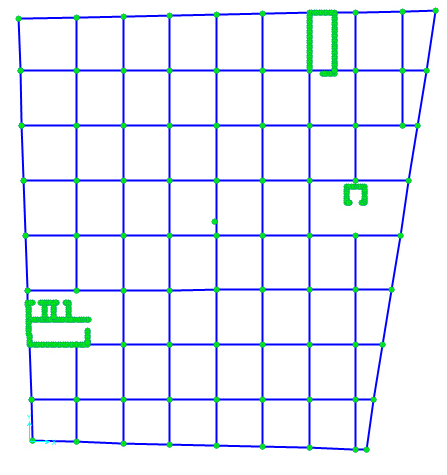
Per impostare l’analisi devo conoscere il valore delle forze orizzontali che devo applicare al centro di massa e per farlo devo considerare il peso totale dell’edificio e moltiplicarlo per un coefficiente sismico di massima pari a 0,2.

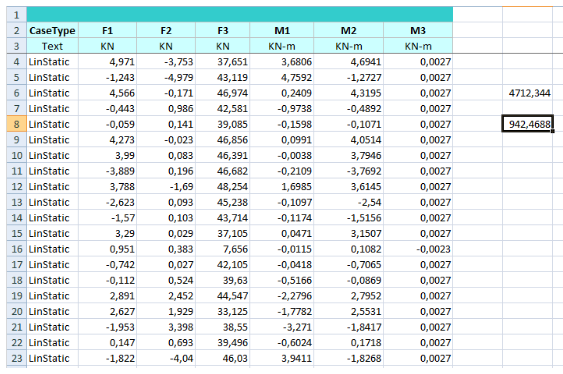
Per trovare il peso dell’edificio eseguo l’analisi dell’impalcato considerando esclusivamente il peso proprio, dalle tabelle di analisi trovo il valore della forza verticale che, sommata in tutte le sue componenti, mi fornisce il peso totale dell’edificio 44712,35 kN; moltiplicato per 0,2 da 942,47 kN, ovvero l’intensità della forza orizzontale che devo applicare. 

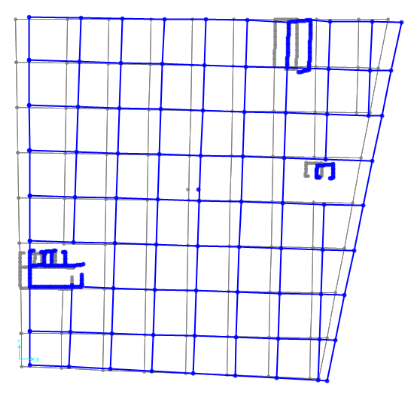
Avvio l’analisi e osservo le deformate dell’impalcato prima per la forza in direzione x e poi per la forza in direzione y.

La deformata dovuta alla forza orizzontale provoca una rotazione dell’impalcato direzione x.

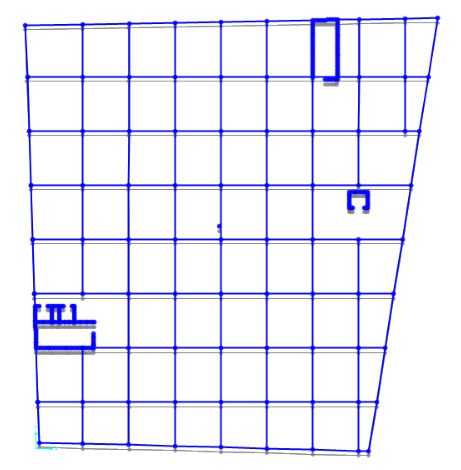
La deformata dovuta alla forza orizzontale provoca una rotazione dell’impalcato anche in direzione y.

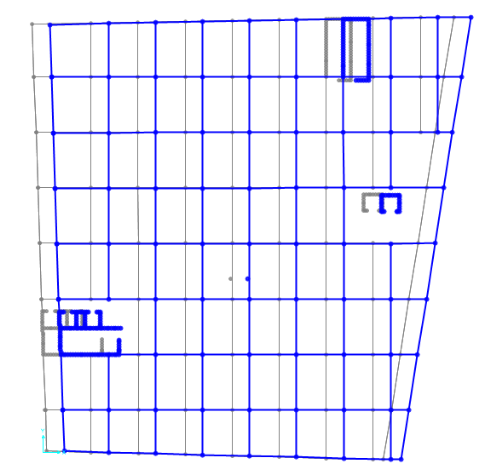
La rotazione mette in evidenza il fatto che il centro di massa non coincide con quello delle rigidezze.

Sposto il centro di massa verso il basso e riavviando l’analisi cerco di trovare il punto in cui la rotazione si annulla. Si abbassa in totale di 5,80 m.  

Risultato direzione x

Risultato direzione y

In collaborazione con Veronica Stefanelli.

L'esercitazione è svolta in coppia con Fabrizio Pontico.

Lo scopo dell’esercitazione è quello di verificare che l’impalcato resista alle forze sismiche:tali forze agiscono nel centro di massa,quindi è necessario che il centro di massa coincida il più possibile con il centro delle rigidezze della struttura. Una struttura può essere resa più rigida attraverso l’utilizzo di controventi,che sono elementi verticali collegati orizzontalmente che portano il carico fino a terra,che possono essere per esempio i vani ascensori,le scale o anche un semplice telaio.

Il nostro impalcato è formato da una struttura semplice a telaio,formato da travi e pilastri. Per motivi di progetto e di struttura abbiamo deciso già dalle prime fasi di considerare i blocchi scale e gli ascensori come una struttura autonoma,collegata al telaio attraverso un giunto strutturale.

L’impalcato ha una struttura in cemento armato con classe di resistenza C40/50 formato da travi 35x50 cm e pilastri 50x50 cm.

Dopo aver disegnato la struttura su Sap passiamo ad assegnare ai vicoli esterni il vincolo di incastro. Si disegna inoltre il centro di massa,corrispondente al centro geometrico della struttura partendo dall’intersezione delle due diagonali.

Selezionando il punto del centro di massa e tutti i punti nel piano xy alla stessa quota delle travi e’ possibile assegnare la condizione di corpo rigido: in questo modo tutti i punti fanno parte dell’impalcato e non possono esserci spostamenti o rotazioni relative. 

Per verificare che il centro di massa e quello di rigidezza coincidano prendiamo in considerazioni le due peggiori combinazioni di casi,ovvero quando la forza sismica è applicata lungo una direzione. Andiamo ad calcolare prima il peso specifico della struttura, imponendo una combinazioni di carico data esclusivamente dal peso proprio della struttura, poi importiamo la tabella su excell e sommando i valori delle reazioni  vincolari verticali otteniamo il peso proprio che è 1909,83 kN. Moltiplichiamo questo valore per 0,2,cioè il coefficiente di riferimento per le zone a basso rischio sisma come Roma, e otteniamo così il valore del carico sismico di 381,94 kN.

A questo punto è possibile applicare il carico sismico come un carico concentrato orizzontale prima nella direzione X e poi nella direzione Y per verificare che la deformata non sia una rotazione ma una traslazione (in entrambe le direzioni).

Da i risultati dell’analisi è evidente che non c’è nessuna rotazione ma due traslazioni,sull’asse X quando la forza è applicata lungo questa direzione, e sull’asse Y quando la forza è lungo quest’altra direzione, quindi è possibile dire che il centro di massa coincida con il centro delle rigidezze,pertanto non è necessario l’aggiunta di controventamenti come scale e ascensori.

Prendendo in esame un piano tipo con relativi corpi scala/ascensore, individuiamo il centro delle rigidezze e facciamo in modo che coincida con il centro di massa; infatti in caso di sisma dobbiamo evitare le rotazioni relative della struttura, questo è possibile solo se i due centri (di massa e delle rigidezze) coincidono.

La struttura considerata è in cemento armato e sono presenti due gabbie scala/ascensore

Viene individuato in maniera geometrica il centro delle masse (baricentro)

Ora riportiamo la struttura su SAP2000 assegnando alle travi in C.A una sezione di 40 x 60 cm, ai pilastri una sezione di 50 x 50 cm ed ai setti delle gabbie scala uno spessore di 25 cm.

La struttura viene vincolata a “terra” tramite incastri ed a tutti i punti che sono alla stessa quota delle travi (compreso il centro di massa) viene assegnata la condizione di corpo rigido

Per calcolare la forza del sisma agente nelle direzioni X ed Y dobbiamo prima calcolare il peso proprio della struttura, lanciando l’analisi, lo ricaviamo tramite le tabelle delle reazioni vincolari per poi moltiplicarlo per 0.2 (coefficiente di riferimento per zone a basso rischio sismico come Roma)

La forza sismica viene applicata nel centro delle masse nelle direzioni X ed Y, lanciamo nuovamente l’analisi e verifichiamo gli spostamenti e le rotazioni relative tramite la vista sul piano XY

Spostamenti in X:

Spostamenti in Y:

La struttura non subisce rotazioni relative, quindi possiamo affermare che il centro delle masse corrisponde al centro delle rigidezze

GRUPPO: Pellegrini - Pasqualino - Rossi