Blog

TRAVE RETICOLARE 2D

La trave reticolare è una struttura composta da un sistema di aste collegate tra loro attraverso cerniere interne. Queste aste costituiscono un sistema formato da tiranti, elemeti tesi, e da puntoni, elementi compressi. Tale struttura è caratterizzata dalla presenza di due correnti continui, uno teso e uno compresso. Le travi reticolari si sviluppano per l'esigenza di realizzare strutture sempre più leggere che superino luci sempre maggiori.

Nella prima esercitazione si è dovuto realizzare un modello bidimensionale di una trave reticolare con il software SAP utilizzando un modello preimpostato.

In tale caso si è deciso, per comodità, di impostare le dimensioni delle aste in modo tale da avere un'altezza della trave di 3m e una campata di lunghezza pari a 6m, per avere un angolo tra le aste di 45°.

In tale caso si ottiene una trave tipo così composta:

Successivamte sono state inserite delle cerniere nei nodi in modo tale che il momento nei nodi sia nullo.

Il passo successivo è stato quello di posizionare dei carichi verticali concentrati nei nodi per vedere il comportamento della trave.

Di seguito si sono determinati sia il materiale che il tipo di sezione che caratterizzano la sezione della trave, nello specifico si è scelta una sezione a doppia C in acciaio, profilato, questo, particolarmente adatto per le strutture reticolari perchè più facilmente lavorabili.

Dopo aver effettuato i passaggi sopra elecati, è stato possibile eseguire con SAP l'analisi del modello preimpostato ottenendo i grafici delle sollecitazioni della trave.

Dai diagrammi delle sollecitazioni così ottenuti si può evincere che:

. dato che la struttura è simmetrica, anche le solleciatazioi sono simmeriche rispetto all'asse centrale della trave;

. l'unica sollecitazione presente all'interno della trave è lo sforzo normale;

. lo sforzo normale è positivo (le aste si comportano come dei tiranti), losforzo normale è negativo (le aste si comportano come dei puntoni).

Dall'analisi della configurazione deformata si evince che:

Il corrente superiore è compress (la lunghezza del corrente si accorcia) mentre quello inferiore è teso (la lunghezza del corrente si allunga).

Il sofware SAP permette anche di esportare i valori delle sollecitazioni otteuti graficamente in una tabella Excel, dove i valori delle sollecitazioni possono essere ordinati, dopo aver dato un nome alle singole aste, per poter vedere meglio quali sono le aste più o meno sollecitate.

Dalla tabella Excel si pò evincere come effettivamente l'unica sollecitazione che agisce è lo sforzo assiale, mentre taglio e momento sono pari a zero, come già si è visto dai grafici, e come l'asta più sollecitata sia la 2-1, cioè quella centrale, in corispondenza della quale, nel grafico delle sollecitazioni, vi si è registrato il valore maggiore dello sforzo assiale.

TRAVE RETICOLARE 3D 

Seguendo gli stessi passaggi utilizzati per costruire il modello di trave reticolare in 2D, si è realizzato un modello di struttura reticolare tridimensionale. Si è aperto un nuovo file ed è stata impostata una griglia utilizzata per costruire le singole unità che poi sono state usate per determinare una struttura a piastra reticolare, che può simulare il solaio di una costrzione.

Utilizzando la griglia è stato costruito il primo modulo, rappresentato da facce controventate su tutti i 6 lati, che poi è stato copiato fino a coprire tutti i moduli della griglia.

Anche nel modello 3D sono state introdotte le cerniere in corrispondenza dei nodi della struttura in modo da rendere nullo il momento.

Anche in questo caso si è proceduti, prima, con l'inserimento di forze in corrisondenza di tutti i nodi dei moduli della faccia superiore della piastra in modo da immaginare che il solaio sia sottoposto ad un carico uniforme, poi si è scelta la tipologia della sezione e il materiale (profilo a doppio C in acciaio).

 

Successivamente sono stati assegnati dei vincoli (cernere) in corrispondenza dei nodi della faccia inferiore ipotizzando che il solaio poggi su dei pilastri.

A questo punto si è avviata l'analisi per vedere quali sono i diagrammi delle sollecitazioni.

Dall'osservazione dei grafici delle sollecitazioni, anche in questo caso, come nella trave reticolare bidimensionale, si può vede come l'unica sollecitazione presente sia quella dello sforzo normale, mentre T e M siano nulli; inoltre i diagrammi sono simmetrici rispetto al baricentro, data la simmetria della struttura stessa, sia sul lato corto che su quello lungo della pastra.

Si è anche realizzato il modello della configurazione deformata della struttura:

Da tali grafici si vede che la struttura si comporta in modo completamente simmetrico, data anche la disposizione regolare e simmetrica degli appoggi (cerniere). La struttura si deforma in corrispondenza delle forze applicate e il modello che questa configurazione ricorda è quello di una qualsiasi trave appoggiata caricata in modo uniforme.

Si considerino un arco a tre cerniere, costituito da due corpi rigidi rappresentabili come travi collegate da cerniere puntuali. Supponiamo che in corrispondenza della cerniera interna agisca un carico concentrato, P.

   

Si può facilmente verificare che il carico agente in sommità viene trasmesso alle due cerniere a terra dalle due aste mediante sole forze di compressione. In altre parole, le due aste sono sollecitate solo da sforzi normali, in questo caso di compressione. Questo elementare modello di struttura a traliccio piana, di frequente impiego nelle prime applicazioni di copertura realizzati in materiale ligneo, è chiaramente ispirata al principio statico della triangolazione. Se inseriamo una catena a collegamento dei due appoggi, come illustrato nella figura precedente, otteniamo la cosiddetta capriata semplice a due spioventi. Tuttavia, l’impossibilità di coprire, mediante tale schema semplice, luci sempre più grandi ha condotto via via all’inserimento di ulteriori elementi strutturali al fine di parzializzarne la luce libera, fino ad ottenere elementi sempre più complessi.

Nascono così le strutture reticolari, le quali offrono una delle più antiche soluzioni al problema delle coperture: le capriate in legno che coprivano le basiliche romane rappresentano un primo esempio. Ma la forma reticolare da anche soluzione ad un altro problema, la necessità di realizzare strutture di notevoli dimensioni con elementi relativamente piccoli. In particolare, l’evoluzione di sistemi costruttivi basati su elementi reticolari ha portato al passaggio dalla trave ad anima piena alla trave reticolare.

Il maggior sviluppo si ebbe nell’ottocento quando si riuscì a produrre industrialmente i laminati di ferro con caratteristiche meccaniche sufficientemente sicure, diffusamente utilizzati nella realizzazione di ponti ferroviari. Contemporaneamente, il reticolo di travi si viene ad orientare verso schemi caratterizzati ciascuno da un preciso funzionamento statico. Si fa così gradualmente strada la tendenza a realizzare composizioni del reticolo mediante una successione di elementi triangolari accostati, come per lo schema Warren considerato come soluzione ottimale per opere da ponte. Il vantaggio di questo schema sta nel fatto che permette di concentrare il materiale secondo le linee di massima concentrazione degli sforzi. Le travature reticolari nascono infatti per ottimizzare lo spazio in cui vengono inserite.

Se però l’altezza necessaria per raggiungere determinati livelli di rigidezza è troppo estesa, nella trave Warren si raggiungono eccessive lunghezze degli elementi che possono provocare nelle aste compresse dei fenomeni di instabilità. Per tali motivi, si affermano altri tipi di travature reticolari, quali i tipi Pratt e Howe.

Tre aste che formano un triangolo costituiscono pertanto una struttura stabile. Il triangolo è quindi la forma più semplice di struttura reticolare di cui costituisce pertanto anche la cellula base per formare un sistema rigido che non può essere deformato dall’applicazione di forze esterne. Le strutture reticolari formate per semplice giustapposizione di triangoli sono dette talora triangolazioni semplici. Definiamo pertanto struttura reticolare, un insieme di aste rettilinee incernierate collegate le une alle altre mediante nodi in modo da formare una struttura portante stabile, piana oppure spaziale. Trave reticolare è un sistema reticolare, formante un’unica membratura, nel quale una dimensione (la lunghezza) è largamente preponderante rispetto all’altra (o alle altre nel caso tridimensionale). Fra le diverse aste che compongono la struttura si distinguono i CORRENTI, costituiti dalle aste essenzialmente orientate nella direzione della dimensione maggiore della trave reticolare, e di cui distinguiamo un CORRENTE SUPERIORE e un CORRENTE INFERIORE,  e un’anima scomposta in elementi lineari di cui distinguiamo le DIAGONALI, disposti inclinati, e i MONTANTI, disposti verticalmente a tale direzione.

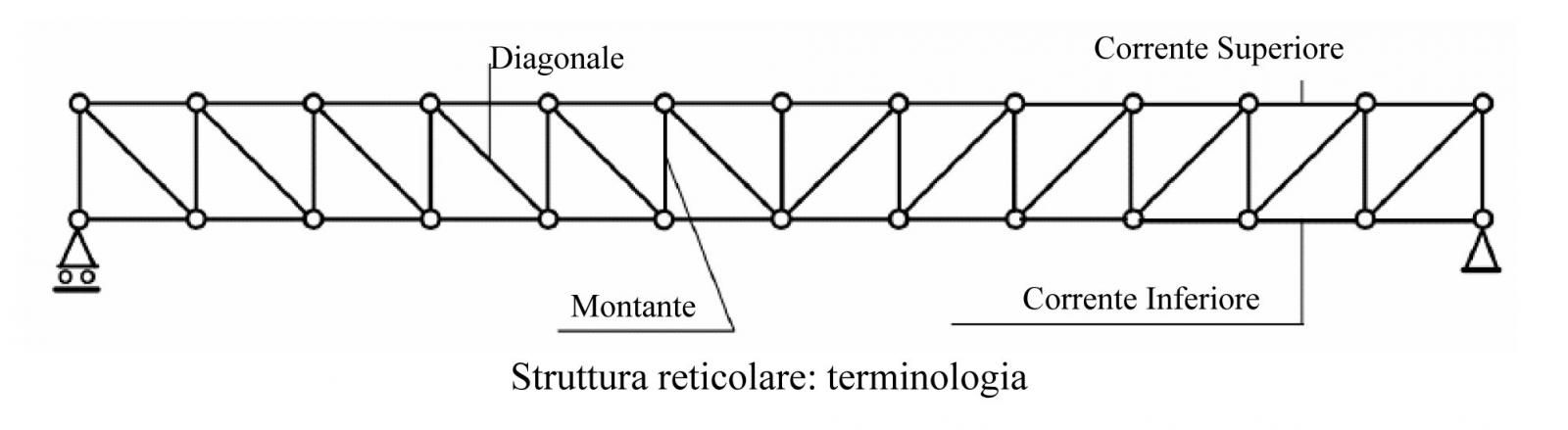
Se i carichi sono costituiti unicamente da forze concentrate sulle cerniere, ogni asta risulterà soggetta a sola azione assiale, o sforzo normale; in virtù di questa ultima ipotesi le aste saranno soggette soltanto a sforzo normale, di trazione o compressione. La generica asta tesa si definisce comunemente come TIRANTE, quella compressa come PUNTONE.

Il problema statico delle strutture reticolari consiste nel calcolo dello sforzo normale in tutte le aste e tale calcolo è possibile servendosi delle sole equazioni di equilibrio. Dei due metodi principali metodi per la determinazione degli sforzi nelle aste di un sistema reticolare, metodo dei nodi e metodo delle sezioni o di Ritter, utilizzerò il secondo per la risoluzione dell’esercizio manualmente.

METODO DELLE SEZIONI

Una travatura reticolare generata a partire da un triangolo iniziale presenta la proprietà di poter essere tagliata da una sezione ideale, che divida la struttura integralmente in due parti sezionando solo tre aste non concorrenti nello stesso punto. Si può quindi disegnare lo schema isolato di una delle due porzioni.  Preventivamente sono state calcolate le reazioni scrivendo l’equilibrio di tutto il traliccio (sommando pertanto tutte le forze esterne agenti sui nodi e dividendola per il numero delle reazioni nei vincoli, in quanto si tratta di una struttura simmetrica), restano come incognite solo gli sforzi normali di tutte le aste tagliate. Poiché l’equilibrio di questa porzione consente di scrivere solo tre equazioni, il taglio non dovrà evidenziare più di tre incognite. Lo sforzo in una delle tre aste viene calcolato mediante un’equazione di equilibrio dei momenti intorno al polo in cui convergono le altre due. Successivamente sono stati operati altri tagli per determinare gli sforzi assiali nelle aste non interessate dal primo taglio.

Successivamente ho verificato la struttura con SAP. Creando un nuovo file con il comando NEW FILE, e dopo aver impostato le unità di misura (KN, m, C), ho scelto come template con cui lavorare 2D TRUSSES, ideale per questo tipo di lavoro. Ho inserito pertanto le indicazioni di tipo geometrico della struttura quali numero delle partizioni, altezza e lunghezza delle aste (L=5m, 2L=10m).

Ottenendo così la struttura richiesta

SAP in realtà riconosce 2 aste unite come un incastro, ma essendo tutte cerniere interne dobbiamo segnalarlo in quanto le aste essendo libere di ruotare non si trasmettono momenti, contrariamente all’incastro. Per questo motivo dopo aver selezionato tutte le aste e seguendo il percorso ASSIGN > FRAME > RELEASES/PARTIAL FIXITY, andiamo ad indicare che all’inizio e alla fine di ogni frame il MOMENT 33 è nullo.

Abbiamo ottenuto così cerniere interne in ogni nodo.

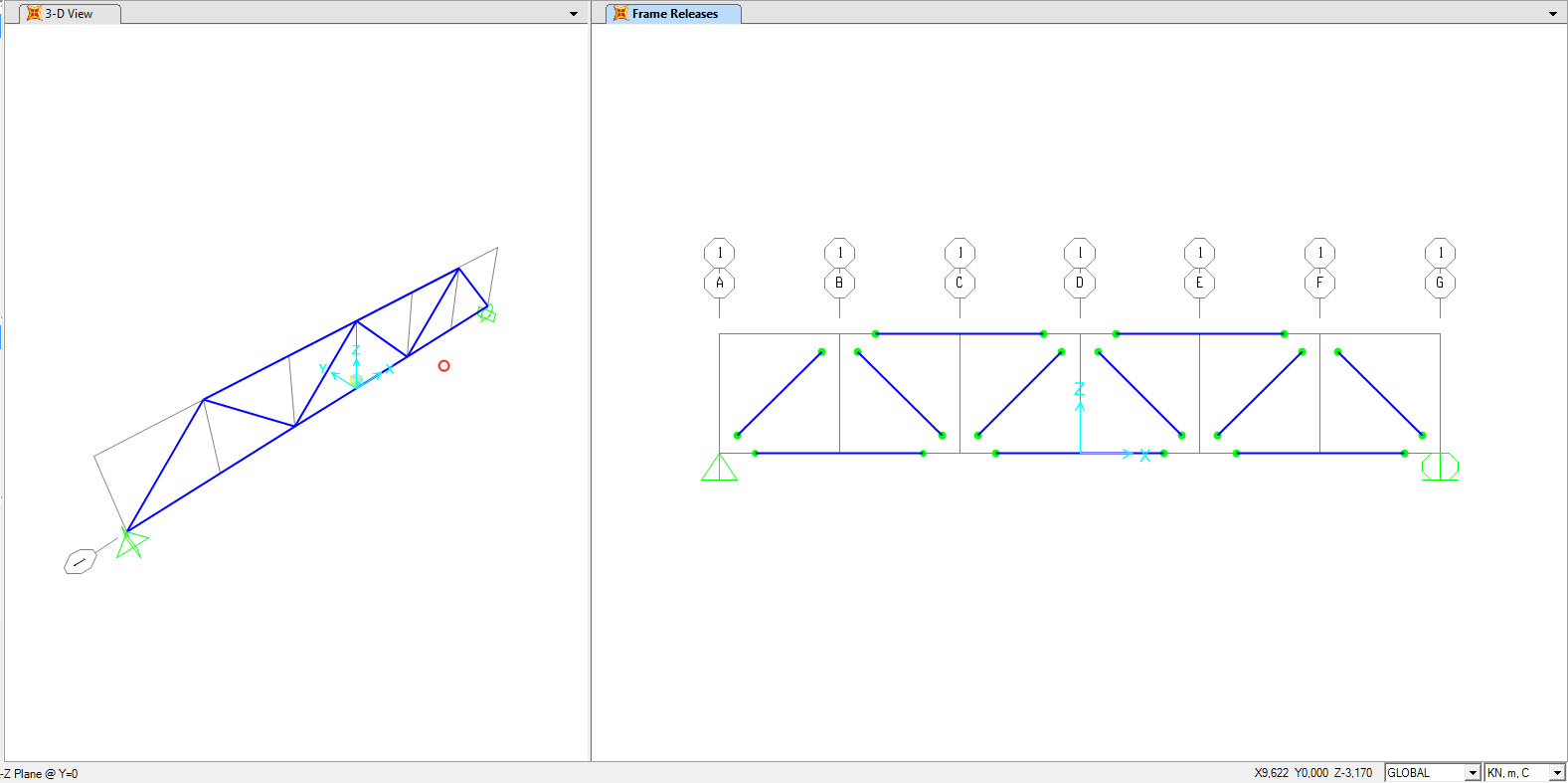
A questo punto ho assegnato i carichi esterni in corrispondenza dei nodi. Dopo averli selezionati, e aver seguito il percorso ASSIGN > JOINT LOADS > FORCES, ho aggiunto  il carico desiderato, ADD NEW LOAD PATTER, nominandolo F e assegnandogli un peso proprio nullo, perché altrimenti lo avrebbe segnalato come carico distribuito 

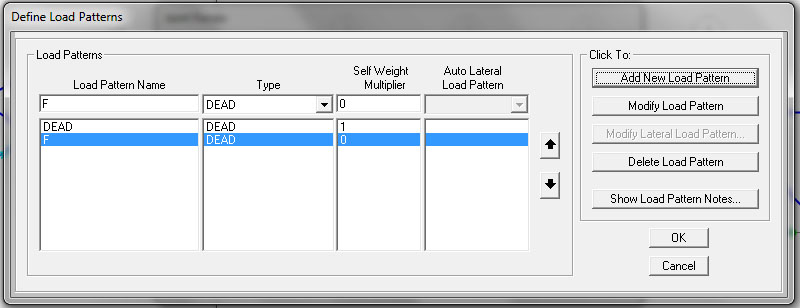
Infine ne stabilisco il valore, in questo caso -200 KN, nel sistema globale in direzione dell’asse z, essendo forze verticali e discordi a tale asse, da cui il segno negativo.  

Occorre arrivati a questo punto assegnare la sezione. Pertanto, dopo aver selezionato tutti gli elementi interessati, attraverso il percorso ASSIGN > FRAME > FRAME SECTION > ADD NEW PROPERTY, scelgo la sezione desiderata. In questo caso è stata scelta la sezione tubolare, rinominata PIPE, per la quale è possibile anche variarne le dimensioni

SAP ci indica sul modello stesso il tipo di sezione scelta

È possibile a questo punto avviare l’analisi, attraverso il comando RUN ANALYSIS. Scelgo al momento di non analizzare né la parte modale nel il carico DEAD, specificandolo attraverso il comando RUN/DO NOT RUN CASE. Avvio infine l’analisi scelta con il comando RUN NOW.

Il primo risultato subito comprensibile è la deformata della struttura, ottenuta  con il comando SHOW DEFORMED SHAPE

È possibile a questo punto verificare le reazioni vincolari, calcolate precedentemente attraverso il comando SHOW FORCES > JOINT

 

Per controllare i diagrammi delle sollecitazioni è possibile invece seguire il percorso SHOW FORCES > FRAME/CLABES/TENDONS e scegliere quale grafico consultare. Scegliendo ad esempio il diagramma del MOMENT 33, risulta un momento nullo così come era stato supposto inizialmente, essendo tutte aste soggette a solo sforzo assiale in cui non viene trasmesso il momento.

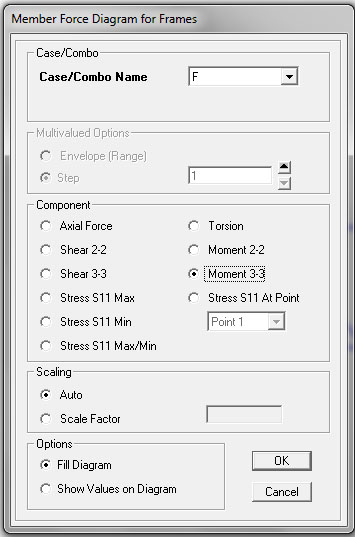
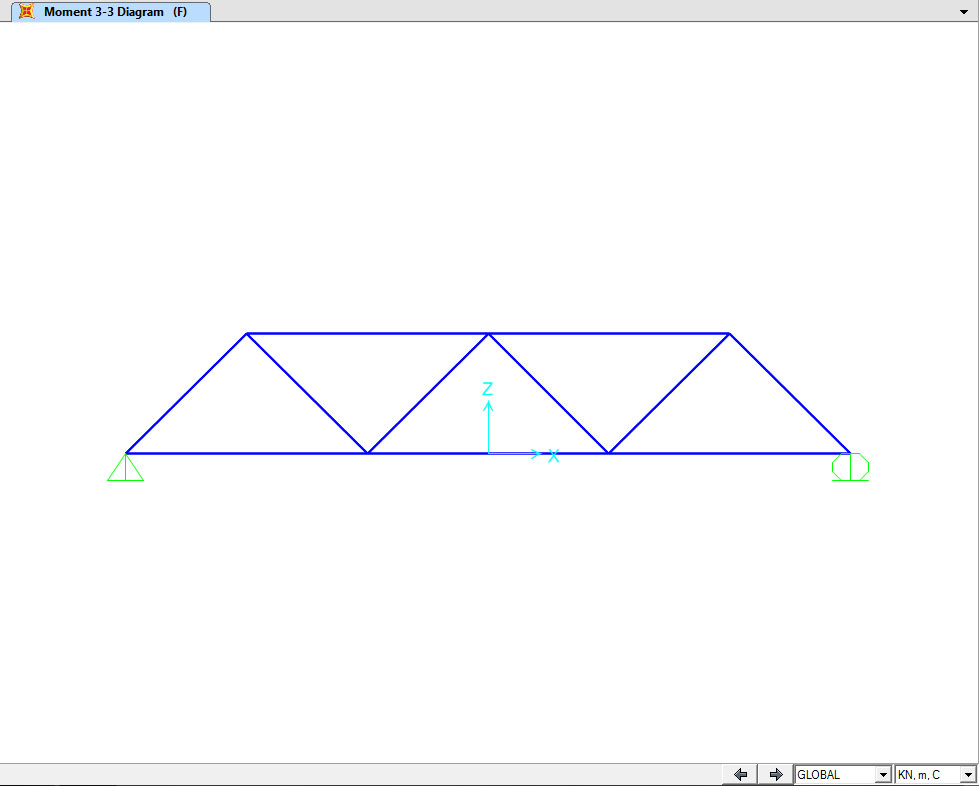
Consultiamo allora il diagramma dello sforzo assiale scegliendo l’opzione AXIAL FORCE nel percorso precedente. Dal diagramma risulta in primo luogo la simmetricità delle sollecitazioni dato dalla struttura simmetrica stessa, da cui dipendono anche la simmetricità delle reazioni vincolari. In secondo luogo è possibile distinguere quali siano le aste compresse, dette PUNTONI, e distinte convenzionalmente dal segno negativo e colore rosso, e le aste tese, ossia i TIRANTI, convenzionalmente con segno positivo e in questo caso colore blu. Detto ciò è possibile notare che tutti gli elementi che corrono a formare il corrente interiore sono dei tiranti mentre quelli del corrente superiore dei puntoni. Al contrario, gli elementi che costituiscono le diagonali sono sia puntoni che tiranti. Dal diagramma è possibile inoltre apprezzare quale siano le aste più sollecitate.

 

Cliccando poi con il tasto destro su ogni singola asta è possibile visualizzare i diagrammi specifici, in cui è possibile notare ulteriormente momento e taglio nullo, al contrario dello sforzo assiale 

 

È possibile a questo punto esportare i valori così ottenuti in una tabella excel per analizzarli qualitativamente, attraverso il percorso DISPLAY > SHOW TABLES. In questo caso ci farà vedere tutte le analisi eseguite, ma deciso di fare una selezione e di farmi mostrare solo quelle ricavate da ANALYSIS RESULTS. Dopo aver cliccato il comando SELECT LOAD PATTER scelgo anche il carico desiderato, e in questo caso continuo ad analizzare solo il carico aggiunto F.

 

Seleziono infine la tabella che intendo esportare ossia ELEMENT JOINT FORCES- FRAME e la esporto attraverso il percorso FILE > EXPORT CURRENT TABLE > TO EXCEL

 

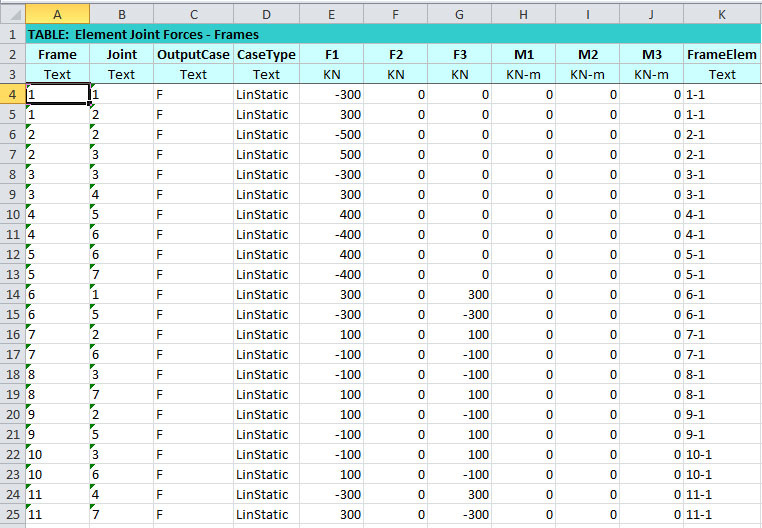
Per analizzare i risultati deciso di riordinarli in ordine decrescente in base al valore di F1

 

Notiamo che la tabella riporta i nomi attribuiti dal programma alle aste (FRAME) e ai nodi (JOINT), allora seleziono direttamente da SAP il comando per vedere tali nomi, attraverso il percorso SET DISPAY OPTIONS > LABLES, sia per le aste che per i nodi.

Seconda tabella esportata ELEMENT FORCES

 

 

Successivamente alla realizzazione delle struttura reticolare in 2D, ho analizzato una struttura reticolare in 3D, la quale, essendo ideale per coprire grandi luci, è stata impostata come una copertura e rappresentata come una piastra di 25x30, con modulo 3x3x3m.

In questo caso, rispetto al modello 2D, si decide di utilizzare come template GRID ONLY, impostata inserendo il numero delle linee per ogni asse e dimensione delle stesse, in modo da ottenere una griglia di base su cui disegnare ogni asta attraverso il comando DRAW FRAME

 

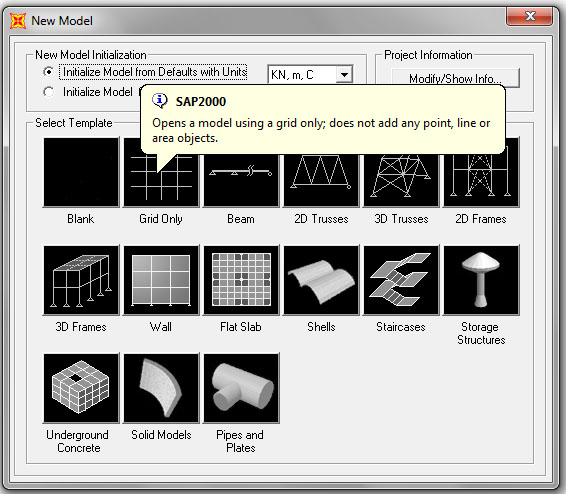
Partendo dalla definizione di un modulo, ho proceduto utilizzando i comandi copia CTRL+C e incolla CTRL+V per ripeterlo e completare la griglia.

 

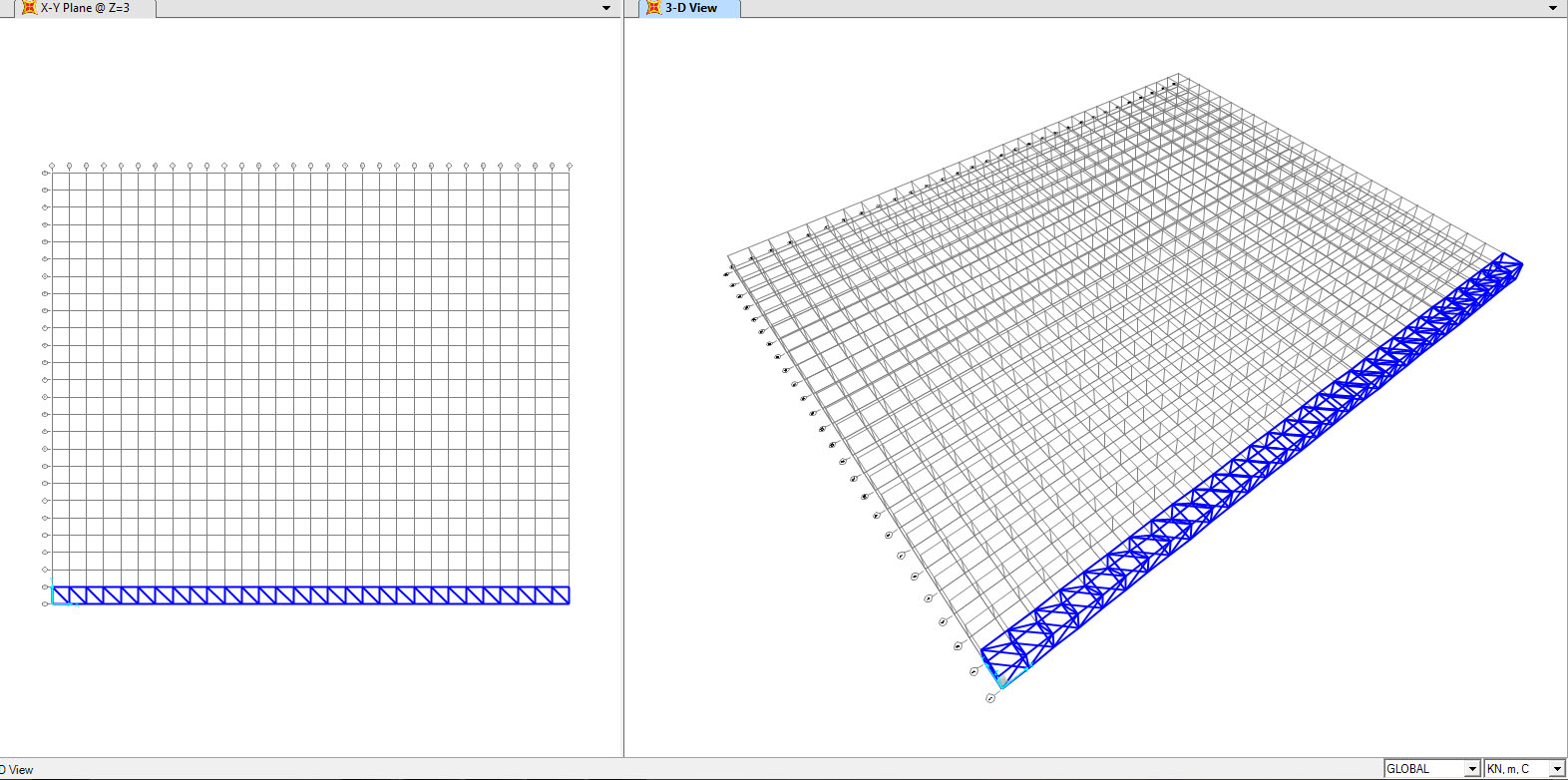
Nel momento in cui si copiano degli elementi si potrebbe non far coincidere i punti, per questo motivo occorre unirli, una volta selezionati, tramite il percorso EDIT > EDIT POINT > MERGE POINT, ed inserendo una tolleranza ad esempio di 10cm Come nel modello 2D, occorre definire che tutti i nodi presenti, essendo una struttura reticolare, sono delle cerniere interne, seguendo per cui il percorso ASSIGN > FRAME > RELEASES/PARTIAL FIXITY, si assegna che all’inizio e alla fine di ogni asta il MOMENT 33 sia nullo, cioè non viene trasmesso momento.

Analogamente ripeto il passaggio per definire la sezione delle aste, ossia attraverso il percorso ASSIGN > FRAME > FRAME SECTION > ADD NEW PROPERTY scelgo la sezione tubolare.

Infine posso definire gli appoggi, ultimo parametro fondamentale per definire la struttura. Si è deciso di porre delle cerniere in corrispondenza dei 4 angoli, come a simulare dei pilastri. Per far ciò bisogna seguire il percorso ASSIGN > JOINT > RESTRAITS, e nel momento in cui scegliamo il vincolo di cerniera verranno selezionati i movimenti bloccati, ossia la traslazione in questo caso

 

 

 

Arrivati a questo punto occorre solo inserire il carico esterno agente prima di avviare l’analisi. In questo caso i carichi vengono applicati a ogni nodo della faccia superiore della struttura. Perciò, così come è stato fatto nel caso 2D, dopo aver selezionato i nodi interessati si segue il percorso ASSIGN > JOINT LOAD > FORCES,  e si aggiunge il carico desiderato denominandolo F e attribuendogli un valore di -5KN.

Definiti i parametri fondamentali delle struttura come cerniere interne, vincoli esterni e sezione, e i carichi esterni agenti, è possibile avviare l’analisi. Anche in questo caso decido di analizzare solamente la parte dovuta ai carichi esterni e di trascurare l’analisi modale e dead. Mostrando la deformata con il comando SHOW DEFORMED SHAPE, si nota come la struttura sopporti abbastanza bene il carico agente, non si riscontrano infatti particolari deformazioni delle configurazione iniziale

Attraverso poi il percorso SHOW FORCES > FRAME CABLES > AXIAL FORCE è possibile visualizzare il diagramma dello sforzo assiale. Da quest’ultimo si nota quali siano i puntoni, la maggior parte nella parte inferiore, e i tiranti, nella parte superiore. Si può notare inoltre come gli sforzi maggiori, sia per gli elementi superiori che inferiori, sia per le diagonali, siano nella parte centrale della struttura, lontana perciò dagli appoggi.

Allo stesso modo si può notare che dal diagramma dei momenti risulta un momento nullo così come era stato supposto inizialmente, essendo tutte aste soggette a solo sforzo assiale in cui non viene trasmesso il momento. Infine esportiamo la tabella dei valori in excel per analizzarli.

 

 

 

 

 

 

 

 

Per la modellazione di una trave reticolare 3d si è pensato di creare un solaio a piastra reticolare rigido, partendo dalla trave reticolare di 9 campate precedentemente creata, e decidendo di ripeterlo per 3 volte dandogli le dimensioni perciò di 54x18 m.

Quindi in realtà la rigidezza serve più che altro per la forte luce di 54 m. Questa piastra è stata modellata attraverso una griglia 3d di SAP, che serviva come base per il disegno delle varie frame, che generavano un modulo a forma di parallelepipedo controventato su tutte e 6 le facce. Questo modulo poi è stato ripetuto sia lungo l’asse delle x creando la trave reticolare di 9 campate in 3d e poi anche lungo l’asse y per creare il lato corto della piastra.

Anche in questo caso, come nella trave 2d è stato necessario specificare che ai nodi non c’era presenza di incastri, bensì di cerniere interne, quindi è stata tolta l’assenza del momento in tutte le aste, sia all’inizio che alla fine, rendendole così affini al comportamento delle cerniere interne.

Si è scelto poi di posizionare i vincoli lungo le campate della trave centrale, concentrandone quattro ai vertici della campata centrale, ed altri quattro a due campate di distanza, sia a destra che a sinistra, immaginando una situazione dove questa piastra rigida viene lasciata solo con tre grandi appoggi interni (per esempio blocchi servizi), cercando di capire quanto riesca a restare rigida, specie nei punti in aggetto che sono i più sensibili.

Per le forze si è deciso di posizionare dei carichi concentrati su tutti i nodi della faccia superiore, per vedere il comportamento della piastra sotto un carico più uniforme possibile.

Anche in questo caso è stato necessario impostare una sezione, utilizzando sempre una trave tubolare cava in acciaio.

.

Dall’analisi dei vincoli è possibile vedere come questi non agiscano in modo simmetrico:

Dall’analisi degli sforzi è possibile vedere come anche in questo caso, sia nulli sia il taglio che il momento Invece è presente lo sforzo assiale.

 Si può vedere sia dal grafico 3d che dalle due viste 2d come le aste si comportino in basso da tiranti, mentre in alto da puntoni. La cosa che non avevo considerato è che come si vede ancor più chiaramente nelle sezioni 2d è come una parte degli sforzi sia assente in alcune aste.

Grazie alla presenza delle tabelle di excel è possibile capire quale sia la trave più sollecitata, e si vede come questa sia una. 

Infine è possibile capire il comportamento effettivo della struttura guardandone la deformata:

da questa si ha la conferma di come la struttura non agisca in modo simmetrico, e di come sia troppo poco vincolata per riuscire a rispondere in modo soddisfacente ai carichi: infatti anche se non si presenta un abbassamento eccessivo della parte centrale, tuttavia la piastra accusa molto i carichi nella parte degli aggetti, in modo anche non simmetrico, andandosi a piegare completamente (deformata di una mensola) e non mostrandosi adatta a sostenere un peso del genere.

Visto il comportamento con un solaio stretto e lungo, si è deciso di provare ad analizzare il comportamento della piastra con una maglia regolare di 9x9 campate. I vincoli sono stati lasciati nella stessa posizione, e ripetuti in modo da lasciare le stesse proporzioni con il solaio precedente, affidando un eventuale miglioramento della sua rigidezza ad una forma geometrica più regolare.

Facendo l’analisi delle forze con SAP , è possibile vedere come ancora una volta, le uniche forze presenti siano quelle assiali.

Il diagramma dello sforzo assiale mostra come anche in questo caso, le aste inferiori siano tese, mentre quelle superiori siano compresse.

 

 

Guardando i grafici della sezione xz e yz è possibile vedere come in un lato sia amplificato l’effetto dei tiranti e molto inferiore quello dei puntoni, e viceversa sull’altro lato si manifesti l’opposto.

grafico lato xz

grafico lato yz

Anche vedendo la deformata, è possibile capire come la forma geometrica più regolare non influisca positivamente nella rigidezza della piastra, in quanto la deformata si comporta esattamente nello stesso modo di quella dei solaio stretto e lungo.

 

La trave reticolare è una struttura caratterizzata da una struttura composta da aste, unite tra loro da cerniere interne che tra loro si trasmettono il momento. Queste aste sono legate in un modulo triangolare, che ripetuto genera una struttura che è caratterizzata da due correnti orizzontali che sono rispettivamente, uno teso e uno compresso.

Con SAP è stato possibile creare una trave reticolare, utilizzando un modello preimpostato, inserendo solo le dimensioni delle varie parti. L’altezza e la lunghezza della campata sono state messe in rapporto 1:2 (rispettivamente 3 e 6m), in modo che l’angolo che si forma tra le aste sia di 45°.

Per fare in modo che il modello di SAP risponda al modello di trave reticolare reale, è necessario trasformare i nodi da incastri a cerniere, andando a togliere un grado di vincolo.

Per capire il comportamento della trave, è necessario sottoporla a dei carichi, che si sceglie di inserire nei nodi in alto, di intensità uguale in ogni nodo.  

Si genera così una struttura simmetrica sia geometricamente che dal punto di vista delle forze.Le reazioni vincolari in una struttura simile si ripartiscono in modo simmetrico, andando a dividersi nelle due cerniere esterne.

Infine è necessario per l’analisi in SAP, stabilire le caratteristiche della sezione della trave: si è scelta perciò una sezione in acciaio tubolare rotonda.

A questo punto è possibile fare l’analisi delle sollecitazioni: guardando i grafici delle varie sollecitazioni è possibile fare alcune considerazioni:

-        I grafici delle sollecitazioni sono simmetrici rispetto all’asse baricentrico della trave;

-        L’unica sollecitazione che avviene all’interno della trave è lo sforzo normale, che si trasmette in modo sia positivo sia negativo sulle aste, rispettando la simmetria precedentemente detta;

-        Le aste dove lo sforzo normale è positivo sono dei tiranti, che vengono allungati, mentre dove lo sforzo normale è negativo si hanno dei puntoni, che vengono compressi;

-        I correnti orizzontali rispettano il modello di trave reticolare, essendo uno teso (inferiore) e uno compresso (superiore);

-        Le aste inclinate interne sono quelle che presentano minore sforzo normale, mentre lungo “il perimetro esterno” lo sforzo normale è molto più concentrato, sia nei tiranti esterni sia lungo i due correnti: tuttavia l’asta più sollecitata è quella centrale del corrente inferiore, in quanto è quella corrispondente al centro di simmetria della trave.

La deformata della trave, coerentemente alle sollecitazioni, si incurva verso il centro, abbassandosi, per permettere l’allungamento delle fibre del corrente teso, che sono massime in corrispondenza dell’asta risulta centrale, mentre risulta accorciata (e quindi presenta fibre compresse) nel corrente superiore. La deformazione avviene verso il basso, coerentemente ai carichi che gli sono stati applicati.

Attraverso l’uso di SAP è stato possibile esportare attraverso una tabella i valori dei vari sforzi assiali, che grazie ad excel sono stati ordinati per capire in modo chiaro quale fossero le aste più sollecitate, e si è potuto avere conferma ulteriore sia di questo sia dei valori nulli di taglio e momento all’interno della trave.

La tabella ha presentato un'analisi delle varie aste, che vengono divisi per intervalli di lunghezza, dimostrando come le varie sollecitazioni restino costanti; inoltre attraverso i segni delle lunghezze è possibile risalire a quali aste si comportino come tiranti (positive) e quali come puntoni (negative). 

Questi dati, vengono confermati dalla tabella sottostante, che invece analizza i risultati delle aste nei nodi, che coincidono con i vincoli. A livello di risultati, l'unica differenza è che nelle aste inclinate, il risultato è diviso per componenti (es. N6sena, N6cosa), però vengono confermati i risultati delle aste orizzontali, che dimostrano come  la reazione del vincolo della cerniera interna coincida con lo sforzo assiale.

Nella risoluzione a mano si è trovato conferma dei risultati ottenuti con SAP. Le reazioni vincolari sono state risolte sfruttando la simmetria della trave, risultando coincidenti con quelle calcolate dal programma. 

L’analisi delle sollecitazioni è stata fatta attraverso l’utilizzo sia del metodo Richter, che attraverso l’equilibrio dei vari nodi:

Con la sezione di Richter si è fatto un taglio nelle prime tre aste (1,4,9), inserendo delle forze incognite che sono gli sforzi normale presenti nelle rispettive aste.

Il primo passaggio è stato il calcolo dell’equilibrio dei momenti nel nodo 2 perché era l’unico dove N1 ed N9 vi convergevano, risultando quindi nulle:

 

N4 x h + 3/2 F x l – F x l/2 =0

N4= ( Fl/2 – 3FL/2) x 1/h  -> N4= (-100 x 6) KNm /3m = -200 KN

Il meno davanti ad N4 significa che la direzione con cui è stato inizialmente ipotizzato non era corretta, ma è diretto in senso opposto.

È stato poi effettuato l’equilibrio a traslazione verticale:

3F/2 – N9senα – F =0

N9senα= (3F/2 –F)= F/2= 50 KN

N9= 50 KN/ senα =70,7 KN

In questo caso il segno positivo, è conferma del fatto che il verso dello sforzo era stato correttamente ipotizzato.

Si è trovata N1 con l’equilibrio a traslazione orizzontale:

N1 – N4 + N9cosα =0

N1= N4- N9cosα= 200 – 50 KN = 150 KN

Si è poi passato allo studio dell’equilibrio delle forze che convergevano nei nodi, in modo di risolvere via via gli sforzi incogniti.

NODO 5

Equilibrio a traslazione orizzontale:

N6cosα + N9cosα – N4=0

N6cosα= N4 – N9 cosα= (200- 50)KN = 150 KN

N6= 150 KN / cosα = 212,1 KN

 

Equilibrio a traslazione verticale: 

N6senα – N9senα – F =0

N6senα= 150 KN

 

NODO 2 

Equilibrio a traslazione verticale:

N9senα + N7senα=0

N7senα= -N9senα= -50 KN

Equilibrio a traslazione orizzontale:

N1 – N2 + N9cosα + N7cosα =0

N2= -N1 - N9cosα - N7cosα= (-150 -50 -50 )KN= -250 KN

NODO 6

Equilibrio a traslazione verticale:

N10 senα + N7senα –F=0

N10senα= - N7senα +F = (-50 + 100) KN= 50 KN

Equilibrio a traslazione orizzontale:

N4 + N7cosα –N10cosα – N5=0

N5= - N4 –N7cosα + N10cosα = (-200 -50 + 50) KN = -200 KN

Infine grazie alla simmetria della trave, senza calcolare ulteriori equilibri ai nodi, è stato possibile andare a scrivere gli sforzi delle restanti aste. In base alla condizione di equilibrio al nodo è stato possibile stabilire anche se gli sforzi erano di trazione o di compressione: quando gli sforzi erano entranti nel nodo di trattava di puntoni, al contrario se lo sforzo era uscente si avevano dei tiranti.

Si è poi ricalcolato lo stesso modello di trave reticolare con SAP, rendendolo più realistico, attraverso l’aumento del numero delle campate, in quanto le travi reticolari sono proprio utilizzate per luci imponenti. Si è così ripetuto il modulo di h=3m e l=6m per 9 campate, lasciando sempre un carico simmetrico e di stessa intensità. 

Attraverso l’analisi di SAP si è potuto constatare come di base il comportamento della trave sia lo stesso, in quanto non sono presenti ne taglio ne momento flettente ma vi è il solo sforzo assiale. Questo è sempre ripartito orizzontalmente in un corrente teso ed uno compresso, ma rispetto al modello di prima, dotato di una luce molto inferiore (18 m), questo che è lungo 54m presenta uno sforzo normale che presenta molte più variazioni di intensità da un’asta all’altra, e non solo sul corrente teso, ma anche su quello compresso crescendo tuttavia come in precedenza verso il centro di simmetria, punto individuato come il più sollecitato. 

 La deformata, tuttavia, avendo una luce maggiore sembra avere un abbassamento molto meno incisivo del modello più corto.

PROVA!

Trave Reticolare 2D

Banalissimo esempio di trave reticolare 2D, operando le sezioni di Ritter, questo mi aiuta a conoscere lo sforzo normale di ogni asta che compone la trave, definendone il ruolo: Tirante (asta sottoposta a trazione) o Puntone (asta sottoposta a compressione).

Su Foglio:

1.       Trovo le reazioni vincolari della struttura, essendo simmetrica suddivido il peso totale (3F) sui due appoggi.

2.       Opero la prima sezione che deve comprendere 3 aste.

3.       Calcolo la prima forza N₁ tramite l'equazione di equilibrio a rotazione nel nodo C poichè qui convergono N₂ ed N₃, quindi l'equazione ha 1 incognita ed è fattibile.

4.       Avendo ipotizzato N₁ con verso uscente e il risultato dell'equazione è negativo, N₁ ha verso entrante, quindi l'asta BD è un puntone.

5.       Calcolo N₃ tramite momento nel nodo B e ottengo che l'asta AC è un tirante.

6.       Calcolo N₂ che essendo inclinata a 45° avrò 2 componenti che conosco tramite trigonometria (modulo x coseno dell'angolo adiacente)( N₂ x cosπ/4 ), posso calcolare indifferentemente tramite equilibrio orizzontale o verticale, e ottengo che l'asta BD è un tirante.

7.       Opero un'altra sezione passante per AB e AC.

8.       Calcolo N₄ tramite equilibrio orizzontale e ottengo che l'asta AB è un puntone.

9.       Opero una terza sezione che comprende le aste BD, CD e CE.

10.   Momento nel nodo D e ottengo che CE è un tirante.

11.   Equilibrio orizzontale e ottengo che CD è un puntone.

12.   Sapendo che la struttura è simmetrica è sufficiente aver calcolato e aver scoperto il ruolo di una metà delle aste.

 

Trave reticolare 2d su SAP 2000:

1.       New Model -> 2D Trusses (Number of Divisions: 3 - Height: 3 - Division Lenght: 6)

2.       Ottengo una trave reticolare simile a quella dell'esercizio su carta; poiché SAP legge i nodi come incastri e non come cerniere bisogna "Rilasciare" il momento: Assign -> Frame -> Relases e spuntare le caselle "Start" e "End" del Momento 33.

3.       Seleziono i 3 punti superiori e applico una forza puntuale di 100 KN: Assign -> Joint Load -> Forces -> + -> F -> su Global Forces Z (asse verticale) immetto il valore (-100).

4.       Per cambiare la sezione delle aste: Assign -> Frame -> Sections -> Add New Property -> Decidere il tipo di sezione e cambiarla a proprio piacimento.

5.       Per visualizzare l'andamento della struttura clicco su "Show Deformed Shape".

6.       Per visualizzare i diagrammi degli sforzi normali clicco su : "Show Forces/Stresses" -> Frame -> Axial Force.

7.       Per salvare le tabelle in Exel: Display -> Show Tables -> Seleziono quello che mi interessa -> Select Load Patterns.

 

 

Trave reticolare 3D

Provo a ricostruire una trave reticolare simile al braccio di una gru:

1.       New Model -> Grid, la mia griglia sarà un modulo di 3x3x3 ripetuto 20 volte.

2.       Costruisco come modulo una piramide controventata alla base.

3.       Copio e incollo il modulo unendo le "punte" delle piramidi.

4.       Applico una forza puntuale sulle "punte" delle piramidi.

5.       "Rilascio" i momenti dei nodi della trave.

6.       Vedo i diagrammi delle forze assiali delle aste.

 

La trave reticolare è composta da un’insieme di aste assemblate in modo tale da comporre dei moduli triangolari, la funzione delle aste diagonali è quella di garantire una certa rigidezza della struttura. Nella parte superiore ed inferiore della trave sono riconoscibili due serie di aste allineate, i correnti superiori hanno un dimetro maggiore mentre quelli inferiori sono più sottili.

Introducendo delle forze esterne agenti sui nodi della trave reticolare potremo verificare, attraverso l’utilizzo del programma Sap 2000 che le aste sono sollecitate da sforzi normali.

FIG.1

                                                                                                                          

 

E’ stata disegnata quindi una  trave reticolare con tre divisori e sono state applicate dei carichi esterni sui tre nodi pari a 10 KN.

FIG.2

Conseguentemente si possono osservare le reazioni vincolari che come si può facilmente verificare sono pari a 15KN su entrambi i vincoli.

FIG.3

Nella deformazione della trave le aste superiori saranno compresse e le inferiori tese, ciò è osservabile facendo riferimento all’immagine della deformata flessionale della trave, visibile in seguito.

FIG.4

Dal diagramma dello sforzo normale e dalle tabelle ottenute si ha un’indicazione grafica e numerica della sollecitazione massima e minima.

FIG.5

FIG.6

Di seguito sono state evidenziate le sollecitazioni normali massime e minime differenziate da colori sia sulla struttura che in tabella.

FIG.7

L’asta maggiormente sottoposta a sforzo normale è quella centrale, seguono le aste superiori, numero 4 e 5, quelle gialle nmero 1, 3, 6, 11 e in fine quelle centrali.

  FIG.8