ESERCITAZIONE 3 - CENTRO DELLE RIGIDEZZE
(Messina Angela, Millozzi Italo, Rubeis Martina)
Per un migliore funzionamento, una struttura deve essere in grado di resistere a forze sismiche: tali forze agiscono nel centro di massa dell’edificio perciò è necessario che esso coincida con il centro delle rigidezze; infatti in caso di sisma dobbiamo evitare le rotazioni relative della struttura. Si può rendere più rigido un edificio grazie ai controventi, ovvero elementi verticali collegati tra loro orizzontalmente, che portano i carichi fino a terra. Il controvento più semplice è il telaio piano, ma importanti sono anche pilastri e muri portanti di blocchi scala e ascensori
Prendiamo in considerazione il piano terra con relativi corpi scala/ascensore.
La struttura considerata è in cemento armato e sono presenti due gabbie scala/ascensore.
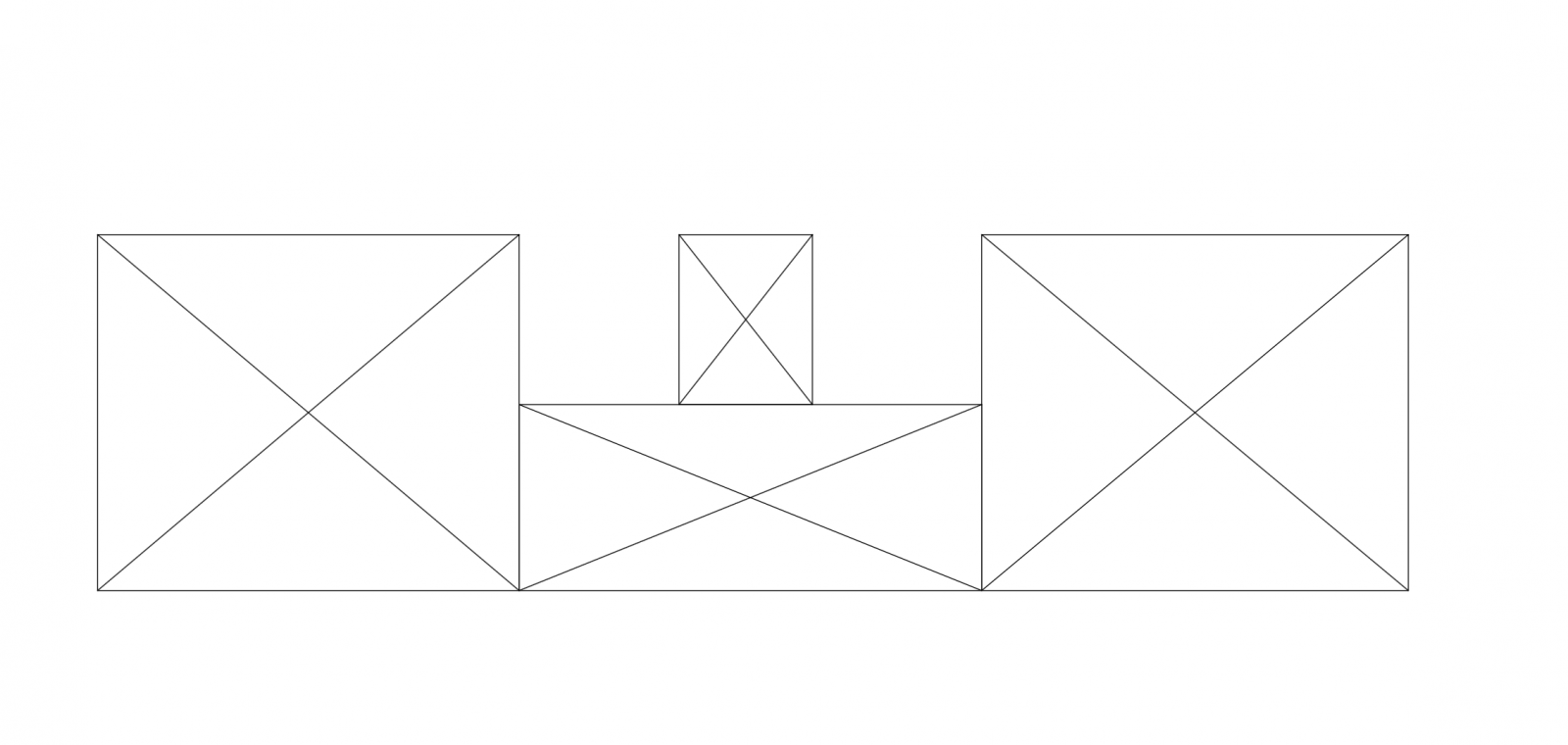
Individuiamo in maniera geometrica il centro delle masse (baricentro); si suddivide l'area in quattro rettangoli minori; individuati i loro centri è stato calcolato con la sommatoria di essi la posizione del centro di tutto l'impalcato.
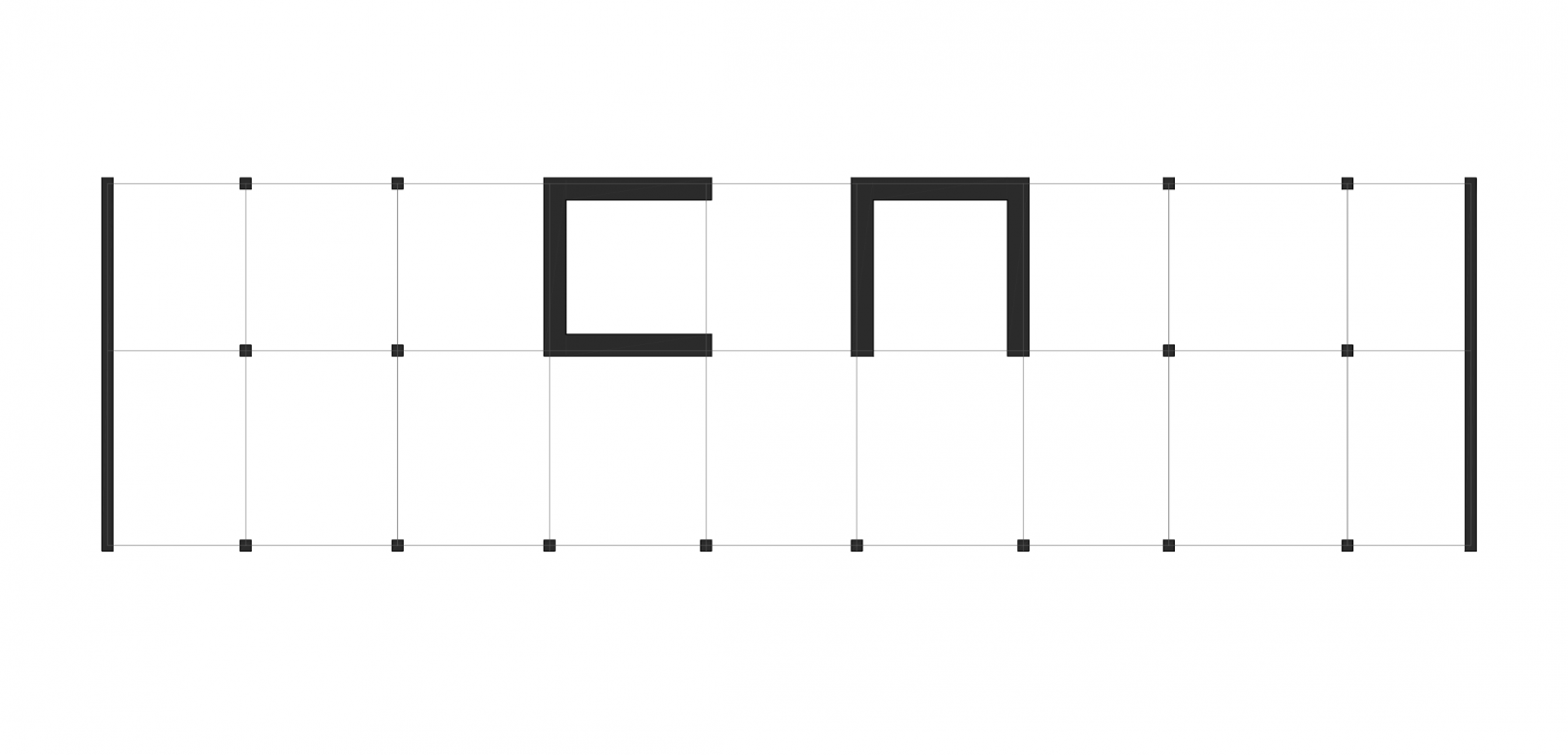
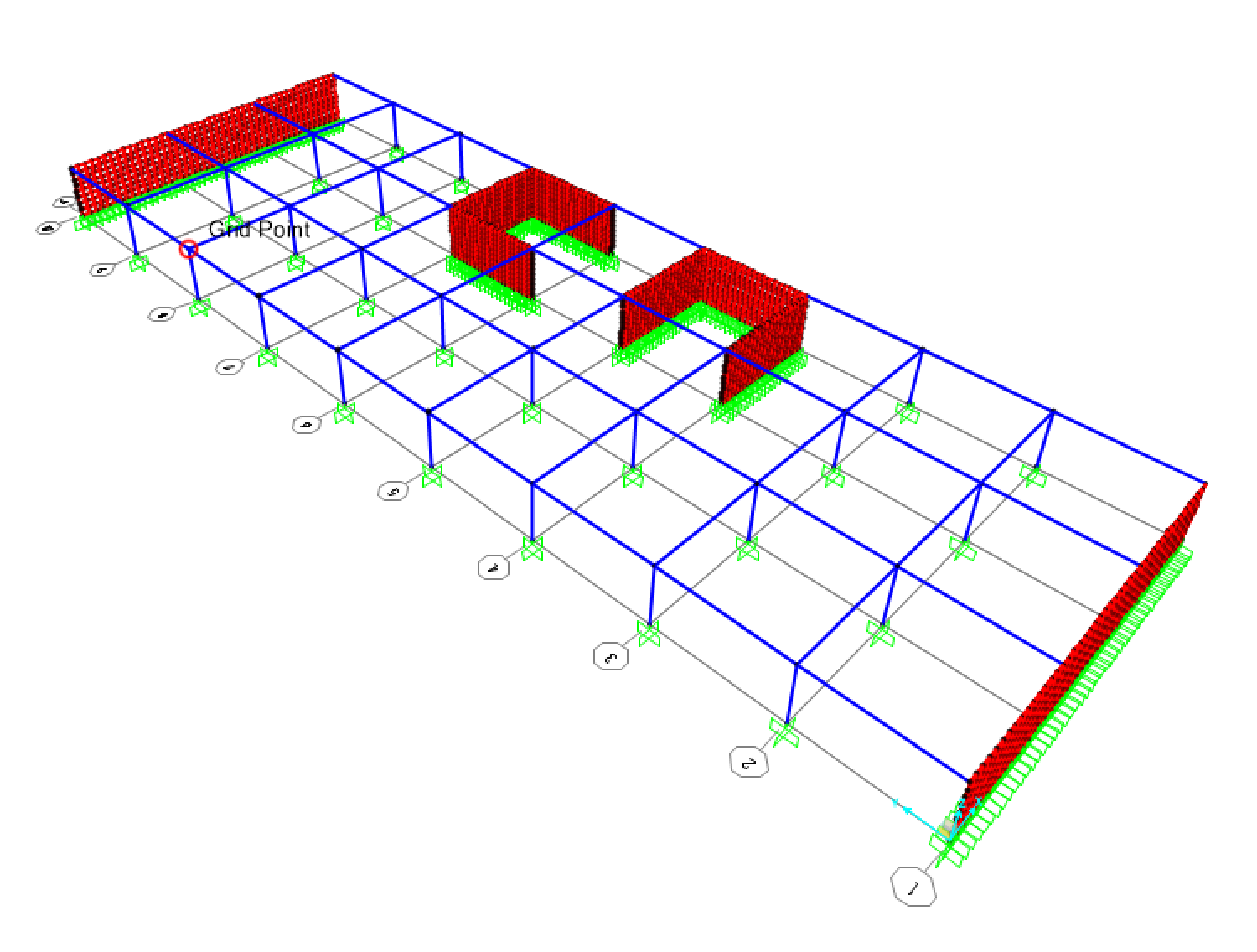
Ora riportiamo la struttura su SAP2000 assegnando alle travi in C.A. una sezione di 40 x 60 cm, ai pilastri una sezione di 40 x 40 cm ed ai setti delle gabbie scala uno spessore di 80 cm.
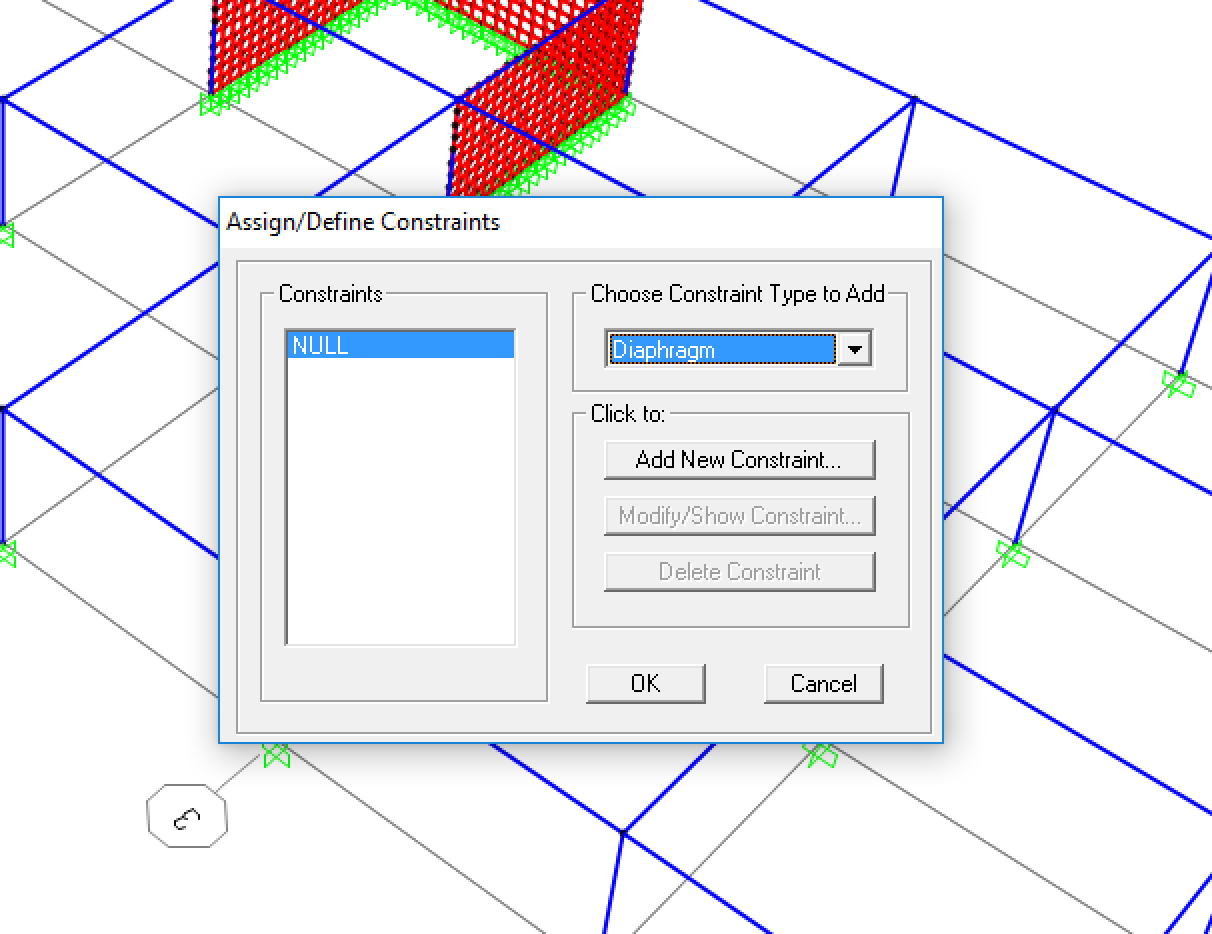
La struttura viene vincolata a “terra” tramite incastri ed a tutti i punti che sono alla stessa quota delle travi (compreso il centro di massa) viene assegnata la condizione di corpo rigido: in questo modo tutti i punti fanno parte dell’impalcato e non possono esserci spostamenti o rotazioni relative.
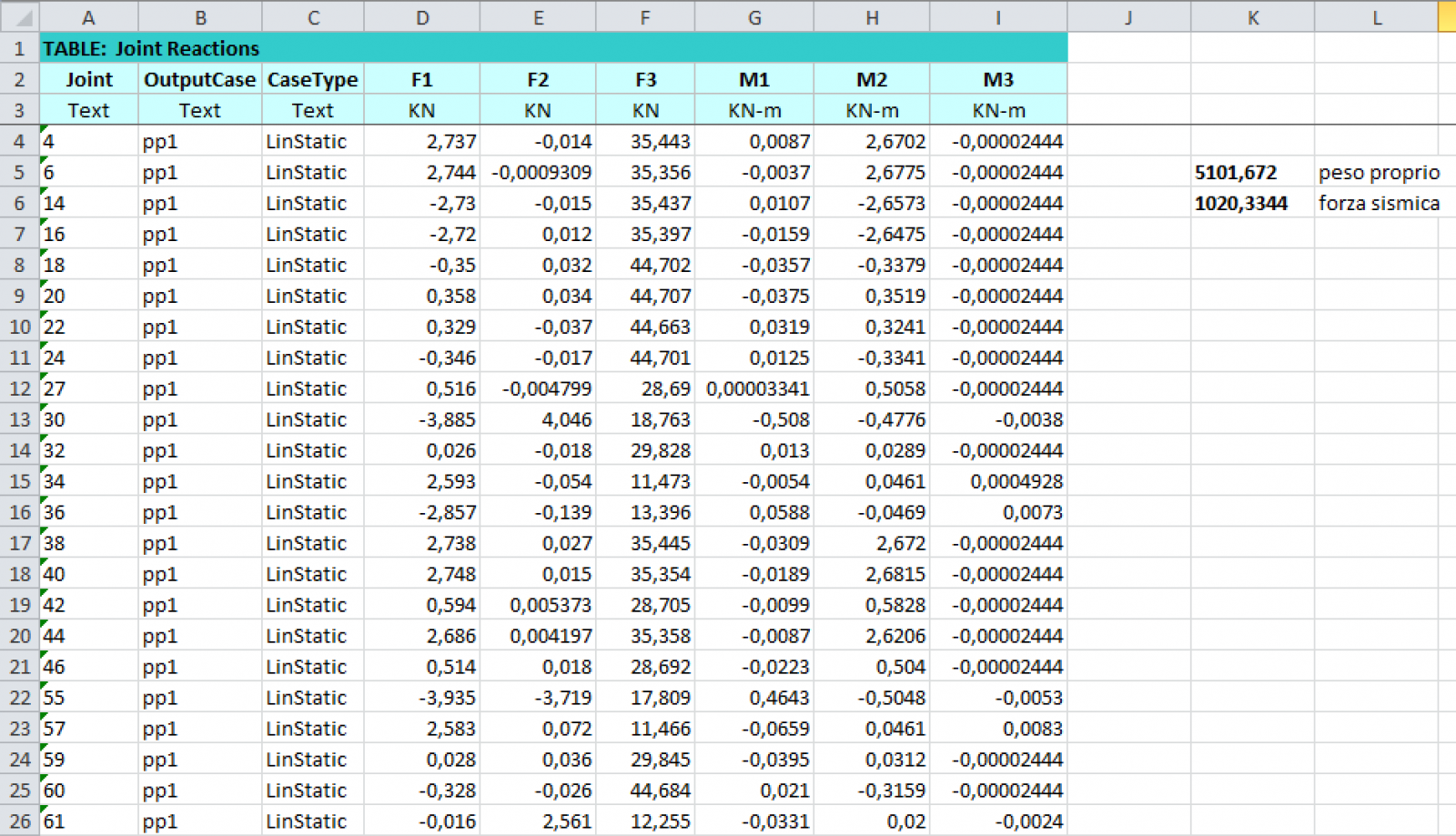
Per verificare che il centro di massa e quello delle rigidezze concidano, o siano molto vicini, assumiamo le due condizioni peggiori in caso di eventi sismici, ovvero che la forza sismica sia applicata interamente lungo una direzione. Per conoscere il valore di carico della forza sismica e’ necessario prima calcolare il peso proprio dell’edificio, quindi si importa la tabella dei carichi su Excel e, sommando tutte le reazioni vincolari verticali, si ottiene il valore del peso proprio pari a 5101,672 kN. E’ quindi possibile definire il carico sismico come percentuale del peso proprio moltiplicandolo per 0,2 (coefficiente di riferimento per zone a basso rischio sismico come Roma): dunque pari a 1020,3344 kN.
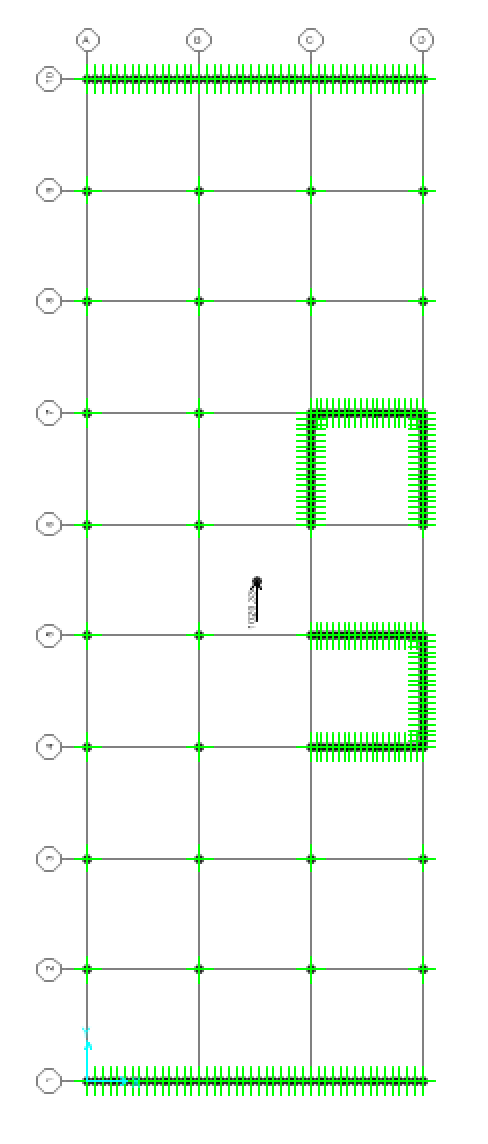
A questo punto è possibile assegnare la forza sismica come carico concentrato orizzontale, in entrambe le direzioni X e Y, e così lanciamo nuovamente l’analisi e verifichiamo gli spostamenti e le rotazioni relative tramite la vista sul piano XY.
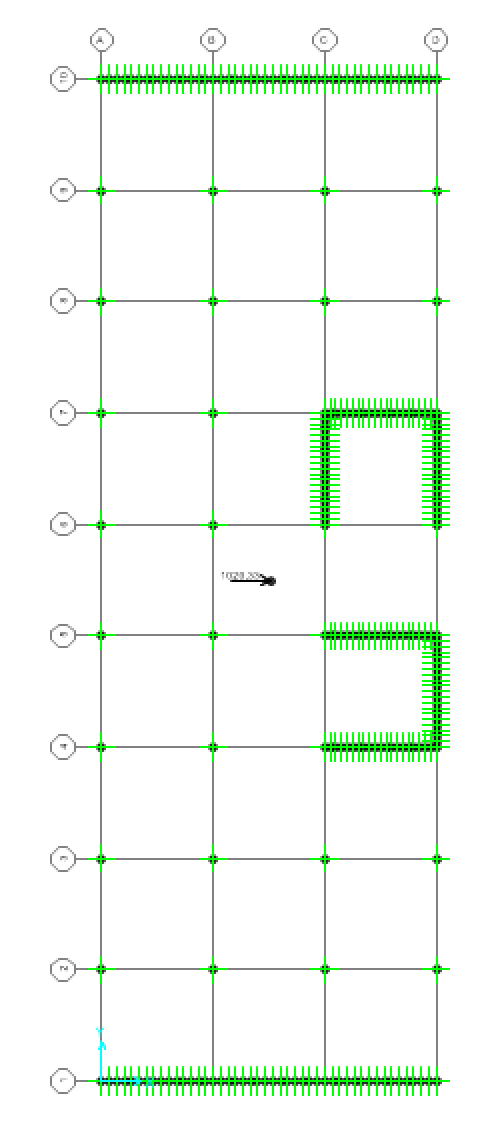
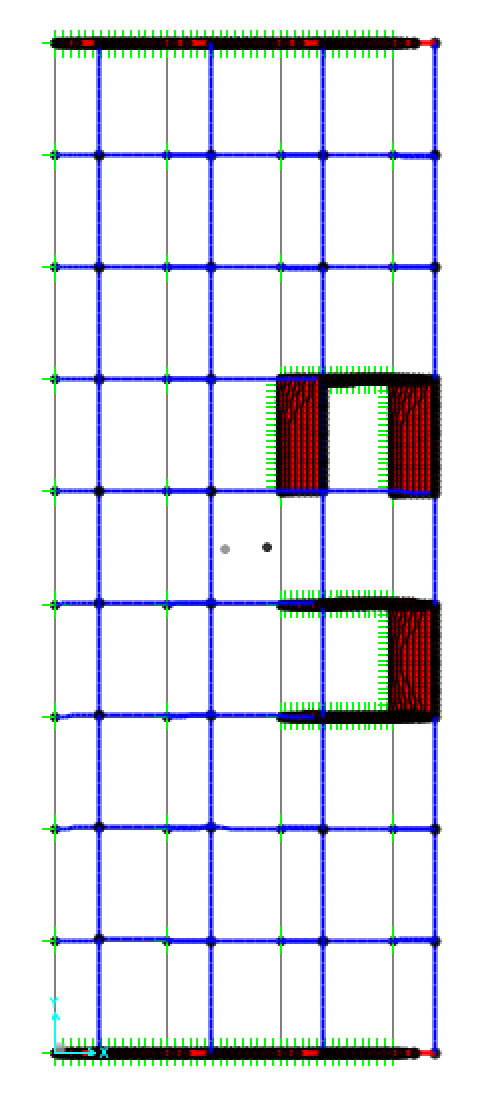
SPOSTAMENTI IN X:
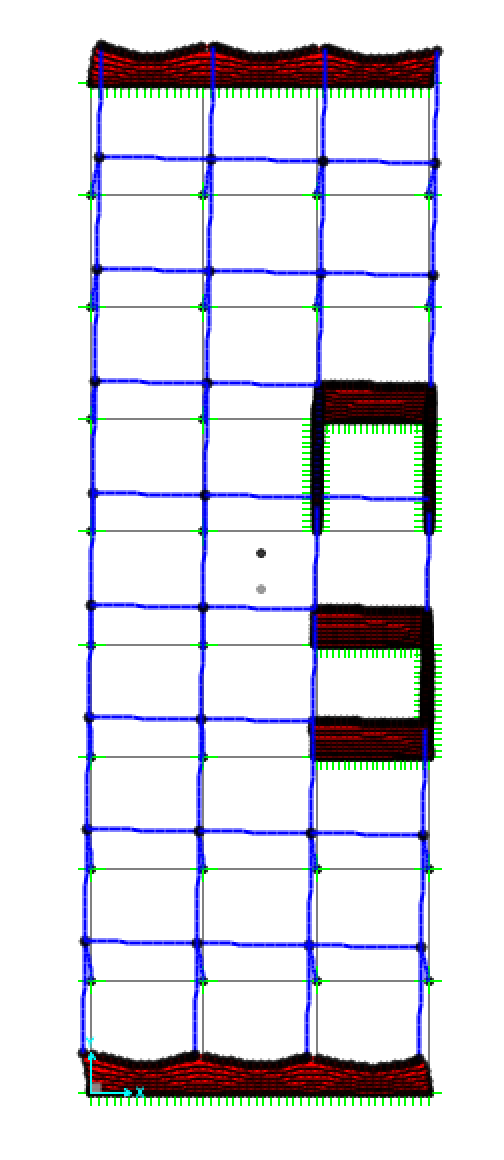
SPOSTAMENTI IN Y:
La deformata dovuta alla forza sismica lungo l'asse X non provoca rotazioni dell'impalcato.
La deformata dovuta alla forza sismica lungo l'asse Y provoca una lieve rotazione dell'impalcato; è necessario dunque spostare il centro di massa affinchè si avvicini il più possibile al centro delle rigidezze e successivamente riavvio l'analisi.
Commenti recenti