Blog

La terza esercitazione consiste nell’analisi di un telaio di un piano di un edificio, in particolare analizzando il centro di massa e il centro delle rigidezze per verificare che questi coincidano o siano molto vicini. Se questo non è verificato l’edificio subirà delle rotazioni quando sul centro di massa agiranno le forze sismiche. 

Per realizzare il piano tipo ho importato da autocad i fili fissi per la creazione di una griglia di riferimento in cui ho incluso tutti gli elementi che costituivano delle gabbie ascensori e corpi scala. Grazie alla griglia ho realizzato un sistema di travi e pilastri ed ho disegnato delle aree poligonali lì dove dovevo definire dei setti.  Alla base di ogni pilastro e di ogni punto appartenente ai setti ho posto un incastro; successivamente ho assegnato le sezioni ai pilastri (circolari e con diametro 60 cm), alle travi (70*45 cm) e ai setti ho assegnato una sezione Shell (0,30*0,30 cm), il tutto in calcestruzzo.  

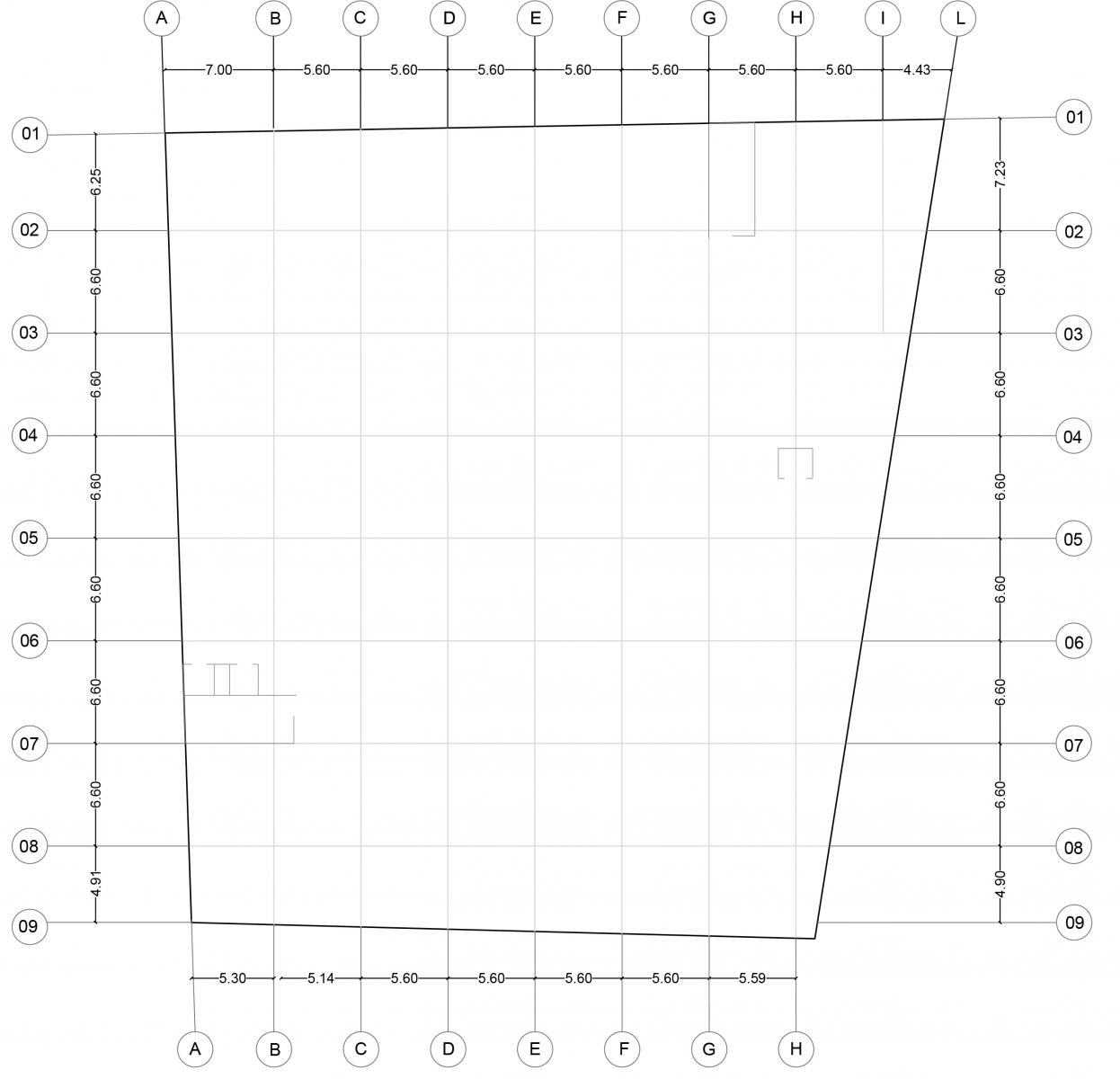
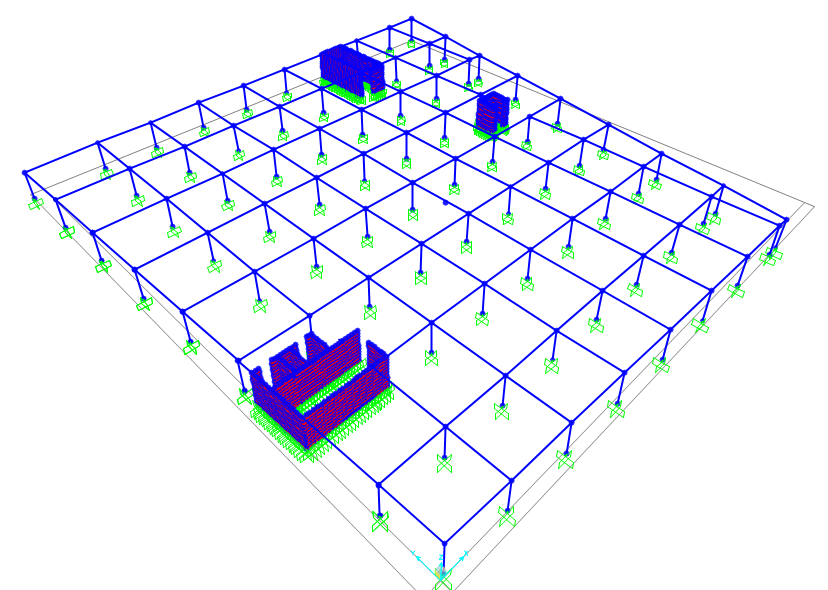
 Descritta e definita la struttura di questo piano dell’edificio ho analizzato la posizione del centro di massa (centro dell’area). Per determinarlo ho ipotizzato il posizionamento del centro d’area suddividendo il trapezio in due triangoli, posizionando i due centri d’area nei baricentri. Ottenute le coordinate dei due centri ho trovato, tramite la formula seguente, le coordinate del centro dell’intera figura: 

G_x = (A₁x₁ + A₂x₂ ) / (A₁+A₂)

G_y = (A₁y₁ + A₂y₂) / (A₁+A₂)

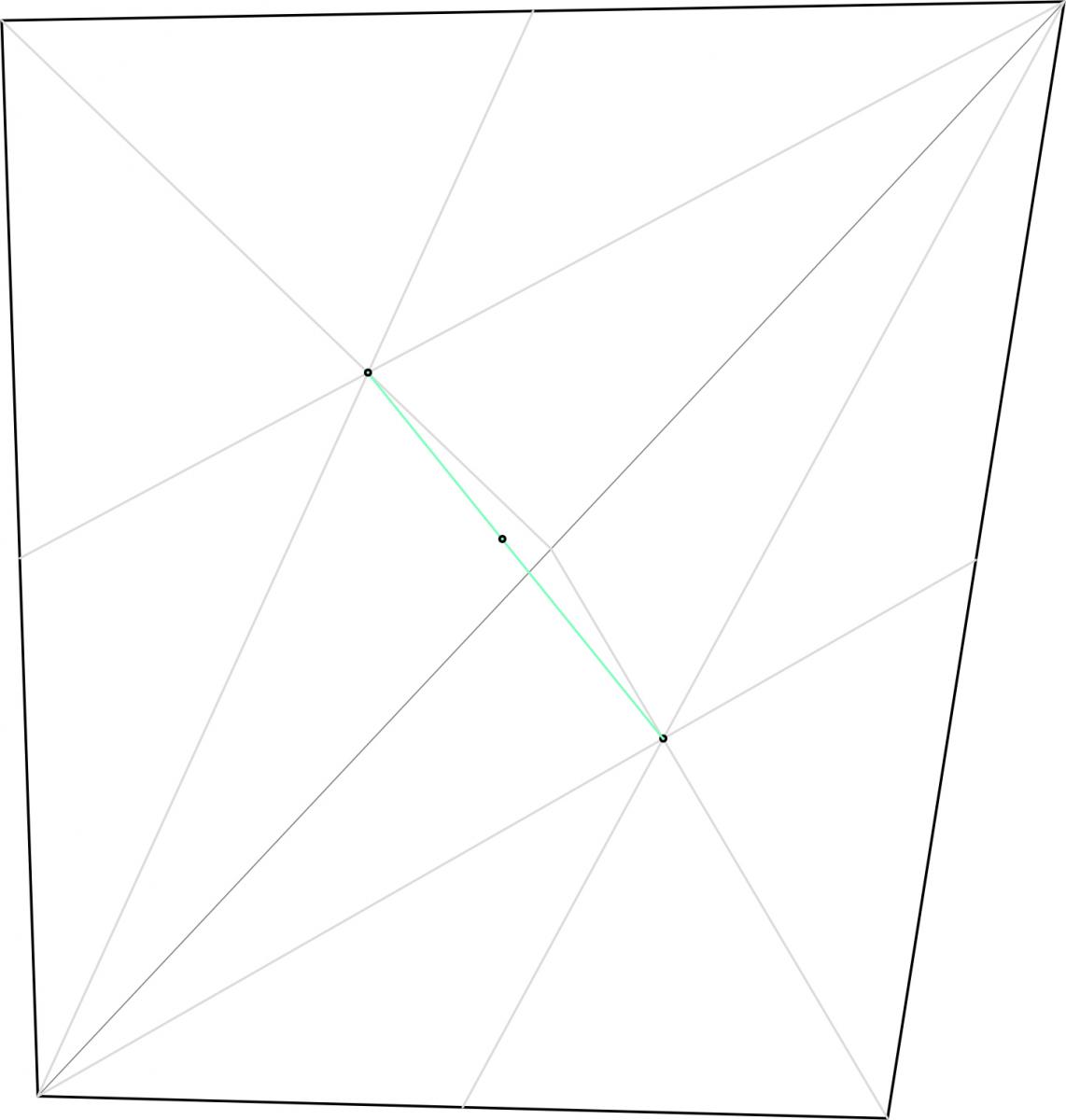
Posizionato il centro di massa su Sap ho selezionato le travi e tutti i punti appartenenti al piano z=3, incluso il centro di massa che deve far parte dell’impalcato, ed ho assegnato una condizione di vincolo interno Diaphragm per imporre la rigidezza del telaio. Questo passaggio riproduce la condizione di impalcato rigido in cui non è consentito il movimento libero di tutti i punti, i quali invece si possono muovere rigidamente, permettendo anche un’uguale rotazione intorno all’asse verticale che devo definire quando assegno questa condizione di vincolo (nel caso specifico attivo la rotazione intorno a z). 

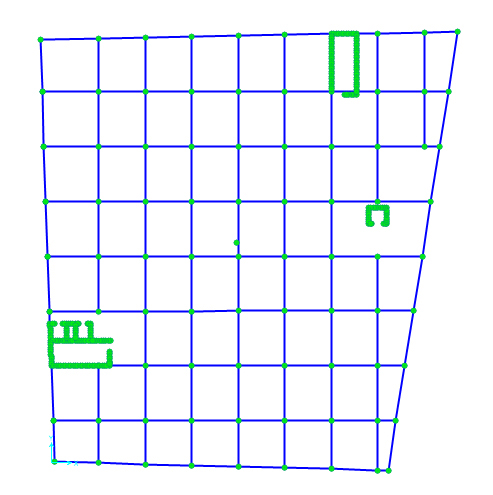
Per impostare l’analisi devo prima conoscere il valore delle forze orizzontali che devo applicare al centro di massa e per farlo devo considerare il peso totale dell’edificio e moltiplicarlo per un coefficiente sismico di massima (0,2). Per trovare il peso dell’edificio eseguo l’analisi dell’impalcato considerando esclusivamente il peso proprio e dalle tabelle di analisi trovo il valore della forza verticale che, sommata in tutte le sue componenti, mi fornisce il peso totale dell’edificio in kN; nel caso specifico è 44712,35 e moltiplicato per 0,2 da 942,47 kN, ovvero l’intensità della forza orizzontale che devo applicare. 

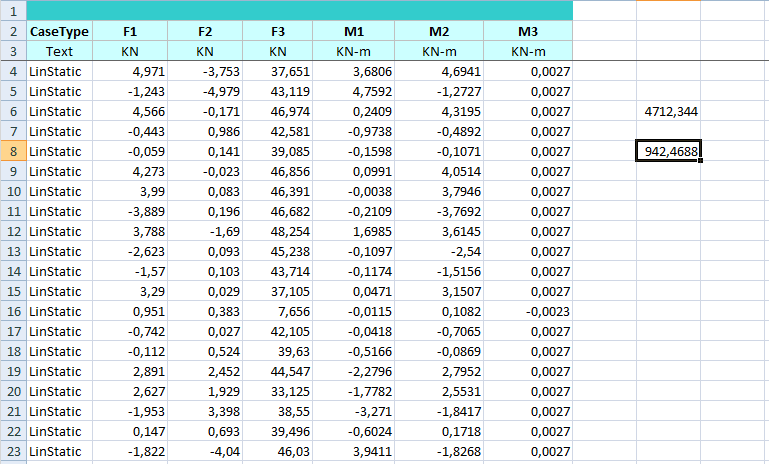
Per avviare l’analisi devo definire i due casi di carico, cioè la fx e la fy, ovvero le due componenti della forza orizzontale nel caso agisca lungo x e lungo y, che analizzo separatamente. Successivamente selezionando il centro di massa gli assegno prima la forza fx che agisce in direzione x con valore pari a 942,47 kN e faccio partire l’analisi; come risultato ottengo che la struttura oltre a traslare in direzione x, ruota.

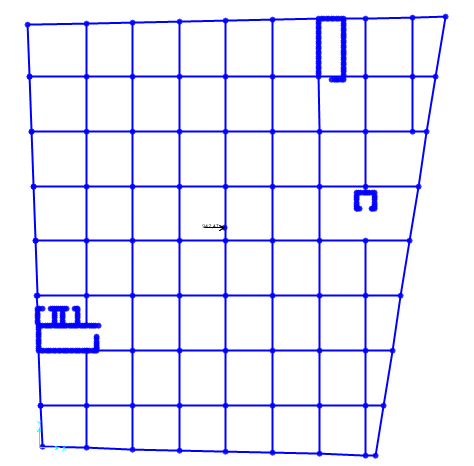
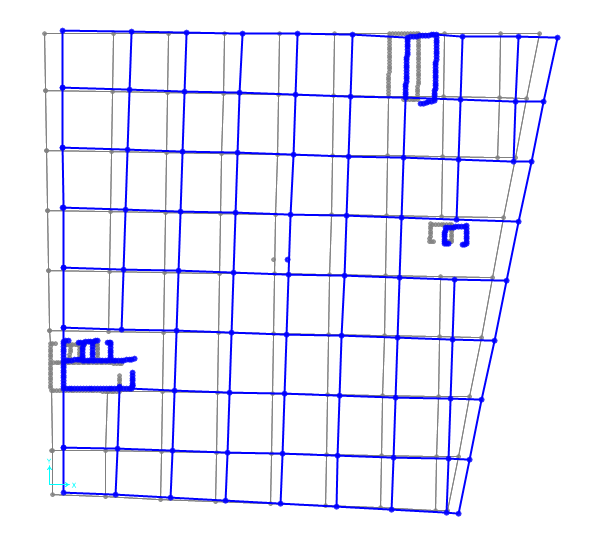
Questo avviene anche applicando la componente lungo y con lo stesso valore di 942,47 kN, ma con direzione lungo y. 

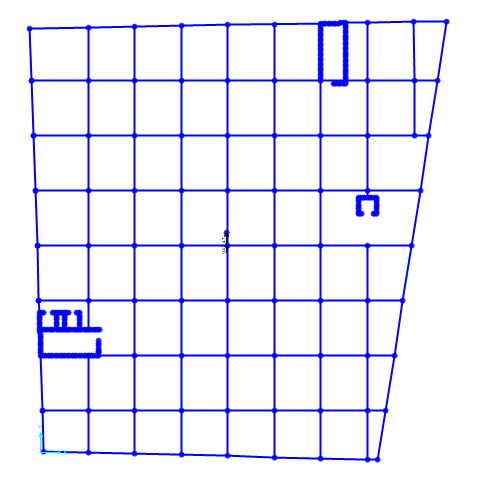
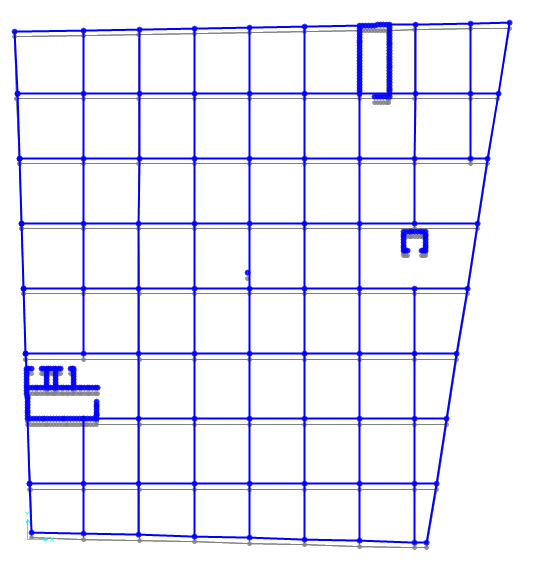
La rotazione mette in evidenza il fatto che il centro di massa non coincide con quello delle rigidezze, per cui nel progetto sarà necessario renderli coincidenti. In questa analisi ho cercato quali fossero le coordinate per cui la rotazione fosse minima in ogni punto cambiando le coordinate del centro di massa lungo y, quindi spostandolo verso il basso visto che la rotazione dell’impalcato era oraria. 

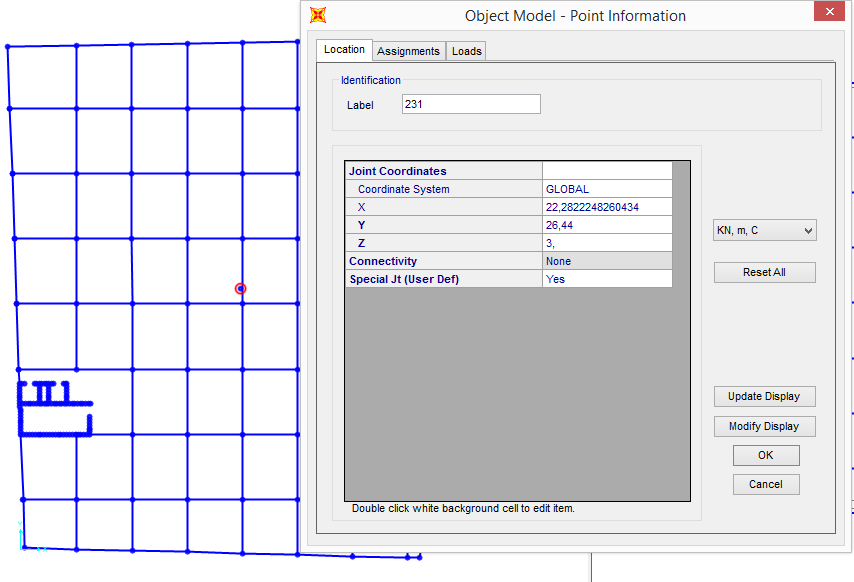
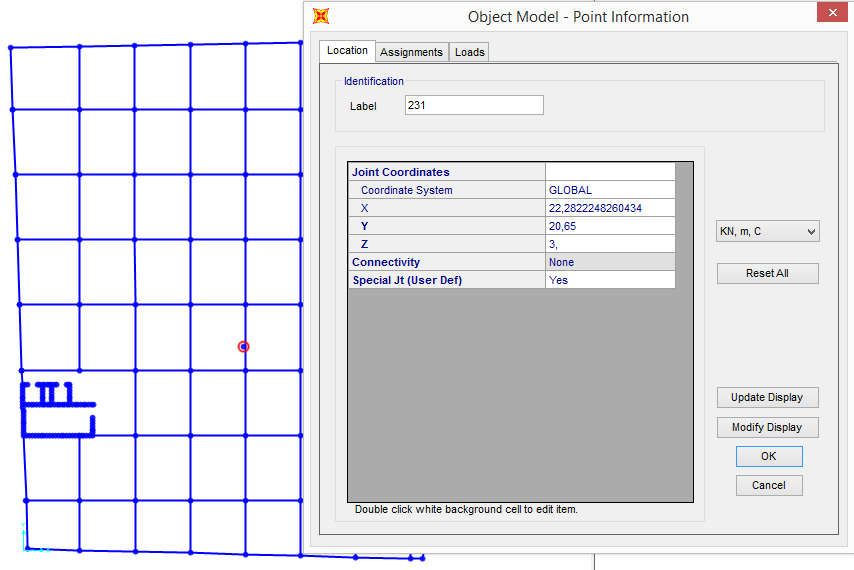
Ho modificato tale coordinata di partenza fino ad ottenere sole traslazioni lungo x e lungo y, in risposta all’azione orizzontale rispettivamente lungo x e lungo y, abbassandolo in totale il centro di massa di 5,80 m. 

Le immagini seguenti mostrano i risultati dell'analisi una volta spostato il centro di massa. 

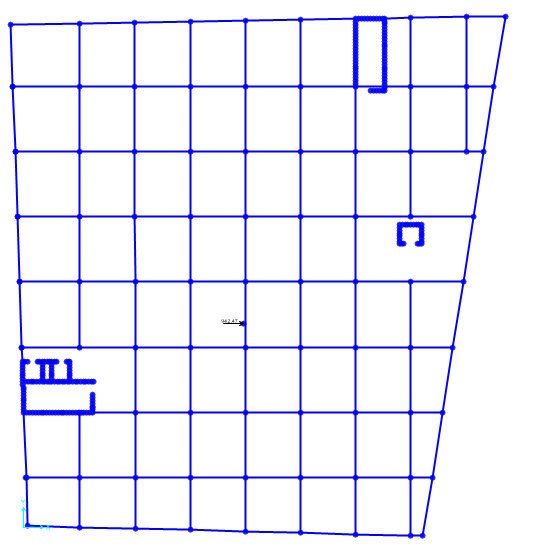
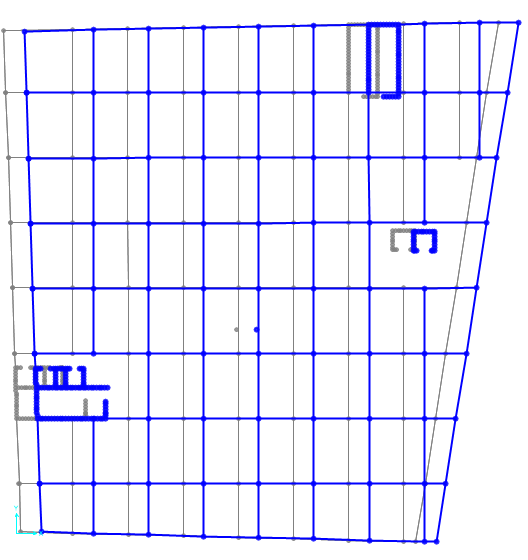
Risultato con la forza agente lungo x. 

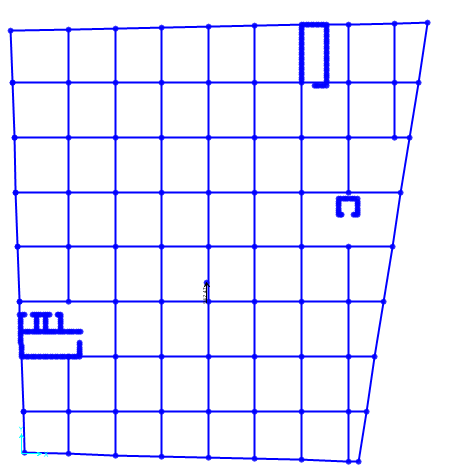
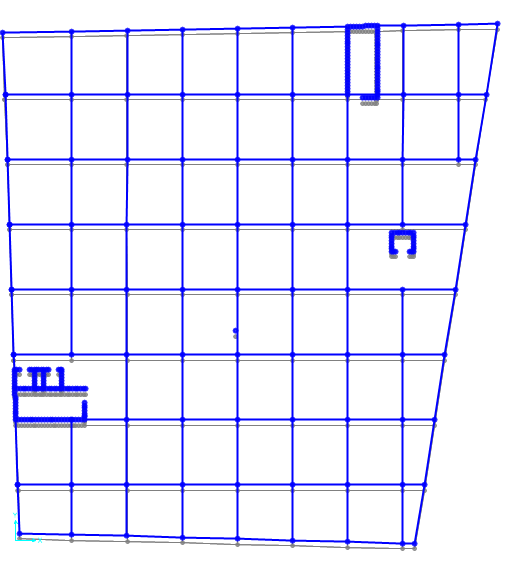
Risultato con la forza agente lungo y. 

In collaborazione con Jessica Sordi. 

Lo scopo dell'esercitazione è quello di verificare che l'impalcato sia in grado di resistere alle forze sismiche, è pertanto necessario accertarsi che il centro delle rigidezze coincida con quello delle masse.
Per fare ciò occorre trovare il centro delle masse a partire dalla geometria dell'edificio.

Si disegna dunque un piano tipo costituito da un telaio semplice di travi e pilastri e due nuclei portanti su Sap2000. 

Si procede dunque con l'assegnazione di sezioni e materiali degli elementi strutturali:

Travi 0,4x0,6 mq di materiale cemento armato C28/35
Pilastri 0,4x0,4 mq di materiale cemento armato C28/35
Nuclei portanti con setti di 0,5 m di spessore e di materiale cemento armato C28/35

Dopo aver definito sezioni e materiali, si procede imponendo i vincoli esterni (incastro) alla base degli elementi verticali, e i nodi rigidi in tutti i nodi superiori.

A questo punto si può procedere con il calcolo del centro delle masse:

Xc = (A3*x3  - A2*x2 - A1*x1)/(A3 - A2 - A1) = 25,34 m

Dove:
           A3 = 765 mq              x3 = 25,5 m
           A2 = 36 mq                x2 = 43,5 m
           A1 = 36 mq                x1 = 10,5 m

Yc = 7,5 m  è stato trovato geometricamente in quanto le tre coordinate della Y1, Y2, Y3, giacciono sullo stesso asse.

Si procede dunque con l'analisi, considerando solo il peso proprio della struttura (DEAD)

Ora è possibile esportare la tabella Excel attraverso la quale si può ricavare il peso totale della struttura che, in questo caso, è pari a 5122,485 KN.
Per calcolare la forza sismica moltiplico il peso della struttura per un coefficiente riduttivo pari a 0,2 considerando una zona a basso rischio sismico.

Per valutare l'azione della forza sismica, si concentra la forza ricavata nel centro di massa, una volta lungo l'asse x e una volta lungo l'asse y e si procede con l'analisi.

Forza sismica lungo asse X

Forza sismica lungo asse Y

Lungo l'asse Y è presente solamente traslazione, mentre lungo l' asse X è presente una rotazione, pertanto il centro delle rigidezze e il centro delle masse non sono coincidenti.
Per fare in modo che i due centri coincidano è necessario intervenire sulla struttura, o in termini di rigidezza o in termini di geometria.

In collaborazione con Paolo La Manna e Giulia Peria

Lo scopo dell'esercitazione è quello di verificare che l'impalcato sia in grado di resistere alle forze sismiche, è pertanto necessario accertarsi che il centro delle rigidezze coincida con quello delle masse.
Per fare ciò occorre trovare il centro delle masse a partire dalla geometria dell'edificio.

Si disegna dunque un piano tipo costituito da un telaio semplice di travi  e pilastri e due nuclei portanti su Sap2000. 

Si procede dunque con l'assegnazione di sezioni e materiali degli elementi strutturali:

Travi 0,4x0,6 mq di materiale cemento armato C28/35
Pilastri 0,4x0,4 mq di materiale cemento armato C28/35
Nuclei portanti con setti di 0,5 m di spessore e di materiale cemento armato C28/35

Dopo aver definito sezioni e materiali, si procede imponendo i vincoli esterni (incastro) alla base degli elementi verticali, e i nodi rigidi in tutti i nodi superiori.

A questo punto si può procedere con il calcolo del centro delle masse:

Xc = (A3*x3  - A2*x2 - A1*x1)/(A3 - A2 - A1) = 25,34 m

Dove:
           A3 = 765 mq              x3 = 25,5 m
           A2 = 36 mq                x2 = 43,5 m
           A1 = 36 mq                x1 = 10,5 m

Yc = 7,5 m  è stato trovato geometricamente in quanto le tre coordinate della Y1, Y2, Y3, giacciono sullo stesso asse.

Si procede dunque con l'analisi, considerando solo il peso proprio della struttura (DEAD)

Ora è possibile esportare la tabella Excel attraverso la quale si può ricavare il peso totale della struttura che, in questo caso, è pari a 5122,485 KN.
Per calcolare la forza sismica moltiplico il peso della struttura per un coefficiente riduttivo pari a 0,2 considerando una zona a basso rischio sismico.

Per valutare l'azione della forza sismica, si concentra la forza ricavata nel centro di massa, una volta lungo l'asse x e una volta lungo l'asse y e si procede con l'analisi.

Forza sismica lungo l'asse x:

Forza sismica lungo l'asse y:

Lungo l'asse Y è presente solamente traslazione, mentre lungo l' asse X è presente una rotazione, pertanto il centro delle rigidezze e il centro delle masse non sono coincidenti.
Per fare in modo che i due centri coincidano è necessario intervenire sulla struttura, o in termini di rigidezza o in termini di geometria.

In collaborazione con Siamak Kavoosi Far e Giulia Peria

Lo scopo dell'esercitazione è quello di verificare che l'impalcato sia in grado di resistere alle forze sismiche,
è pertanto necessario accertarsi che il centro delle rigidezze coincida con quello delle masse.
Per fare ciò occorre trovare il centro delle masse a partire dalla geometria dell'edificio.
Si disegna dunque un piano tipo costituito da un telaio semplice di travi e pilastri e due nuclei portanti su
Sap2000.

Si procede dunque con l'assegnazione di sezioni e materiali degli elementi strutturali:
Travi 0,4x0,6 mq di materiale cemento armato C28/35
Pilastri 0,4x0,4 mq di materiale cemento armato C28/35
Nuclei portanti con setti di 0,5 m di spessore e di materiale cemento armato C28/35
Dopo aver definito sezioni e materiali, si procede imponendo i vincoli esterni (incastro) alla base degli
elementi verticali, e i nodi rigidi in tutti i nodi superiori.

A questo punto si può procedere con il calcolo del centro delle masse:
Xc = (A3*x3 - A2*x2 - A1*x1)/(A3 - A2 - A1) = 25,34 m
Dove:
A3 = 765 mq x3 = 25,5 m
A2 = 36 mq x2 = 43,5 m
A1 = 36 mq x1 = 10,5 m
Yc = 7,5 m è stato trovato geometricamente in quanto le tre coordinate della Y1, Y2, Y3, giacciono sullo
stesso asse.

Si procede dunque con l'analisi, considerando solo il peso proprio della struttura (DEAD).

Ora è possibile esportare la tabella Excel attraverso la quale si può ricavare il peso totale della struttura che,
in questo caso, è pari a 5122,485 KN.
Per calcolare la forza sismica moltiplico il peso della struttura per un coefficiente riduttivo pari a 0,2
considerando una zona a basso rischio sismico.

Per valutare l'azione della forza sismica, si concentra la forza ricavata nel centro di massa, una volta lungo
l'asse x e una volta lungo l'asse y e si procede con l'analisi.

Forza sismica lungo l'asse x.

Forza sismica lungo l'asse y.

Lungo l'asse Y è presente solamente traslazione, mentre lungo l' asse X è presente una rotazione, pertanto il
centro delle rigidezze e il centro delle masse non sono coincidenti.
Per fare in modo che i due centri coincidano è necessario intervenire sulla struttura, o in termini di rigidezza
o in termini di geometria.

In collaborazione con Siamak Kavoosi Far e Paolo La Manna.

Prendendo in esame un piano tipo con relativi corpi scala/ascensore, individuiamo il centro delle rigidezze e facciamo in modo che coincida con il centro di massa; infatti in caso di sisma dobbiamo evitare le rotazioni relative della struttura, questo è possibile solo se i due centri (di massa e delle rigidezze) coincidono.

La struttura considerata è in cemento armato e sono presenti due gabbie scala/ascensore

Viene individuato in maniera geometrica il centro delle masse (baricentro)

Ora riportiamo la struttura su SAP2000 assegnando alle travi in C.A una sezione di 40 x 60 cm, ai pilastri una sezione di 50 x 50 cm ed ai setti delle gabbie scala uno spessore di 25 cm.

La struttura viene vincolata a “terra” tramite incastri ed a tutti i punti che sono alla stessa quota delle travi (compreso il centro di massa) viene assegnata la condizione di corpo rigido

Per calcolare la forza del sisma agente nelle direzioni X ed Y dobbiamo prima calcolare il peso proprio della struttura, lanciando l’analisi, lo ricaviamo tramite le tabelle delle reazioni vincolari per poi moltiplicarlo per 0.2 (coefficiente di riferimento per zone a basso rischio sismico come Roma)

La forza sismica viene applicata nel centro delle masse nelle direzioni X ed Y, lanciamo nuovamente l’analisi e verifichiamo gli spostamenti e le rotazioni relative tramite la vista sul piano XY

Spostamenti in X:

Spostamenti in Y:

La struttura non subisce rotazioni relative, quindi possiamo affermare che il centro delle masse corrisponde al centro delle rigidezze

GRUPPO: Pellegrini - Pasqualino - Rossi

Per un migliore funzionamento, una struttura deve essere in grado di resistere a forze sismiche: tali forze agiscono nel centro di massa dell’edificio percio’ e’ necessario che esso coincida con il centro delle rigidezze. Si puo’ rendere piu’ rigido un edificio grazie ai controventi, ovvero elementi verticali collegati tra loro orizzontalmente, che portano i carichi fino a terra. Il controvento piu’ semplice e’ il telaio piano, ma importanti sono anche pilastri e muri portanti di blocchi scala e ascensori, quindi e’ indispensabile tener conto della loro disposizione gia’ nelle prime fasi di progettazione.

Per l’esercitazione e’ stata presa in considerazione una struttura regolare abbastanza simmetrica costituita da un telaio in cemento armato C40/50 in travi e pilastri, con due blocchi scala e ascensori. 

Dopo aver disegnato la struttura su SAP, assegnando le sezioni ai pilastri 40X40, alle travi 40x60, ai muri delle scale e degli ascensori, si assegnano i vincoli di incastro alle basi dei vari elementi. 

Si crea anche un punto alla quota delle travi per rappresentare il centro di massa, posizionato nel centro geometrico trovato attraverso l’ intersezione delle due diagonali del rettangolo. 

Selezionando il punto del centro di massa e tutti i punti nel piano xy (alla stessa quota delle travi) e’ possibile assegnare la condizione di corpo rigido: in questo modo tutti i punti fanno parte dell’impalcato e non possono esserci spostamenti o rotazioni relative. 

Per verificare che il centro di massa e quello delle rigidezze concidano, o siano molto vicini, assumiamo le due condizioni peggiori in caso di eventi sismici, ovvero che la forza sismica sia applicata interamente lungo una direzione. Per conoscere il valore di carico della forza sismica e’ necessario prima calcolare il peso proprio dell’edificio, quindi si importa la tabella dei carichi su Excel e, sommando tutte le reazioni vincolari verticali, si ottiene il valore del peso proprio pari a 3403,454 kN. E’ quindi possibile definire il carico sismico come percentuale del peso proprio moltiplicandolo per 0,2 (coefficiente di riferimento per zone a basso rischio sismico come Roma).

A questo punto e’ possibile assegnare la forza sismica come carico concentrato orizzontale, in entrambe le direzioni X e Y, per verificare che la deformata sia una traslazione e non una rotazione.

Dai risultati delle analisi si possono notare comportamenti diversi quando la forza e’ applicata lungo direzioni diverse: con la forza direzionata lungo l’asse Y, infatti, la deformata e’ semplice traslazione mentre quando la forza e’ applicata lungo l’asse X e’ presente anche una rotazione, percio’ il centro delle rigidezze e’ lontano da quello delle masse. 

Procendendo per tentativi, spostando il centro delle masse (quindi anche il centro di applicazione delle forze sismiche) lungo l’asse y, si deve trovare una coordinata y tale che la rotazione sia nulla o trascurabile. In questo caso e’ stato necessario traslare il centro delle masse di 90 cm verso il basso.

Dato l'impalcato in figura, progettato in cemento armato, si procede all'individualizzazione del centro delle rigidezze.

Per trovare il centro delle rigidezze, bisogna trovare il centro di massa.

La struttura non ha una forma geometrica di base, quindi per conoscere il suo baricentro si deve suddividere in superfici più piccole con geometrie di cui si conosce la posizione del centro di massa.

Si disegna l'impalcato su SAP con il suo centro di massa e si assegnano le sezioni.

Trave: 30x50m

Pilastro: 35x35m

Si impone a tutti i nodi dell'impalcato e al centro di massa la condizione di nodo rigido, in modo che tutti i punti ruotano dello stesso valore.

Si procede ad una prima analisi per trovare il peso della struttura.

Per trovare la forza sismica, si dovrà moltiplicare il peso dell'impalcato per un coefficente di intensità sismica, dato dalla normativa.

In questo caso, si considera l'edificio costruito in una zona a basso rischio sismico, prendendo come coefficente 0,2.

Applico la forza sismica al centro di massa, nelle due direzioni principali x ed y.

Facendo l'analisi si nota come, lungo x e lungo y l'impalcato subisce delle rotazioni.

Lungo x Lungo y 

Ci si rende conto che il centro di massa ed il centro delle rigidezze non coincidono, quindi si sposta il centro di massa fino ad annullare la rotazione in entrambe le direzioni.

Il centro delle rigidezze dell'impalcato è distante dal centro di massa, in particolare ha coordinate:

In questo caso si procede all'avvicinamento del centro delle rigidezze al centro di massa, agendo o sulla geometria della struttura, per esempio rendendola più simmetrica spostando un setto o aumentando la rigidezza degli elementi nella parte meno rigida della struttura.

Il principale obiettivo dell’esercitazione consiste nella ricerca del centro delle rigidezze e nel confronto tra la posizione di quest’ultimo e del centro di massa della struttura in analisi.

La soluzione ideale sarebbe che i due centri coincidessero, o fossero il più vicino possibile in modo da evitare rotazioni relative in caso di sisma.

La nostra struttura è composta da un solaio in cemento armato e da pilastri in acciaio che reggono la struttura mediante il collegamento con una travatura reticolare posta all’ultimo piano dell’edificio, che poggia su due ulteriori strutture in cemento armato, contenenti le scale e gli ascensori dell’edificio.

Procedendo su SAP abbiamo disegnato la struttura di un piano: i pilastri, le travi e le superfici dei vani scala/ascensori. Assegnato loro le relative sezioni con i materiali e ad ogni punto di base il vincolo di incastro.

Successivamente è necessario trovare il centro delle masse. L’operazione è stata svolta secondo il metodo geometrico, ossia tracciando le diagonali dell’edificio, essendo un rettangolo, e ponendo nell’intersezione di quest’ultime, alla quota delle travi, un punto (centro delle masse).

Abbiamo selezionato tutti i punti alla quota delle travi ed il centro di massa ed abbiamo assegnato loro la condizione di corpo rigido, facendo si che questi appartengano all’impalcato e che si evitino rotazioni e spostamenti relativi.

Per calcolare il peso proprio della struttura abbiamo impostato una condizione di carico ed avviato l’analisi.

Successivamente abbiamo sommato tutte le reazioni verticali in modo da calcolarci il peso proprio della struttura: 5740,25 KN

Per poter definire i carichi sismici, come percentuale del peso proprio, applichiamo al peso proprio della struttura un coefficiente di 0,2 in quanto Roma è una zona a basso rischio. In tal modo otteniamo un valore di : 1148,05 KN

Trovate le forze possiamo assegnare 2 carichi, uno in direzione x e uno in direzione y, pari alla forza sismica, al centro delle masse.

Avviamo l’analisi prima per la direzione x.

Notiamo che l’impalcato non subisce rotazioni relative.

Successivamente avviamo l’analisi in direzione y.

Anche qui notiamo che l’impalcato non subisce rotazioni relative.

In conclusione, dato che il nostro edificio presenta solo traslazioni relative, possiamo affermare che la struttura è perfettamente equilibrato e che il centro delle masse coinciderà con il centro delle rigidezze.

Jlaria Volpi e Giulia Mellano

Il principale obiettivo dell’esercitazione consiste nella ricerca del centro delle rigidezze e nel confronto tra la posizione di quest’ultimo e del centro di massa della struttura in analisi.

La soluzione ideale sarebbe che i due centri coincidessero, o fossero il più vicino possibile in modo da evitare rotazioni relative in caso di sisma.

La nostra struttura è composta da un solaio in cemento armato e da pilastri in acciaio che reggono la struttura mediante il collegamento con una travatura reticolare posta all’ultimo piano dell’edificio, che poggia su due ulteriori strutture in cemento armato, contenenti le scale e gli ascensori dell’edificio.

Procedendo su SAP abbiamo disegnato la struttura di un piano: i pilastri, le travi e le superfici dei vani scala/ascensori. Assegnato loro le relative sezioni con i materiali e ad ogni punto di base il vincolo di incastro.

Successivamente è necessario trovare il centro delle masse. L’operazione è stata svolta secondo il metodo geometrico, ossia tracciando le diagonali dell’edificio, essendo un rettangolo, e ponendo nell’intersezione di quest’ultime, alla quota delle travi, un punto (centro delle masse).

Abbiamo selezionato tutti i punti alla quota delle travi ed il centro di massa ed abbiamo assegnato loro la condizione di corpo rigido, facendo si che questi appartengano all’impalcato e che si evitino rotazioni e spostamenti relativi.

Per calcolare il peso proprio della struttura abbiamo impostato una condizione di carico ed avviato l’analisi. Successivamente abbiamo sommato tutte le reazioni verticali in modo da calcolarci il peso proprio della struttura: 5740,25 KN

Per poter definire i carichi sismici, come percentuale del peso proprio, applichiamo al peso proprio della struttura un coefficiente di 0,2 in quanto Roma è una zona a basso rischio. In tal modo otteniamo un valore di : 1148,05 KN

Trovate le forze possiamo assegnare 2 carichi, uno in direzione x e uno in direzione y, pari alla forza sismica, al centro delle masse.

Avviamo l’analisi prima per la direzione x.

Notiamo che l’impalcato non subisce rotazioni relative.

Successivamente avviamo l’analisi in direzione y.

Anche qui notiamo che l’impalcato non subisce rotazioni relative.

In conclusione, dato che il nostro edificio presenta solo traslazioni relative, possiamo affermare che la struttura è perfettamente equilibrato e che il centro delle masse coinciderà con il centro delle rigidezze.

Di conseguenza i controventi posti sono sufficienti a dare una buona resistenza alle forze orizzontali, quali sisma e vento.

Giulia Mellano - Jlaria Volpi

CENTRO DELLE RIGIDEZZE

L’obiettivo dell’esercitazione è quello di studiare un piano dell’edificio di progetto e trovare la posizione del centro delle rigidezze e confrontarla con la posizione del centro delle masse.

Per avere un buon progetto strutturale i due centri devono essere coincidenti o più vicini possibile in modo che, in caso di sisma, vengano evitate rotazioni dell’impalcato.

Il piano è articolato secondo un telaio regolare in calcestruzzo armato nel quale si trovano due corpi scale/ascensore.

Su SAP definisco la griglia e disegno i pilastri, le travi e le superfici dei corpi scale/ascensori, attribuendo ad ogni elemento la corrispondente sezione in calcestruzzo armato. Assegno a tutti i punti di base dei pilastri e delle superfici il vincolo di incastro.

Traccio le diagonali della pianta e trovo, nell’intersezione, il centro geometrico che assumiamo come centro delle masse. In corrispondenza di questa intersezione inserisco un punto alla quota delle travi. Seleziono il punto e tutti gli altri punti che si trovano alla quota delle travi ed assegno la condizione di corpo rigido in modo che tutti i punti facciano parte dell’impalcato e che quest’ultimo non presenti al suo interno spostamenti e rotazioni relative.

Imposto una condizione di carico per calcolare il peso proprio dell’edificio ed effettuo l’analisi. Dalle tabelle di SAP ricavo tutte le reazioni vincolari verticali e sommandole ottengo il peso proprio, 3830,5 kN.

Definisco i carichi sismici come percentuali del peso proprio: essendo Roma una zona a basso rischio utilizzo il coefficiente 0,2 ed ottengo un valore di 766,1 kN.

Assegno 2 carichi concentrati orizzontali di valore 766,1 kN nel punto trovato come centro delle masse, uno in direzione x ed uno in direzione y: questi sono i carichi sismici.

Avvio l’analisi e osservo le deformate dell’impalcato prima per la forza in direzione x e poi per la forza in direzione y.

La deformata dovuta alla forza sismica lungo y non provoca rotazioni dell’impalcato.

La deformata dovuta alla forza sismica lungo x provoca una lieve rotazione dell’impalcato.

Spostando il centro delle masse verso il basso, quindi verso il centro di rotazione dell’impalcato, e riavviando l’analisi, cerco di trovare il punto in cui la rotazione si annulla. Questo punto è a soli 0,7 m dal centro delle masse.