Blog

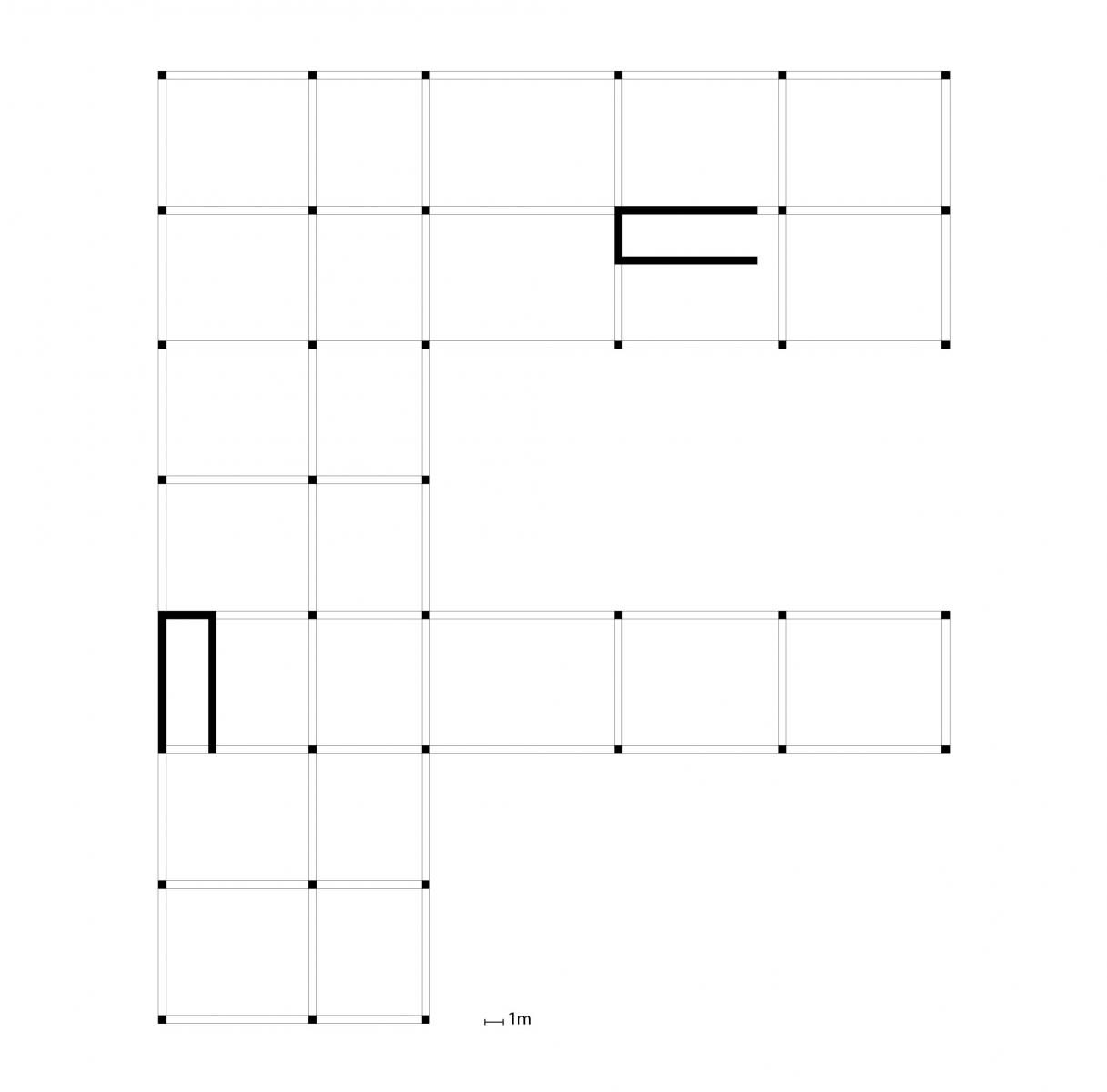
L’edificio è caratterizzato da una struttura a travi e pilastri in calcestruzzo armato. Sono presenti due vani scale/ascensore, formati da setti, anch’essi in calcestruzzo armato.

L’obiettivo dell’esercitazione è quello di individuare la posizione del centro delle masse e di quello delle rigidezze, sottoponendo il telaio all’azione di una forza sismica. Il confronto tra le coordinate dei due centri permetterà di verificare se la distanza tra questi sarà accettabile, oppure se questa debba essere ridotta, attraverso modifiche dell’impianto strutturale.

Per calcolare il centro delle masse si suddivide la struttura nei rettangoli 1,2 e 3 e si individuano geometricamente i relativi baricentri C₁, C₂ e C₃ e le aree A₁, A₂ e A₃.

C₁ : (6,8375; 24,5)

C₂ : (21,175; 42)

C₃ : (21,175; 17,5)

A₁ = 670,075

A₂ = 378

A₃ = 189

Si può quindi procedere con l’individuazione delle coordinate del centro delle masse dell’intera struttura.

x_c = (A₁ x₁ + A₂ x₂ + A₃ x₃) / (A₁ + A₂ + A₃)

x_c = (670,075 x 6,8375 + 378 x 21,175 + 189 x 21,175) / (670,075 + 378 + 189) = 13,4089

y_c = (A₁ y₁ + A₂ y₂ + A₃ y₃) / (A₁ + A₂ + A₃)

y_c = (670,075 x 24,5 + 378 x 42 + 189 x 17,5) / (670,075 + 378 + 189) = 28,7778

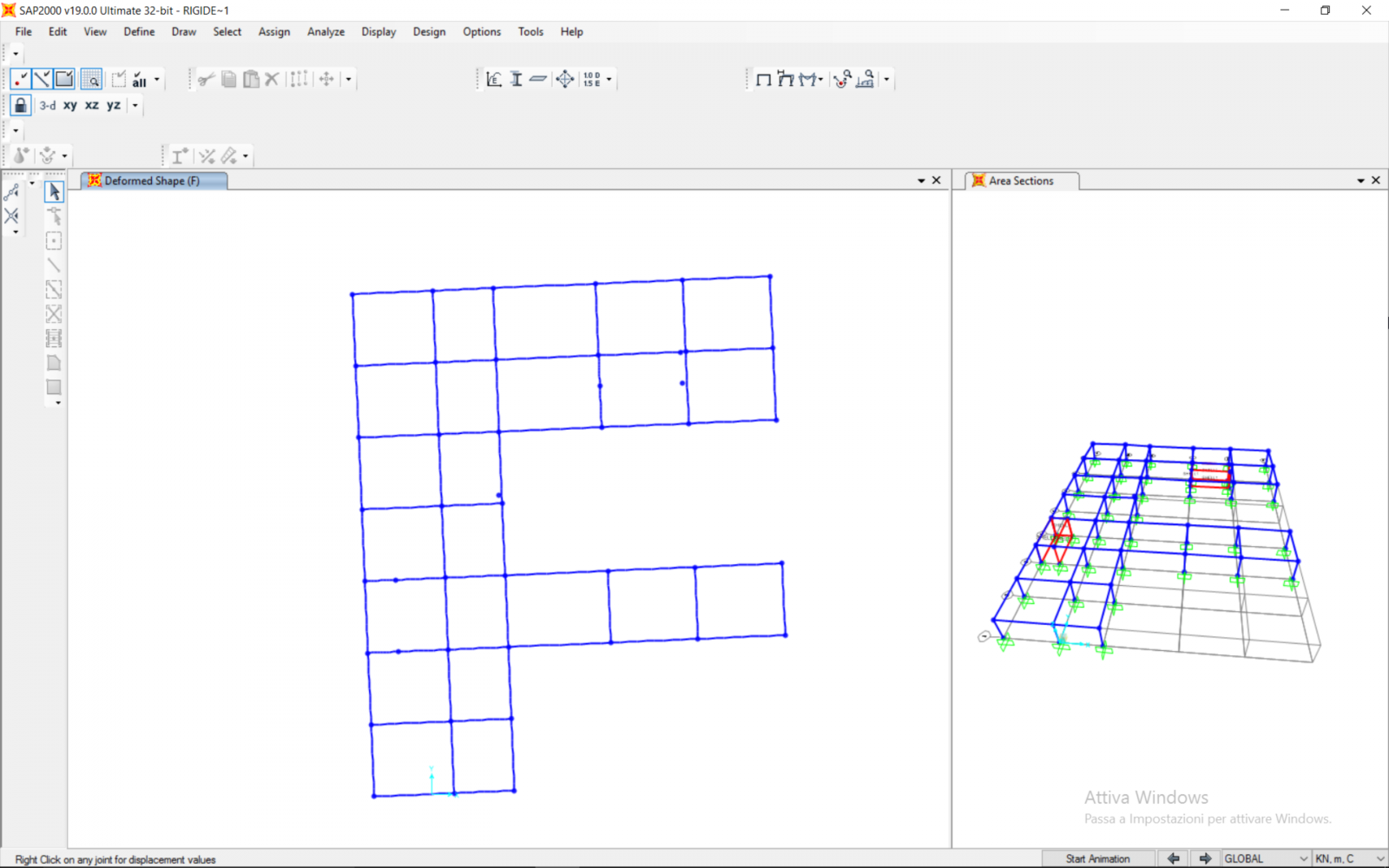
Si impone quindi la condizione di nodo rigido a tutti i punti dell’impalcato, escludendo i pilastri, e al centro delle masse precedentemente individuato.

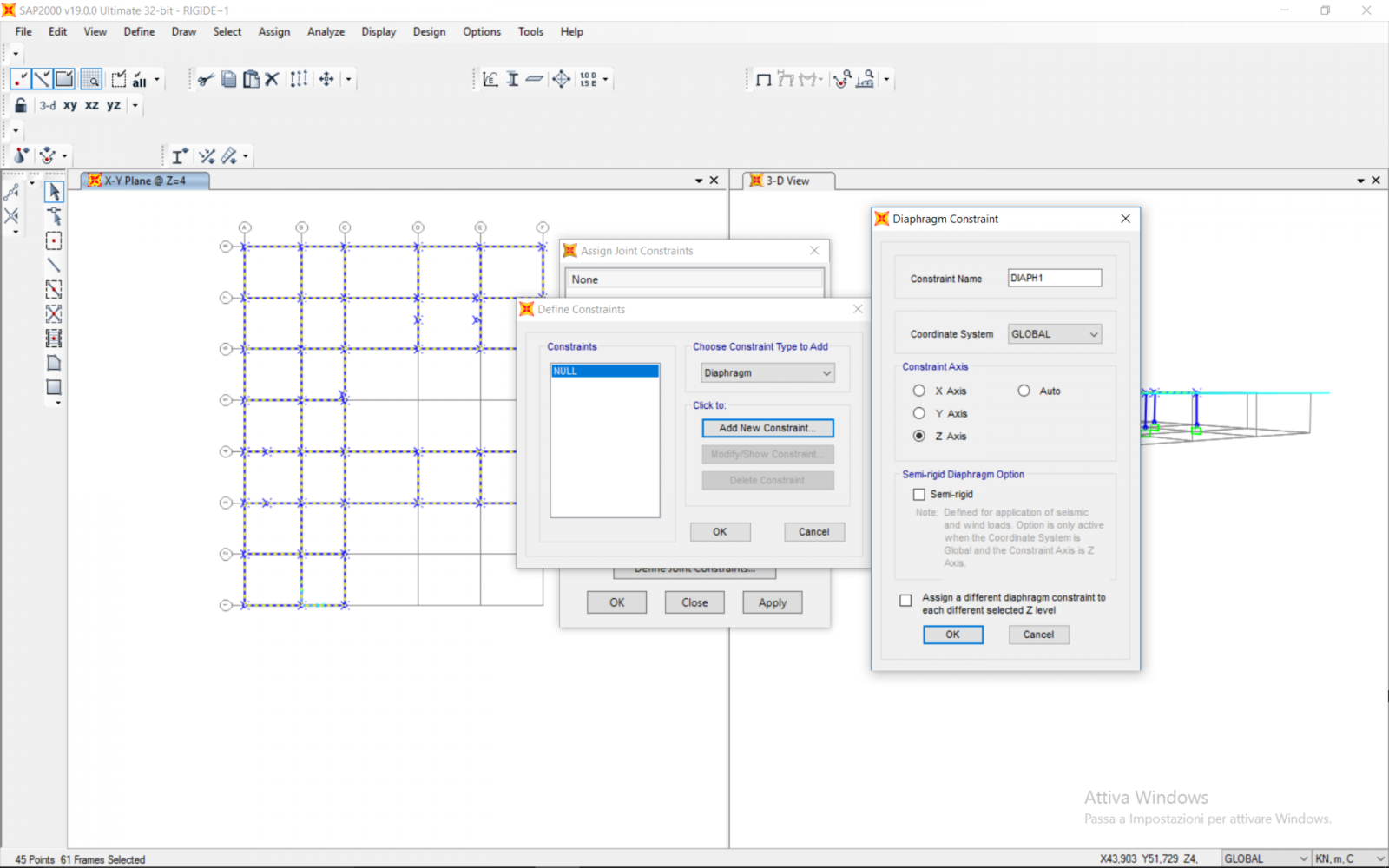
Per calcolare la forza sismica si ricava il peso proprio dell’intera struttura e lo si moltiplica per il coefficiente 0,2.

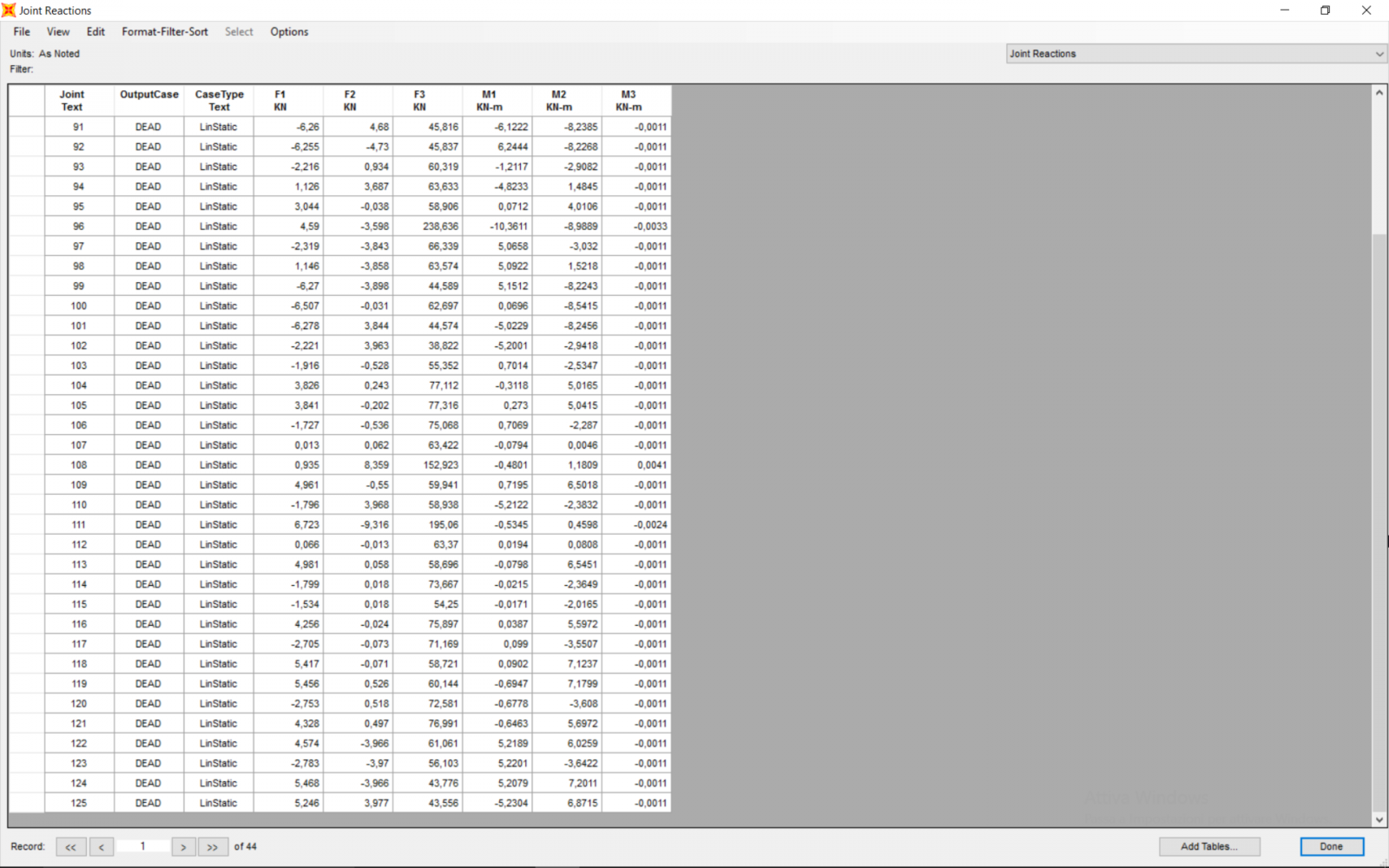
P = 2518,884kN

F = P x 0,2

F = 2518,884kN  x 0,2 = 503,7768kN

La forza sismica individuata deve essere applicata nel punto corrispondente al centro delle masse nelle direzioni x e y. 

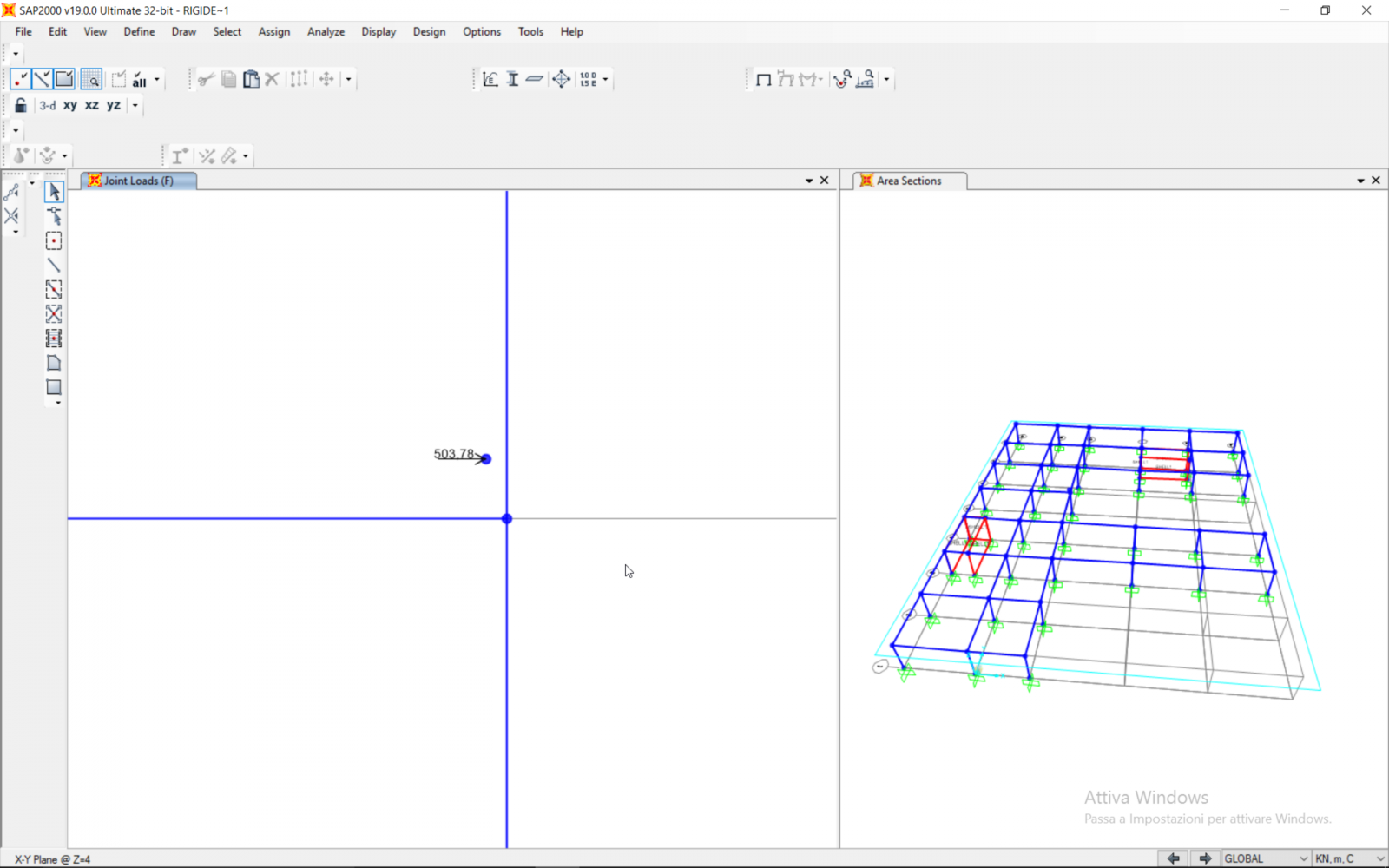
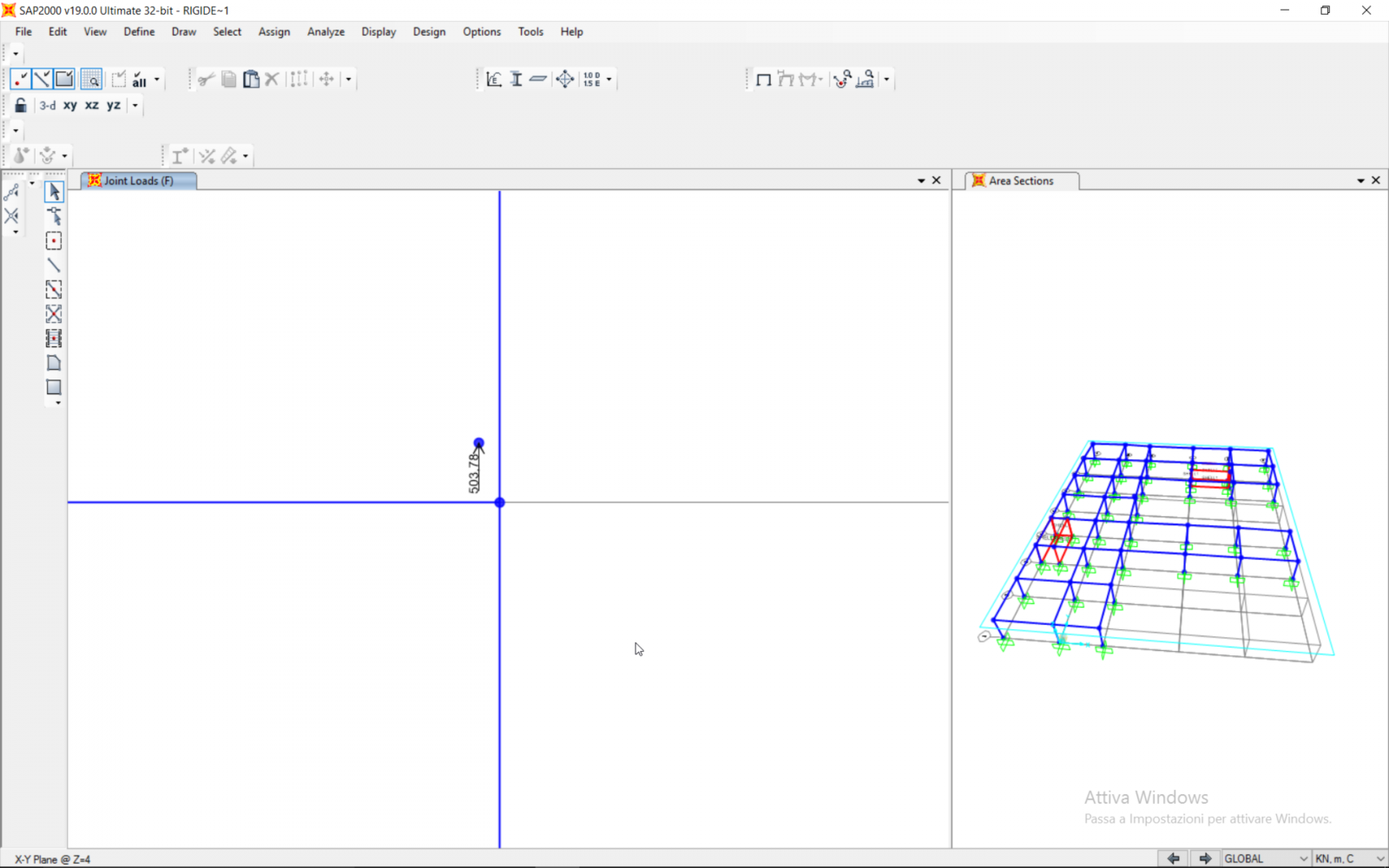
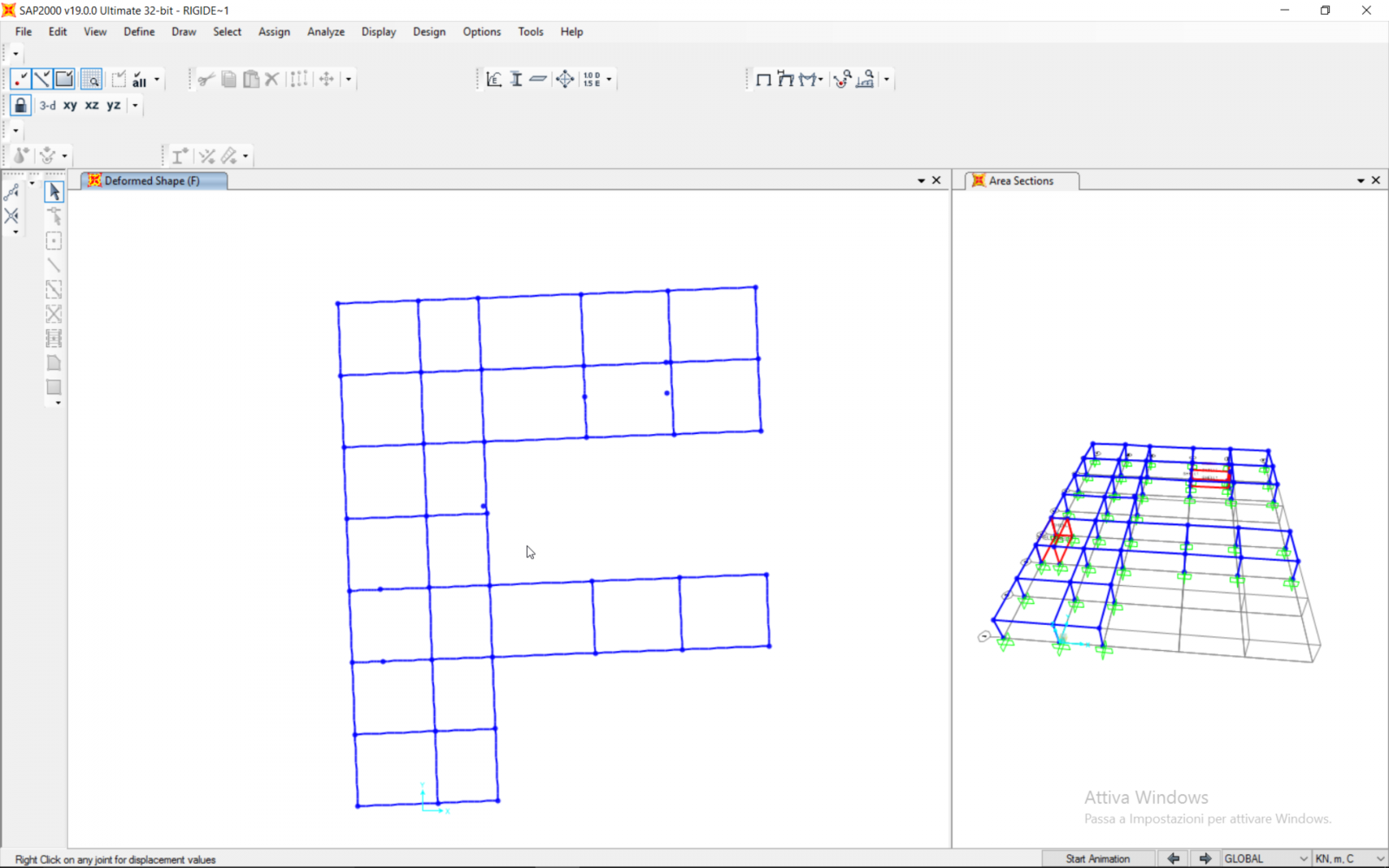
In entrambi i casi si verifica una rotazione in senso antiorario.

Si procede con lo spostamento del centro delle masse e con la ripetizione dell’analisi, finché si giunge ad uno stato di rotazione nulla. Si troveranno così le coordinate del centro delle rigidezze.

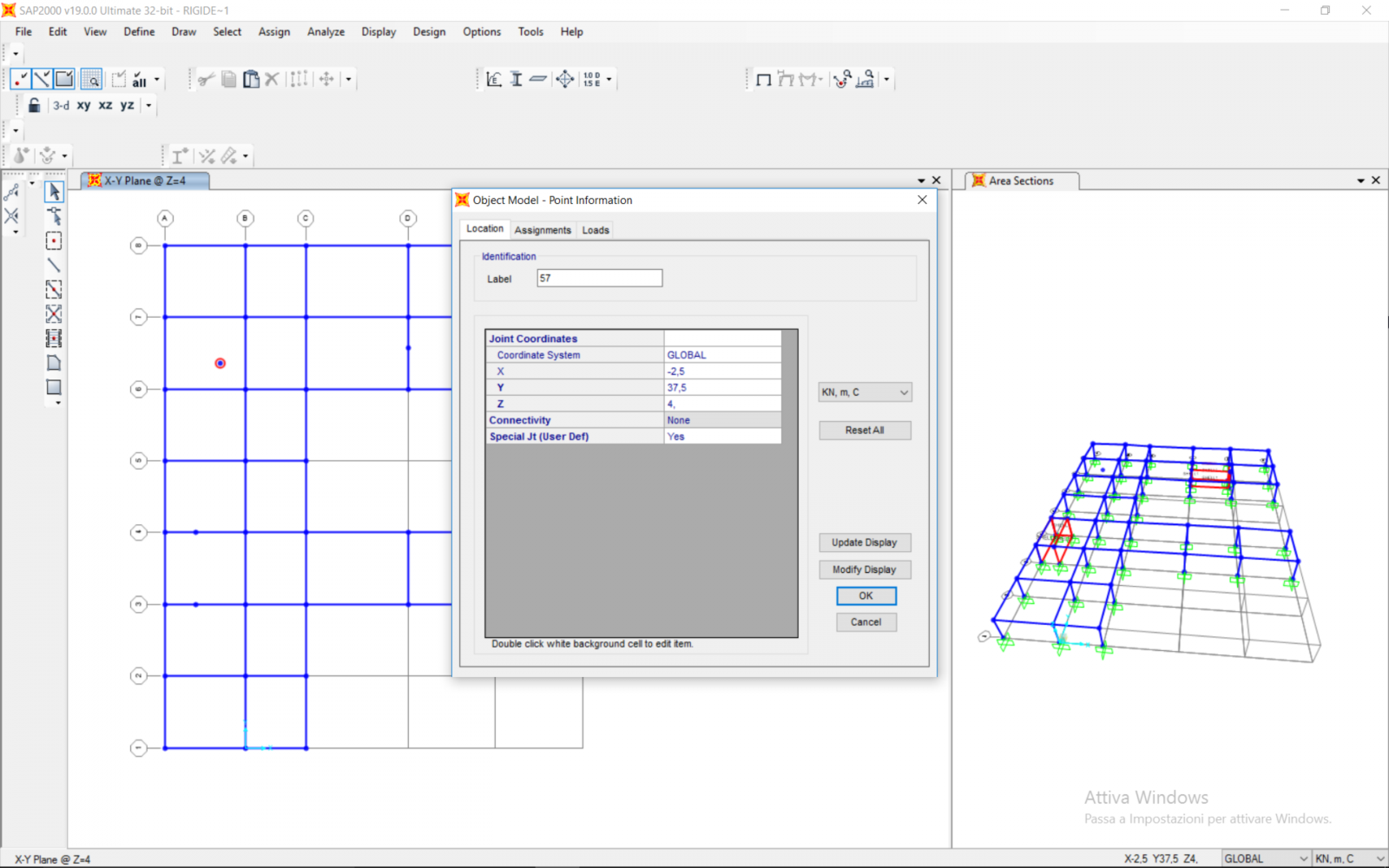
Il centro delle masse e il centro delle rigidezze risultano distanti. Bisognerà dunque agire sulla geometria della struttura, oppure aumentare la rigidezza di determinate porzioni del telaio.

ESERCITAZIONE 03_Svolta con Antonella Peschiera Ghiggo.

L’esercitazione svolta ha il compito di confrontare la posizione del centro di massa della struttura del progetto con quella del centro delle rigidezze, per verificare che la progettazione strutturale sia corretta in quanto questi due punti dovrebbero coincidere; la loro coincidenza garantisce alla struttura di non ruotare.

La struttura presa in esame è il seguente impalcato. 

E’ un  telaio composto da pilastri e travi in cemento armato; le travi sono 40x30 cm, i pilastri sono di due tipi: 30x30cm e 30x60cm dove la luce è maggiore. La presenza del blocco  in cemento armato al piano terra è dovuta alla presenza di una seconda struttura ai piani superiori dove per il volume degli uffici si è utilizzata una reticolare spaziale; questa seconda struttura al piano terra è comunque collegata alla prima con giunti che non sono però strutturali.

Abbiamo modellato l’ impalcato su SAP attribuendo tutte le caratteristiche del caso; calcolato il centro delle masse suddividendo tutto in tre aree distinte:

A₁= 515 m²

A₂= 49 m²

A₃= 169 m²

E trovati i tre centri di ciascuna area di coordinate:

A¹ (15;9)

A² (33;15)

A³ (42;9)

Il centro delle masse avrà coordinate C (X;Y) con

X= (A₁X_A1+ A₂X_A2+ A₃X_A3)/(A₁+A₂+A₃)

Y= (A₁Y_A1+ A₂Y_A2+ A₃Y_A3)/(A₁+A₂+A₃).

Una volta trovato il centro delle masse lo disegno su Sap alla stessa quota delle travi.

Viene poi assegnato il vincolo interno DIAPHRAM, in modo che tutti i punti si muovano contemporaneamente e facciano parte dello stesso impalcato.

Si passa al calcolo del peso proprio della struttura su SAP che si ottiene dalle tabelle di valori ottenute dall'analisi; definiamo secondo la normativa il valore della forza sismica in funzione dell’ area di progettazione . Per Roma, essendo il rischio sismico basso, il valore equivale al 20% del peso proprio e lo calcoliamo. 

Il valore trovato viene applicato come forza concentrata nel centro delle masse C, prima in direzione x e poi in direzione y.

Assegno una forza Fx al centro delle masse.

Posso osservare come la struttura subisca non solo una traslazione ma anche una rotazione oraria.

Definisco ora la forza sismica lungo l'asse y come Fy.

Osservo come anche in questo caso la struttura non solo subisca una traslazione lungo l'asse y ma anche una rotazione.

Possiamo dedurre che centro delle masse e centro delle rigidezze non coincidono dunque bisognerà ridisegnare l'impalcato.

ESERCITAZIONE 3_Svolta con Alice Grondona

L’esercitazione svolta ha il compito di confrontare la posizione del centro di massa della struttura del progetto con quella del centro delle rigidezze, per verificare che la progettazione strutturale sia corretta in quanto questi due punti dovrebbero coincidere; la loro coincidenza garantisce alla struttura di non ruotare.

La struttura presa in esame è il seguente impalcato.

E’ un  telaio composto da pilastri e travi in cemento armato; le travi sono 40x30 cm, i pilastri sono di due tipi: 30x30cm e 30x60cm dove la luce è maggiore. La presenza del blocco  in cemento armato al piano terra è dovuta alla presenza di una seconda struttura ai piani superiori dove per il volume degli uffici si è utilizzata una reticolare spaziale; questa seconda struttura al piano terra è comunque collegata alla prima con giunti che non sono però strutturali.

Abbiamo modellato l’ impalcato su SAP attribuendo tutte le caratteristiche del caso; calcolato il centro delle masse suddividendo tutto in tre aree distinte:

A₁= 515 m²

A₂= 49 m²

A₃= 169 m²

E trovati i tre centri di ciascuna area di coordinate:

A¹ (15;9)

A² (33;15)

A³ (42;9)

Il centro delle masse avrà coordinate C (X;Y) con

X= (A₁X_A1+ A₂X_A2+ A₃X_A3)/(A₁+A₂+A₃)

Y= (A₁Y_A1+ A₂Y_A2+ A₃Y_A3)/(A₁+A₂+A₃).

Una volta trovato il centro delle masse lo disegno su Sap alla stessa quota delle travi.

Viene poi assegnato il vincolo interno DIAPHRAM, in modo che tutti i punti si muovano contemporaneamente e facciano parte dello stesso impalcato.

Si passa al calcolo del peso proprio della struttura su SAP che si ottiene dalle tabelle di valori ottenute dall'analisi; definiamo secondo la normativa il valore della forza sismica in funzione dell’ area di progettazione . Per Roma, essendo il rischio sismico basso, il valore equivale al 20% del peso proprio e lo calcoliamo.

Il valore trovato viene applicato come forza concentrata nel centro delle masse C, prima in direzione x e poi in direzione y.

Assegno una forza Fx al centro delle masse

Posso osservare come la struttura subisca non solo una traslazione ma anche una rotazione oraria.

Definisco ora la forza sismica lungo l'asse y come Fy

Osservo come anche in questo caso la struttura non solo subisca una traslazione lungo l'asse y ma anche una rotazione.

Possiamo dedurre che centro delle masse e centro delle rigidezze non coincidono dunque bisognerà ridisegnare l'impalcato.

L'esercitazione è stata in .jpeg perchè il blog non salva gli avanzamenti, ma solo una parte dell'esercitazione caricata.

Esercitazione svolta con Francesco Petrelli.

NOTA: Ho dovuto caricare l'esercitazione in formato jpeg, perché il blog non salva gli avanzamenti del lavoro, ma salva solo una parte dell'esercitazione caricata.

Esercitazione svolta con Susanna Terreri.

Per questa esercitazione dobbiamo trovare il centro delle rigidezze e verificare che sia coincidente o vicino al centro delle masse, così da evitare rotazioni della struttura in caso di sisma.

Abbiamo preso in considerazione un piano dell'edificio. Il telaio è in cemento armato, con una griglia strutturale di 6m per 5m.

Dopo aver disegnato la griglia possiamo inserire i setti (sempre in cemento armato) in cui andranno posizionati i corpi scala.

Poi assegnamo le sezioni alle travi ed ai pilastri, troviamo il centro delle masse e assegniamo la condizione di corpo rigido a tutti i punti che si trovano sulla quota delle travi (compreso il centro delle masse).

A questo punto avviamo l'analisi per ricavare il peso proprio della struttura, tramite le tabelle. Si moltiplica il peso per il coefficiente 0,2 (Roma è a basso rischio sismico).

 Assegniamo un carico concentrato del valore trovato in direzione X e poi in direzione Y e avviamo di nuovo l'analisi e verifichiamo che ci sia solo una traslazione e non una rotazione.

In conclusione il nostro centro delle masse coincide con il centro delle rigidezze.

La terza esercitazione consiste nel trovare il centro delle rigidezze e verificare che coincida, o sia abbastanza vicino al centro delle masse, così da avere solo traslazione e non rotazione della struttura in caso di sisma.  

Consideriamo solo un piano dell'edificio. La nostra struttura ha un telaio in cemento armato di 6m per 5m.  

Una volta disegnata la griglia strutturale mettiamo i vincoli e assegniamo la sezione di travi e pilastri, infine inseriamo i setti (sempre in cemento armato) con i corpi scala.  

Troviamo il baricentro e assegniamo la condizione di corpo rigido ai punti che si trovano sulla quota delle travi (compreso il centro delle masse).

Avviamo l'analisi e ricaviamo il peso proprio della struttura, tramite le tabelle. Lo moltiplichiamo per 0,2 dato che Roma è a basso rischio sismico. 

Assegniamo un carico concentrato del valore trovato in direzione X e poi in direzione Y.  Infine avviamo l'analisi e verifichiamo che non ci sia una rotazione. In conclusione il nostro centro delle masse coincide con il centro delle rigidezze.  

L'esercitazione consiste nell'analisi del telaio di un piano tipo dell'edificio progettato, nell'individuazione del centro di massa e del centro delle rigidezze. Per una buona progettazione il centro di massa e quello delle rigidezze devono essere più vicini possibile, in modo che sotto azione di forze orizzontali si evitino  rotazioni e traslazioni dell'impalcato. Il fine dell'esercitazione è quello di garantire una resistenza strutturale dell'impalcato sottoposto all'azione di una forza sismica.

La struttura utilizzata per il progetto è una travatura reticolare spaziale, quindi sono stati rappresentati soltanto gli elementi strutturali, quali travi e setti murari.

Per determinare la posizione del centro di massa suddivido la struttura in tre rettangoli e vado a definire le coordinate x e y di ogni area.

C1_ (9-24)                    A1_ 864

C2_(9-6)                      A2_216

C3_(7,5-21)                 A3_630

Xc= (A1 X1+A2 X2+A3 X3) / (A1+A2+A3) = 8,44

Yc=(A1 Y1+A2 Y2+A3 Y3) / (A1+A2+A3) = 20,62            

Quindi le coordinate del centro di massa saranno:           X= (8,44 - 20,62)

Disegno quindi il centro di massa come un punto sulla pianta strutturale.

Disegnato il centro di massa assegno a tutti gli elementi la condizione di nodo rigido, questo affinché non si verifichino spostamenti e rotazioni relative.
Per calcolare il peso proprio dell'impalcato eseguo l'analisi considerando soltanto il peso proprio e verificando i valori sulle tabelle.

        Dalla tabella ricavo il peso proprio sommando tutti i valori della voce F3.

Il peso proprio dell'impalcato risulta   Pp= 4438,202 KN

La normativa mi fornisce il coefficiente di sicurezza da applicare alla struttura che è pari al 20% del peso dell'impalcato e che varia a seconda della zona in cui viene studiato il progetto.

quindi: 4438,202 x 0,2= 887,64              

Definisco ora idue casi di carico Fx ed Fy, ovvero le due componenti della forza orizzontale che andrò ad applicare nelle due differenti direzioni sul centro di massa. Una volta assegnati i carichi avvio l'analisi senza considerare il peso proprio e verifico la posizione del centro delle rigidezze.

   COMPONENTE X_         

COMPONENTE Y_

Dall'analisi risulta che il centro delle rigidezza non è coincidente con quello di massa.

Per un corretto comportamento dell'impalcato bisegerà far coincidere i due punti, effettuando delle modifiche sulla posizione degli elementi strutturali.