Portale di Meccanica

In questa seconda esercitazione analizzerò una struttura reticolare spaziale. Questo è un sistema costruttivo molto usato per realizzare coperture di luci importanti, poichè permette di realizzare grandi campate per mezzo di un numero limitato di supporti verticali, poichè la struttura trae forza dalla rigidità del telaio triangolare.

Utilizzo il software SAP 2000 per realizzare il modello su cui lavorare. I passaggi che bisogna seguire sono i seguenti:
1. Modellazione
2. Caratterizzazione: materiale e carichi
3. Analisi
4. Dimensionamento.

1. Modellazione
Come modulo base scelgo quello piramidale. Inizio con il disegnare quindi una piramide con il vertice verso il basso, inscritta all’interno di un cubo di lato l=1,5m. La griglia di riferimento usata è:
x= 5
y= 6
z= 2

2. Caratterizzazione: materiale e carichi
Per evitare di aver disegnato delle aste doppie seleziono tutti gli elementi e vado su Edit_Merge duplicate, in modo da unirli ed evitare anomalie nel corso delle analisi. Un ulteriore attenzione riguarda invece la tolleranza dei nodi; essendo la struttura costruita copiando un’unica base correggo la tolleranza. Seleziono tutta la struttura e vado su Edit_Edit points_Merge joints e confermo il valore pari a 0,1. Ultimo passaggio è quello di aggiungere i vincoli sui 4 appoggi (cerniere).

Dato che la struttura reticolare lavora a sforza normale di trazione o compressione, bisogna svincolare i nodi al momento. Seleziono quindi tutta la struttura e poi vado su Assign_Frame_Release/Partial Fixity e pongo il doppio flag al Moment (2-2) e Moment (3-3).

Procedo con la caratterizzazione di questo definendo un materiale (tubolare in acciaio) ed assegnando ai nodi superiori una forza F pari ad F=-80 KN. Seleziono quindi i nodi superiori e poi vado su Assign_Joints Load, scelgo la forza F che ho definito precedentemente ed imposto z=-80 KN

3. Analisi
Dopo aver impostato e caratterizzato la struttura faccio partire l’analisi lineare statica che ha come oggetto la forza F generata precedentemente.

Per conferma controllo la sollecitazione N,T,M. Quest’ultimi due non sono presenti, vista la caratterizzazione fatta prima, mentre il risultato dello sforzo assiale è qui riportato. Esporto tutti i dati relativi alla mia struttura su di un foglio di calcolo elettronico Excel per poter procedere con il dimensionamento delle aste.

4. Dimensionamento

Dopo aver ordinato il foglio Excel esportato, avrò per ogni singola asta il valore dello sforzo normale di trazione (+) o compressione (-).
Avendo un modulo piramidale devo considerarlo composto da aste di lunghezza diversa:
- Aste orizzontali = 1,5 m
- Aste diagonali = 2,12 m
- Aste inclinate = 1,67 m
Adesso ho tutti i ati per poter compilare i due fogli Excel.

4.1 Trazione  

Compilo il foglio riportando i valori di N di trazione (+) ottenuti precedentemente; aggiungo le caratteristiche dell'acciaio di carpenteria scelto (f_yk=235 MPa) ed il coefficiente γ_m=1,05. In questo modo per ogni singola asta ottengo una A_min (cm²⁾, risultato di A_min=(N*10)/f_yd. Procedo con il dimensionamento delle aste scegliendo i profili in base a questo valore ingegnerizzandolo.

4.2 Compressione

Per la compressione (+) la prima parte da compilare è identica alla precedente, ma devo considerare il fenomeno di instabilità, che non riguardava invece la trazione. Aggiungo quindi i valori di E=210000 MPa, beta=1, e la lunghezza dell'asta considerata. Ottengo così tre dati fondamentali per il dimensionamento:
-Lambda= pi*sqrt(E/f_cd)
-Rho_min= (l₀*100)/Lambda
-I_min= E*(Rho_min)².

Inizio il dimensionamento delle aste in base ai valori di Rho_min e I_min. Una verifica ulteriore di cui devo tenere conto è la Lambda finale che deve risultare <200.

 

Progetto di una trave in CEMENTO ARMATO,LEGNO ed ACCIAIO:

Una volta disegnata la mia carpenteria, prendo in considerazione la trave più sollecitata, ovvero quella centrale.

Prendendo in considerazione 1mq di solaio vado a calcolarmi tutti i carichi agenti sulla trave diversificandoli in carichi strutturali (qs) , carichi permanenti (qp) e carichi accidentali (qa). Per fare ciò io devo studiare e capire quanto volume ho in questo mq di ogni materiale e poi moltiplicare tale dato per il relativo peso specifico

Andiamo perciò a progettare una trave in CEMENTO ARMATO

 

Carichi strutturali : PIGNATTE,TRAVETTI, SOLETTA COLLABORANTE

PIGNATTE 9,1kg/mq x 8 = 0,73KN/mq  

SOLETTA COLLABORANTE CLS 24 KN/mc x ( 0,04m x 1m x 1m ) =0,96 KN/mq

TRAVETTI 24KN/mc x 2 (0,1m x 1m x 0,16m) =0,77 KN/mq 8 PIGNATTE 9 kg/mq x 8 = 0,77KN/mq

Carichi permanenti : PAVIMENTO GRANITO, MALTA D'ALLETTAMENTO,ISOLANTE ACUSTICO,MASSETTO,INTONACO

PAVIMENTO 27 KN/mc x ( 0.02 x 1m x 1m ) = 0,54 KN/mq

MALTA DI ALLETTAMENTO 770 1.400 Kg/mc x (0,03m x 1m x 1m ) = 0,42 KN/mq

ISOLANTE LANA DI VETRO 0,2 KN/mc x (0,06m x 1m x 1m ) = 0,012 KN/mq

MASSETTO ALLEGERITO 18KN/mc x (0,04m x 1m x 1m) = 0,72KN/mq

INTONACO 18KN/mc x (0,01m x 1m x 1m) = 0,18 KN/mq

IMPIANTI e TRAMEZZI 1,5 KN/mq (tale voce viene aggiunta per un'ulteriore sicurezza -

-dalla normativa)

 

Carichi accidentali : Ipotizzando un uso residenziale del mio progetto, il carico sarà di 2 KN/mq dato dalla normativa

qs = 2,46 KN/mq                                      qp = 3,37 KN/mq qa                                = 2 KN/mq

 

Adesso andando ad inserire tutti i carichi nella tabella EXEL si andrà a calcolare il carico ultimo (qu) cioè la somma di tutti i carichi moltiplicati per i propri coefficienti di sicurezza ed infine moltiplicati per l'interasse trovando intal modo il carico lineare distribuito sulla trave.

Lo scopo dei coefficienti di sicurezza è quello di aumentare il carico ultimo cosicchè la progettazione della trave risulti sovradimensionata e quindi più sicura.

 

qu = ( qs x 1,3 + qp x 1,5 + qa x 1,5 ) x 3 = 33.76 KN/m

 

Una volta trovato il mio carico qu che andrà a pesare sulla mia trave, posso trovare il Momento massimo che sarà pari a 151.92

 

FASE PROGETTUALE

 

Per il dimensionamento della mia trave scelgo

Acciaio S450 con Fyk = 450 Mpa

Cls di categoria "alte prestazioni" = C 55/67

 

Avendo scelto il materiale e quindi le forze caratteristiche è possibile ricavare la tensione di progetto sia dell'acciaio che del cemento armato.

Successivamente troviamo l'altezza utile e quindi l'altezza minima (per trovare l'altezza utile sarà necessario ricavare tramite le apposite formule i valori di “r” e di “beta”

 

Scegliendo arbitrariamente la base della nostra trave di 30 cm e un copriferro di 5cm, si ottiene un Hmin = 35,62 cm che consiste nel valore minimo dell'altezza della trave, lo vado ad ingegnerizzare cioè ad aumentare il suo valore.

Ipotizzo un altezza ultima della mia trave pari a H= 50cm

Il profilo della mia trave sarà di 30cm x 50cm ed è VERIFICATO

 

Andiamo a progettare una trave in LEGNO:

Carichi strutturali: TRAVETTI e TAVOLATO

TRAVETTI ( castagno) 10KN/mc x 2( 0,1m x 0,015 ) = 0,30 KN/mq

TAVOLATO( castagno) 6KN/mc x (0,025m x 1m x 1m) = 0.15 KN/mq

 

Carichi permanenti : PARQUET , MALTA ALLETTAMENTO, MASSETTO CEMENTIZIO

 

PARQUET(acero) 6KN/mc x (0,025m x 1m x 1m ) = 0,15 KN/mq

MALTA ALLETTAMENTO 18 KN/mc x ( 0,03m x 1m x 1m) = 0,54 KN/ mq

ISOLANTE (lana di legno) 0.18 KN/mc x (0.04m x 1m x 1m) = 0.0072

MASSETTO ALLEGERITO 18 KN/mc x (0,04m x 1m x1m ) = 0.72 KN/mq

IMPIANTI e TRAMEZZI +1,5 KN/mq

 

Carichi accidentali : Ipotizzando un uso residenziale del mio progetto, il carico sarà di 2 KN/mq dato dalla normativa

 

 

qs = 0,45 KN/mq qp = 2,92 KN/mq qa = 2 KN/mq

 

qu = ( qs x 1,3 + qp x 1,5 + qa x 1,5 ) x 3 = 23.9KN/mq

 

Una volta trovato il mio carico qu che andrà a pesare sulla mia trave, posso trovare il Momento massimo che sarà pari a 107,53 KNm .

 

FASE PROGETTUALE

Per il progetto del solaio scelgo un legno lamellare GL24h che ha una resistenza a flessione di fmk= 24Mpa

Ora vado ad impostare una possibile base della mia trave pari a 30cm che porterà tramite il calcolo un altezza minima della trave. Ingegnerizzando l'Hmin arriverò alla mia altezza ultima. H= 50cm

Il profilo della mia trave sarà di 30cmx50cm

 

FASE DI VERIFICA

Nella fase di verifica dovrò andare a considerare anche il peso proprio della trave appena progettata che andrò ad inserire nei carichi strutturali.

TRAVE: 10KN/mc x( 1m x 0,50m x 0,30m) = 1,5 KN/mq

 

il nuovo carico qu prevede una trave di Hmin= 45.32cm quindi il mio profilo è VERIFICATO in quanto avevo considerato un altezza H pari a 50cm.

 

 

 

Andiamo a progettare una trave in ACCIAIO

 

Carichi strutturali:TRAVETTO,MASSETTO e LAMIERA GRECATA

TRAVETTO(IPE100) 78,5KN/mc x (0,001 mq x 1m) = 0.078

LAMIERA GRECATA spessore della lamiera 5mm = 0,4 KN/mq (tabellato dalla casa produttrice)

MASSETTO ALLEGERITO 24KN/mc x (0,09m x 1m x 1m) = 2.16 KN/mq

Carichi permanenti: PAVIMENTO , MALTA ALLETTAMENTO, ISOLANTE

PAVIMENTO (granito) 30KN/mq x (0.02 x 1m x 1m) = 0,6 KN/mq

MALTA ALLETTAMENTO 18KN/mq x (0,03m x 1m x 1m) = 0,54 KN/mq

ISOLANTE (lana di roccia) 90kg/mc x (0,04m x 1m x 1m) = 0,36KN/mq

IMPIANTI e TRAMEZZI +1,5 KN/mq

 

 

Carichi accidentali: Ipotizzando un uso residenziale del mio progetto, il carico sarà di 2 KN/mq dato dalla normativa

 

qs = 2,64 KN/mq qp = 3 KN/mq qa = 2 KN/mq

 

qu = ( qs x 1,3 + qp x 1,5 + qa x 1,5 ) x 3 = 30,69 KN/mq

 

Una volta trovato il mio carico qu che andrà a pesare sulla mia trave, posso trovare il Momento massimo che sarà pari a 138,11 KNm .

 

FASE PROGETTUALE

Scelgo l'acciaio Fe 430/S275 che avrà una tensione di snervamento pari a 275Mpa e otterrò un modulo di resistenza Wxmin pari a 563,49 cmc che equivale ad un IPE 300 perchè considero un Wx pari a 628.36 cmc.

 

FASE DI VERIFICA

Nella fase di verifica dovrò andare a considerare anche il peso proprio della trave appena progettata che andrò ad inserire nei carichi strutturali.

Peso trave IPE 300 = 0,005381 mc x 78 KN/mc = 0,42 KN/m

 

Andando a considerare anche il peso della trave progettata, il Wxmin equivale a 591.64 cmc, e non superando il valore preso di Wx scelto posso dire che la sezione è VERIFICATA 

 

 

Per questa consegna ho deciso di studiare una struttura reticolare che prendesse spunto da quelle usate per fare coperture di grandi luce, come ad esempio quella della stazione Tiburtina(2.1)

      

2.1

Per prima cosa ho cercato di capire come fossero realizzate queste strutture, ed ho visto che il più delle volte sono realizzate con moduli reticolari tridimensionali piramidali uniti in testa da aste, per costituire una struttura solidale(2.2).

 

(2.2)

Quindi ho realizzato in SAP 2000 il modello di questa struttura realizzata con moduli piramidali, composti da aste di 2m, ed ho disposto due moduli di questi in larghezza e 5 in lunghezza. Dopo avere vincolato esternamente la struttura con delle cerniere agli spigoli estremi, ho assegnato i vincoli interni alle aste. In fine, dopo aver deciso di realizzare la struttura con dei tubolari in acciaio, ho caricato la struttura nei vertici superiori delle piramidi con un carico di 200 kN (2.3).

2.3

A questo punto con l’ausilio del software ho potuto vedere come la struttura si deformerebbe sotto lo sforzo del carico da me ipotizzato, trascurando il peso proprio della stessa (2.4).

2.4

Con il programma ho anche potuto ricavare il grafico degli sforzi normale a cui è sottoposta la struttura (2.5).

2.5

In questo modo ho potuto osservare quante delle 90 aste componenti la struttura sono soggette a compressione e quante a trazione ovvero 53 a compressione e 37 a trazione.

A  questo potuto ho potuto estrarre il valore esatto dello sforzo a cui è sottoposta ogni singola asta e quindi le ho potute dimensionare tutte con l’ausilio di un foglio di calcolo excel.

 

ASTE TESE

Come prima cosa scelgo il tipo di acciaio da utilizzare per i profili che comporranno il modulo, nel mio caso un acciaio con una resistenza pari a 235 Mpa. Dopo di che ricavo la resistenza di progetto, fyd, facendo il rapporto tra la resistenza del materiale ed il coefficiente di sicurezza, γ m0 (1,05). A questo punto conoscendo impongo che fyd sia la tensione che deve sopportare la mia asta e quindi facendo il rapporto tra lo sforzo normale a cui è sottoposta l’asta e la resistenza di progetto trovo l’area minima che deve avere l’elemento per resistere a tale sforzo. Amin= N/fyd. In questo modo ho potuto dimensionare tutte le aste.

Ad esempio per la coppia di aste “12-65” sottoposte allo stesso sforzo di  11,592 kN, ho potuto ricavare l’area minima della sezione seguendo i procedimenti sopra elencati (2.6).

2.6

Dopo di che, ho cercato sul profilario un’asta a sezione cilindrica con l’area della sezione uguale o subito superiore  all’area necessaria per sopportare tale sforzo  (2.7).

2.7

2.8

In questo modo ho dimensionato tutte le altre aste sottoposte a tensione (2.9).

2.9

 

ASTE COMPRESSE

Per dimensionare le aste soggette a compressione ho dovuto considerare più parametri, in quanto, la compressione oltre alla rottura dell’asta porta anche allo sbandamento della stessa, quando va in carico di punta, e ciò è da tenere in considerazione in sede di progetto per cercare di evitarlo. Per questo ai parametri citati prima ho dovuto aggiungere: il modulo di elasticità del materiale (E) pari a 210000 Mpa per l’acciaio; la lunghezza dell’asta considerata (L) , nel mio caso 2 metri; le condizioni di vincolo a bordo dell’asta e quindi il modo in cui essa può sbandare in tale configurazione con in coefficiente (β), nel mio caso pari a 1;la snellezza dell’asta (λ) uguale a π √E/√fyd; il raggio d’inerzia dell’elemento (ρ) , ricavato dal rapporto tra la lunghezza dell’asta e la sua snellezza(λ); il momento d’inerzia(I) pari all’area della sezione per il quadrato del raggio d’inerzia.

Questa volta per la scelta del profilo non pasta vedere l’area della sezione ma bisogna verificare anche se il raggio d’inerzia sia verificato nella sezione scelta. Un  caso esemplare, a tal proposito, mi è venuto nel dimensionamento della coppia di aste “26-60” sottoposte ad uno sforzo di -132 kN. Seguendo i procedimenti sopra elencati, infatti, avevo ricavato che tali aste, per contrastare lo sforzo a cui sono sottoposto, avrebbero dovuto avere un area minima di 6,04 cmq. Quindi ho scelto un profilo rispondente a quell’area. Tuttavia tale profilo non aveva un raggio d’inerzia che eguagliasse quello minimo richiesto per resistere alla compressione a cui era sottoposto e  per questo il profilo non risultava adeguato e quindi troppo snello (2.10),(2.11)

2.10

2.11

Per questo sono stato costretto a prendere la sezione con area immediatamente superiore e con un raggio di ineriza che soddisfacesse quello richiesto dal predimensionamento .(2.12),(2.13)

2.12

2.13

In questo modo ho dimensionato tutte le altre aste compresse (2.14).

2.14

 

 

 

 

La prima esercitazione prevede il dimensionamento della travell più sollecitata del telaio nelle tre tecnologie: calcestruzzo, acciaio e legno.La trave su cui grava più carico è quella centrale, evidenziata in rosso. La sua aerea di influenza è pari 24 mq. Ossia 6m di luce e 4 di interasse.

Analisi carichi solaio in laterocemento

 

 

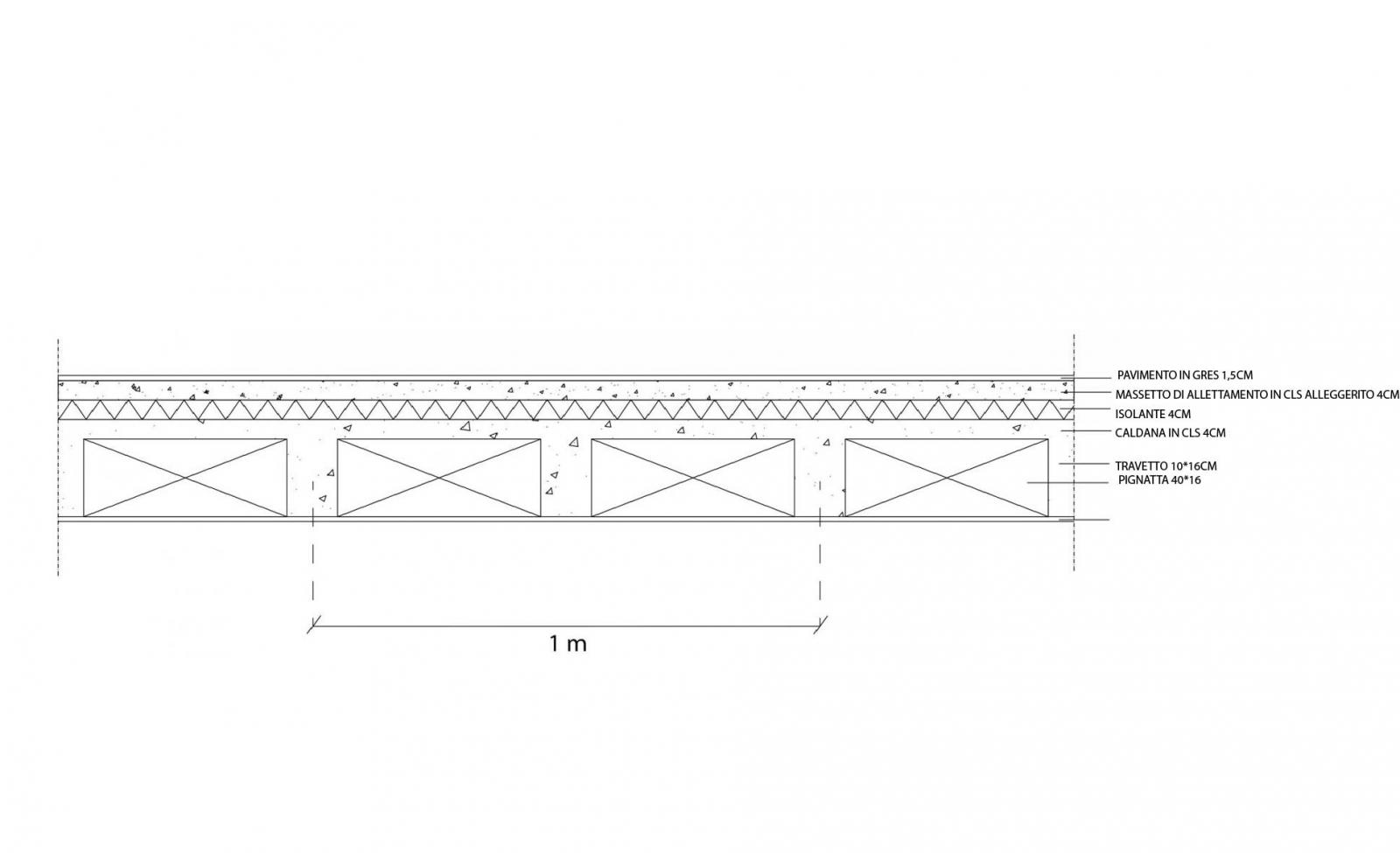
Il primo step per l’analisi dimensionale della trave, è lo studio dei carichi che questa deve sopportare. Questi si dividono in carichi strutturali q_s, carichi permanenti q_p, carichi accidentali q_A

 

CARICHI STRUTTURALI q_s :

caldana 0,04 m * 24kN/m³ = 0,96 kN/m²
travetti   2 * 0,10 m* 0,16 m * 24 kN/m³ = 0,77 kN/m² 
totale q_{s =} 1,73 kN/m²

 

CARICHI PERMANENTI q_p 

pavimento in gres porcellanato  0,015 m * 20 kN/m³ = 0,3 kN/m²
massetto in cls leggero 0,02 m * 14 kN/m³ = 0,28 kN/m²
isolante 0,04 m * 0,4 kN/m³ = 0,016 kN/m²
pignatte 2 * 0,4 m * 0,16 m * 8 kN/m³ = 1,02 kN/m²
incidenza impianti 1 kN/m²
incidenza tramezzi 0,5 kN/m²
totale q_p = 3,12 kN/m²

 

CARICHI ACCIDENTALI q_A:

ambiente residenziale 2,00 kN/m²
totale q_A: 2,00 kN/m²

totale carichi 6,85 kN/m²

 

Tali valori possono essere ora inseriti in un foglio di calcolo excel che a partire dal q_s, dal q_p e dal q_A ricaverà q (kN/m) tenendo conto di un fattore di accrescimento pari a 1,3 per i carichi permanenti strutturali e non strutturali (q_s e q_p) e 1,5 per i carichi accidentali (q_A)

In questa prima fase del dimensionamento non è stato considerato il peso proprio della trave, che incide nei carichi strutturali, in quanto non si conoscono le dimensioni della sezione. Tuttavia, una volta ricavata la sezione con il predimensionamento, verrà moltiplicata per il peso specifico del materiale con cui è composta. Verrà poi effettuato un nuovo dimensionamento, aggiungendo il valore del peso della trave ai carichi strutturali, ottenendo così un nuovo momento flettente, e valutando così la resistenza della trave.

 

Dimensionamento

Dal valore di carico calcolato su un mq di solaio moltiplicato per l’interasse della trave si è calcolati il carico che agisce sulla trave scelta. q =39,72 kN/m

Successivamente è possibile calcolare il momento massimo M_max che insiste sulla sezione della stessa. In questo caso, la trave trattata è una semplice trave appoggiata dotata di un momento massimo pari a M_max = ql²/8:  M_max =178,2 kN * m

Definito il momento massimo di progetto, è necessario calcolare le resistenze dei due materiali che compongono la trave scegliendo un acciaio per le armature con una resistenza caratteristica f_y pari a 450 MPa e un calcestruzzo con resistenza a compressione R_ck pari a 40 MPa e impostando la base b della nostra trave sui 30 cm, avremo un altezza utile h pari a 36,58 cm, che diventa H = 41,58 cm aggiungendo il delta = 5 cm., per una sezione finale della trave in cemento armato pari a 30 x 45 cm. 

 

Verifica del dimensionamento

Per verificare il dimensionamento appena svolto è opportuno calcolare il carico q aggiungendo il peso proprio della trave p, moltiplicato per un coefficiente pari a 1,3.

p = (0,30 x 0,45 x 1)m³ x 25 kN/m³= 3,375 kN/m²
Questo valore bisogna sommarlo al valore di q_s  precedentemente trovato:

q_s= 1,73 kN/m² + 3,375 kN/m²= 5,105 kN/m²

Andando a svolgere gli stessi calcoli svolti in precedenza avremo:

Carico distribuito q= 57.27 kN/m
momento M_max =257,7 kN * m
altezza utile hu= 43,92 cm, aggiungendo il coefficient δ per ottenere l’altezza H=48,93

Servirà quindi una trave di altezza di 50 cm.

 

Dati di progetto nella tabella Excel

Nella prima riga della tabella Excel c’è il dimensionamento della trave senza considerarne il peso proprio, nella seconda invece c’è il dimensionamento che tiene conto anche al peso proprio della trave.Come si può osservare dalla figura la verifica non risulta soddisfatta pertanto si dovrà utilizzare una trave con un’altezza H di 55cm

Conclusioni

Dai due diversi dimensionamenti si è potuto constatare come aggiungendo il peso proprio della trave, si ha avuto un incremento dell’altezza della trave molto incisivo: si passa da un’altezza utile di 36,58 cm ad un valore di 43,92, di oltre 7 cm superiore.
Questo è dovuto dal valore elevato del peso specifico del calcestruzzo armato, che influenza il dimensionamento quando si considera anche la trave con il suo peso.

 

Analisi carichi solaio in legno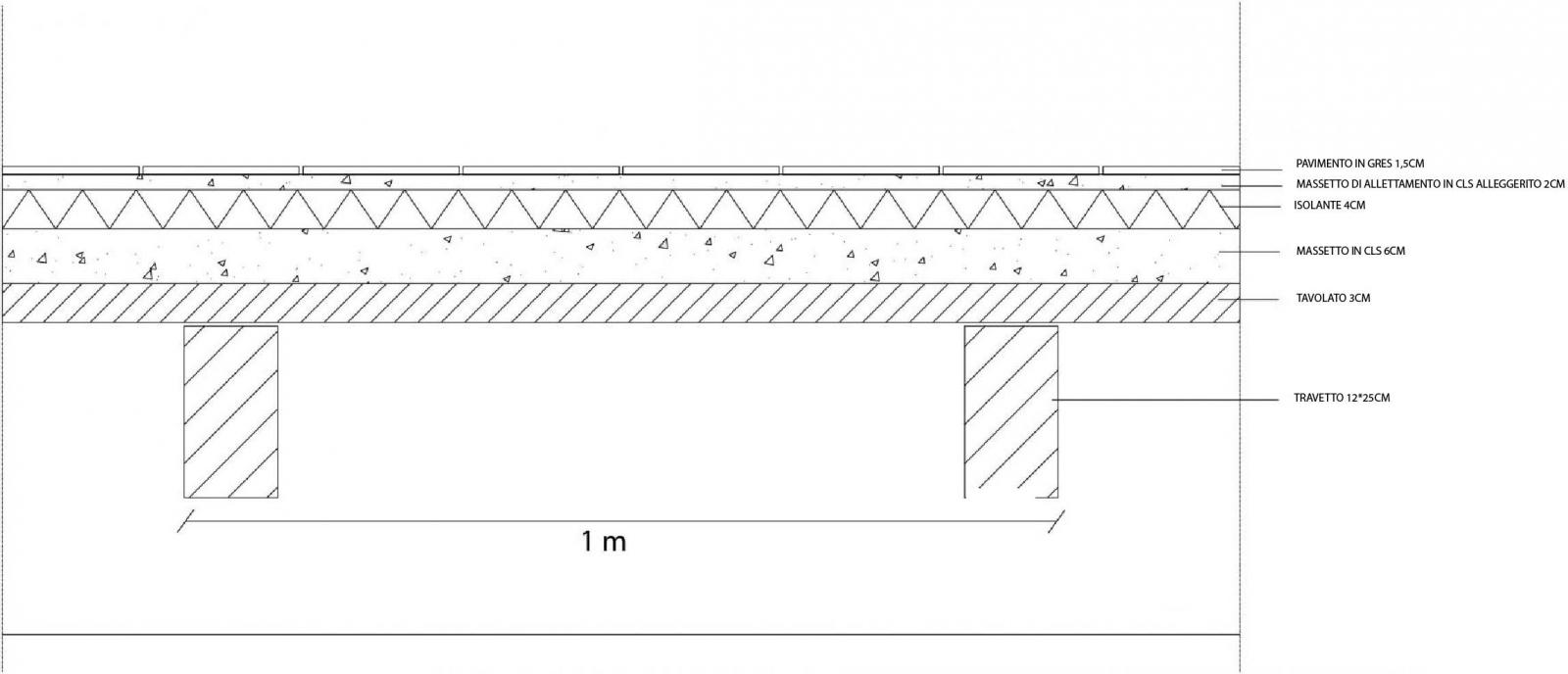

CARICHI STRUTTURALI q_s 

tavolato 0,03 m * 4kN/m³ = 0,12 kN/m²
travetti   2 * 0,25 m* 0,12 m * 6 kN/m³ = 0,36 kN/m² 
totale q_{s =} 0,48 kN/m²

 

CARICHI PERMANENTI q_p 

massetto in cls leggero 0,02 m * 14 kN/m³ = 0,28 kN/m²
isolante 0,04 m * 0,4 kN/m³ = 0,016 kN/m²
massetto cls  0,06 m * 24 kN/m³ = 1,44 kN/m²
incidenza impianti 1 kN/m²
incidenza tramezzi 0,5 kN/m²
totale q_p = 3,54 kN/m²

 

CARICHI ACCIDENTALI q_A:

ambiente residenziale 2,00 kN/m²
totale q_A: 2,00 kN/m²

totale carichi 6,02 kN/m²

 

Tali valori possono essere ora inseriti in un foglio di calcolo excel che a partire dal q_s, dal q_p e dal q_A ricaverà q (kN/m) tenendo conto di un fattore di accrescimento pari a 1,3 per i carichi permanenti strutturali e non strutturali (q_s e q_p) e 1,5 per i carichi accidentali (q_A)

In questa prima fase del dimensionamento non è stato considerato il peso proprio della trave, che incide nei carichi strutturali, in quanto non si conoscono le dimensioni della sezione. Tuttavia, una volta ricavata la sezione con il predimensionamento, verrà moltiplicata per il peso specifico del materiale con cui è composta. Verrà poi effettuato un nuovo dimensionamento, aggiungendo il valore del peso della trave ai carichi strutturali, ottenendo così un nuovo momento flettente, e valutando così la resistenza della trave.

 

Dimensionamento

Dal valore di carico calcolato su un mq di solaio, si è risaliti alla quantità di carico del pezzo di solaio che grava sulla trave scelta. q =35,74 kN/m

Successivamente al calcolo del carico distribuito che insiste sulla trave, è possibile calcolare il momento massimo M_max che insiste sulla sezione della stessa. In questo caso, la trave trattata è una semplice trave appoggiata dotata di un momento massimo pari a M_max = ql²/8: M_max =160,1 kN * m

In fase progettuale viene scelto il tipo di legno che si vuole utilizzare, in questo caso è stato preso in considerazione un legno lamellare GL 24h la cui resistenza caratteristica f_m,k è pari a 24 MPa. Ora è possibile calcolare la tensione ammissibile sig_am e impostando la base b, ricavare l'altezza h.

L’altezza minima per la trave è di 49,28 cm. Tuttavia visto che è un predimensionamento di minima, si sceglie di utilizzare una sezione di h= 50 cm.

 

Verifica del dimensionamento

Per verificare il dimensionamento appena calcolato è necessario andare a ricalcolare i carichi, aggiungendo il peso proprio della trave  p, calcolato in base alla sezione. Il peso specifico del legno lamellare classe GL 24 h è di 3,80 kN/ m^3.

p = (0,3 m x 0,5m) x 3,8 kN/m³= 0,57 kN/m²

Questo valore bisogna sommarlo al valore di q_s  precedentemente trovato:

q_s= 0,48 kN/m² + 0,57 kN/m²= 1,05 kN/m²

Andando a svolgere gli stessi calcoli svolti in precedenza avremo:

Carico distribuito q= 38,7 kN/m
momento M_max =174,15 kN * m
altezza utile hu= 52,16 cm,

Servirà quindi una trave di altezza di 55 cm.

 

 Dati di progetto nella tabella Excel

Conclusioni

Dai due diversi dimensionamenti si è potuto constatare come aggiungendo il peso proprio della trave, si ha avuto un incremento dell’altezza della trave di oltre 5cm.

 

 

Analisi carichi solaio in acciaio

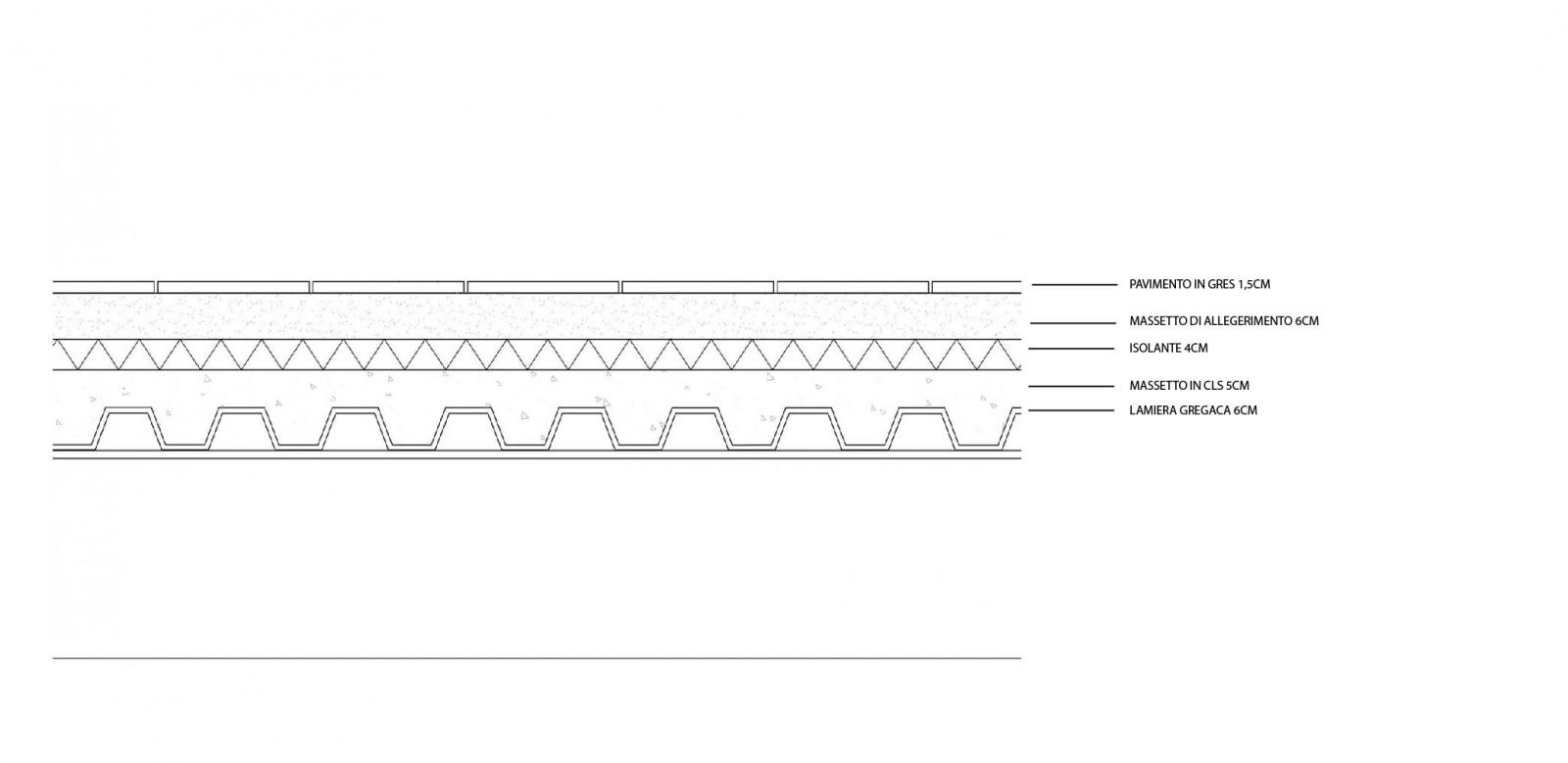
CARICHI STRUTTURALI q_s :

massetto in cls spessore 0,11 m= 2,15 kN/m²
lamiera grecata tipo HI-BOND spessore 0,7mm = 0,09 kN/m²
totale q_{s =} 2,24 kN/m²

 

CARICHI PERMANENTI q_p 

pavimento in gres porcellanato 0,015 m * 20 kN/m³ = 0,3 kN/m²
massetto in cls leggero 0,06 m * 14 kN/m³ = 0,84 kN/m²
isolante 0,04 m * 0,4 kN/m³ = 0,016 kN/m²
incidenza impianti 1 kN/m²
incidenza tramezzi 0,5 kN/m²
totale q_p = 2,66 kN/m²

 

CARICHI ACCIDENTALI q_A:

ambiente residenziale 2,00 kN/m²
totale q_A: 2,00 kN/m²

totale carichi 6,9 kN/m²

 

Tali valori possono essere ora inseriti in un foglio di calcolo excel che a partire dal q_s, dal q_p e dal q_A ricaverà q (kN/m) tenendo conto di un fattore di accrescimento pari a 1,3 per i carichi permanenti strutturali e non strutturali (q_s e q_p) e 1,5 per i carichi accidentali (q_A

In questa prima fase del dimensionamento non è stato considerato il peso proprio della trave, che incide nei carichi strutturali, in quanto non si conoscono le dimensioni della sezione. Tuttavia, una volta ricavata la sezione con il predimensionamento, verrà moltiplicata per il peso specifico del materiale con cui è composta. Verrà poi effettuato un nuovo dimensionamento, aggiungendo il valore del peso della trave ai carichi strutturali, ottenendo così un nuovo momento flettente, e valutando così la resistenza della trave.

 

Dimensionamento

Dal valore di carico calcolato su un mq di solaio, si è risaliti alla quantità di carico del pezzo di solaio che grava sulla trave scelta. q =39,61 kN/m

Successivamente al calcolo del carico distribuito che insiste sulla trave, è possibile calcolare il momento massimo M_max che insiste sulla sezione della stessa. In questo caso, la trave trattata è una semplice trave appoggiata dotata di un momento massimo pari a M_max = ql²/8 M_max =178,24 kN * m

Definito il momento massimo di progetto, è necessario stabilire il materiale con cui si vuole realizzare la trave, dal quale dipenderà la resistenza f_yd.

f_yd = 275 N/mm²  /1,15 f_yd = 239,13 N/mm²

I risultati restituiti dalla tabella excel riportano un valore del modulo di resistenza W_x pari a 680,54 cm³, è perciò opportuno selezionare come profilo un IPE 330 in cui W_x è pari a 713cm³.

 

Verifica del dimensionamento

Per verificare il dimensionamento appena calcolato è necessario andare a ricalcolare i carichi, aggiungendo il peso proprio della trave p, calcolato in base alla sezione. Il peso specifico dell'acciaio è di 78,5 kN/m³ e l’area dell’IPE330 è pari a 62,60 cm² (=0,00626 m²)

p = (62.60 x 10^-4 x 1) m³/m x 78,50 kN/m³ = 0,491 kN/m

Questo valore bisogna sommarlo al valore di q_s  precedentemente trovato:

q_s= 2,24 kN/m² + 0,49 kN/m²= 2,73 kN/m²

Andando a svolgere gli stessi calcoli svolti in precedenza avremo:

Carico distribuito q= 42,16 kN/m
momento M_max =189,7 kN * m
W_xmin=724,32 cm³

È necessario dunque scegliere una IPE superiore, perchè la IPE330 non copre tale valore di modulo di resistenza a flessione, si adotta perciò una IPE 360 ( W_x = 904 cm³).

 

Conclusioni

Anche tramite la tabella di Excel è possibile vedere come il calcolo del peso della trave incida anche in questo caso molto sulla scelta della trave, e ancora una volta questo è dovuto dall’elevato peso specifico del materiale.

 

 

 

Dati di progetto nella tabella Excel

 

 

 

 

cari ragazzi e care ragazze, in allegato trovate due fascicoletti, uno relativo alle caratteristiche geometriche delle sezioni in acciaio di tubi quadrati e rettangolari e l'altro relativo ai tubi circolari. 

Buon lavoro

la prof.