La terza esercitazione consiste nel progetto di una trave a sbalzo nelle tre tecnologie di costruzione più comuni (legno, acciaio, cemento armato), con l’ausilio di un foglio elettronico Excel.
Piante di carpenteria di riferimento per solaio in legno,cls e acciaio
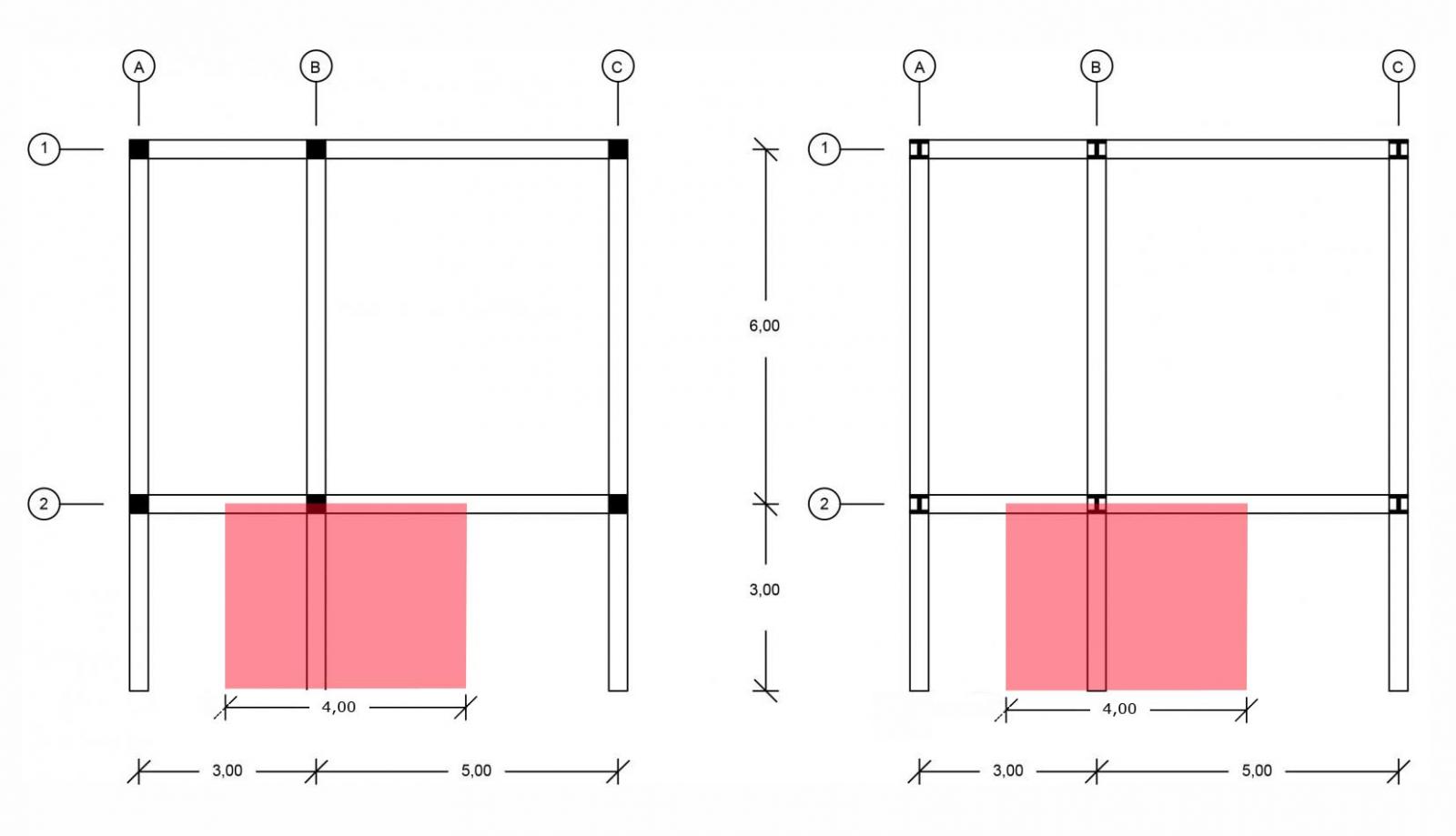
La prima carpenteria rappresenta un solaio in cls e legno; la seconda un solaio in acciao.
La trave a sbalzo maggiormente sollecitata è quella sull’asse B, con un’ area di influenza pari a 12 m2 (luce: 3m, interasse: 4m).
Lo scopo dell’esercitazione è verificare che la deformabilità della trave non provochi un abbassamento (spostamento verticale) maggiore di 1/250 della luce della trave stessa; il foglio Excel ci permettere di conoscere il valore dello spostamento verticale della trave allo stato limite di esercizio.
Nel caso di una trave a sbalzo, si prende in considerazione il modello statico della mensola
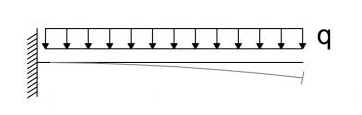
il cui momento massimo è dato dalla formula Mmax = ql²/2
CEMENTO ARMATO
Considero i valori dei carichi strutturali, permanenti ed accidentali relativi al calcestruzzo della prima esercitazione:
qs= 3,23 kN/m2
qp= 2,64 KN/m2
qa= 2kN/m2
I tre carichi vengono sommati, moltiplicati per i loro coefficienti di sicurezza e moltiplicati per l’interasse ottenendo qu pari a 44,64 kN/m. Conoscendo la luce (3 m) , si ottiene il valore del Momento massimo di una mensola pari a 200,86 KNm.
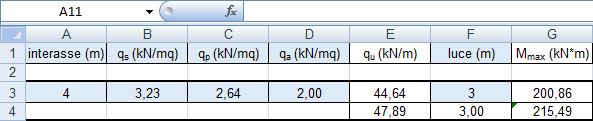
Per le armature scelgo un acciaio con coefficiente di resistenza caratteristica pari a fyk=450 MPa e un calcestruzzo con resistenza a compressione pari a fck=60 MPa. Imposto una base b pari a 25 cm; i calcoli del foglio Excel mi danno un’altezza minima della sezione che ingegnerizzo a 40 cm. Di conseguenza, ho una sezione di 25 cm X 40 cm.
Dopo aver dimensionato la sezione, effettuo la verifica a deformabilità controllando l’abbassamento massimo dell’elemento strutturale in rapporto alla sua luce.
Il procedimento, che è uguale in tutte e tre le tecnologie, si effettua allo SLE (Stato Limite di Esercizio) poiché la verifica è finalizzata a controllare che non vi siano spostamenti e deformazioni che possano limitare l’uso della costruzione, la sua efficienza e il suo aspetto.
A tal motivo i carichi incidenti sulla struttura vengono ricombinati seguendo la combinazione frequente, generalmente impiegata per gli stati limite di esercizio reversibili:
qe= (G1 + G2 + ¥11 × Q1) × i
Nel cemento armato, il peso proprio dell’elemento strutturale veniva calcolato anche nella prima esercitazione, poiché era necessario verificare allo stato limite ultimo (SLU) che la sezione scelta fosse idonea a sopportare tutti i pesi gravanti su di sé anche dopo aver aggiunto il peso proprio. Dopo questa verifica, l’informazione relativa al peso verrà riutilizzata per calcolare il carico totale qe.
Infine, per calcolare lo spostamento è necessario conoscere il modulo elastico del materiale E e il suo momento d’inerzia Ix
Calcolato il carico totale allo SLE qe, specificato il modulo elastico E ed il momento di inerzia Ix, è ora possibile calcolare l’abbassamento massimo che è pari a:
vmax = qe* l4 / 8EIx
e verificare che il rapporto tra la luce della trave e il suo spostamento massimo sia maggiore di 250, come imposto dalla normativa in base al tipo di elemento strutturale considerato:
l / vmax ≥ 250
Lo spostamento verticale massimo è pari a 1,08 cm e il rapporto tra la luce e lo spostamento massimo è maggiore di 250.
LEGNO
qs= 0,18 kN/m2
qp= 3,74 KN/m2
qa= 2kN/m2
qu pari a 35,376 kN/m
Conoscendo la luce (3 m) , si ottiene il valore del Momento massimo di una mensola pari a 159,192 KNm
Dopo aver impostato il modulo elastico del materiale, scelgo una base di lunghezza pari a 25 cm; i calcoli del foglio Excel mi danno un’altezza minima della sezione che ingegnerizzo a 50 cm. Di conseguenza, ho una sezione di 25 cm X 50 cm. Dopo aver dimensionato la sezione, è necessario effettuare la verifica a deformabilità controllando l’abbassamento massimo dell’elemento strutturale in rapporto alla sua luce.
Nel caso del legno, per quanto riguarda il calcolo del carico totale allo stato limite di esercizio, il peso proprio della trave viene trascurato in quanto è un materiale leggero.
qe= (G1 + G2 + ¥11 × Q1) × i = 20 kN/m
Calcolato il carico totale allo SLE qe, specificato il modulo elastico E ed il momento di inerzia Ix, è ora possibile calcolare l’abbassamento massimo che è pari a:
vmax = qe l4/ 8EIx= 0,96 cm.
Di conseguenza:
l / vmax> 250
ACCIAO
qs= 1,18 kN/m2
qp= 1,74 kN/m2
qa= 2kN/m2
qu pari a 28,576 kN/m
Conoscendo la luce (3 m) , si ottiene il valore del Momento massimo di una mensola pari a 128,592 KNm
Dopo aver definito la resistenza del materiale, dal foglio Excel si ottiene un modulo di resistenza a flessione Wx,min pari a 490,99 cm3. Quindi è opportuno utilizzare come profilato una IPE 300 che ha Wx pari a 557,0 cm3 e Ix pari a 8356 cm4.
Dopo aver dimensionato la sezione, è necessario effettuare la verifica a deformabilità controllando l’abbassamento massimo dell’elemento strutturale in rapporto alla sua luce. Come per il cemento, anche per l’acciaio va considerato il peso proprio (0,422 KN/m); informazione che verrà riutilizzata per calcolare il carico totale qe.
qe= (G1 + G2 + ¥11 × Q1) × i = 16,102 kN/m
Calcolato il carico totale allo SLE qe, specificato il modulo elastico E ed il momento di inerzia Ix, è ora possibile calcolare l’abbassamento massimo che è pari a:
vmax = qe l4/ 8EIx= 0,929 cm.
Di conseguenza:
l / vmax> 250
SdC(b)
ed uno schema dei diagrammi delle sollecitazioni che, come ho gia detto, in una reticolare è relatvo solo allo sforzo normale: di trazione o di compressione.
Per i valori di compressione ho ricavato allo stesso modo un'area minima ma prima di passare al dimensionamento ho dovuto inserire altri valori: questo perchè per la compressione bisogna tener conto dell'instabilità e considerare quindi anche la luce delle aste, la loro geometria, qundi l'inerzia ed anche l'elasticità del materiale. Una volta inseriti i valori relativi a queste caratteristiche, in particolare lambda, rho_min e I_min ho potuto dimensionare le aste tramite la tabella dei profilati.
Commenti recenti