Portale di Meccanica

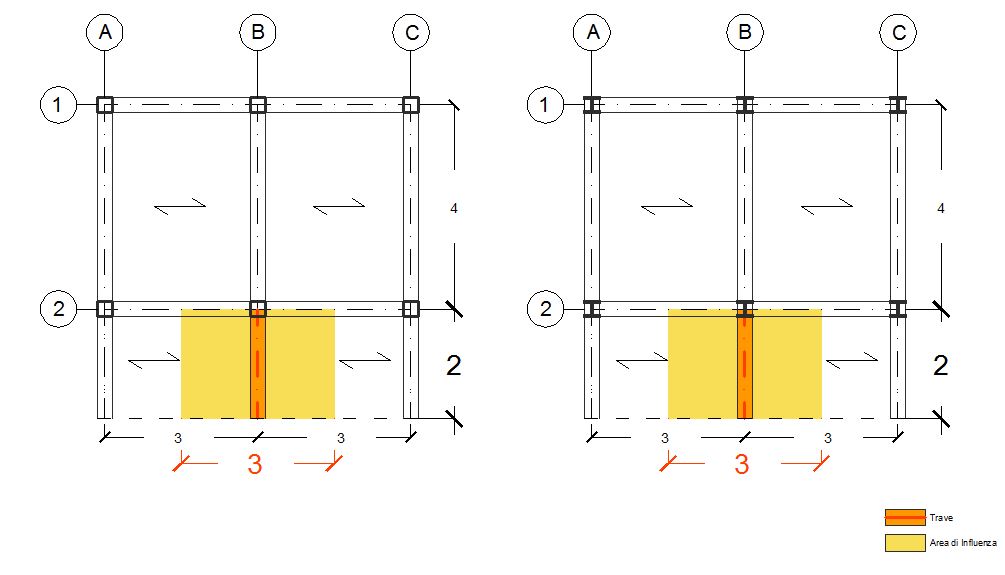
L’esercitazione prevede il dimensionamento di una mensola nelle tre tecnologie: legno, acciaio e cls armato.

Osservando la struttura è evidente che la mensola su cui grava più carico è quella centrale e la sua area è pari a 6 m², con Luce = 2m e Interasse = 3m

Iniziamo il calcolo prendendo come riferimento gli stessi carichi dell’ Esercitazione 1 - Dimensionamento di una trave in Legno, Acciaio e Cls Armato

(vedi collegamento Esercitazione 1 - Dimensionamento Trave)

Legno

Scelta degli elementi di calcolo

• Carico strutturale: qs = 0,438 kN/m²
• Carico permanente: qp = 2,69 kN/m²
• Carico accidentale: qa = 2,00 kN/m²

Inserendo il valore di ogni singolo carico nel foglio excel darà come risultato il carico totale:

qu = 15,2088 kN/m

Inserendo la luce l=2 m, possiamo ricavare il Momento Massimo di una mensola:

Mmax = ql²/2

Fase progettuale

Dobbiamo scegliere:

1– La tipologia di legno: Legno lamellare GL 24h con

     resistenza a flessione caratteristica fm,k = 24 MPa    

2 – coefficiente della durata del carico kmod = 0,8 (fornito dalla normativa)

3 – coefficiente parziale di sicurezza del materiale γm = 1,45 (legno lamellare) con questi dati possiamo calcolare la tensione ammissibile f_d c (N/mm²) = fm,k x kmod / γm

4 – impostando la base b= 20 cm, ricaviamo l’altezza hmin:

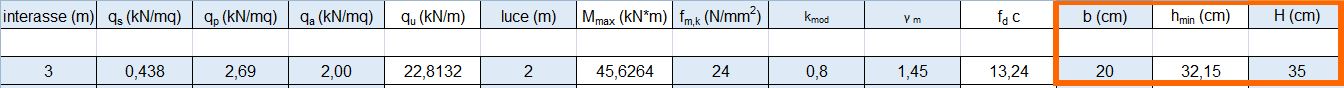
hmin è il valore minimo che deve avere l’altezza della sezione, tale va ingegnerizzata cioè va scelto un valore di altezza superiore ad hmin, cioè H= 35 cm quindi non avendo considerato il peso proprio della trave è giusto scegliere la sezione con un profilo pari a 20 x 35 cm

5 – determiniamo il valore del modulo elastico E = 8.000 N/mm²

6 – il foglio excel ci determina il momento d’inerzia I_x = b x h³/12 e i carichi incidenti come q_e = (q_s + q_p + q_a x 0,5) x i come vediamo non inseriamo il peso proprio del trave perché è materiale leggero (mentre verrà inserito per l’acciaio e il cls)

7– avendo ottenuto il carico totale q_e, specificato E e il I_x, il foglio di calcolo ci determina l’abbassamento massimo v_max = q_e x l⁴/ 8 x E x I_x e il suo rapporto con la luce:

Fase di verifica _ Limiti Di Deformabilità:

1 – la verifica è molto semplice dobbiamo determinare che il rapporto tra la luce e l’abbassamento sia maggiore o uguale a 250, quindi l/ v_max ≥ 250:

                                                                                La sezione 20 x 35 cm è stata verificata!

2- definiamo un altro esempio di sezione con base b=30 cm e poniamo un H=35 cm, come si vede dalla tabella il rapporto tra la luce e l’abbassamento è minore di 250 quindi la mensola supera i limiti di deformabilità:

                                                                                La sezione 30 x 35 cm non è verificata!

Acciaio

                                  

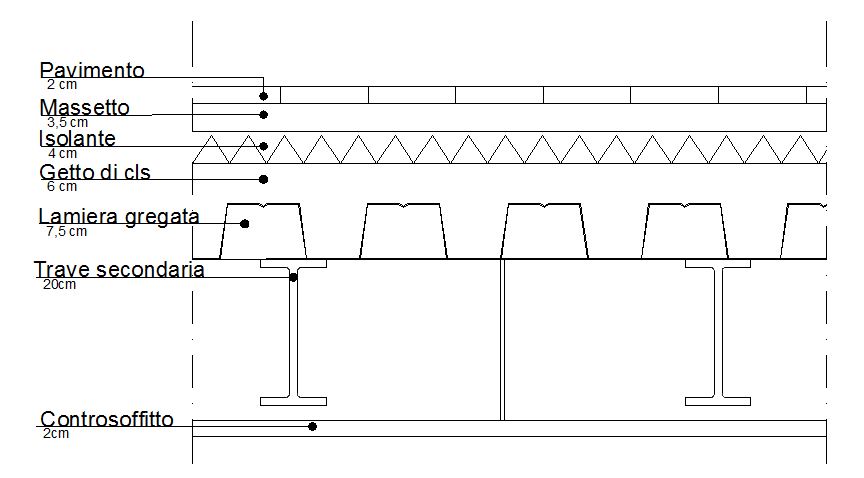
Scelta degli elementi di calcolo

• Carico strutturale: qs =  2,01 kN/m²
• Carico permanente: qp = 2,84 kN/m²
• Carico accidentale: qa = 2,00 kN/m²

Inserendo il valore di ogni singolo carico nel foglio excel darà come risultato il carico totale:

qu = 29,619 kN/m

Inseriamo la luce l= 2 m ricaviamo il Momento Massimo di una mensola:

Mmax = ql²/2

Fase progettuale

1 - la tensione di snervamento del Fe 430/ S275 è fy,k = 275 MPa quindi otteniamo un modulo di resistenza pari a W_x,min = 226,18 cm³:

Dopo aver ottenuto il modulo di resistenza, per ingegnerizzare la sezione si inserisce nella colonna affianco il valore del momento d’inerzia I_x del profilo, che ha come modulo di resistenza W_x,min un valore maggiore di quello trovato:

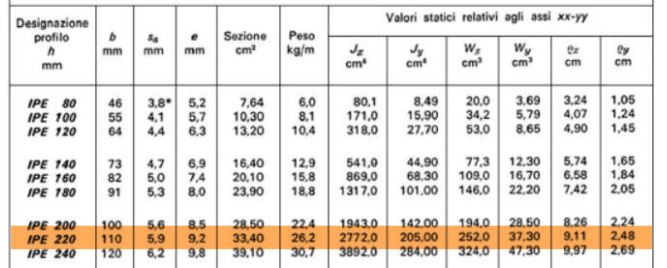
Il profilo scelto è un IPE 220 con:

• Ix=2772 cm⁴;
• Peso=26,2 kg/m = 0,262 kN/m

2- Al carico totale q_e si inserisce il peso proprio dell’elemento strutturale e otteniamo:

3 – determiniamo il valore del modulo elastico E = 210.000 N/mm²

4– avendo ottenuto il carico totale q_e, specificato la luce l, E e il I_x, il foglio di calcolo ci determina l’abbassamento massimo v_max = q_e x l⁴/ 8 x E x I_x e il suo rapporto con la luce:

Fase di verifica _ Limiti Di Deformabilità

1 – Determiniamo che  il rapporto tra la luce e l’abbassamento deve essere maggiore o uguale a 250, quindi l/ v_max ≥ 250:

                                                                           Il profilo IPE 220 è stato verificato!

CLS

 

Scelta degli elementi di calcolo

• Carico strutturalo: qs =  2,368 kN/m²
• Carico permanente: qp = 2,654 kN/m²
• Carico accidentale: qa = 2,00 kN/m²

Inserendo il valore di ogni singolo carico nel foglio excel darà come risultato il carico totale:

qu = 30,18 kN/m

Inseriamo la luce l= 2 m ricaviamo il Momento Massimo di una mensola:

Mmax = ql²/2

Fase progettuale

1 - acciaio per il cls: B450C avremo come tensione di snervamento fyk = 450 MPa, con queste scelte è possibile ricavare la tensione di progetto con la formula:           

fyd = fyk / γs

2 –tensione di progetto del cls fcd = αcc x fck/γc quindi fck = 60 MPa

3 – β = 0,53 e r = 2,14

4 – consideriamo una base b = 15 cm

otteniamo un Hmin pari a 28,29 cm, quindi ingegnerizzando possiamo scrivere H = 30 cm.

Quindi la sezione finale della trave in cls sarà 15 x 30 cm.

5 - Al carico totale q_e si inserisce il peso proprio dell’elemento strutturale

6 – determiniamo il valore del modulo elastico E = 21000 N/mm²

7 – avendo ottenuto il carico totale q_e, specificato la luce l, E e il I_x, il foglio di calcolo ci determina l’abbassamento massimo v_max = q_e x l⁴/ 8 x E x I_x e il suo rapporto con la luce l/ v_max ≥ 250:

Fase di verifica _ Limiti Di Deformabilità

1- Calcoliamo il peso unitario:

p = (0,15 x 0,30x 1) m³/m² x 25 kN/m³ = 1,125 kN/m²

quindi il carico totale con l’aggiunta del peso proprio del cls moltiplicato per 1,3 è

qu = 31,64 kN/m

                                                                             La sezione 15 x 30 cm è stata verificata!

 

 

Disegniamo la geometria 

SAP2000 è un programma che utilizza il metodo degli elementi finiti e si basa sulla Teoria di Eulero-Bernoulli. Per le unità di misura lavora con gruppi prestabiliti e  per questa esercitazione utilizzeremo kN,m,°C.

Per quanto riguarda gli assi utilizzeremo come ordinata z = gravità mentre come gli assi locali si decide tramite regola della mano destra:

                                                                       

Il programma ci permette di creare una struttura reticolare cubica o piramidale. Noi disegneremo quella cubica con:

1. New Model – Grid Only

Assi Locali:

X =3 m

Y =5 m

Z =2 m

Spazio Griglia:

X =2 m

Y =2 m

Z =2 m

           

2. Tasto Frame (per disegnare i lati e le diagonali del cubo)

Importante

-Prima di andare avanti con la struttura bisogna verificare che le aste non siano doppie:

Selezionare struttura – Edit –Merge Duplicates – OK

-Controllare che tutti i nodi siano uniti:

Selezionare la struttura – Edit – Edit Points - Merge Joints – 0,1 - OK

(0,1 = raggio entro cui tutti i nodi vicini coincidono nello stesso nodo)

Vincoli esterni

Vincoliamo esternamente la struttura con quattro cerniere agli spigoli esterni e assegniamo i vincoli interni alle aste:

-Assign – Joint – Restraints – selezionare la cerniera – OK

-Selezionare la struttura - Assign – Frame – Releases (accendere Moment 2-2 e 3-3) e ricontrollare l’unità di misura

          

          

Scelta del Profilo:

Selezionare la struttura – Assign – Frame – Frame Sections – Add New Property – Pipe Section – OK

           

 

Forze Concentrate

Dopo aver deciso di realizzare la struttura con dei tubolari in acciaio, l’ho caricata superiormente, con carichi di 50kN:

- Creare F ed eliminare il peso proprio:

Define – Load Patterns – “F” – (non considerare il peso proprio quindi scrivere 0 su "Self Weight Multiplier”) - cliccare su Add New Load Pattern – Selezionare il carico “F” – OK

- Assegnare il Carico 50kN:

Selezionare la parte superiore sella struttura – Assign – Joint Loads – Forces – Scegliere il carico F – Force Global Z – inserire –50kN – OK

          

 

Analisi della struttura - deformata

A questo punto, clicco Play per far partire l’analisi della struttura. Come vediamo dall’immagine la struttura si è deformata a causa del carico che ho ipotizzato dato che non ho considerato il peso proprio della struttura:

           

Analisi della struttura – sforzi normali

       

Tabella

Il programma SAP2000 riassume in una tabella tutti i valori che ho inserito e i relativi risultati. Il valore che ci interesserà  è lo Sforzo Normale (N) di ogni singola asta. Con SAP è possibile estrarre la tabella in formato Excel, così da facilitare i calcoli in seguito:

Display – Show Tables – Analysis Results – selezionare Select Load Patters, il carico F –Ok – Element Forces – Frames – File – Export Curren Table –To Excel – Labels – OK

Il sistema della tabella è molto semplice bisogna eliminare i valori che non vengono impiegati per il calcolo e lasciare:

lo sforzo normale = N

il numero delle aste = n°

le lunghezze delle aste = L

Dato che abbiamo scelto un cubo dobbiamo considerare solo le lunghezze di

 L=2 m (lati)

 L=2,82843 m (diagonali)

 

Dividiamo le Aste

Aste Tese _ Fase di Progetto

Prima cosa da fare è scegliere il tipo di acciaio dalla Normativa Tecnica per le costruzione – del 2008 ed identificare:

• La resistenza a tensione di snervamento fyk = 235MPa (Acciaio Classe Fe 360/S235);
• Il Coefficiente di sicurezza del materiale γm = 1,05
• Calcolare la resistenza a tensione di progetto: fyd (MPa) = fyk/γ

Calcolare l’area minima che deve avere l’elemento: A_min = N/fd

Scegliamo dalla Tabella Profilati metallici (scaricabile dal sito Profili Acciaio) i profili con:

A_design > A_min

Per le aste a trazione ho scelto 3 tipi di profilati in acciaio:

A=2,54 cm² - 33,7 x 2,6 mm

A=3,94 cm² - 42,4 x 3,2 mm

A=5,74 cm² - 60,3 x 3,2 mm

Fase di verifica _ σ<fd o N/A<fd

Consideriamo l’asta più sollecitata:

N/A = 126130 N / 574 mm² = 219,73 N/mm²   

fd = 223,81MPa

                                                                              N/A≤fd è VERIFICATA!

Asta Compressa _ Fase di Progetto

1 Fase di Progetto _ I calcoli per trovare A_min in un asta a compressione sono uguali come per l’asta a trazione:

• La resistenza a tensione di snervamento fyk = 235MPa (Acciaio Classe Fe 360/S235);
• Coefficiente di sicurezza del materiale γm=1,05;
• Calcolare la resistenza a tensione di progetto: fyd (MPa) = fyk/γ
• Calcolare l’area minima che deve avere l’elemento: A_min=N/fd

Per l’asta a compressione non basta la verifica dell’A_min, anzi bisogna considerare oltre alla rottura dell’asta anche lo sbandamento.

2 Fase di Progetto  _ Per questo bisogna considerare:

• Il modulo di elasticità del materiale E = 210000 MPa (acciaio);
• Lunghezza dell’asta l = 2m;
• Coefficiente del vincolo β= 1;
• Coefficiente di sicurezza del materiale γm=1,05;
• Sforzo Normale di progetto euleriano (kN) N_ed = N x γ
• Momento d’inerzia minimo (cm⁴) I_min = N_ed x (β x l)²/ π² x E

1-2 Fase di progetto_ Scegliere dalla Tabella dei Profili metallici:

• L’area di Progetto (cm²) A_design > A_min;
• Momento d’inerzia di progetto (cm⁴) I_design > I_min;
• Scrivere il raggio d’inerzia (cm)  ρ_design del profilo;
• Nell’asta di compressione bisogna conoscere la SNELLEZZA λ

Fase di Verifica  _ N/A < fd e λ ≤ 200

Asta n°67 più sollecitata

1- Come per l’asta a trazione verifichiamo anche per quella a compressione la più sollecitata:

N/A = -157445 N / 820 mm² = 192,0 N/mm²   

fd = 223,81MPa

                                                                             N/A≤fd è VERIFICATA!

2- Verifichiamo la snellezza λ ≤ 200 considerando sempre la stessa asta:

λ = 110,06

                                                                             λ ≤ 200 è VERIFICATA!

 

Per il dimensionamento di aste d’acciaio di una struttura reticolare il procedimento utilizzato prevede come primo passo di disegnare su SAP una griglia 3mx3m nella quale inserire la mia struttura reticolare, avendo cura di intelaiarla. Inserisco successivamente ai vertici il vincoli di cerniera esterni ed interni.

Proseguo scegliendo la sezione più consona delle travi (nel caso specifico tubolare in acciaio) e assegnando le forze, alle quali attribuisco arbitrariamente il valore di -150 kN.

                             

A questo punto posso avviare l’analisi che  produrrà una serie di risultati che esporterò su un foglio excell, il quale una volta “pulito” dei risultati inutili al fine dell’esercitazione e messo in ordine, apparirà così:

dove possiamo leggere tutte le aste in trazione e compressione, ed evidenziate in giallo le aste diagonali (dato che ci sarà utile successivamente nel calcolo delle aste in compressione).

Sul foglio excell fornitoci ora procedo per prima cosa con le aste in trazione, aggiornando, asta per asta, il mio sforzo N espresso in kN.

Dato il valore della tensione caratteristica di snervamento dell’acciaio f_yk e attribuito il coefficiente di sicurezza ϒ_m , si può trovare f_d , tensione di progetto, facendo f_yk / ϒ_m . A questo punto l’area minima sarà determinata da N / f_d , con l’accortezza di eseguire la giusta equivalenza in quanto espressa in cm². 

Infine l’ultima colonna sarà dedicata all’inserimento dei valori dell’area di design ricavata dalle tabelle dei profilati in base all’area min ottenuta. Ad esempio qui sotto il profilato più piccolo della tabella associato ai primi risultati ottenuti.

Proseguendo con le aste in compressione vado ad inserire i valori di N. I valori di f_yk, ϒ_m e f_d rimangono invariati rispetto al procedimento precedente, elaborando immediatamente l’area min. A questo punto però per le aste in compressione vanno fatti dei calcoli aggiuntivi che prevedono: l’inserimento del modulo di elasticità E, il valore β, pari ad 1 (in quanto siamo nel caso dell’asta appoggiata-appoggiata), la luce (che dovrà tener conto delle aste diagonali, misurate come l*√2), il ϒ_m, ed infine il calcolo dell’inerzia minima.

Infine in base ai risultati ottenuti andiamo ad ingegnerizzare l’area, l’inerzia e ρ (raggio d’inerzia minima). Ultimo dato ricavato sarà la snellezza, che tiene conto del raggio d’inerzia minima e della luce, secondo la relazione λ= l/ ρ.

La travatura reticolare è una struttura composta da un insieme di aste vincolate ai nodi, in modo da costituire un elemento resistente in grado di superare luci molto grandi. È formata da due elementi continui chiamati correnti, uno superiore e uno inferiore, collegati da altri elementi disposti alcuni in verticale e altri inclinati. Gli elementi verticali vengono denominati montanti, quelli inclinati diagonali. 
Questa seconda esercitazione prevede dunque la modellazione in tre dimensioni di una travatura reticolare, sui cui nodi superiori vengono applicati dei carichi concentrati, al fine di analizzare la deformazione e fare la verifica a sforzo normale. Essendo le travi reticolari sollecitate solo a sforzo normale, non troveremo sollecitazioni di taglio e momento. Il disegno tridimensionale della travatura può avvenire su cad o rhino, importandolo poi in sap, oppure direttamente su sap, preimpostando una griglia. Scelgo quest’ultimo metodo, quindi mi costruisco la griglia andando su File->New Model->Grid Only

Impostata la griglia, ricalco con Draw Frame un cubetto di dimensioni 2x2x2, controventato su ogni faccia con una diagonale, che poi ripeto per tutta la griglia. Questo è il risultato.

Adesso devo assegnare i vincoli ai quattro punti in basso all’estremità della griglia, e scelgo delle cerniere, andando su Assign->Joint->Restraints

Trasformo poi le aste della travatura in aste incernerate al loro interno, selezionando tutto, andando su

Assign->Frame->Releases/Partial Fixity e spuntando Moment 22 (minor) e Moment 33 (major).

Il passo successivo è quello di assegnare una sezione alla travatura reticolare, ad esempio una sezione tubolare, che rinomino “pipe”: Assign->Frame->Frame Section

 

Ora stabilisco i carichi concentrati che andrò ad applicare sui nodi superiori della travatura: su Define->Load patterns aggiungo un modello di carico che chiamo “F” e, dopo aver selezionato la fascia superiore della travatura: Assign->Joint Loads->Forces. In questo modo assegno il valore di carico che ho stabilito, ovvero di 80 KN verso il basso lungo l’asse verticale z.

Posso a questo punto avviare l’analisi (Run Analysis), ottenendo la deformata derivante dal carico da me stabilito.

Visualizziamo il grafico dello sforzo normale andando su Frames/Cables/Tendons e spuntando Axial Forces, e mettiamolo a confronto con i diagrammi dello sforzo di taglio e del momento, che essendo nulli, non di segnano alcun grafico.

Per visualizzare i risultati dello sforzo normale di trazione e di compressione a cui le aste sono soggette, si va su Display->Show Tables e spunto la casella Analysis Results, specificando che siano i risultati derivanti dal carico F che ho applicato inizialmente. Mi si apre così la finestra dei risultati, dove imposto la voce Element Forces Frames.

Ottenendo il valore dello sforzo normale per ogni singola asta, posso esportare il foglio dei dati su un documento di calcolo excel e procedere con il dimensionamento delle aste. 
Avendo inizialmente impostato una lunghezza delle aste pari a 2*2*2, sotto la colonna “station” troverò due dimensioni: 2m per le aste dritte e 2,82843m per le diagonali.

Come passo successivo mi riordino la colonna degli sforzi normali di trazione (+) e compressione (-)  dal più piccolo al più grande, in modo tale da copiare i valori positivi nel foglio di dimensionamento a trazione e quelli negativi nel foglio di dimensionamento a compressione.

ACCIAIO ASTA RETICOLARE-TRAZIONE

Scelta la tipologia di acciaio, in questo caso S275, con una resistenza caratteristica di 275 MPA, trovo la resistenza di progetto, dividendo la resistenza caratteristica per il coefficiente di sicurezza 1,05 (fyd=fyk/1,05). Dopodichè facendo il rapporto tra lo sforzo normale e la resistenza di progetto, posso conoscere l’area minima che l’asta deve avere per potere resistere alla sollecitazione (Amin=N/fyd). Andando sulla tabella dei profilati metallici cerco un sezione circolare >/= all’area minima calcolata.

Per esempio se prendo in considerazione la prima riga, avendo un’area minima di 24,06 cm2 trovo sul profilario un’area superiore pari a 39,50 relativa al profilo 219*5,9 (mm).

Chiaramente avendo in tutto 366 aste, 171 per quelle tese e 194 per quelle compresse, non attribuirò a ciascuna  un profilo diverso, bensì quattro-cinque profili, a ognuno dei quali corrisponderà un intervallo di valori più o meno ampio. Alla fine allegherò le  intere pagine calcolate per la trazione e per la compressione. Qui proseguo nel mostrare giusto qualche esempio utile ai fini della spiegazione.

ACCIAIO ASTA RETICOLARE-COMPRESSIONE

Mantenuto l’acciaio S275 e calcolata prima la resistenza di progetto e poi l’area minima, seguendo lo stesso procedimento della trazione, per trovare l’area di progetto devo prendere in considerazioni più elementi, poichè un’asta soggetta compressione è esposta non solo alla crisi di rottura, ma anche a quella dello sbandamento, ovvero quando presenta una configurazione non rettilinea. Quest’ultimo fenomeno si verifica quando il carico raggiunge una soglia massima e l’oggetto in questione è piuttosto snello (snellezza λ=lunghezza libera d’inflessione l0/raggio d’inerzia ρ ). Ecco quindi che entrano in gioco altri parametri, dal momento che per progettare un’asta compressa si necessita di AREA e di INERZIA.
-Lunghezza asta
-Modulo di elasticita: E=210000 MPa
-Coefficiente di vincolo che ci dice come sbanda l’asta: β = 1
-Snellezza asta: l0/ρ = λ =  π √E/√fcd
-Raggio d’inerzia: ρ = l0/λ
-Momento d’inerzia: I = A*(ρ)2

In particolare effettuo il dimensionamento considerando il momento d’inerzia e il raggio d’inerzia.

Prendendo come esempio la prima riga, con un’area minima di 33,90 cm2, un raggio d’inerzia minimo di 3,18 cm e un momento d’inerzia minimo di 343 cm4, ho considerato sempre il profilo 219*5,9 (mm), notando che I_design=2247>I_min=343, che rho_min_design=7,54>rho_min=3,18 e che A_design=39,5>A_min=33,90.

 

Allegherò in seguito due file PDF riguardanti le tabelle excel di tutte le aste sia tese che compresse con relativi 5 profilati metallici scelti, in modo da fornire eventuale approfondimento a chi interessato e mi scuso per l'ordine talvolta "creativo" della numerazione dei punti dove ho notato ripetersi due volte 4. e il salto del punto 12. (saltati solo nell'elencazione ma non nella storyboard)

 

La terza esercitazione riguarda il dimensionamento di una trave a sbalzo, usando un foglio di calcolo elettronico Excel, con tre tecnologie diverse:

- cemento armato
- legno
- acciaio.

Per il progetto del solaio, con ognuna di queste tre tecnologie, considero un’unica pianta di carpenteria:

La prima la posso utilizzare per rappresentare il solaio in legno ed in cemento armato, mentre la seconda riguarda la tecnologia dell’acciaio. La trave a sbalzo più sollecitata è quella lungo l’asse B, per questo motivo procedo con il dimensionamento di quest’ultima, che ha interasse 4m e luce 3m:

Il foglio elettronico che adesso andremo a compilare sarà diviso in due parti. Una prima parte sarà identico al foglio della prima esercitazione, quindi ragioniamo in termini di SLU poichè otteniamo una h_min tramite il q_u. Mentre la seconda parte, quella che riguarda questa nuova esercitazione, ragiona in termini di SLE in quanto dal q_e ottengo il dato relativo al v_max.
Ovviamente queste analisi presuppongono coefficienti di sicurezza diversi, poichè con l’analisi allo stato limite ultimo consideriamo lo stato più grave del danno, ovvero il collasso; mentre con l’analisi allo stato limite elastico consideriamo dei fenomeni come la deformabilità del solaio o la vibrazione di quest’utimo, quindi fenomeni che non compromettono il funzionamento generale della struttura ma arrecano fastidio agli occupanti di essa.
Ricordiamoci che adesso non stiamo più considerando il modello meccanico della trave appoggiata appoggiata, ma quello di una mensola. Quindi il M_max = (ql^2)/2
Procedo con l’analisi dell’abbassamento della trave nelle tre diverse tecnologie.

CEMENTO ARMATO

Come solaio e carichi di riferimento considero la mia prima esercitazione postata su questo blog (http://design.rootiers.it/strutture/node/1681). Per il cemento armato il calcolo del  q_u:
qu = (1,3qs + 1,5qp + 1,5qa) x interasse = 46,82 KN/m 
Mentre il M_max:
M_max = (ql^2)/2 = 210,7 KN/m
Impostando i dati relativi al materiale scelto (f_yk ed f_ck) ottengo per una base di 30 cm un'altezza minima di 54,10 cm che ingegnerizzo ad 60 cm. La trave ipotizzata ha un peso unitario di 4,5 KN/m, che va a sommarsi ai carichi e va a confermare la trave progettata: 
Adesso inizia la parte relativa allo SLE, poichè il foglio si calcola il q_e:
q_e = (1qs + 1qp + 0,5qa) x interasse = 33,02 KN/m
Imposto il Modulo elastico del c.a. pari a 21000 MPa ed ottengo una I_x:
I_x = (b*h^3)/12 = 540000cm⁴
Come risultato avrò un v_max = 0,29 cm, dato che mi conferma il progetto poichè I_x/ v_max >250

LEGNO

Come solaio e carichi di riferimento considero la mia prima esercitazione postata su questo blog (http://design.rootiers.it/strutture/node/1681). Per il legno il calcolo del  q_u:
qu = (1,3qs + 1,5qp + 1,5qa) x interasse = 31,60 KN/m 
Mentre il M_max:
M_max = (ql^2)/2 = 142,20 KN/m
Impostando i dati relativi al materiale scelto (f_mk) ottengo per una base di 30 cm un'altezza minima di 54,43 cm che ingegnerizzo ad 60 cm. A differenza del c.a. non considera il peso della trave progettata poichè il legno è un materiale leggero.

Adesso inizia la parte relativa allo SLE, poichè il foglio si calcola il q_e:
q_e = (1qs + 1qp + 0,5qa) x interasse = 19,00 KN/m
Imposto il Modulo elastico del c.a. pari a 8000 MPa ed ottengo una I_x:
I_x = (b*h^3)/12 = 540000cm⁴
Come risultato avrò un v_max = 0,45 cm, dato che mi conferma il progetto poichè I_x/ v_max >250

ACCIAIO
Come solaio e carichi di riferimento considero la mia prima esercitazione postata su questo blog (http://design.rootiers.it/strutture/node/1681). Per l'acciaio il calcolo del  q_u:
qu = (1,3qs + 1,5qp + 1,5qa) x interasse = 46,04 KN/m 
Mentre il M_max:
M_max = (ql^2)/2 = 207,20 KN/m
Impostando i dati relativi al materiale scelto (f_yk) ottengo W_x,min:
W_x,min = (M_max/ f_d)*1000 = 928,78 cm³

Scelgo il mio profilato ingegnerizzando quest'ultimo dato, avendo così un IPE 400

Inserisco sul foglio Excel i dati relativi al I_x ed il peso KN/m del profilato:

Adesso inizia la parte relativa allo SLE, poichè il foglio si calcola il q_e:
q_e = (1qs + 1qp + 0,5qa) x interasse = 26,46 KN/m
Imposto il Modulo elastico del c.a. pari a 8000 MPa ed ottengo una I_x:
I_x = (b*h^3)/12 = 210000cm⁴
Come risultato avrò un v_max = 0,552 cm, dato che mi conferma il progetto poichè I_x/ v_max >250

Nei nostri laboratori di progettazione capita spesso di finire a disegnare cose che, lontanamente ricordano questo edificio per uffici di Herzog & de Meuron.

Ma sugli aggetti c'è molto da imparare; innanzitutto è necessario considerare che sono molto deformabili, ossia si abbassano troppo!  

Per evitare la progettazioni di un trampolino di lancio da piscine olimpioniche scaricate i file in allegato:

un file Excel, utile per il dimensionamento a resistenza di una mensola nei tre materiali (acciaio, legno e Cemento armato) con annessa verifica a deformabilità. 

un file pdf contenente un commento del file Excel.