Si vuole, nella seguente esercitazione, analizzare come un impalcato reagisce a forze orizzontali tramite l'azione dei controventi.
IMPALCATO DI RIFERIMENTO - piano tipo in c.a. -
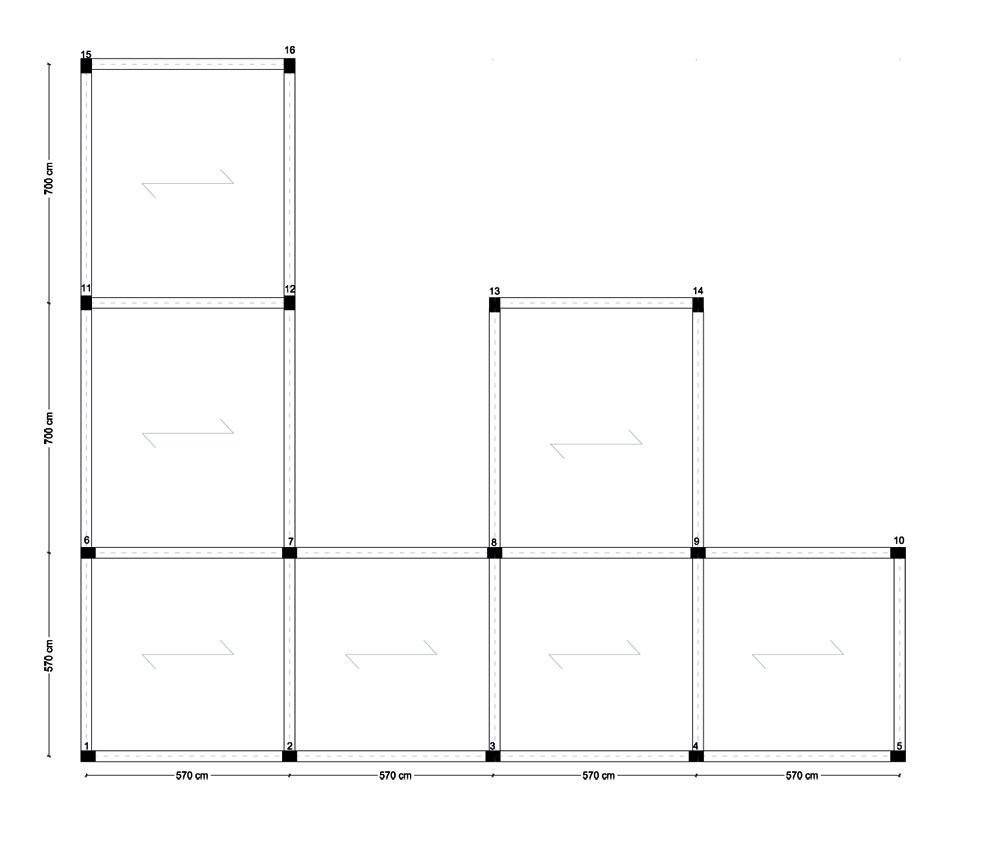
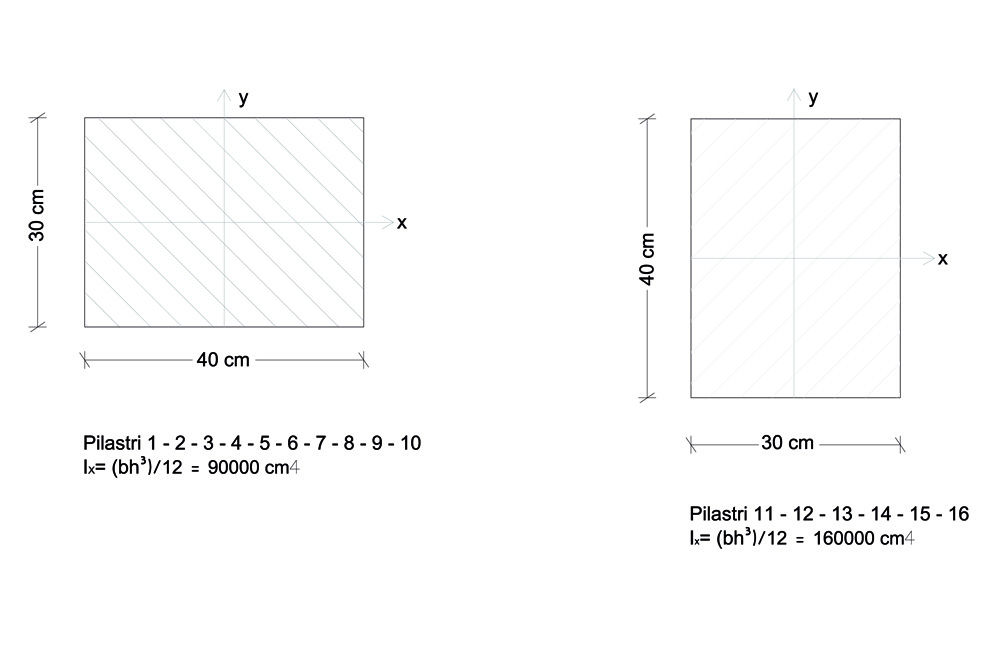
L'impalcato presenta due diverse orditure di solaio. Abbiamo pilastri di forma rettangolare, le cui dimentsioni sono le seguenti :
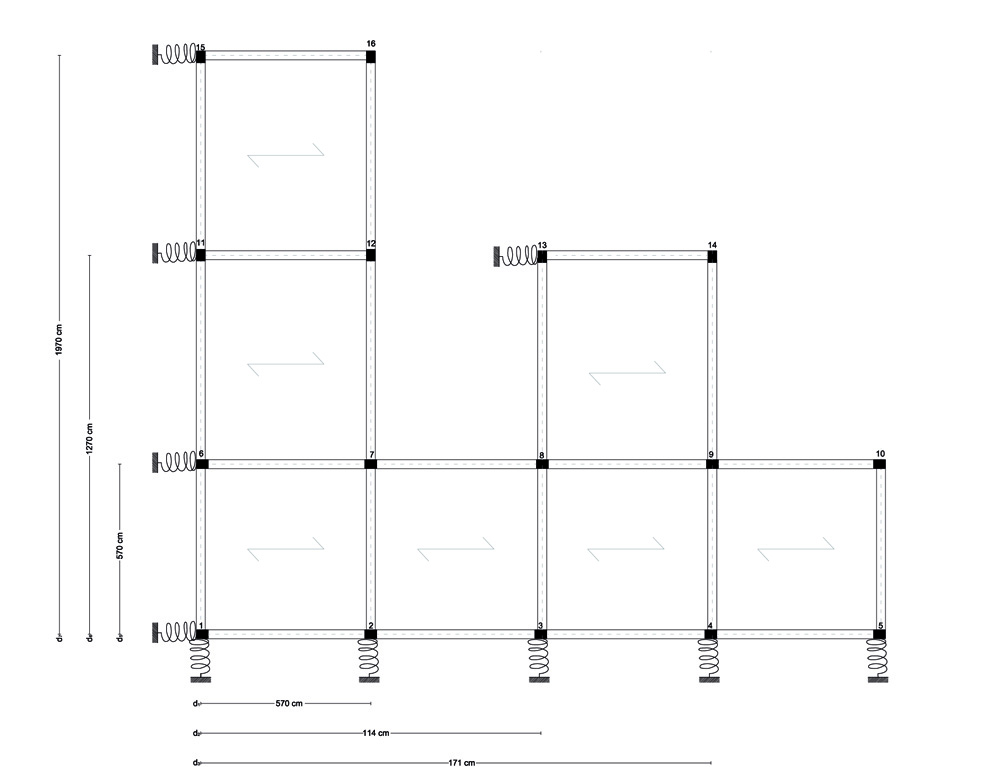
I controventi presentano un'elasticità che ci permette di considerarli cedevoli. Possono dunque essere semplificati con delle molle.
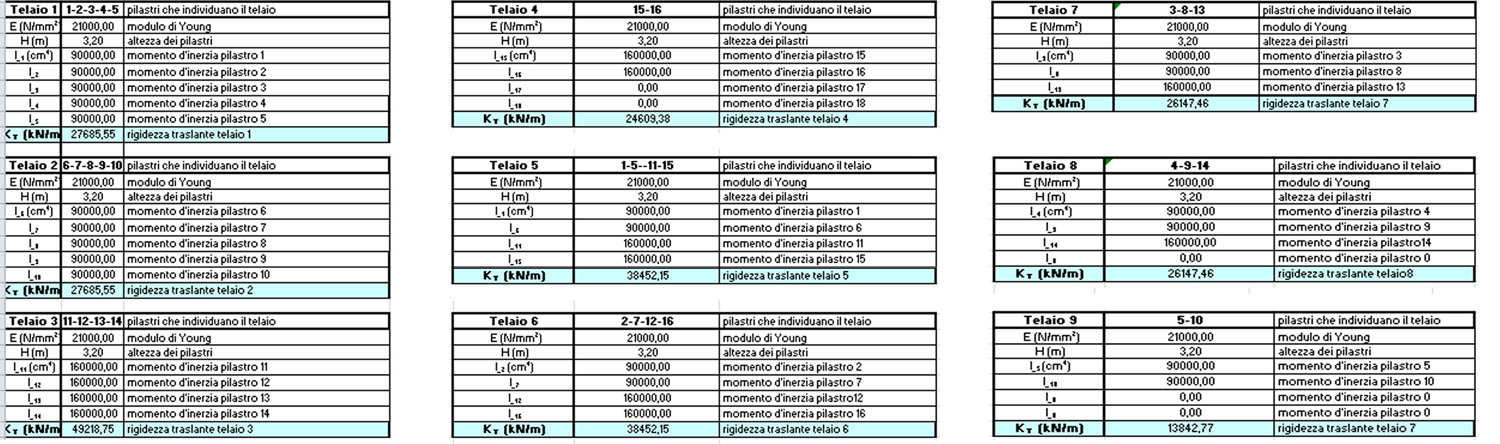
Verifichiamo l'efficacia dei controventi analizzando le loro rigidezze. Per farlo, occorre trovare il centro delle rigidezze e ripartire le forze orizzontali. Analizziamo il calcolo utilizzando un foglio excel.
STEP 1 : Calcolo delle rigidezze traslanti e dei controventi dell'edificio
Inserendo i seguenti dati nella tabella :
-
modulo di elasticità del Cls E=21000 N/mm2;
-
momento d'inerzia di ciascun pilastro ;
-
altezza dei pilastri (320 cm);
possiamo calcolare qual'è la rigidezza che i vari telai oppongono alla translazione lungo i loro assi.
STEP 2 : Tabella sinottica controventi e distanze
Vengono riportate le distanze verticali e orizzontali dei telai dal punto di origine O
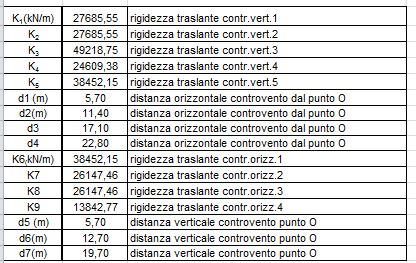
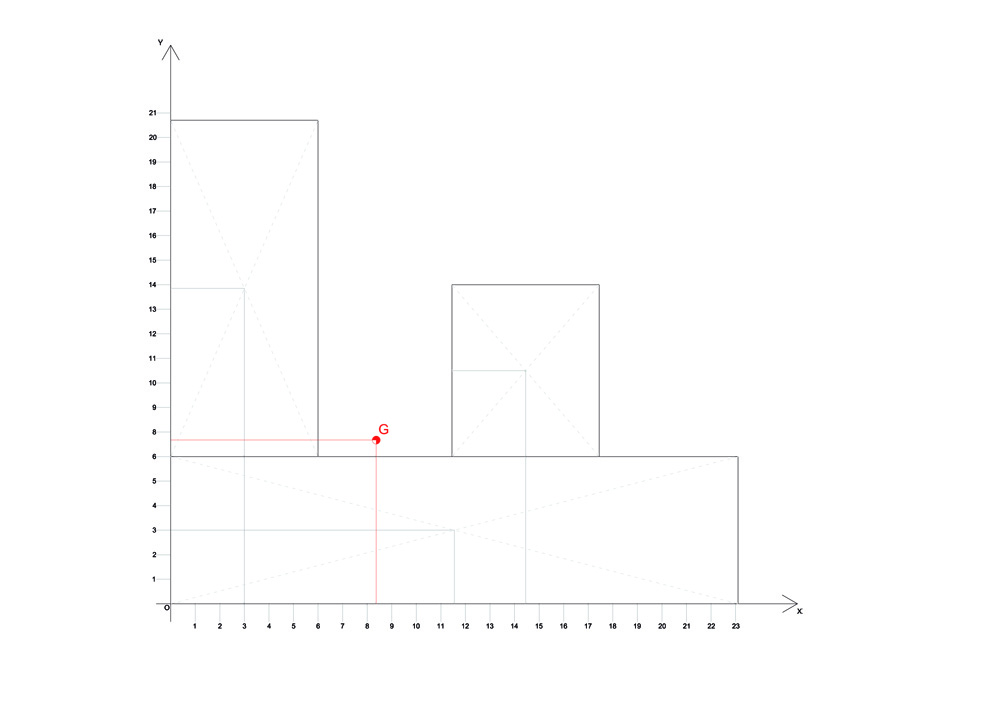
STEP 3 : Calcolo del centro di massa
Semplificando l'impalcato in forme semplici (rettangoli) , mi calcolo facilmente l'area di ogni rettangolo e calcolo il centro di massa facendo la somma delle cordinate lungo gli assi x e y, per l'area di ogni rettangolo suddiviso, diviso l'area totale.
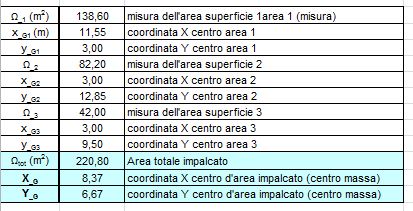
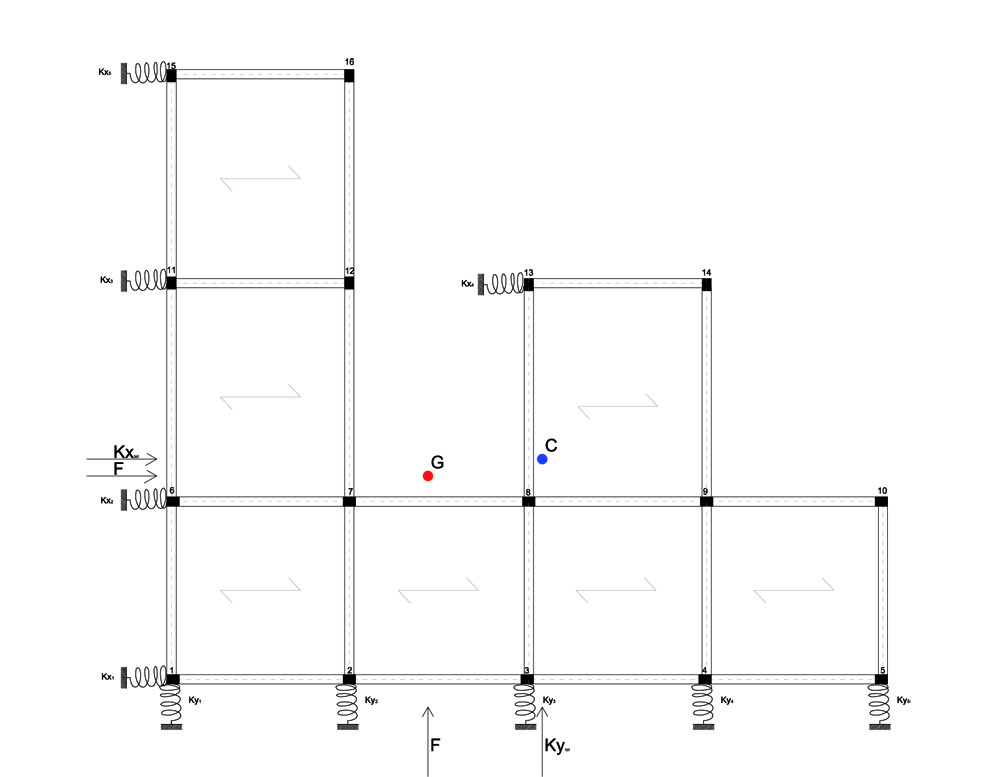
STEP 4 : Calcolo del centro di rigidezze e delle rigidezze globali
Il centro delle rigidezze è il centro del sistema di forze considerate, in cui viene applicata la risultante delle rigidezze traslanti dei controventi lungo l’asse x ed y. Nella tabella vengono indicate le distanze di ogni telaio dal centro di rigidezza e la rigidezza torsionale Kϕ, che è la rigidezza a rotazione di tutte le molle.
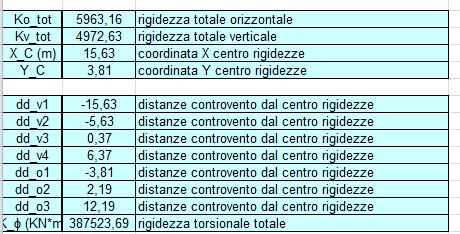
STEP 5 : Analisi dei carichi sismici
Vieni ora definita la forza sismica, applicata nel centro di massa. La somma del carico permanente totale e del carico totale accidentale , moltiplicata per il coefficiente di contemporaneità, ci dà il valore dei pesi sismici che divisi per il coefficiente di intensità sismica, ci danno il valore della forza sismica orizzontale.
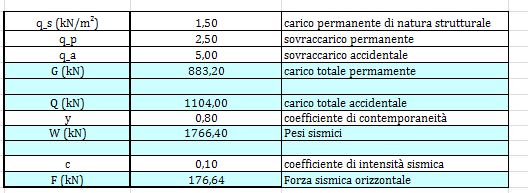
STEP 6 - 7 : Ripartizione della forza sismica lungo x e y
Possiamo ora analizzare come si ripartisce la forza sismica lungo gli assi x e y per ognuno dei controventi; trovando il momento torcente , moltiplicando la forza sismica per il suo braccio. Calcoliamo poi la traslazione orizzontale, dividendo la forza F per la rigidezza traslante orizzontale, e la traslazione verticale, dividendo la forza F per la rigidezza traslante verticale, e le rotazioni, dividendo i momenti torcenti, lungo x e y, per la rigidezza rotazionale.
Ripartizione della forza lungo l'asse x
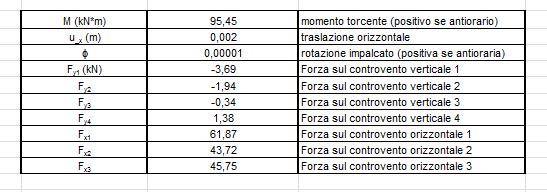
Ripartizione della forza lungo l'asse y
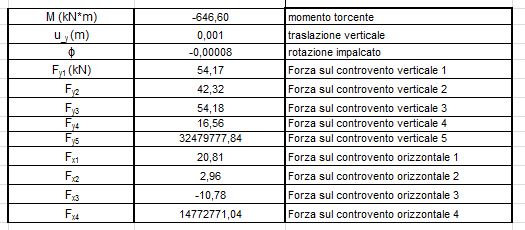
Commenti recenti