 Edificio della Prefettura - L'Aquila
Edificio della Prefettura - L'Aquila
Era il 6 aprile 2009 alle ore 3:32 quando la città de L'Aquila e i paesi circostanti venivano colpiti da una scossa sismica dell'VIII grado della scala Mercalli. I danni furono ingenti, sia per le vittime che per la molteplicità di beni storici e artistici devastati. In molti, subito dopo la sciagura, si appellarono alla negligenza dei progettisti, i quali avevano deliberatamente ignorato il DM 2008, il quale prevede una serie di normative atte alla progettazione di impalcati idonei a resistere all'azione delle spinte orizzontali, quali appunto il sisma. Per questo, oggigiorno, risulta assolutamente indispensabile per un progettista avere un bagaglio di conoscenze che gli permettano di progettare un edificio, la cui struttura comprenda degli elementi irrigidenti finalizzati all'assorbimento delle spinte orizzontali. Tali elementi vengono chiamati controventi.
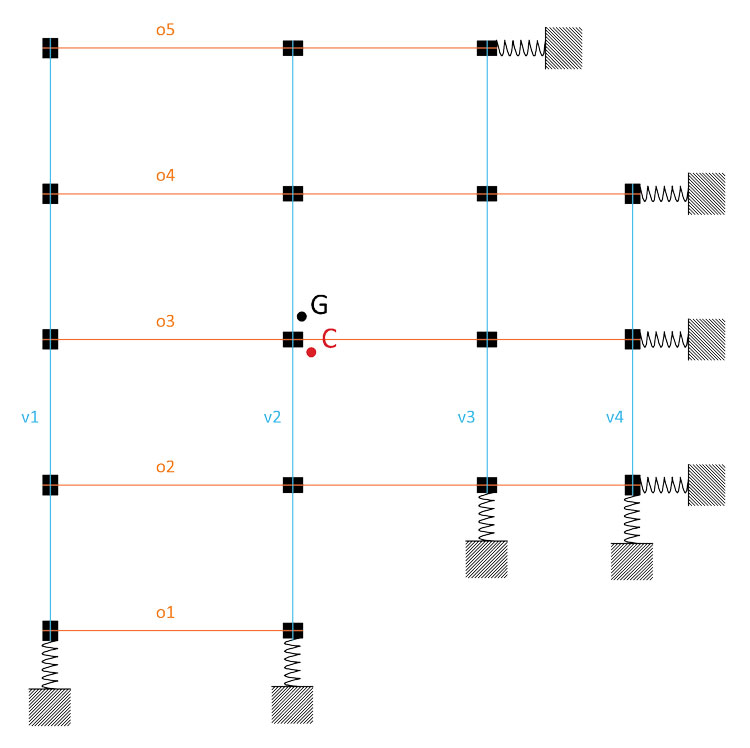
In questa esercitazione andremo quindi ad esaminare qual è l'azione di una forza orizzontale su di un impalcato così strutturato: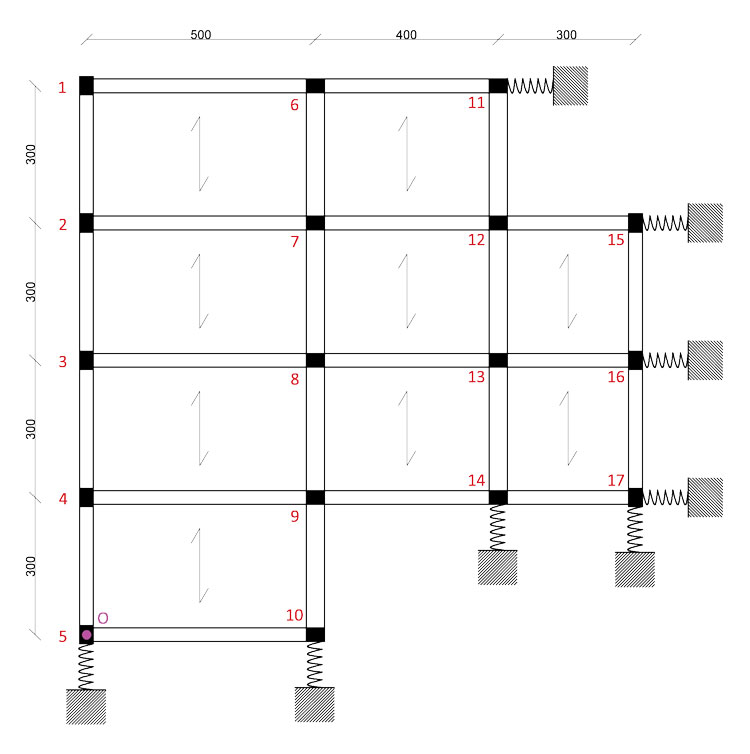
Dobbiamo innanzitutto fare due considerazioni:
- ipotizzando che il solaio sia un diaframma rigido, il suo comportamento meccanico sarà tale da poterlo equiparare a quello di un corpo rigido. Gli spostamenti che esso potrà compiere saranno, quindi, la traslazione orizzontale, la traslazione verticale e la rotazione;
- il comportamento meccanico dei telai invece è quello dei corpi elastici, che si deformano assorbendo il carico orizzontale come se fossero delle molle.
Giova inoltre sottolineare che, avendo i controventi delle rigidezze diverse, la struttura non trasla solamente, bensì, generandosi un braccio pari alla distanza del centro delle masse dal centro delle rigidezze, essa è soggetta anche a rotazione. Nel caso in cui il braccio fosse eccessivo, la struttura sarebbe soggetta ad un momento troppo grande che la porterebbe inevitabilmente al collasso.
Da notare, infine, che i pilastri dell'impalcato (30x40 cm) sono disposti secondo due orientamenti diversi e avranno quindi momenti d'inerzia diversi:
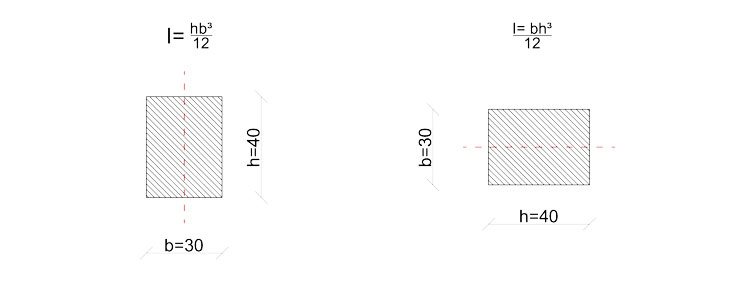
Ora, tramite un foglio di calcolo Excel, vediamo come si comporta il suddetto impalcato, quando è soggetto ad una forza orizzontale.
STEP 1: calcolo delle rigidezze traslanti dei controventi dell'edificio
Come primo passo, abbiamo calcolato la rigidezza traslante di ogni controvento costituente l'impalcato. A sinistra vi sono i telai paralleli l'asse y, mentre a destra lungo l'asse x. In tutto e due i casi la K_T risultante di ogni telaio deriva dalla formula:

che non è nient'altro che la formula del taglio in un corpo rigido, dove:
E = modulo di Young (21000 per il calcestruzzo)
ΣiJi = sommatoria dei momenti di inerzia di pilastri del telaio
h = altezza dei pilastri dell'impalcato

STEP 2: tabella sinottica controventi e distanze
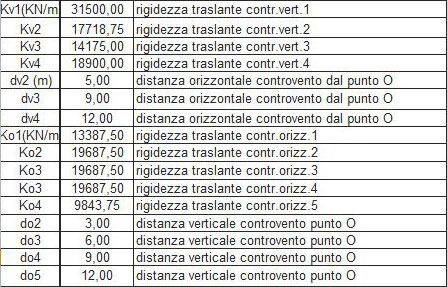
In questa tabella riassuntiva sono semplicemente riportate le rigidezze calcolate precedentemente e le distanze dei controventi dal punto O.
STEP 3: calcolo del centro di massa
Una volta stabilite le rigidezze dei telai e le loro distanze dall’origine O, l’impalcato è stato suddiviso in tre aree:
A1= 60 m² A2 = 36 m² A3 = 18 m²
delle quali sono stati calcolati i rispettivi centri di massa, semplicemente tracciando le diagonali di ogni rettangolo. Ottenute le coordinate relative, abbiamo calcolato il centro di massa dell’intera struttura tramite questa semplice formula:
XG = (A1 xG1 + A2 xG2 + A3 xG3) / (A1 + A2 + A3) = 5,18 m
YG = (A1 yG1 + A2 yG2 + A3 yG3) / (A1 + A2 + A3) = 6,47 m

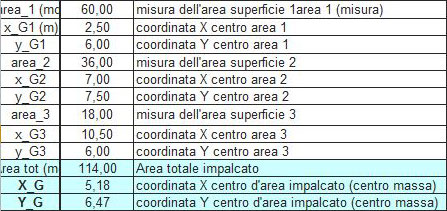
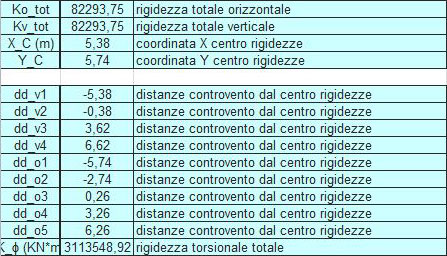
STEP 4: calcolo del centro di rigidezze e delle rigidezze globali
Con i dati fin qui raccolti possiamo trovare le coordinate del centro delle rigidezze, calcolando il rapporto tra la sommatoria delle rigidezze di ogni singolo telaio per la rispettiva distanza dal punto O, e la somma di tutte le rigidezze (prima verticali, poi orizzontali) :
Xc = Σi kvdv / kv tot.
Yc = Σi kodo / ko tot.
Nella tabella troviamo inoltre la variabile dd, che indica la distanza dei controventi dal centro delle rigidezze C, dato che C è il punto attorno al quale il corpo ruota nel caso in cui la forza orizzontale fosse applicata nel centro di massa G non coincidente con C. Quindi il centro delle rigidezze è posto vicino al controvento più rigido. Inoltre le distanze dd hanno un segno, perchè a seconda di dove sono posti i telai ho, rispetto a C, una rotazione oraria o antioraria.
Infine è possibile calcolare anche la rigidezza torsionale totale pari a:
kΦ = Σiki ddi2
STEP 5: analisi dei carichi sismici
La forza sismica è data dal prodotto della massa dell’edificio e dell’accelerazione di trascinamento del suolo. Quest’ultimo valore è stabilito dalla normativa e corrisponde ad una frazione dell’accelerazione di gravità.
F = m a
a = c g dove c < 1 che corrisponde al coefficiente di intensità sismica.
quindi F = m c g = c (mg) dove mg = Peso
--> F = c P
La forza sismica è una frazione della forza peso, quindi, più un elemento è pesante, più è vulnerabile alla forza sismica.
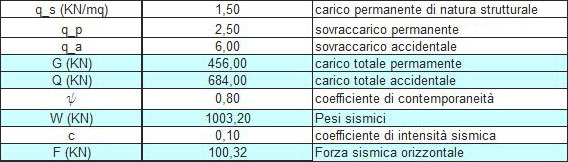
Per trovare la forza sismica calcoliamo, quindi, il peso dell'impalcato P, dopo aver definito i carichi strutturali, accidentali e permanenti che agiscono sulla struttura:
W = G + (Q ψ)
W = peso sismico
G = carico totale permanente = (qs + qp) Atot
ψ = coefficiente di contemporaneità, dato dalla normativa, che diminuisce il carico accidentale.
Q = carico totale accidentale = qa Atot
STEP 6: ripartizione della forza sismica lungo l'asse x e lungo l'asse y
Ora non rimane che analizzare la ripartizione della forza sismica lungo entrambi gli assi, dato che, come sappiamo, l’azione del sisma è particolarmente incerta ed aleatoria. Infatti, con buona pace dei naturalisti, è impossibile prevedere con esattezza la data della manifestazione dell'episodio sismico e tantomeno definire l'asse secondo cui esso si scatenerà.
Inoltre, come detto, la forza sismica non agisce mai secondo la direttrice su cui giace il centro delle rigidezze, generando così un momento torcente che provoca la rotazione dei controventi in entrambe le direzioni.
Per calcolare perciò suddetto momento torcente nelle due direzioni, possiamo applicare:
My = F (XC - XG)
Mx = F (YC - YG)
dove (YC - YG) è il braccio della forza, ovvero la distanza tra la coordinata Y del centro delle rigidezze e quella del centro di massa.
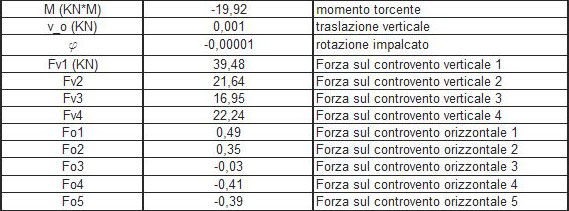
Dopo aver calcolato il momento torcente, la traslazione (orizzontale e verticale) e la rotazione è possibile definire come la forza sismica si ripartisce su ogni controvento in base alla rigidezza dei controventi stessi:
FxO= KxO * ddxO * ϕx per i controventi orizzontali
FyO= KyO * ddyO * ϕy per i controventi verticali
Ripartizione della forza sismica lungo l'asse X:
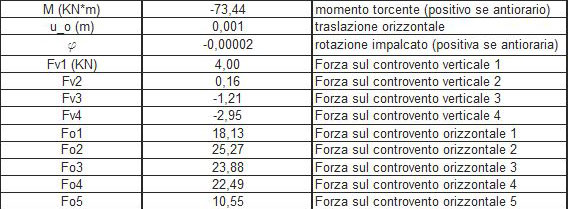
Ripartizione della forza sismica lungo l'asse Y:
Commenti recenti