
GRATICCIO
Si fa riferimento al modello di telaio utilizzato nella prima esercitazione e del relativo dimensionamento di travi e pilastri in calcestruzzo armato.
CALCOLO “N” PILASTRI SUPERIORI
Calcolo dell’area di influenza del pilastro “1”
a = 4m (vedi pianta strutturale)
b = 6m (vedi pianta strutturale)
Ainfl. pilastro = a x b
Ainfl. pilastro = 4m x 6m = 24m2
Calcolo del peso delle travi presenti nell’area di influenza
Calcolo dell’area della sezione della trave precedentemente dimensionata:
Asez. trave = bsez. trave x hsez. trave
bsez. trave = 30cm (vedi “dimensionamento travi”)
hsez. trave = 40cm (vedi “dimensionamento travi”)
Asez. trave = 30cm x 40cm = 1200 cm2 = 0,12m2
Individuazione del peso specifico del materiale della trave:
gmater. trave = 25kN/m3 (calcestruzzo armato)
Calcolo del carico a metro lineare esercitato delle travi:
traveprincipale = travesecondaria = Asez. Trave x gmater. trave
traveprincipale = travesecondaria = 0,12m2 x 25kN/m3 = 3kN/m
Calcolo del carico esercitato dalle travi nell’area di influenza del pilastro maggiormente sollecitato:
qtravi = 1,3 x a x travesecondaria + 1,3 x b x traveprincipale
qtravi = 1,3 x 4m x 3kN/m + 1,3 x 6m x 3kN/m = 39kN
Calcolo del peso della porzione di solaio presente nell’area di influenza
qsolaio = (1,3 x qs + 1,5 x qp + 1,5 x qa) x Ainfl. pilastro
qs = 3,058kN/m2 (vedi “dimensionamento travi”)
qp = 2,84kN/m2 (vedi “dimensionamento travi”)
qa = 2kN/m2 (vedi “dimensionamento travi”)
qsolaio = (1,3 x 3,058kN/m2 + 1,5 x 2,84kN/m2 + 1,5 x 2kN/m2) x 24m2 = 269,6496kN
CALCOLO DELLO SFORZO NORMALE AGENTE SUL PILASTRO “1”
N = (qtravi + qsolaio) x n°piani
n°piani = 2 (vedi sezione strutturale)
N = (39kN + 296,6496kN) x n°piani = 617,2992Kn
Calcolo dell’area di influenza del pilastro “2”
a = 2m (vedi pianta strutturale)
b = 6m (vedi pianta strutturale)
Ainfl. pilastro = a x b
Ainfl. pilastro = 2m x 6m = 12m2
Calcolo del peso delle travi presenti nell’area di influenza
Calcolo dell’area della sezione della trave precedentemente dimensionata:
Asez. trave = bsez. trave x hsez. trave
bsez. trave = 30cm (vedi “dimensionamento travi”)
hsez. trave = 40cm (vedi “dimensionamento travi”)
Asez. trave = 30cm x 40cm = 1200 cm2 = 0,12m2
Individuazione del peso specifico del materiale della trave:
gmater. trave = 25kN/m3 (calcestruzzo armato)
Calcolo del carico a metro lineare esercitato delle travi:
traveprincipale = travesecondaria = Asez. Trave x gmater. trave
traveprincipale = travesecondaria = 0,12m2 x 25kN/m3 = 3kN/m
Calcolo del carico esercitato dalle travi nell’area di influenza del pilastro maggiormente sollecitato:
qtravi = 1,3 x a x travesecondaria + 1,3 x b x traveprincipale
qtravi = 1,3 x 2m x 3kN/m + 1,3 x 6m x 3kN/m = 31,2kN
Calcolo del peso della porzione di solaio presente nell’area di influenza
qsolaio = (1,3 x qs + 1,5 x qp + 1,5 x qa) x Ainfl. pilastro
qsolaio = (1,3 x 3,058kN/m2 + 1,5 x 2,84kN/m2 + 1,5 x 2kN/m2) x 12m2 = 134,82kN
CALCOLO DELLO SFORZO NORMALE AGENTE SUL PILASTRO “2”
N = (qtravi + qsolaio) x n°piani
n°piani = 2 (vedi sezione strutturale)
N = (31,2kN + 134,82kN) x n°piani = 332,04kN
Calcolo dell’area di influenza del pilastro “3”
a = 4m (vedi pianta strutturale)
b = 3m (vedi pianta strutturale)
Ainfl. pilastro = a x b
Ainfl. pilastro = 4m x 3m = 12m2
Calcolo del peso delle travi presenti nell’area di influenza
Calcolo dell’area della sezione della trave precedentemente dimensionata:
Asez. trave = bsez. trave x hsez. trave
bsez. trave = 30cm (vedi “dimensionamento travi”)
hsez. trave = 40cm (vedi “dimensionamento travi”)
Asez. trave = 30cm x 40cm = 1200 cm2 = 0,12m2
Individuazione del peso specifico del materiale della trave:
gmater. trave = 25kN/m3 (calcestruzzo armato)
Calcolo del carico a metro lineare esercitato delle travi:
traveprincipale = travesecondaria = Asez. Trave x gmater. trave
traveprincipale = travesecondaria = 0,12m2 x 25kN/m3 = 3kN/m
Calcolo del carico esercitato dalle travi nell’area di influenza del pilastro maggiormente sollecitato:
qtravi = 1,3 x a x travesecondaria + 1,3 x b x traveprincipale
qtravi = 1,3 x 4m x 3kN/m + 1,3 x 3m x 3kN/m = 27,3kN
Calcolo del peso della porzione di solaio presente nell’area di influenza
qsolaio = (1,3 x qs + 1,5 x qp + 1,5 x qa) x Ainfl. pilastro
qsolaio = (1,3 x 3,058kN/m2 + 1,5 x 2,84kN/m2 + 1,5 x 2kN/m2) x 12m2 = 134,82kN
CALCOLO DELLO SFORZO NORMALE AGENTE SUL PILASTRO
N = (qtravi + qsolaio) x n°piani
n°piani = 2 (vedi sezione strutturale)
N = (27,3kN + 134,82kN) x n°piani = 324,24kN
Calcolo dell’area di influenza del pilastro “4”
a = 2m (vedi pianta strutturale)
b = 3m (vedi pianta strutturale)
Ainfl. pilastro = a x b
Ainfl. pilastro = 2m x 3m = 6m2
Calcolo del peso delle travi presenti nell’area di influenza
Calcolo dell’area della sezione della trave precedentemente dimensionata:
Asez. trave = bsez. trave x hsez. trave
bsez. trave = 30cm (vedi “dimensionamento travi”)
hsez. trave = 40cm (vedi “dimensionamento travi”)
Asez. trave = 30cm x 40cm = 1200 cm2 = 0,12m2
Individuazione del peso specifico del materiale della trave:
gmater. trave = 25kN/m3 (calcestruzzo armato)
Calcolo del carico a metro lineare esercitato delle travi:
traveprincipale = travesecondaria = Asez. Trave x gmater. trave
traveprincipale = travesecondaria = 0,12m2 x 25kN/m3 = 3kN/m
Calcolo del carico esercitato dalle travi nell’area di influenza del pilastro maggiormente sollecitato:
qtravi = 1,3 x a x travesecondaria + 1,3 x b x traveprincipale
qtravi = 1,3 x 2m x 3kN/m + 1,3 x 3m x 3kN/m = 19,5kN
Calcolo del peso della porzione di solaio presente nell’area di influenza
qsolaio = (1,3 x qs + 1,5 x qp + 1,5 x qa) x Ainfl. pilastro
qsolaio = (1,3 x 3,058kN/m2 + 1,5 x 2,84kN/m2 + 1,5 x 2kN/m2) x 24m2 = 67,41kN
CALCOLO DELLO SFORZO NORMALE AGENTE SUL PILASTRO
N = (qtravi + qsolaio) x n°piani
n°piani = 2 (vedi sezione strutturale)
N = (19,5kN + 67,41kN) x n°piani = 173,82Kn
Il pilastro “1” trasmette al graticcio una forza concentrata pari a 617kN.
I pilastri “2” trasmettono al graticcio una forza concentrata pari a 332kN.
I pilastri “3” trasmettono al graticcio una forza concentrata pari a 324kN.
I pilastri “4” trasmettono al graticcio una forza concentrata pari a 174kN.
PESO SOLAIO GRATICCIO
Si ipotizza:
qu = 10kN/m2
CALCOLO MOMENTI MASSIMO GRATICCIO
Si utilizzano i carichi individuati per l’analisi del graticcio scelto in Sap2000.
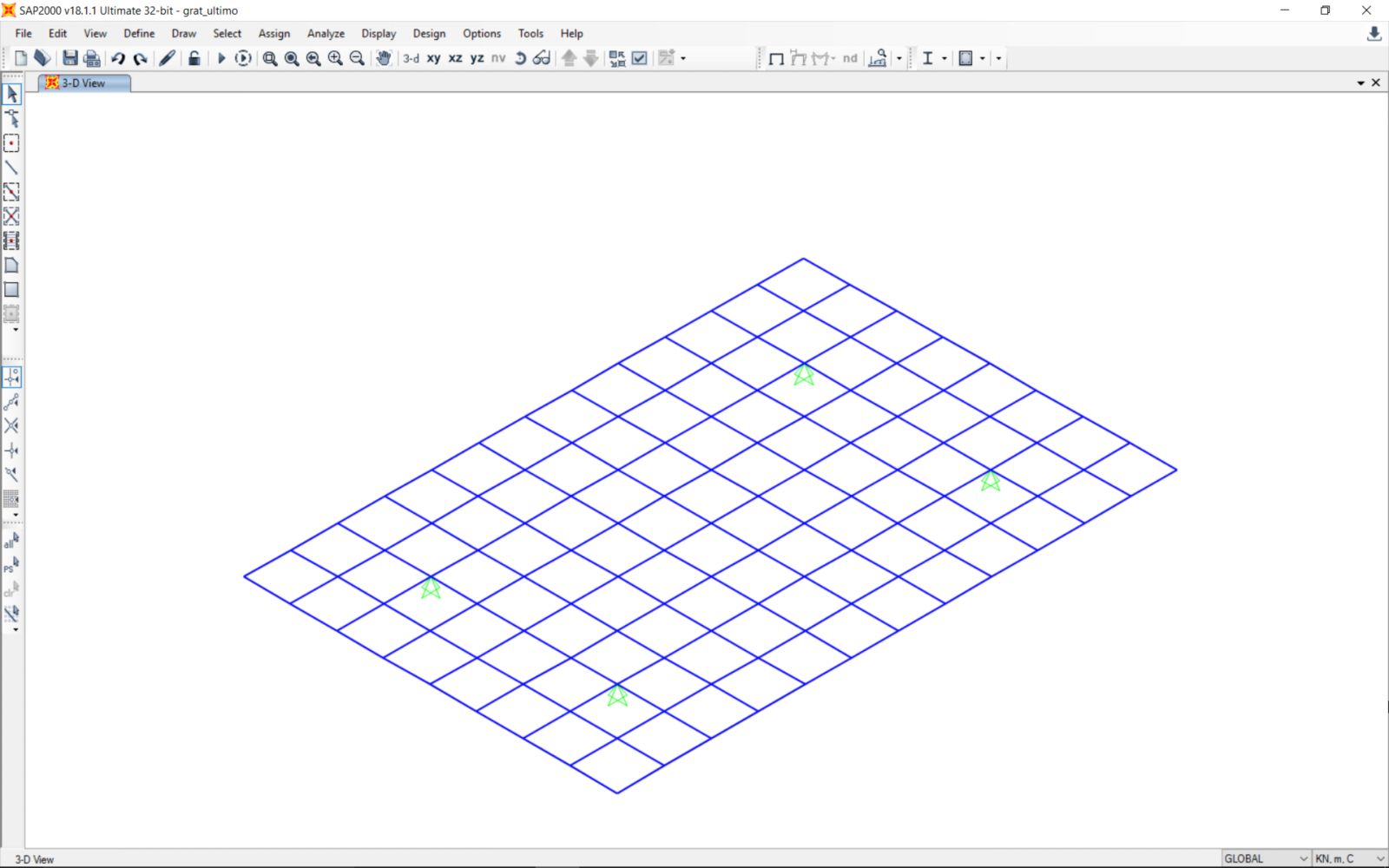
Una volta importata la griglia 8m x 12m in formato .dxf, si pongono i vincoli nei nodi corrispondenti ai pilastri inferiori. Ci si assicura quindi che ogni tratto della griglia corrisponda ad una singola trave (comando “break at intersection”).
Si ipotizza per le travi in calcestruzzo armato classe C35/45 che compongono il graticcio una sezione rettangolare di 30cm x 50 cm.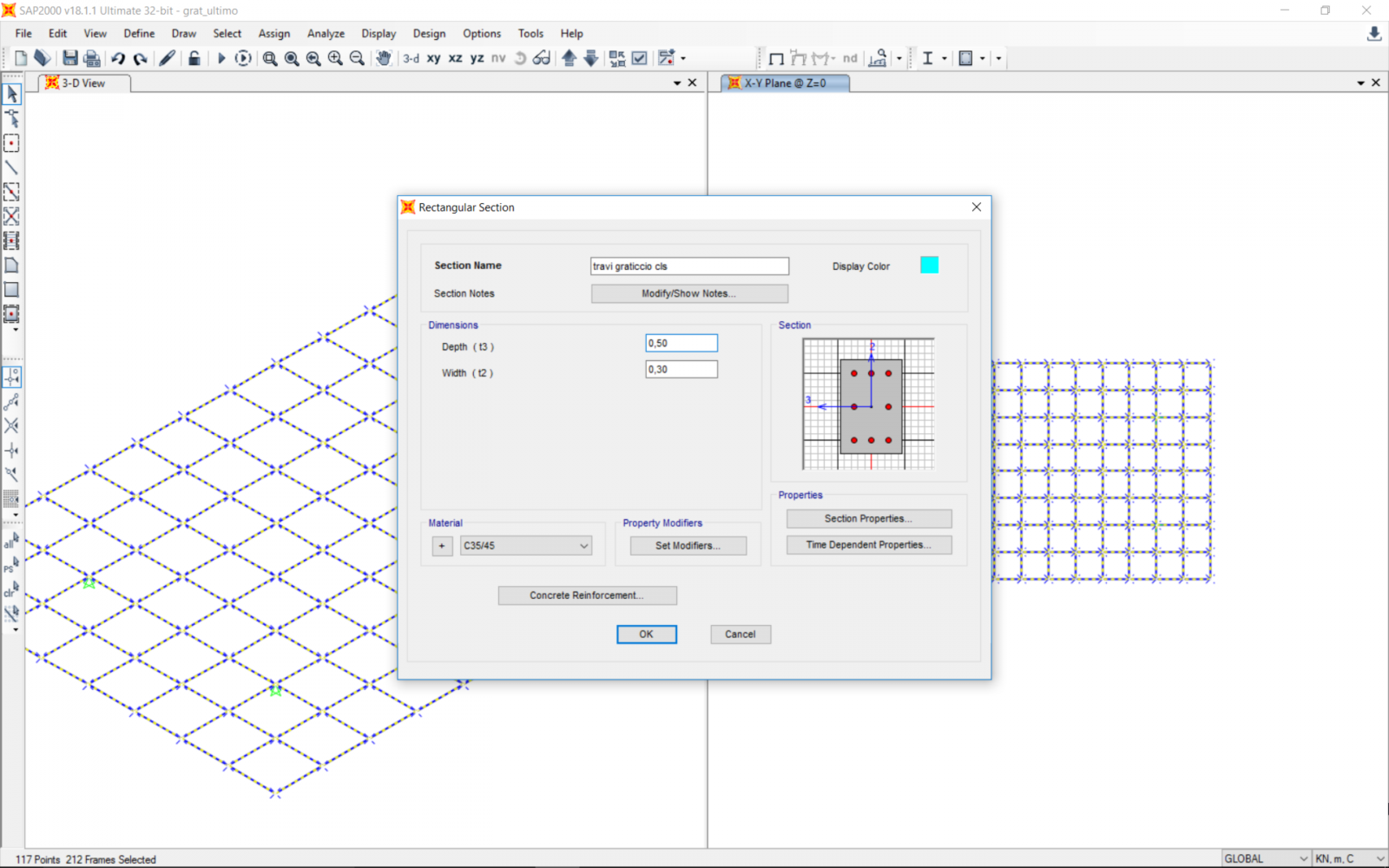
Segue la definizione dei carichi relativi ai pilastri del telaio superiore, agenti nei relativi nodi, e quella di qu, che corrisponde a 5kN/m sulle travi centrali e a 2,5kN/m su quelle di bordo.
Si può quindi lanciare l’analisi di Sap2000, considerando tutti i carichi inseriti.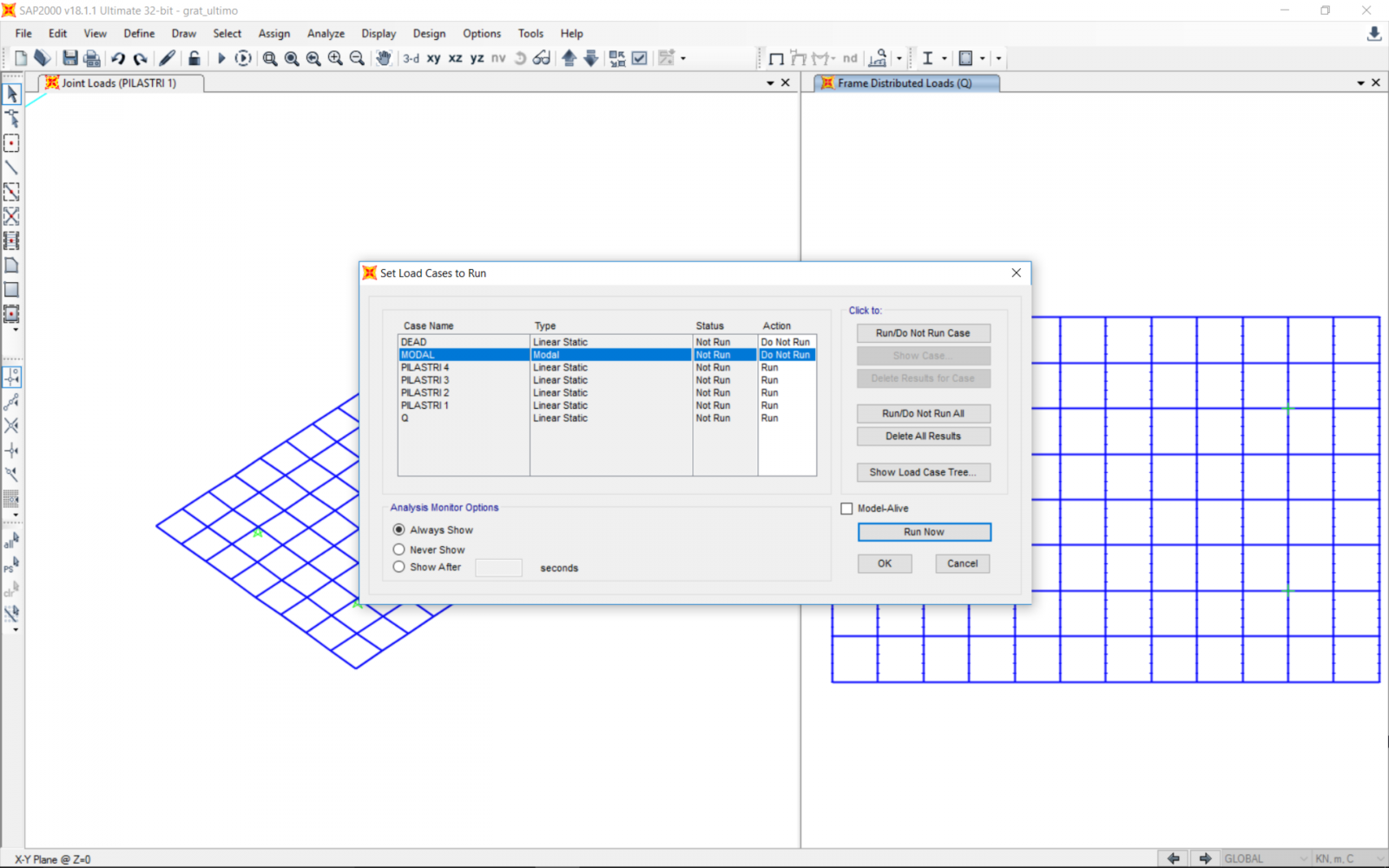
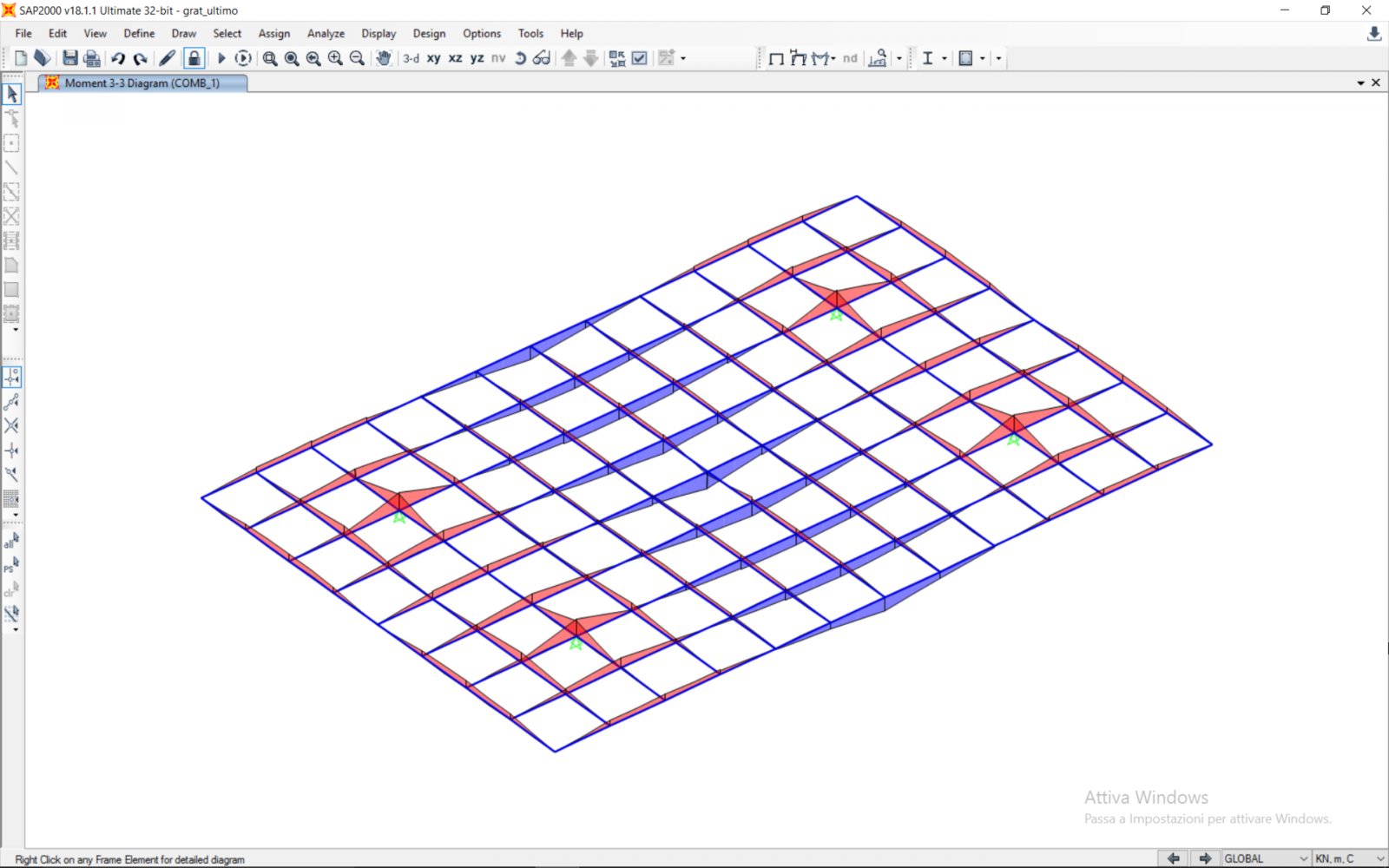
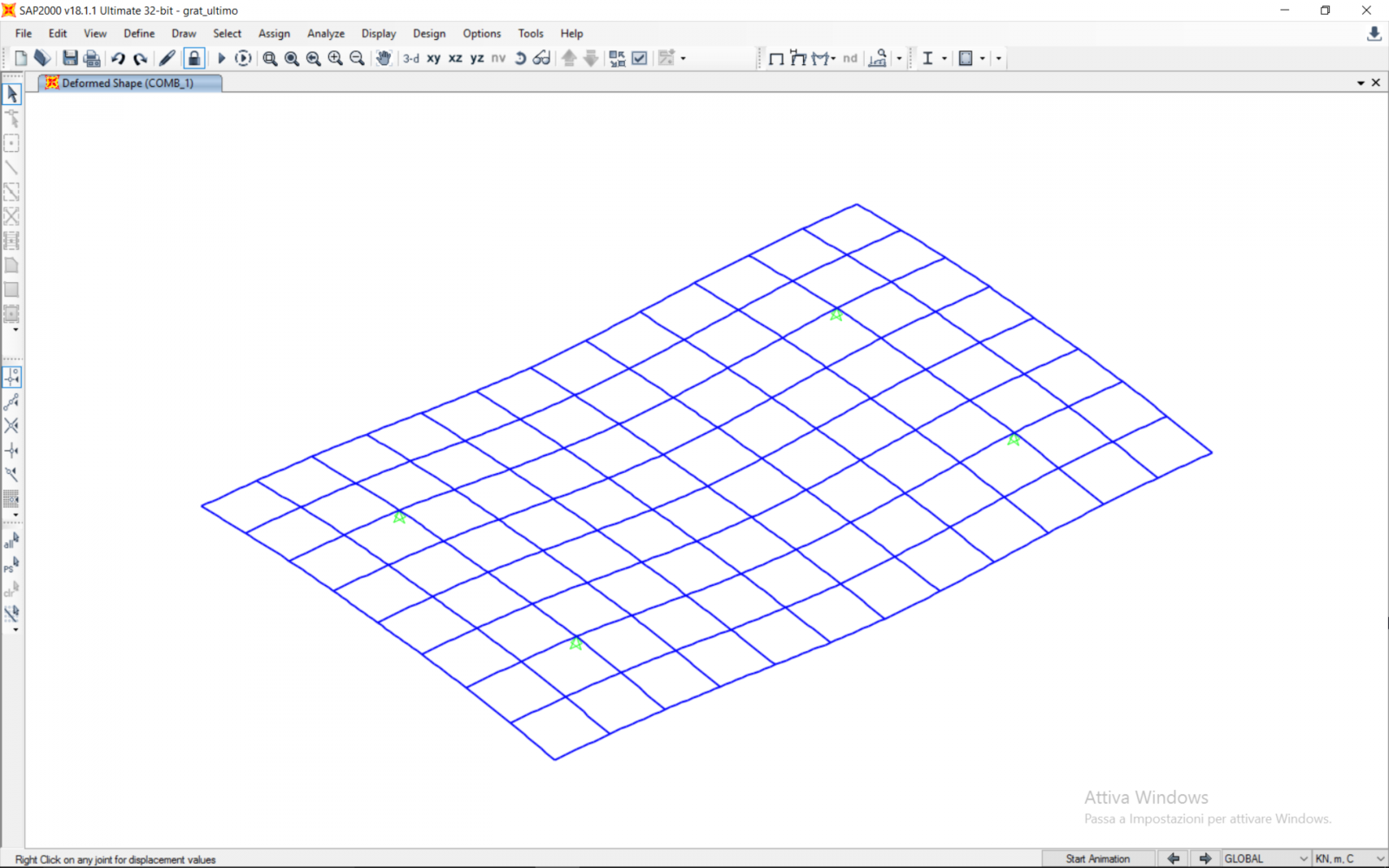
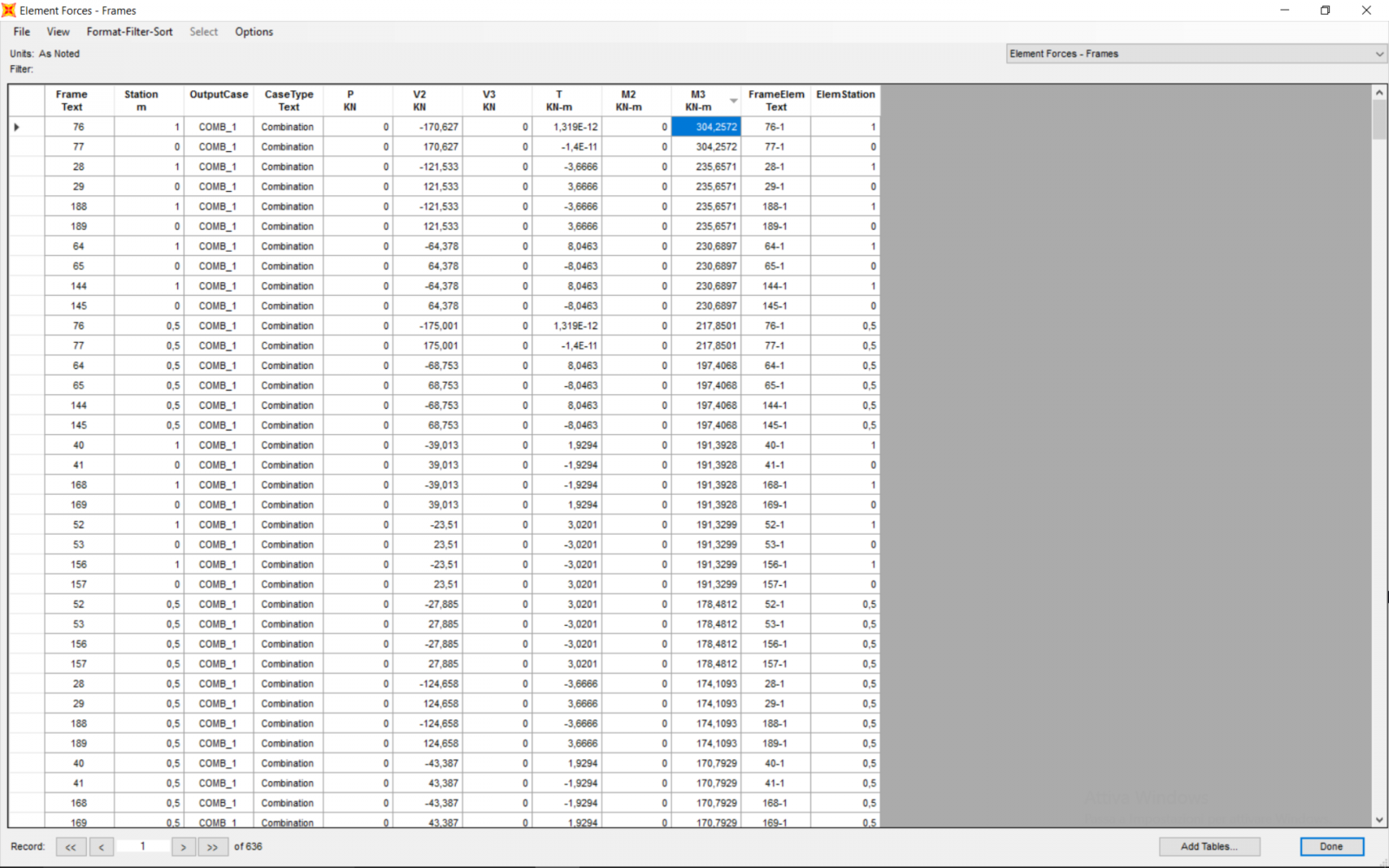
Secondo i risultati dell’analisi:
Mmax = 304,2572 kNxm
Questo momento interessa i tratti sotto evidenziati:
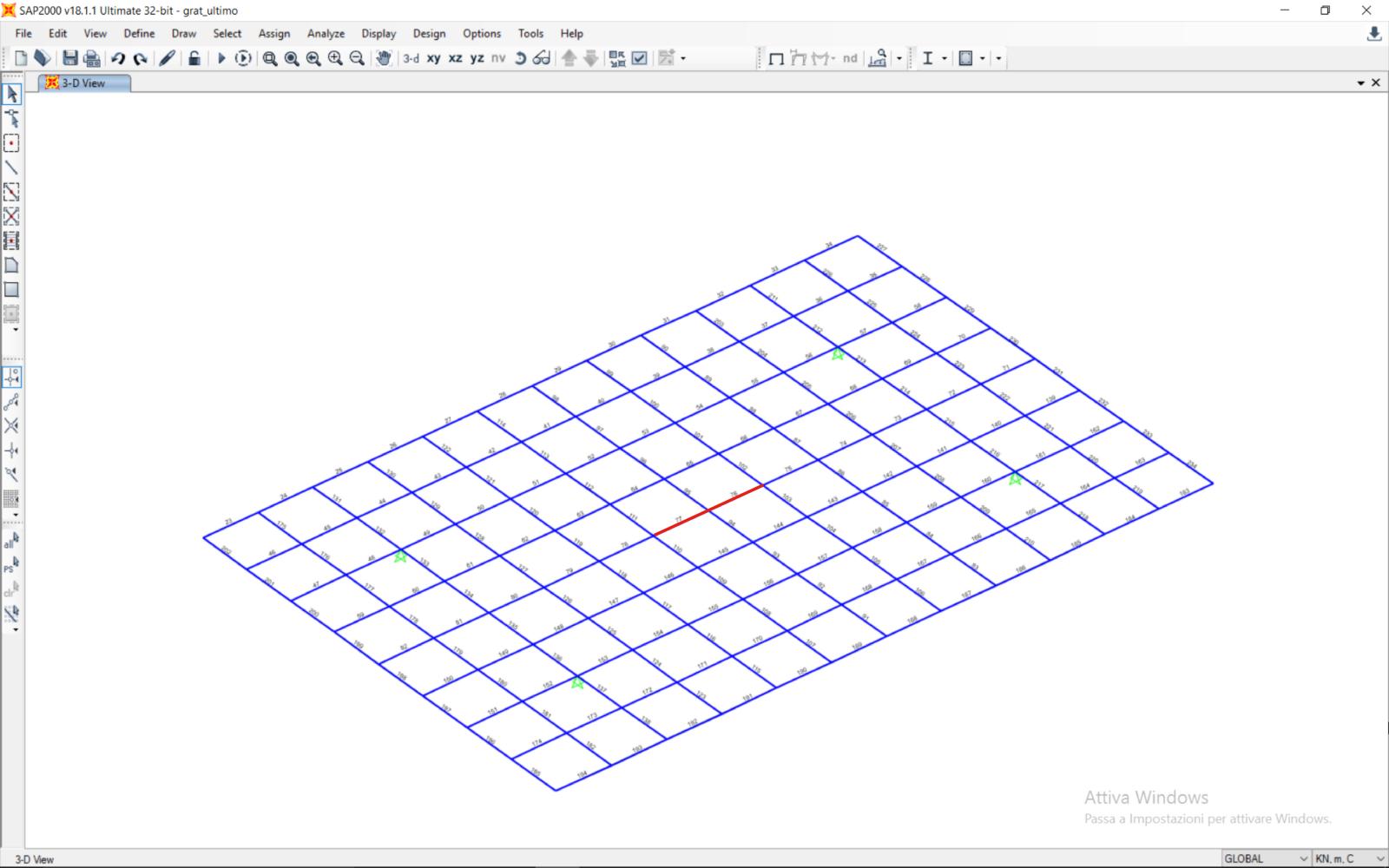
DIMENSIONAMENTO TRAVE GRATICCIO
Conoscendo il momento massimo, è possibile dimensionare la trave utilizzando il medesimo procedimento della prima esercitazione e il relativo file .xls.
Le travi del graticcio avranno dunque una sezione di dimensioni 30cm x 45cm.
Il peso proprio della trave non viene considerato, poiché già imposto durante l’analisi su Sap2000, attraverso il comando “self weight multiplier”.


Commenti recenti