La trave reticolare è una struttura caratterizzata da una struttura composta da aste, unite tra loro da cerniere interne che tra loro si trasmettono il momento. Queste aste sono legate in un modulo triangolare, che ripetuto genera una struttura che è caratterizzata da due correnti orizzontali che sono rispettivamente, uno teso e uno compresso.
Con SAP è stato possibile creare una trave reticolare, utilizzando un modello preimpostato, inserendo solo le dimensioni delle varie parti. L’altezza e la lunghezza della campata sono state messe in rapporto 1:2 (rispettivamente 3 e 6m), in modo che l’angolo che si forma tra le aste sia di 45°.
Per fare in modo che il modello di SAP risponda al modello di trave reticolare reale, è necessario trasformare i nodi da incastri a cerniere, andando a togliere un grado di vincolo.
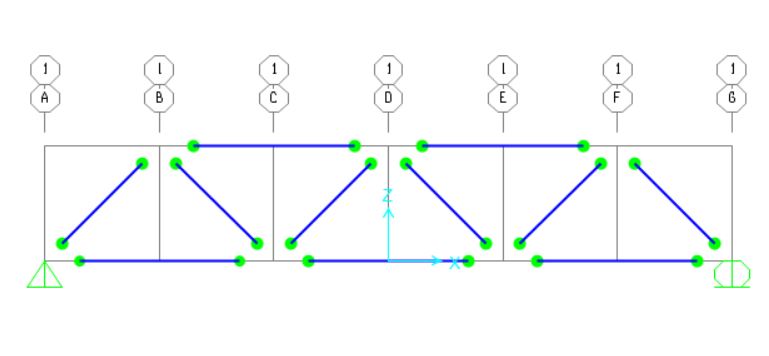Per capire il comportamento della trave, è necessario sottoporla a dei carichi, che si sceglie di inserire nei nodi in alto, di intensità uguale in ogni nodo.
Si genera così una struttura simmetrica sia geometricamente che dal punto di vista delle forze.Le reazioni vincolari in una struttura simile si ripartiscono in modo simmetrico, andando a dividersi nelle due cerniere esterne.
Infine è necessario per l’analisi in SAP, stabilire le caratteristiche della sezione della trave: si è scelta perciò una sezione in acciaio tubolare rotonda.
A questo punto è possibile fare l’analisi delle sollecitazioni: guardando i grafici delle varie sollecitazioni è possibile fare alcune considerazioni:
- I grafici delle sollecitazioni sono simmetrici rispetto all’asse baricentrico della trave;
- L’unica sollecitazione che avviene all’interno della trave è lo sforzo normale, che si trasmette in modo sia positivo sia negativo sulle aste, rispettando la simmetria precedentemente detta;
- Le aste dove lo sforzo normale è positivo sono dei tiranti, che vengono allungati, mentre dove lo sforzo normale è negativo si hanno dei puntoni, che vengono compressi;
- I correnti orizzontali rispettano il modello di trave reticolare, essendo uno teso (inferiore) e uno compresso (superiore);
- Le aste inclinate interne sono quelle che presentano minore sforzo normale, mentre lungo “il perimetro esterno” lo sforzo normale è molto più concentrato, sia nei tiranti esterni sia lungo i due correnti: tuttavia l’asta più sollecitata è quella centrale del corrente inferiore, in quanto è quella corrispondente al centro di simmetria della trave.
La deformata della trave, coerentemente alle sollecitazioni, si incurva verso il centro, abbassandosi, per permettere l’allungamento delle fibre del corrente teso, che sono massime in corrispondenza dell’asta risulta centrale, mentre risulta accorciata (e quindi presenta fibre compresse) nel corrente superiore. La deformazione avviene verso il basso, coerentemente ai carichi che gli sono stati applicati.
Attraverso l’uso di SAP è stato possibile esportare attraverso una tabella i valori dei vari sforzi assiali, che grazie ad excel sono stati ordinati per capire in modo chiaro quale fossero le aste più sollecitate, e si è potuto avere conferma ulteriore sia di questo sia dei valori nulli di taglio e momento all’interno della trave.
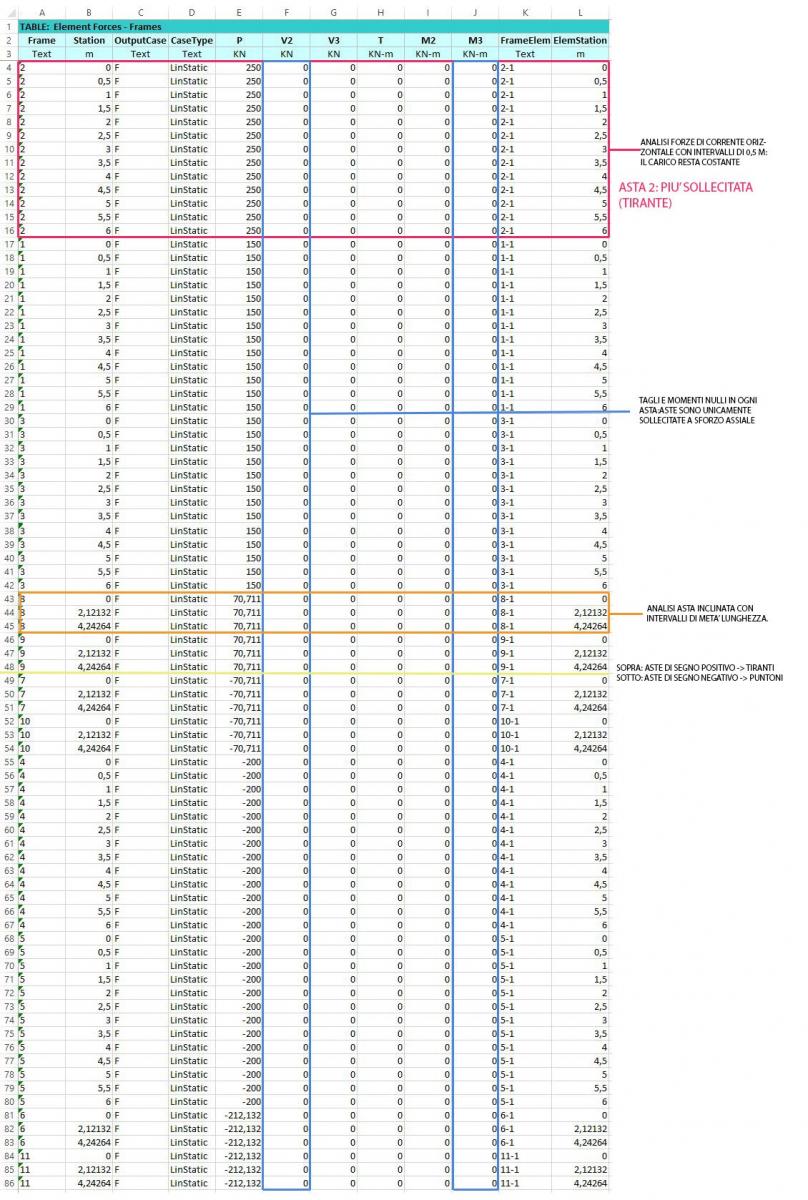
La tabella ha presentato un'analisi delle varie aste, che vengono divisi per intervalli di lunghezza, dimostrando come le varie sollecitazioni restino costanti; inoltre attraverso i segni delle lunghezze è possibile risalire a quali aste si comportino come tiranti (positive) e quali come puntoni (negative).
Questi dati, vengono confermati dalla tabella sottostante, che invece analizza i risultati delle aste nei nodi, che coincidono con i vincoli. A livello di risultati, l'unica differenza è che nelle aste inclinate, il risultato è diviso per componenti (es. N6sena, N6cosa), però vengono confermati i risultati delle aste orizzontali, che dimostrano come la reazione del vincolo della cerniera interna coincida con lo sforzo assiale.
Nella risoluzione a mano si è trovato conferma dei risultati ottenuti con SAP. Le reazioni vincolari sono state risolte sfruttando la simmetria della trave, risultando coincidenti con quelle calcolate dal programma.
L’analisi delle sollecitazioni è stata fatta attraverso l’utilizzo sia del metodo Richter, che attraverso l’equilibrio dei vari nodi:
Con la sezione di Richter si è fatto un taglio nelle prime tre aste (1,4,9), inserendo delle forze incognite che sono gli sforzi normale presenti nelle rispettive aste.
Il primo passaggio è stato il calcolo dell’equilibrio dei momenti nel nodo 2 perché era l’unico dove N1 ed N9 vi convergevano, risultando quindi nulle:
N4 x h + 3/2 F x l – F x l/2 =0
N4= ( Fl/2 – 3FL/2) x 1/h -> N4= (-100 x 6) KNm /3m = -200 KN
Il meno davanti ad N4 significa che la direzione con cui è stato inizialmente ipotizzato non era corretta, ma è diretto in senso opposto.
È stato poi effettuato l’equilibrio a traslazione verticale:
3F/2 – N9senα – F =0
N9senα= (3F/2 –F)= F/2= 50 KN
N9= 50 KN/ senα =70,7 KN
In questo caso il segno positivo, è conferma del fatto che il verso dello sforzo era stato correttamente ipotizzato.
Si è trovata N1 con l’equilibrio a traslazione orizzontale:
N1 – N4 + N9cosα =0
N1= N4- N9cosα= 200 – 50 KN = 150 KN
Si è poi passato allo studio dell’equilibrio delle forze che convergevano nei nodi, in modo di risolvere via via gli sforzi incogniti.
NODO 5
Equilibrio a traslazione orizzontale:
N6cosα + N9cosα – N4=0
N6cosα= N4 – N9 cosα= (200- 50)KN = 150 KN
N6= 150 KN / cosα = 212,1 KN
Equilibrio a traslazione verticale:
N6senα – N9senα – F =0
N6senα= 150 KN
NODO 2
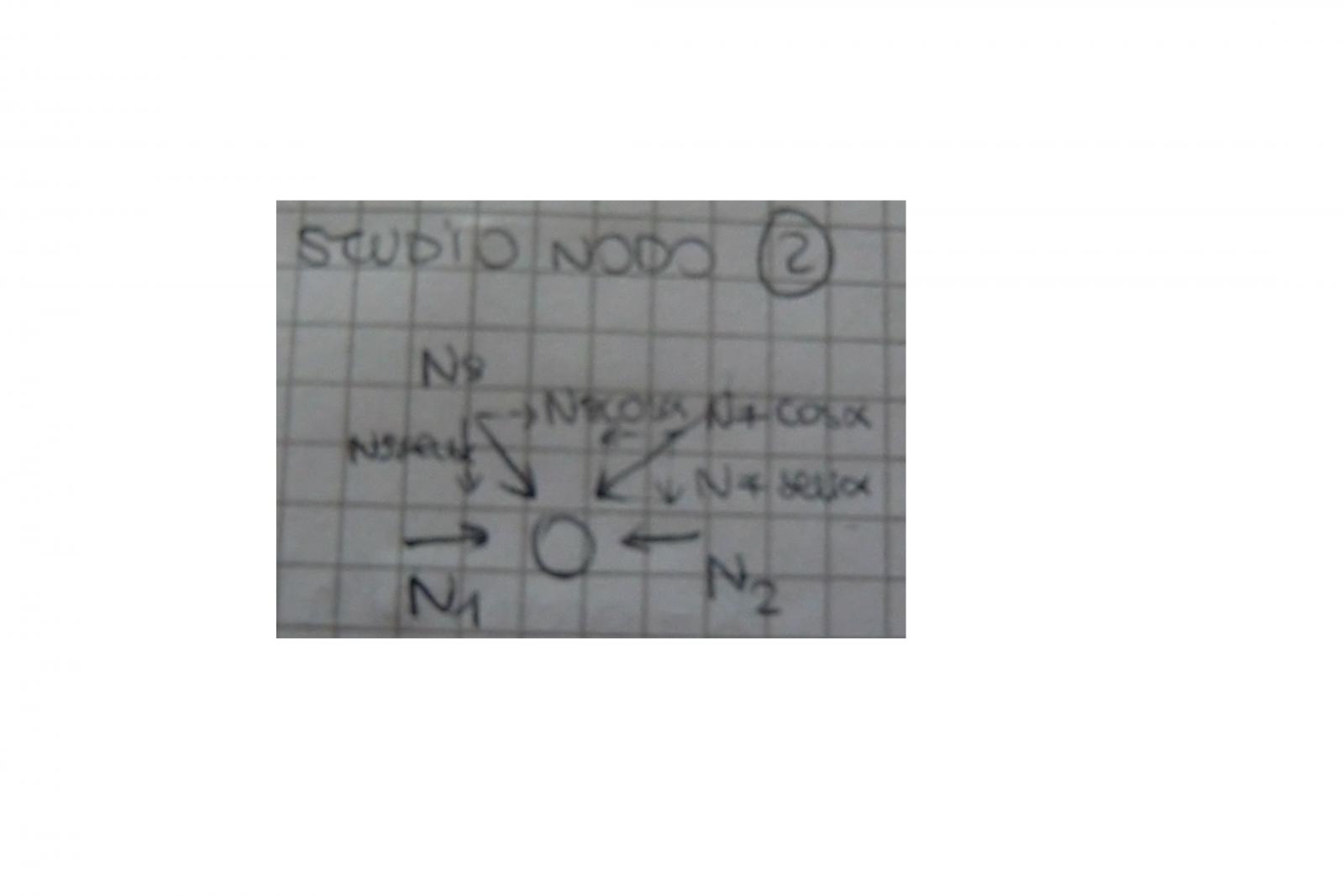Equilibrio a traslazione verticale:
N9senα + N7senα=0
N7senα= -N9senα= -50 KN
Equilibrio a traslazione orizzontale:
N1 – N2 + N9cosα + N7cosα =0
N2= -N1 - N9cosα - N7cosα= (-150 -50 -50 )KN= -250 KN
NODO 6
Equilibrio a traslazione verticale:
N10 senα + N7senα –F=0
N10senα= - N7senα +F = (-50 + 100) KN= 50 KN
Equilibrio a traslazione orizzontale:
N4 + N7cosα –N10cosα – N5=0
N5= - N4 –N7cosα + N10cosα = (-200 -50 + 50) KN = -200 KN
Infine grazie alla simmetria della trave, senza calcolare ulteriori equilibri ai nodi, è stato possibile andare a scrivere gli sforzi delle restanti aste. In base alla condizione di equilibrio al nodo è stato possibile stabilire anche se gli sforzi erano di trazione o di compressione: quando gli sforzi erano entranti nel nodo di trattava di puntoni, al contrario se lo sforzo era uscente si avevano dei tiranti.
Si è poi ricalcolato lo stesso modello di trave reticolare con SAP, rendendolo più realistico, attraverso l’aumento del numero delle campate, in quanto le travi reticolari sono proprio utilizzate per luci imponenti. Si è così ripetuto il modulo di h=3m e l=6m per 9 campate, lasciando sempre un carico simmetrico e di stessa intensità.
Attraverso l’analisi di SAP si è potuto constatare come di base il comportamento della trave sia lo stesso, in quanto non sono presenti ne taglio ne momento flettente ma vi è il solo sforzo assiale. Questo è sempre ripartito orizzontalmente in un corrente teso ed uno compresso, ma rispetto al modello di prima, dotato di una luce molto inferiore (18 m), questo che è lungo 54m presenta uno sforzo normale che presenta molte più variazioni di intensità da un’asta all’altra, e non solo sul corrente teso, ma anche su quello compresso crescendo tuttavia come in precedenza verso il centro di simmetria, punto individuato come il più sollecitato.
La deformata, tuttavia, avendo una luce maggiore sembra avere un abbassamento molto meno incisivo del modello più corto.
FIG.1
FIG.2
FIG.3
FIG.4
FIG.5
FIG.6
FIG.7
FIG.8
