SdC(b) (LM PA)

Nell’analisi meccanica di una struttura travi-pilastri, il più delle volte, o almeno per me,  si pone particolare attenzione alle sollecitazioni dovute a momento, taglio e sforzo normale. Nell’esercizio seguente si vuole capire, invece, in quale misura la torsione influisce nel comportamento di sistema della struttura stessa.

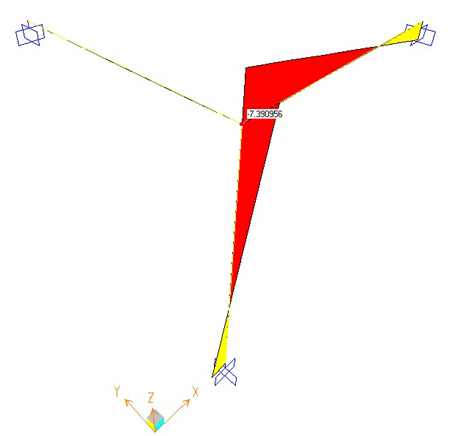
SCHEMA DI CALCOLO                                                                                             DEFORMATA

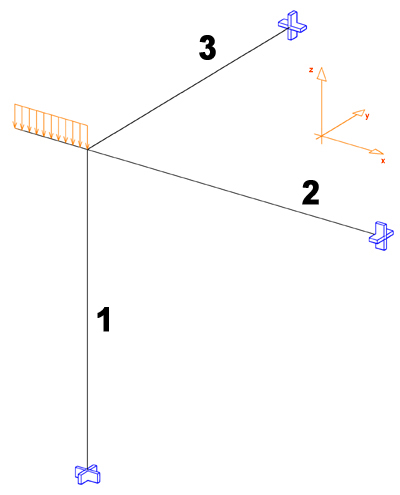
Lo sbalzo soggetto al carico distribuito è stato sostituito con il corrispondente valore del momento flettente applicato nel nodo, il quale ruota provocando nell’asta 3 una torsione. Le aste 1 e 2 hanno lo stesso comportamento che è riconducibile allo schema notevole già esaminato nei blog in precedenza.

Il problema presenta un’incognita (rotazione “ϕ” del nodo) che sarà trovata scrivendo l’equilibrio contro la rotazione del nodo:

 

ql²/2 = ϕ ( 4EI/l1 + 4EI/l2 + GJT/l3)

 

L’esercizio sarà svolto utilizzando il programma SAP2000 dal quale otterremo i valori delle caratteristiche di sollecitazione delle aste considerando, in un primo momento, che queste siano di calcestruzzo ed abbiano una sezione circolare. Successivamente si cambierà di volta in volta sezione e materiale all’asta 3.

L’obiettivo è quello di capire se e quanto, al variare della rigidezza torsionale dell’asta 3, i valori delle sollecitazioni nelle aste 1 e 2 cambiano.

Si ricorda che per una generica sezione il momento torsionale vale:

MT = (G*JT/l) ϑ(l) dove:

G = modulo di elasticità tangenziale (dipende dal materiale)

                         Calcestruzzo:      Gcls = 10⁷KN/m²

                         Acciaio:               Gsteel = 8*10⁷KN/m²

JT = momento di inerzia polare (dipende dalla sezione)

ϑ(l) = angolo unitario di rotazione

(G*JT/l) rappresenta la RIGIDEZZA TORSIONALE delle generica asta di lunghezza "l".

 

Di seguito vengono esaminate le diverse sezioni. Per ognuna sarà riportato il valore del momento e del taglio massimo nelle aste 1 e 2.

1

     

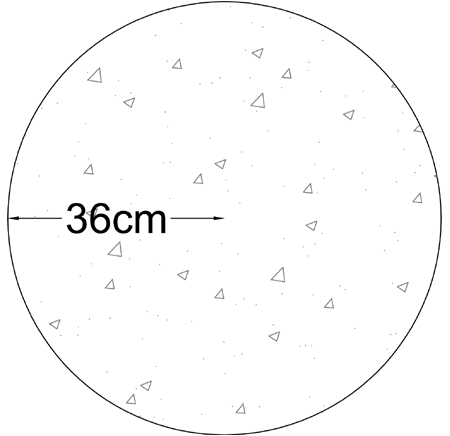
      MATERIALE: calcestruzzo

      SEZIONE: circolare piena   →   Jt = Ip = πR⁴/2 = π (0,36)⁴/2 = 0,026 m⁴

     

 

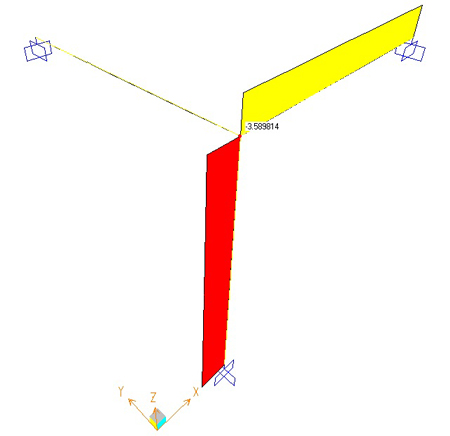
Deformata                                  Taglio=3,36 Kn                       Momento = -6,78 Kn m

2

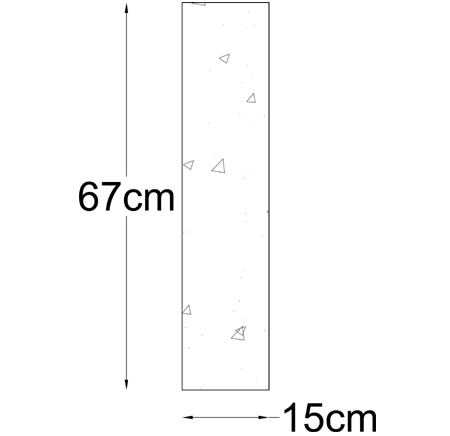
MATERIALE: calcestruzzo

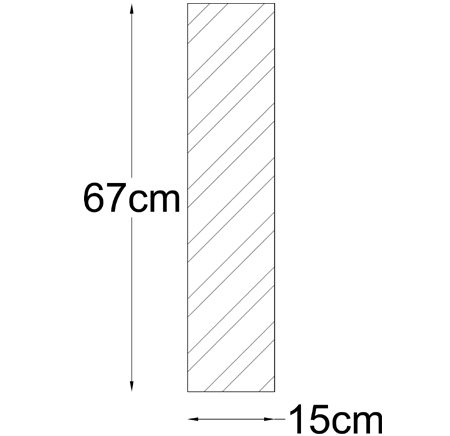
SEZIONE: rettangolare   →   Jt = c2 ab³ = (0,281) 0,67 * (0.15)³ = 6,3 e-4 m⁴

Il valore di c2 è tabellato e viene definito dal rapporto di forma della sezione e cioè altezza/base.In questo caso a/b = 0.67/0.15 = 4,444 →c2 = 0,281

 

 

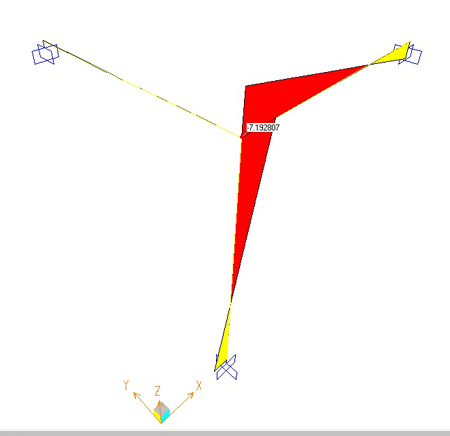
Deformata                                Taglio= 3,56Kn                          Momento = -7,19 Kn m

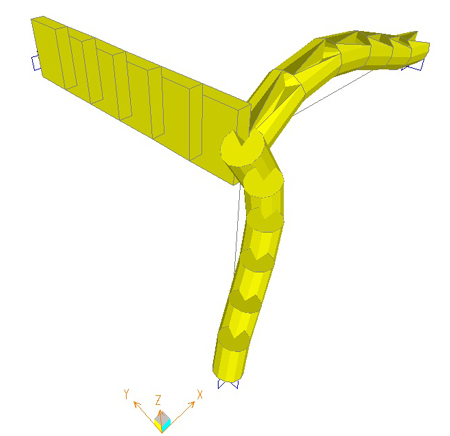
3

MATERIALE: acciaio

SEZIONE: rettangolare   →   Jt = c2 ab³ = (0,281) 0,67 * (0.15)³ = 0,026 m⁴

In questo caso a/b = 0.67/0.15 = 4,444 →c2 = 0,281

 

 

Deformata                                  Taglio= 2,81Kn                        Momento= -5,69 Knm

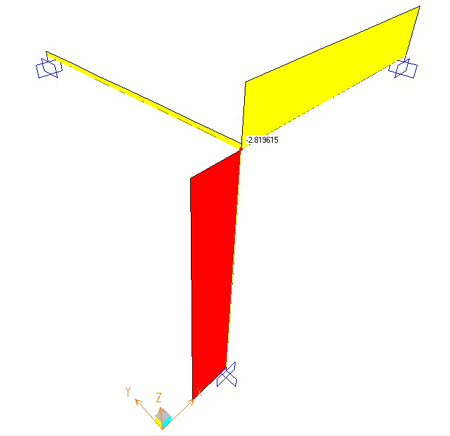
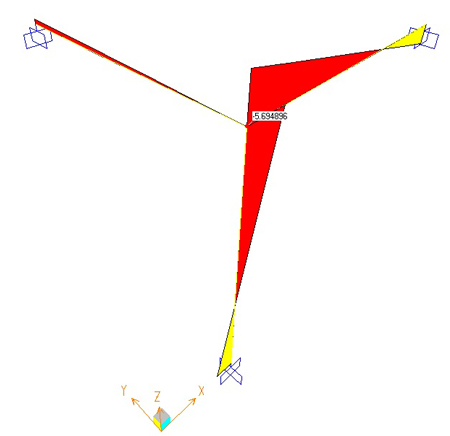
4

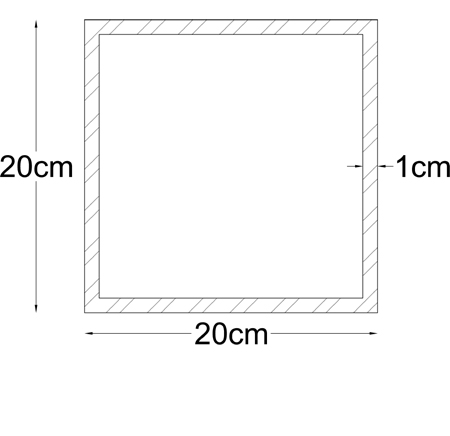
      MATERIALE: acciaio

      SEZIONE: quadrata cava   →   Jt = 4 Ω² t / lm = 4 * (0,038 m²)²  (0,01) / (0,78 m) = 7,4 e-5 m⁴

 

 

Deformata                                 Taglio= 3,58 Kn                            Momento = -7,25 Kn m

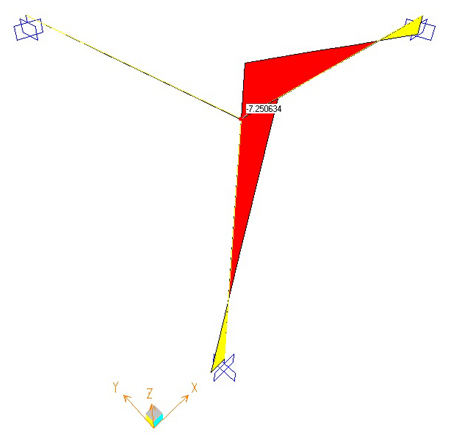
5

     

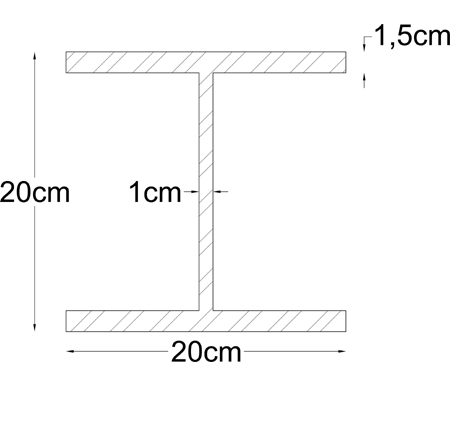
      MATERIALE: acciaio

      SEZIONE: doppio T   →   Jt = ΣJTi = 2,13 e-7 + 5,55 e-8 + 2,13 e-7 = 4,81 e-7 m⁴

 

 

Deformata                                 Taglio= 3,71 Kn                           Momento = -7,49 Kn m

6

      MATERIALE: calcestruzzo

      SEZIONE: quadrata piena   →   Jt = c2 ab³ = (0,14) 0,20 * (0,20)³ = 2,2 e-4 m⁴

      a/b = 0.20/0.20 = 1 →c2 = 0,14

 

 

Deformata                                 Taglio= 3,66 Kn                                Momento = -7,39 Kn m

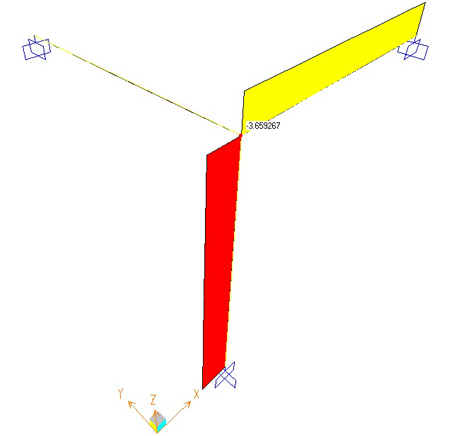
7

     

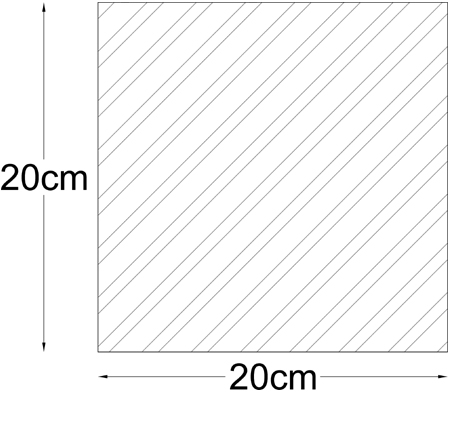
      MATERIALE: acciao

      SEZIONE: quadrata piena   →   Jt = c2 ab³ = (0,14) 0,20 * (0,20)³ = 2,2 e-4 m⁴

      a/b = 0.20/0.20 = 1 →c2 = 0,14

 

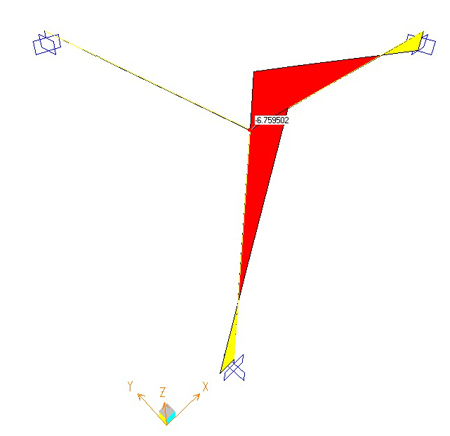
Deformata                                  Taglio= 3,34Kn                       Momento = -6,75 Kn m

 

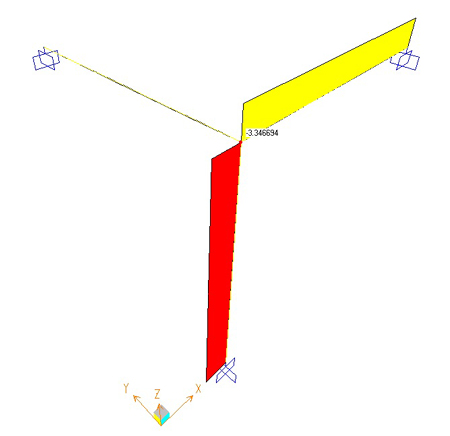
Nella tabella che segue viene stilata “una classifica” delle sezioni esaminate in base alla rigidezza torsionale.

Si può notare che:

Le sezioni in acciaio offrono una maggiore resistenza torsionale rispetto a quelle in calcestruzzo in quanto queste ultime hanno un modulo di elasticità tangenziale 8 volte superiore a quello in cls.

Le sezioni piene, grazie ad un maggiore valore di JT, offrono maggiore rigidezza torsionale rispetto alle sezioni cave.

Le sezioni chiuse resistono meglio a torsione rispetto alle sezioni aperte.

 

In questa esercitazione, analizzeremo il comportamento di un impalcato strutturale soggetto a spinte orizzontali (ad esempio il vento o il sisma).

L’insieme di travi e pilastri, non solo riescono a resistere alle forze verticali ma se disposti correttamente nello spazio, possono anche fungere da controvento. I telai agiscono dunque come vincoli elastici, reagendo alle forze orizzontali lungo il loro stesso piano e proporzionalmente alla oro rigidezza, queste caratteristiche ci permettono di rappresentarli come vere e proprie molle!

 

A questo punto, consideriamo un impalcato in calcestruzzo armato (E=21000 N/mmq) composto da quattro  telai lungo X e quattro lungo Y, sorretti da dodici pilastri, questi ultimi avendo una dimensione di 30x40 cm e due momenti d’inerzia, uno lungo X e uno lungo Y.

 

Ora riportiamo lo stesso impalcato con rappresentate le molle e le loro distanze dall’origine.

 

Passiamo al foglio Excel grazie al quale ci ricaveremo i valori di reazione alle forze sismiche:

 

STEP 1: CALCOLO DELLE RIGIDEZZE TRASLANTIDEI CONTROVENTI DELL’EDIFICIO.

 

In queste tabelle inseriamo i valori di modulo elastico, dell’altezza dei pilastri e dei momenti d’inerzia dei pilastri (prendendo ovviamente quelli lungo l’asse del telaio studiato) per ricavarci la rigidezza traslante di ciascun telaio.

 

 

STEP 2: TABELLA SINOTTICA CONTROVENTI E DISTANZE.

 

Qui riportiamo le distanze verticali e orizzontali dei controventi dall’origine O.

 

 

STEP 3: CALCOLO DEL CENTRO DI MASSA.

 

Come prima cosa dividiamo la struttura in tre aree per poi inserire i valori delle distanze dei loro baricentri dall’origine in modo da ricavarci le coordinate del baricentro dell’intero impalcato.

Xg = (A1 x  Xg1 + A2 x Xg2 + A3 x Xg3) / (A1 + A2 + A3)

Yg = (A1 x  Yg1 + A2 x Yg2 + A3 x Yg3) / (A1 + A2 + A3)

 

STEP 4: CALCOLO DEL CENTRO DELLE RIGIDEZZE E DELLE RIGIDEZZE GLOBALI.

 

In questa tabella vengono riportate le coordinate del centro delle rigidezze, punto intorno al quale ruota la struttura in caso di momento.  Considerando invece che il centro di massa è il punto nel quale vengono applicate le forze, la distanza tra i due punte risulta essere il braccio, di conseguenza più questi due punti si avvicinano e meno sarà importante il valore del momento!

 

Questa tabella ci permette inoltre di ricavarci la rigidezza torsionale totale (somma delle rigidezze di ogni telaio, moltiplicato per la loro distanza dal centro delle rigidezze.)

 

 

 

 

STEP 5: ANALISI DEI CARICHI SISMICI.

 

 

 

STEP 6-7: RIPARTIZIONE DELLA FORZA SISMICA LUNGO X E Y.

Queste ultime due tabelle ci riportano i valori del momento torcente della struttura, le traslazioni,  e le rotazioni lungo X  Y.

Si procede alla compilazione del foglio Excel fornitoci, scegliendo di analizzare il seguente impalcato costituito da un telaio in c.a..

La maglia strutturale è regolata sul modulo di 4.50 m; nell'ultima campata viene raddoppiata la luce e conseguentemente invertita l'orditura del solaio in virtù di ragioni spaziali e progettuali

Vediamo così che la ripartizione sui due assi della forza sismica tra i controventi avviene proporzionalmente alla rigidezza di quest'ultimi:

METODO DELLE RIGIDEZZE – MENSOLA

 

 

Questa è una trave Vierendeel ed ha lo stesso comportamento di un telaio shear-type ( travi infinitamente rigide e quindi resistenti a flessione). Mentre i pilastri sono soggetti a traslazioni provenienti da azioni esterne.

 

Questo telaio si deformerebbe così

Questo solaio può essere visto come uno shear-type ruotato di 90°.

Consideriamo i tratti verticali come travi doppiamente appoggiate.

 

Questa trave è iperstatica ed è soggetta ad un cedimento vincolare δ, da cui si ricavano i seguenti valori del taglio e del momento:

 

M = 6 EI/l² * δ T = 12 EI/l³ * δ

 

TRATTO 1

 

-F + 2T = 0

F = 2T

Applicando i valori notevoli

F = 2 (12 EI/l³ * δ1) = 24 EI/ l³ * δ1

 

δ1 = F l³/24 EI

 

T = 12 EI/ l³ * δ1 = F/2

 

M = 6 EI/ l² * δ1 = Fl/4

 

TRATTO 2

 

T + T – F – F/2 – F/2 = 0

2F = 2T

Applicando i valori notevoli

F = 12EI/ l³ * δ2

 

δ2 = F l³/12 EI

 

T = 12 EI/ l³ * δ2 = F

 

M = 6 EI/ l² * δ2 = FL/2

 

 

TRATTO 3

 

T + T – F -F – F = 0

3F = 2T

Applicando i valori notevoli

3F = 24 EI/l³ * δ3

 

δ3 = Fl/8 EI

 

T = 12 EI/ l³ * δ3 = 3/2 F

 

M = 6 EI/ l² * δ3 =3/4Fl

 

TRATTO 4

 

T + T – F – 3/2 F – 3/2 F = 0

4F = 2T

Applicando i valori notevoli

4 F = 24EI/ l³ * δ4

 

δ4 = F l³/6EI

 

T = 12 EI/ l³ * δ4 = 2F

 

M = 6 EI/ l² * δ4 = Fl

 

TRATTO 5

 

T + T – F – 2F – 2F = 0

5F = 2T

Applicando i valori notevoli

5F = 24 EI/ l³ * δ5

 

δ5 = 5 F l³/24 EI

 

T = 12 EI/ l³ * δ5 = 5/2 F

 

M = 6 EI/ l² * δ5 = 5/4 Fl

 

TRATTO 6

 

T + T – F – 5/2 F – 5/2 F = 0

6F = 2T

Applicando i valori notevoli

6F = 24 EI/ l³ * δ6

 

δ6 = F l³/4 EI

 

T = 12 EI/ l³ * δ6 = 3F

 

M = 6 EI/ l² * δ6 = 3/2 Fl 

 

 

DIAGRAMMA DEL TAGLIO

 

 

DIAGRAMMA DEL MOMENTO

 

 

Ora bisogna calcolare il taglio e i momenti delle shear-type facendo l'equilibrio ai nodi

 

MOMENTI

 

TRATTO 1 VERTICALE

 

 

MV1 – Fl/4 = 0

MV1 = Fl/4

 

TRATTO 2 VERTICALE

 

MV2 – Fl/4 – Fl/2 = 0

MV2 = 3/4Fl

 

TRATTO 3 VERTICALE

 

MV3 – 3/4Fl – Fl/2 = 0

MV3 = 5/4 Fl

 

TRATTO 4 VERTICALE

 

MV4 – Fl – 3/4Fl = 0

MV4 = 7/4 Fl

 

TRATTO 5 VERTICALE

 

MV5 – Fl – 5/4 Fl = 0

MV5 = 9/4 Fl

 

TRATTO 6 VERTICALE

 

MV6 - 5/4 Fl – 3/2 Fl = 0

MV6 = 11/4 Fl

 

DIAGRAMMA MOMENTI VERTICALI

 

Per ricavarci i valori del taglio a questo punto ci basterà fare la somma dei momenti agenti sull'asta dividendoli per la luce e mettendo il taglio in equilibrio

 

TAGLIO

TRATTO 1 VERTICALE

 

Tv1 = (Fl/4 + Fl/4) 1/l = F/2

 

TRATTO 2 VERTICALE

 

Tv2 = (3/4Fl + 3/4Fl) 1/l = 3/2F

 

TRATTO 3 VERTICALE

 

Tv3 = (5/4Fl + 5/4Fl) 1/l = 5/2 F

 

TRATTO 4 VERTICALE

 

Tv4 = 7/4Fl + 7/4Fl) 1/l = 7/2 F

 

TRATTO 5 VERTICALE

 

Tv5 = (9/4 Fl + 9/4Fl) 1/l = 9/2 F

 

TRATTO 6 VERTICALE

 

Tv6 = (11/4 Fl + 11/4 Fl) 1/l =11/2 F

 

DIAGRAMMA TAGLIO VERTICALE

 

Gli sforzi di taglio in un tratto diventano sforzi normali per i tratti ortogonali adiacenti, quindi possiamo disegnare il diagramma dello sforzo normale

 

DIAGRAMMA SFORZO NORMALE

Possiamo parlare di graticcio quando vi è collaborazione tra due sistemi ortogonali di travi. Va distinto dalla gerarchia di travi, nella quale c’è sempre un’orditura principale e una secondaria.

Ne graticcio non vi sono differenze nelle sezioni degli elementi, a prescindere dalla loro orditura e per questo motivo abbiamo momenti d’inerzia pressoché identici nei due assi x e y.

 

Un parametro che assume notevole importanza nel graticcio è la rigidezza torsionale, dal momento che avendo flessione in una direzione, inevitabilmente avremo torsione nell’altra. Il problema della Torsione è legata principalmente alla sezione dell’elemento strutturale poiché nella formula della rigidezza compare il Momento d’inerzia Polare (Ip), diverso a seconda della sezione in esame. Per questo motivo analizziamo un graticcio semplice, comparando i valori delle rotazioni indotte da una forza concentrata a travi di sezioni differenti. Va ricordato, infatti, che la rotazione è indirettamente proporzionale alla rigidezza.

RISOLUZIONE DI UN GRATICCIO

Il nodo ha 6 gradi di libertà: esso può avere 3 differenti traslazioni, secondo i 3 assi x, y e z; inoltre, può essere soggetto a rotazioni intorno ai 3 assi. In questo caso specifico, però, la condizione di carico non genera traslazioni lungo x e lungo y, così come non vi sono rotazioni in x e in z. Le incognite, dunque, sono soltanto due, ossia lo spostamento e la rotazione.

Analizziamo le deformate delle due travi separatamente:

Sulla trave BD la forza F agisce esattamente al centro, quindi la deformata è simmetrica e in quel punto abbiamo uno spostamento δ, ma nessuna rotazione della sezione essendo un punto di tangenza orizzontale. Sulla trave AC, invece, F agisce ad un terzo della lunghezza e, sebbene il punto trasli della stessa quantità lungo z, stavolta non ci troviamo nel punto a tangenza orizzontale della deformata, quindi avremo anche una rotazione della sezione intorno all’asse y.

Per questo motivo separiamo idealmente le due incognite, facendole agire separatamente e sovrapponendo poi i loro effetti.

Analizziamo innanzitutto le due deformate prodotte dalla spostamento δ:

• deformazione dovuta solo allo spostamento δ per la trave AC:

come detto in precedenza il punto soggetto alla forza F deve abbassarsi senza ruotare. Conoscendo già i valori della rigidezza in una trave doppiamente incastrata possiamo quantificare gli sforzi di Taglio e Momento flettente, concentrandoci in particolare su quelli che agiscono sul nodo:

• deformazione dovuta solo allo spostamento δ per la trave BD:

anche nell’asta BD soggetta alla sola traslazione il nodo si abbassa senza ruotare, quindi analogamente a quanto fatto in precedenza procediamo rapidamente al calcolo degli sforzi di Taglio e Momento Flettente, i quali per via della simmetria dello schema stavolta saranno identici:

(questi due moment oltre ad elidersi perché uguali in valore assoluto e opposti nel verso, si riferiscono ad una rotazione attorno all’asse x, quindi non verranno presi in considerazione nell’equazione di equilibrio dei momenti)        

A questo punto analizziamo le deformate provocate dalla sola rotazione:

• deformazione dovuta solo alla rotazione  per la trave AC:

la rotazione imposta al nodo prova un’inflessione nella trave AC e il punto stesso ruota intorno all’asse y. Anche in questo caso, come in precedenza, ci affidiamo a schemi notevoli dal momento che abbiamo già affrontato la questione della rigidezza flessionale e conosciamo i valori dei momenti agli estremi in una trave doppiamente incastrata:

noto il diagramma dei Momenti, possiamo calcolare anche gli sforzi di Taglio:

La flessione della trave AC intorno all’asse y corrisponde inevitabilmente alla torsione di quella BD:

• deformazione dovuta solo alla rotazione per la trave BD (TORSIONE):

il Momento Torcente agente sulla trave genera due momenti reagenti di verso opposto, cosa non trascurabile per determinare poi il segno di questi due contributi nell’equazione di equilibrio dei momenti:

A questo punto conosciamo tutti i contributi degli sforzi di Taglio e Momento Flettente agenti sul nodo e generati sia dalla traslazione che dalla rotazione. Possiamo, quindi, scrivere le due equazioni di equilibrio:

Risoluzione delle equazione distinte:

Sostituzione di δ/L  all’interno della prima equazione e ricerca dell’incognita rotazione:

 

VERIFICA DEL GRATICCIO SU SAP

Scopo di questo esercizio è quantificare le variazioni degli abbassamenti e delle rotazioni relativi al nodo, punto d’incontro delle 2 travi doppiamente incastrate, al variare delle proporzioni di lunghezza e delle sezioni assegnate agli elementi strutturali. Infatti, come già sottolineato in precedenza, la rigidezza torsionale è direttamente proporzionale al Momento d’inerzia Polare, il quale dipende dal tipo di sezione.

• Immagine dello schema di partenza

• la forza F agente sul nodo provoca le deformate qualitativamente descritte precedentemente nella risoluzione a mano:

• Questi sono i rispettivi diagrammi di Taglio, Momento flettente e Momento torcente:

Ad una delle due travi, quella con la forza applicata ad un terzo della luce, è stata associata una sezione costante in acciaio di tipo scatolare, con spessori ridotti in modo da consentire abbassamenti sensibili che mettessero in evidenza il contributo dell’altra trave. Inoltre, così facendo essa mantiene costante la sua rigidezza flessionale, quindi le differenze nei valori delle rotazioni finali tra i diversi casi studio saranno dovute soltanto al contributo della rigidezza torsionale.

A quest’ultima  state assegnate 3 sezioni differenti con due condizioni di luce distinte, in modo da avere una gamma di risultati relativamente ampia che consentisse un qualunque discorso comparativo.

• La prima è una sezione scatolare in acciaio:

 

• La seconda è una sezione rettangolare con la base molto minore dell’altezza:

• La terza e ultima è una sezione tubolare:

Le stesse sezioni sono state applicate dopo aver dimezzato la luce della trave. Di seguito lo schema iniziale e la deformata:

• Questi sono i rispettivi diagrammi di Taglio, Momento flettente e Momento torcente:

In queste tabelle sono riassunti i dati esportati da SAP relativi  all’abbassamento  e alla rotazione jdel punto in comune alle 2 travi, nel quale viene applicata la forza agente F.

Le tabelle di sinistra fanno riferimento al caso di luce pari a 6 m, mentre quelle di destra al caso con luce pari a 3 m.

Come prevedibile, nei casi in cui alla trave soggetta a torsione sono stati associati profili chiusi (gli scatolari e i tubolari) essa ha garantito una maggiore rigidezza torsionale, limitando la rotazione del punto d’incontro delle travi.

Ricordiamo che la rotazione è inversamente proporzionale alla rigidezza del sistema, la quale in questo caso è data dalla somma della rigidezza flessionale della trave AC (mantenuta costante) e di quella torsionale della trave BD che abbiamo fatto variare per quantificare il suo contributo ai fini della rigidezza totale.

•