Portale di Meccanica

Prova Blog!!

Ciao a tuttiiii!! Ci sono anche io!! Vi auguro una buonanotte prima dell'esercitazione numero uno!

anche se in ritardo, salve prof!

ciao a tuttiiiiii!!!!!

Ciao!!! 

sa sa prova prova

dfdfdfdfd

cari studenti e care studentesse

in allegato troverete i risultati della prova di lunedì scorso. Mediamente non sono andati male, ma nei voti abbiamo anche largheggiato per incoraggiamento. Mi preoccupano soprattutto quelli di voi campiti in rosso. 

Buon lavoro

la prof.
 

In quest'ultima esercitazione farò un veloce studio del comportamento degli archi.

Arco a tutto sesto - F (freccia dell'arco) = L (distanza dall'imposta dell'arco alla proiezione a terra della chiave)

Arco a sesto acuto - F > L

Arco a sesto ribassato - F < L

Ho disegnato i tre archi in Rhino per poi importarli in Sap. Ho sistemato il modello per evitarne "errori":

- ho usato il comando Merge Joints perché le curve importate erano in verità segmenti accostati. Questo comando mi permette di garantire una curva continua

- alla chiave di ogni arco ho annullato il trasporto del momento usando il comando Release/Partial Fixity. (come se ci fosse una cerniera)

Ad ogni imposta dell'arco ho assegnato un vincolo cerniera. Infine imposto anche la sezione della trave.

Impongo un carico uniformemente distribuito (20KN)che agisca su una luce pari a quella degli archi (Gravity Projected)

Ora posso far partire l'analisi. Ecco la deformata.

Posso anche vedere i diagrammi di Sforzo Normale, Taglio e Momento.

N   

T    

M   

Soprattutto Sforzo Normale e Taglio sono interessanti da analizzare in quanto essi sono strettamente legati alle reazioni vincolari delle cerniere all'imposta. Si può notare infatti che più ci si sposta verso l'imposta dell'arco e più la spinta dell'arco aumenta. Essa è infatti l'opposto delle reazioni vincolari.

In particolare questa, dipende dalla freccia dell'arco che più è bassa e più è alta la spinta. Se andiamo a vedere nelle tabelle SAP le reazioni vincolari delle cerniere possiamo notare che l'arco a tutto sesto ha una spinta quasi due volte superiore a quella dell'arco acuto ma molto inferiore rispetto a quella dell'arco ribassato.

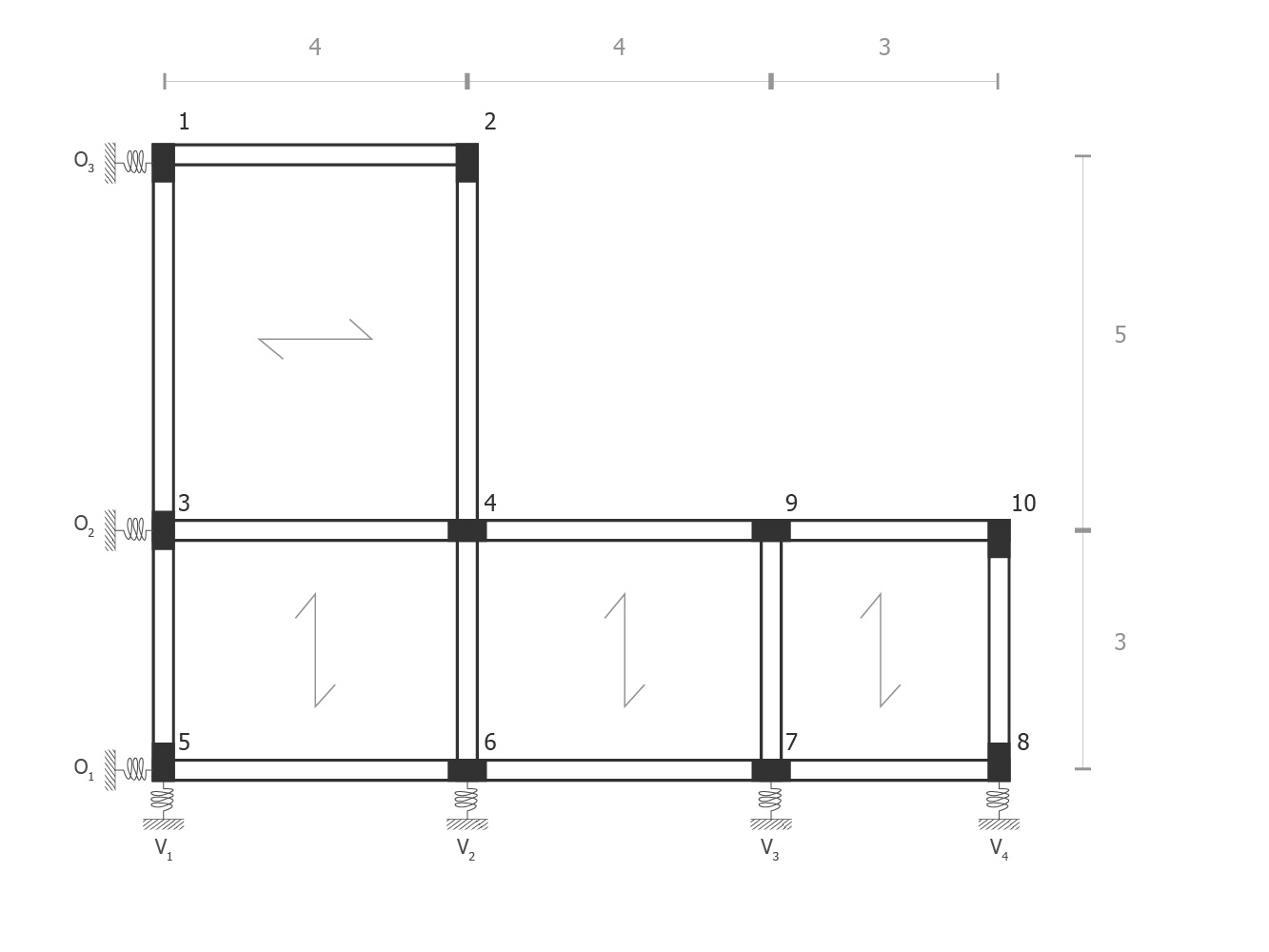
In questa esercitazione analizzo un IMPALCATO STRUTTURALE, considerato come un CORPO INFINITAMENTE RIGIDIO (struttura Shear Type) alle azioni che agiscono lungo il suo piano, si comporti sotto l’effetto di FORZE ESTERNE ORIZZONTALI come ad esempio in questo caso il SISMA; il suo comportamento dipende:

- dai CONTROVENTI considerati VINCOLI ELASTICI CEDEVOLI, assimilabili a molle che reagiscono alle forze agenti lungo il loro stesso piano in proporzione della loro rigidezza;

- dalla distanza tra il CENTRO DELLE MASSE, baricentro geometrico dell’impalcato, e il CENTRO DELLE RIGIDEZZE, dato dalla risultante di tutte le rigidezze.

Questi due aspetti determinano infatti la RIGIDEZZA TRASLANTE K_δ e di conseguenza laTRASLAZIONE δ lungo la direzione della FORZA AGENTE e la RIGIDEZZA ROTAZIONALE Kφ e di conseguenza la ROTAZIONE φ intorno al CENTRO DELLE RIGIDEZZE.7

I diversi telai hanno controventi, i quali sono indicati con delle molle V per quelli VERTICALI e O per quelli ORIZZONTALI.

H pilastri: 3,20 m
Si tratta di pilastri in cemento armato che hanno un Modulo di Young E= 21000 Nmm
Sezione dei pilastri  30x40 cm

A seconda del posizionamento del pilastro avremo diversi Momenti di Inerzia I_x=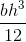 

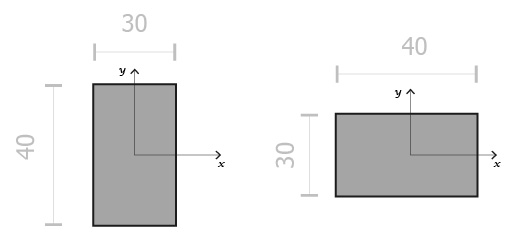
I_x= 4000 cm⁴                        I_x=3000 cm⁴

Prima di procedere al foglio excel definisco la suddivisione dei telai con le rispettive numerazioni dei pilastri, a seconda che io stia analizzando l’impalcato rispetto l’asse x e poi lungo l’asse y.                                   

(STEP 1) Calcolo delle rigidezze traslanti dei controventi dell'edificio

La rigidezza traslante viene calcolata secondo la formula 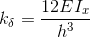 dove I_x in questo caso è la somma di tutti i momenti di inerzia di ogni pilastro.

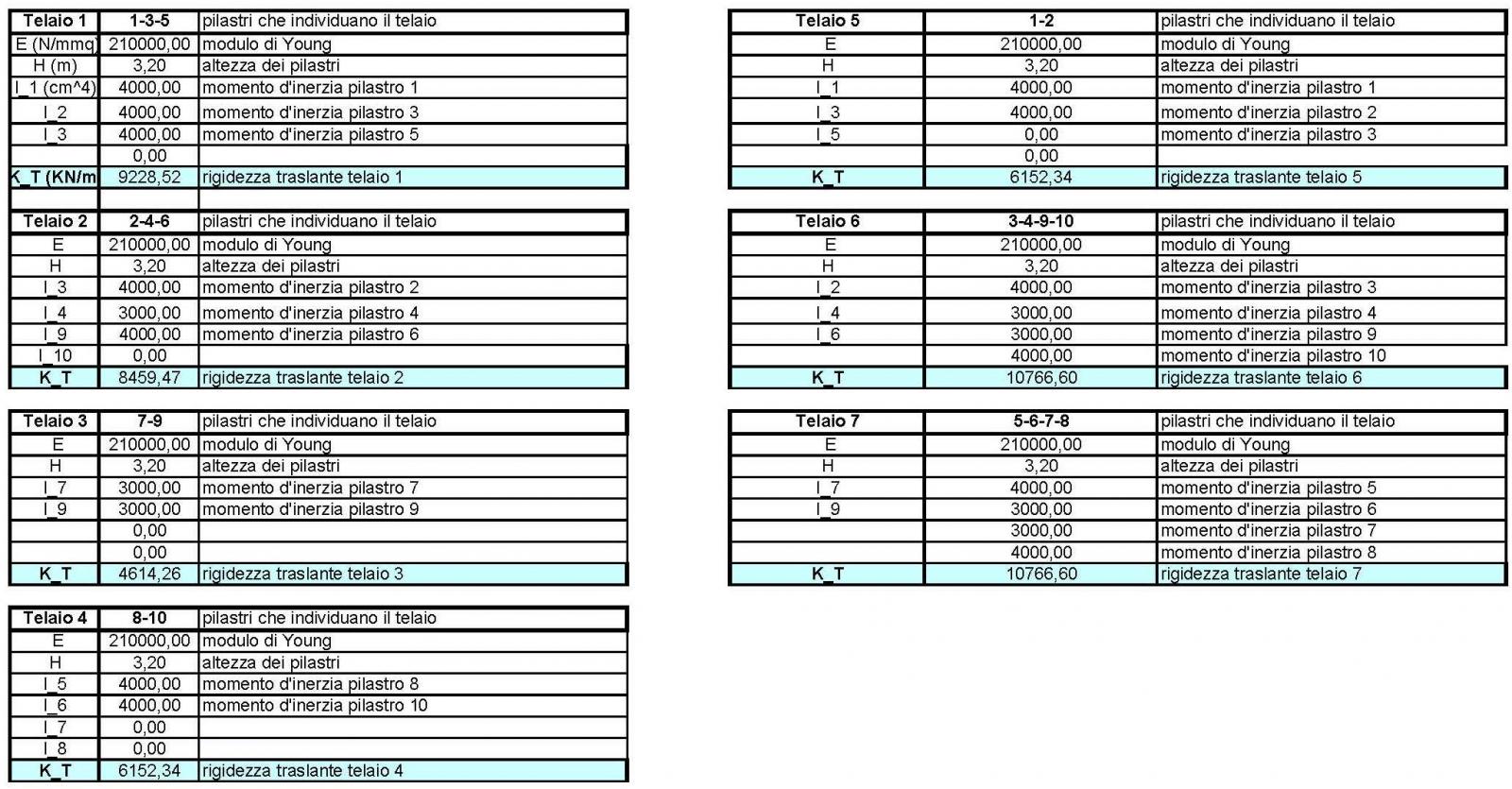
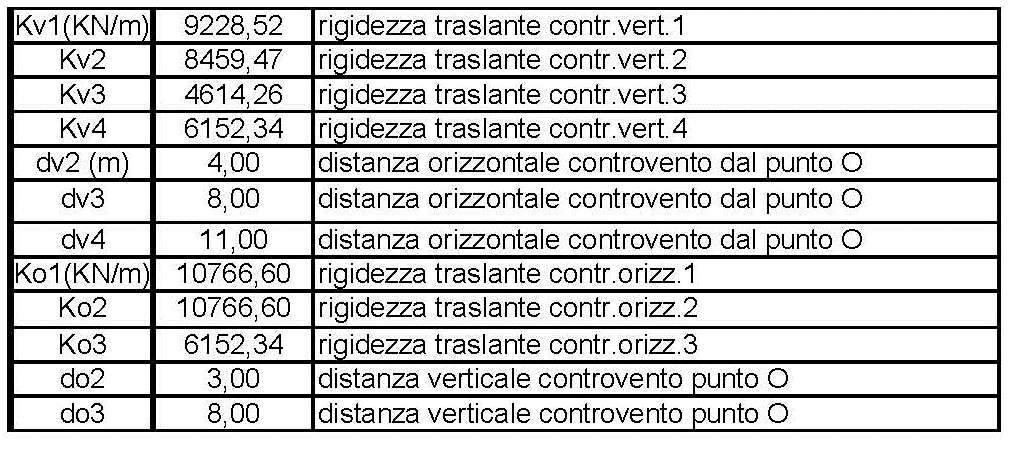
(STEP 2) Tabella sinottica controventi e distanze

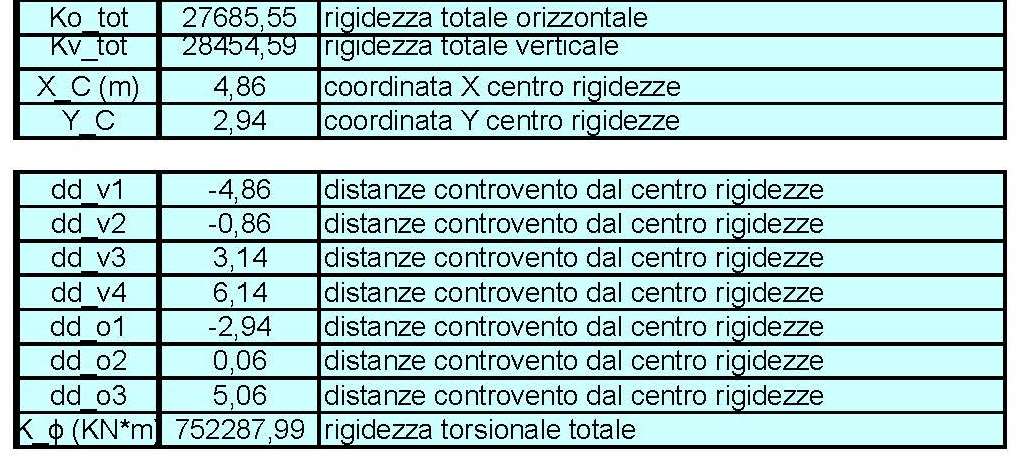
Considerando come origine l'angolo in basso a sinistra considero le distanze di ogni molla da esso.

(STEP 3) Calcolo del centro di massa

Dividendo l'impalcato in aree semplici possiamo calcolare la posizione del centro delle masse, ovvero il punto di applicazione delle forze esterne. Ogni area avrà il suo baricentro e la sua area. Nel foglio di calcolo il dato si basa su queste formule:

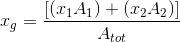
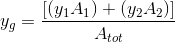
(STEP 4) Calcolo del centro di rigidezze e delle rigidezze globali

Il centro delle rigidezze si calcola mediante le seguenti formule:

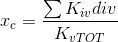
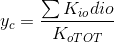
Il calcolo delle rigidezze torsionali globali invece lega la distanza di ogni controvento con la sua rigidezza traslante.

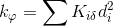
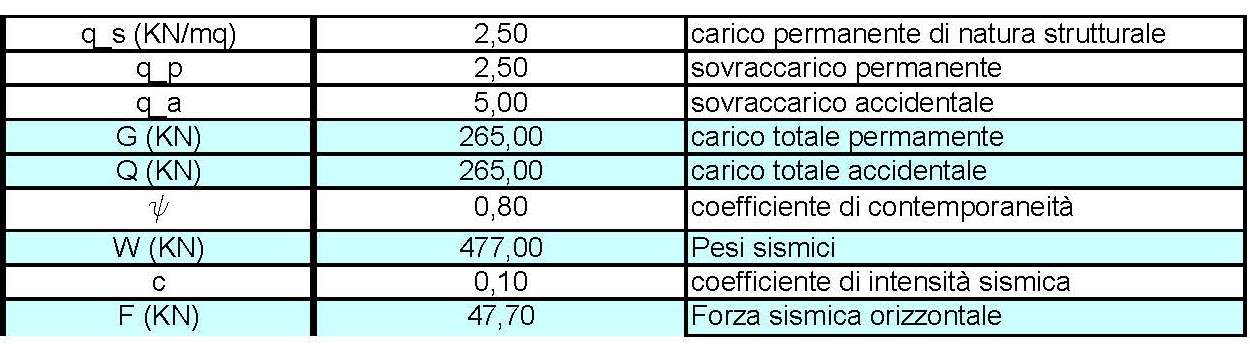
(STEP 5) Analisi dei carichi sismici

Per trovare la forza sismica calcolo il carico totale permanente G della struttura (definito per somma di carichi strutturali, accidentali e permanenti moltiplicata per l'area) e il coeficente di contemporaneità Y (dato dalla normativa, che diminuisce il carico accidentale).

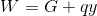
La forza sismica orizzontale F (kN) è data dal prodotto dei pesi sismici totali per il coefficente di intensità sismica c (che dipende dalla zona sismica).

(STEP 6-7) Ripartizione forza sismica

Individuo come l’ipotetica forza sismica si ripartisce nelle due direzioni e viene assorbita dai controventi. Nel mio caso il centro delle rigidezze e il centro delle masse NON coincidono, pertanto avrò una rotazione data da un momento (momento torcente) creatro dalla forza sismica che ha un braccio, il cui valore coincide con la differenza tra il centro delle masse e il centro delle rigidezze, rispettivamente all’asse x e all’asse y.

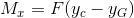
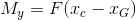
In seguito cerco il valore della traslazione lungo x e lungo y che equivale a

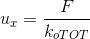
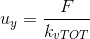
Poi calcolo la rotazione dell'impalcato che equivale al rapporto tra il momento e le rigidezze torsionali totali 

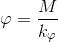
Ricavo infine le reazioni con cui ciascuna molla reagisce e contrasta la forza orizzontale sismica.

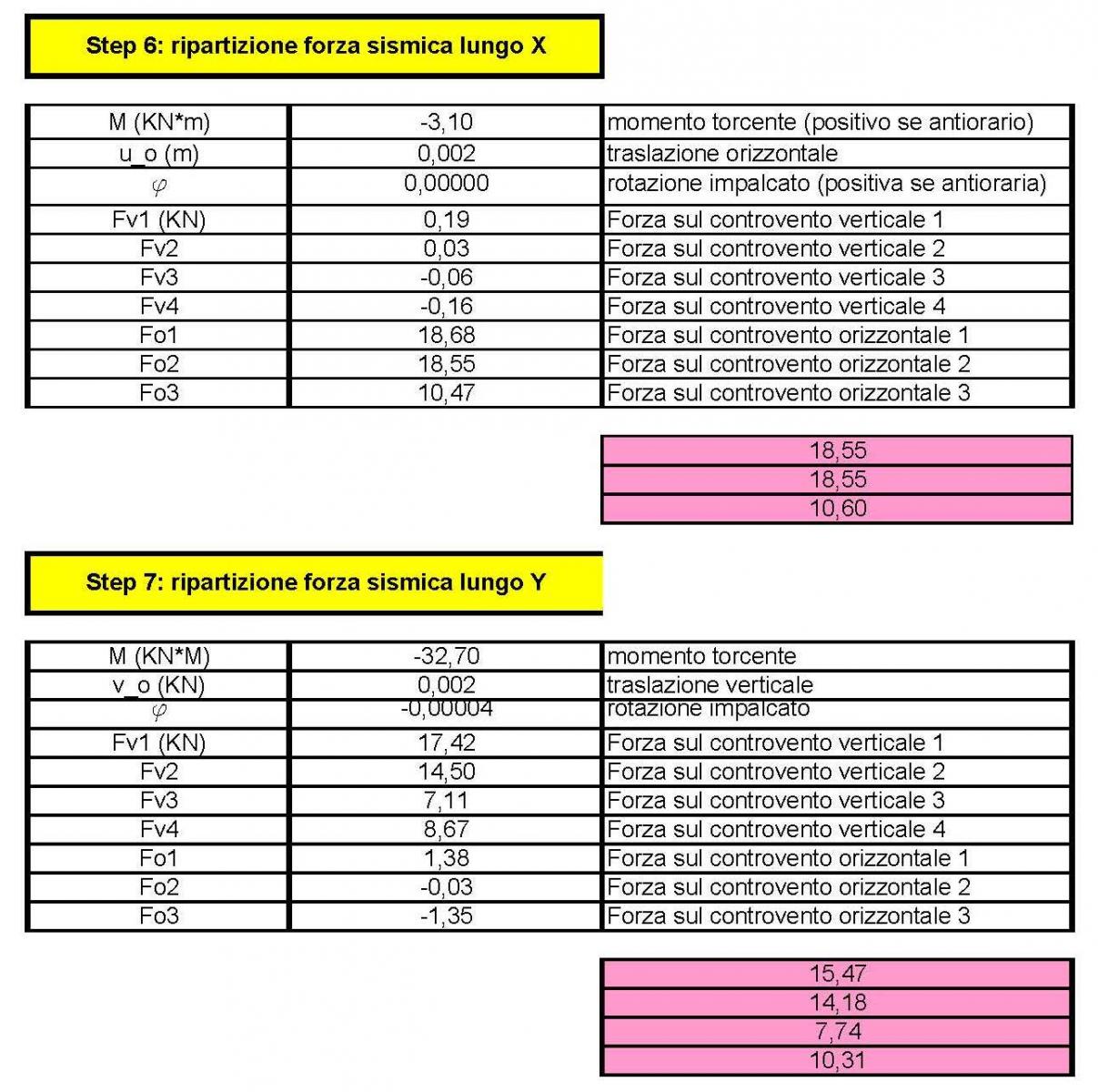
 Passo ora su SAP 2000

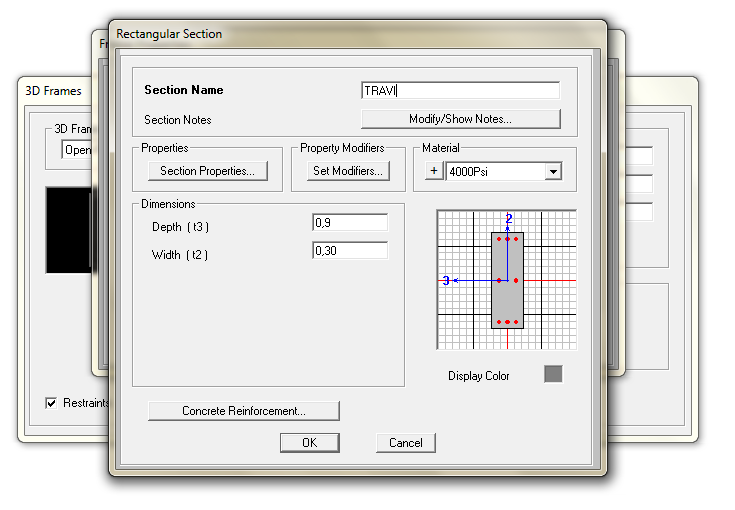
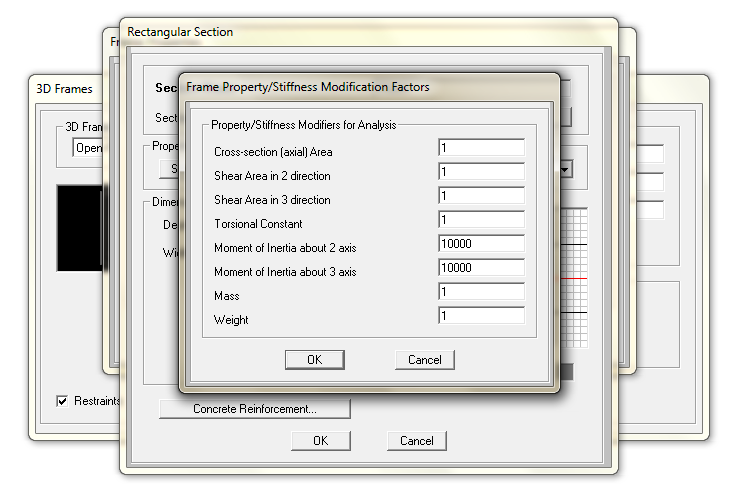
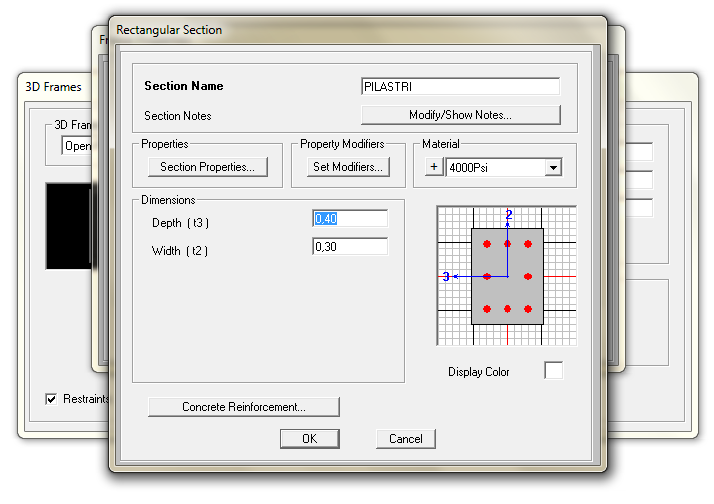
  Disegno la struttura direttamente nel programma con l'accortezza di predisporre le sezioni di travi e pilastri nel modo corretto. Nel caso delle travi, abbiamo immaginato di lavorare con un ipotetico modello Shear Type. Questo richiederà non solo una trave particolarmente alta ma dovremo aumentare il momento di inerzia in modo importante. Ricordiamoci anche di assegnare la giusta sezione al giusto pilastro secondo com'era stata immaginata la disposizione.

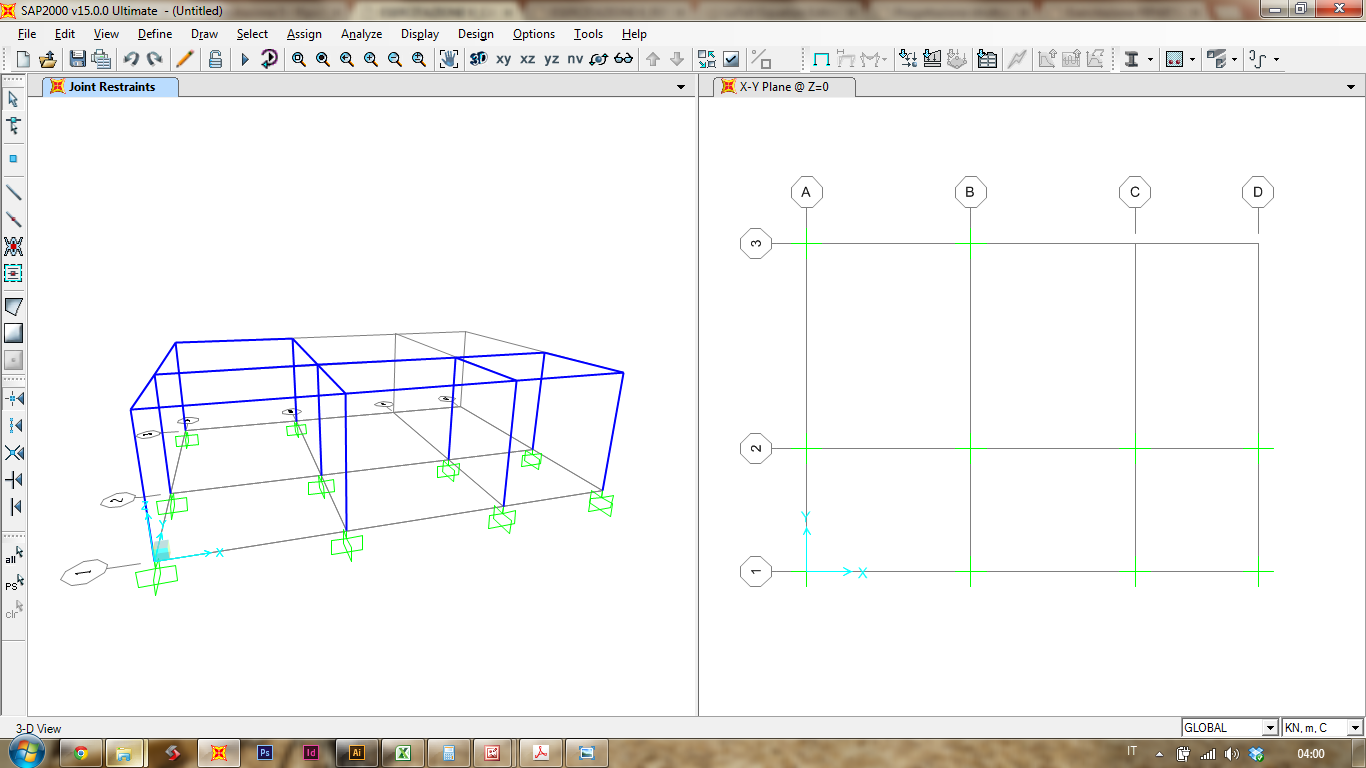
E' il momento di disegnare due punti, ovvero il Centro delle Rigidezze e il Centro delle Masse.

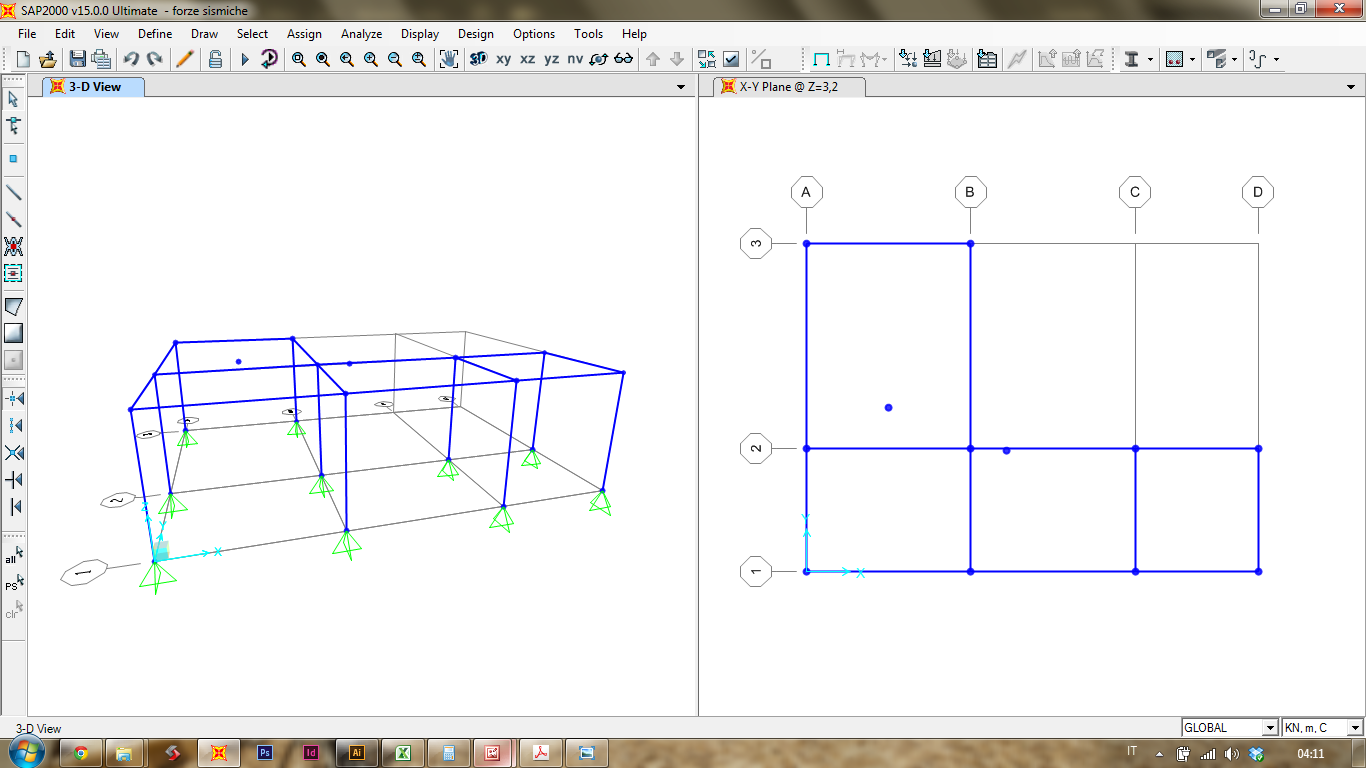
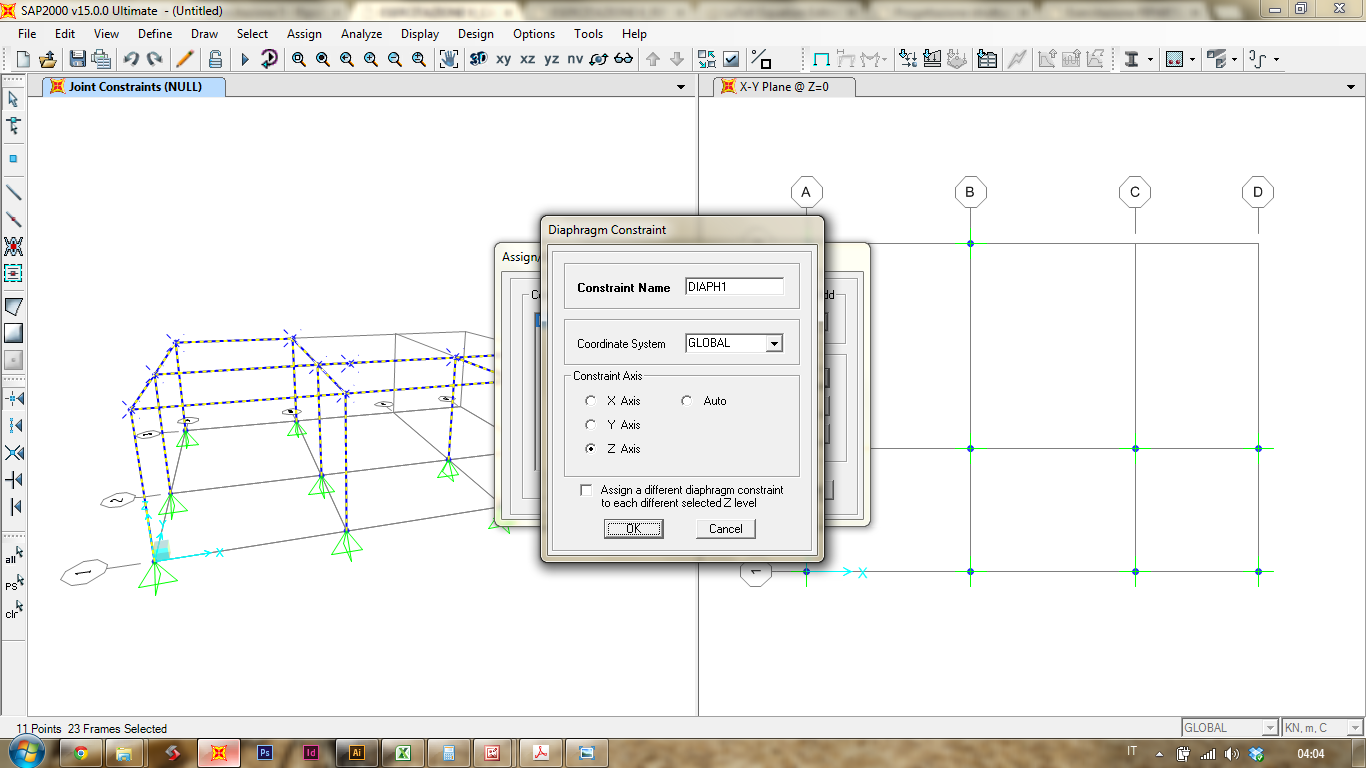
Prima di procedere "leghiamo insieme tutti i nodi superiori, in modo che si muovino come elemento unico. Impongo il vincolo Diaphragm

[Assign] > [Joints] > [Constraints]

Ora al centro delle Rigidezze applichiamo una forza, la Forza Sismica Orizzontale, lungo l'asse y. Una volta avviata l'analisi ecco come si presenta la deformata.

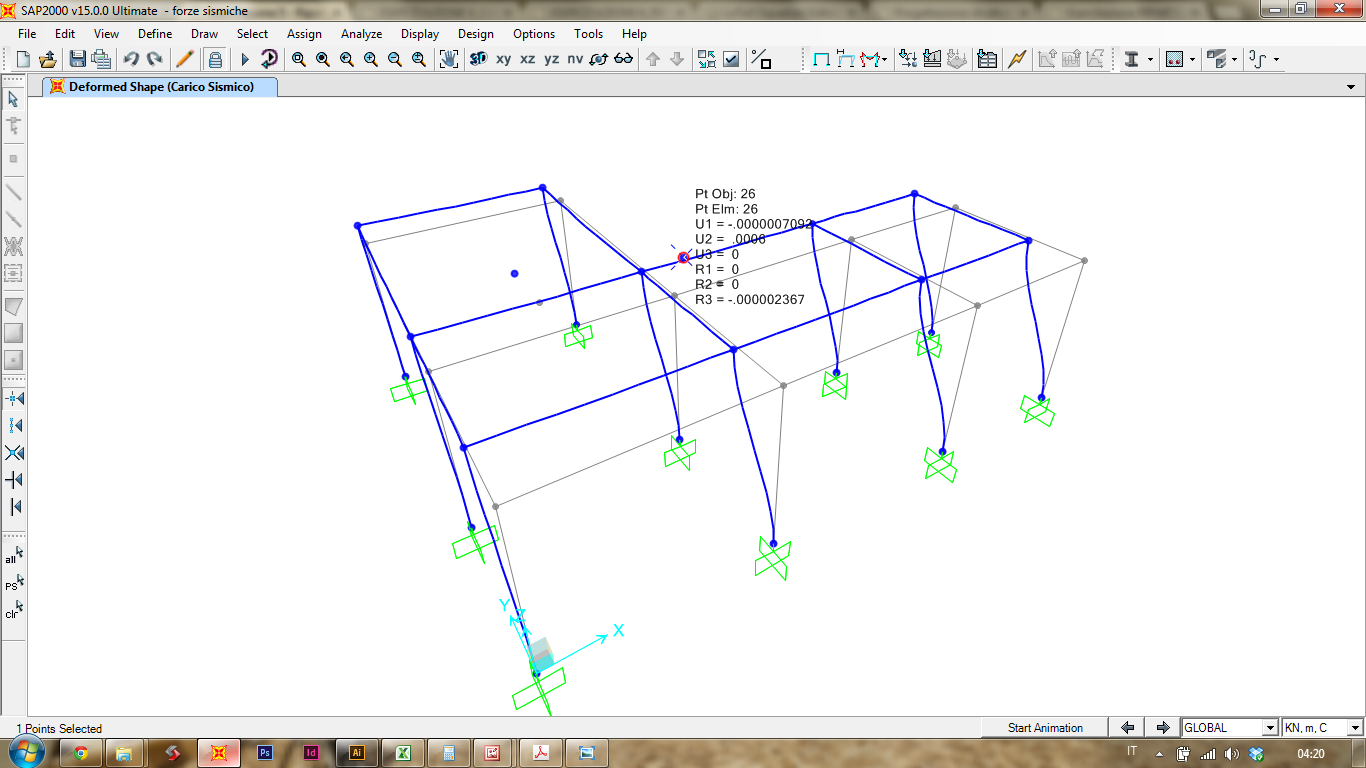
Si può vedere come gli spostamenti del punto siano infinitesimali.

Molto di quanto sviluppato in questa esercitazione fa riferimento anche a procedure utilizzate durante l'esercitazione 2.

Ipotizzo di essere alle prese con un solaio composto come quanto segue (del quale ho evidenziato l'area di influenza di una della trave). 

Voglio dimensionare questa trave in funzione di tre ipotetici pacchetti murari: legno, acciaio e laterocemento. Di conseguranza si tratteranno di tre tipologia di trave diverse. Per questa operazione mi avvalgo di un file excel all'interno del quale si "nascondono" diverse formule fondamentali che andrò a spiegare man mano. Molti dei valori sono stati spiegati nel posto precedentemente citato, bisogna però fare subito una distinzione. Nel caso precedente si trattava di una trave doppiamente appoggiata con momento massimo calcolato come . In questo caso, trattandosi di una mensola bisogna considerare che .

Area di influenza = 12 m²

(1) TRAVE E SOLAIO IN LEGNO

I dati da A a K, come detto in precedenza, sono già stati ricavati in precedenza con l'aiuto della scorsa esercitazione (a differenza del momento, anche questo già detto). Procedo.

K) h - altezza della trave calcolata come = 52,75 cm

L) h_D - altezza di progetto assegnata =55 cm

M) E - modulo di elasticità parallelo alle fibre (come da normativa)= 8000 N/mm²

N) I_X - momento di inerzia calcolato come  =415938 cm⁴

O) V_MAX - spostamento massimo della trave calcolato come =1,25 cm⁴

P) L/V_MAX - rapporto che deve essere soddisfatto per >250= 240,87  Non verificato!

Non essendo verificato devo decidere di alzare il valore dell'altezza della trave. Con 60 cm viene verificato.

(2) TRAVE E SOLAIO IN ACCIAIO

La tabella fornisce il valore (in J) W_x=643,58 cm³ ovvero il modulo di resistenza a flessione dell'acciaio. Per scegliere il profilato corretto scelgo quello con valore immediatamente superiore. Nel mio caso IPE330 (W_x=713 cm³).

N) I_X - momento di inerzia (tabellato) =11770 cm⁴

L) peso della trave (tabellato)=0,49 KN/m

P) L/V_MAX - rapporto che deve essere soddisfatto per >250= 211,11  Non verificato!

Cerco un nuovo profilo dal profilario in modo da soddisfare il rapporto. IPE360 (W_x=904 cm³ - I_x=16270 cm³ - 0,57 KN/m - valori da sistemare in tabella) soddisfa il rapporto.

(3) TRAVE IN CALCESTRUZZO ARMATO E SOLAIO LATEROCEMENTO

A seguito del calcolo l'altezza ricavata è di 63,61 cm. 

Q) H_d=65 cm

Y) P) L/V_MAX - rapporto che deve essere soddisfatto per >250= 115,95  Non verificato!

Correggo l'altezza della trave fino a verificare il rapporto. Il rapporto è soddisfatto con una trave alta 85 cm. (251,13 rapporto verificato)