Portale di Meccanica

SdC(b)
A.A. 2015-2016

Commenti recenti

Correzione tavola 6 2 anni 2 settimane fa
diagrammi graticcio 5 anni 9 mesi fa
ultima domanda 5 anni 9 mesi fa
no ho ancora un'ultima 5 anni 9 mesi fa
sì sì tutto chiaro. 5 anni 9 mesi fa
Load Pattern peso proprio 5 anni 9 mesi fa
Ciao Fabiana, 5 anni 10 mesi fa
Ciao Giuliana, 5 anni 10 mesi fa
Modellazione setto - Giuliana Nardi 5 anni 10 mesi fa
assegnare sezione a setti su sap 5 anni 10 mesi fa

ES 3 - Il metodo di integrazione della linea elastica

Inviato da nicola.moscheni il Dom, 28/09/2014 - 20:04

La trave qui presentata non è altro che una struttura iperstatica.

Si calcoli quindi il valore v_MAX e la sua posizione sulla lunghezza della trave attraverso l'equazione della linea elastica.

Scriviamo le equazioni di riferimento:

$\large \left\{\begin{matrix} \frac{\mathrm{d} N}{\mathrm{d} s}+q_{2}=0\\ N=EA\xi \\ \xi=\frac{\mathrm{d} u}{\mathrm{d} s} \end{matrix}\right.$ $\left\{\begin{matrix} \frac{\mathrm{d} T}{\mathrm{d} s}+q_{2}=0\\ \frac{\mathrm{d} M}{\mathrm{d} s}+T=0\\ M=EJ\chi\\ \chi=\frac{\mathrm{d} \varphi }{\mathrm{d} s}\\ \varphi=\frac{\mathrm{d} v }{\mathrm{d} s} \end{matrix}\right.$

Di cui le prime tre si riferiscono allo sforzo normale perciò possono essere ignorate.

$\frac{\mathrm{d} T}{\mathrm{d} s}+q_{2}=0$ di cui $T=-\frac{\mathrm{d} M}{\mathrm{d} s}$ quindi $\frac{\mathrm{d} }{\mathrm{d} s}\left ( -\frac{\mathrm{d} M}{\mathrm{d} s} \right )+q_{2}=0 \Rightarrow -\frac{\mathrm{d^{2}} M}{\mathrm{d} s^{2}}+q_{2}=0$

$\chi=\frac{\mathrm{d} \varphi }{\mathrm{d} s}$ di cui $\varphi=\frac{\mathrm{d} v }{\mathrm{d} s}$ quindi $\chi=\frac{\mathrm{d} }{\mathrm{d} s}\left ( \frac{\mathrm{d} v}{\mathrm{d} s} \right )\Rightarrow \chi =\frac{\mathrm{d^{2}} v}{\mathrm{d} s^{2}}$

$M=EJ\chi \Rightarrow M =EJ\frac{\mathrm{d^{2}} v}{\mathrm{d} s^{2}}$ perciò $-\frac{\mathrm{d} ^{2}}{\mathrm{d} s^{2}}\left ( EJ\frac{\mathrm{d^{2}} v}{\mathrm{d} s^{2}} \right )+q_{2}=0$

di cui $EJ$ è una costante perché dipende dal materiale della struttura che consideriamo sempre uguale in tutte le sezioni, e $q_{2}$ rappresenta un carico uniformemente distribuito, abbiamo quindi che:

$\frac{\mathrm{d^{4}} v}{\mathrm{d} s^{4}}=\frac{q_{2}}{EJ}$ $\frac{\mathrm{d^{3}} v}{\mathrm{d} s^{3}}=\frac{q_{2}}{EJ}s+c_{1}$

$\frac{\mathrm{d^{2}} v}{\mathrm{d} s^{2}}=\frac{q_{2}}{EJ}\frac{s^{2}}{2}+c_{1}s+c_{2}$

$\frac{\mathrm{d} v}{\mathrm{d} s}=\frac{q_{2}}{EJ}\frac{s^{3}}{6}+\frac{c_{1}s^{2}}{2}+c_{2}s+c_{3}$

$v\left ( s \right )=\frac{q_{2}}{EJ}\frac{s^{4}}{24}+\frac{c_{1}s^{3}}{6}+c_{2}s^{2}+c_{3}s+c_{4}$

Ci troviamo quindi con quattro differenti costanti additive. Per trovarle dobbiamo esprimere le condizioni al bordo.

$V(0)=0\Rightarrow c_{4}=0$

$\varphi(0)=0\Rightarrow {\frac{\mathrm{d} v}{\mathrm{d} s}}=0\Rightarrow c_{3}=0$

$v(l)=0\Rightarrow v\left ( l \right )=\frac{q_{2}}{EJ}\frac{l^{4}}{24}+\frac{c_{1}l^{3}}{6}+c_{2}l^{2}=0$

$M(l)=0\Rightarrow EJ\left (\frac{q_{2}}{EJ}\frac{l^{2}}{2}+c_{1}l+c_{2} \right )=0$

Non ci resta che trovare i valori di c₁ e c₂. Mettiamo quindi a sistema le due equazioni, tenendo conto che per convenzione di segno q₂ ha segno negativo.

$\large \left\{\begin{matrix} \frac{q_{2}}{EJ}\frac{l^{4}}{24}+\frac{c_{1}l^{3}}{6}+c_{2}l^{2}=0\\ \frac{q_{2}}{EJ}\frac{l^{2}}{2}+c_{1}l+c_{2}=0 \end{matrix}\right.$

Dalla seconda equazione si può ricavare c₂: $c_{2}=\frac{q_{2}}{EJ}\frac{l^{2}}{2}-c_{1}l$

E sostituirlo nella prima: $\frac{-q_{2}}{EJ}\frac{l^{4}}{24}+\frac{c_{1}l^{3}}{6}+\left ( \frac{q_{2}}{EJ}\frac{l^{2}}{2}-c_{1}l \right )\frac{l^{2}}{2}=0$

Svolgendo le equazioni (risparmio tutto lo svolgimento in quanto si tratta della soluzione di un normale sistema a due equazioni) si hanno le due soluzioni c₁e c₂:

$\large \left\{\begin{matrix} c_{1}=\frac{5}{8}\frac{q_{2}l}{EJ}\\ c_{2}=-\frac{q_{2}l^{2}}{8EJ} \end{matrix}\right.$

Ora bisogna trovare la posizione dove lo spostamento è massimo, in quel punto cioè dove $\varphi=0$ .

Essendo $\varphi=\frac{\mathrm{d} v}{\mathrm{d} s}\Rightarrow \frac{\mathrm{d} v}{\mathrm{d} s}=0$

$\frac{\mathrm{d} v}{\mathrm{d} s}=\frac{q_{2}}{EJ}\frac{s^{3}}{6}+\frac{c_{1}s^{2}}{2}+c_{2}s+c_{3}$ $\Rightarrow \frac{q_{2}}{EJ}\frac{s^{3}}{6}+\frac{5}{8}\frac{q_{2}l}{EJ}\frac{s^{2}}{2}+\frac{q_{2}l^{2}}{8EJ}s=0$ $\Rightarrow \frac{s^{2}}{2}+\frac{5}{8}ls+\frac{l}{4}=0$

di cui le soluzioni sono:

$\left\{\begin{matrix} s_{1}=1,29l\\ s_{2}=0,57l \end{matrix}\right.$

Di cui solo s₂ è valida in quanto inferiore al valore di l e perciò interno alla trave. A questo punto è sufficente sostituire il valore nella funzione $v(s)$ per trovare il valore dello spostamento massimo.

$v\left _{( MAX) \right}=\frac{q_{2}}{EJ}\frac{(0,57l)^{4}}{24}+\frac{5}{8}\frac{q_{2}l}{EJ}\frac{(0,57l)^{3}}{6}+\frac{q_{2}l^{2}}{8EJ}(0,57l)^{2}$

Ma perché affrontare un difficile calcolo quando possiamo usare SAP2000 per scoprire tale valore?

(alcune procedute verranno date per per scontate, si rimanda perciò ai post precedenti)

Iniziamo. Aprite SAP2000 e impostate il modello [Grid Only] e impostate i parametri [Number of Grid Lines] e [Grid Spacing] tenendo conto che stiamo progettando in 2D quindi il valore Z=1.

Nel mio caso i parametri saranno rispettivamente per (X, Y): [Number of Grid Lines]=(2, 1) ; [Grid Spacing]=(1, 1). Cioè ho previsto una griglia composta da due serie di linee lungo X, una lungo Y; distanziate di 1 m.
Impostare vista xz.

Disegnare la trave seguendo le linee della griglia. Impostare vincoli e forza agente sulla struttura [Assign > Frame Loads > Distributed...] e assegnare il valore del peso distribuito in [Load]. (Nel mio caso 12). Quindi assegnamo il peso proprio della struttura e la sezione della trave. Questa volta ho scelto una sezione rettangolare 20cm x 20 cm di spessore 1 cm.

Ecco la struttura.

A questo punto bisogna dare un punto di riferimento per misurare lo spostamento e tutte le forze che agiscono a quel 0,57L. Quindi [Draw > Draw Special Point]. Puntarlo sulla struttura, quindi clic destro, menù [Location], doppio clic su [Joint Cordinates] e impostare X=0,57 (e controllare che Y,Z=0).

[Run Analysis]

Ecco la struttura "in azione".

A questo punto è possibile conoscere tutti i dati che ci interessano, ma soprattutto lo spostamento massimo perché nelle tabelle è stato preso in considerazione il punto che abbiamo assegnato precedentemente. Lo troviamo nella tabella [Joint Displacements] indicato nella colonna U3.

$v\left _{( MAX) \right}=16\times 10^{-6}$

SdC(b) (LM PA)

Esercitazione

ES 2 - Dimensionamento trave

Inviato da nicola.moscheni il Dom, 28/09/2014 - 04:48

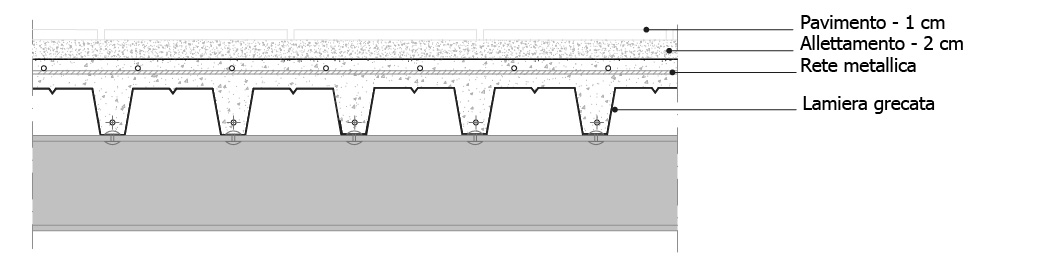
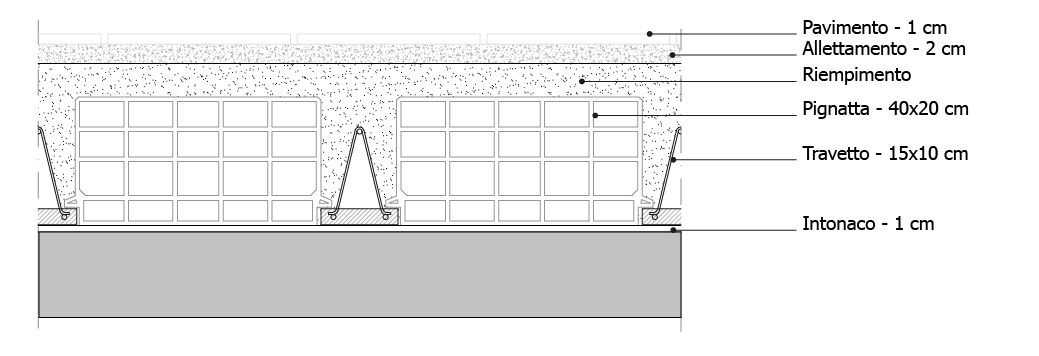
Ipotizzo di essere alle prese con un solaio composto come quanto segue (del quale ho evidenziato l'area di influenza di una delle travi).

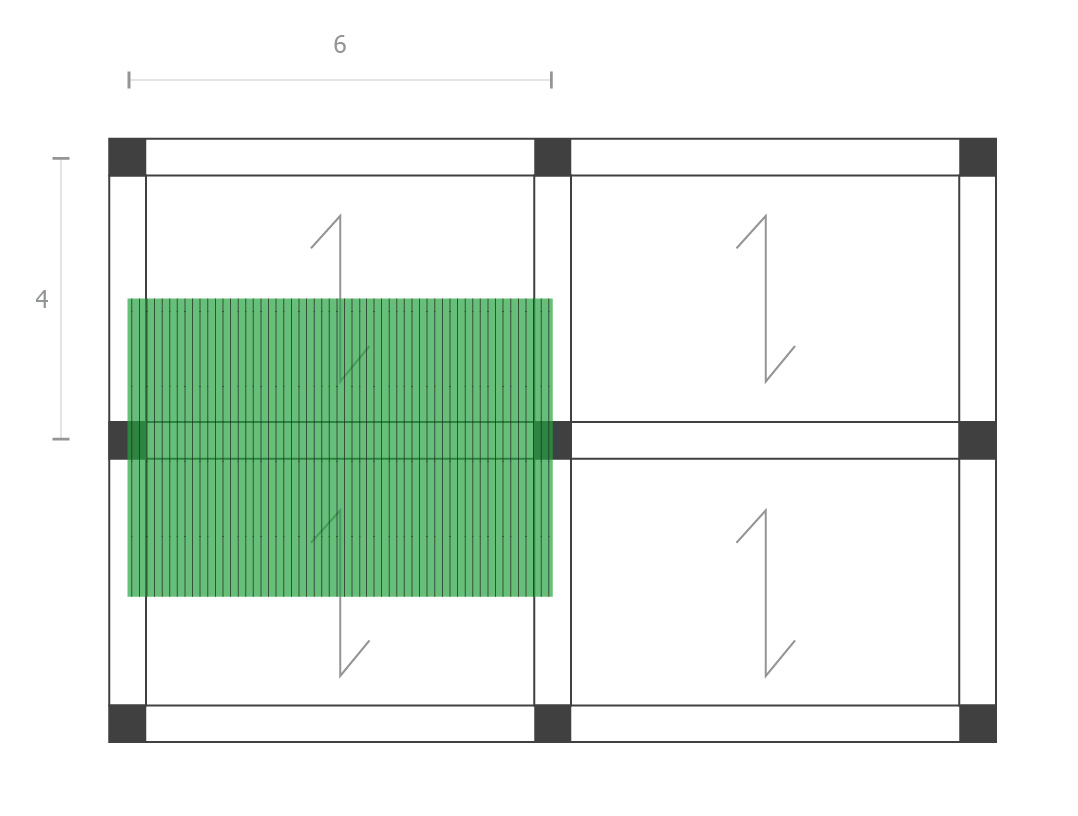
Voglio dimensionare questa trave in funzione di tre ipotetici pacchetti murari: legno, acciaio e laterocemento. Di conseguranza si tratteranno di tre tipologia di trave diverse. Per questa operazione mi avvalgo di un file excel all'interno del quale si "nascondono" diverse formule fondamentali che andrò a spiegare man mano. (il file completo è in allegato)

Area di influenza = 24 m²

(1) TRAVE E SOLAIO IN LEGNO

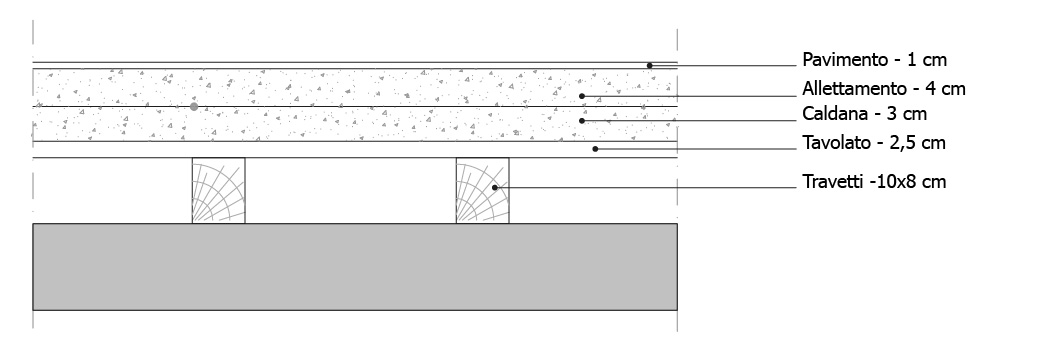
I dati inseriti nell'excel corrispondono a:

A) Interasse =4 m

B) q_{S -}CARICHI STRUTTURALI il peso proprio delle parti strutturali del solaio ovvero i travetti e il tavolato (in questa fase di dimensionamento non considero il peso della trave oggetto di analisi, in quanto, non conoscendone le dimensioni, non lo posso ancora calcolare - NDR) =0,46 KN/m²

C) q_{P -}CARICHI PERMANENTI il peso proprio delle parti non strutturali del solaio, ovvero tutto quello che viene portato. A questo aggiungo il peso dei tramezzi (1 KN/m²)e degli impianti (0,5 KN/m²), definiti dalla normativa =2,48 KN/m²

D) q_{A -}CARICHI ACCIDENTALI un valore aggiuntivo che tiene conto della destinazione d' uso dell edificio, in questo caso residenziale =2 KN/m²

E) q - somma dei precedenti carichi distribuito sull'interasse =27,28 KN/m

F) Luce della trave =6 m

G) M - momento massimo della trave considerato come momento massimo di una trave doppiamente appoggiata caricata uniformemente 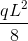=122,80 KNm

H) f_MK- resistenza caratteristica con valore dato dalla normativa (nel caso di legno lamellare)=24 N/mm²

I) k_MOD - coefficiente riduttivo che tiene conto della durata del carico e dell'umidità della struttura (sostanzialmente il livello di degrado della struttura) dato dalla normativa =0,8

J) σ_AM- tensione ammissibile calcolata come 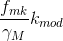dove al denominatore c'è un coefficiente di sicurezza (per il legno lamellare 1,45)=13,24 N/mm²

K) Base della trave che scelgo essere di 30 cm

L) h - altezza della trave calcolata come 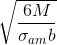=43 cm

Ora che abbiamo un valore ipotetico della trave devo scegliere un profilo chiaro. Opto per 30x48 cm. Questo valore mi permette di calcolare il peso proprio della trave da aggiungere a q_Sper poi verificare nuovamente l'altezza corretta della trave.

(2) TRAVE E SOLAIO IN ACCIAIO

In questo caso non andrò a ricavarmi base ed altezza della trave, ma trattandosi di un profilato ci sono delle sezioni già pronte. Questo vuol dire che mi baserò sul Modulo di Resistenza W_x.

A) Interasse =4 m

B) q_{S -}CARICHI STRUTTURALI =2,5 KN/m²

C) q_{P -}CARICHI PERMANENTI =1,2 KN/m²

D) q_{A -}CARICHI ACCIDENTALI =2 KN/m²

E) q - somma dei precedenti carichi distribuito sull'interasse =27,28 KN/m

F) Luce della trave =6 m

G) M - momento massimo della trave =122,80 KNm

H) f_YK- tensione di snervamento caratteristica (avendo scelto un acciaio FE430/S275)=275 N/mm²

I) σ_AM- tensione ammissibile calcolata come 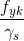dove al denominatore c'è un coefficiente di sicurezza (per l'acciaio 1,15)=239,13 N/mm²

J) W_x - modulo di resistenza calcolato come 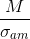=587,88 cm³

Ora che ho questo valore devo cercare nel profilario un profilato con un W_x immediatamente superiore, ovvero una IPE330 (W_x=713 cm³). Una volta trovato il profilato, faccio la verifica finale inserendo il peso proprio della trave ai carichi strutturali.

W_xè ancora verificato.

(3) TRAVE IN CALCESTRUZZO ARMATO E SOLAIO LATEROCEMENTO

A) Interasse =4 m

B) q_{S -}CARICHI STRUTTURALI =3,75 KN/m²

C) q_{P -}CARICHI PERMANENTI =3,4 KN/m²

D) q_{A -}CARICHI ACCIDENTALI =2 KN/m²

E) q - somma dei precedenti carichi distribuito sull'interasse =49,18 KN/m

F) Luce della trave =6 m

G) M - momento massimo della trave =221,31 KNm

H) f_Y- tensione di snervamento caratteristica dell'acciaio da armatura (da normativa dev'essere sopra i 450 N/mm²)=450 N/mm²

I) σ_AM- tensione ammissibile dell'acciaio =391,30 N/mm²

J) R_CA- resistenza caratteristica del calcestruzzo (da normativa, nel mio caso scelgo C40/50)=40 N/mm²

K) σ_CA- tensione ammissibile del calcestruzzo =391,30 N/mm²

L) α calcolata come 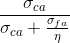dove η è un coefficiente di omogeneizzazione che lega i moduli elastici di acciaio e calcestruzzo =0,46

M) r calcolata come 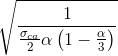=2,26

N) base =20 cm

O) h altezza della trave senza considerare il copriferro inferiore calcolata come 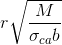=49,89 cm

P) δ copriferro inferiore =5 cm

Q) H altezza totale della trave =54,89 cm

Questa volta però per fare la verifica della trave decido non solo di aumentare l'altezza della trave fino a che non ottengo un valore adeguato, ma di intervenire anche su R_CA in modo da aumentare la resistenza del calcestruzzo in modo da non dovre avere una trave troppo alta.

In effetti dopo varie prove mantenendo R_CA=40 N/mm² avrei dovuto utilizzare una trave da 75 cm, aumentando invece tale valore sono riuscito ad ottenere un profilo non esagerato.

SdC(b) (LM PA)

Esercitazione

ES 1b - Reticolare 3D

Inviato da nicola.moscheni il Dom, 28/09/2014 - 00:26

In questa esercitazione provvederò ad analizzare una struttura reticolare spaziale. Molte nozioni base per il procedimento di questa nalisi sono contenuti nel mio precedente post.

Alcune considerazioni. La struttura può essere disegnata in un altro programma, nel mio caso Autocad. Importante è non disegnare nel Layer 0 e le aste devono essere disegnate tutte separatamente. Salvare in .dxf.

Nel momento in cui importiamo il file, seleziono nel menù Frames il layer dove ho disegnato le aste. [File] > [Import] > [Autocad .dxf File]

Ecco qui la struttura.

Come nel post precedente, nel caso della stuttura reticolare piana, devo "sistemare" il modello. Perciò impongo il Momento 0 ai nodi, imposto la Sezione (tubolare) e oltretutto devo assicurarmi che i nodi vengano riconosciuti come tali per ovviare ad una tolleranza troppo alta. Perciò [Edit] > [Edit Points] > [Merge Joints] quindi inserisco un valore di tolleranza relativamente basso (nel mio caso 0,05).

A questo punto impongo le forze sui nodi (80KN).

E' il momento di posizionare i vincoli. [Assign] > [Joints] > [Restraints] selezionando i soli nodi che vengono interessati.

Nel mio caso ho deciso di inserire due carrelli e due cerniere.

Via all'analisi. Ecco la deformata, sempre meno rincuorante.

Ora passo al diagramma dello sforzo normale.

Quello che si può notare è che in in questo caso, le aste maggiormente sollecitate sono quelle più vicine ai carrelli. Questo perché, a differenza del post precedente, questa stuttura presenta uno sbalzo. Questo, non ha la possibilità di scaricare le forze, quindi di contrastarle che gli vengono esercitate sopra e quindi lo sforzo maggiore lo subiscono le aste più vicino al vincolo dove esse trovano un'opposizione.

A questo punto individuo le aste maggiormente sollecitate e quindi i loro valori tensionali.

Di tutte e 280 le aste quella più sollecitata ha un valore σ=250 N/mm². Questo significa che dovremmo considerare un acciaio di classe Fe430/S275 oppure Fe510/S355 che hanno tensioni di snervamento caratteristiche adeguate.

SdC(b) (LM PA)

Esercitazione

tabella sforzo normale reticolare3D.pdf

ES 1a - Reticolare 2D

Inviato da nicola.moscheni il Sab, 27/09/2014 - 19:39

Mi appresto a risolvere questa reticolare piana. Si tratta di una struttura composta da triangoli equilateri. Così composta oltretutto, la struttura può essere considerata simmetrica, ecco perché posso permettermi di concentrarmi su una delle due parti della struttura, al suo simmetrico il comportamento sarà appunto, simmetrico.

Prima procederò con il Metodo delle Sezioni di Ritter (1) e in seconda battuta con il programma SAP2000 (2).

(1) Metodo delle Sezioni di Ritter

In questa fase farò un'analisi cercando di trovare quali siano le parti più sollecitate della struttura e quindi le aste poste a maggior sforzo (siano esse tiranti o puntoni), le quali immagino già siano in corrispondenza del modulo centrale. Posso ricavarmi le reazioni vincolari R=9/2 F

Il metodo, in sostanza, taglia tre aste. Ognuna delle aste ha un suo sforzo normale che vado a rappresentare uscente da essa (con verso completamente casuale, NDR).

Procedo considerando l'equilibrio a rotazione per i nodi C e D

NODO C M_c=0 ⇒ -N₁₄(3^½/2)L+F(L/2)+F(3L/2)+F(5L/2)+F(7L/2)+F(9L/2)-(9F/2)5L=0 ⇒ N₁₄=(-20*3^½*F)/3

Il valore dello sforzo normale dell'asta 14 è negativo, siamo quindi in presenza di un'asta compressa, ovvero di un puntone. [Attenzione! Il verso di N₁₄ così disegnato è sbagliato, si tratterebbe dell'opposto in quanto negativo] Allo stesso modo tutte le aste superiori della struttura saranno dei puntoni. L'intensità di N diminuirà all'avvicinarsi verso il vincolo in quanto sempre meno forze agiscono sulla parte di struttura presa in considerazione. Per esempio: N₁₀=(-8*3^½*F)/3

NODO D M_D=0 ⇒ N₅(3^½/2)L+FL+F2L+F3L+F4L+F5L-(9F/2)5/2L=0 ⇒ N₅=(5*3^½*F)/2

Il valore dello sforzo normale dell'asta 1 è positivo, siamo quindi in presenza di un'astra in trazione, ovvero di un tirante. Allo stesso modo tutte le aste superiori della struttura saranno dei tiranti. L'intensità di N diminuirà all'avvicinarsi verso il vincolo in quanto sempre meno forze agiscono sulla parte di struttura presa in considerazione. Per esempio: N₁=(13*3^½*F)/3

Procedo considerando l'equilibrio a traslazione verticale

-5F+9F/2-N₃₁*3^½/2=0 ⇒ N₃₁=-(3^½*F)/3

Il valore dello sforzo normale dell'asta 31 è positivo, siamo quindi in presenza di un'astra in trazione, ovvero di un tirante.

Ecco quindi come si presenta il diagramma dello sforzo normale della struttura, utile per individuare puntoni e tiranti, nonché le aste maggiormente sollecitate.

(2) SAP2000

Cercherò di riprodurre la stessa struttura in SAP2000.

Creando il file nuovo seleziono [2D Trusses] e imposto i valori della reticolare: numero di moduli di base, lunghezza (3 m) e altezza (2,60 m) di questi.

Ed ecco qui la mia struttura.

In primo luogo devo "sistemare" alcuni difetti del modello per assicurarmi il corretto funzionamento della struttura.

Impongo che i nodi non trasmettano momento. Selezionando tutta la struttura vado al comando [Assign]>[Frame]>[Release/Partial Fixity]

Selezionando Moment 22 e Moment 33 dando valore 0.

La struttura ora viene visualizzata così.

Imposto ora la sezione delle aste. [Assign]>[Frame]>[Frame Section] e clicco su Add New Property per creare una nuova proprietà disezione.

E seleziono il profilato cilindrico in acciaio. Al quale do parametri diametro 18 cm e spessore 6 mm.

E' ora di imporre le forze che esercitano sulla struttura. Essendo una reticolare le forze insistono sui nodi, ecco perché devo stare attento a selezionare solo quelli che mi interessano.

[Assign]>[Joint Loads]>[Forces]

Clicco su + per aggiungere una nuova entità di carico. Scrivo il nome Carico e clicco Add New Load Pattern

Stando attento a selezionare Carico dal menù a tendina impongo una forza dall'alto che insista sulla struttura. Quindi su Globale Z inserisco il valore -80KN. (Negativo perché verso il basso)

Sono pronto per l'analisi. [Analyze]>[Run Analysis]. Devo solo avere l'accortezza di inserire in analisi solo l'azione delle forze che ho imposto. Quindi dando Run/Do not Run Case in modo che resti selezionato solo Carico.

SAP2000 mostra subito la deformata, poco rassicurante, della struttura.

Adesso posso andare a vedere il diagramma dello sforzo normale. Ma prima voglio vedere il numero delle aste in modo da poter confrontare i risultati.

[View]>[Set Display Options] e selezionare Labels dalla seconda colonna. In questo modo ogni asta avrà un suo "nome", o meglio un numero.

[Display]>[Show Forces/Stresses]>[Frame/Cables/Tendons] e selezionando Axial Forces posso vedere il diagramma che mi interessa. In basso alla finestra si può Anche selezionare Fill Diagram o Show Values on Diagram, i quali rispettivamente mostrano un semplice diagramma colorato oppure permette di vedere i valori direttamente sul diagramma.

Beh sembra proprio che c'abbia preso.

Ora posso visualizzare anche le tabelle con tutti i valori. [Display]>[Show Table]. Selezionando dal sottomenù di Analysis Results > Element Output. La tabella che mi interessa è Element Forces - Frames.

La tabella che mi si presenta ha molti valori. Per ogni asta vengono mostrate molte sezioni, essendo però lo sforzo normale costante posso selezionare solo una delle sezioni per ogni asta. Questo e molto altro per "pulire" la tabella ancor prima di esportarla si può fare dal menù [Format-Filter Sort] > [Filter Table]. Il valore che ci interessa dello sforzo normale è nella colonna P

[File] > [Export Current Table] > [To Excel]

I valori delle aste più sollecitate sono:

ASTA 5 = 981,338 KN tirante ASTA 13 = ASTA 14 = -957,824 KN puntone

E' anche interessante valutare la tensione esercitata sulle aste. Per questo una volta calcolata l'area della sezione (6669mm²) ho anche valutato σ=N/A.

ASTA 5 = 147,14 N/mm² ASTA 13 = ASTA 14 = -143,6 N/mm²

Questi valori ci permettono di controllare se questa struttura può reggere il carico senza superare il limite di snervamento (quello cioè di una tensione ammissibile). Secondo normativa gli acciaio partono da un valore di Tensione di snervamento caratteristica pari a 235 MPa, direi che ci siamo.

Per tutti gli altri valori, allego la tabella excel.

SdC(b) (LM PA)

Esercitazione

tabella sforzo normale reticolare.pdf

ESERCITAZIONE 5 - CONTROVENTI, CENTRI DELLE RIGIDEZZE E RIPARTIZIONE DELLE FORZE SISMICHE

Inviato da Ottavio Minella il Mer, 16/07/2014 - 09:51

Per questa esercitazione abbiamo preso in oggetto una porzione dell'edificio progettato per il corso di progettazione architettonica lm2. Questo fabbricato è pensato per essere realizzato con struttura in acciaio e quindi con i conseguenti controventi. Siamo partiti dal predimensionamento degli elemnti strutturali, alla definizione del centro delle rigidezze e al calcolo delle forze sismiche. Abbiamo calcolato gli spostamenti e rotazioni confrontandoli con i risultati del software SAP200 constatando la corrispondenza degli stessi.

In allegato l'esercitazione per esteso.

SdC(b) (LM PA)

Esercitazione

ES. 4 Ripartizione delle forze sismiche.

Inviato da Giovanni.Saja il Gio, 10/07/2014 - 18:12

Costruendo un impalcato con travi e pilastri in cls armato di tipo shear - type studiamo come reagisce sotto l'azione di una forza sismica orizzontale, la struttura per resistere necessita di essere controventata. I controventi di un impalcato sono rappresentati proprio dai telai che assorbono la spinta e rispondono come una molla sottoposta a compressione.

F= K*∂

L'impalcato viene costruito con una trave di altezza h= 70cm e pilastri di sezione 30x30 cm. Viene scelto un cls con classe di resistenza 25/30 che avrà un modulo elastico E= 25000 N/mmq.

Per calcolare la rigidezza traslante di ogni telaio abbiamo bisogno del momento d'inerzia rispetto all'asse in cui agisce la forza sismica, nel nostro caso l'asse X.

I x = b* h³/12 =67500 cm⁴

Adesso calcoliamo la rigidezza per ogni telaio con la formula : 12 EIx/ h³

Riassunto delle rigidezze di ogni telaio

Calcolo del centro di massa dell'impalcato.

Con un procedimento simile, moltiplicando la rigidezza di ogni telaio per la distanza dell'origine ( pilastro 11),

si calcola il centro di rigidezza.

Considerando un pacchetto di solaio in cls armato già calcolato in un esercitazione precedente si analizzano i carichi sismici agenti sulla struttura considerando i coefficenti di contemporaneità ed intensità sismica.

Le tabelle seguenti riportano come la forza si distribuisce lungo le direzioni orizzontale e verticale nella pianta della struttura.

Adesso verifichiamo i calcoli applicandoli su un modello costruito con SAP.

Il modello rappresenta l'impalcato disegnato precedentemente , i pilastri vengono fissati alla base con un vincolo incastro mentre per rendere le travi di tipo shear - type aumentiamo con diversi zeri il momento d'inerzia di quest'ultime rispetto agli assi X e Y . Inoltre diciamo al programma con il comando Diaphragm di traslare allo stesso modo i nodi trave - pilastro.

Tramite il comando offset definiamo i rispettivi centri di rigidezza e massa.

Adesso assegnamo la forza F nel centro di massa e verifichiamo con l'analisi.

Il solaio trasla e ruota leggermente subendo una minima rotazione poichè il centro delle masse e quello delle rigidezze non coincidono, per diminuire ancora di più tale rotazione si può irrigidere i pilastri aumentandone la dimensione in sezione.

Esercitazione Piastre e gusci

Inviato da LuigiOlivieri il Mer, 09/07/2014 - 20:00

SdC(b) (LM PA)

Esercitazione

Esercitazione 6_archi

Inviato da micol.pucciarelli il Lun, 07/07/2014 - 09:29

SdC(b) (LM PA)

Esercitazione

ESERCITAZIONE ARCHI

Inviato da Tommaso il Dom, 06/07/2014 - 21:43

L'esercitazione mira a verificare che un arco è "più arco" (cioè si configura come una struttura spingente) quando la propria freccia diminuisce in rapporto alla luce, questa variazione di dimensione fa sì che il carico applicato sull'arco si trasformi prevalentemente in sforzo assiale a discapito dello sforzo di taglio e del momento flettente all'interno delle sezioni che compongono l'arcata.

Per quanto riguarda la tipologia dell'arco parabolico, ci aspettiamo di ottenere risultati dai diagrammi di taglio e momento flettente nulli, in quanto questa tipologia di arco, per la sua particolare forma geoemetrica è ingrado di trasformare tutto il carico gravante sull'arco in sforzo assiale.

Cominciamo con l'arco a tutto sesto, luce 12m, freccia 6m.

Importiamo il file IGES della struttura all'interno dell'ambiente sap20014.

Assegniamo INCASTRO alle imposte dell'arco, e in chiave CERNIERA interna selezionando le due aste più vicine al nodo e assegnando che rilasci il momento da sinistra a destra.

Definiamo le sezioni rettangolari (0,4m x 0,3m) del concio che compone l'arco.

[vista estrusa]

Definiamo il carico distribuito assegniamo 0 a peso proprio.

Selezioniamo tutte le aste.

Asseganiamo il carico distribuito con un valore di 10 KN in modalità Gravity Projected.

Selezioniamo la combinazione di carico, carico distribuito e lanciamo l'analisi.

Deformata dell'arco.

Reazioni vincolari, notiamo come la componente Y è perfettamente il doppio della componente X che rappresenta la forza di spinta(ql²/2f).

Sforzo assiale:

all'imposta 52,21 KN DI COMPRESSIONE.

Momento flettente.

Sforzo di taglio.

Vediamo come si comporta l'arco a sesto ribassato ricordando che la luce è la stessa, così come il carico distribuito e che invece la freccia è la metà dell'arco a tutto sesto.

Deformata dell'arco.

Reazioni vincolari, notiamo come la componente X (della spinta) comincia a crescere rispetto a quella Y pareggiandola essendo la freccia in questo caso la perfetta metà della luce.