RISOLUZIONE DI UN GRATICCIO SEMPLICE MEDIANTE IL METODO DELLE RIGIDEZZE
Possiamo parlare di graticcio quando vi è collaborazione tra due sistemi ortogonali di travi che non presentano strutture gerarchiche: ogni elemento strutturale (in ognuna delle 2 direzioni di orditura) ha la stessa valenza, e per questo le sezioni delle travi sono analoghe.
Un parametro che assume notevole importanza nel graticcio è la rigidezza torsionale, dal momento che avendo flessione in una direzione, inevitabilmente avremo torsione nell’altra. Nella rigidezza torsionale gioca un ruolo fondamentale il Momento d’inerzia Polare (Ip), un parametro legato alla geometria della sezione.
In questo esercizio si analizza un graticcio semplice, comparando i valori delle rotazioni indotte da una forza concentrata ottenuti associando diverse sezioni alla trave soggetta a torsione(al contrario di quanto si constata normalmente in strutture di questo tipo). Va ricordato, infatti, che la rotazione è indirettamente proporzionale alla rigidezza torsionale.
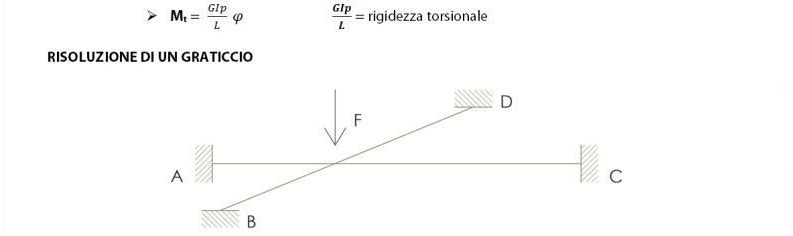
Il nodo ha 6 gradi di libertà: esso può traslare lungo i 3 assi x, y e z, inoltre può ruotare attorno agli stessi. In questo caso specifico la condizione di carico non genera traslazioni lungo x e lungo y, così come non vi sono rotazioni in x e in z, date le proporzioni dello schema strutturale.
Le incognite, dunque, sono soltanto due, ossia lo spostamento Delta(z) e la rotazione Fi(y).
Analizziamo le deformate delle due travi separatamente:

Sulla trave BD la forza F agisce esattamente al centro, quindi la deformata è simmetrica e in quel punto abbiamo uno spostamento δ, ma nessuna rotazione della sezione essendo un punto di tangenza orizzontale. Sulla trave AC, invece, F agisce ad un terzo della lunghezza e, sebbene il punto trasli della stessa quantità lungo z, stavolta non ci troviamo nel punto a tangenza orizzontale della deformata, quindi avremo anche una rotazione della sezione intorno all’asse y.
Per questo motivo separiamo idealmente le due incognite, facendole agire separatamente e sovrapponendo poi i loro effetti.
Analizziamo innanzitutto le due deformate prodotte dalla spostamento δ:
- deformazione dovuta solo allo spostamento δper la trave AC:
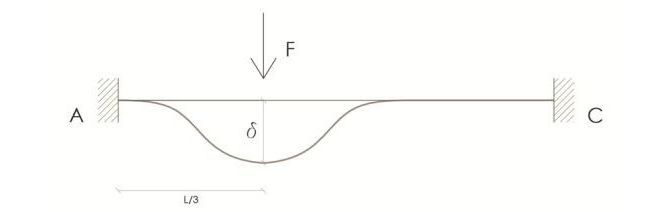
come detto in precedenza il punto soggetto alla forza F deve abbassarsi senza ruotare. Conoscendo già i valori della rigidezza in una trave doppiamente incastrata possiamo quantificare gli sforzi di Taglio e Momento flettente, concentrandoci in particolare su quelli che agiscono sul nodo:

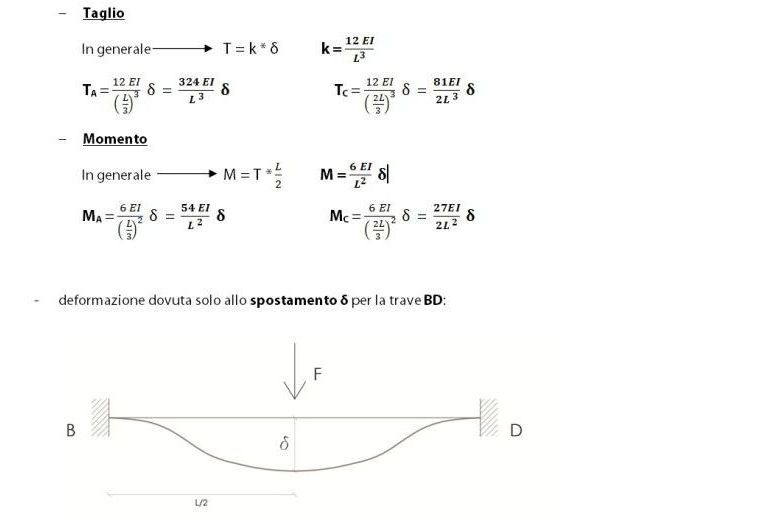
Anche nell’asta BD soggetta alla sola traslazione il nodo si abbassa senza ruotare, quindi analogamente a quanto fatto in precedenza procediamo rapidamente al calcolo degli sforzi di Taglio e Momento Flettente, i quali per via della simmetria dello schema stavolta saranno identici:

(questi due momenti oltre ad elidersi perché uguali in valore assoluto e opposti nel verso, si riferiscono ad una rotazione attorno all’asse x, quindi non verranno presi in considerazione nell’equazione di equilibrio dei momenti)
A questo punto analizziamo le deformate provocate dalla sola rotazione Fi(y):
- deformazione dovuta solo alla rotazione Fi(y) per la trave AC:

la rotazione imposta al nodo prova un’inflessione nella trave AC e il punto stesso ruota intorno all’asse y. Anche in questo caso, come in precedenza, ci affidiamo a schemi notevoli dal momento che abbiamo già affrontato la questione della rigidezza flessionale e conosciamo i valori dei momenti agli estremi in una trave doppiamente incastrata:
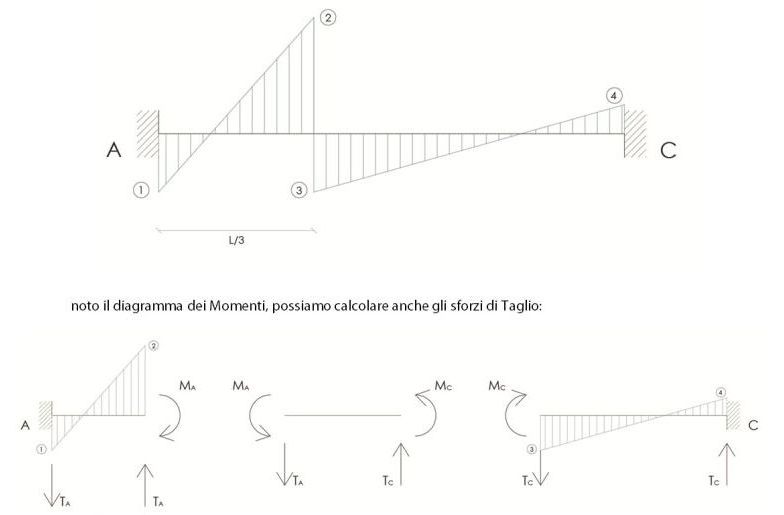
La flessione della trave AC intorno all’asse y corrisponde inevitabilmente alla torsione di quella BD:
deformazione dovuta solo alla rotazione Fi(y) per la trave BD (TORSIONE):

il Momento Torcente agente sulla trave genera due momenti reagenti di verso opposto, cosa non trascurabile per determinare poi il segno di questi due contributi nell’equazione di equilibrio dei momenti:

A questo punto conosciamo tutti i contributi degli sforzi di Taglio e Momento Flettente agenti sul nodo e generati sia dalla traslazione Delta(z) che dalla rotazione Fi(y). Possiamo, quindi, scrivere le due equazioni di equlibrio:

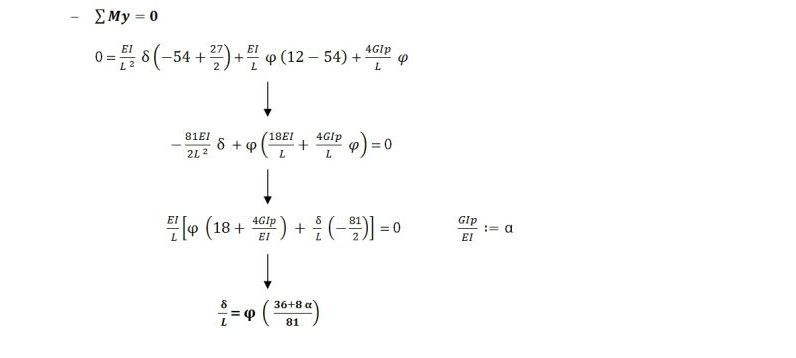

VERIFICA DEL GRATICCIO SU SAP
Lo scopo di questo esercizio è di constatare le variazioni di abbassamenti e rotazioni del punto d’incontro delle 2 travi doppiamente incastrate al variare della luce e della sezione assegnate alla trave la cui rigidezza torsionale influenza il comportamento del sistema.
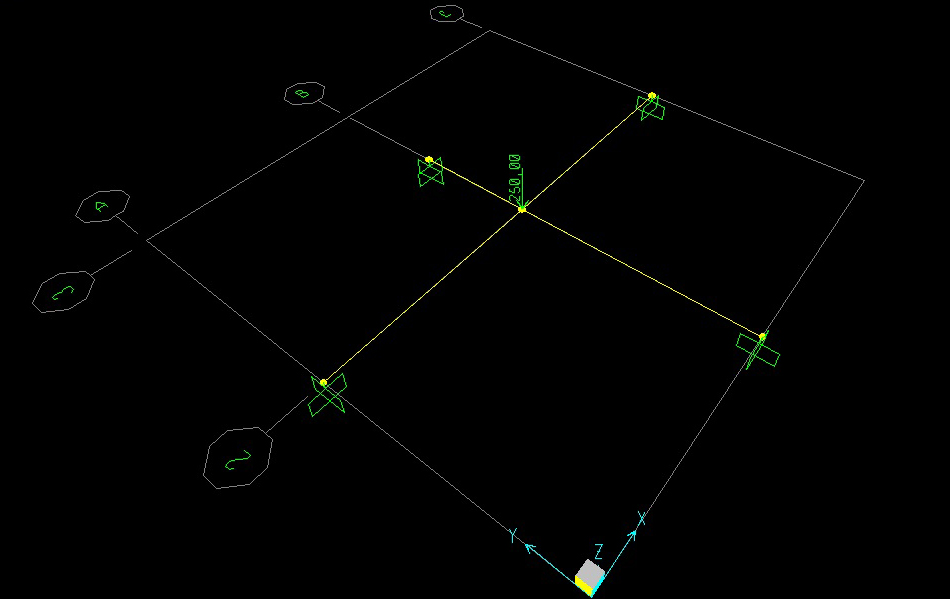
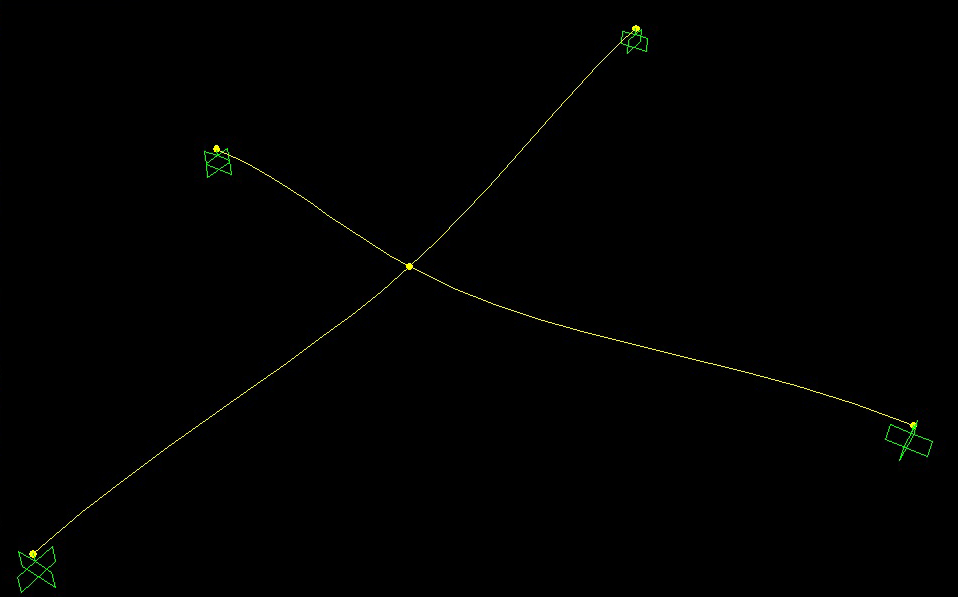
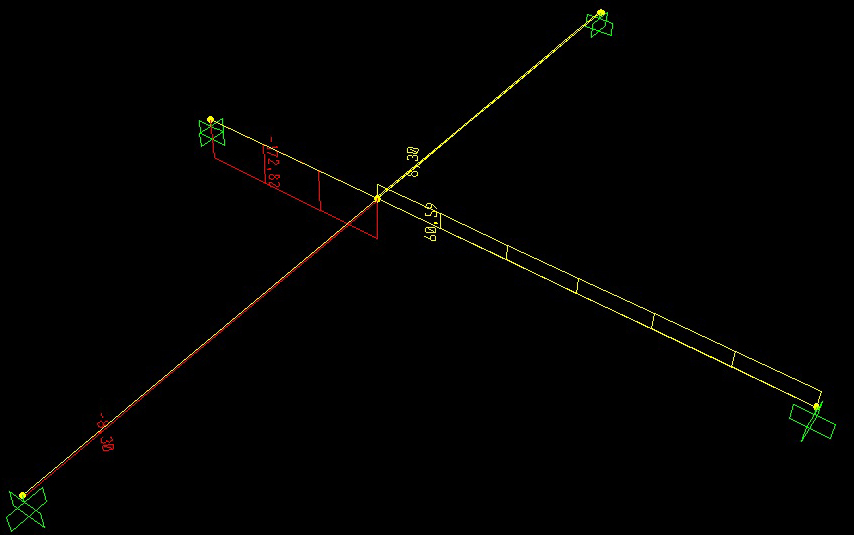
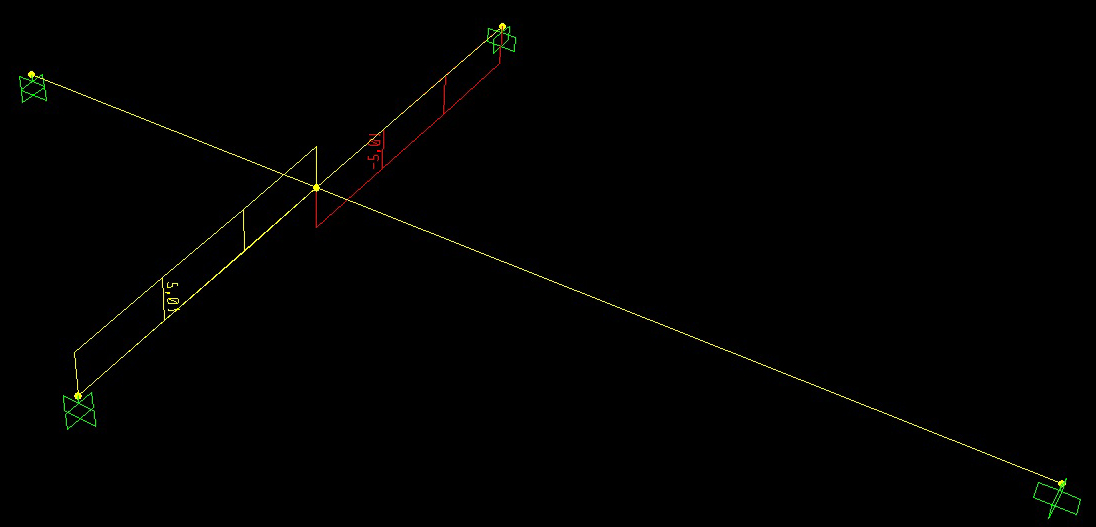
Questi sono i rispettivi diagrammi di Taglio, Momento flettente e Momento torcente.

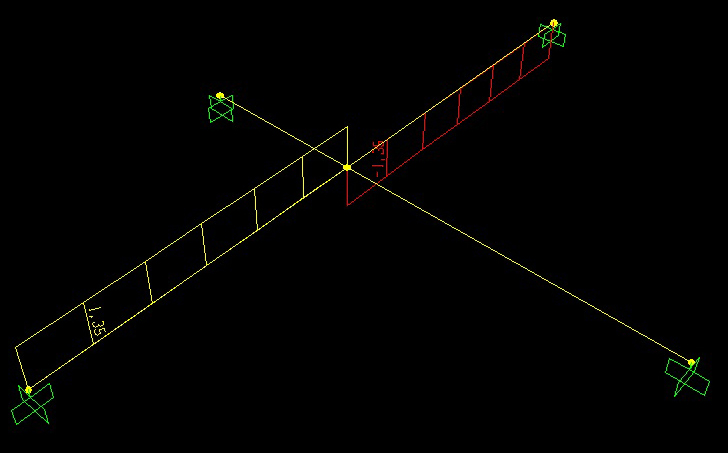
Alla trave con luce costante è stata associata una sezione in acciaio di tipo scatolare, con spessori ridotti in modo da consentire abbassamenti sensibili che mettessero in evidenza il contributo dell’altra trave.
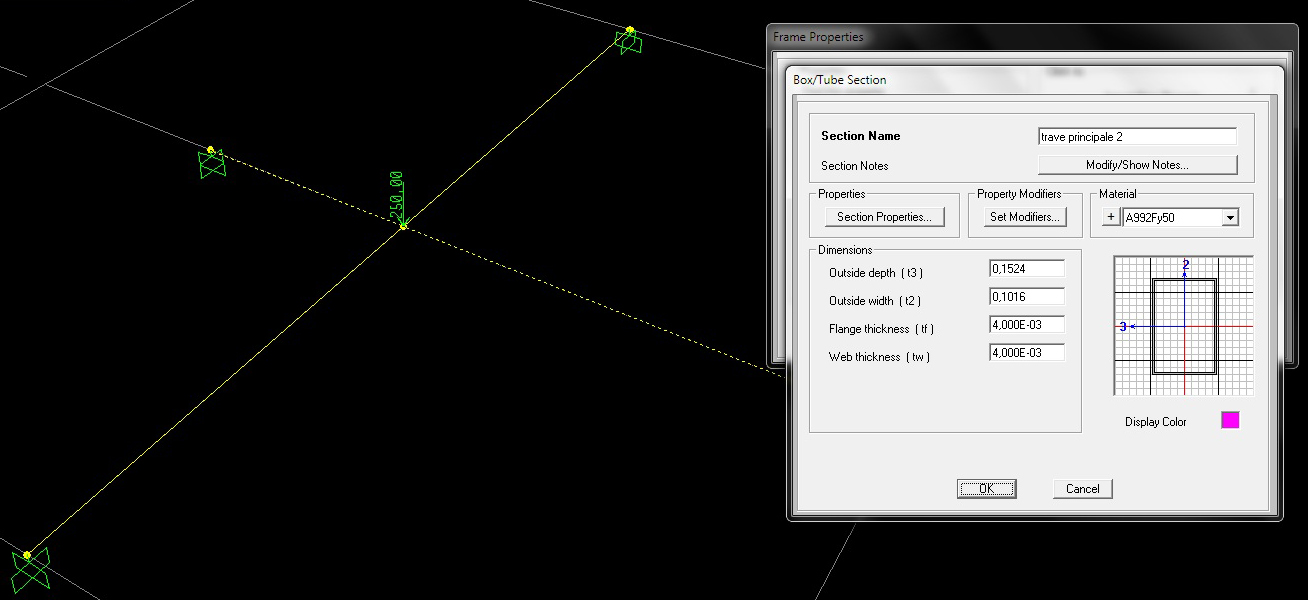
A quest’ultima state messe a confronto 3 sezioni in 2 condizioni di luce distinte.
La prima è una sezione scatolare in acciaio.
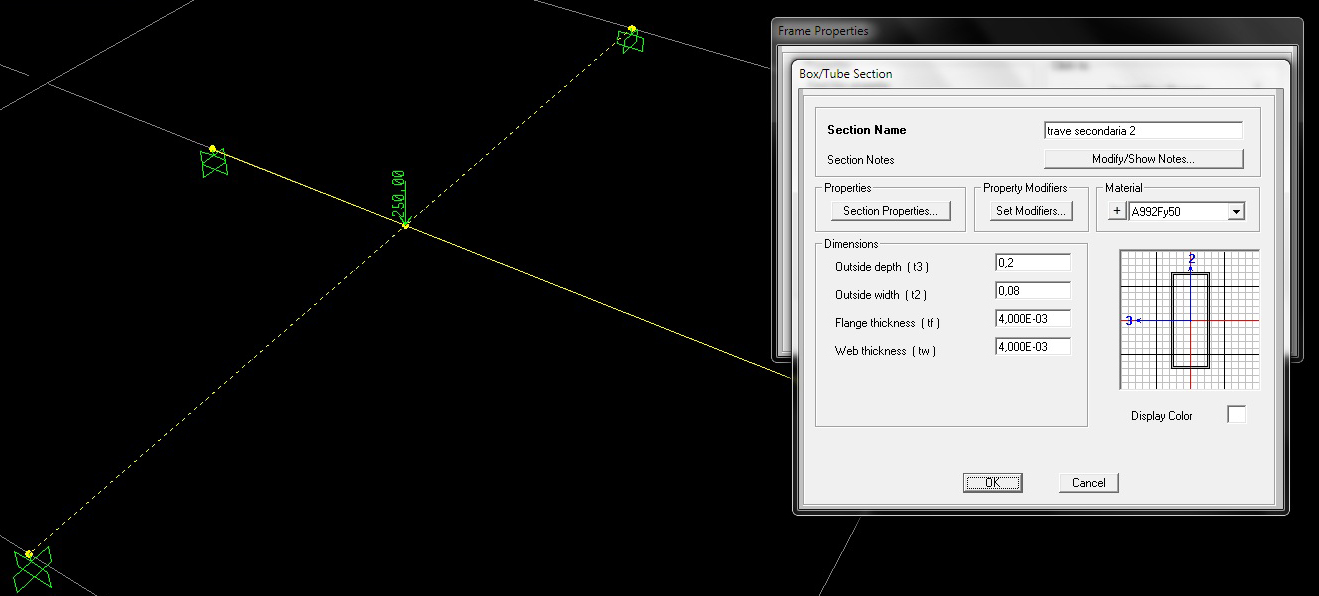
La seconda è una sezione rettangolare con la base molto minore dell’altezza.
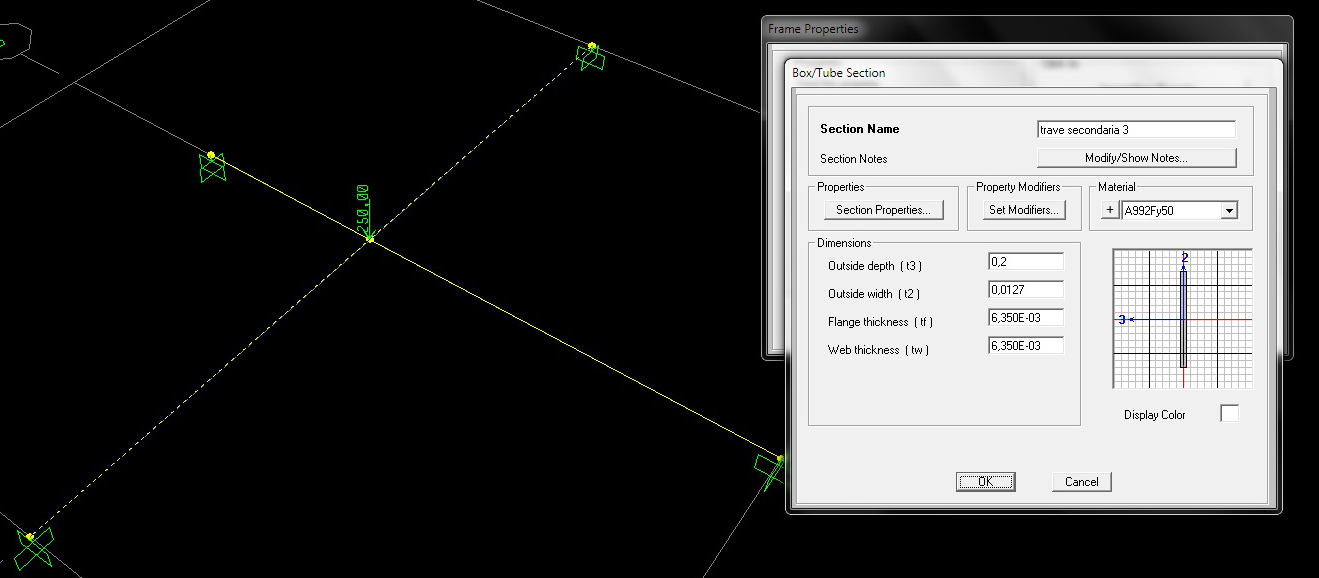
La terza e ultima è una sezione tubolare.
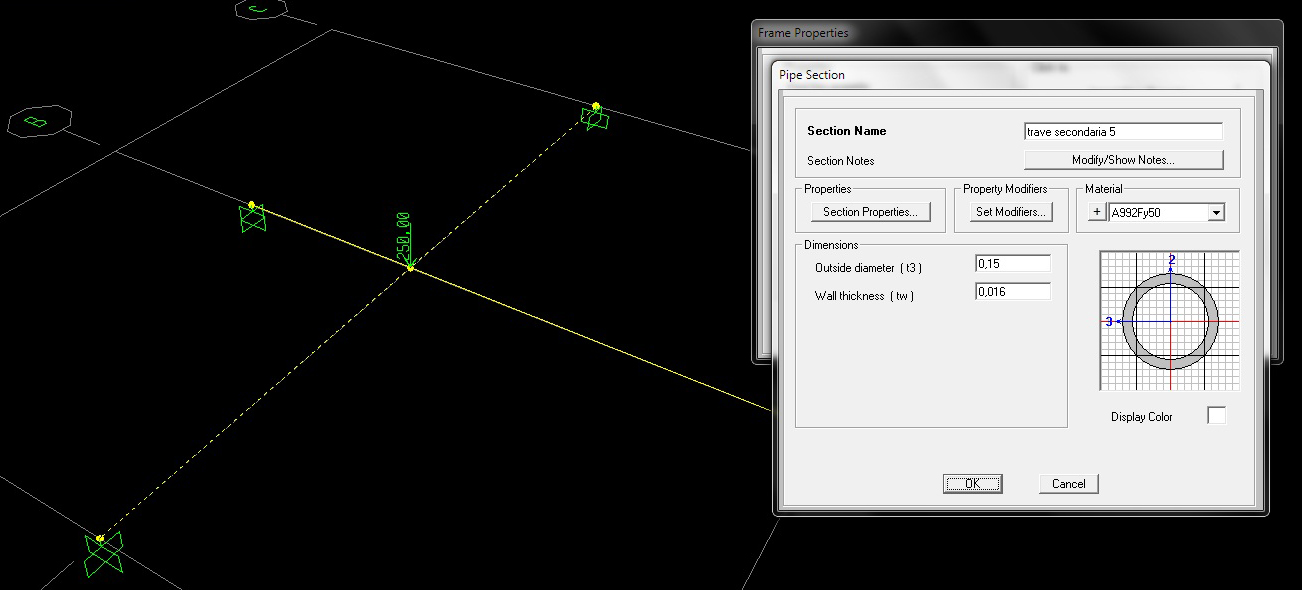
Le stesse sezioni sono state applicate dopo aver dimezzato la luce della trave.

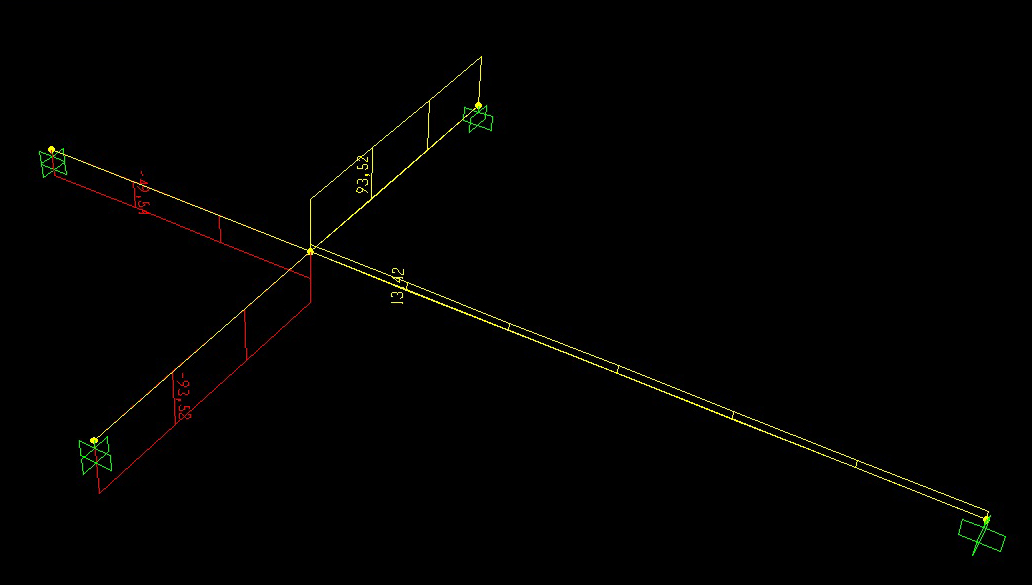
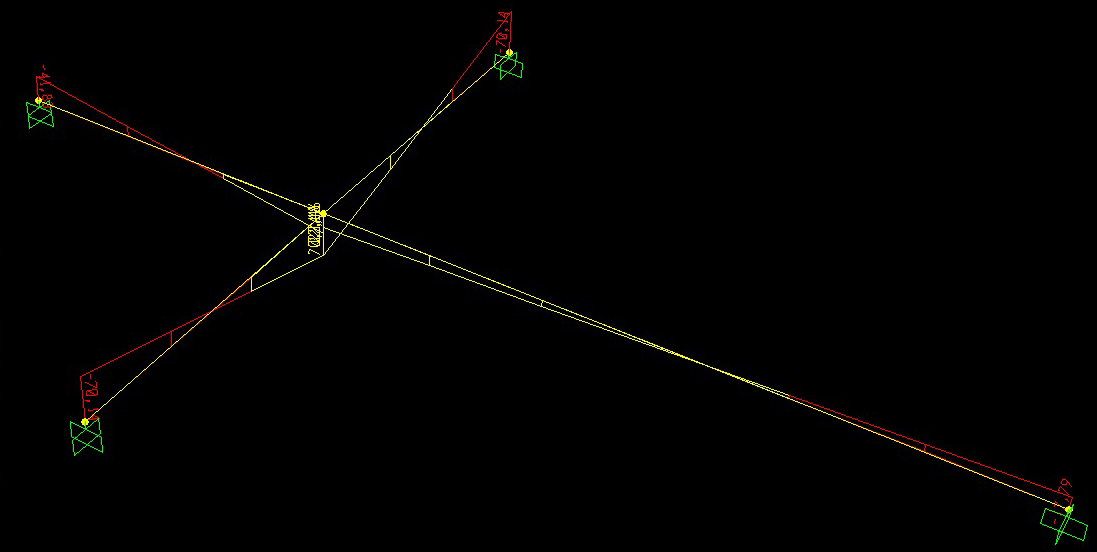
Questi sono i rispettivi diagrammi di Taglio, Momento flettente e Momento torcente.
In questa tabella sono riassunti i dati esportati da SAP che descrivono l’abbassamento e la rotazione del punto in comune delle 2 travi, dove viene applicata la forza agente, nelle 2 condizioni di luce (le tabelle a sinistra fanno riferimento al caso di 6m di luce, a destra il caso di 3m di luce).
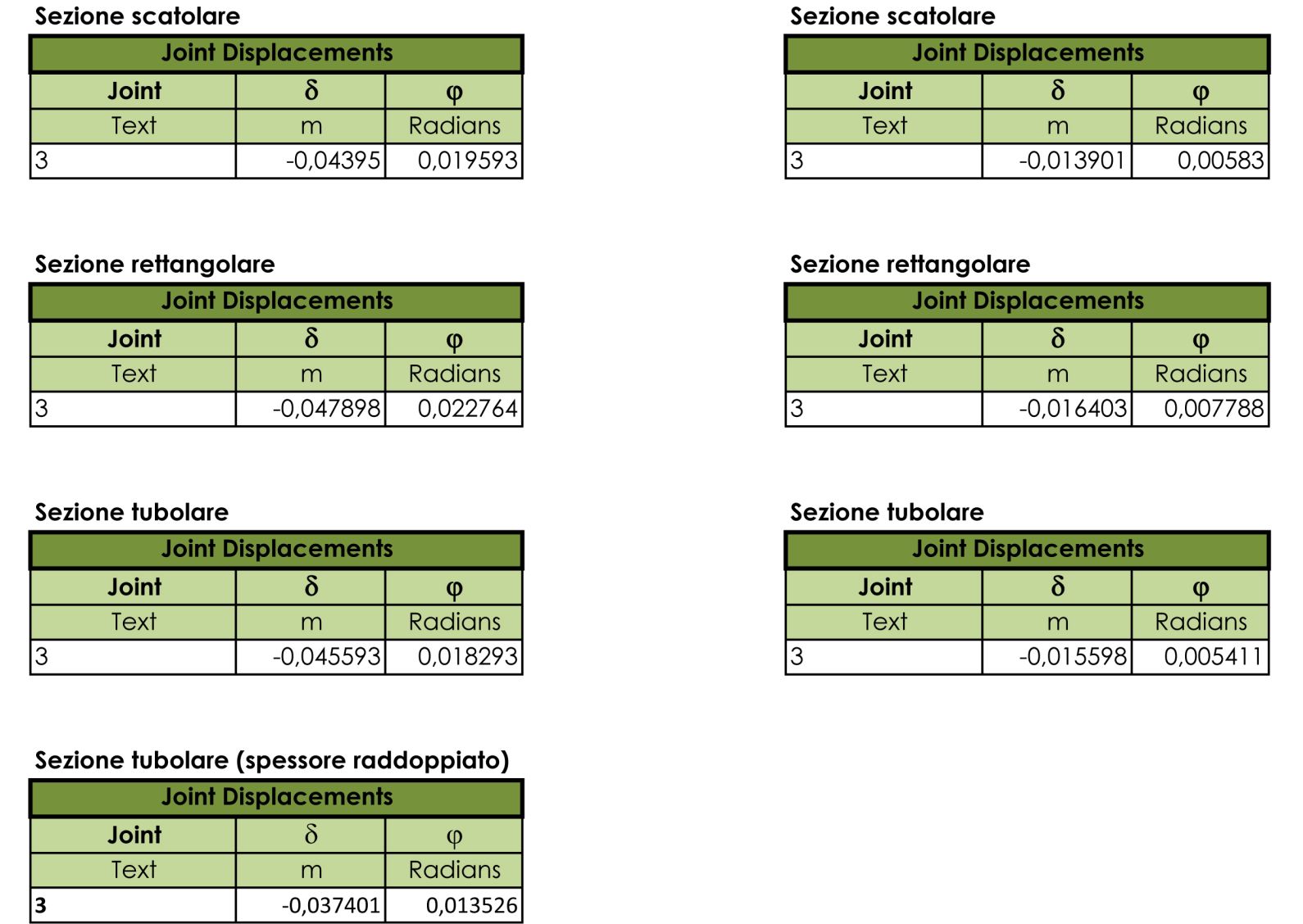
Come prevedibile, nei casi in cui alla trave soggetta a torsione sono stati associati profili chiusi (gli scatolari e i tubolari) essa ha garantito una maggiore rigidezza torsionale, limitando la rotazione del punto d’incontro delle travi. Gli abbassamenti dipendono da parametri diversi, come il Momento d'inerzia, di conseguenza essi non vanno di pari passo con le rotazioni. Per esempio il profilo rettangolare si comporta molto peggio degli altri a torsione, permettendo una rotazione maggiore. Anche a flessione risulta essere il peggiore, ma lo scarto dell'abbassamento rispetto agli altri profili è decisamente inferiore a quello della rotazione. questo per merito dell'altezza del profilo, che ne incrementa il momento d'inerzia.
Commenti recenti