Esercitazione

Vediamo cosa cambia se consideriamo un nodo incastro in 3D invece che in 2D: intanto non bloccherà più 3 gradi di libertà ma 6 e renderà solidali delle travi tra loro perpendicolari.

Eliminiamo per un attimo l'asse DC (che sarebbe "uscente" dallo schermo) e osservo il comportamento di questa struttura:

- la mensola produce un MOMENTO FLETTENTE che arriva direttamente al nodo D; assumo inoltre che il pilastro sia assialmente indeformabile e che quindi assorba lui tutto lo sforzo qL.

                                              configurazione equivalente:

- il momento genera sul nodo una ROTAZIONE che diventa: FLESSIONE nelle travi AD e BD, TORSIONE nella trave DC. Da qui nasce l'esigenza di una nuova RIGIDEZZA, che contrasti le deformazioni derivanti dal momento torcente.

Risolviamo il sistema con il METODO DELLE FORZE facendo cedere l'incastro in A alla rotazione.

1) INTEGRO:

2) METTO LE CONDIZIONI AL BORDO:

3) SOSTITUISCO I VALORI NELLE EQUAZIONI:

4) DIAGRAMMI

In questo caso il MOMENTO non si ribalta sul pilastro! Ci vuole altro per equilibrarlo!

Il MOMENTO si è diviso esattamente a metà perchè la RIGIDEZZA delle due aste è la stessa!

SAP

Ripartizione di forze sismiche

Per un edificio a un solo livello, si consideri la pianta strutturale dell’impalcato:

La struttura tridimensionale è sottoposta a carichi verticali ed azioni orizzontali, quest’ultime interpretabili come sismiche.

I pilastri in calcestruzzo vengono considerati con sezione rettangolare di base b=40 cm e altezza h=30 cm:

L’impalcato descrive la presenza di 8 telai piani,

4 lungo l’asse x, piano x-z:

1_O) 1-2-3-4

2_O) 5-6-7-8

3_O) 9-10-11

4_O) 12-13

telaio 1_O

 e 4 lungo l’asse y, piano y-z:

1_V) 1-5-9-12

2_V) 2-6-10-13

3_V) 3-7-11

4_V) 4-8

telaio 1_V

che hanno il ruolo di sostenere il peso della costruzione ma anche di reagire alle forze orizzontali agenti sul piano x-y.

Associando quindi il comportamento di questi telai fungenti da controventi a quello dei telai shear-type, per solaio sufficientemente rigido e pilastri elastici, si rappresentano i controventi applicati alla costruzione grazie a delle molle di adeguata rigidezza sul piano x-y.

La ridistribuzione delle forze sismiche avviene seguendo una sequenza di passaggi:

1) calcolo delle rigidezze traslanti dei controventi;

2) calcolo del centro di massa;

3) calcolo del centro delle rigidezze;

4) calcolo delle rigidezze globali;

5)calcolo delle forze sismiche;

6) ridistribuzione delle forze sismiche lungo gli assi di riferimento x e y.

1_ calcolo delle rigidezze traslanti dei controventi.

Il valore della rigidezza traslante è valutabile grazie al modulo di Young E= 210 000 N/mm^2, all’altezza dei pilastri h=4,00 m, e ai momenti di inerzia dei pilastri di sezione rettangolare, per cui I=(bh^3)/(12)=(40cm*(30cm)^3)/12=90000cm^4.

Rigidezza traslante dei telai orizzontali:

es: telaio 1:

Rigidezza traslante dei telai verticali:

2_ Calcolo del centro di massa

Per il calcolo del centro di massa è possibile immaginare di dividere la struttura in aree rettangolari, valutare il centro di ognuna e poi determinare quello complessivo.

3_ Calcolo del centro delle rigidezze

Il centro delle rigidezze invece richiede le distanze dv e do dei controventi dal centro degli assi di riferimento O e le rigidezze di ogni controventokv e ko, la cui somma definisce la rigidezza totale k_vtot lungo i due assi.

4_Calcolo della rigidezza torsionale totale:

con dd_on e dd_vn distanze dei controventi dal centro delle rigidezze:

5_Calcolo delle forze sismiche

Dopo aver assegnato i carichi permanenti strutturali e accidentali, è possibile, grazie al coefficiente di intensità sismica

6a_ Ridistribuzione delle forze sismiche lungo x

La ridistribuzione delle forze sismiche richiede la conoscenza del momento torcente M, delle traslazioni u_o e v_o e delle rotazioni dell'impalcato.

Forze sui controventi verticali:

Forze sui controventi orizzontali:

6b_ Ridistribuzione delle forze sismiche lungo y

Se consideriamo gli impalcati come corpi rigidi sul proprio piano, gli spostamenti che essi potranno compiere saranno: traslazione verticale U_v (m), orizzontale Uo (m) e rotazione φ.

Per esempio la forza orizzontale (forza sismica o la forza del vento) tende a spostarli, ma i controventi contrastano questa azione grazie alla loro elasticità.

Il controvento nell’impalcato piano può essere definito come un appoggio cedevole elasticamente infatti essi sono come molle con una data rigidezza K (kN/m). In un impalcato queste rigidezze possono essere differenti e causare una rotazione.

In questa esercitazioni ci viene chiesto di progettare una trave a RESISTENZA utilizzando il metodo delle TENSIONI ammissibili che consiste nell’eguagliare la tensione massima del materiale alla sua tensione ammissibile. L’esercizio prevede il dimensionamento di una trave maggiormente sollecitata in un solaio in LEGNO, un solaio in ACCIAIO e un solaio in C.A.

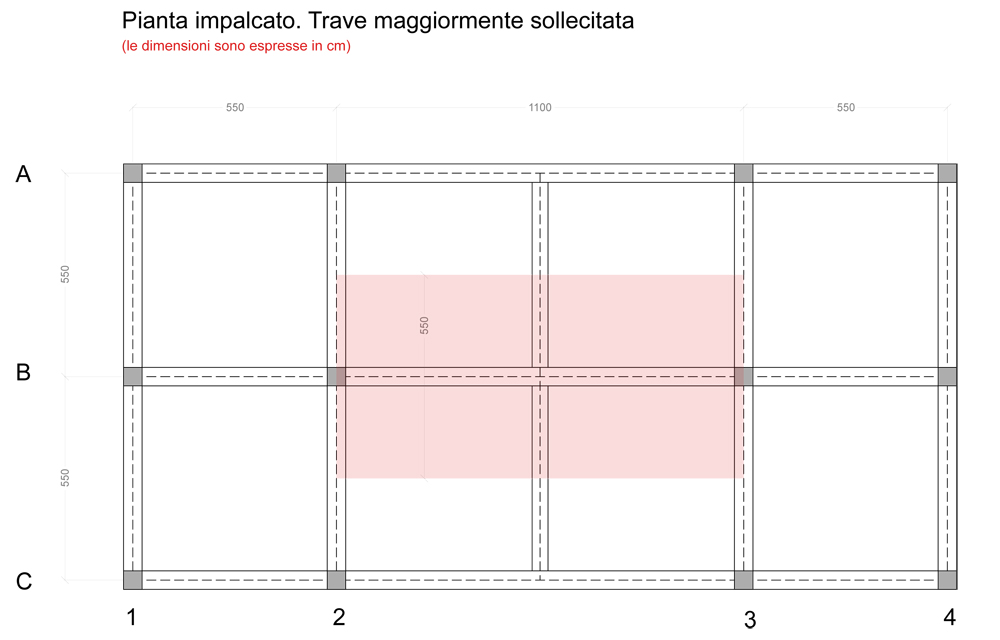
La trave evidenziata in rosso è soggetta a maggior carico e quindi a maggior momento flettente.

L'impalcato in questione è di un edificio nel centro di Roma. Ho bisogno di luci molto grandi come quella di 11m per questioni distributive degli spazi interni.

In questo caso l’area d’influenza per la trave caricata è:

A= 11 x 5.5 = 60,5 m²

L = 11m

I = 5,5m 

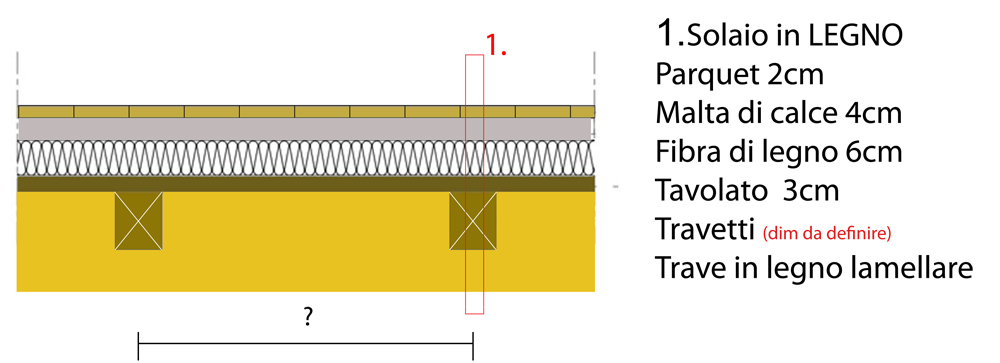
1.     Analisi dei carichi

Per dimensionare al meglio una trave ho bisogno di conoscere ed analizzare tutti i carichi che agiscono sulla struttura.

1. Il carico strutturale qs[KN/mq]: il peso di tutti gli elementi stutturali.
2. Il carico permanente qp[KN/mq]: i carichi che fanno parte del pacchetto solaio, il carico degli impianti 0,5 KN/mq, il carico dato dai tramezzi pari a 1KN/mq.
3. Il carico accidentale qa[KN/mq]: legato alla destinazione d’uso dell’edificio e viene dato dalla normativa he per edifici residenziali è stimato pari a 2 KN/mq(considera la variazione di carico data dagli arredi, persone che possono variare nel corsodel tempo) per uffici 3 KN/mq.

SOLAIO IN ACCIAIO

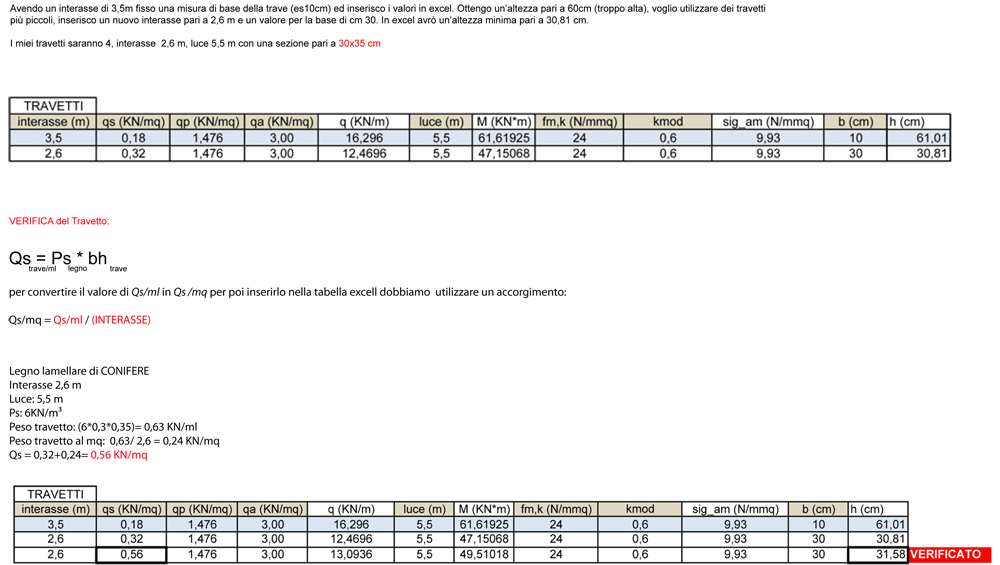
Per poter dimensionare la trave, devo tener conto nei carichi strutturali anche del peso dei travetti, che è necessario dimensionare.

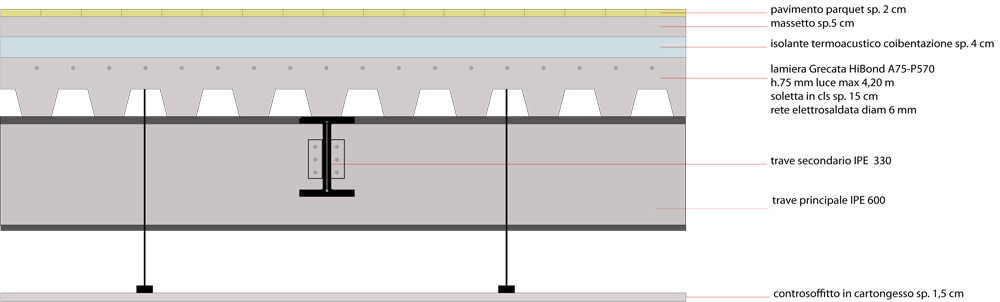
Dimensionamento travetti del solaio

Carico strutturale Qs [KN/mq]: lamiera Grecata, soletta

lamiera Grecata HiBond A55-P600 h.55 mm (luce max ≤2,80m)+ soletta cls sp. 9 cm =14,5 cm

Qs= 1,65 (kN/mq)

Carico permanente Qp [KN/mq]

(massetto, rete elettrosaldata, controsoffitto, impianti, tramezzi)

Massetto sp 40 mm

Peso Specifico = 2100  Kg/mc    F=m.a

F=2100x(9,81)

=21 kN/mc

Volume  al mq =  0,04 m x 1m x 1m = 0,04 mc

Peso al mq = 0,04 m x 21 Kg/mc = 0,84 KN/mq

Rete elettrosaldata 620/2  AD (diam. 6mm_ 200mm x 200mm)

Peso al mq = 2,29 Kg/mq

= 0,02 KN/mq

Controsoffitto in cartongesso (sp. 15 mm):

Peso Specifico = 1325  Kg/mc

Volume  al mq =  0,015 m x 1m x 1m = 0,015 mc

Peso al mq = 0,015 m x 1325 Kg/mc = 19,875 Kg/mq = 0,2 KN/mq

Incidenza Impianti:

0,5 KN/mq

Incidenza Tramezzi:

1 KN/mq

Qp = 2,56 kN/ mq

Carico accidentale Qa [KN/mq]: legato alla destinazione d’uso.

Nel progetto questo ambiente è destinato ad uffici quindi 3 kN/mq

Qa = 3 kN/ mq

Qtotale mq= 1,65+2,56+3 =  7,18 KN/mq

Per trasformare Q in metri lineari = 7,18*interasse

TRAVETTI-a: ( interasse 2,75m; luce 5,5m)

Inserisco i valori ottenuti nella scheda di Excel e scelgo il tipo di acciaio Fe 430/S275 fy,k=275 (tensione di snervamento dell’acciaio)

La tensione σ amm è data dal valore di fy,k/ il COEFFICENTE DI SICUREZZA Y (1,15 nell’acciaio).

σamm = fy,k/y = 275/1,15= 239,13 N/mm²

Il modulo di RESISTENZA A FLESSIONE (minimo) lo ricavo dalla formula di Navier per poi poter scegliere il profilo appropriato (sulle tabelle dei profili in acciaio).

Wxmin= M/σ amm = 74,9/0,23913 = 313,21 cm³

Inserendo tutti i valori in excell trovo che il mio  Wx = 313,5 cm3

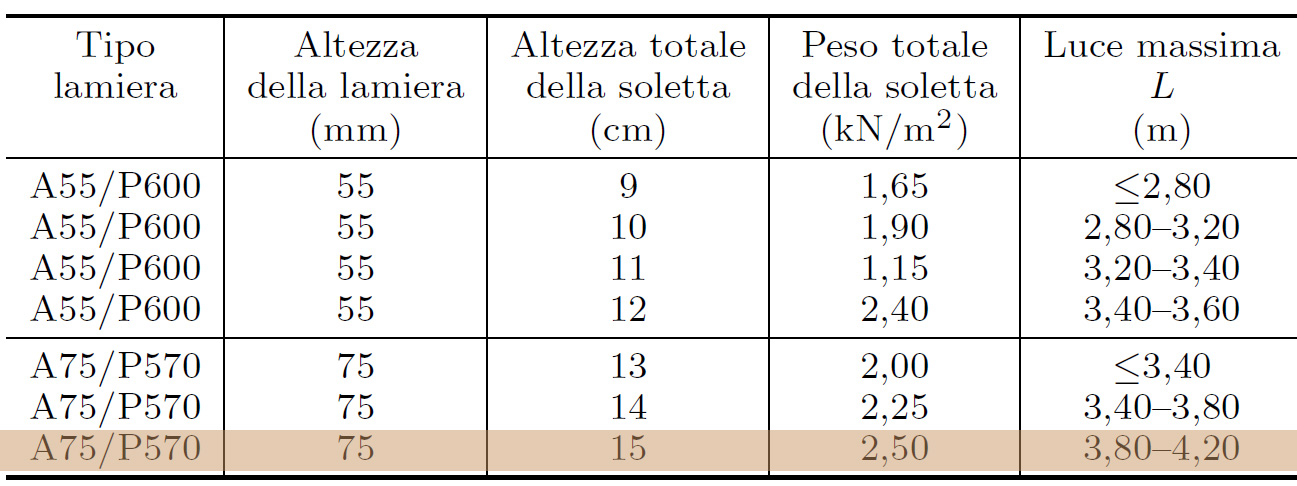
Nella tabella dei profili metallici (sotto riportata) scelgo un profilo adatto che abbia 

un modulo di resistenza a flessione Wx maggiore di quello da me trovato,

scelgo un IPE 240 con Wx =324 cm3,  Peso travetto = 30,7 Kg/m

Peso travetto al mq: 0,307/2,75 (interasse) =  0,111 kN/mq

che vado a sommare al Qs = 1,65 kN/ mq per un totale di 1,76 kN/mq

inserisco il nuovo valore di Qs in excell e verifico la trave (vedi tabella sotto)

Utilizzo questo esercizio per dimensionare le travi per il mio progetto di uffici, per poi scegliere la strategia migliore da adottare guardando anche all'aspetto economico e della messa in opera delle travi in cantiere (per velocizzare il lavoro e ridurre gli errori)

TRAVE 1: ( interasse 5,5 m; luce 6,5m)

Qs= 1,76 kN/mq

Qp = 2,56 kN/ mq

Qa = 3 kN/ mq

Il modulo di resistenza a flessione (minimo) é Wx = 890 cm3

Quindi un scelgo un IPE 360

un IPE 360 con Wx =904 cm3,  Peso travetto = 57,1 Kg/m

Peso TRAVE 1 al mq: 0,571/5,5 (interasse) =  0,103 kN/mq

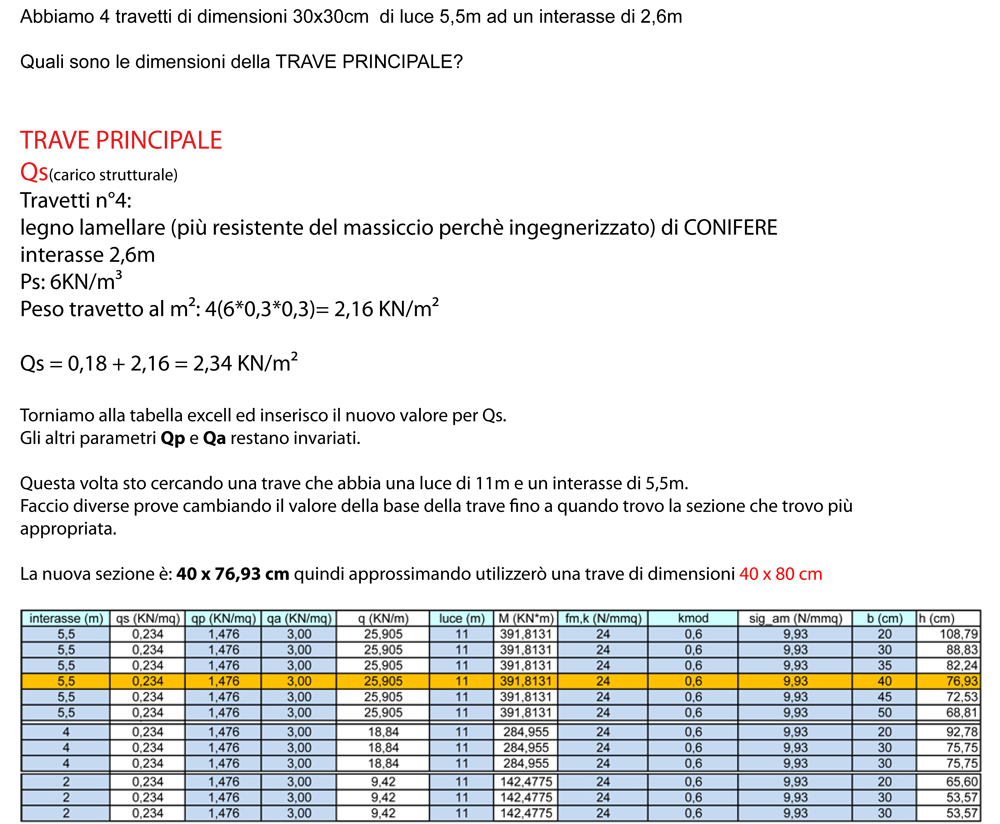
TRAVE 2: ( interasse 5,5 m; luce 11m) è la trave maggiormente caricata

Qs= 1,76 kN/mq

Qp = 2,56 kN/ mq

Qa = 3 kN/ mq

Il modulo di resistenza a flessione (minimo) é Wx = 2546,45 cm3

Quindi un scelgo un IPE 600

un IPE 600 con Wx =3070 cm3,  Peso trave = 122 Kg/m

Peso TRAVE 2 al mq: 1,22/11 (interasse) =  0,110 kN/mq

TRAVE 3: ( interasse 5,5 m; luce 5,5m)

Qs= 1,76 kN/mq

Qp = 2,56 kN/ mq

Qa = 3 kN/ mq

Il modulo di resistenza a flessione (minimo) é Wx = 637 cm3

Quindi un scelgo un IPE 330

un IPE 330 conWx =713 cm3,  Peso travetto = 49,1 Kg/m

Peso TRAVE 3 al mq: 0,491/5,5 (interasse) =  0,089 kN/mq

Nel nostro progetto utilizzeremo le seguenti IPE:

TRAVE 1: ( interasse 5,5 m; luce 6,5m) IPE 360

TRAVE 2: ( interasse 5,5 m; luce 11m) IPE 600 la trave più caricata

TRAVE 3: ( interasse 5,5 m; luce 5,5m) IPE 330

TRAVETTI-a: ( interasse 2,75m; luce 5,5m) IPE 240

TRAVETTI-b: ( interasse 3,29m; luce 5,5m) IPE 270

Utilizzeremo la IPE 600 e la IPE 360 anche se questo vorrà dire un aumento dei costi però evitiamo errori di cantiere avendo solo due grandezze di travi.

Prendendo in esame il telaio shear-type abbiamo studiato il concetto di rigidezza tenendo conto che i medesimi elementi strutturali possono avere una doppia funzione, sia come elementi di sostegno verticale della struttura ma anche come elementi di sostegno orizzontale (controvento).

Per rendere efficace un sistema di controventi è necessario considerare l’impalcato infinitamente rigido sul piano orizzontale. I controventi vengono assimilati a molle perché si comportano in modo elastico e hanno una data rigidezza. Sappiamo anche che più sarà la rigidezza e meno sarà lo spostamento. Come possiamo vedere in figura uno dei telai shear-type che andremo poi di seguito ad analizzare sul nostro impalcato.

Nel caso più semplici di controventi con eguale rigidezza avremmo una medesima ripartizione della forza agente sull’impalcato così che il corpo traslerà. Mentre se i controventi hanno una diversa rigidezza tra di loro l’impalcato a questo punto non traslerà solamente ma ci sarà anche un effetto di rotazione.

Andiamo ad analizzare un impalcato strutturale. Questo impalcato è individuato da 8 telai piani. 

I telai hanno il compito non solo di portare il peso dell’edificio ma anche di controventare la struttura interna resistendo alle forze orizzontali. Il nostro compito sarà quello di:

·         Calcolare le rigidezze traslanti dell’edificio per ogni telaio presente in esso;

·         Calcolare il centro di massa;

·         Calcolare il centro delle rigidezze e la rigidezza torsionale totale;

·         Analizzare i carichi sismici attraverso l’analisi dei carichi permanenti e accidentali;

·         Infine ripartizione delle forze sismiche lungo gli assi X e Y

STEP 1

Come abbiamo detto prima il nostro impalcato è composto da 8 telai ed a ognuno viene assegnato un materialo, in questo caso il C.A., una sezione pari a b = 30 cm e h = 40 cm. Calcoliamo come prima cosa la rigidezza traslante per ogni telaio, ovvero la somma delle rigidezze dei singoli pilatri che dipende dal modulo di Young, dal momento d’Inerzia e dall’altezza. L’inerzia è calcolata attraverso l’equazione  .  La rigidezza del telaio è calcolata con la sommatoria di tutte le rigidezze. La rigidezza di un singolo pilastro è uguale a k = 12EI/h³

TELAIO 1

TELAIO 2

TELAIO 3

TELAIO 4

TELAIO 5

TELAIO 6

TELAIO 7

TELAIO 8

STEP 2

In questa fase raccogliamo in una tabella sinottica le rigidezze traslanti trovate nei controventi e indichiamo la distanza delle molle da un punto O ritenuto origine del sistema di riferimento XY. Questa tabella ci servirà per trovare il centro di massa e delle rigidezze.

STEP 3

Prima di andare avanti vediamo cos’è il centro di massa.

Il centro di massa è il punto di applicazione di tutte le forze, cioè il baricentro di un corpo. Un esempio chiaro del centro di massa è la torre di Pisa che non è mai crollata perché il centro di massa cade all’interno della sua proiezione in pianta.

Per trovare le coordinate prima di tutto dividiamo in due aree rettangolari il nostro impalcato così da trovare il loro baricentro. Misuriamo le coordinate X e Y dei due punti e li andiamo a scrivere nel foglio Excel. Sappiamo che per trovare il baricentro di tutto l’impalcato non dobbiamo far altro che, per il punto X_G, sommare la coordinata X_G1 moltiplicata per l’area 1 (corrisponde a 24m*14m) e la coordinata X_G2 moltiplicata per l’area 2 (corrisponde a 8m*16m) il tutto diviso per l’area totale. Lo stesso procedimento verrà fatto per la coordinata Y così che troviamo le due coordinate del centro di massa dell’impalcato.

STEP 4

Calcolato il centro di massa ora troviamo il centro delle rigidezze. A differenza del suddetto discorso fatto il centro delle rigidezze è il punto in cui la reazione dell’edificio si concentra.

Per trovare le coordinate del punto X_C sommiamo tutte le rigidezze verticali moltiplicate per le rispettive distanze verticale dall’origine il tutto diviso per la somma delle rigidezze verticali. Lo stesso discorso vale per la coordinata Y_C.

Dopo aver individuato il centro delle rigidezze annotiamo le distanze da esso di ogni controvento (esempio: dd_v2 = d_v2 – X_c)poiché sono necessarie ai fini del calcolo della rigidezza torsionale totale k_φ che si trova con:

STEP 5

In questo STEP facciamo l’analisi dei carichi sismici agenti sull’implacato. Facciamo un’analisi dei carichi permanenti e sovraccarichi accidentali. I pesi sismici li troviamo con la somma dei carichi totali permanenti e quelli accidentali moltiplicate per il coefficiente di contemporaneità. Mentre la forza sismica orizzontale è calcolata dal prodotto tra pesi sismici totali e il coefficiente di intensità sismica.

STEP 6-7

Ora ci occupiamo della ripartizione delle forze sismiche sia lungo l’asse X e lungo l’asse Y. Possiamo dire che come prima cosa troviamo il momento torcente che è calcolato con la forza F (forza sismica) e le coordinate del centro di massa e del centro delle rigidezze.

Mx = F * (Yg – Yc)

My = F * (Xg – Xc)

Calcolato il momento, vediamo quant’è la traslazione sia orizzontale e verticale ed si trova con la forza sismica diviso la rigidezza totale.

Ci calcoliamo dal foglio excel le forze sui vari controventi attraverso il prodotto di diversi fattori come la rigidezza traslante, la distanza dal controvento al centro delle rigidezze e la rotazione dell’impalcato (per quelli verticali). Mentre per le forze orizzontali è data dal prodotto della rigidezza traslante che moltiplica la somma della traslazione orizzontale e la distanza dal controvento al centro delle rigidezze e quest’ultima moltiplicata per la rotazione traslante.

Trovate tutte le forze corrispondente a ogni controvento possiamo trovarci le reazioni vincolare calcolate con :

Il Metodo delle Forze

Il Metodo delle forze viene utilizzato per la risoluzione di strutture iperstatiche e si adatta perfettamente al caso di strutture iperstatiche composte da travi come la tave singola, la trave continua su più appoggi.

Il metodo si articola in quattro passi:

1.     la scelta di una struttura isostatica di riferimento e l’individuazione delle incognite iperstatiche.

2.     la scrittura delle equazioni di compatibilità cinematica.

3.     la risoluzione del sistema di equazioni per la determinazione delle incognite iperstatiche.

4.     la sistematica applicazione del principio di sovrapposizione degli effetti per la determinazione delle azioni di contatto sulla struttura iperstatica.

Trave continua su cinque appoggi_ La trave è 3 volte iperstatica

GDV= 6 

GDL= 3

1.     scelta di una struttura isostatica di riferimento e l’individuazione delle incognite iperstatiche.

Scelgo una struttura  isostatica di riferimento. Trasformo le cerniere in B, C e D in cerniere interne applicando dei momenti X1, X2. Essendo la trave simmetrica nel punto C posso applicare X1 anche in D. Le incognite sono X1e X2.

Trattare una trave continua su più appoggi come un insieme di travi appoggiate rende più semplice la soluzione del problema iperstatico.

2.     la scrittura delle equazioni di compatibilità cinematica.

Per ripristinare le condizione di vincolo di continuità della trave devo imporre le equazioni di compatibilità cinematica, la rotazione relativa nei punti sia a sinistra (S) che a destra (D)  in cui ho rimosso il vincolo:

ΔφB = 0 

φBS – φBD = 0

φBS = ql³/24EJ – X1l/3EJ

φBD = - ql³/24EJ + X1l/3EJ + X2l/6EJ

ΔφC = 0 

φCS – φCD = 0

φCS = + ql³/24EJ - X2l/3EJ – X1l/6EJ

φCD = - ql³/24EJ + X2l/3EJ + X1l/6EJ

ΔφB = ΔφC

3.    la risoluzione del sistema di equazioni per la determinazione delle incognite iperstatiche.

Consideriamo i seguenti tratti:

Troviamo le incognite X1e X2:

ΔφB = 0  

φBS – φBD = 0

ql³/24EI - X1L/3EI+ ql³/24EI - X1L/3EI - X2L/6EI=0

2ql³/24EI - 2X1L/3EI - X2L/6EI=0

X2/2 = -2X1+ ql²/4

X2= -4X1+ ql²/2     

ΔφC = 0 

φCS – φCD = 0

ql³/24EI – X2l/3EI - X1l/6EI+ ql³/24EI - X2l/3EI - X1l/6EI=0

2ql³/24EI – 2X2l/3EI - 2X1l/6EI=0

-X1/2 = X2 - ql²/8  

X1= - 2X2- ql²/4    sostituisco in ΔφB = 0 

X2= -4(-2X2- ql²/4)+ ql²/2    

X2= 8X2- ql² + ql²/2   

ql² - ql²/2 = 7X2

X2= ql²/14

X1= 3/28 ql²

4.   la sistematica applicazione del principio di sovrapposizione degli effetti per la determinazione delle azioni di contatto sulla struttura iperstatica.

Trovate le incognite X1 e X2 posso cercare le reazioni vincolari:

Sommiamo q con il momento in ogni punto:

ΣFv(A) = ql/2 – 3ql/28 = 11ql/28

ΣFv(B) = ql + (2) 3ql/28 - ql/14 = 8ql/7

ΣFv(C) = ql - (2) 3ql/28 + (2) ql/14 = 13ql/14

ΣFv(D) =  ΣFv(B) = 8ql/7 (simmetria)

ΣFv(E) = ΣFv(A) = 11ql/28 (simmetria)

Disegno i grafici di Taglio e Momento: