
Vestibolo d'antico tempio - Giovanbattista Piranesi
Nell'immaginario collettivo, quando si parla della monumentalità dell'architettura romana, si manifesta immediatamente l'immagine dell'ormai dimenticato arco. Nonostante esso sia già riscontrabile in età molto antica presso popoli culturalmente molto differenti (vd. Egitto 3500 a.C.), divenne celebre durante la fase repubblicana di Roma, grazie all'uso massivo che se ne fece, adottando generalmente l'arco a tutto sesto poggiato su pilastri. Con l'avvento del Cristianesimo, la cui architettura è mutuata da quella classica, l'arco continuò a dominare la scena architettonica, raggiungendo forse la sua catarsi nel Medioevo, in funzione di più complesse esigenze statico-costruttive, che portarono all'implementazione di nuovi tipi (archi acuti, lobati, ecc.). La cultura occidentale, dal Rinascimento al sec. XIX, ne ripropose invece i tipi e gli usi desunti dallo studio degli esempi romani. Il Movimento Moderno, dall'alto della sua arrogante necessità di fare tabula rasa, cancellò dal suo lessico l'arco, che fu relegato ad un malinconico ruolo di comprimario eccellente.
Dal punto di vista del comportamento statico, gli archi possono distinguersi in: incastrati, a due cerniere, a tre cerniere o a spinta eliminata. L'arco incastrato, tre volte iperstatico, è molto rigido ed è difficilmente soggetto a spostamenti eccessivi sotto carico,ma la sua analisi può risultare molto complessa. Il vantaggio della maggiore resistenza degli archi molto rigidi viene però controbilanciato dai problemi che proprio la loro rigidezza crea (specie se la luce è considerevole), allorquando nascano tensioni interne di origine termica o dovute a deformazioni lente nel tempo. Diminuendo la rigidezza si passa all'arcoa due cerniere, il quale, appunto perché più deformabile, mantiene tali tensioni entro limiti accettabili, per giungere all'arcoa tre cerniere isostatico, altamente deformabile, ma che permette di calcolare con precisione le spinte orizzontali e le forze interne (vd. Galerie des Machines). Gli archia spinta eliminata, infine, possono considerarsi archi a due cerniere nei quali l'incognita iperstatica è costituita dalla tensione della catena, che ne collega le imposte per assorbirne quella spinta che altrimenti sarebbe destinata ai piedritti.
In questa ultima esercitazione ci limiteremo ad analizzare gli archi a tre cerniere isostatici, sia dal punto di vista teorico che da quello pratico, verificando il loro comportamento meccanico su SAP2000. Iniziamo col sottolineare che gli archi fanno parte di quegli elementi architettonici che resistono per forma, lavorano a compressione e possono essere in alcuni casi (vd. arco parabolico) strutture altamente ottimizzate, ovvero in grado di assorbire i carichi e di trasformarli in sforzo normale. Ciò ovviamente andrà a discapito della riserva di resistenza, utile, ad esempio, nel caso del sisma. Questa attitudine degli archi a trasformare tutto il carico in sforzo normale, ignorando la flessione, si chiama architudine.
ARCO A TUTTO SESTO a 3 cerniere

San Lorenzo fuori le mura - Roma
Trattiamo innanzitutto l'arco a tutto sesto a tre cerniere. Esso è sostanzialemente definito da una semicirconferenza e può essere considerato alla stregua del portale a 3 cerniere, in quanto è caratterizzato dalle stesse reazioni vincolari:

Considerando la simmetria della struttura, le reazioni vincolari sono facilmente ricavabili dall'equazione di equilibrio alla rotazione, in quanto, non essendoci taglio in chiave, il carico verrà contrastato dalla reazione verticale all'imposta:
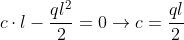
Una volta trovate le reazioni vincolari, si passa allo studio delle azioni di contatto all'interno di una sezione generica dell'arco. Per fare ciò è necessario adottare il metodo delle parti, utilizzando qualsivoglia sezione contenuta all'interno dell'intervallo definito da 0<α<90:
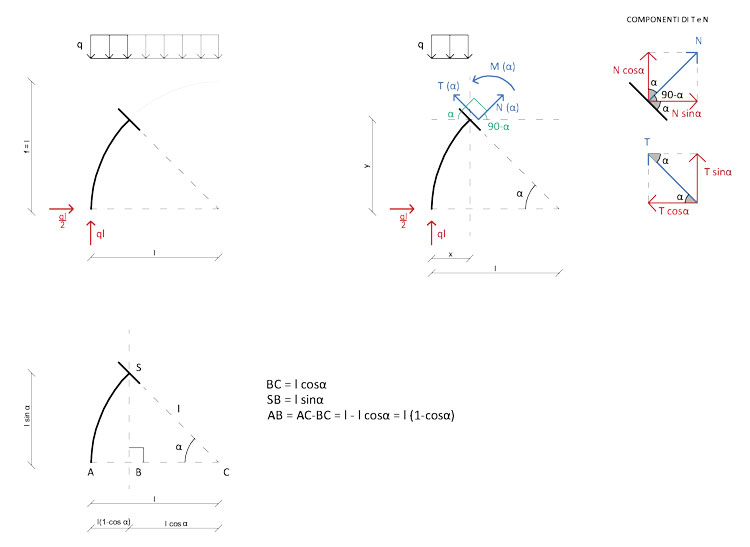
Nelle azioni di contatto subentreranno quindi semplici nozioni di trigonometria, che ci permettono di scomporre le risultanti inclinate nelle canoniche forze orizzontali o verticali, cosicchè sia possibile procedere alla scrittura delle equazioni di equilibrio (con polo in B):
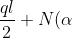sen\alpha&space;-T(\alpha&space;)cos\alpha=0)
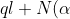cos\alpha&space;+T(\alpha&space;)sen\alpha-ql(1-cos\alpha&space;)=0)
-ql^2(1-cos\alpha&space;)+\frac{ql^2}{2}sen\alpha&space;+ql^2\frac{(1-cos\alpha)^2}{2}=0)
Come si nota nelle prime 2 equazioni N e T sono accoppiati (e lo sarebbero stati anche nella 3° se non avessimo preso il polo in B), caratteristica essenziale delle strutture curve. Se provassimo a prendere ad esempio un arco a tutto sesto di raggio e freccia pari ad l sottoposto ad un carico distribuito pari a 10 KN/m, avremmo i seguenti risultati:

Gli sforzi assiali varieranno da -80KN all'imposta a -40 KN in chiave, quelli di taglio da 40 KN all'imposta a 0 KN in chiave e i momenti flettenti saranno ovviamente 0 KNm agli estremi fino a raggiungere un picco di -80 KNm all'interno della sezione dell'arco. Confronteremo successivamente questi risultati con la seguente tipologia di arco.
Nel frattempo portiamo su SAP2000 l'arco a tutto sesto per verificare se quanto detto finora sia valido. Modelliamo il nostro arco su AUTOCAD, disegnando una circonferenza di 5 m di raggio e tagliandone solo la metà che ci occorre. Spezziamo il nostro arco in corrispondenza della chiave di volta e ruotiamolo in 3D affinchè la sua freccia sia orientata secondo il piano z. Dopo aver salvato in dxf 2004 lo importo su SAP2000:

Assegno 2 cerniere alle imposte dell'arco e col solito comando (ASSIGN - FRAME - RELEASE/PARTIAL FIXITY spuntando la casella del momento M 3-3) assegno il rilascio in chiave:
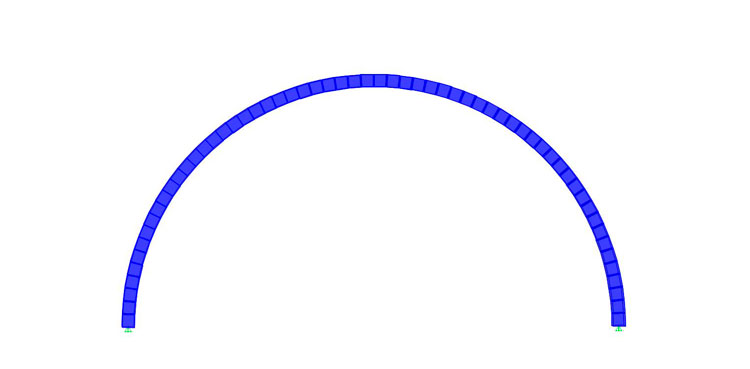
Assegno delle sezioni di calcestruzzo con lato maggiore uscente dal piano di dimensione 0,25m x 0,50m:
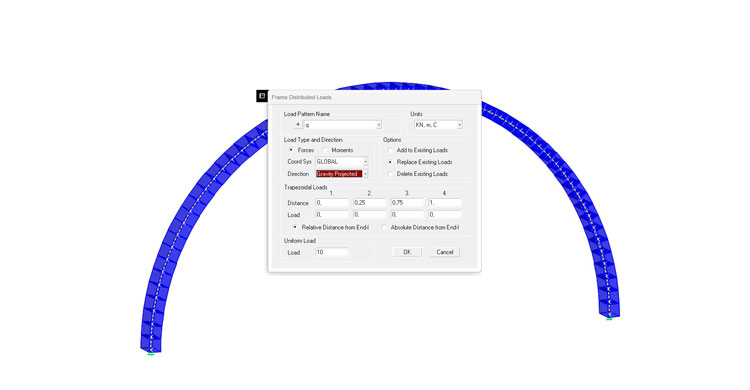
Assegno un carico distribuito di 10 KN/m, avendo la premura di scegliere come opzione GRAVITY PROJECTED, in modo tale che venga spalmato sull'orizzontale dell'arco. Rimuovo inoltre il peso proprio della struttura:
Faccio partire l'analisi:
Deformata

Sforzo normale

Taglio

Momento flettente

Reazioni vincolari:
I dati di SAP2000 non fanno che confermare quanto detto sopra. Sotto la spinta del carico, l'arco tende a spanciare lateralmente e viene riportato al suo posto dall'azione dei vincoli alle imposte. I valori dello sforzo normale tendono a diminuire man mano che si va dall'imposta alla chiave, per poi effettuare il processo inverso. I momenti sono ovviamente 0 in corrispondenza delle cerniere e massimi nelle parti mediali dei due semi-archi. Ci annotiamo inoltre i valori max delle sollecitazioni per metterli a confronto dopo con l'arco ribassato: Nmax = 50KN; Tmax = 23,65 KN; Mmax = 31,16 KNm.
ARCO CIRCOLARE RIBASSATO a 3 cerniere

Ponte degli Annibaldi - Insula
Come suggerisce il nome, l'arco circolare ribassato è costruito sempre a partire dalla circonferenza, di cui però sfrutta non più l'esatta metà, bensì un intervallo più piccolo, tale che f < l. Trattandosi comunque di un arco a 3 cerniere, le sue reazioni vincolari saranno sempre le stesse:
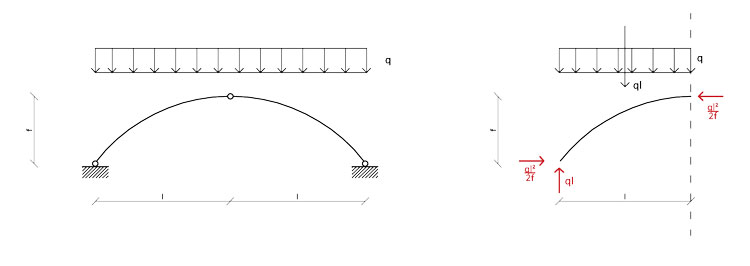 A differenza della precedente tipologia più immediata, in questo caso la prima cosa da fare è trovare l'angolo α0 che rispetto al centro della circonferenza individua la sezione di imposta:
A differenza della precedente tipologia più immediata, in questo caso la prima cosa da fare è trovare l'angolo α0 che rispetto al centro della circonferenza individua la sezione di imposta:
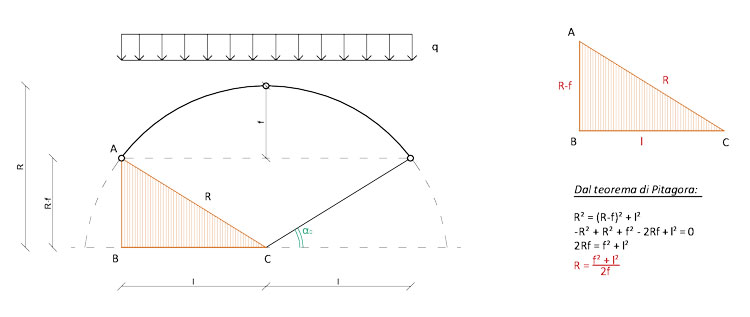
Grazie al teorema di Pitagora ricaviamo il valore della retta R che collega il centro dell'ipotetica circonferenza con la sezione d'imposta dell'arco. Visto che l'arco da 0 ad α0 non esiste, introduciamo un secondo angolo α e procediamo come prima grazie al metodo delle parti:
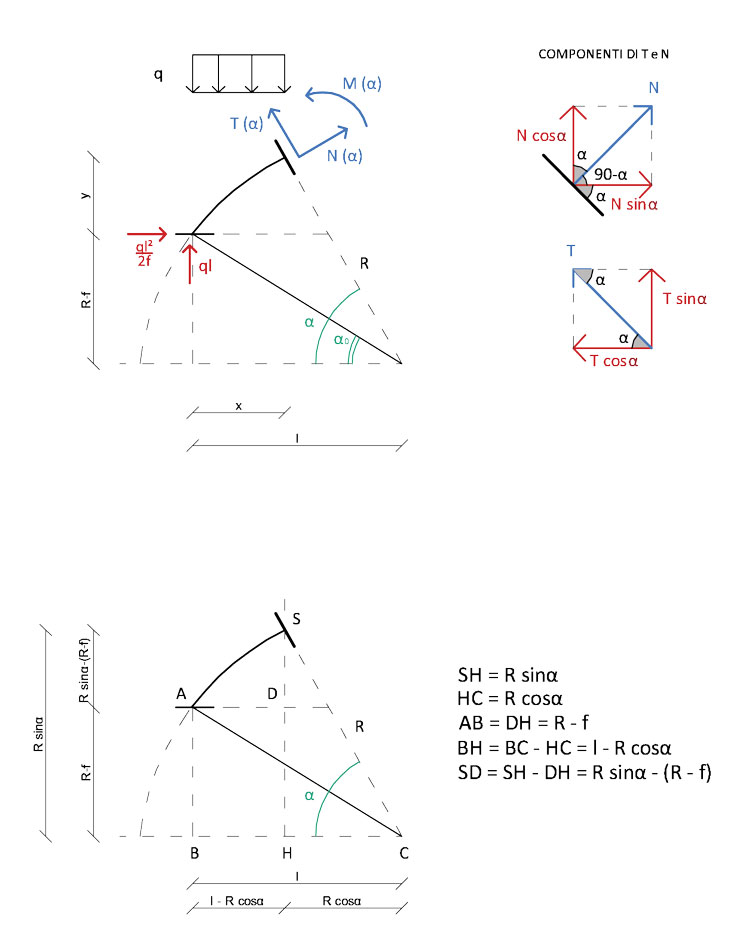
Con la scomposizione delle azioni di contatto N(α) e T(α) nelle loro componenti elementari e dopo aver trovato il valore di ogni braccio, possiamo scrivere le equazioni di equilibrio (con polo in S):
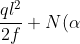sen\alpha&space;-T(\alpha&space;)cos\alpha&space;=0)
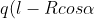+N(\alpha&space;)cos\alpha&space;-T(\alpha&space;)sen\alpha&space;+ql=0)
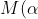-ql(l-Rcos\alpha&space;)+\frac{ql^2}{2f}(Rsen\alpha-R+f&space;)+q\,&space;\,&space;\frac{(l-Rcos\alpha)^2}{2}=0)
Se proviamo ad applicare i valori dell'esempio precedente all'arco ribassato, curandoci di portare la freccia da 8m a 4 m, avremmo i seguenti risultati (con α0=0,64 rad) :

Notiamo subito che la spinta dell'arco è raddoppiata rispetto all'arco a tutto sesto, mentre consultando un apposito tabellario sappiamo che gli sforzi assiali raggiungono valori di 115 KN, gli sforzi di taglio 15 KN e i momenti flettenti 20 KNm (vedi immagine). Possiamo quindi concludere che lo sforzo normale è decisamente incrementato, mentre il taglio risulta essere meno della metà e il momento flettente addirittura 4 volte inferiore.

Vediamo ora su SAP2000 se le nostre conclusioni vengono confermate. Disegnamo su AUTOCAD un arco di circonferenza con raggio 5m e freccia di 2,5m e lo importiamo su SAP2000 come fatto in precedenza, assegnando poi i vincoli, il rilascio in chiave, le sezioni in calcestruzzo ed il carico distribuito:


Deformata
 Sforzo normale
Sforzo normale
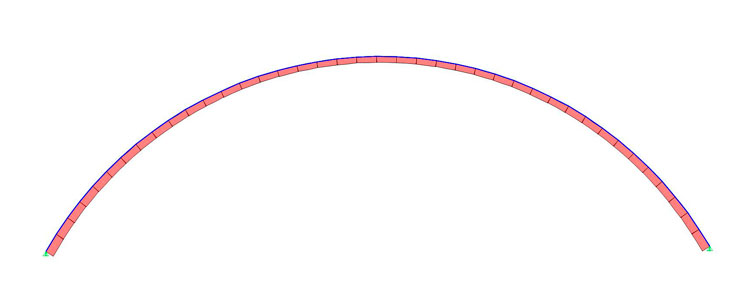
Taglio

Momento flettente

Reazioni vincolari

Le riflessioni fatte in precedenza rimangono valide anche per questo modello di arco, ma balza subito all'occhio come la spinta dell'arco all'imposta sia il doppio dell'arco a tutto sesto. Inoltre analizzando i valori massimi delle sollecitazioni abbiamo ottenuto i seguenti valori: Nmax = 70,25 KN; Tmax = 9,40 KN; Mmax = 7,8 KNm.
Lo sforzo normale è sensibilmente aumentato, mentre il taglio è inferiore alla metà e il momento flettente addirittura 4 volte inferiore al precedente.
ARCO PARABOLICO a 3 cerniere

Miho Museum - Arco parabolico d'ingresso
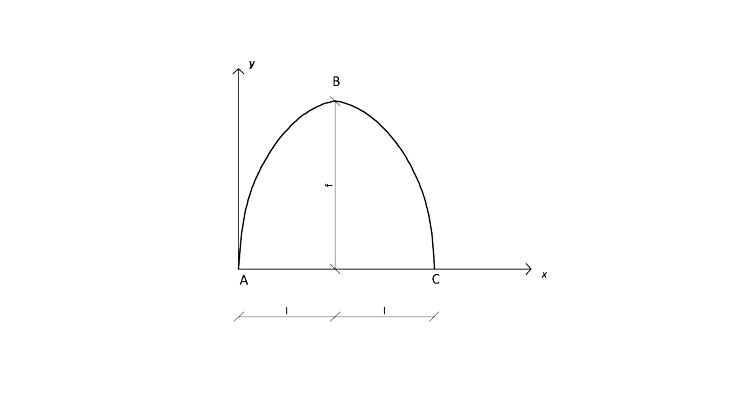
L'arco parabolico isostatico, a differenza dei due precedenti, è una struttura perfettamente ottimizzata. La sua capacità, come detto in precedenza, consiste nel trasformare la densità di carico ripartita uniformemente sull'orizzontale in sforzo normale puro, all'interno di ogni singola sezione. Si dice quindi che l'arco parabolico isostatico è funicolare rispetto al carico ripartito. Non essendo più in presenza di una struttura definita dalla funzione circonferenza, per dimostrare che effettivamente l'unica tensione interna diversa da 0 è lo sforzo normale, dobbiamo innanzitutto analizzare l'equazione della parabola:
 La famiglia di parabole che descrive il nostro arco è:
La famiglia di parabole che descrive il nostro arco è:
y = ax2 + bx + c
Imponiamo l'appartenenza dei punti A,B,C alla parabola e troviamo l'equazione esatta che descrive la nostra parabola:
A ► x=0; y=0; -> c = 0
B ► x=l; y=f; -> al2 + bl2 + c = f
C ► x=2l; y=0; -> 4al2 + 2bl + c = 0
Mettiamo le 3 equazioni a sistema e otterremo che:
a = - f/l2 b = 2 f/l c = 0
L'equazione sarà quindi:
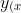}=&space;-\frac{f}{l^2}x^2+2\frac{f}{l}x)

Dato che siamo in presenza di una struttura curva più complessa delle precedenti e non potendo utilizzare l'angolo α come prima, ci calcoliamo la tangente alla parabola tramite la derivata, cosicchè sia possibile scomporre le azioni di contatto dopo aver applicato il metodo delle parti:
&space;=&space;\frac{sen\beta}{cos\beta&space;}&space;=-\frac{2fx}{l^2}+2\frac{f}{l})

cos\beta&space;-T(x)sen\beta&space;=0\\&space;ql+N(x)sen\beta&space;+T(x)cos\beta&space;-q(l-x)-qx=0\\&space;M(x)-ql\cdot&space;x+\frac{ql^2}{2f}\cdot&space;y+q\frac{x^2}{2}=0&space;\end{matrix}\right.)
Dalla prima equazione ricaviamo:
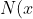=T(x)&space;tan\beta&space;-\frac{ql^2}{2f}\cdot&space;\frac{1}{cos\beta&space;})
Sostituendo nella seconda:
&space;tan\beta&space;-\frac{ql^2}{2f}\cdot&space;\frac{1}{cos\beta&space;}&space;\right&space;)sen\beta&space;+T(x)cos\beta&space;=0)
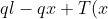&space;\left&space;(&space;tan\beta&space;sen\beta&space;+cos\beta\right&space;)&space;+\frac{ql^2}{2f}\cdot&space;tan\beta&space;=0)
Sostituisco a tanβ il valore precedentemente ricavato:
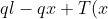&space;\left&space;(&space;\frac{sen^2\beta+cos^2\beta&space;}{cos^2\beta&space;}&space;\right)&space;+\frac{ql^2}{2f}\cdot&space;\left&space;(-\frac{2f}{l^2}&space;x+\frac{2f}{l}&space;\right&space;)&space;=0)
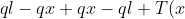&space;\left&space;(&space;\frac{1&space;}{cos^2\beta&space;}&space;\right)&space;=0)
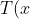&space;\left&space;(&space;\frac{1&space;}{cos^2\beta&space;}&space;\right)&space;=0\:&space;\rightarrow&space;\:&space;T(x)=0)
Vediamo ora il momento flettente:
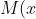&space;-qlx+\frac{ql^2}{2f}\cdot&space;y+\frac{qx^2}{2}=0)
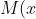&space;-qlx+\frac{ql^2}{2f}\cdot&space;\left&space;(-\frac{f}{l^2}x^2+\frac{2f}{l}x&space;\right&space;)+\frac{qx^2}{2}=0)
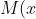&space;-qlx-\frac{qx^2}{2}+qlx+\frac{qx^2}{2}=0\:&space;\rightarrow&space;\:&space;M(x)=0)
Come anticipato quindi, essendo M(x) e T(x) nulli, l'arco parabolico costringe il materiale a lavorare solo a compressione, risultando così come una struttura altamente ottimizzata.Vediamo in ultimo come si comporta l'arco parabolico su SAP2000. Lo modelliamo su AUTOCAD tramite il comando spline, spezzandolo come usuale in chiave, e avendo la premura di trasformare la spline in polilinea (con una precisione >5) e di esplodere il tutto prima di salvare. Questo è quello che si ottiene importandolo su SAP2000:

Assegno di nuovo i vincoli alla base, il rilascio in chiave, le sezioni di calcestruzzo ed il carico distribuito:

Deformata

Sforzo normale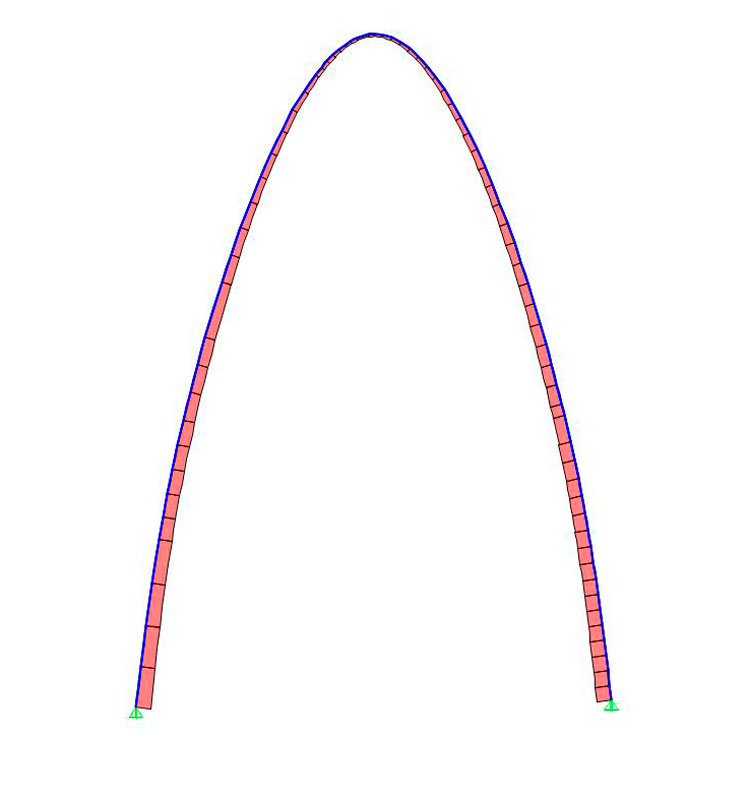
Nel caso in cui il taglio e il momento non siano pari a 0, basterà reimportare l'arco su SAP2000 dopo aver convertito la spline in polilinea con una precisione più alta.
Commenti recenti