La TORSIONE in un elemento si verifica quando esso è soggetto a momenti uguali e opposti che agiscono all’estremità, paralleli al piano di sezione cioè intorno al suo asse longitudinale; l’elemento risponderà a tali sollecitazioni in base alla sua RIGIDEZZA TORSIONALE Rt data dalla geometria della sezione (MOMENTO D’INERZIA POLARE Jt), dal materiale (MODULO DI ELASTICITA’ TANGENZIALE G) e dalla LUNGHEZZA l dell’elemento stesso.
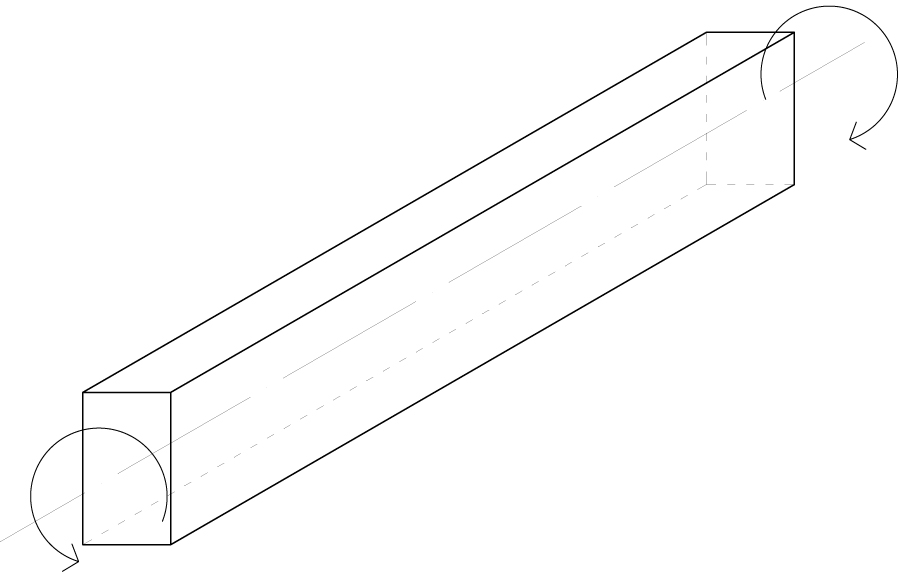

Questo ci interessa soprattutto nelle strutture tridimensionali poiché i momenti flettenti che agiscono su una trave generano MOMENTI TORCENTI Mt in quelle perpendicolari ad essa in base alla ROTAZIONE φcausata dall’inflessione della trave e a Rt della trave soggetta a torsione.

TELAIO 3D
Analizzeremo ora una struttura tridimensionale composta da travi e pilastri di lunghezza l pari a 3m; le due travi sono poste ortogonalmente tra loro nel piano xy, il carico uniformemente distribuito sulla mensola di l 1m è pari a 10 kN/m (q); lo scopo dell’esercitazione è osservare come la sezione di una trave e il suo materiale influisca sul momento torcente a parità di azioni esterne.
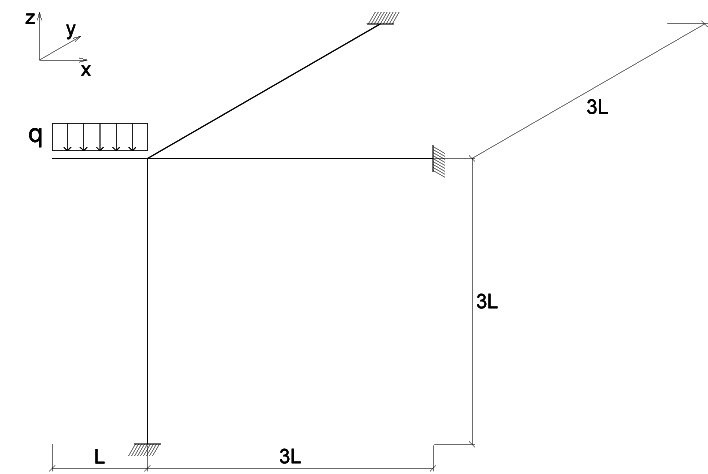
Per prima cosa possiamo semplificare la struttura adottando un sistema equivalente, per farlo bisogna sostituire la mensola e il suo carico distribuito con il momento concentrato M al nodo pari a ql2/2 (ovvero pari all’azione del carico distribuito); questo momento che ruota intorno all’asse y genererà una flessione nella trave e nel pilastro posti nel piano xz e di conseguenza una torsione nella trave che giace nel piano yz.
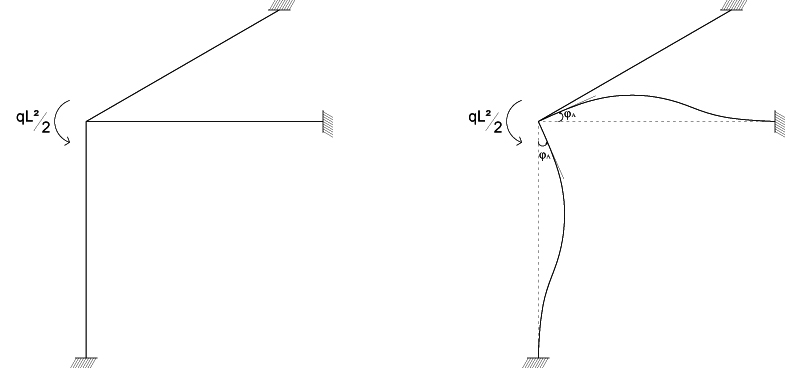
Conoscendo la deformata possiamo ricavare il valore dei momenti flettenti e di quello torsionale in funzione della ROTAZIONE φa grazie agli schemi notevoli e fare così l’equilibrio alla rotazione nel nodo.
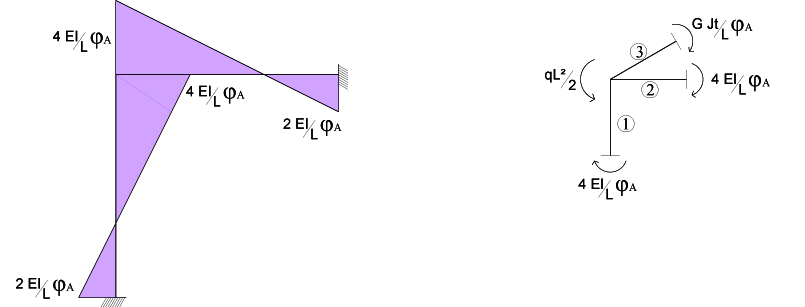
)
Possiamo indicare come rigidezza nel nodo A






Ora possiamo inserire nelle formule sopra ottenute i valori corrispondenti ad una sezione rettangolare 15x67cm in C.A. e successivamente verificare il risultato in SAP.



})


Sappiamo che C2 è un coefficiente tabellato che tiene conto del rapporto del lato maggiore sul lato minore della sezione (a/b).


Possiamo utilizzare SAP per controllare i valori da noi ottenuti (essendo il programma più accurato) e utilizzare tali dati per il calcolo in modo d’avere un riscontro migliore con le verifiche finali.
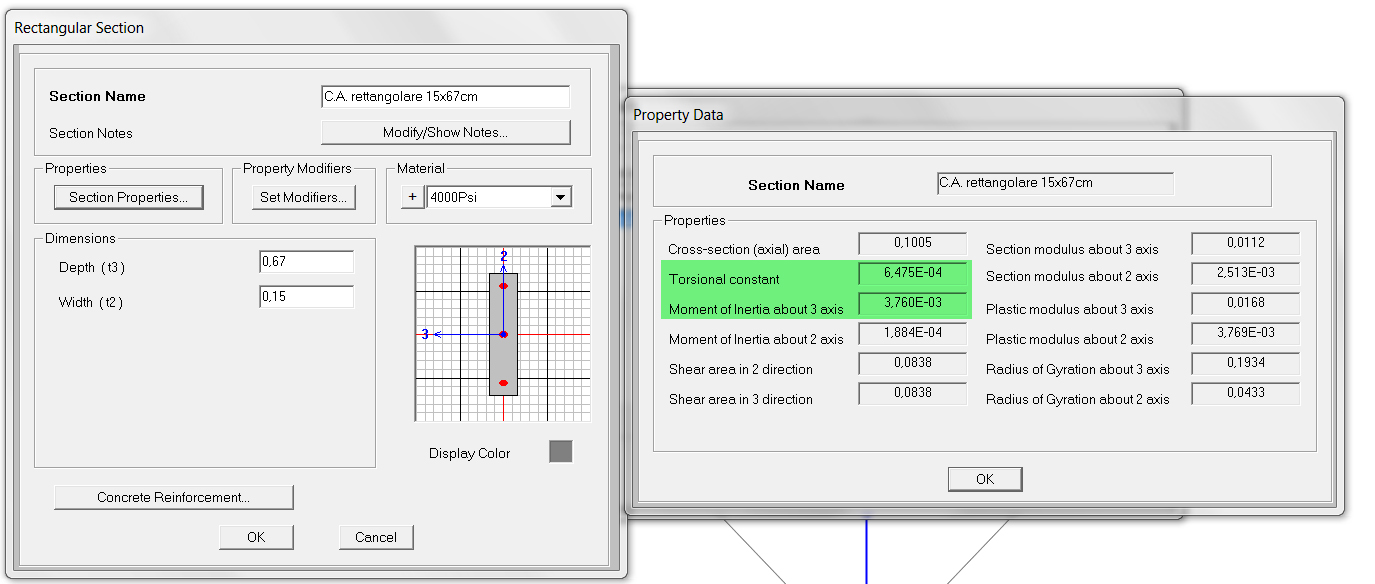


Eseguendo i calcoli otteniamo
+\left ( \frac{4*21*10^{6}*3.76*10^{-3}}{3} \right )+\left ( \frac{10356491*6.475*10^{-4}}{3} \right )=105280+105280+2235.276=212795.276 KNm)



Verifichiamo se l'equazione è soddisfatta:

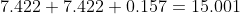
Passiamo ora a modellare la struttura in SAP utilizzando una 3D Grid applicando questa volta direttamente il momento concentrato equivalente all’azione del carico distribuito sulla mensola.
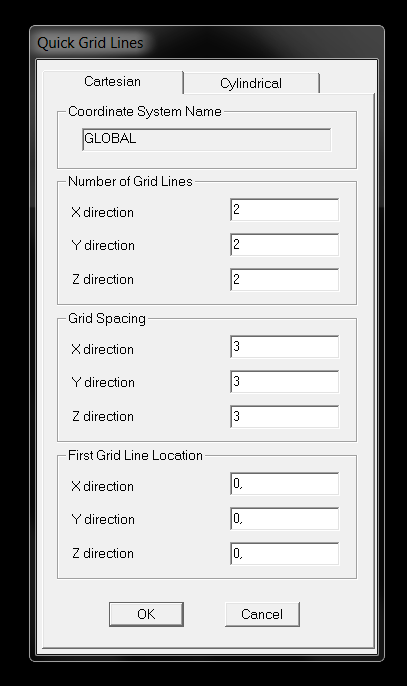
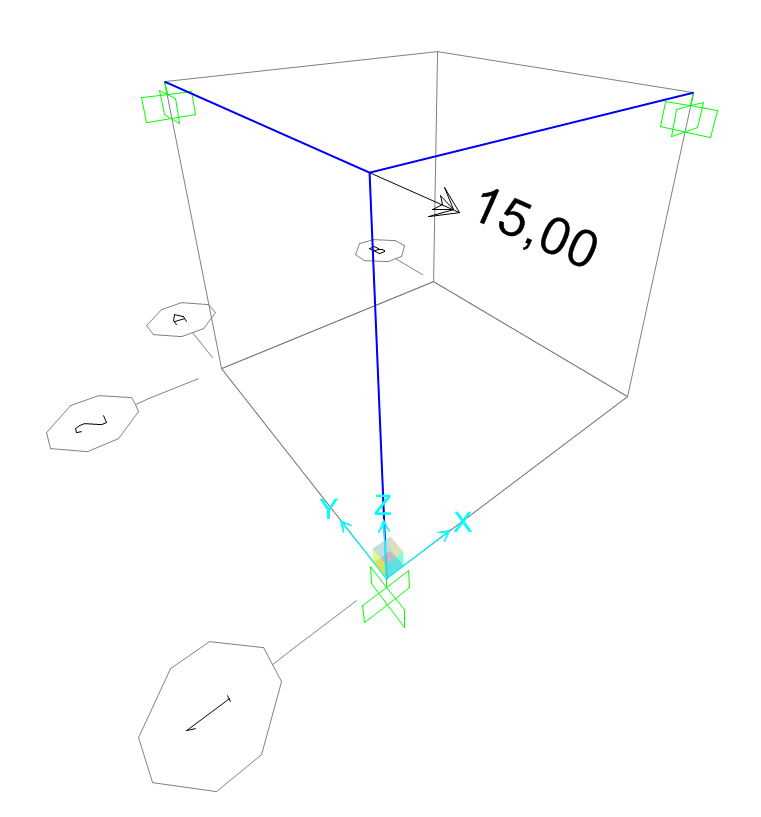
Iniziamo verificando il comportamento della struttura con una sezione generica.
DEFORMATA

SFORZO ASSIALE

TAGLIO

MOMENTO
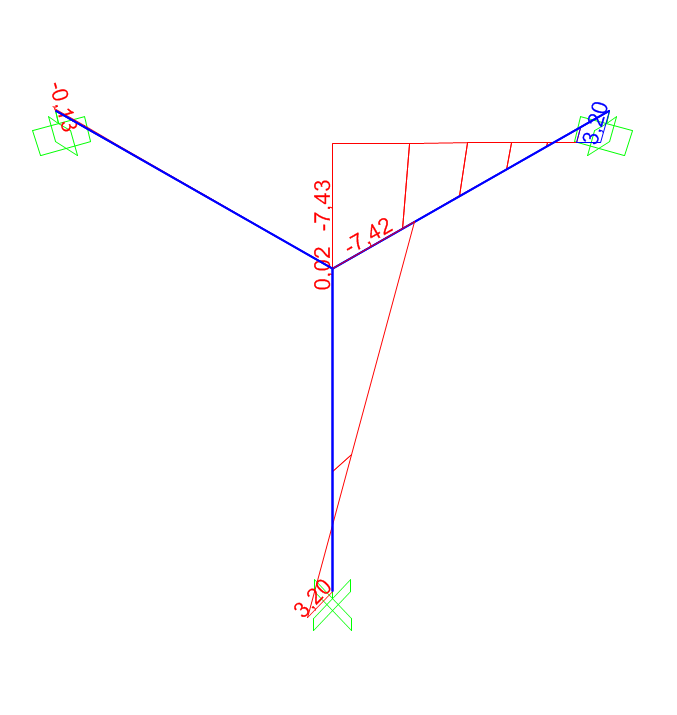
TORSIONE
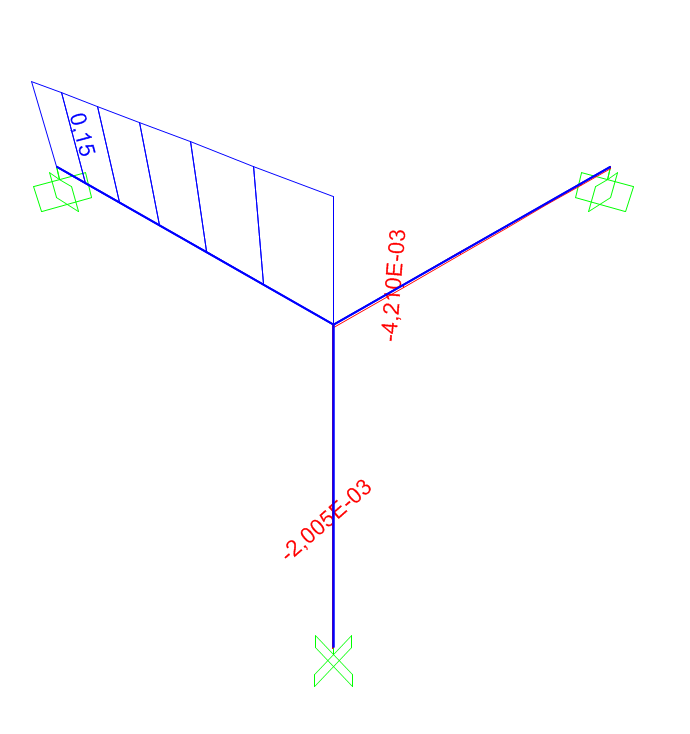
Impostiamo ora la sezione RETTANGOLARE 15x67 cm in C.A. e lanciamo il calcolo.
Possiamo vedere che il risultato ottenuto è pressoché identico a quello ricavato dal calcolo a mano.
ROTAZIONE φA = 6,8 * 10^-5
Ripetiamo l’analisi con una sezione CIRCOLARE PIENA in C.A. di diametro 36 cm (stessa area della sezione rettangolare).

Cambiamo materiale e vediamo come cambi la rotazione utilizzando tre diversi profili in ACCIAIO:
- HEA 20x20 cm
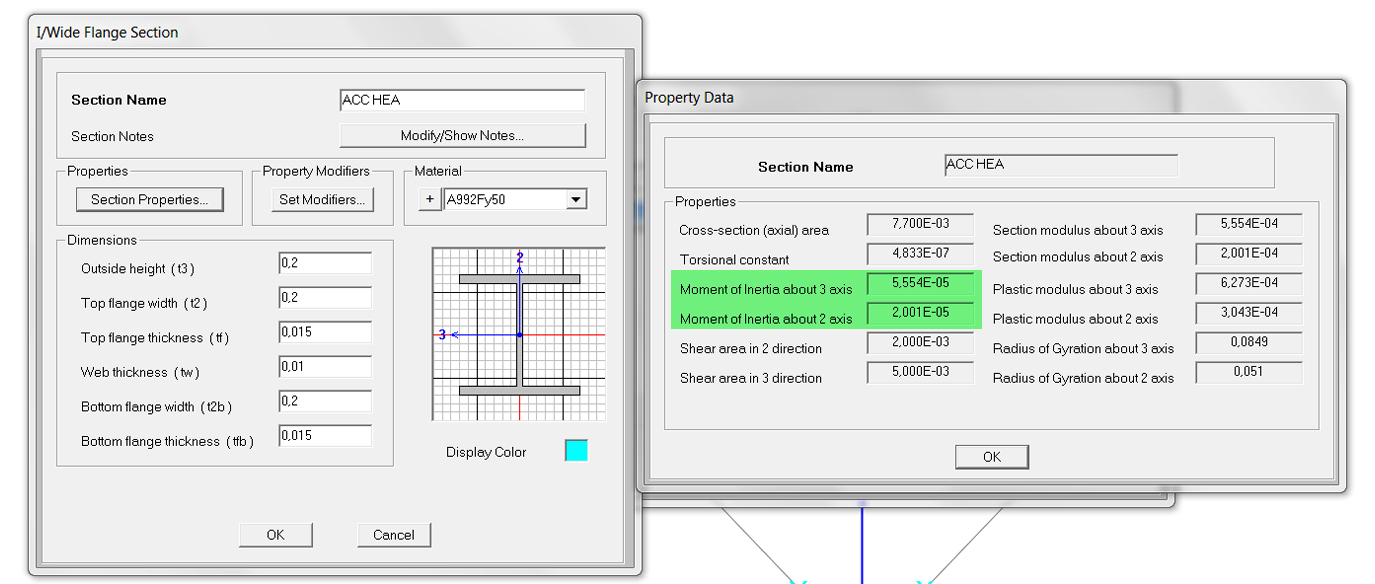
- SCATOLARE 20x20 cm
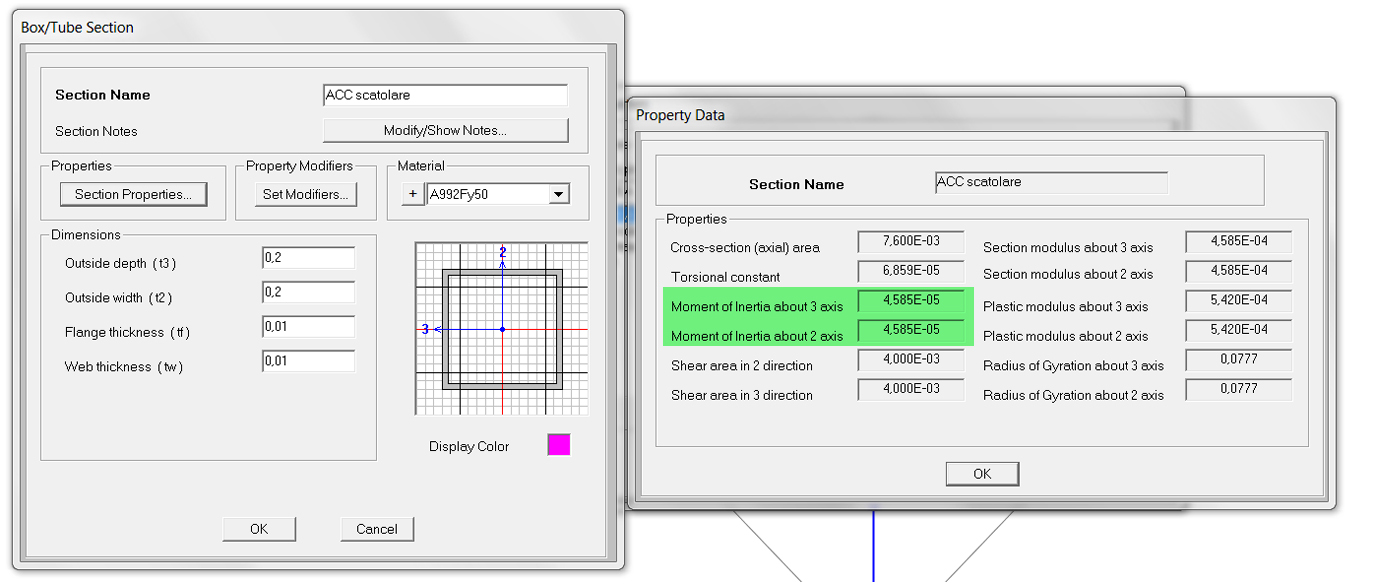
- TUBOLARE d. 25 cm
Riassumiamo ora nella seguente tabella i valori delle rotazioni ed il contributo di ciascuna asta in base alla sezione ed al materiale adottato.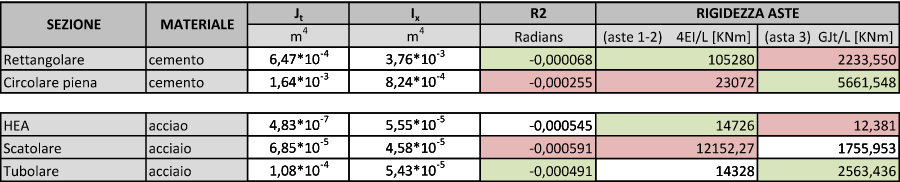
Osservando la tabella ed in particolare la rigidezza dell’asta 3 (quella soggetta a torsione) si può concludere che sezioni dello stesso materiale reagiscano meglio (cioè ricevono più carico) se hanno un profilo chiuso rispetto a quelle aperte; questo perché le tensioni tangenziali, che aumentano all’aumentare della distanza dall’asse torsionale, riescono a distribuirsi ad una distanza media maggiore, ciò spiega perché il tubolare funzioni meglio dello scatolare e perché il profilo HEA invece sia il peggiore avendo l’asse dell’anima che passa per il centro torsionale e molta della sua area abbia una reazione molto piccola.
E’ interessante inoltre come profili in acciaio nonostante le dimensioni delle sezioni molto minori reagiscano meglio rispetto a sezioni piene in C.A., questo è dovuto al modulo di elasticità tangenziale che è circa 8 volte maggiore.
Nel complesso però bisogna ammettere che in questa struttura la sezione rettangolare in calcestruzzo è quella che garantisce una deformazione minore, questo si spiega perché il contributo dato dalla rigidezza torsionale nell’assorbimento del momento concentrato è molto minore rispetto a quello fornito dalla rigidezza flessionale data dal modulo di elasticità e dal momento d’inerzia (molto più elevati nel calcestruzzo e nella sezione rettangolare rispetto alle altre ipotesi fatte).
GRATICCIO
Analizzeremo ora un graticcio composto da due travi di lunghezza l totale pari a 6m; le due travi sono poste ortogonalmente tra loro nel piano xy (incastrandosi a l/2 di una trave e a l/3 dell’altra, questo causa un momento torcente in una delle travi); il carico concentrato nell’incastro tra le due travi è pari a 10 kN (F); lo scopo dell’esercitazione è osservare come la sezione di una trave e il suo materiale influisca sul momento torcente a parità di azioni esterne.
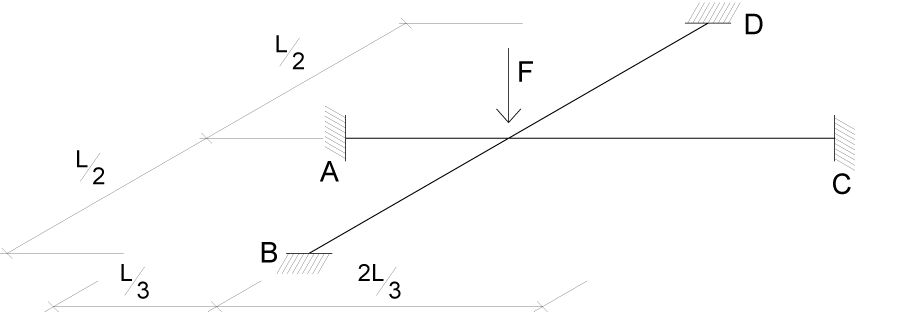
Il nodo centrale oggetto di analisi ha 6 GDL ovvero 3 rotazioni e 3 traslazione possibili, la condizione di carico da noi studiata però non genera traslazione lungo l’asse x e y inoltre non ci sono rotazioni intorno ad x e z; rimangono da determinare quindi solo lo SPOSTAMENTO δ e la ROTAZIONE φy.
Otteniamo così le seguenti deformate:
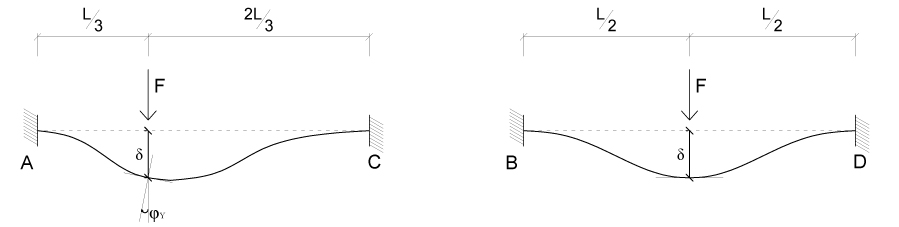
Nella trave BD, in essa F agisce esattamente al centro quindi si avrà solamente uno spostamento δ dato che la tangente della deformata in quel punto è orizzontale e di conseguenza la rotazione è nulla.
Nella trave AC invece F agisce a l/3 questo comporta che a parità di spostamento δ ci sarà anche una rotazione, questo perché la tangente alla deformata non orizzontale e si avrà di conseguenza anche una rotazione φy.
Possiamo sfruttare il principio di sovrapposizione degli effetti separando le incognite in modo da poter analizzare gli effetti di ciascuna per poi sommarli.
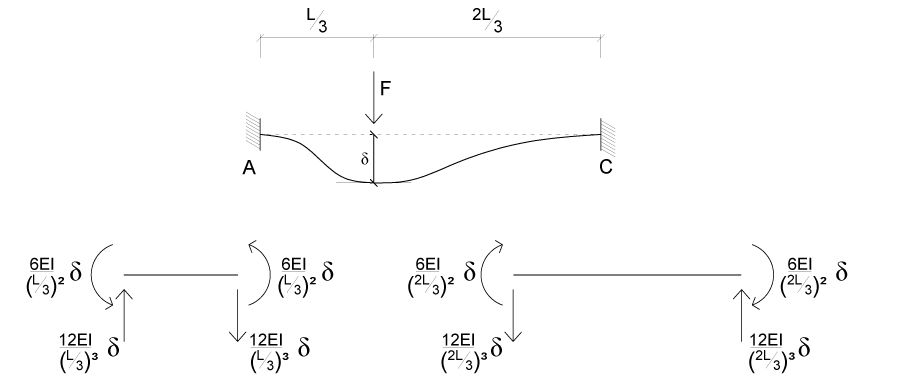
Iniziamo con lo studio della deformata della trave BD dovuta allo SPOSTAMENTO δ, possiamo ricondurci agli schemi notevoli di una trave doppiamente incastrata per conoscere i valori della rigidezza e ottenere così gli sforzi di TAGLIO e MOMENTO FLETTENTE.
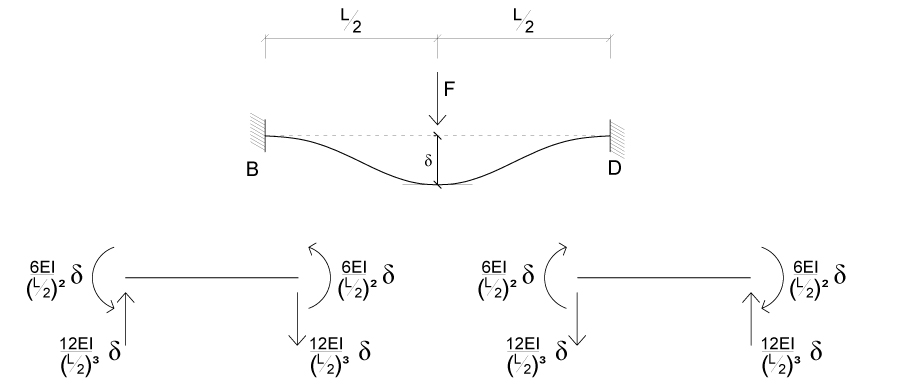
Ripetiamo lo stesso procedimento studiando la deformata della trave AC dovuta solo allo SPOSTAMENTO δ.
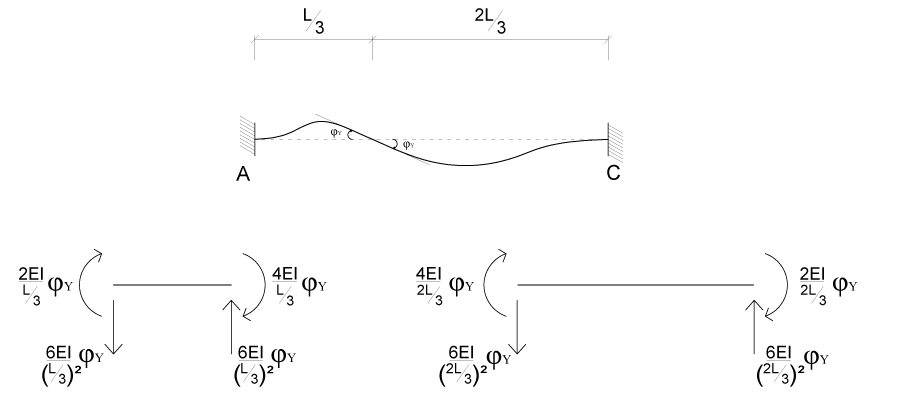
Nella trave AC è presente anche la ROTAZIONE φy, possiamo quindi dalla deformata e dagli schemi notevoli ricavarci i valori del MOMENTO FLETTENTE e di conseguenza del TAGLIO.
La ROTAZIONE φy nel nodo causa anche un MOMENTO TORCENTE nella trave BD, questo si ripartisce nelle due campate con un momento proporzionale alla lunghezza di ciascuna campata e con verso opposto a quello della rotazione.

Conosciamo ora le azioni generate dallo in ciascuna trave SPOSTAMENTO δ e dalla ROTAZIONE φy e possiamo sommare i loro effetti e scrivere le equazioni di equilibrio.
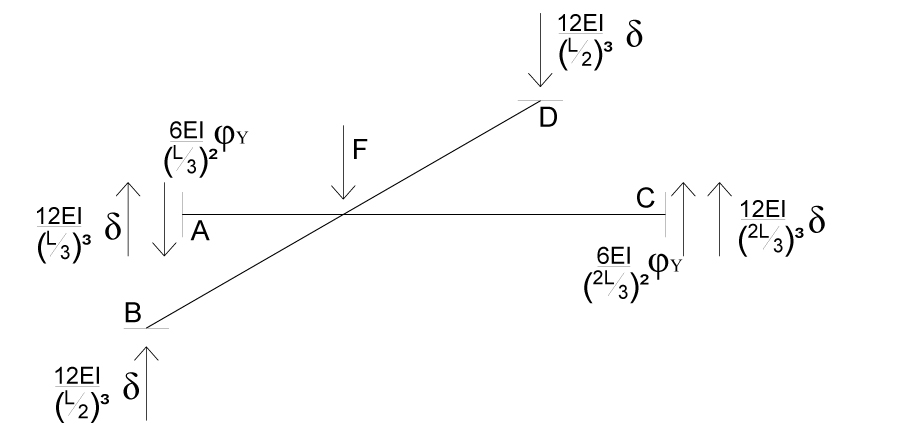
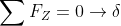
^{3}}\delta -\frac{12EI}{\left ( \frac{l}{3} \right )^{3}}\delta -\frac{12EI}{\left ( \frac{2}{3}l \right )^{3}}\delta-\frac{6EI}{\left ( \frac{2}{3}l \right )^{2}}\varphi _{Y}+\frac{6EI}{\left ( \frac{l}{3} \right )^{2}}\varphi _{Y}=0)

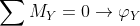
^{2}}}\delta +\frac{2GJ_{t}}{\frac{l}{2}}\varphi _{Y}+\frac{6EI}{\left ( \frac{2}{3\right l)^{2}}}\delta +\frac{4EI}{\frac{2}{3}l}\varphi _{Y}=0)
Ora dobbiamo solamente mettere a sistema le due equazioni e ricavarci le incognite.
^{2}}\delta -\frac{12EI}{(\frac{l}{3})^{3}}\delta -\frac{12EI}{(\frac{2}{3}l)^{3}}\delta -\frac{6EI}{(\frac{2}{3}l)^{2}}\varphi _{Y}+\frac{6EI}{(\frac{l}{3})^{2}}\varphi _{Y}=0 \\ \frac{4EI}{\frac{l}{3}}\varphi _{Y}-\frac{6EI}{(\frac{l}{3})^{3}}\delta +2\frac{GJ_{t}}{\frac{l}{2}}\varphi _{Y}+\frac{6EI}{(\frac{2}{3}l)^{2}}\delta +\frac{4EI}{\frac{2}{3}l}\varphi _{Y}=0 \end{matrix}\right.)
Risolvendo la prima equazione abbiamo:
+\delta \left (- \frac{54EI}{l^{2}}+\frac{27}{2}\frac{EI}{l^{2}} \right )=0)
+\delta \frac{EI}{l^{2}} \left (- 54+\frac{27}{2} \right )=0)
![\frac{EI}{l}\left [\varphi _{Y}\left ( 18+\frac{4GJ_{t}}{EI} \right )+\frac{\delta}{l} \left (- \frac{81}{2} \right )\right ]=0](http://latex.codecogs.com/gif.latex?\frac{EI}{l}\left [\varphi _{Y}\left ( 18+\frac{4GJ_{t}}{EI} \right )+\frac{\delta}{l} \left (- \frac{81}{2} \right )\right ]=0)
Possiamo imporre che: 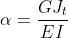
Otteniamo così:
=\frac{81}{2}\frac{\delta }{l})
\varphi _{Y}=\frac{36+8\alpha }{81}\varphi _{Y})
\varphi _{Y})
Risolvendo la seconda equazione otteniamo:
=0)

\varphi _{Y}=0)
+\frac{81}{2}\varphi _{Y}=0)

\varphi _{Y}+\frac{81}{2}\varphi _{Y}=0)
\varphi _{Y}+\frac{81}{2}\varphi _{Y}=0)
\varphi _{Y}-\frac{81}{2}\varphi _{Y})
)
)
)
![\varphi _{Y}=\frac{Fl^{2}}{EI\left [ \frac{1241}{6}+\frac{1484}{27}\alpha \right ]}](http://latex.codecogs.com/gif.latex?\varphi _{Y}=\frac{Fl^{2}}{EI\left [ \frac{1241}{6}+\frac{1484}{27}\alpha \right ]})
Ora possiamo inserire nelle formule sopra ottenute i valori corrispondenti ad una sezione rettangolare 15x67cm in C.A. con F=10KN, l=6m e successivamente verificare il risultato in SAP.





Sappiamo che C2 è un coefficiente tabellato che tiene conto del rapporto del lato maggiore sul lato minore della sezione (a/b).


Possiamo utilizzare SAP per controllare i valori da noi ottenuti (essendo il programma più accurato) e utilizzare tali dati per il calcolo in modo d’avere un riscontro migliore con le verifiche finali.



Eseguendo i calcoli otteniamo
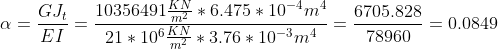
![\varphi _{Y}=\frac{Fl^{2}}{EI\left [ \frac{1241}{6}+\frac{1484}{27}\alpha \right ]}](http://latex.codecogs.com/gif.latex?\varphi _{Y}=\frac{Fl^{2}}{EI\left [ \frac{1241}{6}+\frac{1484}{27}\alpha \right ]})
![\varphi _{Y}=\frac{10KNm*m^{2}}{21*10^{6}\frac{KN}{m^{2}}*3.76*10^{-3}m^{4}\left [206.8+54.96*0.849 \right ]}=2.15*10^{-5}](http://latex.codecogs.com/gif.latex?\varphi _{Y}=\frac{10KNm*6m^{2}}{21*10^{6}\frac{KN}{m^{2}}*3.76*10^{-3}m^{4}\left [206.8+54.96*0.0849 \right ]}=2.15*10^{-5})
\varphi&space;_{Y}=0.45*2.15*10^{-5}=0.000009)
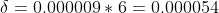
Passiamo ora a modellare la struttura in SAP utilizzando una 3D Grid impostando le condizioni di carico e vincolo come nella struttura sopra esaminata ricordiamoci inoltre di assegnare alle travi la sezione RETTANGOLARE 15x67 cm in C.A.
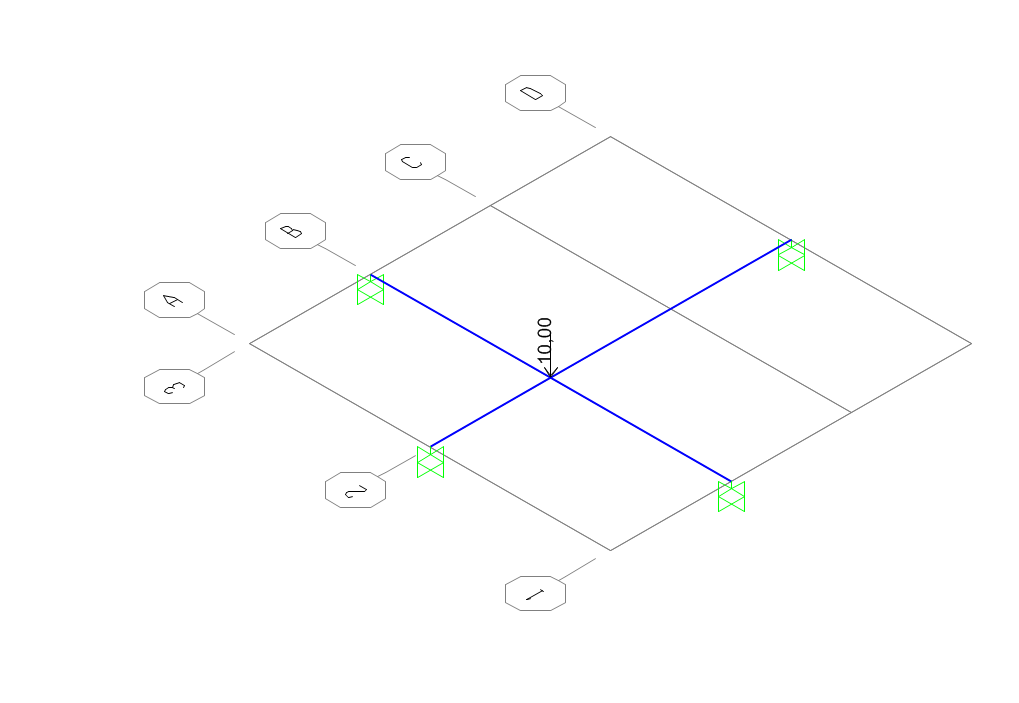
Lanciamo il calcolo e otteniamo:
DEFORMATA
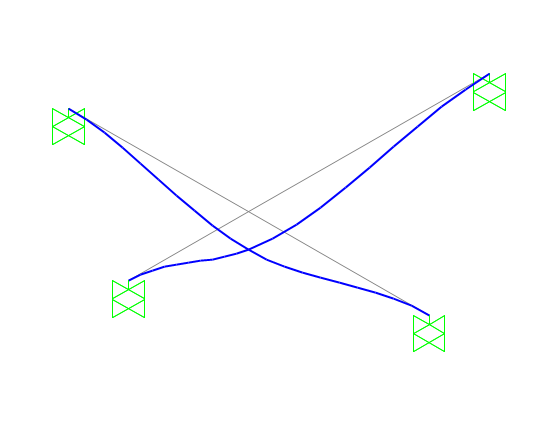
TAGLIO

MOMENTO FLETTENTE

MOMENTO TORCENTE
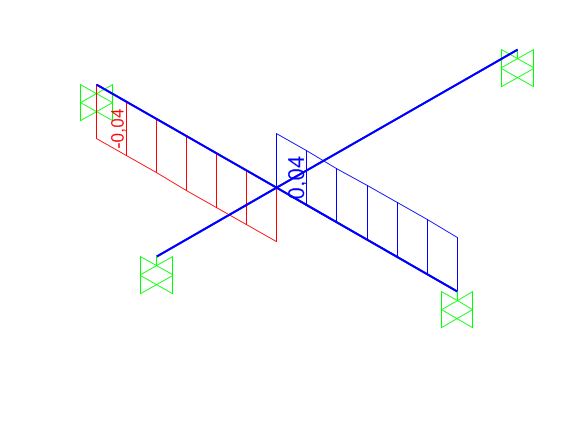
Possiamo vedere che il risultato ottenuto è pressoché identico a quello ricavato dal calcolo a mano.
ROTAZIONE φy = 2 * 10^-5
SPOSTAMENTO δ = 5,8 * 10^-5
Ripetiamo l’analisi con una sezione CIRCOLARE PIENA in C.A. di diametro 36 cm (stessa area della sezione rettangolare).
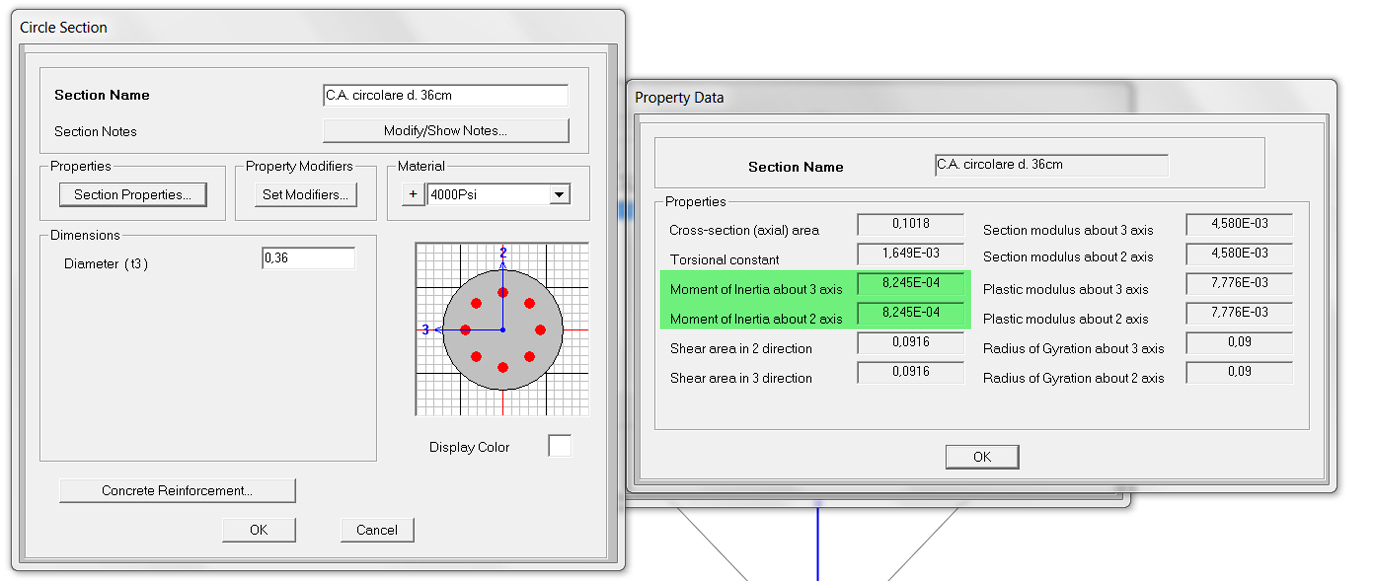
Cambiamo materiale e vediamo come cambi la rotazione e lo spostamento utilizzando tre diversi profili in ACCIAIO:
- HEA 20x20 cm

- SCATOLARE 20x20 cm
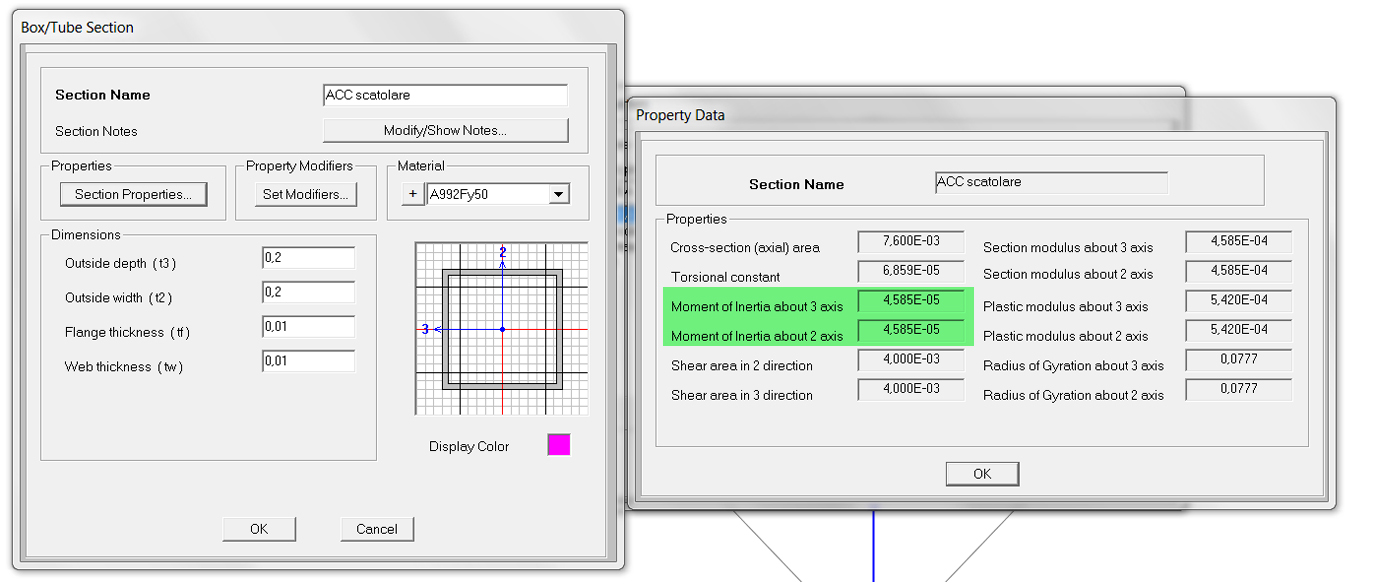
- TUBOLARE d. 25 cm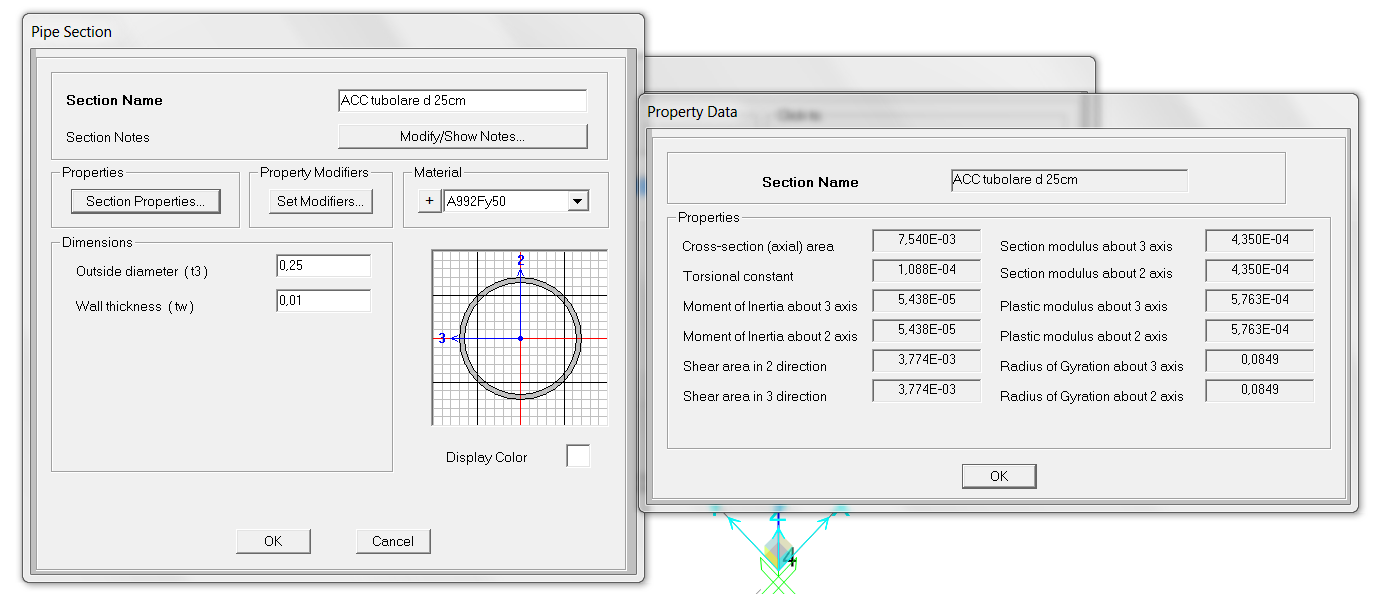
Riassumiamo ora nella seguente tabella i valori delle rotazioni ed il contributo di ciascuna asta in base alla sezione ed al materiale adottato.
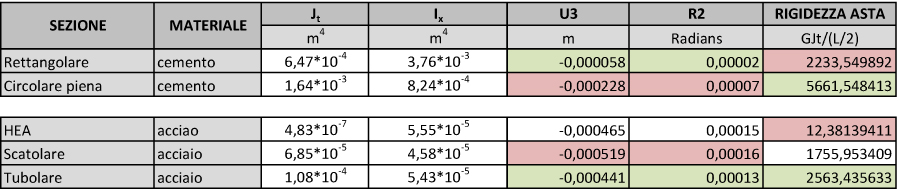
Dalla tabella ottenuta vengono confermate le osservazioni fatte per il telaio 3d.
Commenti recenti