Esercitazione

Un impalcato è infinitamente rigido nel suo piano, ma se sottoposto a forze orizzontali, quali sisma e vento, può subire spostamenti. L’esercitazione vuole farci analizzare come tale impalcato reagisce tramite l’azione dei controventi.

I controventi  vengono rappresentati come molle, dato il loro comportamento elastico che ci permette di considerarli vincoli cedevoli. Ogni molla reagisce alle forze esterne in proporzione alla propria rigidezza che varia a seconda  della sezione e dal numero di pilastri presenti su quel telaio.

Ipotizziamo un impalcato in calcestruzzo armato con pilastri 30x40 cm e altezza 3,20 m diversamente orientati a seconda dell’orditura del solaio. Esso è composto da 10 telai ognuno collegato ad una molla, dove Kv sono i telai verticali e Ko quelli orizzontali.

Stabilito il materiale con il relativo modulo di Young (E=21000 N/mm), la sezione dei pilastri con il loro momento d’inerzia in base all’orientamento, e conoscendo la distanza delle molle dal punto d’origine dell’impalcato, possiamo compilare il foglio di calcolo.

1 CALCOLO DELLE RIGIDEZZE TRASLANTI DEI CONTROVENTI DELL’EDIFICIO

Si prendono in esame uno per volta i telai relativi ad ogni controvento per determinarne la rigidezza , ovvero la forza con la quale si oppongono alla traslazione lungo l’asse

2 TABELLA SINOTTICA CONTROVENTI E DISTANZE

3 CALCOLO DEL CENTRO DELLE MASSE

In strutture non propriamente simmetriche la ricerca del centro delle masse non è intuitiva.

Si semplifica l’impalcato in forme semplici, nel nostro caso 3 aree di cui è facile trovare il baricentro, conoscendo le coordinate di ciascun baricentro e l’area delle forme semplici possiamo trovare il centro dell’intero impalcato

4 CALCOLO DEL CENTRO DI RIGIDEZZE E DELLA RIGIDEZZA GLOBALE

Il centro delle rigidezze (C) è il punto dove viene applicata la risultante delle rigidezze traslanti dei controventi sia lungo l’asse x che lungo l’asse y.

Per trovarlo si sommano le rigidezze verticali K_v-tote quelle orizzontali K_o-tot, e le coordinate saranno:

Trovato il centro di rigidezza ci calcoliamo la distanza di ogni telaio da questo puto (dd), e di conseguenza ci troviamo la rigidezza complessiva a rotazione delle molle

5 ANALISI DEI CARICHI SISMICI

Definiamo la forza sismica applicata nel centro delle masse, come prodotto tra la massa dell’impalcato (W) e il coefficiente di intensità sismica (c)

6 RIPARTIZIONE DELLA  FORZA SISMICA LUNGO L’ASSE X

Il centro delle masse (dove agisce la forza sismica) non coincide con il centro della rigidezza (dove agisce la risultante delle rigidezze del nostro sistema di forze) quindi si genera una traslazione ed una rotazione dell’impalcato.

Troviamo il momento torcente

Traslazione orizzontale

Rotazione

Ora possiamo quantificare come la forza si ripartisce nei controventi

Analogamente per l'asse y

In conclusione i telai con una rigidezza maggiore assorbono una maggiore forza sismica.

Con la seguente esercitazione si vuole analizzare come un IMPALCATO STRUTTURALE, considerato come un CORPO INFINITAMENTE RIGIDIO alle azioni che agiscono lungo il suo piano, si comporti sotto l’effetto di FORZE ESTERNE ORIZZONTALI come ad esempio in questo caso il SISMA; il suo comportamento dipende:

- dai CONTROVENTI considerati VINCOLI ELASTICI CEDEVOLI, assimilabili a molle che reagiscono alle forze agenti lungo il loro stesso piano in proporzione della loro rigidezza;

- dalla distanza tra il CENTRO DELLE MASSE, baricentro geometrico dell’impalcato, e il CENTRO DELLE RIGIDEZZE, dato dalla risultante di tutte le rigidezze.

Questi due aspetti determinano infatti la RIGIDEZZA TRASLANTE K_δ e di conseguenza la TRASLAZIONE δ lungo la direzione della FORZA AGENTE e la RIGIDEZZA ROTAZIONALE Kφe di conseguenza la ROTAZIONE φintorno al CENTRO DELLE RIGIDEZZE.

Si è scelto di analizzare il seguente impalcato:

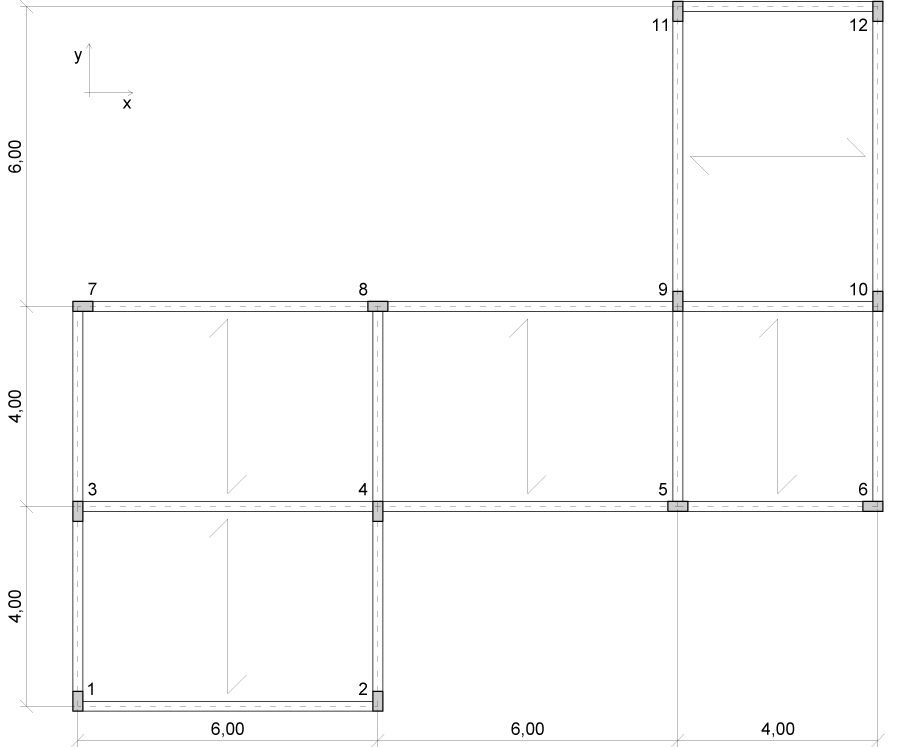
Esso è costituito da diversi telai indicati con delle molle K_V per quelli VERTICALI e K_O per quelli ORIZZONTALI.

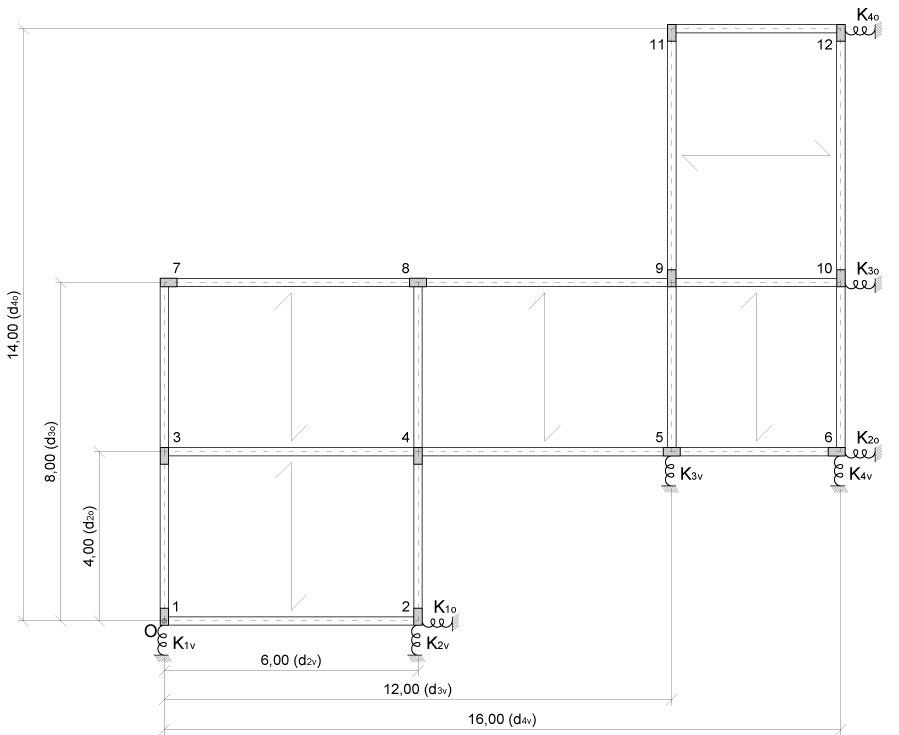
Ciascun telaio e formato da PILASTRI in CALCESTRUZZO (E=21000 N/mm²) 20x40cm di base e alti 3,2m i cui MOMENTI D’INERZIA I_x = (B x H³)/12 e I_y = (H x B³)/12 sono rappresentati in figura:

STEP 1

Una volta noto il MODULO DI YOUNG (E), l’ALTEZZA DEL PILASTRO, i MOMENTI D’INERZIA (facendo attenzione di utilizzare quello reagente, ad esempio se analizziamo un telaio verticale cioè reagente lungo y dovremmo usare I_x) possiamo calcolare la RIGIDEZZA TRASLANTE K_δ del telaio dato dalla somma delle rigidezze di ciascun pilastro ovvero:

K = 12EI/h³                       K_δ= ∑ K_i

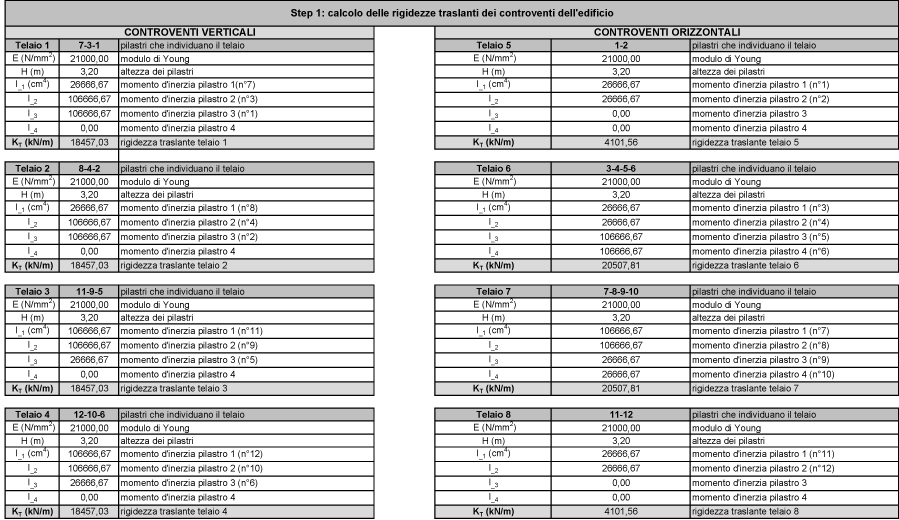
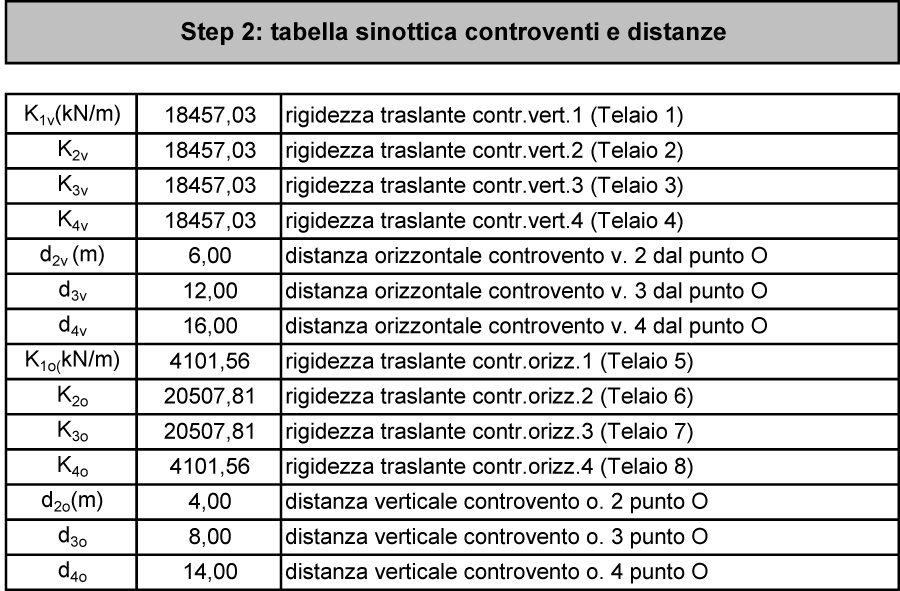
STEP 2

Possiamo ora raccogliere ciascuna rigidezza traslante e la rispettiva distanza dal centro O in una tabella.

STEP 3

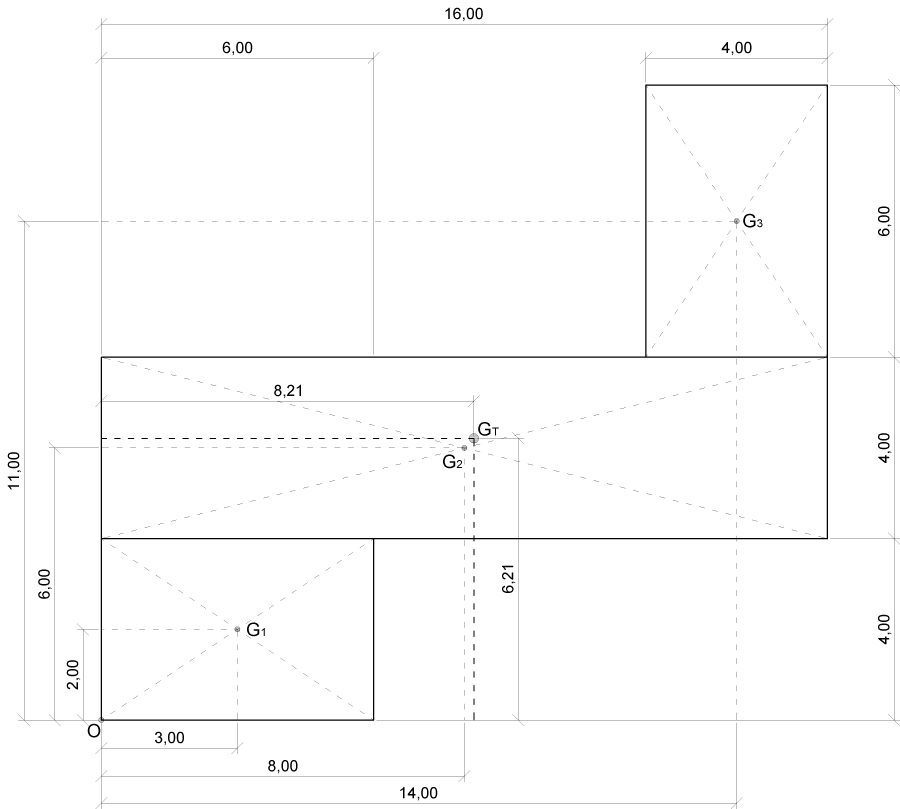
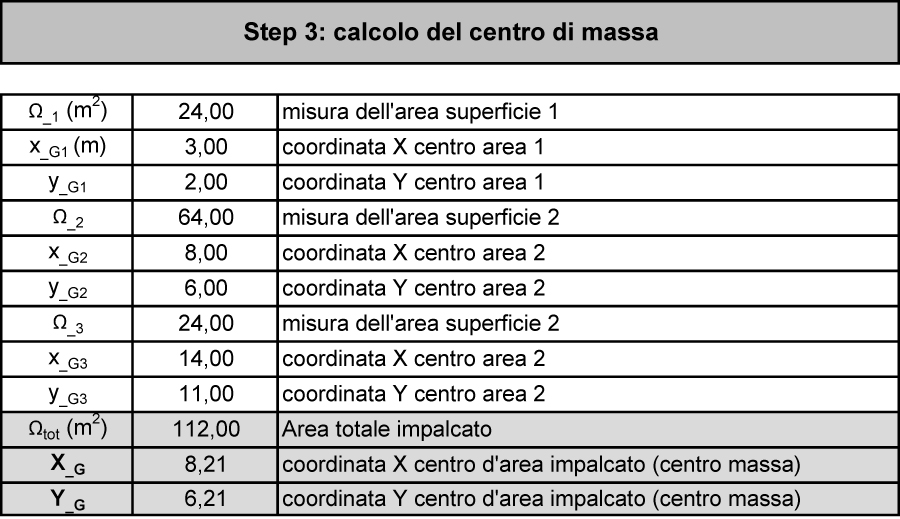
Dobbiamo ora individuare il CENTRO DELLE MASSE, per farlo è consigliabile suddividere la pianta in aree geometriche semplici come ad esempio RETTANGOLI di cui siamo in grado di determinare il BARICENTRO; otteniamo così le coordinate del baricentro di ogni area, ora ci rimane di ottenere le coordinate del centro delle masse attraverso una MEDIA PONDERATA poiché nel nostro caso la superficie totale è stata divisa in 3 aree più piccole abbiamo:

x_{_G}= [(x₁* A₁) + (x₂* A₂) + (x₃* A₃)] / A_tot                    

y_{_G}= [(y₁* A₁) + (y₂* A₂) + (y₃* A₃)] / A_tot

STEP 4

Si passa ora alla determinazione del CENTRO DELLE RIGIDEZZE (C).

Per prima cosa dobbiamo sommare tutte le rigidezze verticali e poi quelle orizzontali; dopodiché dobbiamo fare una media ponderata dove abbiamo:

x_C = (∑_i K_iv * d_iv) / K_{v_tot}                       y_C = (∑_i K_io * d_io) / K_{o_tot}

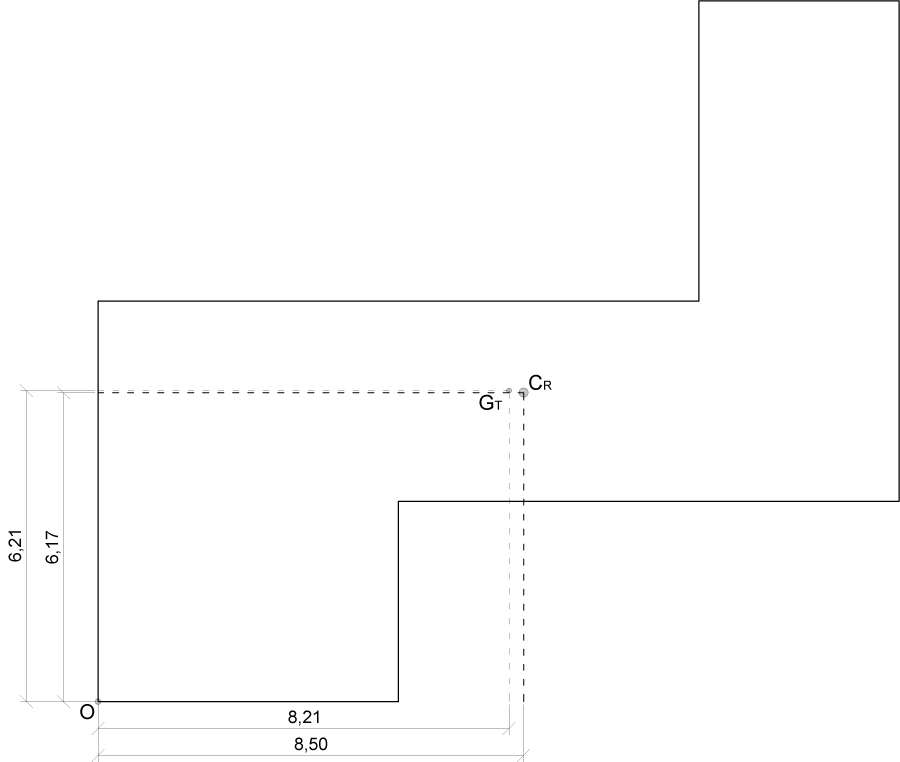
Ora che il centro delle rigidezze è noto possiamo calcolare la distanza di ogni telaio da C; non rimane ora che calcolare la RIGIDEZZA ROTAZIONALE Kφche è data dalla sommatoria dei prodotti delle rigidezze traslanti di ciascun telaio per la distanza al quadrato di ognuno di essi rispetto a C.

Kφ = ∑_i K_i * dd_i²

STEP 5

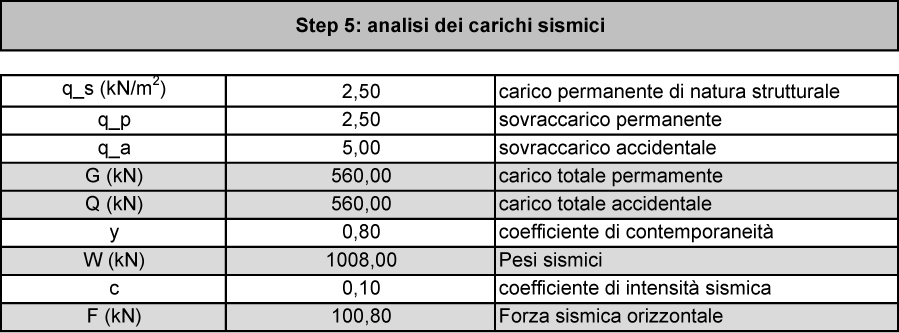
Dobbiamo ora eseguire l’analisi dei carichi (allo stato limite di esercizio poiché non si tiene conto di γ), per farlo dobbiamo ottenere il CARICO TOTALE PERMANTE G (somma del carico strutturale e quello permanente, moltiplicata per l’area dell’impalcato) ed il CARICO TOTALE ACCIDENTALE Q (prodotto del carico accidentale per l’area); successivamente ci possiamo ricavare i PESI SISMICI W dalla seguente formula:

W = G + (Q * y)               dove y indica il COEFFICIENTE DI CONTEMPORANEITA’.

L’ultima forza da ricavare è la FORZA SISMICA ORIZZONTALE F data dal rapporto tra i pesi sismici e il COEFFICIENTE DI INTENSITA’ SISMICA c (dipende dalla zona sismica).

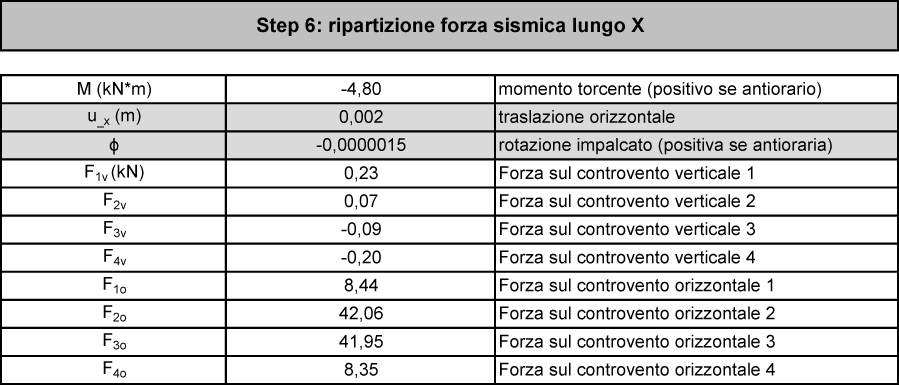
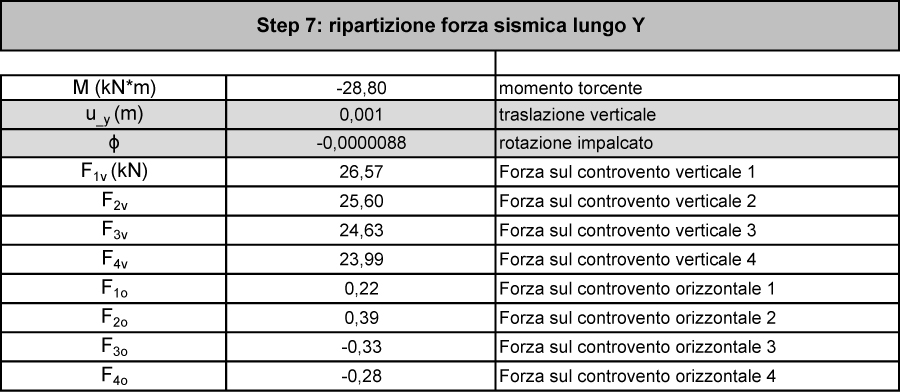
STEP 6-7

Arriviamo infine a quantificare la ripartizione della FORZA SISMICA ORIZZONTALE Flungo l’asse x e lungo l’asse y per ognuno dei controventi.

Poiché il nostro centro delle masse (dove si applica la forza sismica) non coincide con il centro delle rigidezze il sisma genera sia una TRASLAZIONE δ (una volta u_{_x} lungo l’assex e una voltau_{_y} lungo l’asse y in base alla direzione del sisma) ed unaROTAZIONE φ (anche questa diversa in base alla direzione del sisma).

Dobbiamo quindi calcolare il MOMENTO TORCENTE M, per l’asse x abbiamo M = F *(Y_{_c} – Y_{_G}) mentre per l’asse y abbiamo M = F *(X_{_c} – X_{_G}).

Successivamente possiamo ricavarci la TRASLAZIONE ORIZZONTALE u_{_x} = F / K_{o_tot} , TRASLAZIONE VERTICALE u_{_Y} = F / K_{V_tot} e la ROTAZIONE φ una volta per il sisma in direzione x e una volta per quello in direzione y (φ = M / Kφ facendo attenzione nell’utilizzare il rispettivo momento torcente).

In conclusione possiamo conoscere la ripartizione della forza sismica sia quando agisce lungo x sia quando agisce lungo y per ciascun controvento.

ASSE X:

        F_oi = K_oi (u_{_x} + dd_oi * φ)

        F_vi = K_vi (dd_vi * φ)

ASSE Y:

        F_oi = K_oi (dd_oi * φ)

        F_vi = K_vi (u_{_y}  + dd_vi * φ)

Per questa esercitazione ci è stato richiesto di fare il dimensionamento della trave in legno lamellare più sollecitata di un solaio tipo.

Questo è il solaio preso in considerazione e evidenziata la trave più sollecitata.

Innanzitutto quello che si dovrà andare a fare è il calcolo dei pesi gravanti sulla struttura i quali si dividono in tre categorie: Qs-Carichi strutturali (il peso della struttura atta a ripartire le forze che arrivano su di essa), Qp-Carchi permanenti (tutti quei carichi che pesano sulla struttura ma che non saranno mai levati o spostati), Qa-Carichi accidentali (in base alla destinazione d’uso dell’edificio il valore cambierà da tabella).

Calcolati i pesi li andremo a sommare tra loro e li moltiplichiamo per l’interasse di influenza in modo da sapere quanto sarà la forza che la trave dovrà reggere. A questo punto, una volta calcolati i carichi, si potrà calcolare il momento flettente. In questo caso io mi trovo davanti ad una trave doppiamente appoggiata e quindi il momento massimo si troverà in mezzeria con un valore pari a: ql^2/8, dove q sono i carichi e L la luce della trave.

Si inseriscono in tabella i valori del valore di resistenza a flessione caratteristica (che sarà diviso per il coefficiente di sicurezza gamma) e il coefficiente riduttivo kmod che ci daranno la nostra sigma (tensione) ammissibile 

Ora si può quindi procedere al calcolo dell’altezza della trave scegliendo a piacere la grandezza della base. Tramite la formula di Navier riusciamo infatti a ricavarci il Modulo di restenza W e quindi l’altezza della trave.

Una volta calcolata l’altezza della trave devo ripetere tutto in quanto il procedimento mancava appunto del peso proprio della trave che però ora, in quanto so la grandezza, conosco quindi devo procedere ad aggiungerla alla somma dei carichi strutturali e riposizionare i nuovi valori in tabella. Mi verrà quindi una trave con una altezza maggiore visto l’aumento della tensione massima a cui la trave dovrà resistere e quindi, come nel mio caso, se la trave calcolata regge un peso minore di quello che in realtà ci serve, dovrò ripetere una terza volta il processo.

h=45cm

altezza trave 50cm