SdC(b) (LM PA)

Consideriamo un impalcato di un piano tipologia shear type.

Siano affiancati all’impalcato dei controventi, i quali sono considerati vincoli cedevoli, rappresentati come molle. Questi ultimi intervengono a favorire la resistenza della struttura , quando forze orizzontali, come sisma e vento agiscono su di essa. Studiamo quindi come la struttura reagisce alle forze, supportata anche dall’azione dei controventi.

 

Siano:

Kv= rigidezza traslante dei controvento verticale

Ko=rigidezza traslante del controvento orizzontale

dv=distanza orizzontale del controvento dal punto O, origine degli assi

do=distanza verticale del controvento dal punto O

STEP 1: Calcolo rigidezze traslanti nell’edificio

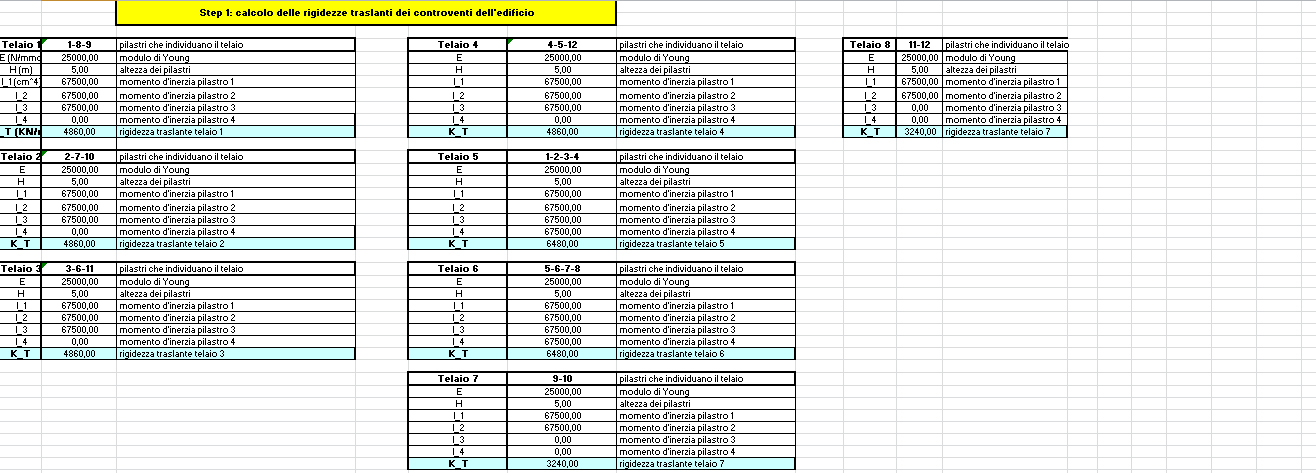
Nel file exel, prendendo in esame ogni singolo controvento , e individuando gruppi di essi secondo l’allineamento del telaio orizzontale e verticale, possiamo conoscere la rigidezza di ognuno di essi K_T.

Dato E=21000 N/mmq e h = 5 m .

KT (KN/m) =12EItot/h^3  

Calcolo la rigidezza per gruppi di elementi strutturali, ossia per gruppi di pilastri che compongono il telaio.

Siccome ogni telaio raggruppa almeno tre pilastri, (o comunque più di due) il calcolo della rigidezza del telaio terrà conto di questo fatto. Infatti la rigidezza del telaio, a partire dal primo telaio orizzontale, sarà data dal modulo di elasticità, moltiplicato per la somma delle inerzie dei pilastri che ne fanno parte, per 12 il tutto diviso l’altezza, ossia la distanza su cui la forza applicata agisce.

Applicheremo questo metodo per i seguenti telai orizzontali e lo stesso faremo per i telai verticali. 

 

Step 2 Tabella controventi e distanze

La tabella seguente è una tabella riassuntiva delle rigidezze traslanti precedentemente trovate e delle rispettive distanze orizzontali e verticali rispetto un centro di riferimento dato un sistema di assi cartesiani in cui la struttura è inserita. Da cui 0 è il punto di origine da cui si calcolano le distanze. 

 

 

Step 3 Calcolo centro masse

Calcoliamo ora il centro delle masse.

Per semplificare il calcolo, abbiamo suddiviso la superficie in aree semplici , ossia in aree di rettangoli.

Questo servirà per poter calcolare di ognuna di queste aree il centro di massa, e di conseguenza partire da tre punti, tanti quanti il numero di aree scelte, per trovare il centro delle masse tra questi.

Il centro delle masse è quindi dato dalle due coordinate X e Y. Troviamo X , distanza del centro G (chiamo così il centro delle masse) dall’origine. Il suo valore sarà dato dalla somma del prodotto di ogni area con la sua rispettiva distanza dall’origine, il tutto diviso per la somma delle aree.

Usiamo lo stesso procedimento per trovare la distanza di tutto l’impalcato dall’origine a G, muovendoci sull’asse Y.

Step 4: Calcolo delle rigidezze globali e del centro delle rigidezze

 

Ora che conosciamo le rigidezze dei telai , possiamo procedere con lo studio.

Calcoliamo ora la rigidezza globale della struttura e di seguito il centro delle rigidezze assoluto.

La rigidezza globale è pari alla somma delle rigidezze del telaio che sto considerando.  

Adesso , il centro delle rigidezze, che mi consente di conoscere il punto di applicazione della forza orizzontale di natura sismica ( o atmosferica come il vento) , dunque molto importante, sarà il valore da cui parto per svolgere l’esercizio nella prova simulata.

Esso è dato da due coordinate X e Y calcolate rispetto all’origine . Il centro avrà nome C. Per la prima coordinata X, tengo conto dei telai verticali e delle loro distanze dall’origine; la seconda coordinata Y , tiene a sua volta conto dei telai orizzontali e la loro distanza dall’origine.

Le due coordinate si trovano con un rapporto , pari alla somma dei prodotti della distanza del singolo telaio dall’origine, moltiplicato per la sua rigidezza, il tutto diviso per la rigidezza totale sull’asse corrispondente, come prima specificato.

 

Step 5: Analisi dei carichi sismici  

 

Tale tabella è riassuntiva dei carichi che sono applicati sulla struttura, con i corrispettivi coefficienti di contemporaneità.

Tali coefficienti , servono per considerare l’improbabilità che le azioni agiscano simultaneamente.

E un calcolo del risultato complessivo della forza agente, di natura sismica o atmosferica che muoverà la struttura nel senso orizzontale.

Step 6/7 ripartizione della forza sismica su X eY:

 

La forza risultante sarà ripartita sui due assi X e Y , specificando con i valori della tabella , come cambia l’intensità di volta in volta e su quale telaio.

Le tabelle indicano anche , a seconda del punto di applicazione della forza, valori di angoli e spostamenti.

Siccome il tipo di spostamento della struttura dipende strettamente dal punto in cui è applicata la forza, l’angolo è quell’angolo che si crea tra il punto iniziale e quello della deformata quando avviene rotazione, mentre lo spostamento si ha laddove la forza è applicata nel punto che genera solo traslazione. 

Vediamo ora cosa accade riportando la struttura in SAP

Con i passi e gli svolgimenti indicati sopra abbiamo inserito e ricavato valori dalla tabella.

Ho disegnato la struttura della tabella in SAP e mi sono servita dei valori calcolati per applicare la forza e vedere cosa succede.

Ho disegnato la struttura su una griglia tridimensionale su SAP , per ricostruire la situazione che avevo in alto nella tabella , dove il numero di pilastri e di telai e le loro reciproche distanze era specificato. 

 

Scegliamo e applichiamo i vincoli, il materiale e la sezione. 

Dunque passando alla pratica, selezioni tutti i punti ai piedi della struttura e inserisco gli incastri : bisogna cliccare su :

assign>joint>Incastro.

 

Quindi clicchiamo su ogni elemento strutturale e affidiamogli una sezione per materiale e dimensioni:

Assign> Frame > Frame sections> Add new property

Scegliamo concrete per la prima , e per tutti gli elementi strutturali. Differenzieremo però le travi dai pilastri dando ai pilastri una sezione 0,30 mx 0,30 m e alle travi una sezione di 0,70 m x 0,30 m, dove l’altezza è più marcata, per avere una rigidezza molto alta.   

Scegliamo di applicare la forza sul centro delle rigidezze, e verifichiamo cosa accade.

Cosa ci aspettiamo ?

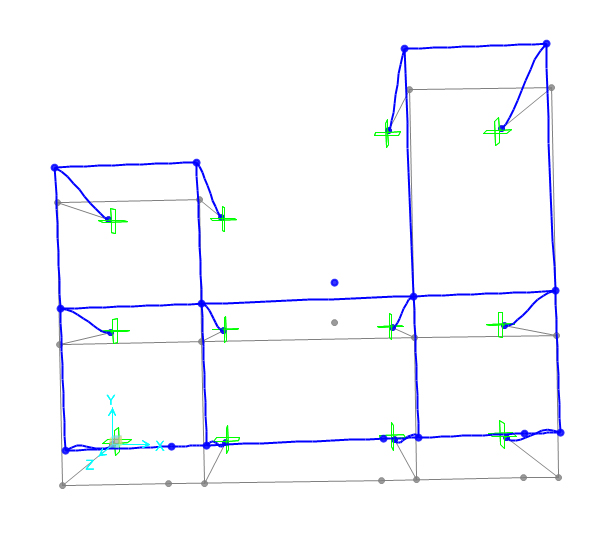
Che data una forza orizzontale, applicata lungo Y , sul punto del centro delle rigidezze, la struttura non ruoti , ma trasli solamente.

Ora ci occupiamo di rendere infinitamente rigida la struttura , applicando diaphragm ai nodi, in modo che tutta la struttura si muova insieme.

Selezioniamo dunque tutti i punti sulla sommità della struttura, compreso il centro della rigidezza e applichiamo Assign> Joints> Constraints> nel menù a tendina a destra in alto : diaphragm>ok.

 

Adesso è il momento di verificare il nostro obiettivo.

Applicata la forza , per la quale dobbiamo cliccare su Assign>Joint loads>Forces>Load Pattern Name ( Creiamo una nuova forza ) >Applichiamo la forza su Y , per la direzione dovuta alla sua natura sismica.

 

Applichiamo l’analisi con >Run.

La struttura , per verificare la prova, dovrà traslare. 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

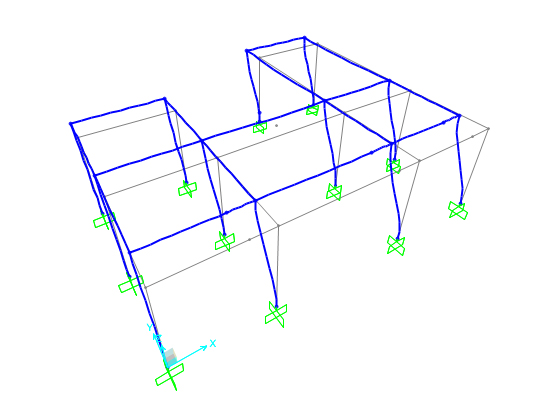
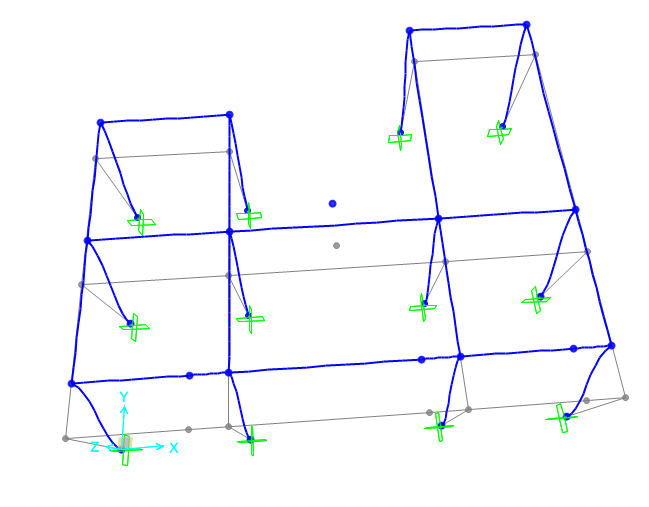
Possiamo fare lo stesso , solo applicando la forza sul centro delle masse.

Cosa ci aspettiamo adesso?

Che a struttura non trasli solamente , ma ruoti anche.

 

 

Il punto deve cadere dunque su centro delle masse, e sarà la prima cosa che disegneremo, al posto di quello precedente.

Le procedure da seguire sono le stesse eseguite per il caso precedente.

Dopo aver unito i punti insieme al centro delle masse, dovremo applicare la forza.

Essa sarà applicata su Y come prima. 

 

 

Se tutto va bene, vedremo adesso cosa succederà , e sarà diverso dalla situazione precedente.

Infatti , adesso dovrà verificarsi che la struttura, non trasla solamente ma ruota anche , intorno al punto di applicazione della forza.  La rotazione , per inciso, la sappiamo, dalle tabelle.

Dobbiamo dunque inserire la forza su SAP, avviare l’analisi, e verificare che questo avvenga.   

 

 

La seguente esercitazione ci è stata utile per affrontare il problema del comportamento di reazione che una struttura ha se sottoposta a carichi orizzontali, quali il sisma o il vento, quesito che va necessariamente messo in relazione con i concetti di centro delle rigidezze e di spostamento rigido.

Si è scelto di analizzare una struttura con intelaiatura trave-pilastro in cemento armato, avente la seguente carpenteria:

Avendo concepito le travi come elementi infinitamente rigidi a flessione, dunque indeformabili, possiamo considerare la struttura scelta come facente parte della tipologia idealizzata di telaio “shear-type”, avente nodi trave-pilastro rigidi, a incastro. Questa tipologia strutturale risponde meglio alle forze orizzontali, rispetto ad una tipologia intelaiata i cui collegamenti trave-pilastro sono incernierati: in questo caso, i pilastri, sottoposti a carichi orizzontali, tendono a deformarsi come se fossero mensole, nel caso scelto, invece, le travi, progettate come elementi molto alti e, quindi, robusti, “spingono” i pilastri a lavorare come elementi di un portale generico: la continuità strutturale data dal nodo incastro favorisce, infatti, un comportamento di collaborazione tra elementi verticali (pilastri) e trasversali (travi), creando ciò che viene definito un controvento.

La sezione A-A’ in basso mostra la deformata generalizzata dei sistemi shear-type, oltre ad evidenziare l’altezza dei pilastri scelti, dato fondamentale quando si affronta il problema della rigidezza: sappiamo, infatti, che la rigidezza di un pilastro facente parte di un sistema di controvento shear-type è pari a k=12EJ/L^3, dove E= modulo di elasticità dipendente dal materiale scelto, (nel nostro caso E=24855 Mpa, scelto in conformità a quanto previsto dal programma SAP2000 che utilizzeremo nella fase finale di verifica dell’esercitazione), J= momento di inerzia di sezione del pilastro (cm^4), ed L= all’altezza nel caso di elementi verticali, dunque uguale ad H nel nostro caso. Dalla formula si evince che più un pilastro è basso e più la sua rigidezza sarà elevata, essendo questi due parametri inversamente proporzionali tra loro, di conseguenza più un pilastro è alto e più la sua rigidezza sarà minore, tra l’altro L nella formula è un termine elevato al cubo, ciò significa che l’indiretta proporzionalità che sussiste tra queste due grandezze è regolata da un potenza al cubo e quindi che se l’altezza del pilastro cresce, la sua flessibilità (coefficiente inverso alla rigidezza) aumenta esponenzialmente di ben tre volte.

In basso riporto la sezione dei pilastri, ipotizzati di 30x30 cm, con il loro momento di inerzia Ix, altro dato strettamente legato al concetto di rigidezza, in quanto direttamente proporzionale ad essa. 

                                                             

Essendo la struttura come composta da elementi piani, possiamo considerare  il solaio come un unico corpo rigido inquadrato in un piano X-Y, di cui stabiliremo il punto di origine O (0;0), e considerare i controventi come vincoli elastici cedevoli, e rappresentarli allora come molle sottoposte a forze concentrate, il cui comportamento è regolato dalla Legge di Hooke che stabilisce che una forza F agente su una molla fa nascere una reazione della molla stessa uguale e contraria, pari ad F= ku, dove k è la rigidezza della molla e u individua lo spostamento, o meglio l’allungamento o l’accorciamento cui la molla è stata sottoposta, a seconda che la forza sia di compressione o di trazione.

Di seguito l’impalcato ed i vincoli elastici ognuno indicato con la propria rigidezza, che sarebbe cioè la rigidezza totale del telaio cui corrispondono, data dalla somma delle rigidezze dei pilastri che ne fanno parte (kv1, kv2, etc…).

Disponendo a questo punto di tutte i dati costituenti le caratteristiche geometriche e intrinseche della sezione dei pilastri, possiamo iniziare a compilare la prima parte (STEP 1) della tabella excel, che ci aiuterà a situare la posizione del centro di massa e del centro delle rigidezze. Di seguito le tabelle contenenti il calcolo della rigidezza traslante di ogni controvento, verticale e orizzontale, della struttura scelta:

A questo punto, si è passati allo STEP 2, in cui si sono riportate tutte le rigidezze dei controventi e la loro distanza dal punto di origine O (0;0) prefissato arbitrariamente all’inizio:

Si è giunti, quindi, al calcolo delle coordinate spaziali nel piano X-Y del centro di massa, cui è preceduta una fase di suddivisione dell’impalcato in tre aree chiuse e di individuazione delle coordinate dei rispettivi baricentri di quest’ultime, valori che, poi, sono stati inseriti nella tabella dello STEP 3:

Le coordinate del centro di massa G (X_G; Y_G) sono state ricavate in questo modo:

X_G= Sommatoria coordinate dei tre centri lungo X moltiplicate ognuna per le rispettive aree, il risultato diviso per l’area totale (Atot=A1+A2+A3)=∑ XiG*Ai/Atot

Y_G= Sommatoria coordinate dei tre centri lungo Y moltiplicate ognuna per le rispettive aree, il risultato diviso per l’area totale (Atot=A1+A2+A3)= ∑ YiG*Ai/Atot

A questo punto si è affrontato lo STEP 4 della tabella excel, mirato al calcolo della rigidezza traslante orizzontale totale Ko_Tot e della rigidezza traslante verticale Kv_tot, entrambe ottenute rispettivamente tramite la somma delle singole rigidezze dei controventi orizzontali e la somma delle singole rigidezze dei controventi verticali. Lo STEP 4 è servito fondamentalmente a stabilire le coordinate del centro delle rigidezze C (X_C;Y_C), ottenute, un con la stessa metodologia attuata precedentemente per calcolare il centro di massa, cioè sommando i prodotti di ogni rigidezza per la sua distanza dall’origine (orizzontale per quanto riguarda i controventi verticali e verticale per quanto riguarda i controventi orizzontali) e dividendo il risultato per la rigidezza traslante orizzontale totale Ko_Tot nel caso di X_C, e per Kv_Tot nel caso di Y_C.

A questo punto si sono riportate tutte le distanze dei controventi dal centro delle rigidezze, sempre orizzontali per quanto riguarda i controventi verticali e verticali per quanto riguarda i controventi orizzontali. Sommando la moltiplicazione, dunque, di ogni rigidezza per la sua distanza al quadrato dal centro delle rigidezze appena trovato si è ottenuta la rigidezza torsionale traslante K_ϕ (KN*m).

Gli ultimi tre STEP della tabella excel hanno riguardato il calcolo dei carichi sismici e la loro ripartizione lungo l’asse X e l’asse Y.

Dallo STEP 5, abbiamo ottenuto il valore della forza sismica orizzontale F=167,20 KN:

Dallo STEP 6 e 7 abbiamo ottenuto i valori di traslazione orizzontale e verticale della struttura, i suoi valori rotazionali, infinitamente piccoli, oltre ai valori ripartiti dei carichi sismici su ogni controvento, in proporzione alla loro rigidezza:

La seconda parte dell’esercitazione ha riguardato una sorta di verifica dei concetti teorici e, precisamente, si è andato a vedere se, ponendo il centro delle rigidezze come punto di applicazione di una data forza sismica orizzontale, la struttura subisse solo una traslazione, ossia uno spostamento rigido lungo la direzione di applicazione della forza, ma non una rotazione. Viceversa, applicando la medesima forza sul centro delle masse, non essendo esso coincidente con il centro delle rigidezze, si è visto come la struttura tenda a ruotare, creandosi un braccio tra centro delle masse e centro delle rigidezze, ossia tra punto di applicazione della forza e CR. La rotazione in questo caso, tuttavia, è molto esigua, in quanto la distanza, ossia il braccio rotazionale, tra CM e CR è molto piccolo, per questo motivo, per buona norma, si dovrebbe progettare in modo tale da avere questi due punti poco distanti tra loro, così da assimilare le forze orizzontali in maniera più adeguata, sottoponendo la struttura a rotazioni molto poco elevate.

Dunque, si è ridisegnata la struttura su SAP2000. Questa è la sua configurazione in pianta e in prospettiva:

Si sono assegnati i vincoli a terra come incastri, andando su ASSIGN--> JOINT-->RESTRAINTS e selezionando il vincolo incastro:

Successivamente, si sono assegnate le sezioni alle travi, selezionando quest’ultime e andando su ASSIGN-->FRAME->FRAME SECTIONS, si è scelto il cemento armato come materiale (concrete nel programma) e si sono imposte le caratteristiche geometriche di sezione, supponendo di avere un’altezza pari a 60 cm e una base pari a 30 cm. 

Andando poi su SET MODIFIERS, sempre nella finestra di assegnazione delle caratteristiche di sezione, si è aumentato il momento di inerzia aggiungendo tanti zeri, in modo da aumentare la rigidità flessionale delle travi.

Si sono assegnate, poi, le sezioni ai pilastri 30x30 cm:

Questa è la configurazione della struttura con, vincoli a terra, travi e pilastri assegnati:

A questo punto, si è riportato il centro delle rigidezze, utilizzando il tasto punto e assegnato i valori di offset rispetto ai vari assi X,Y e Z:

Per far in modo di generare una continuità strutturale, e, quindi, di considerare come parte di uno stesso piano i punti di incastro trave-pilastro, si sono selezionati e poi si è loro assegnato il comando DIAPHRAGM, andando su ASSIGN-->JOINT-->CONSTRAINTS:

Se il comando ha funzionato, dovremmo ottenere questa schermata, tutti i punti superiori della struttura devono cambiare colore rispetto al resto:

Infine, si è potuta applicare la forza nel centro delle rigidezze, andando su ASSIGN-->JOINT LOADS-->FORCES, assegnando un nuovo livello F (con self multiplier pari a zero) e immettendo un valore lungo l’asse Y pari a quello calcolato tramite l’ausilio della tabella excel:

La deformata ottenuta è stata la seguente:

Come si può notare, la struttura è stata sottoposta solo ad un atto di moto rigido, traslando lungo l’asse y, ma non ruotando. Cliccando col destro sul punto che individua il centro delle rigidezze, si è potuto ulteriormente prendere atto del fatto che le rotazioni sono state nulle, ma che c’è stata una traslazione, seppure molto piccola:

Questa è l’andamento lineare a farfalla del momento 2-2, relativo al nostro caso, tipico di un telaio shear-type:

Si è voluto, infine, vedere cosa succedeva nel caso in cui si fosse applicata la forza non nel centro delle rigidezze, ma nel centro di massa e il risultato è stato quello di una rotazione! In basso le fasi di applicazione della forza sul CM e la relativa deformazioni della struttura:

 

 

 

 

Affrontiamo l’analisi del comportamento di un impalcato, munito dei dovuti controventi, sollecitato alle forze esterne orizzontali, a simulazione delle azioni sismiche, del vento, della spinta della terra, etc., e di conseguenza le risposte dei controventi a tali sollecitazioni.

E’ importante quindi ripartire in modo adeguato le forze orizzontali, in quanto una struttura, nella sua vita tridimensionale, non deve impegnarsi ad affrontare solo le azioni dovute ai carichi verticali.

In questo modo nel momento di cui si progetta una struttura si deve tener presente che gli elementi strutturali hanno questa duplice funzione; ne è un esempio il telaio, il più semplice controvento, costituito da un collegamento in testa ai pilastri, quindi nel piano verticale, che è capace di sopportare sia i carichi verticali che le azioni orizzontali.

Si è deciso di esaminare un impalcato formato da un telaio shear-type, ossia un insieme di travi e pilastri piano, in cui le travi sono elementi infinitamente rigidi a flessione, perciò non si deformano assialmente ma si avrà solo una traslazione orizzontale δ, conseguenza della deformata dei pilastri soggetti a flessione; le travi quindi avranno un momento d’inerzia molto più grande rispetto ai pilastri e i nodi sono tutti rigidi per cui saranno degli incastri.

 

Si ipotizza quindi un impalcato di un piano, come in figura, costituito da 10 telai shear-type, di cui 5 lungo la direzione orizzontale e 5 lungo quella verticale; ogni telaio è costituito da pilastri con sezione (40 x 30) cm e altezza 3 m, e con modulo si inerzia maggiore nella direzione di massima inflessione pari a:

Ix= (b x h^3)/12= (40 x 30^3)/12= 90000 cm^4

 

 

 

Ogni telaio è considerato un controvento, e siccome sono dei vincoli elastici, possiamo rappresentarli come delle molle; il concetto di rigidezza di questi controventi, k, nasce allora nel piano dei prospetti e per comodità la trasportiamo in pianta. Analizziamo quindi come reagiscono gli impalcati a causa delle azioni orizzontali.

Per comodità inseriamo l’impalcato in un sistema di riferimento e indichiamo con kv rigidezza controventi verticali, lungo y, ko rigidezza controventi orizzontali, lungo x, dv distanza orizzontale dei controventi dall’origine degli assi, posto nel pilastro 1, e do distanza verticale dei controventi dall’origine degli assi.

Ogni controvento si prenderà una parte delle forza orizzontale applicata all’impalcato, a seconda della rigidezza dei controventi, come somma delle rigidezze dei pilastri che lo compongono, e della sua distanza dal punto detto centro di istantanea rotazione o centro di rigidezza.

 

1-Calcolo della rigidezza traslante dei controventi

Si calcola la rigidezza traslante di ogni controvento, come la somma delle rigidezze dei pilastri che lo compongono, considerando che la rigidezza di un pilastro del telaio shear-type è pari a k= 12EI/h^3;

pertanto la rigidezza totale del controvento sarà k_t= 12EItot/h^3, con E= 21000 N/mmq, Ix= (b x h^3)/12=90000 cm^4 e h= 3m

 

2-Tabella sinottica controventi e distanze

Riassumiamo il una tabella i valori delle rigidezze e le loro rispettive distanze dal punto di origine degli assi.

3-Calcolo del centro di massa

Calcoliamo ora il centro di massa dell’impalcato, come centro dell’area, e siccome siamo di fronte ad un’area più complessa si può dividere in aree geometricamente più semplici e calcolare per ognuno il centro delle masse.

Sappiamo infatti che se la forza applicata all’impalcato ha la retta d’azione passante per questo il centro di massa, l’impalcato non ruoterà ma traslerà solamente, compromettendo quindi in misura minore la sicurezza dell’impalcato, mentre al contrario nel momento in cui la retta d’azione è distante dal centro, l’impalcato ruoterà nel piano.

Per questo motivo è importante quando di progetta un edificio, che centro di massa e centro di rigidezza siamo il più possibile vicini per ridurre al minimo la rotazione dello stesso.

G1 (12;2)

G2 (21;6)

G3 (3;8)

Con G (xG;yG) = (10,71;4,29)

xG= (∑Ai x xG)/Atot

yG= (∑Ai x yG)/Atot

4-Calcolo del centro di rigidezze e delle rigidezze globali

Con C (xC;yC)= (10,88;4,75)

xC= (∑kvi x dvi)/ ∑kvi

yC= (∑koi x doi)/ ∑koi

 

Calcoliamo poi le distanze dei rispettivi controventi dal centro di rigidezza, è infine la rigidezza a rotazione dei controventi data dalla somma dei prodotti delle rigidezze di ogni controvento e la sua distanza al quadrato rispetto al centro delle rigidezze.

kφ= (∑ki x ddi^2)/ ∑kvi

5-Analisi dei carichi sismici

Calcoliamo infine i carichi sismici partendo dal carico totale gravante sulla area dell’impalcato. Ricaviamo quindi il valore della forza sismica agente sull’impalcato dato dal peso sismico W(KN) e dal coefficiente di intensità sismica c=0,10

F= W x c= 202,61 KN

6-7-Ripartizione della forza sismica lungo x e lungo y

Calcoliamo il momento torcente prodotto dalla forza sismica rispetto al centro delle rigidezze per cui con braccio pari alla distanza tra centro di rigidezza e centro di massa dove è applicata la forza, rispettivamente rispetto all’asse x e all’asse y.

Calcoliamo poi le traslazioni orizzontali e verticali.

uo= F/kotot

vo= F/kvtot

Infine la rotazione dei controventi

φ= M/ kφ

Infine le reazioni vincolari dei controventi da:

Ri= ki x ( u x ddi x φ)

Ri= ki x ( v x ddi x φ)

Dall’analisi fatta sembrerebbe che l’edificio sottoposto alla forza sismica F subisca solo una traslazione, in quanto siccome i due centri, di massa e delle rigidezze, sono abbastanza vicini, portano ad una rotazione quasi nulla. Verifichiamo ora anche su SAP.

Si disegna l’impalcato su sap e indichiamo che i vincoli a terra sono incastri

Definiamo la sezione delle travi, che saranno abbastanza alte per simulare un telaio shear-type.

Si assegna la sezione ai pilastri.

Si disegna il centro delle rigidezze

Definiamo ora che il punto disegnato fa parte dell’impalcato e che quest’ultimo è di tipo rigido attraverso il vincolo interno (constrain) DIAPHRAM, che attribuisce all’intero impalcato una rigidezza tale ma non ammettere deformazioni ma sono traslazioni.

Per aumentare ancora di più la rigidezza del solaio possiamo aumentare il modulo di inerzia delle travi.

Infine applichiamo la forza sismica nel centro delle rigidezze.

Possiamo avviare a questo punto l’analisi da cui possiamo ricavare la deformata dei pilastri dovuta alla forza F, ad “s” tipica del telaio shear-type, che sta ad indicare un diagramma del taglio costante e un diagramma dei momenti lineare ed in particolare a forma di “farfalla”.

Possiamo anche notare che il centro di rotazione come previsto subirò solo una piccola traslazione e non ruoterà nel piano.

Nel documento PDF allegato abbiamo voluto approfondire il comportamento di una struttura in acciaio su due livelli sottoposta all' azione di forze orizzontali come possono essere quelle sismiche.

Abbiamo preso spunto da una parte dell' edificio che stiamo progettando come tema del semestre e abbiamo provato a disporre i controventi tipici della tecnologia dell' acciaio, in modo da valutare il centro delle rigidezze di ciascuno dei due impalcati, la sua relazione con il centro di massa e come questa influisce sul comportamento dell' edificio.

Abbiamo fatto alcune considerazioni su come converrebbe agire per avvicinare centri delle rigidezze e centri di massa, tenedo conto dei vincoli che la struttura e il progetto impongono.

Abbiamo completato l' esercitazione verificando su SAP la struttura, non prima di aver effettuato un predimensionamento di travi e pilastri, trovando conferma delle nostre previsioni (a meno di lievi margini di errore nei valori) sugli andamenti di spostamenti e rotazioni.

Analizziamo la struttura che presenti un arco a tutto sesto su sap.

Dopo aver provveduto nel disegnare su cad il 3d della struttura di interesse, la importiamo come *.dxf su sap, avendo cura di utilizzare un solo layer, che non sia 0.

 

Impostiamo la cerniera sia nell’ imposta a destra sia in quella a sinistra.

E’ necessario trovare la chiave dell’ arco, in modo tale da poter assegnare in quel punto una cerniera. Dopo aver selezionato i due vertici in chiave, [Assign --> Frame --> Releases/ Partial Fixity] spuntiamo al Momento 33 “Start” per il vertice che si trova a sinistra, “End” per il vertice che si trova a destra, in modo tale da imporre che il momento  sia nullo. 

Assegnamo una sezione rettangolare in cls armato all’ arco.

Assegnamo all’ arco un carico distribuito [Assign --> Frame Load--> Distribuited Loads]

E’ necessario assegnare il carico sull’ ipotetica trave che presenta la stessa luce dell’ arco (proiezione a terra dell’ arco), non sulla reale lunghezza dell’ arco. Se abbiamo una luce di mt 6 e un carico di 10 KN, sappiamo che dovremo avere come reazioni vincolari alle due imposte dell’arco rispettivamente 30 KN.

Avviamo l' analisi con il carico distribuito:

Dobbiamo ora verificare che le reazioni vincolari ottenute siano quelle corrette: